0 引言
基于电压源换流器的柔性直流输电(VSC-HVDC)是新一代的高压直流输电技术。换流器由于采用全控型开关器件,不需要换相电压,可以独立控制有功功率和无功功率输出,在新能源发电并网、孤岛供电、多端直流互联等领域应用广泛。在众多的电压源换流器拓扑中,模块化多电平换流器(modular multilevel converter,MMC)因具有输出特性好、运行效率高、可扩展性强等优点脱颖而出,成为柔性直流输电的首选技术方案 [1-3] 。
目前,投入运行的MMC-HVDC工程的换流阀大多采用半桥子模(half-bridge sub-module,HBSM)的MMC拓扑,尽管其具有器件数目少、运行损耗低的优势,但是由于不具备直流故障阻断能力,限制了其往更高电压、更大容量方向发展 [4] 。因此,设计研制具有直流故障穿越能力的MMC拓扑结构,成为近年来MMC研究热点之一。2011年,MMC拓扑的提出者R.Marquart提出的全桥子模块(full-bridge sub-m odule, FBSM)等拓扑具备直流故障穿越能力,但是FBSM的开关器件数目比HBSM整整多了一倍,器件利用率低。而全/半桥子模块混合型的MMC兼顾了运行效率和直流故障穿越能力,同时FBSM具有负电平输出能力增加了MMC的运行灵活性 [5-7] 。文献[4]提出可以利用子模块提供的反向电压来抑制直流侧短路故障电流;进一步地,文献[8]-[9]提出通过配置桥臂全桥子模块数目,在直流短路故障期间不用闭锁换流器,让MMC维持对交流侧的无功支撑。文献[10]-[11]研究发现让混合型MMC主动运行在过调制状态,可以降低子模块电容电压波动。文献[12]提出利用FBSM负电平输出能力,可以使交流输出电压幅值不再受限于直流母线电压,可以实现某些运行条件下的MMC直流母线降压运行。文献[13]提出在定直流电压和功率传输的情况下,通过提升电压调制比升高交流电压输出,减小桥臂电流峰值,进而降低换流器损耗。同时也有研究发现在定直流母线电压和交流输出电流工况下,通过提升电压调制比来提升交流输出电压,进而提升MMC传输容量,可以提升混合型MMC运行效率 [14-16] 。
文献[17]-[21]基于子模块投入占空比的概念研究了基于半桥子模块拓扑的MMC子模块器件损耗特性及结温波动特性,并给出了解析表达式。文献[22]-[24]对全桥子模块拓扑MMC在不同工况下的损耗和结温特性,并分别给出了优化的调制策略以降低系统损耗或均衡子模块内部器件损耗。文献[25]提出一种基于不同子模块的MMC-HVDC 阀损耗的通用计算方法,但实际仍是针对一种子模块拓扑的MMC进行单独计算。文献[26]等研究了全/半桥子模块混合型MMC的损耗情况并比较了不同调制方式下的总损耗,但是系统总损耗的降低并不能保证其可靠性的提高,因为损耗在子模块间和子模块内部器件间的分布问题亦可能对系统稳定性造成影响。混合型MMC在过调制运行条件下的运行特性与调制策略相比传统半桥子模块拓扑的MMC有很大差异,电流—热应力在全/半桥子模块中的分布特性尚不清楚,目前少有文献涉及。针对上述问题,本文根据混合型MMC过调制运行的工作特性,结合PLECS仿真软件,对过调制下子模块器件电流分布和热应力进行研究,旨在为混合型MMC的设计与优化提供指导。
1 混合型MMC过调制工作原理
1.1 运行原理
如图1所示的混合型MMC拓扑,每相有两个桥臂,每个桥臂由H个半桥子模块(HBSM)和F个全桥子模块(FBSM)串联而成。图中U dc 和i dc 分别为直流电压和直流电流,u jp /u jn 和i jp /i jn (j=a,b,c)为j相上、下桥臂电压和桥臂电流,u j 和i j 代表MMC三相交流电压和交流电流。子模块中,C sm 和U C 分别代表模块电容值和额定电压值。

图1 混合型MMC拓扑及两种子模块结构图
Fig.1 Circuit configuration of hybrid MMC
根据图1所示的变量及参考方向,MMC桥臂电压可以表示为
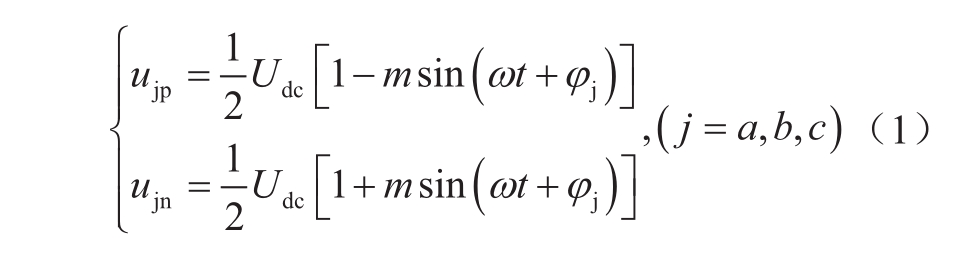
式中,φ j 为j相交流电压相角;m为换流器电压调制比,定义为
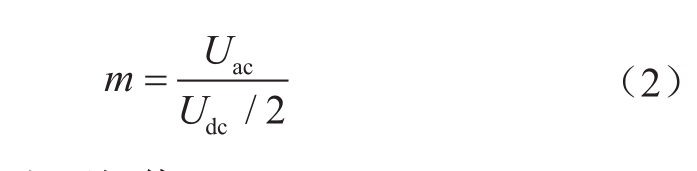
式中U ac 为交流相电压幅值。
由于全桥子模块可以输出负电平,因此混合型MMC桥臂可以输出负电压。根据式(3),桥臂可以输出最大电压为桥臂所有半桥、全桥子模块电容电压之和;桥臂可以输出最小电压为全桥子模块负电压之和。
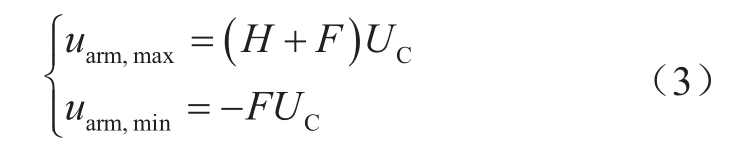
另一方面,根据式桥臂输出最大电压为(1+m)U dc /2,最小输出电压为(1-m)U dc /2。为了满足MMC正常工作,桥臂输出电压应满足直流和交流电压需求,即有
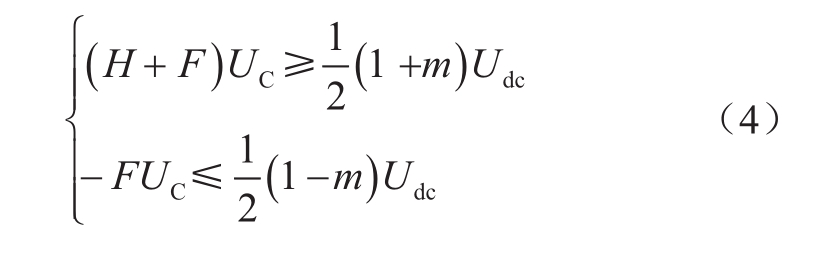
从式(2)发现由于全桥子模块具备负电平输出能力,混合型MMC电压调制比m可以大于1,本文将m>1的运行状态定义为过调制。
当混合型MMC运行在过调制状态时,桥臂将会有负电平输出,因此混合型MMC的调制与排序方式也与传统有所差异,图2展示了混合型MMC一种常见的过调制运行下的子模块排序方式 [27] 。当根据桥臂电压调制波计算所需投入子模块个数n为正,桥臂电流为正时,从桥臂所有子模块中选择电压最低的n个子模块正投入(当桥臂电流为负时,从桥臂所有子模块中选择电压最高的n个子模块正投入);当计算所需投入子模块个数n为负,桥臂电流为正时,从桥臂的全桥子模块中选择电压最高的-n个子模块负投入(当桥臂电流为负时,从桥臂所有子模块中选择电压最低的-n个子模块负投入)。

图2 混合型MMC电容电压平衡排序方式
Fig.2 Sorting algorithmin hybrid MMC
1.2 全桥子模块配置原则
为了提高子模块器件利用率,尽可能减少混合型MMC中全桥子模块数目比例,需要根据过调制需求和直流故障处理能力进行计算全桥子模块最低数目配比。
设桥臂子模块总数为N=H+F,在调制比m>1过调制运行的条件下,根据式(4),在不考虑子模块冗余的情况下,桥臂所需子模块总数N为
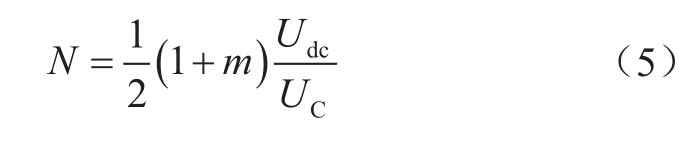
桥臂所需全桥子模块个数F为
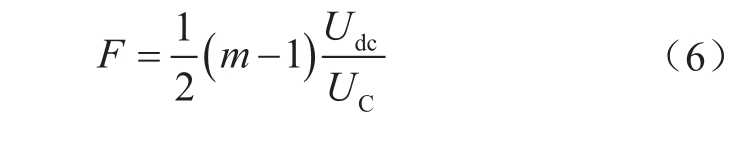
根据式(5)、(6)可以发现,在保持直流电压U dc 一定的情况下,随着换流器电压调制比的增加,桥臂需要的子模块总数随之增多。
由式 (5)和 (6),得到全桥子模块比例f最低为
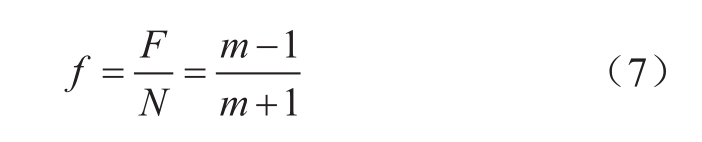
另一方面,为了让混合型MMC具有直流故障穿越能力,要求在直流两极短路故障时换流器可以维持交流电压输出和对网侧的无功支撑。任意时刻上、下桥臂电压之和为0,则桥臂输出电压范围应在[-FU C ,FU C ],为了维持交流电压,因此有
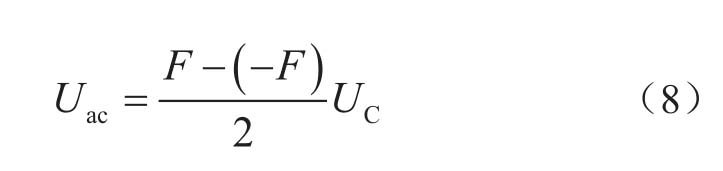
将调制比定义式(2)代入上式,则所需全桥子模块数目F为
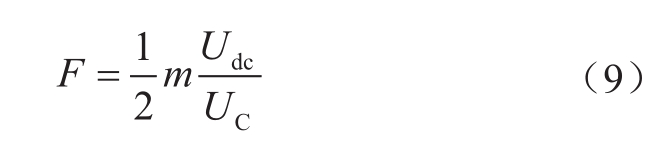
可以验证,该配置比例也满足直流侧单极接地故障穿越要求 [4] 。
此时,桥臂需要的全桥子模块数目比例f最低为
2 混合型MMC过调制热应力分析
2.1 子模块工作模式
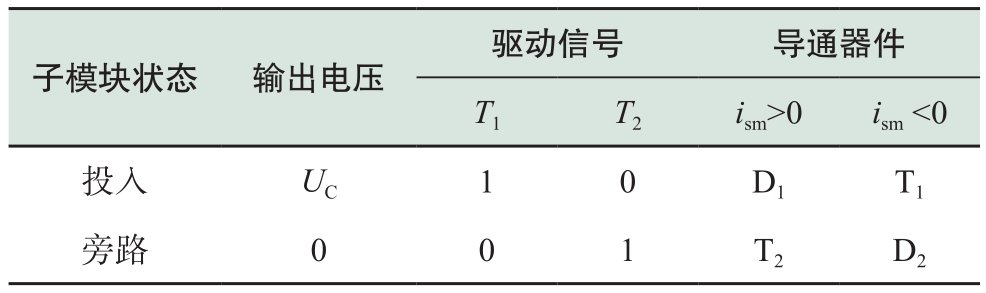
对于如图3所示的半桥子模块,在正常工作模式下,可以输出两种电平0和U C ,具体的工作状态和电流路径见表1。当半桥子模块处于投入状态时,若桥臂电流为正,则电流流经D 1 ;若桥臂电流为负,电流流经T 1 。当子模块被旁路时,若桥臂电流为正,电流流经T 2 ,若桥臂电流为负,电流流经D 2 。
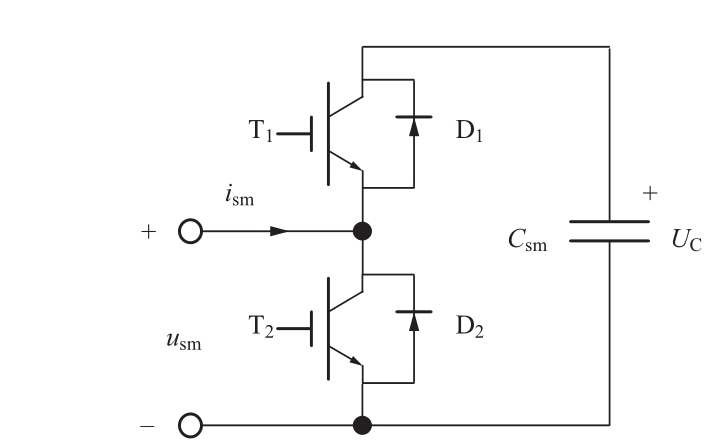
图3 半桥子模块结构图
Fig.3 Structure of HBSM
表1 正常工作下半桥子模块状态
Table 1 HBSMstate under normal operation
对于图4所示的全桥子模块,在换流器工作在m<1条件下输出0和+U C 两种电平,而在过调制下需要输出0, -U C 和+U C 3种电平。表2为FBSM器件具体的开关信号和工作状态。可以发现,FBSM有两种0电平输出的驱动方式,FBSM既可以一直工作在旁路1模式或旁路2模式,也可以两种模式交替工作。为了简化控制和后文分析的简便,设FBSM输出0电平时工作在旁路1模式。当全桥子模块处于正投入状态时,若桥臂电流为正,电流流经D 1 D 4 ;若桥臂电流为负,电流流经T 1 T 4 。当全桥子模块处于负投入状态时,若桥臂电流为正,电流流经T 2 T 3 ;若桥臂电流为负,电流流经D 2 D 3 。当全桥子模块处于旁路状态时,若桥臂电流为正,电流流经D 1 T 3 ;若桥臂电流为负,电流流经T 1 D 3 。
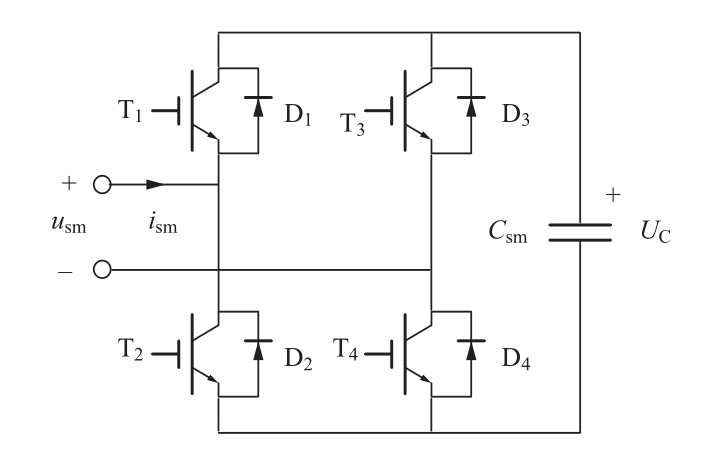
图4 全桥子模块结构图
Fig.4 Structure of FBSM
表2 正常工作下全桥子模块状态
Table 2 FBSMstate under normal operation
2.2 子模块器件电流分布
混合型MMC j相桥臂电流表达式为 [13]
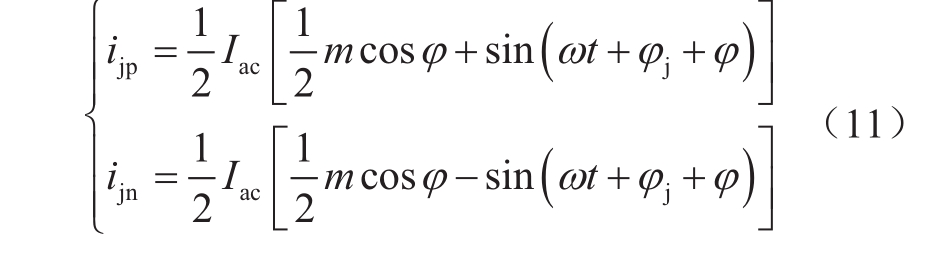
以a相上桥臂为例,设换流器工作在纯有功工作状态,设直流电压和交流电流一定,根据式和的桥臂电压和桥臂电流表达式可以分别绘出逆变状态和整流状态下,m<1和m>1时的桥臂电压和桥臂电流波形,蓝线为a相上桥臂电压,红线为a相上桥臂电流。

图5 不同调制比下的桥臂电压和桥臂电流波形
Fig.5 Arm voltage and current under different m
从图5可以发现,当MMC运行在过调制工况时,相比于m<1,桥臂电流直流偏置增大导致流过子模块的电流峰值增大。另一方面,不论换流器处在逆变状态还是整流状态,在桥臂电流瞬时值较大时刻,而桥臂电压较小,因此桥臂投入的子模块数较少,绝大多数子模块处在旁路状态。根据子模块内部器件电流路径,这就会使旁路的半桥子模块器件T 2 (逆变时)或D 2 (整流时)和旁路的全桥子模块器件D 1 T 3 (逆变时)或T 1 D 3 (整流时)的电流应力较大。而当桥臂电压较大时(即投入子模块数目较多时),桥臂电流瞬时值较小,此时器件的电流应力较小。综上,桥臂电流的直流分量影响了子模块内部器件电流分布,从而使子模块内部器件的电流应力变得更加不均。
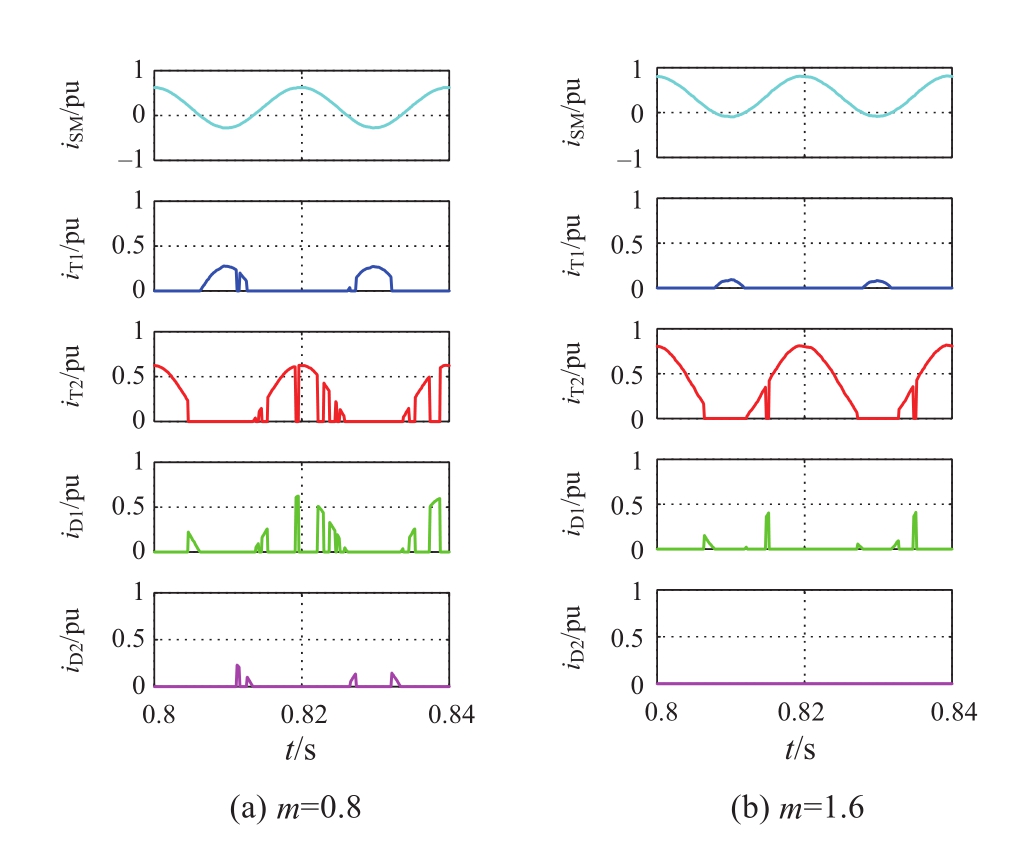
图6 不同调制比下的半桥子模块器件电流分布
Fig.6 Current in HBSMswitches under different m
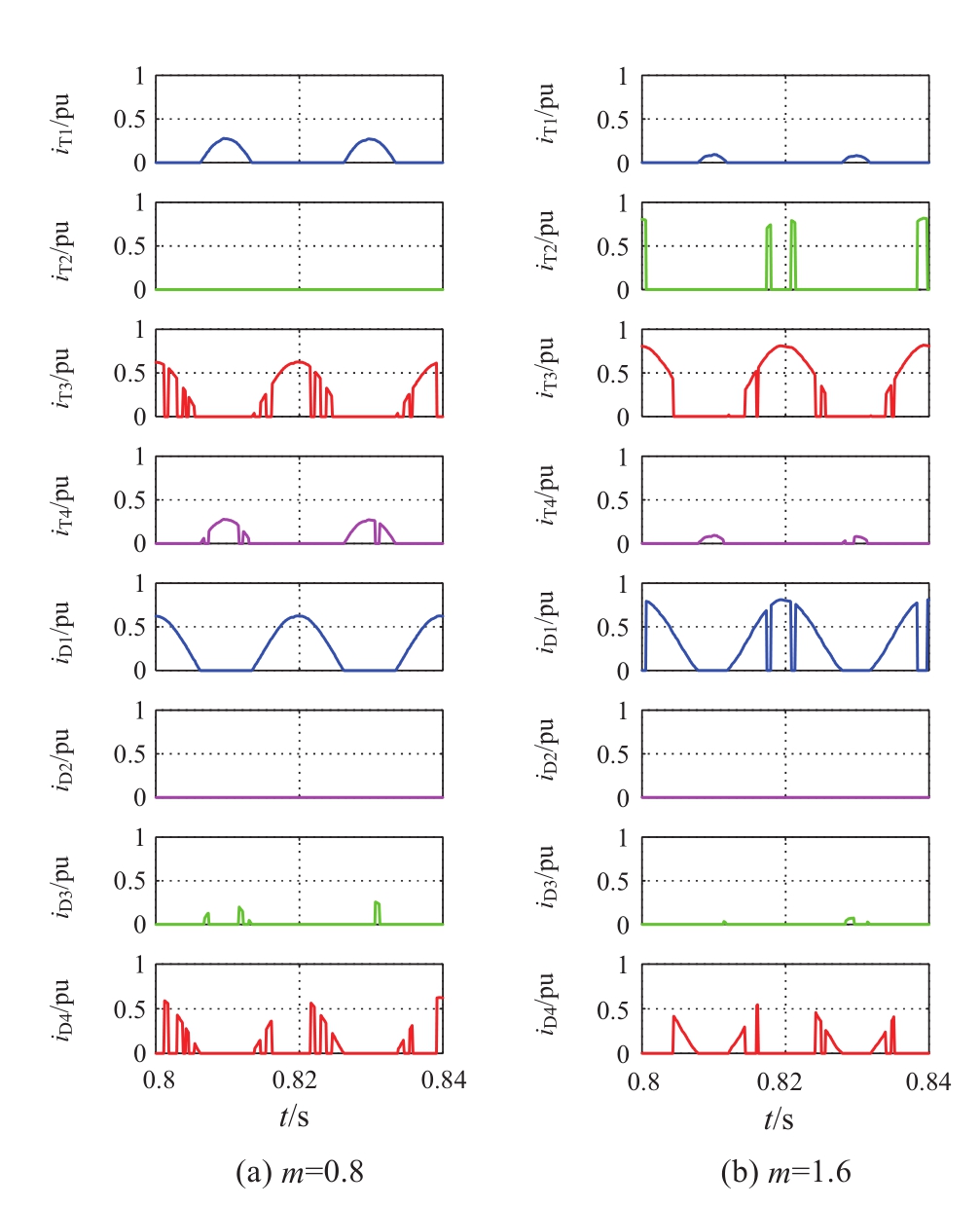
图7 不同调制比下的全桥子模块器件电流分布
Fig.7 Current in FBSMswitches under different m
根据式(11),影响桥臂电流的直流分量因素为m和cosφ的乘积,因此本文定义MMC直流电流调制比k为桥臂电流直流分量幅值与交流分量幅值的比值,即
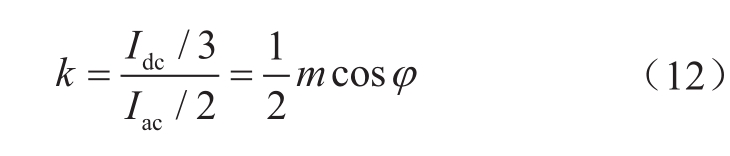
图6和图7为半桥子模块和全桥子模块在m=0.8和m=1.6两种电压调制比下流经子模块电流在全/半桥各个开关器件间分布情况(变换器工作在逆变状态)。在过调制状态下,一个工频周期里半桥子模块的T 2 和全桥子模块的T 3 D 1 和T 2 导通电流幅值变大,导通时间变长,而其他开关器件导通电流幅值变小,导通时间变短。
2.3 结温分析
MMC子模块开关器件的损耗主要来自于IGBT 通态损耗、IGBT开关损耗、二极管通态损耗和二极管反向恢复损耗,而IGBT断态损耗、二极管断态损耗和二极管开通损耗均相对较小,可以忽略 [18] 。
由于在过调制状态下,由于桥臂电压需要输出负电平,全/半桥子模块器件开关函数也变得较为复杂,除了基频分量外还存在高倍频的分量,较难得到一个精简的解析式。以逆变为例,结合图8所示的过调制下桥臂电压和桥臂电流波形,桥臂电压过零点相位为θ 1 和θ 2 ,桥臂电流过零点相位为θ 3 和θ 4 ,θ 1 ~θ 4 可以表示为
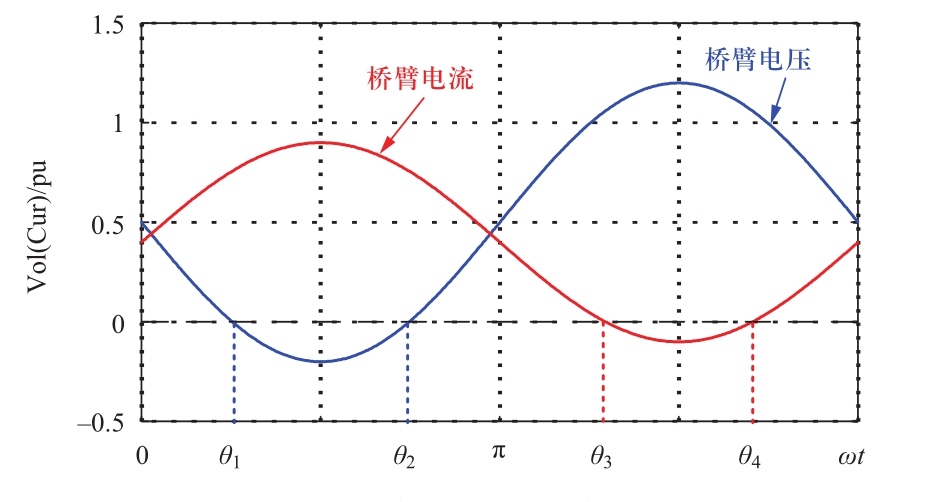
图8 过调制下桥臂电压和桥臂电流(逆变)
Fig.8 Arm current arm voltage under over-modulation
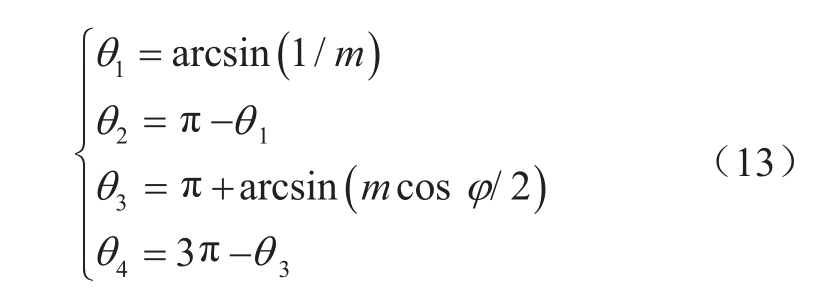
以半桥子模块为例,当桥臂电压大于零时,半桥子模块器件T 1 和T 2 的开关函数为
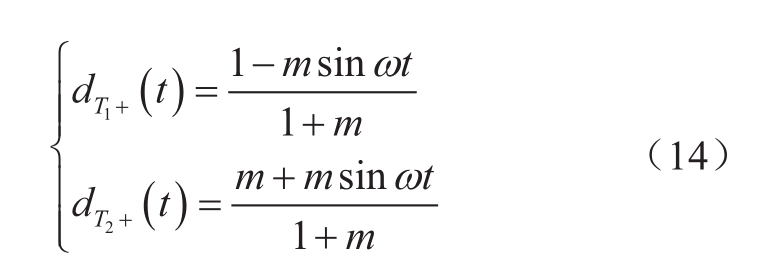
当桥臂电压小于零时,半桥子模块一直被旁路,器件T 1 和T 2 的开关函数为
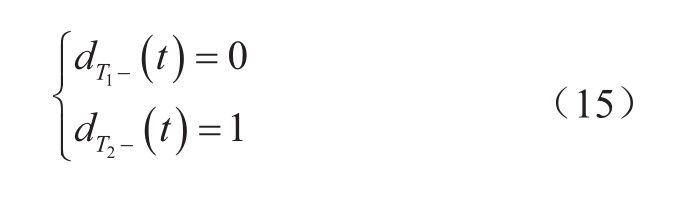
因此,半桥子模块器件T 1 T 2 D 1 D 2 在一个工频周期内的导通损耗可以分别表示为

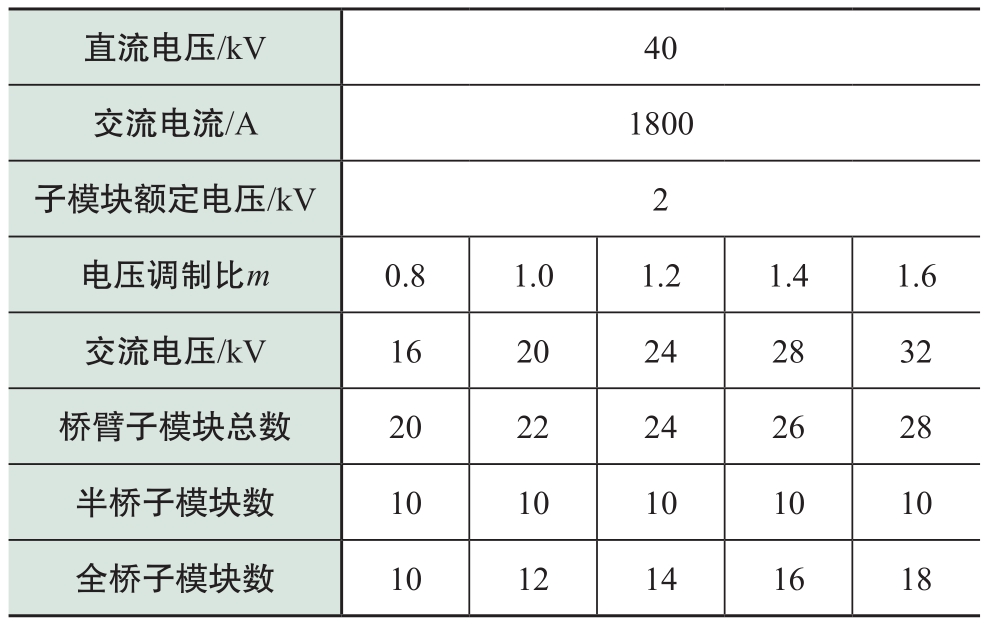
根据式(16),可以利用MATLAB等数学工具计算出半桥子模块每个器件损耗随着电压调制比m和功率因数cosφ的变化关系。但是由于一个工频周期内半、全桥子模块电容电压充放电机制存在差异,导致半、全桥子模块投入切除存在不对等关系,难以得到每个器件精确的损耗解析表达式。为此下面结合仿真来归纳分析混合型MMC在过调制运行状态下热的分布情况。仿真模型参数如表3所示:在几种不同电压调制比和功率因数下,直流电压固定为40 kV,交流电流幅值固定为1800 A,子模块电压额定值为2 kV,全桥子模块数目配置按照1.2节全桥子模块数目配置原则进行配置,采用NLM调制策略以减小器件开关频率。器件损耗热模型采用ABB公司的型号为5SNA 1200E330100的IGBT模块。
表3 几种调制比下仿真系统参数
Table 3 Simulation parameter of hybrid MMC
为了获取器件的结温,通过PLECS仿真软件提取到IGBT的导通损耗和开关损耗以及二极管的导通损耗和反向恢复损耗后,采用图9所示的IGBT模块的热阻网络模型对芯片结温进行估算。芯片到外壳的热阻用4层RC网络描述,外壳到散热板的热阻用一个R c-h 描述。设散热片基板温度T h 为60℃。
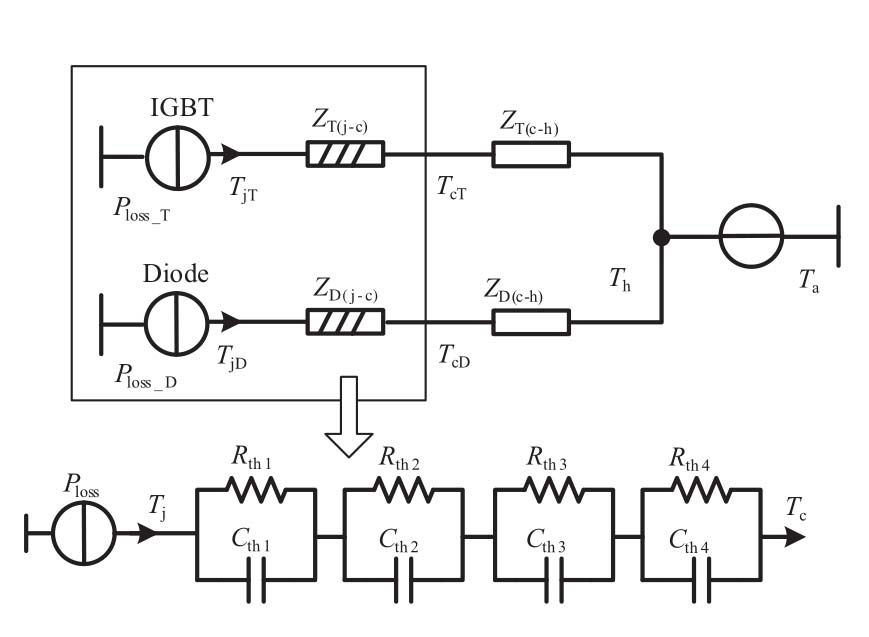
图9 IGBT模块热阻网络模型
Fig.9 IGBT module thermal resistance network model
因此,芯片温度可以用式(17)表示
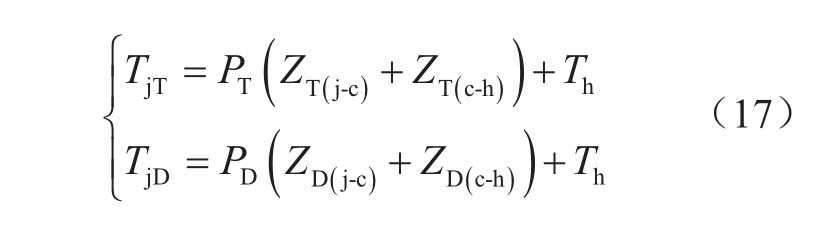
图10为m=0.8和m=1.6调制比下半桥子模块各个器件的结温。当换流器工作在常规调制比下,T 2 芯片结温较其他3个器件高,而且当换流器工作在过调制工况下,T 2芯片的结温变得更高,从m=0.8时的95℃增大到112℃,同时其他3只管子结温反而下降。m=0.8时,最热的T 2 和次热的D 1 温差为17℃;而当m=1.6时,最热的T 2 和次热的D 1 温差达到46℃。图11为m=0.8和m=1.6调制比下全桥子模块各个器件的结温。其中T 3 D 1 结温较高,且过调制下器件结温差异增大。验证了前文所分析的用于子模块旁路的器件其电流应力、热应力较大。同时可以发现半桥子模块和全桥子模块的最热芯片的结温相等,也反映了混合型MMC全半桥子模块间的热应力分布是较均衡的。
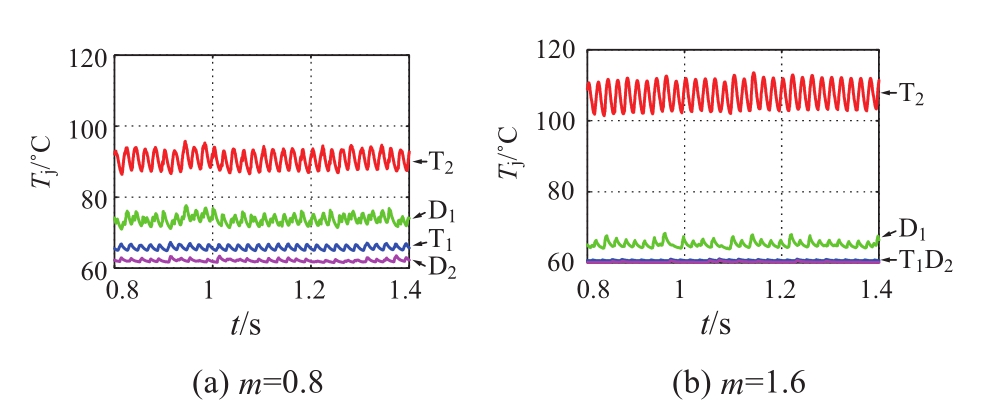
图10 两种调制比下半桥子模块器件结温
Fig.10 T j of HBSMunder different m
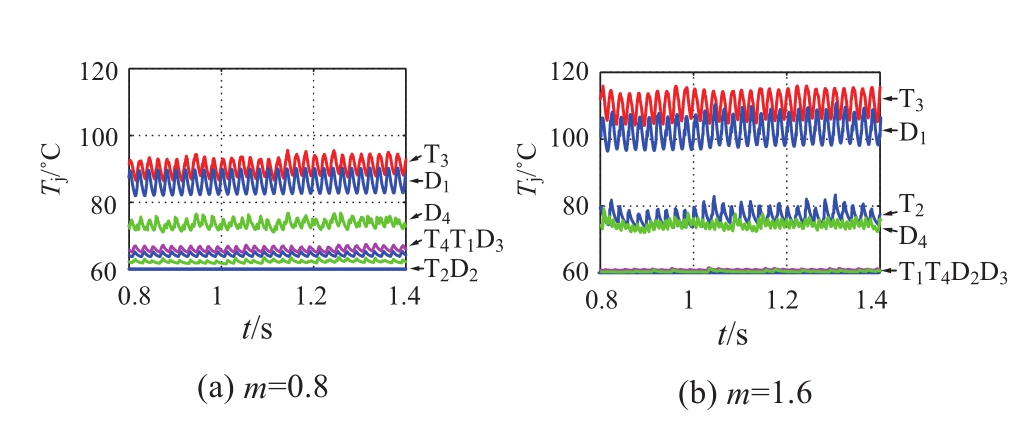
图11 两种调制比下全桥子模块器件结温
Fig.11 T j of FBSMunder different m
图12为半桥子模块器件的芯片最高结温随电压调制比的变化关系,可以发现,随着电压调制比的增大,T 2 芯片结温随之增大,而其他3只芯片最高结温随之降低。图13为全桥子模块器件的各个芯片最高结温随电压调制比的变化关系。随着电压调制比的增大,T 3 D 1 芯片结温随之增大,而其他芯片的结温大多随着调制比的增大而减小。当m由0.8增大至1.6后,子模块内器件的最大温差由约30℃增大至50℃以上,严重威胁混合型MMC在过调制下的安全运行。
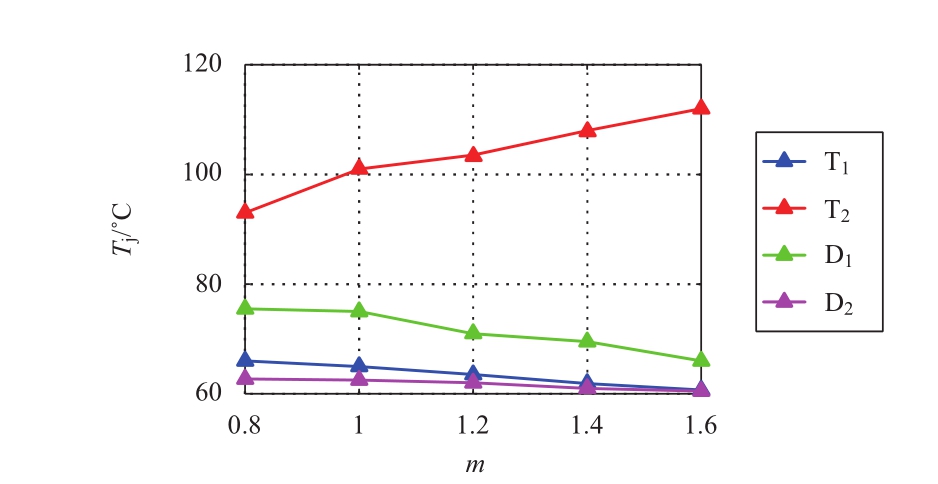
图12 半桥子模块器件最高结温随电压调制比变化关系
Fig.12 Maximum T j of HBSMwith m

图13 全桥子模块器件最高结温随电压调制比变化关系
Fig.13 Maximum T j of FBSMwith m
图14和图15研究了过调制状态下m=1.6时,子模块器件芯片最高结温与交流侧功率因数的关系。其中,半桥子模块的T 2 结温随着功率因数的增大而增大,其他3个器件结温均随着功率因数增大而减小。当cosφ=0,即MMC换流器作为STATCOM运行只传输无功时,半桥子模块4个器件结温最为接近。全桥子模块的T 3 D 1 和T 2 的结温随着功率因数的增大而升高,而其他器件均随着功率因数增大而降低。当cosφ=0时,全桥子模块的器件除了T 2 和D 2 其他器件热应力较均匀。因此,功率因数的提升也使得子模块内部器件热应力变得不均。
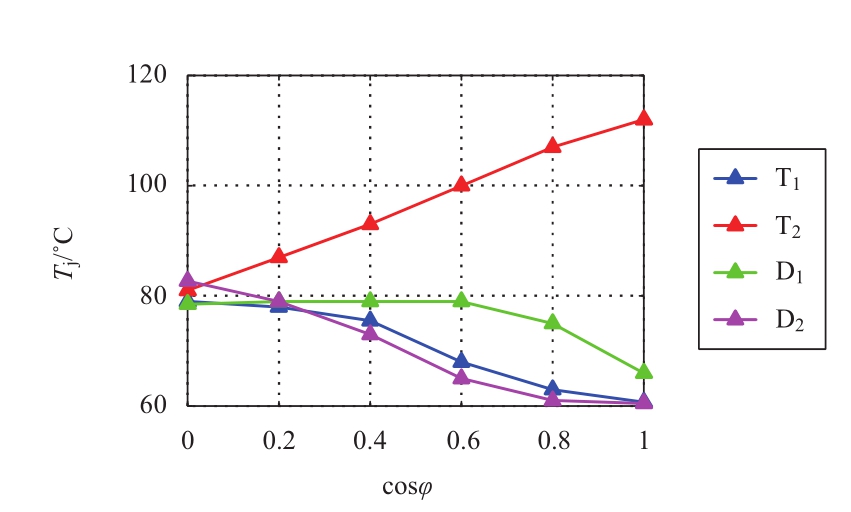
图14 半桥子模块器件最高结温随功率因数变化关系
Fig.14 Maximum T j of HBSMwith cos φ
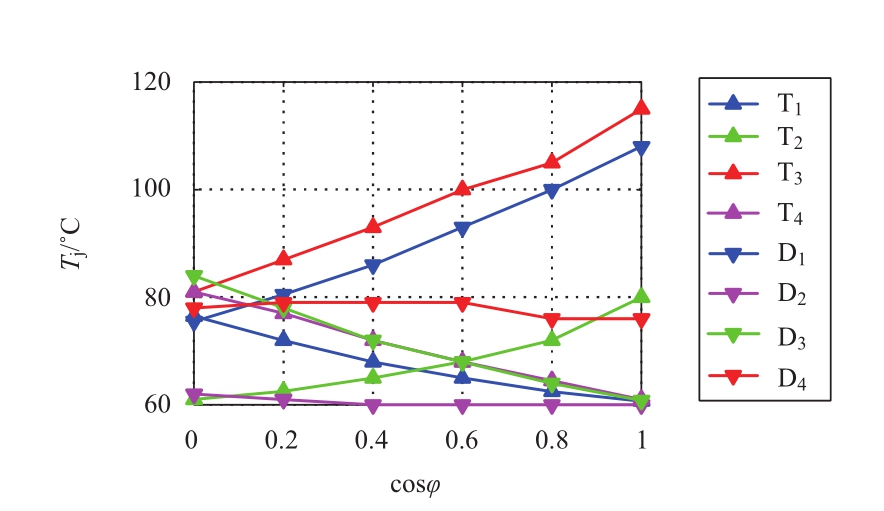
图15 全桥子模块器件最高结温随功率因数变化关系
Fig.15 Maximum T j of FBSMwith cos φ
图16和图17为相同直流电流调制比k=0.4,不同电压调制比m和功率因数cosφ组合下,子模块器件芯片最高结温随调制比变化关系。对于半桥子模块,保持直流电流调制比k一致,增大电压调制比,减小功率因数,T 2 管最高结温基本保持一定,其他3只管最高结温略微上升,4个开关器件热应力分布变得略微均匀。对于全桥子模块,相同直流电流调制比下,子模块各个器件最高结温均变化不大。
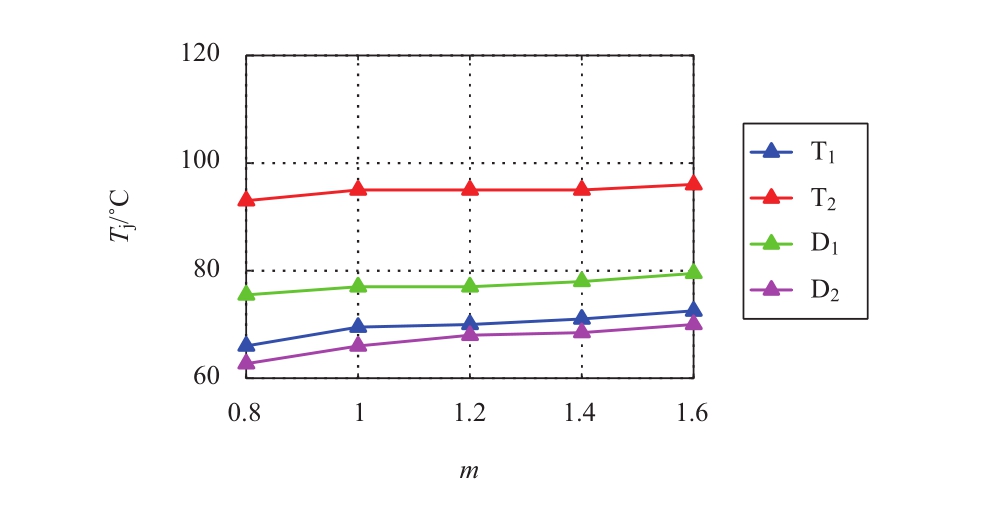
图16 相同电流调制比下半桥子模块器件最高结温
Fig.16 Maximum T j of HBSMwith same k
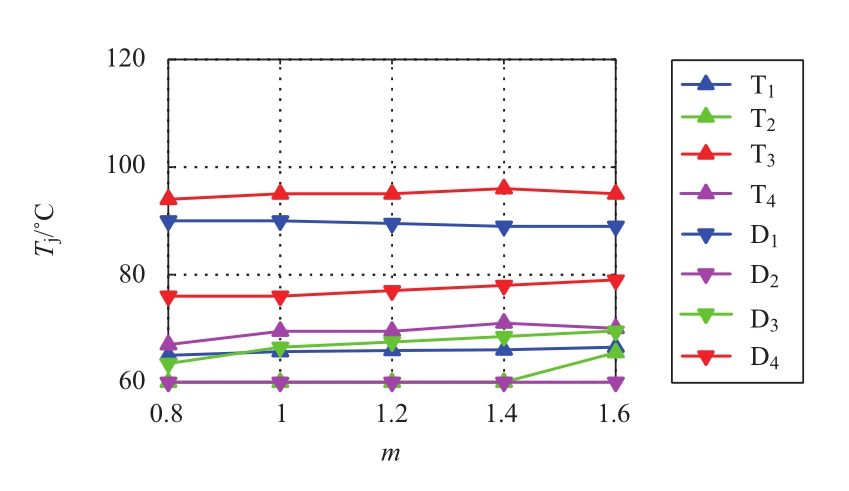
图17 相同电流调制比下全桥子模块器件最高结温
Fig.17 Maximum T j of FBSMwith same k
3 结论
本文主要针对混合型MMC过调制下子模块器件的热—电应力分布展开研究。结合仿真探究了混合型MMC电压调制比与功率因数对半桥子模块以及全桥子模块内部器件热分布的影响,并归纳出直流电流调制比的概念。分析发现,直流电流调制比通过影响桥臂电流的直流分量大小,进而影响子模块内部器件负载电流及损耗分布。并且直流电流调制比越大,全/半桥子模块内部器件热应力分布不均程度越严重,降低了器件的利用率,甚至危及MMC安全运行。因此,为了提升混合型MMC效率和安全运行裕度,需要对子模块热分布进行优化。
参考文献
[1] 周孝信,鲁宗相,刘应梅,等.中国未来电网的发展模式和关键技术[J].中国电机工程学报,2014,34(29):4999-5008.Zhou Xiaoxin, Lu Zongxiang, Liu Yingmei, et al.Development Models and Key Technologies of Future Grid in China[J].Proceedings of the CSEE, 2014, 34(29): 4999-5008(in Chinese).
[2] 姚良忠,吴婧,王志冰,等.未来高压直流电网发展形态分析[J].中国电机工程学报,2014,34(34):6007-6020.Yao Liangzhong, Wu Jing, Wang Zhibing, et al.Pattern Analysis of Future HVDC Grid Development[J].Proceedings of the CSEE, 2014, 34(34): 6007-6020(in Chinese).
[3] 汤广福,贺之渊,曹均正,等.2012年国际大电网会议系列报道—高压直流输电和电力电子技术最新进展[J].电力系统自动化,2012,36(24):1-3.Tang Guangfu, He Zhiyuan, Cao Junzheng, et al.A Review of CIGRE 2012 on HVDC Transmission and Power Electronic Technology[J].Automation of Electric Power Systems, 2012,36(24): 1-3(in Chinese).
[4] 张帆.子模块混合型MMC-HVDC直流故障控制策略研究[D].北京:华北电力大学,2017.
[5] 许建中,赵鹏豪,江伟,等.具备直流故障穿越能力的混合MMC可靠性分析和冗余配置方法[J].中国电机工程学报,2016,36(4):953-960.Xu Jianzhong, Zhao Penghao, Jiang Wei, et al.Reliability Analysis and Redundancy Configuration of Hybrid MMCs with DC Fault Blocking Capability[J].Proceedings of the CSEE, 2016, 36 (4): 953-960(in Chinese).
[6] 李少华,王秀丽,李泰,等.混合式MMC及其直流故障穿越策略优化[J].中国电机工程学报,2016, 36(7):1849-1858.Li Shaohua, Wang Xiuli, Li Tai, et al.Optimal Design for Hybrid MMC and Its DC Fault Ride-through Strategy[J].Proceedings of the CSEE, 2016 , 36 (7): 1849-1858(in Chinese).
[7] 孟新涵,李可军,王卓迪,等.混合型MMC拓扑及应用于MTDC直流故障穿越能力分析[J].电力系统自动化,2015,39(24):72-79.Meng Xinhan, Li Kejun, Wang Zhoudi, et al.A Hybrid MMC Topology and Its DC Fault Ride-through Capability Analysis When Applied to MTDC System[J].Automation of Electric Power Systems, 2015, 39 (24): 72-79(in Chinese).
[8] Cui S, Sul S K.A Comprehensive DC Short-Circuit Fault Ride Through Strategy of Hybrid Modular Multilevel Converters (MMCs) for Overhead Line Transmission[J].IEEE Transactions on Power Electronics, 2016, 31(11): 7780-7796.
[9] Lin L, He Z, Hu J, et al.Pole-to-ground fault ride through strategy for half-/full-bridge hybrid MMC-based radial multi-terminal HVDC systems with low-impedance grounded[J].Iet Generation Transmission & Distribution, 2018, 12(4): 1038-1044.
[10] Hu J, Xiang M, Lin L, et al.Improved Design and Control of FBSMMMC with Boosted AC Voltage and Reduced DC Capacitance[J].IEEE Transactions on Industrial Electronics,2017, PP(99): 1-1.
[11] Judge P D, Chaffey G, Merlin MMC, et al.Dimensioning and Modulation Index Selection for the Hybrid Modular Multilevel Converter[J].IEEE Transactions on Power Electronics, 2017,PP(99): 1-1.
[12] W.Lin, D.Jovcic, S.Nguefeu, and H.Saad.Full-bridge MMC Converter Optimal Design to HVDC Operational Requirements[J].IEEE Transactions on Power Delivery, vol.31, no.3, pp.1342–1350, June 2016.
[13] Lu M, Hu J, Zeng R, et al.Imbalance Mechanism and Balanced Control of Capacitor Voltage for a Hybrid Modular Multilevel Converter[J].IEEE Transactions on Power Electronics, 2017,PP(99): 1-1.
[14] Hofmann V, Bakran MM.An Optimized Hybrid-MMC for HVDC[C].PCIMEurope 2016; International Exhibition and Conference for Power Electronics, Intelligent Motion,Renewable Energy and Energy Management; Proceedings of.VDE, 2016.
[15] Hofmann V, Bakran MM.Optimized Design of a Hybrid-MMC and Evaluation of Different MMC Topologies[C].European Conference on Power Electronics and Applications.IEEE, 2016:1-9.
[16] Lin W, Jovcic D, Nguefeu S, et al.Full bridge MMC Converter Optimal Design to HVDC Operational Requirements[C].Power and Energy Society General Meeting.IEEE, 2016: 1-1.
[17] 李强,庞辉,贺之渊.模块化多电平换流器损耗与结温的解析计算方法[J].电力系统自动化,2016,40(4):85-91.Li Qiang, Pang Hui, He Zhiyuan.Analytic Calculating Method for Loss and Junction Temperature of Modular Multilevel Converter[J].Automation of Electric Power Systems, 2016,40(4): 85-91(in Chinese).
[18] 王海田,汤广福,贺之渊,等.模块化多电平换流器的损耗计算[J].电力系统自动化,2015,39(2):112-118.Wang Haitian, Tang Guangfu, He Zhiyuan, et al.Power Loss Calculation of Modular Multilevel Converter[J].Automation of Electric Power Systems, 2015, 39 (2): 112-118(in Chinese).
[19] 饶宏,李建国,宋强,等.模块化多电平换流器直流输电系统损耗的计算方法及其损耗特性分析[J].电力自动化设备,2014,34(6):101-106.Rao Hong, Li Jianguo, Song Qiang, et al.Loss Calculation Method and Characteristics Analysis for MMC-HVDC System[J].Electric Power Automation Equipment, 2014 , 34 (6) : 101-106(in Chinese).
[20] Schoen A, Birkel A, Bakran MM.Modulation and Losses of Modular Multilevel Converters for HVDC Applications[C].PCIMEurope 2014; International Exhibition and Conference for Power Electronics, Intelligent Motion, Renewable Energy and Energy Management; Proceedings of.VDE, 2014:1-8.
[21] Li J, Zhao X, Song Q, et al.Loss Calculation Method and Loss Characteristic Analysis of MMC Based VSC-HVDC System[C].IEEE International Sym posium on Industrial Electronics.IEEE, 2013: 1-6.
[22] 董玉斐,杨贺雅,李武华,等.MMC中全桥子模块损耗分布优化的调制方法研究[J].中国电机工程学报,2016,36(7):1900-1907.Dong Yufei, Yang Heya, Li Wuhua, et al.An Optimal Strategy for Loss Distribution of Full-bridge Submodules in Modular Multilevel Converters[J].Proceedings of the CSEE, 2016, 36(7): 1900-1907(in Chinese).
[23] 谢晔源,曹冬明,姜田贵,等.基于模块化多电平换流器的新型全桥损耗优化调制策略[J].电力系统自动化,2016,40(6):78-84.Xie Yeyuan, Cao Dongming, Jiang Tiangui, et al.A New Full-bridge Loss Optimization Modulating Strategy Based on Modular Multilevel Converter[J].Automation of Electric Power Systems, 2016, 40 (6): 78-84(in Chinese).
[24] Li K, Zhao Z, Yuan L, et al.An im proved phase-shifted carrier-based modulation and loss distribution analysis for MMC using full bridge sub-modules[C].Power Electronics and Motion Control Conference.IEEE, 2016: 1252-1258.
[25] 薛英林,徐政,张哲任,等.采用不同子模块的MMCHVDC阀损耗通用计算方法[J].电力自动化设备,2015,35(1):20-29.Xue Yinglin, Xu Zheng, Zhang Zheren, et al.General Method of Value Loss Calculation for MMC-HVDC with Different Submodules[J].Electric Power Automation Equipment, 2015 ,35 (1): 20-29(in Chinese).
[26] X.Shi, S.Filizadeh, D.A.Jacobson.Loss Evaluation for the Hybrid Cascaded MMC under Different Voltage-Regulation Methods[J].IEEE Transactions on Energy Conversion, 2018,PP(99): 1-1.
[27] Lin Y, Lin L, Xu C, et al.A design method of hybrid modular m ultilevel converter with negative output generated by FBSM[C].IECON 2017 -, Conference of the IEEE Industrial Electronics Society.IEEE, 2017: 4465-4471.
Thermal and Electrical Stress Distribution Characteristics of Hybrid MMC Converters Under Over-modulation Operation
SHENG Jing, DONG Yufei, LI Wuhua, HE Xiangning
(State Key Laboratory of Power Electronics(Zhejiang University), Hangzhou 310027, Zhejiang Province, China)
Abstract: Hybrid modular multilevel converter (Hybrid-MMC)using both half-bridge sub-modules (HBSM) and full-bridge sub-modules (FBSM) in arms can ride through DC fault and reduce the switches compared with FBSM-MMC, which is considered as a promising topology in Voltage Source Converter based High Voltage Direct Current (VSC-HVDC).Additionally,the voltage modulation ratio m can be promoted by utilizing the negative arm voltage output so that the power transmission and efficiency can be enhanced.However, under over-modulation operation (m>1), the current and thermal distribution in HBSMand FBSMbecome different from that of traditional modulation (m<1) due to the more complex modulation mode and operation principle.So in this paper, based on the analysis of the characteristics of hybrid MMC under over-modulation operation, the current stress and power loss under different modulation index and different pow er factor operation is emphasized in research with simulation.The concept of current modulation ratio is generalized finally and based on the concept the conclusion is made that the power loss in SMs’ switching devices becomes more imbalanced with the increase of current modulation ratio.
Keywords: hybrid MMC; over-modulation; loss distribution;thermal stress
Youth Scientist Subject of National Basic Research Program of China (973 Program) (2014CB247400); National Natural Science Foundation of China (51490682).

盛景
作者简介:
盛景 (1993),男,博士研究生,主要研究方向为模块化多电平换流器的热管理,E-mail:zjdxsj2013@zju.edu.cn。
董玉斐 (1990),男,博士研究生,主要研究方向为模块化多电平换流器的热管理。
李武华 (1979),男,博士,教授,博士生导师,主要研究方向为柔性直流输配电技术,包括大容量器件的动态测试与健康管理、高性能变流器的拓扑理论与调制策略、可再生能源的灵活接入与柔性并网、直流配电网的系统架构与运行控制等。
何湘宁 (1961),男,博士,教授,博士生导师,IEEE Fellow,IET Fellow,研究方向为电力电子技术及其工业应用,包括大功率变换器与智能控制系统,特种电源及其网络化系统,电力电子器件、电路和系统的建模、仿真和测试等。
(责任编辑 张鹏)
