0 引言
目前,基于模块化多电平换流器(modular multilevel converter, MMC)的柔性直流输电技术 [1-2] 正朝着高压大容量方向发展。柔性直流输电系统也正经历由两端输电到多端输电,并逐渐过渡到直流电网的发展过程。基于柔性直流输电技术的架空线柔性直流电网 [3-6] 是实现大规模可再生能源广域协调互补和可靠送出的有效解决方案,是未来高压大容量柔性直流输电的重要应用方向。
架空线的应用势必会造成柔性直流电网线路故障概率的大幅增加 [7-10] 。针对模块化多电平柔性直流输电系统(MMC-HVDC)直流故障暂态特性,专家、学者们做了大量的相关研究工作。文献[11]分析了MMC直流双极短路故障机制,建立了其闭锁前和闭锁后两个阶段过电流分析的电路模型,推导出了过电流应力的解析方程。文献[12]研究了MMC-HVDC直流故障瞬间电气应力的暂态特性,建立了短路故障状态下的等值电路模型,给出了故障电压、电流的数学表达式。文献[13]-[14]在研究MMC直流侧双极短路故障机理的基础上,建立了故障发展过程各阶段的故障电流解析表达式。文献[15]对MMC-HVDC直流故障特性进行了深入分析,提出了故障情况下MMC的等效电路模型。文献[16]针对伪双极柔性直流电网直流线路双极短路故障,提出了故障电流通用计算方法。然而,关于双极柔性直流电网直流线路短路电流暂态特性的定量分析计算,尚属空白。
本文建立了双极柔性直流电网中单个换流器在直流线路不同短路故障类型下的等效电路数学模型,建立了故障时刻双极柔性直流电网等效电路网络模型,提出了一种适用于双极柔性直流电网的单极接地、单极接中性线及双极短路的暂态短路电流定量分析方法,实现了双极柔性直流电网任意故障类型、任意故障位置的短路电流暂态特性定量分析计算。最后,通过PSCAD/EMTDC仿真,验证了该分析方法的有效性和精确性。
1 MMC等效电路模型
柔性直流电网是一个“低惯量”系统 [4] ,直流线路一旦发生故障,各换流站将在毫秒级短时间内均向故障点注入短路电流。为保障柔性直流电网的供电可靠性,国际大电网会议(CIGRE)等国内外学术组织和科研机构提出的基于直流断路器 [17-19] 的保护方案 [20] ,可避免直流电网线路故障时换流阀闭锁先于直流断路器跳闸动作,即出现“局部故障,全网停运”的现象,该方案要求在故障发生后,直流电网保护系统能够在短时间内迅速检测出故障 [7] ,并在几毫秒内通过跳开故障线路两侧直流断路器实现直流故障的快速隔离 [7-8] 。
如图1所示,直流侧发生双极短路故障情况下,基于半桥子模块的MMC在故障后、闭锁前的短时间内,在电容电压平衡控制作用下,子模块电容通过故障点迅速放电。此时,MMC直流侧故障电流特性主要由子模块电容放电电流决定 [11,13,14] ,MMC可等效为RLC串联电路,其等效电路模型如图2所示 [15,16] 。
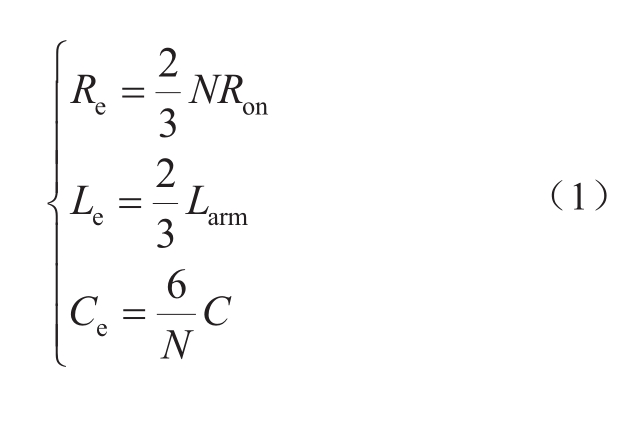
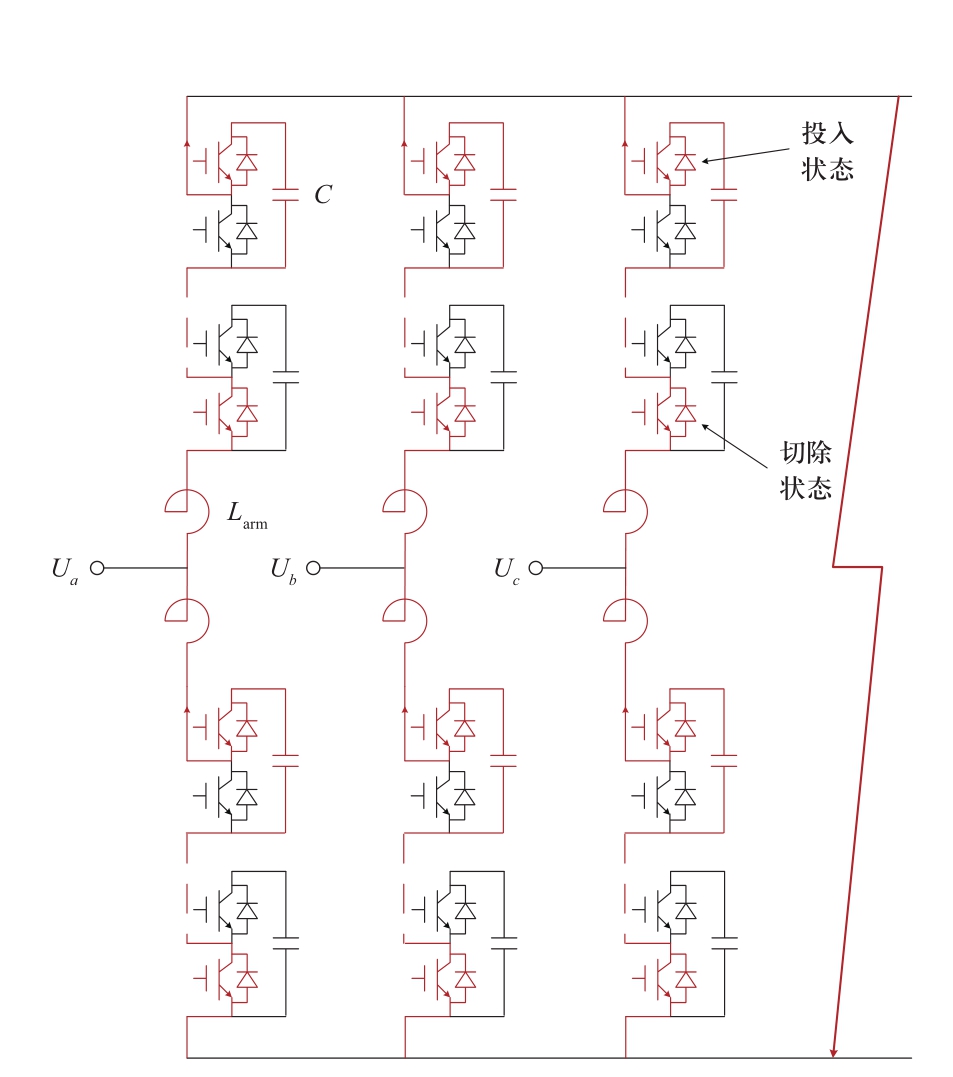
图1 闭锁前,MMC等效放电示意图
Fig.1 Schematic diagram of MMC equivalent discharge before blocking
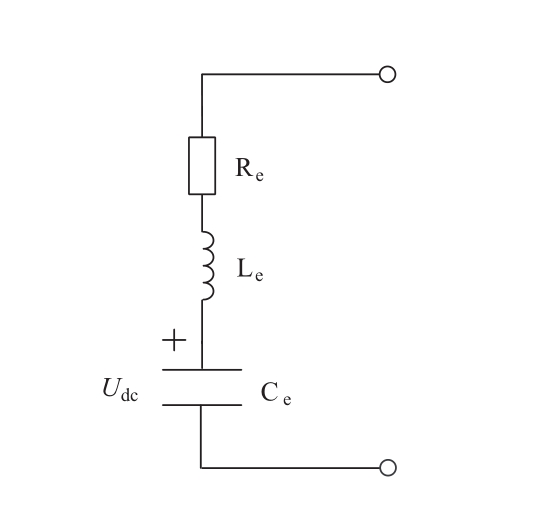
图2 闭锁前,MMC等效电路模型
Fig.2 Model of the MMC equivalent discharge circuit before blocking
图2中,R e 、L e 和C e 分别为故障后、闭锁前MMC串联等效电路的电阻、电感和电容,其大小如式(1)所示。式中,N为MMC单桥臂子模块个数,R on 为开关管导通电阻,L arm 为MMC桥臂电抗,C为MMC桥臂子模块电容。
2 换流站等效电路模型
双极柔性直流电网单个换流站示意图如图3所示,正极换流器MMC p 和负极换流器MMC n 分别为直接连于正负极线的MMC,金属回线作为中性线通过电抗L p 分别回连于MMC p 和MMC n 的负极和正极,其中,MMC p 和MMC n 均采用如图1所示基于半桥子模块的MMC。
与伪双极接线方式相比,双极接线方式更灵活、可靠性更高 [20] 。对称运行的双极柔性直流电网,正常运行或者直流线路双极短路故障时,中性线无电流流过;直流线路发生单极接地故障或单极接中性线短路故障时,不平衡电流通过中性线流回相应换流器。
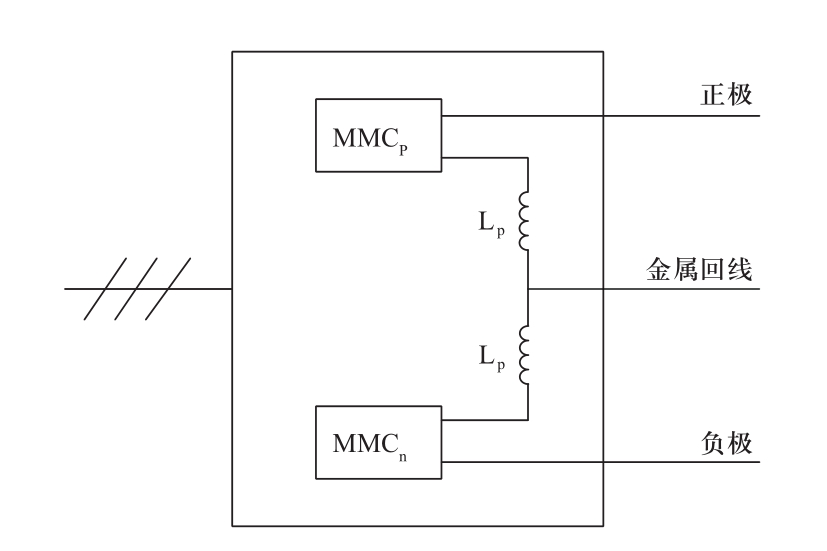
图3 双极拓扑换流站示意图
Fig.3 Schematic diagram of bipolar topology converter station
2.1 单极短路故障
双极柔性直流电网单极短路故障可分为单极接地短路故障和单极接中性线短路故障。以正极直流线路短路故障为例,双极柔性直流电网发生如图4(a)所示的单极接地故障时,故障电流通过MMC p 、正极线路、故障接地点、直流系统接地点、金属回线和极线电抗L p 形成闭合回路。换流站闭锁前,MMC p 所有子模块均通过该回路迅速放电。此时,正极换流器MMC p 和其极线电抗可串联等效为如图4(b)所示的RLC电路,其中,R为单个桥臂所有子模块IGBT导通电阻之和,L arm 为桥臂电抗,L p 为连接金属回线的极线电抗,C为子模块电容,N为单个桥臂子模块个数。

图4 单极接地故障
Fig.4 Pole-to-ground fault
双极柔性直流电网发生如图5(a)所示的正极线路接中性线短路故障时,故障电流通过MMC p 、正极线路、故障通路、中性线(金属回线)和极线电抗L p 形成闭合回路。此时,正极换流器MMC p 和极线电抗可串联等效为如图5(b)所示的RLC电路,其等效电阻、电感、电容与直流线路单极接地故障时换流站等效电路对应参数相同。
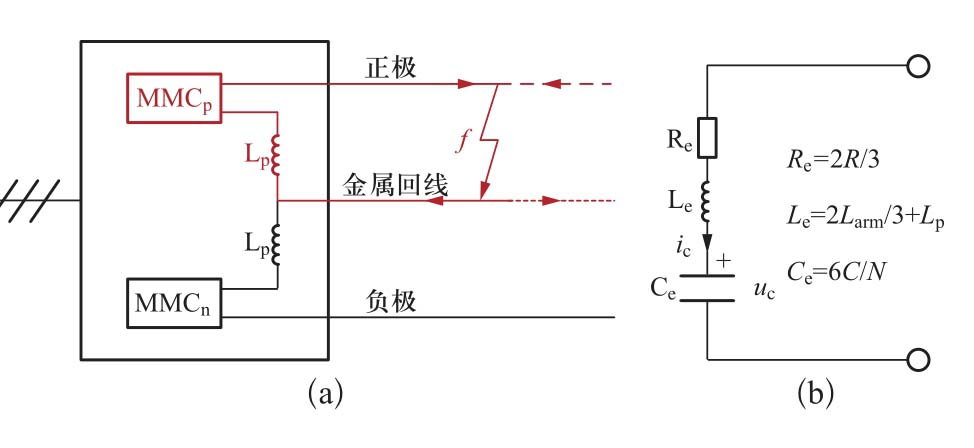
图5 极线与中性线短路故障
Fig.5 Pole-to-neutral line fault
2.2 双极短路故障
双极柔性直流输电系统发生如图6(a)所示的直流线路双极短路故障时,故障电流通过MMC p 、正极线路、故障通路、负极线路、MMC n 及两个极线电抗L p 形成闭合回路。换流站闭锁前,MMC p 和MMC n 所有子模块均通过该回路迅速放电。此时,正极换流器MMC p 、负极换流器MMC n 及两个极线电抗可串联等效为如图6(b)所示的RLC电路,其等效电阻、电感均为直流线路单极接地故障时等效电路对应参数的两倍,其等效电容为直流线路单极接地故障时等效电路对应参数的50%。
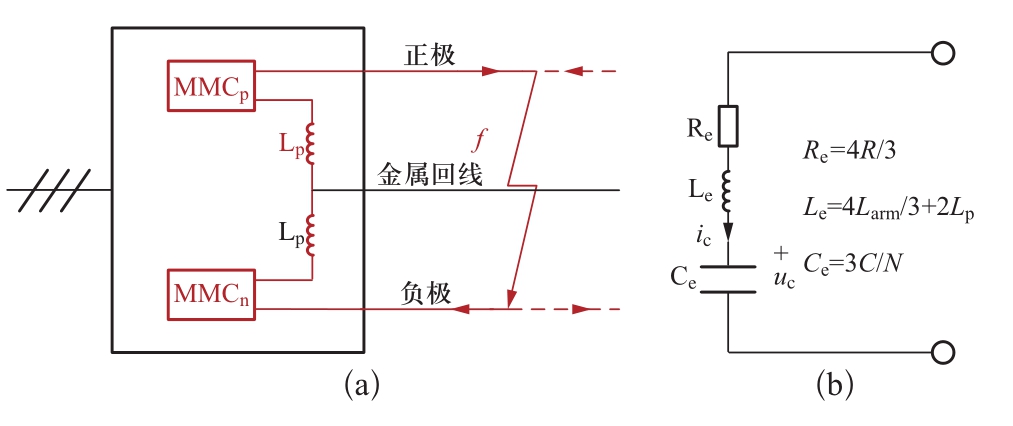
图6 双极短路故障
Fig.6 Pole-to-pole fault
3 柔性直流电网等效电路网络模型
3.1 系统介绍
图7为省去交流系统的对称运行双极四端环形柔性直流电网示意图,其中,S 1 、S 2 、S 3 和S 4 为基于MMC的柔性直流换流站,换流站站间正、负极线路由架空线连接而成,各换流站正、负极中点通过金属回线作为中性线相连接,直流系统接地点位于换流站S 4 ,电抗器配置方式采用集中式配置和分散式配置相结合的混合式配置方式。
3.2 等效电路网络模型
柔性直流电网发生短路故障后,由于电路中电容电压和电感电流不能突变,即在故障时刻有

式中,U c 为直流电网中所有换流站等效电容电压的集合;I L 为直流电网中所有直流线路等效电感电流的集合;t f 为故障发生时刻。
以图7所示的双极柔性直流电网为例,根据换流站等效电路模型,可得故障时刻该柔性直流电网的等效电路网络模型,如图8所示。需要指出的是,该等效电路网络模型只在直流电网故障后短时间内有意义,在直流电网正常运行时或故障长时间后无任何意义。基于该等效电路网络模型,可以对双极柔性直流电网不同短路故障类型下的暂态短路电流进行定量分析计算。

图7 四端环形柔性直流电网示意图
Fig.7 Schematic of four-terminal VSC-based DC grid
4 短路电流分析计算
柔性直流电网中,每种短路故障工况只涉及电网中的局部变化,而网络的大部分没有发生变化。网络方程修正解法的基本思想是有效利用变化前网络方程的解,进行少量的修正计算得到变化后网络方程的解 [21] 。基于此思想,可分别建立故障前柔性直流电网的初始矩阵方程组和故障后该柔性直流电网的修正矩阵方程组,对不同运行工况下的柔性直流电网短路电流暂态特性进行定量分析,从而成倍地提高计算效率。
4.1 初始矩阵方程组
基于图8所示的故障时刻柔性直流电网等效电路网络模型和文献[16]提出的针对伪双极柔性直流电网直流线路双极短路故障电流计算方法,从简单实用角度出发,对处于对称运行状态的不含汇流站 [16] 的双极柔性直流电网,根据故障时中性线有无电流流过,建立不同故障类型下该柔性直流电网的初始矩阵方程组。

图8 故障时刻,直流电网等效电路网络模型
Fig.8 Equivalent circuit network model at fault time
4.1.1 故障时,中性线无电流流过
与伪双极柔性直流电网直流线路双极短路故障类似,此工况对应于对称运行的双极柔性直流电网发生直流线路双极短路故障情况。根据柔性直流电网的对称性,为方便起见,可将换流站等效为一个节点,站间线路等效成一条支路。因此,图8所示的直流电网等效电路网络模型中,存在n个节点n 1 , n 2 , n 3 和n 4 ,b条支路b 12 , b 23 , b 34 和b 41 。此时,柔性直流电网中各换流站可用图6所描述的双极短路故障时的换流站等效电路模型表示,上平面n 1 -n 2 -n 3 -n 4 代表正极回线,下平面n 1’-n 2 ’-n 3 ’-n 4 ’代表负极回线。
根据基尔霍夫电压定律,回路n 1 -n 2 -n 2 ’-n 1 ’的电压方程为
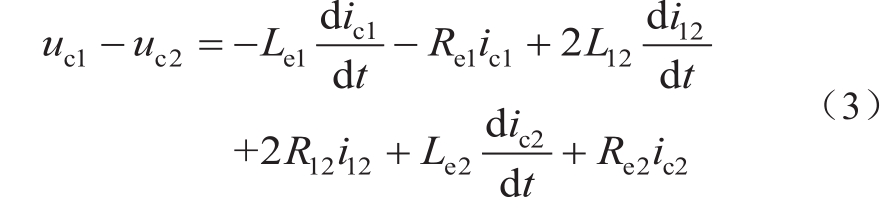
根据基尔霍夫电流定律,有

将式(4)带入式(3),可得该回路矩阵电压方程
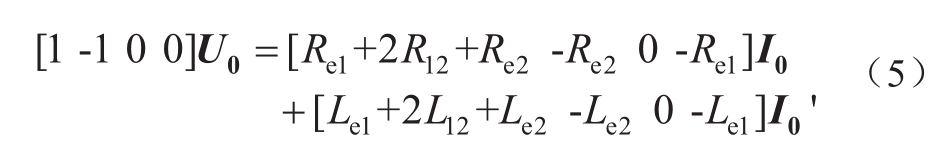
式中,U 0 =[u c1 , u c2 , u c3 , u c4 ] T 为换流站等效电容电压矩阵;I 0 =[i 12 , i 23 , i 34 , i 41 ] T 为站间线路电流矩阵。
故障时刻,该柔性直流电网换流站等效电容电压矩阵和站间线路电流矩阵的关系为
式中,A 0 为b×n阶初始关联矩阵;R 0 为b×b阶初始电阻矩阵;L 0 为b×b阶初始电感矩阵,具体数学形式如下:
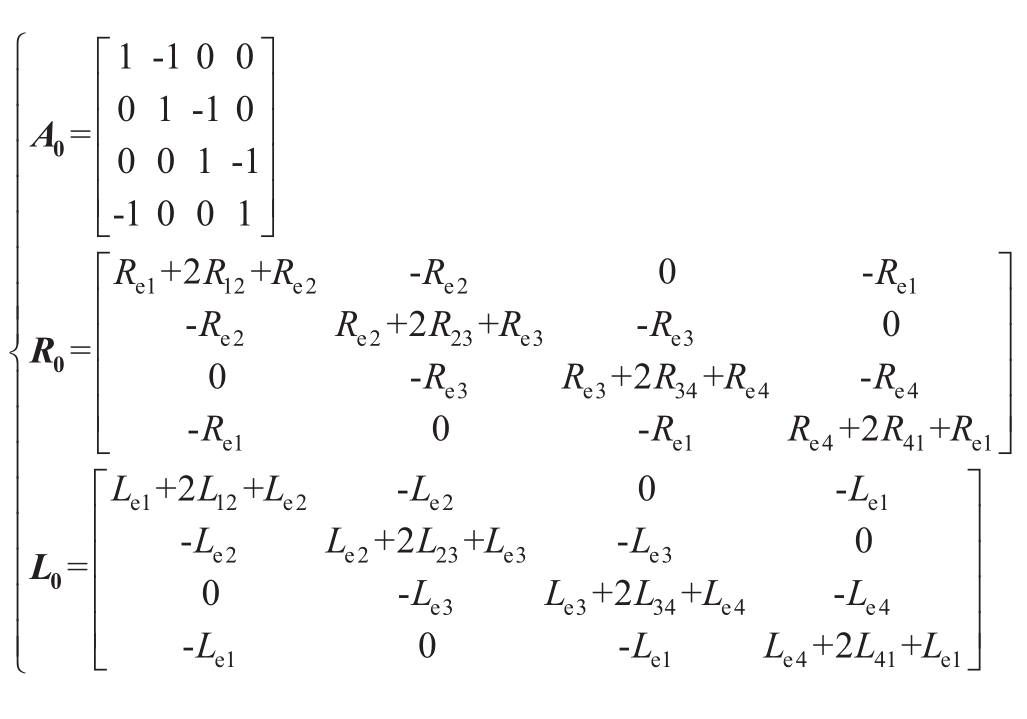
4.1.2 故障时,中性线有电流流过
此情况对应于对称运行的双极柔性直流电网直流线路发生单极接地故障或单极接中性线短路故障情况。图8所示的直流电网等效电路网络模型中,各换流站可分别用图4和图5描述的单极接地故障和单极接中性线故障时所对应的换流站等效电路模型表示,上平面n 1 -n 2 -n 3 -n 4 代表正极回线,下平面n 1 ’-n 2 ’-n 3 ’-n 4 ’代表中性线回线。
正常运行时,中性线无电流流过,对应于图8中,线路n 1 ’-n 2 ’、n 2 ’-n 3 ’、n 3 ’-n 4 ’及n 4 ’-n 1 ’均无电流流过,因此,图8中各换流站负极出口可视为等电位点,回路n 1 -n 2 -n 2 ’-n 1 ’的电压方程为
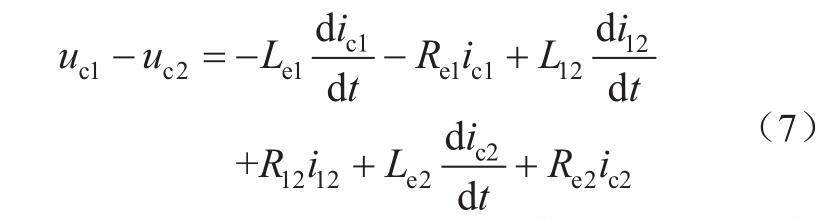
结合式(4)和式(7)可得,故障时刻该柔性直流电网初始矩阵电压方程中的关联矩阵A 0 、电阻矩阵R 0 和电感矩阵L 0 分别为
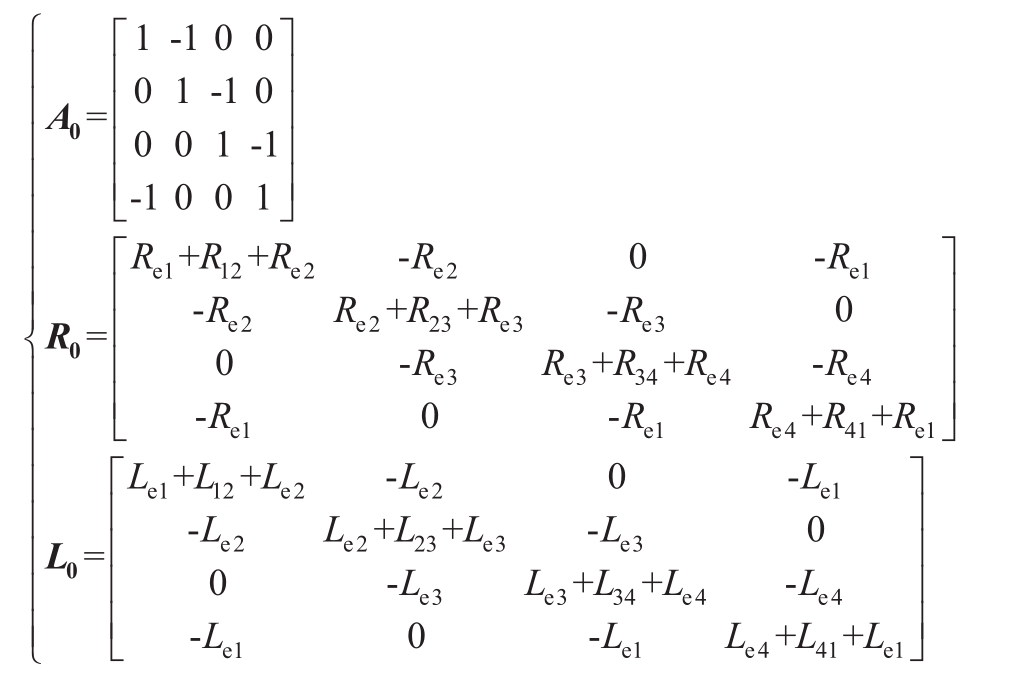
各换流站等效电容电压矩阵与站间线路电流矩阵之间的关系式为
其中,
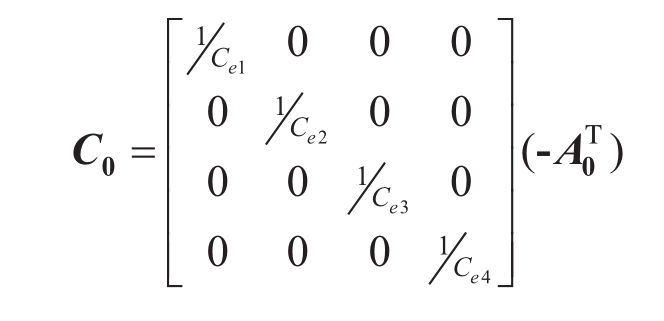
联立式(6)和式(8),该柔性直流电网初始矩阵方程组为
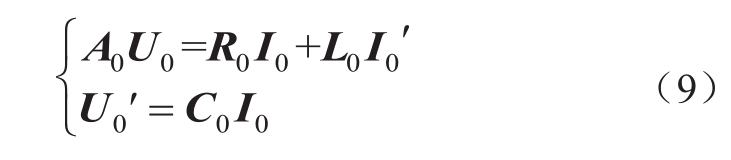
式中,U 0 为故障时刻所有换流站等效电容电压;I 0 为故障时刻所有直流线路等效电感电流,具体可表示为
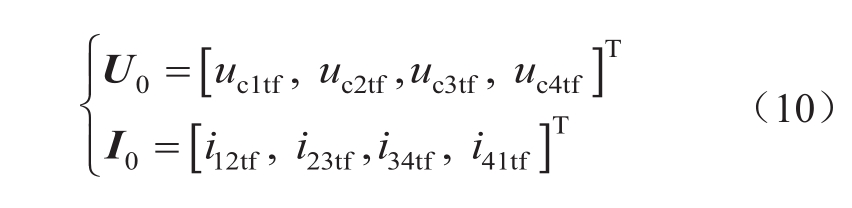
4.2 修正矩阵方程组
假设短路故障发生在支路b ij 上,且故障位置距节点n i 的距离占节点n i -n j 总距离的百分比为x。故障后,整个柔性直流电网的节点数由n变为n+1,支路数由b变为b+1。如图9所示,定义故障节点为n 0 ,故障过渡电阻为R n ,则故障后,支路b ij 更新为b i0 和b 0j ,支路电阻R ij 更新为R i0 和R 0j ,支路电感L ij 更新为L i0和L 0j ,支路电流i ij 修正为i i0 和i 0j ,更新后的电阻和电感具体表示如式(11)所示。
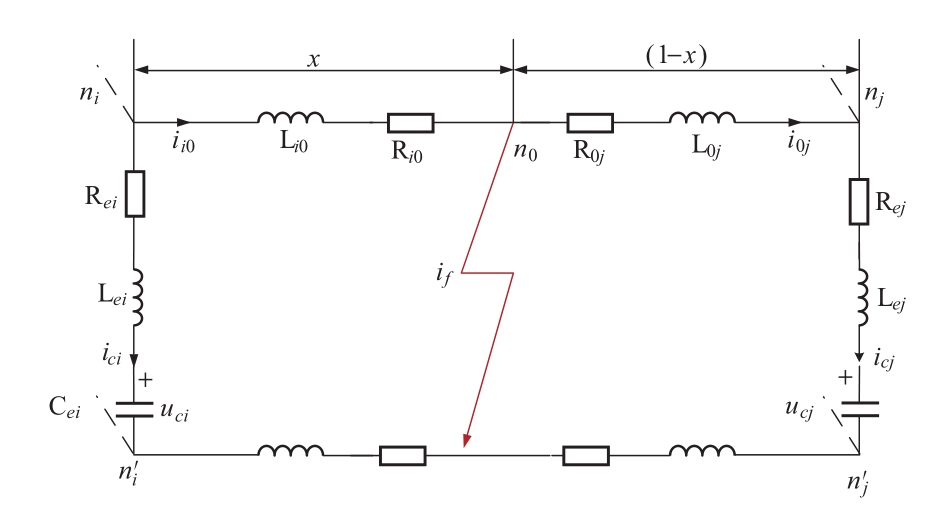
图9 故障支路b ij 等效电路
Fig.9 Equivalent circuit model of line b ij

为便于柔性直流电网短路电流的计算机求解,保持换流站等效电容电压矩阵U = U 0 = [u c1 , u c2 , u c3 , u c4 ] T 维数不变,将站间线路电流矩阵I 0 = […i ij…] T 修正为I = […i i0 , i 0j …] T 。
相应地,将初始关联矩阵A 0 中计算电压u ci -u cj 的对应行修正为两行,此两行分别产生电压u ci 和-u cj ,如图10所示。
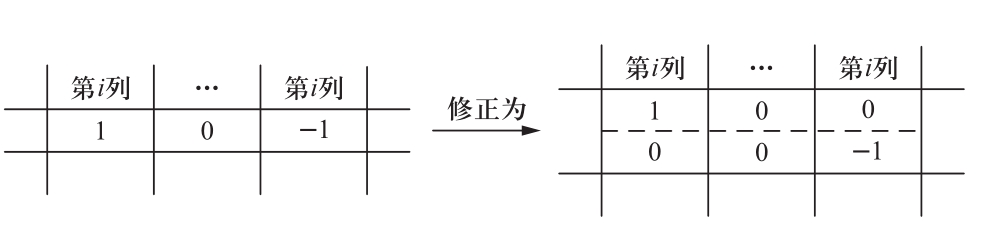
图10 关联矩阵A 0 修正
Fig.10 Modification of the incidence matrix A 0
对于双极短路故障,将初始电阻矩阵R 0 和电感矩阵L 0 中对应于原电流i ij 的对角线元素修正为两行,此两行分别对应故障电流i i0 和i 0j ,如图11和图12所示。
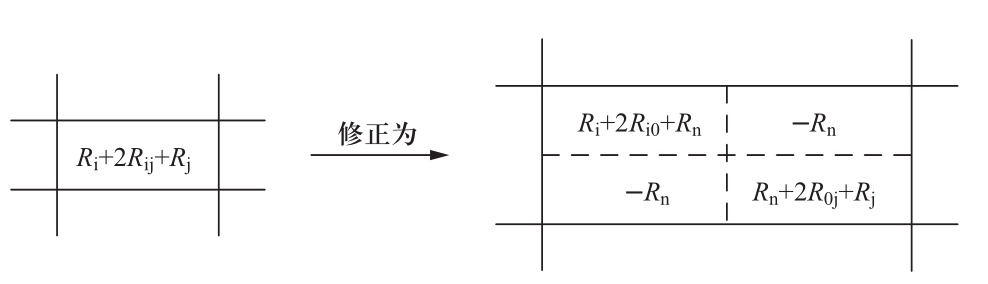
图11 双极故障时,电阻矩阵R 0 修正
Fig.11 Modification of the resistance matrix R 0 under DC bipolar fault
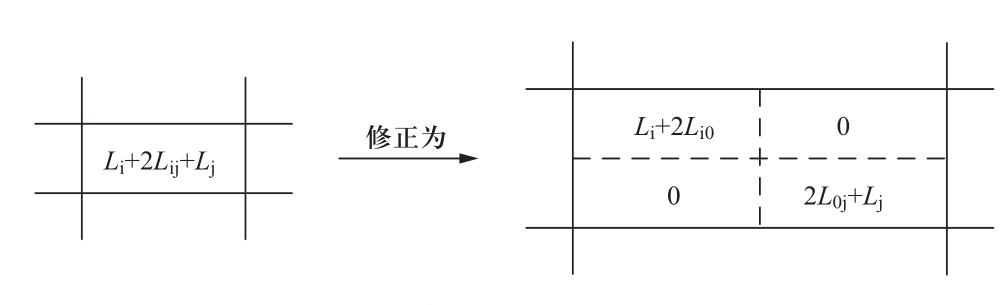
图12 双极故障时,电感矩阵L 0 修正
Fig.12 Modification of the inductance matrix L 0 under DC bipolar fault
对于单极接地故障和单极接中性线短路故障,需考虑故障后电流通路发生变化后,中性线等效电感和电容计入故障回路的问题。此时,初始电阻矩阵R 0 和电感矩阵L 0 中修正关系如图13和图14所示。
图13和图14中,R ex1 、R ex2 和L ex1 、L ex2 为考虑故障电流通路发生变化后,中性线计入不同故障回路时的附加电阻和电感。
假设修正后的关联矩阵、电阻矩阵和电感矩阵分别为A t , R t 和L t ,则该柔性直流电网故障后的修正矩阵方程组为
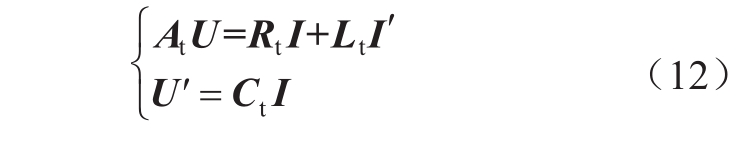
联立式(10)和式(12),结合双极柔性直流电网单个换流站在不同短路故障类型下的等效电路模型,可计算机程序求解定量分析双极柔性直流电网任意故障类型、任意故障位置的短路电流暂态特性。
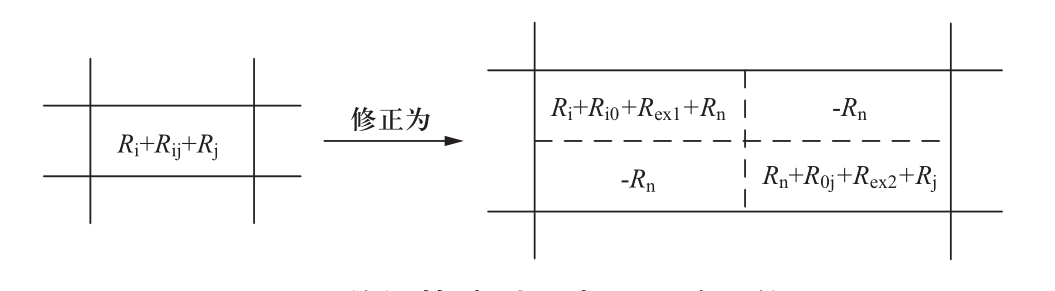
图13 单极故障时,电阻矩阵R 0 修正
Fig.13 Modification of the resistance matrix R 0 under DC unipolar fault
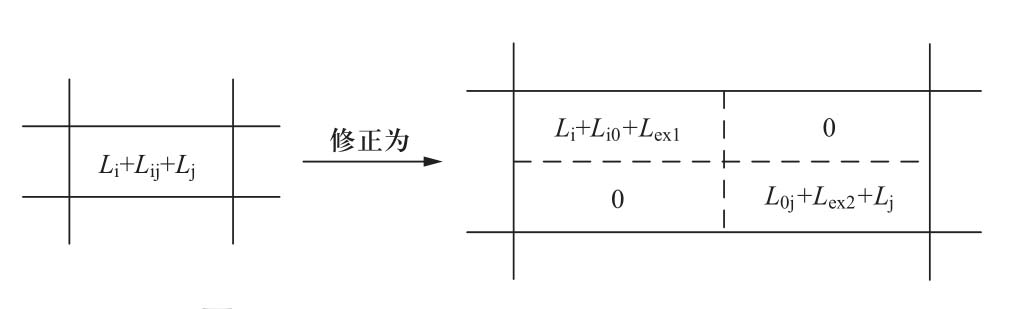
图14 单极故障时,电感矩阵L 0 修正
Fig.14 Modification of the inductance matrix L 0 under DC unipolar fault
5 仿真分析
为验证本文所提出的双极柔性直流电网短路电流暂态特性分析方法的有效性和精确性,在PSCAD/EMTDC仿真平台中,搭建了如图7所示的四端环形柔性直流电网相应电磁暂态仿真模型,其基本参数如表1~表5所示。
基于所搭建的四端环形柔性直流电网电磁暂态仿真模型和本文提出的柔性直流电网短路电流暂态特性分析方法,对双极柔性直流电网不同短路故障类型下的短路电流暂态特性进行对比分析,结果如下。
表1 直流电网系统参数
Table 1 System Parameters of DC Grid
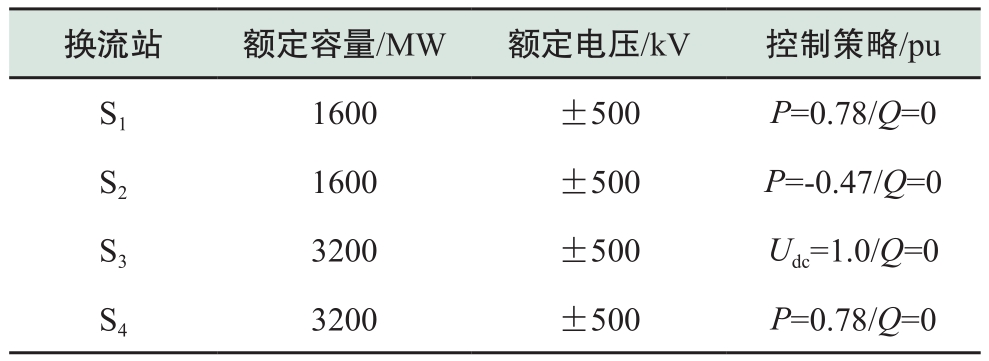
表2 MMC参数
Table 2 Parameters of MMC

续表
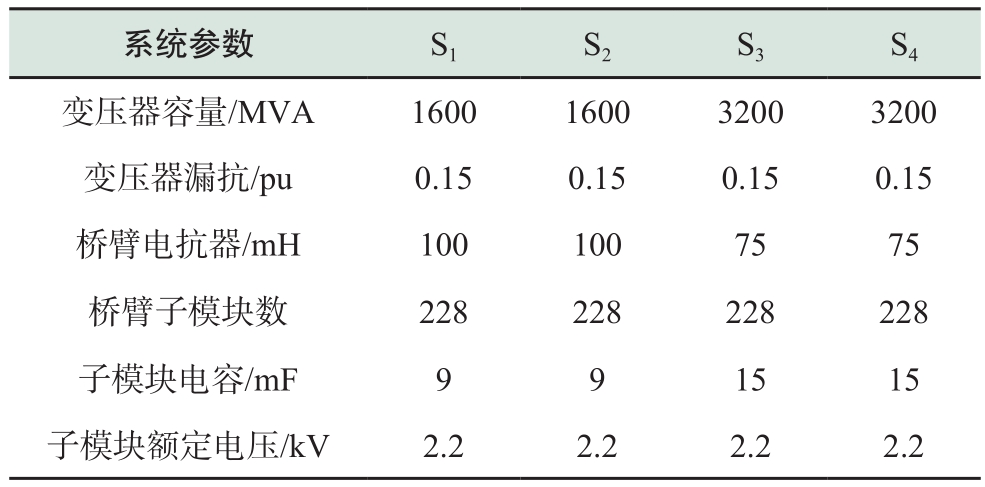
表3 直流线路参数
Table 3 Parameters of DC Transmission Lines

表4 站间距离
Table 4 Distance between stations

表5 电抗器参数
Table 5 Parameters of Reactors

5.1 单极接地故障
1.5 s时刻,故障点1处发生正极接地故障,记录故障后10 ms内各条直流线路的暂态电流波形,计算值与仿真值对比结果如图15所示。
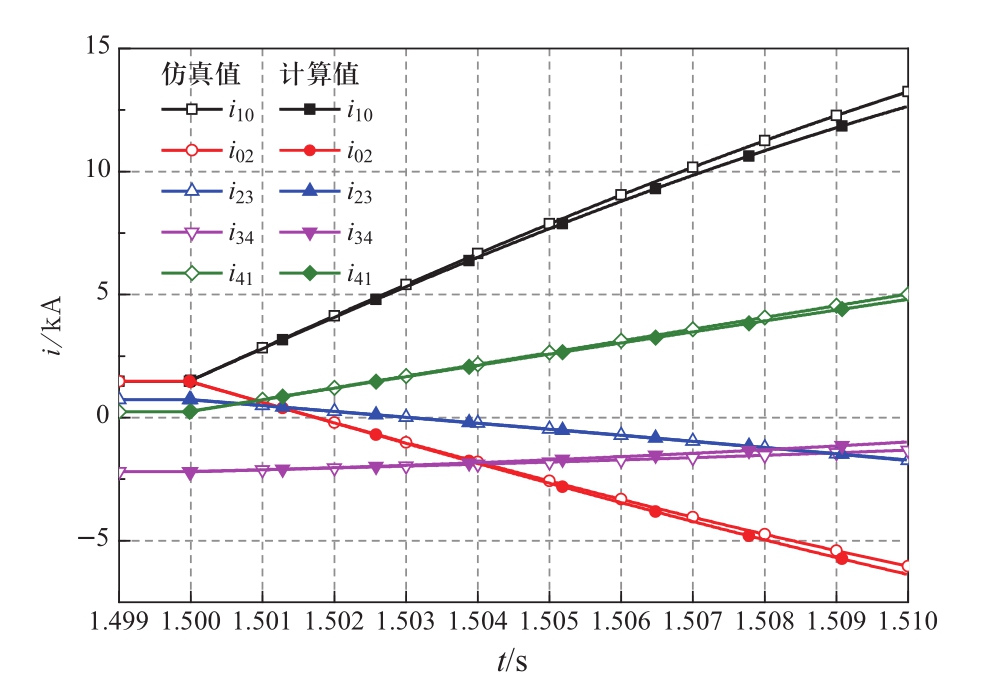
图15 单极接地故障时,故障电流对比
Fig.15 Fault current comparison under pole-to-ground fault
对故障点1处两侧的馈入电流i 10 、i 02 进行定量误差分析,以仿真数据为基准,i 10 和i 02 在故障后10 ms内的平均误差百分比分别为2.52%和4.27%。在1.510 s时刻,馈入电流i 10 、i 02 发展到最大,此时二者的误差百分比分别为4.5%和5.5%。
对S 1 -S 2 站间线路不同位置,即距离S 1 为站间线路长度的10%、50%、和90%处分别设置单极接地故障,故障后10 ms时刻,故障两侧馈入电流i 10 、i 02 仿真值、计算值及误差百分比如表6所示。
表6 故障点1两侧馈入电流对比
Table 6 Infeed current comparison from both sides of fault point 1

5.2 单极接中性线短路故障
1.5 s时刻,故障点19处发生正极接中性线短路故障,记录故障后10 ms内各条直流线路的暂态电流波形,计算值与仿真值对比结果如图16所示。
对故障点19处两侧的馈入电流i 40 、i 01 进行定量误差分析,以仿真数据为基准,i 40 和i 01 在故障后10 ms内的平均误差百分比分别为1.67%和1.74%。在1.510 s时刻,馈入电流i 40 、i 01 发展到最大,此时二者的误差百分比分别为2.7%和2.1%。
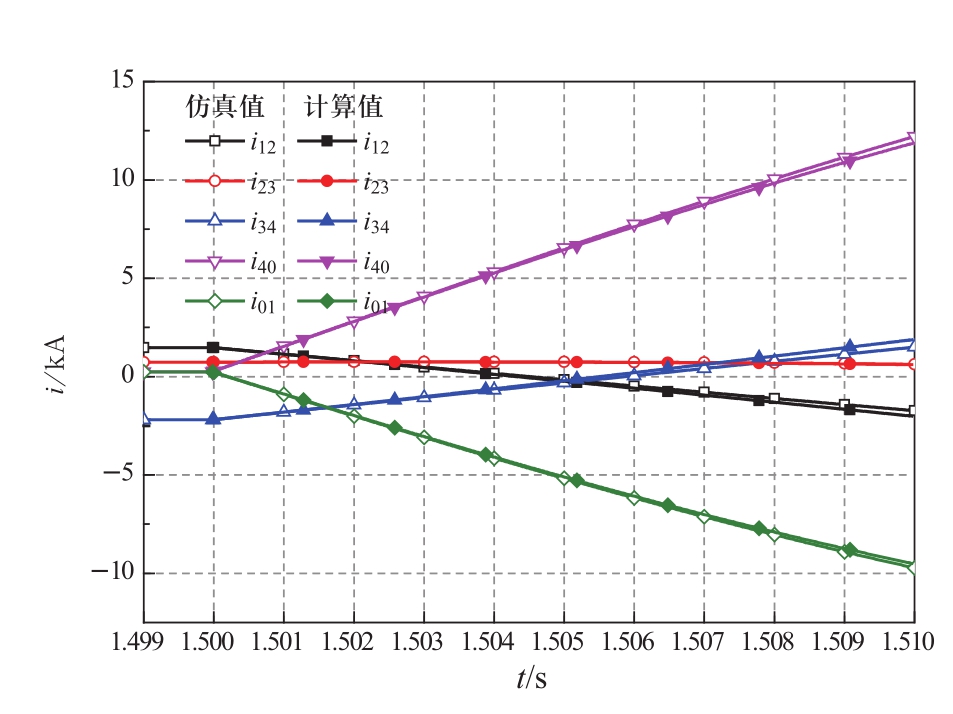
图16 单极接中性线故障时,故障电流对比
Fig.16 Fault current comparison under pole-to-neutral line fault
对S 4 -S 1 站间线路不同位置,即距离S 4 为站间线路长度的10%、50%和90%处分别设置单极接地故障,故障后10 ms时刻,故障两侧馈入电流i 40 、i 01 仿真值、计算值及误差百分比如表7所示。
表7 故障点19两侧馈入电流对比
Table 7 Infeed current comparison from both sides of fault point 19

5.3 双极短路故障
1.5 s时刻,故障点13和16处发生双极短路故障,记录故障后10 m s内各条直流线路的暂态电流波形,计算值与仿真值对比结果如图17所示。
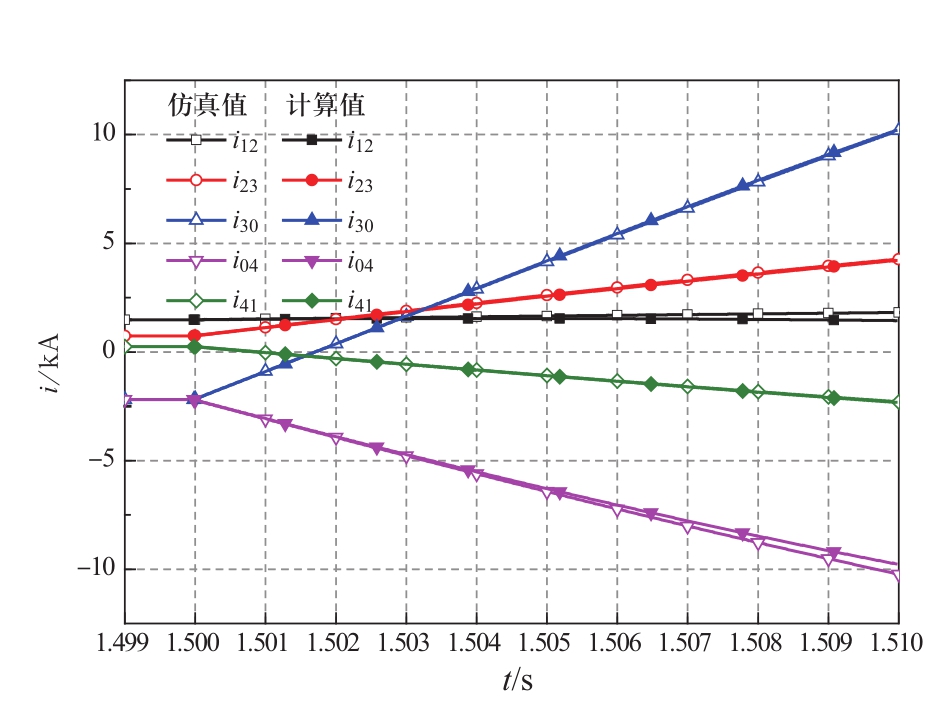
图17 双极短路故障时,故障电流对比
Fig.17 Fault current comparison under pole-to-pole fault
对故障点13处两侧的馈入电流i 30 、i 04 进行定量误差分析,以仿真数据为基准,i 30 和i 04 在故障后10 ms内的平均误差百分比分别为0.96%和2.13%。在1.510 s时刻,馈入电流i 30 、i 04 发展到最大,此时二者的误差百分比分别为1.6%和4.4%。
对S 3 -S 4 站间线路不同位置,即距离S 3 为站间线路长度的10%、50%和90%处分别设置双极短路故障,故障后10 ms时刻,故障两侧馈入电流i 30 、i 04 仿真值、计算值及误差百分比如表8所示。
表8 故障点13两侧馈入电流对比
Table 8 Infeed current comparison from both sides of fault point 13
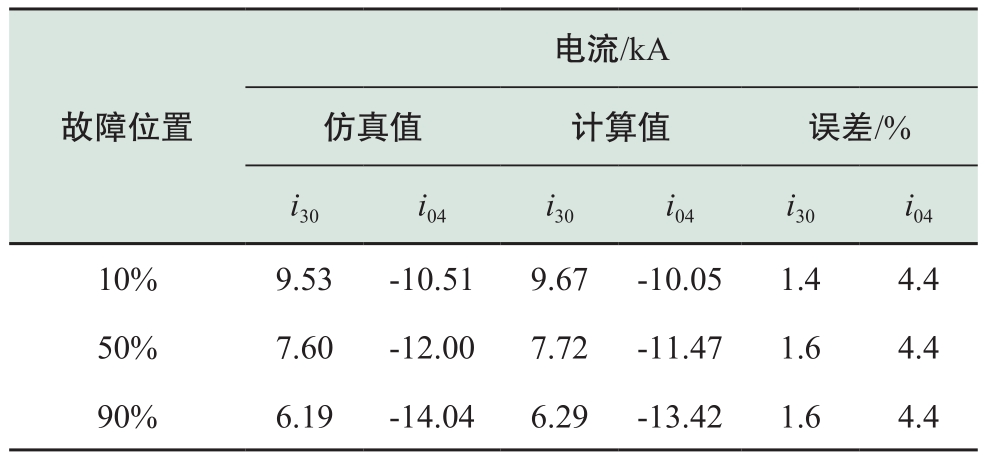
对比分析双极柔性直流电网任意故障类型、任意故障位置的直流线路短路故障暂态电流的仿真值和计算值可知,在子模块电容放电电流占主导地位的故障后、闭锁前短时间内,故障暂态电流的仿真值和计算值高度一致,从而证明了本文所提出的双极柔性直流电网短路电流暂态特性分析方法的有效性和精确性。
6 结论
本文提出了一种适用于双极柔性直流电网短路电流暂态特性定量分析方法,通过仿真分析验证了该方法的有效性和精确性,得到如下结论:
1)建立了双极柔性直流电网在直流线路不同短路故障类型下的单个换流站等效电路数学模型,为双极柔性直流电网的短路电流定量分析计算提供了理论支撑。
2)构建了故障时刻双极柔性直流电网等效电路网络模型,该模型层次结构明确,物理概念清晰,适用于双极柔性直流电网的短路电流定量分析计算。
3)实现了双极柔性直流电网任意故障类型、任意故障位置的短路电流定量分析计算,为换流阀、直流断路器和电抗器等柔性直流电网关键主设备参数选取提供了理论依据。
参考文献
[1] 汤广福.基于电压源换流器的高压直流输电技术[M].北京:中国电力出版社,2010:34-37.Tang Guangfu.HVDC based on voltage source converter.Beijing: China Electric Power Press, 2010: 34-37(in Chinese).
[2] 汤广福,贺之渊,庞辉.柔性直流输电工程技术研究及发展[J].电力系统自动化,2013,37(15):3-14.Tang Guangfu, He Zhiyuan, Pang Hui.Research, application and development of VSC-HVDC engineering technology[J].Automation of Electric Power Systems, 2013, 37(15): 3-14(in Chinese).
[3] 汤广福,罗湘,魏晓光.多端直流输电与直流电网技术[J].中国电机工程学报,2013,33(10):8-17.Tang Guangfu, Luo Xiang, Wei Xiaoguang.Multi- terminal HVDC and DC-grid technology[J].Proceedings of the CSEE,2013, 33(10):8-17(in Chinese).
[4] 姚良忠,吴婧,王志冰,等.未来高压直流电网发展形态分析[J].中国电机工程学报,2014,34(34):6007-6020.Yao Liangzhong, Wu Jing, Wang Zhibing, et al.Pattern analysis of future HVDC grid development [J].Proceedings of the CSEE, 2014, 34(34):6007-6020(in Chinese).
[5] 周孝信,鲁宗相,刘应梅,等.中国未来电网的发展模式和关键技术[J].中国电机工程学报,2014,34(29):4999-5008.Zhou X iaox in, Lu Zongx iang, Liu Y ingm ei, et al.Development models and key technologies of future grid in China[J].Proceedings of the CSEE, 2014, 34(29): 4999-5008(in Chinese).
[6] 温家良,吴锐,彭畅,等.直流电网在中国的应用前景分析[J].中国电机工程学报,2012,32(13):7-12.Wen Jialiang, Wu Rui, Peng Chang, et al.Analysis of DC grid prospects in China[J].Proceedings of the CSEE, 2012, 32(13):7-12(in Chinese).
[7] 吴亚楠,吕铮,贺之渊,等.基于架空线的直流电网保护方案研究[J].中国电机工程学报,2016,36(14) :3726-3733.Wu Yanan, Lyu Zheng, He Zhiyuan, et al.Study on the Protection Strategies of HVDC G rid for Overhead Line Application[J].Proceeding of the CSEE, 2016, 36(14): 3726-3733(in Chinese).
[8] 孙栩,曹士冬,卜广全,等.架空线柔性直流电网构建方案[J].电网技术,2016,40(3) :678-682.Sun Xu, Cao Shidong, Bu Guangquan, et al.Construction Scheme of Overhead Line Flexible HVDC Grid [J].Power System Technology, 2016, 40(3): 678-682(in Chinese).
[9] 徐政,薛英林,张哲任.大容量架空线柔性直流输电关键技术及前景展望[J].中国电机工程学报,2014,34(29):5051-5062.Xu Zheng, Xue Y ing lin, Zhang Zheren.VSC-HVDC techno logy suitab le for bu ll power overhead line transmission[J].Proceedings of the CSEE, 2014, 34(29): 5051-5062(in Chinese).
[10] Li X Q, Song Q, Liu WH, et al.Protection of nonpermanent faults on DC overhead lines in MMC-based HVDC systems[J].IEEE Transactions on Power Delivery, 2013, 28(1): 483-490.
[11] 王姗姗,周孝信,汤广福,等.模块化多电平换流器HVDC直流双极短路子模块过电流分析[J].中国电机工程学报,2010,31(1) :1-7.Wang Shanshan, Zhou Xiaoxin, Tang Guangfu, et al.Analysis of Submodule Overcurrent Caused by DC Pole-to-Pole Fault in Modular Multilevel Converter HVDC System[J].Proceeding of the CSEE, 2010, 31(01): 1-7(in Chinese).
[12] 杨海倩,王玮,荆龙,等.MMC-HVDC 系统直流侧故障暂态特性分析[J].电网技术,2016,40(1) :40-46.Yang Haiqian, Wang Wei, Jing Long, et al.Analysis on Transient Characteristic of DC Transmission Line Fault in MMC Based HVDC Transmission System [J].Power System Technology, 2016, 40(1):40-46(in Chinese).
[13] 吴婧,姚良忠,王志冰,等.直流电网MMC 拓扑及其直流故障电流阻断方法研究[J].中国电机工程学报,2015,35(11) :2681-2694.Wu Jing, Yao Liangzhong, Wang Zhibing, et al.The Study of MMC Topologies and Their DC Fault Current Blocking Capacities in DC Grid[J].Proceeding of the CSEE, 2015,35(11): 2681-2694(in Chinese).
[14] 李斌,李晔,何佳伟,等.具有直流故障清除能力的MMC 子模块关键性能研究[J].中国电机工程学报,2016,36(8) :2114-2122.Li Bin, Li Ye, He Jiaw ei, et al.Research on the Key Properties of MMC Sub-modules With DC Fault Eliminating Capability[J].Proceeding of the CSEE, 2016, 36(8): 2114-2122(in Chinese).
[15] Xue Yinglin Xu Zheng.On the bipolar MMC-HVDC topology suitable for bulk power overhead linetransmission:configuration, control, and DC fault analysis[J].IEEE Transactions on Power Delivery, 29(6): 2420-2429.
[16] Chengyu Li, Chengyong Zhao, Jianzhong Xu, etal.A Pole-to-Pole Short-Circuit Fault Current Calculation Method for DC Grids[J].IEEE Transactions on Power System, 2017, 32(6):4943-4953.
[17] Wang Wen yuan, Barnes M, Marjanovic O, et al.Impact of DC breaker systems on multiterminal VSC-HVDC stability[J].IEEE Transactions on Power Delivery, 2016, 31(2): 769-779.
[18] Zhou WD, Wei X G, Zhang S, et al.Development and test of a 200 kV full-bridge based hybrid HVDC breaker[C]//Proceedings of the 2015 17th European Conference on Power Electronics and Applications.Geneva, Switzerland: IEEE,2015: 1-7.
[19] 魏晓光,高冲,罗湘,等.柔性直流输电网用新型高压直流断路器设计方案[J].电力系统自动化,2013,37(15):95-102.Wei Xiaoguang, Gao Chong, Luo Xiang, et al.A novel design of high-voltage DC circuit breaker in HVDC flexible transmission grid[J].Automation of Electric Power Systems,2013, 37(15): 95-102(in Chinese).
[20] Leterme W, Van Hertem D.Classification of fault clearing strategies for HVDC grids[C]//CIGRE Session.Paris,France:CIGRE, 2015: 1-10.
[21] 胡文旺,唐志军,林国栋,等.柔性直流控制保护系统方案及其工程应用[J].电力系统自动化,2016,40(21):27-33.Hu Wenwang, Tang Zhijun, Lin Guodong, et al.Scheme and Engineering Application of Flexible DC Control and Protection System[J].Automation of Electric Power Systems, 2016,40(21): 27-33(in Chinese).
[22] 张伯明,陈寿孙,严正.高等电力网络分析(第二版)[M].北京:清华大学出版社,2013:89-114.Zhang Boming, Chen Shousun, Yan Zheng.Advanced Electric Power Net work Analy sis(The secondedition).Beijing:Tsinghua University Press, 2013: 89-114(in Chinese).
Analysis on Transient Characteristics of Short-circuit Current for Bipolar VSC-based DC Grid
PEI Xiangyu 1 , TANG Guangfu 2 , ZHANG Shengmei 3 , XIE Sujuan 3 , WU Yanan 2 ,YANG Jie 2
(1.China Electric Power Research Institute, Haidian District, Beijing 100192, China;2.State Key Laboratory of Advanced Power Transmission Technology(Global Energy Interconnection Research Institute),Changping District, Beijing 102209, China; 3.North China Electric Power University, Changping District, Beijing 102206, China)
Abstract: Overhead transmission lines of VSC-based Directcurrent (DC) grid is an effective solution for the wide-area coordination, complementarity and reliable delivery of the largescale renewable energy sources, and therefore is an important application direction of VSC-HVDC charactered by highvoltage and large-capacity in the future.Short-circuit current of DC lines is one of the important basis for the selection of the key equipment parameters such as converter valve, reactor and DC circuit breaker in DC grid.In this paper, the equivalent circuit model of a single converter station under different shortcircuit fault types is studied.Based on this, the equivalent circuit network model of VSC-based DC grid at fault time is established.Furthermore, a quantitative analysis method of transient short-circuit current for bipolar VSC-based DC grid under short-circuit faults including pole-to-ground, poleto-neutral line and pole-to-pole is proposed.As a result, the quantitative calculation of transient short-circuit current of any fault type and fault location for bipolar VSC-based DC grid is realized.Finally, the validity and accuracy of the proposed method is verified by PSCAD/EMTDC simulation.
Keywords: overhead transmission line; MMC; VSC-based DC Grid; short-circuit current; fault characteristic analysis
National Key Research and Development Program of China(2017YFB0902400).

裴翔羽
作者简介:
裴翔羽 (1986),男,博士研究生,CSEE学生会员,研究方向为柔性直流电网技术,E-mail:peixiangyu@geiri.sgcc.com.cn。
汤广福 (1966),男,博士,中国工程院院士,教授级高级工程师,博士生导师,从事灵活交流输电、高压直流输电、柔性直流输电和直流电网等装备的设计与研发。
(责任编辑 张鹏)
