0 引言
随着化石能源的大量消耗,环境污染与气候问题成为人类社会亟待解决的重点课题。电动汽车作为一种清洁的交通工具,以其低能耗、低排放的特点,受到社会的广泛关注[1-2]。在政府的大力支持下,我国电动汽车数量近几年呈现高速增长态势:2015年我国电动汽车保有量达到58.3万辆,成为保有电动汽车最多的国家;2016年数量飞速跃升至109万辆,占全球总量的一半[3]。
随着电动汽车渗透率的提高,大规模电动汽车的充电负荷将成为电网运行中不可忽视的影响因素[4-6]。尽管电动汽车的无序充电将加大电网调峰难度,为电网调度运行带来挑战;但另一方面,电动汽车作为柔性负荷,可通过有序调控实现平滑负荷[7]、降低成本[8-9]、减小网损[10-11]、消纳新能源[12-14]等多种目标,增加运行收益,改善电网运行环境。考虑负荷平滑因素,文献[7]提出了一种基于负荷预测的有序充电方法,可实现充电负荷向低谷转移,从而平抑负荷波动。考虑用户充电费用因素,文献[8]从电网的角度以减小峰谷差为目标提出了分时电价时段划分方法,并建立了以用户充电费用最小与电池充电起始时间最早为目标的有序充电优化模型。文献[9]基于分时电价制度和电动汽车可入网的情况,针对电动汽车调度机构建立了计及电网负荷波动及用户成本的多目标优化模型,采用交叉遗传粒子群算法求解得到次日优化充放电计划。以配电网网损最小为考虑因素,文献[10]证明了网损与负荷率及方差的关系,网损的减少在一定程度上可转化为负荷波动的减少,从而可以避免在优化模型中引入复杂的潮流约束。文献[11]考虑了电压约束与用户需求,通过线性化电压约束建立了凸二次规划模型。在考虑新能源发电的情形下,文献[12]提出了同时计及电动汽车负荷与风电、光伏出力不确定性的随机协同调度优化模型,以降低可再生能源出力波动。文献[13]以最小化可再生能源出力波动与最大化电动汽车用户收益为目标的多目标协同调度模型,并利用多目标改进化学反应优化算法(chemical reaction optimization algorithm,CROA)加以求解。上面的文献仅考虑了日前的优化,未考虑日内的实时运行。文献[14]考虑光伏与空调负荷,提出了含电动汽车与可控负荷智能小区的两阶段优化调度策略,日前以运营方收益最大为目标确定实时电价,再引入实时调度修正预测偏差带来的不平衡量。
近几年,随着数学规划算法的发展,以二阶锥规划为代表的规划模型逐步应用到电力系统优化当中,涉及最优潮流[15]、无功优化[16]、储能配置[17]与网络重构[18]等多个方向。其中文献[15]提出了一种精确的凸松弛方法并给出其适用条件,通过二阶锥规划解出辐射状配电网中潮流问题的最优解。
本文针对含电动汽车充电负荷、分布式电源及无功补偿装置的配电网络系统,提出了一种配电网两阶段优化运行策略。首先进行节点电动汽车负荷建模,并基于此以最小化总购电成本为目标建立了日前优化混合整数二阶锥规划模型。日内滚动优化同样以最小化总购电成本为目标,求解在日前无功补偿最优动作策略下分布式电源预测出力存在偏差时电动汽车功率的修正量。
1 基于混合整数二阶锥规划的日前优化模型
在日前阶段,调度中心可以按照次日配电网内各节点的分布式电源出力、基础负荷与电动汽车充电负荷的预测数据,计算得到日前电动汽车最优充电策略与无功补偿最优动作策略。
配电网通常工作在开环状态下。同时我们合理地假设配电网仅通过根节点处的单一母线与外部无限大电网相连,因此根节点可以视为松弛节点。电动汽车负荷接在除根节点之外的其他节点。在配电网内的部分节点接有光伏或风电等分布式电源,在部分节点接有分档投切式补偿电容器等无功补偿装置。
1.1 节点充电负荷建模
当进行配网级电动汽车功率优化时,往往不需要像充电站内优化一样求解每辆车的充电曲线。实际上,当网络中节点接入的电动汽车数量较多时按车辆求解也会带来较大的计算量。相比而言,从节点的角度考虑,将车辆充电负荷汇集,视为一个集总的等效充电负荷,会给求解带来很大的便利。为此,本文将首先进行节点电动汽车充电负荷的建模。
利用接入某节点电动汽车的具体信息,如到达时间、离开时间、初始荷电状态、终止荷电状态等,可以建立节点充电负荷的能量边界模型。在某一具体时刻,节点已完成充电电量应当不小于在此时刻前要离开的车辆需求电量之和,同时应当不大于在此时刻前接入的车辆需求电量之和。即
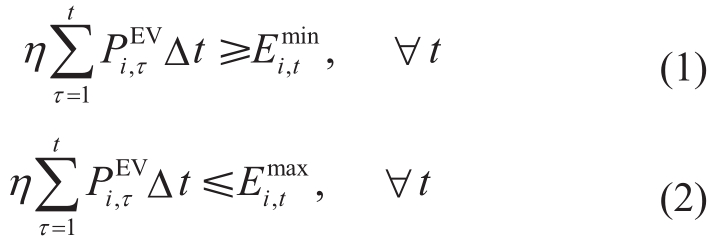
式中,η为电动汽车充电效率,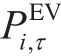 为τ时刻节点i处电动汽车的有功充电功率
为τ时刻节点i处电动汽车的有功充电功率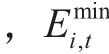 为t时刻及之前时刻离开节点i的电动汽车总充电需求,
为t时刻及之前时刻离开节点i的电动汽车总充电需求, 为t时刻及之前时刻到达节点i的电动汽车总充电需求。
为t时刻及之前时刻到达节点i的电动汽车总充电需求。
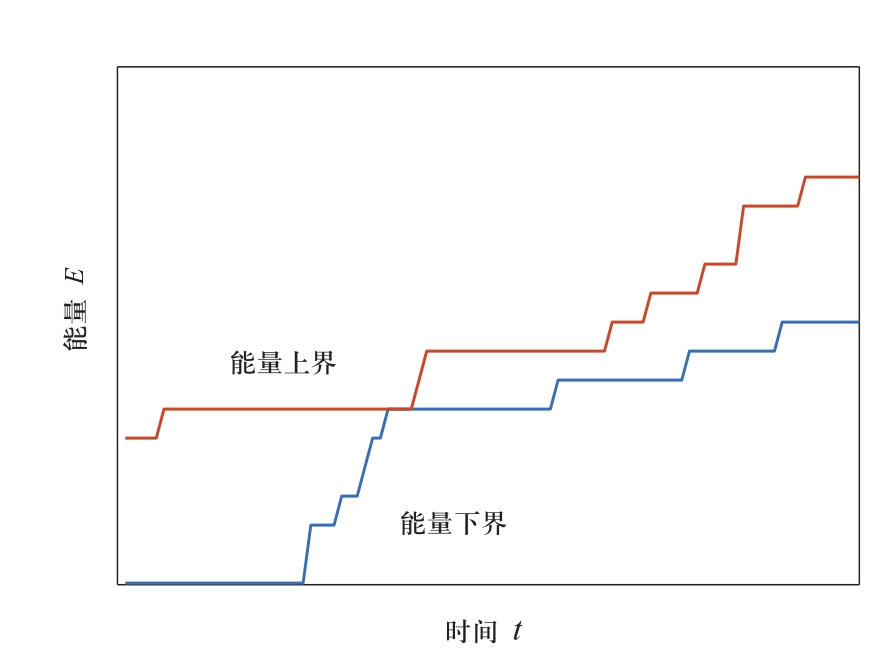
图1 电动汽车节点充电能量边界示意
Fig. 1 Nodal EV charging electricity boundary
电动汽车节点充电能量边界如图1所示。t时刻之前离开的车辆需求电量给出当前节点已完成充电电量的下界,而t时刻之前接入的车辆需求电量给出已完成充电电量的上界,实际节点上的充电策略对应的充电电量曲线应当位于上下界之间区域内。
同时,t时刻节点充电功率应当不超过节点处实际接入电动汽车的最大充电功率和与节点处充电设施最大充电功率中的较小值,即
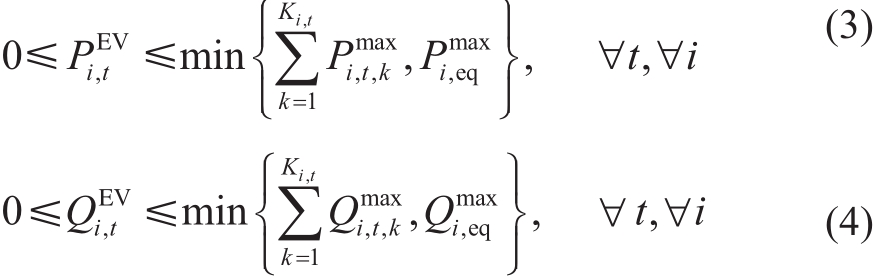
式中,K 为t时刻节点i接入电动汽车的数量,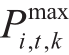 与i,t
与i,t 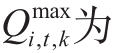 t时刻节点i连接的第k辆车的最大允许充电有功及无功功率,
t时刻节点i连接的第k辆车的最大允许充电有功及无功功率,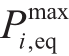 与
与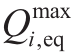 为节点i充电设施允许的最大充电有功及网侧无功功率。
为节点i充电设施允许的最大充电有功及网侧无功功率。
1.2 日前优化模型建立
日前优化模型将综合考虑充电需求、潮流约束等条件,在预测分布式电源出力场景下,求得最优无功补偿装置动作策略与电动汽车有序充电策略。
1.2.1 优化目标
日前优化模型以最小化配电网总购电成本为优化目标,即
式中,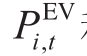 和
和 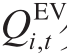 分别为节点i处电动汽车有功和充电功率和电动汽车充电负荷网侧无功功率,0-1变量 u i , t , s为t时刻节点i处第s档电容器的投切状态(1表示切入,0表示切出),
分别为节点i处电动汽车有功和充电功率和电动汽车充电负荷网侧无功功率,0-1变量 u i , t , s为t时刻节点i处第s档电容器的投切状态(1表示切入,0表示切出),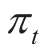 为t时刻的购电电价,
为t时刻的购电电价,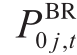 表示根节点与节点j之间支路在t时刻的支路有功潮流,
表示根节点与节点j之间支路在t时刻的支路有功潮流, 为所有支路的集合,T为时间间隔数目,Δt为时段长度。
为所有支路的集合,T为时间间隔数目,Δt为时段长度。
1.2.2 约束条件
日前优化模型需满足支路潮流、节点电压、充电需求、无功补偿等约束条件。
(1)支路潮流约束。
配电网内各条支路的有功、无功潮流需满足潮流方程等式约束与潮流上下限约束
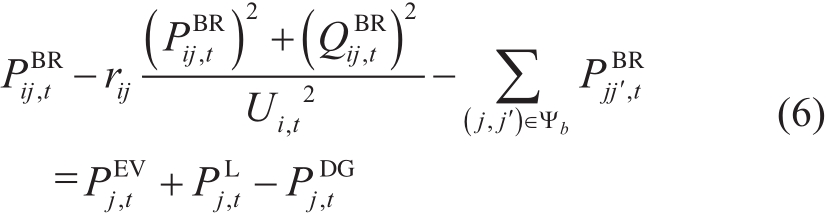
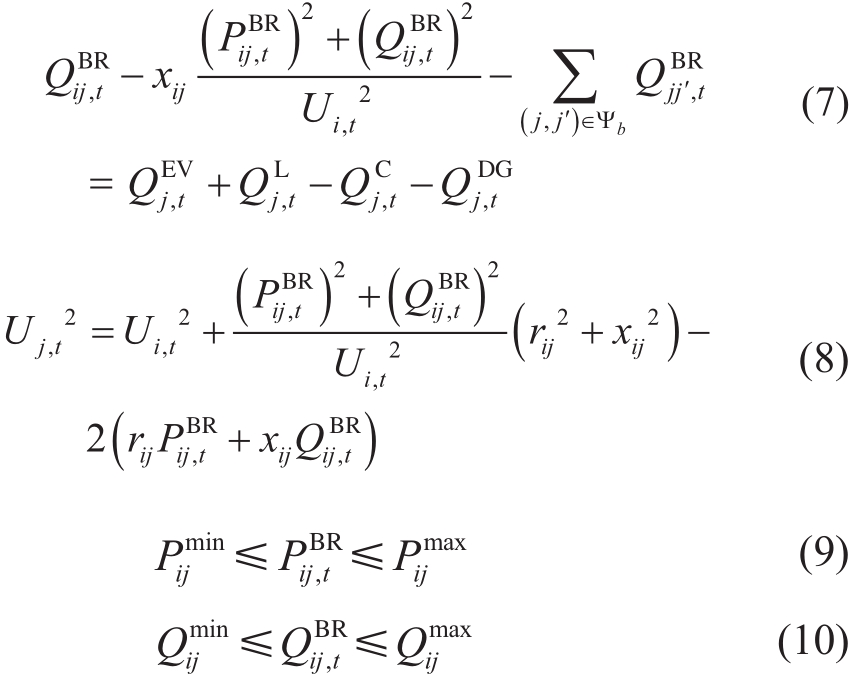
式中,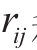 和
和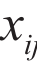 j 分别为支路ij的电阻与电抗值,
j 分别为支路ij的电阻与电抗值,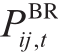 和
和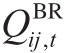 分别为t时刻支路ij的有功和无功潮流, U 为t时刻i,t节点i的电压幅值,
分别为t时刻支路ij的有功和无功潮流, U 为t时刻i,t节点i的电压幅值,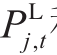 和
和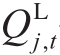 分别为t时刻节点j处的有功与无功基础负荷,
分别为t时刻节点j处的有功与无功基础负荷,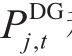 和
和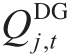 为t时刻节点j处分布式电源的有功与无功实际出力
为t时刻节点j处分布式电源的有功与无功实际出力 为t时刻节点j处的无功补偿功率。
为t时刻节点j处的无功补偿功率。
(2)充电需求约束。
配电网内可接入电动汽车的各个节点,在t时刻的节点充电功率需要满足前述节点充电负荷建模中的能量边界及功率上下限要求,即(1)~(4)式。
此外,本文考虑电动汽车充电有最低功率因数要求(记为λ),因此充电负荷的网侧无功功率需满足
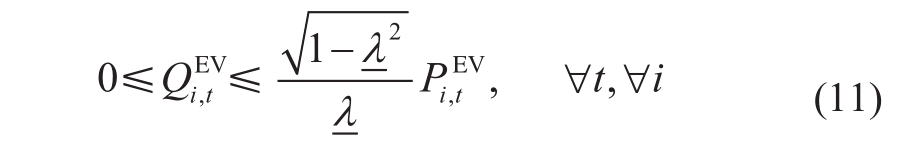
(3)无功补偿约束。
考虑配电网中某些节点配置了分档投切的补偿电容器。假设同一节点处补偿电容器各档位容量相同,但不同节点处电容器档位与容量有所差别。则各节点无功补偿功率应满足
式中,Δ Q i 为节点i处每档电容器的无功容量,Si为节点i处投切电容器的档位数,Λ表示接有分档投切电容器的节点集。
电容器各档位之间应满足较低档位先于较高档位切入,切出则相反。同时考虑到电容器的投切会带来时间与设备损耗,单日电容器动作次数应设置上限,因此有

式中,Ni为节点i单日允许最大电容器动作次数。
通过引入辅助变量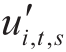 与
与 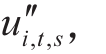 可以将式(13)转换为如下所示的线性形式约束:
可以将式(13)转换为如下所示的线性形式约束:
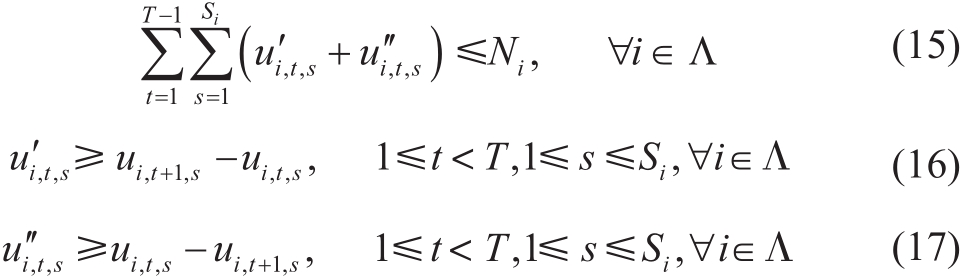
(4)节点电压约束。
配电网内各节点电压应满足上下限约束

至此,建立了含电动汽车、分布式能源与无功补偿装置的配电网日前运行优化模型。
1.2 二阶锥松弛
由于交流潮流约束(6)~(8)的存在,上述日前优化模型是典型的非线性模型,求解较为困难。文献[15]证明了一种以购电成本最小为优化目标的辐射状配电网优化模型可引入精确的二阶锥松弛来将交流潮流约束转换为二阶锥形式。
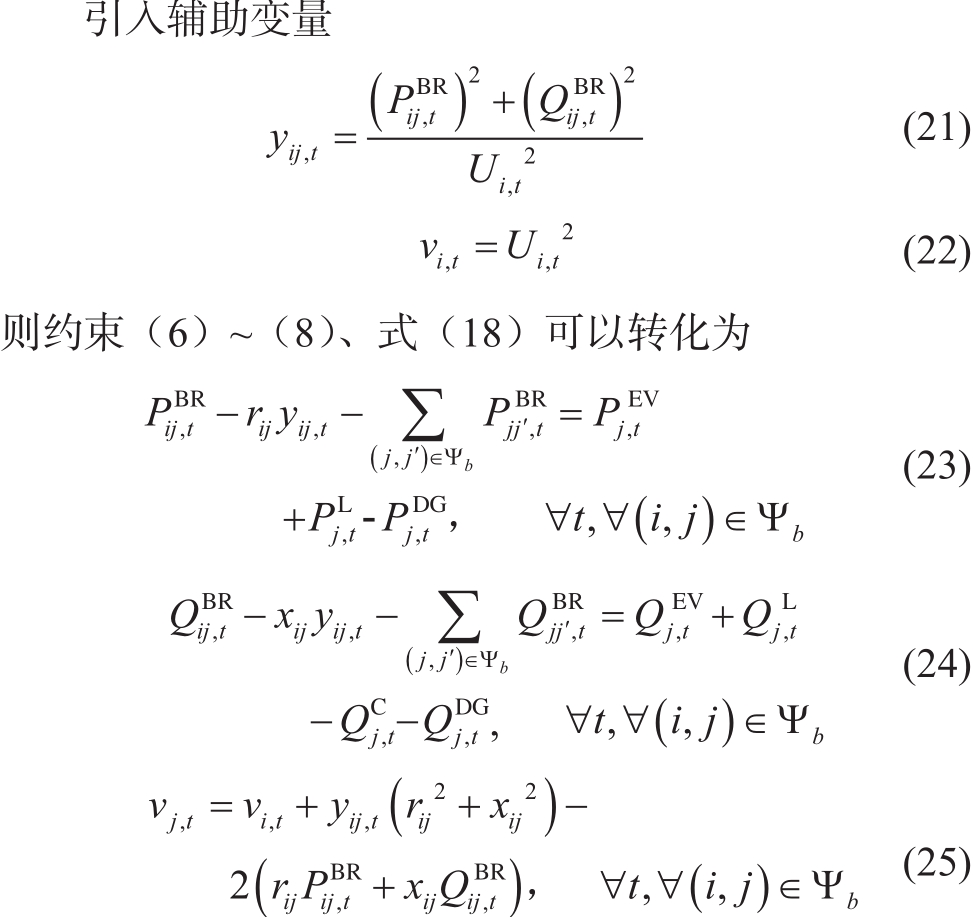

至此,本文以最小化总购电成本为目标建立了配电网日前运行优化的混合整数二阶锥规划模型。相比于此前的非线性规划,二阶锥规划模型便于求解,CPLEX[19]等商业软件均可提供求解支持。
2 日内滚动优化
通过上述日前优化可得到在分布式电源预测出力下的电动汽车最优充电策略及无功补偿装置的最优动作计划。而实际上,光伏等分布式电源的出力都具有一定的不确定性,日前预测存在偏差在所难免。因此还需要在日内针对实际情况进行调整。考虑到无功补偿装置动作具有一定时间延迟,日内的滚动优化仅针对电动汽车充电功率进行,而无功补偿装置仍采用日前优化得出的动作策略。
2.1 日内优化模型
日内滚动优化目标与日前相同,即总购电成本最小。在t0时刻,应当有
其中,ΔT为滚动优化考虑的时间长度。对于某时刻,其滚动优化时应考虑的时间长度等于当前时刻接入各节点的电动汽车的最晚离开时间与当前时间之差。
同样地,与日前相同,日内滚动优化也需要考虑充电需求、潮流约束、分布式能源出力等约束条件,但由于无功补偿策略已在日前阶段确定,日内将不考虑无功补偿约束,因而不含有整数变量。日内滚动优化的约束条件包括以下3点。
(1)充电参数约束。
各时刻各节点的已完成充电电量应不少于在此前离开车辆的充电电量需求之和
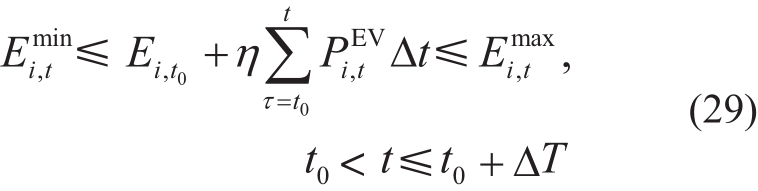
其中,Ei,t0为 t 0 时刻i节点已完成的充电电量。
除此之外,有功充电功率及网侧无功功率应当符合节点充电功率模型中的边界要求与功率因数要求,分别如式(3)、(4)及(11)所示。
(2)分布式能源出力。
分布式能源出力也应满足式(19)、式(20)所示的约束条件。
(3)潮流约束。
同样地,配电网各支路潮流及节点电压应当满足式(23)~(25)、(27)所示的二阶锥形式潮流方程,以及式(9)、(10)、(26)所示的支路潮流及节点电压上下限约束。
2.2 日内优化计算流程
日内滚动优化每隔15 min,在每个时段开始时更新一次光伏出力的实时预测信息与电动汽车车辆信息,并据此进行日内滚动优化,取当前时刻到已接入电动汽车的最晚离开时刻之间的时段作为研究对象,求解前述日内滚动优化策略得到研究时段内的电动汽车最优充电策略。计算得到的下一时段充电策略即作为下一时段的实际充电策略,在下一时段结束后再次进行数据更新并重新进行优化计算。
3 算例分析
3.1 算例参数设置
本算例采用33节点配电网系统进行分析,系统示意如图2所示。节点0为根节点,连接主网,其余32个节点均为PQ节点。假设在12、28、32号节点上配置有相同的分档投切电容器,每节点共3档,每档无功容量均为0.1 MVar。考虑到投切电容器的动作成本,每节点每天各档位动作总次数不应超过10次。在负荷较大的23、24、31号节点接入分布式光伏,每节点光伏装机容量为200 kW。
考虑到配网覆盖范围面积较小,简单起见,假设所有PQ节点处的基础负荷及光伏出力变化趋势相同,而不同节点的值仅在峰值上有差别。基础负荷选用华北地区冬季典型日负荷曲线(如图3所示),有功与无功负荷峰值分别为2836 kW与1756 kVar。光伏日前预测出力与实际出力采用华北地区典型日数据,如图4所示。
日前优化时各节点处连接的电动汽车平均数量随机产生。在区域内共有300辆电动汽车接入配电网,按照每户平均峰值时负荷4 kW且平均每户拥有一辆汽车计算,电动汽车渗透率约为42.31%。日内滚动优化时的电动汽车充电需求信息采用蒙特卡洛方法根据文献[2]中的参数抽取得到。每辆电动汽车电池容量均为32 kW·h,起始与期望荷电状态均分别为0.20与0.90,额定充电功率为7 kW,最小充电功率因数为0.95,充电效率为0.95。在日前优化中,为了对比有序充电与无序充电的效果,我们根据上面的电动汽车充电需求得到电动汽车无序充电功率,如图5所示,在无序充电情况下电动汽车一旦到达即开始充电。
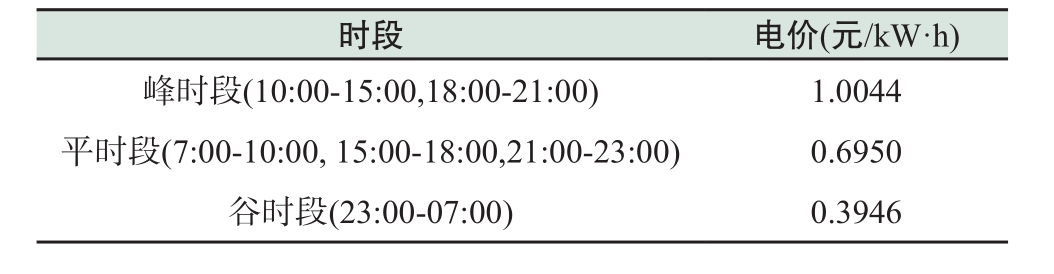
算例分析中使用的分时电价信息采用北京市非居民分时电价[20],如表1所示。
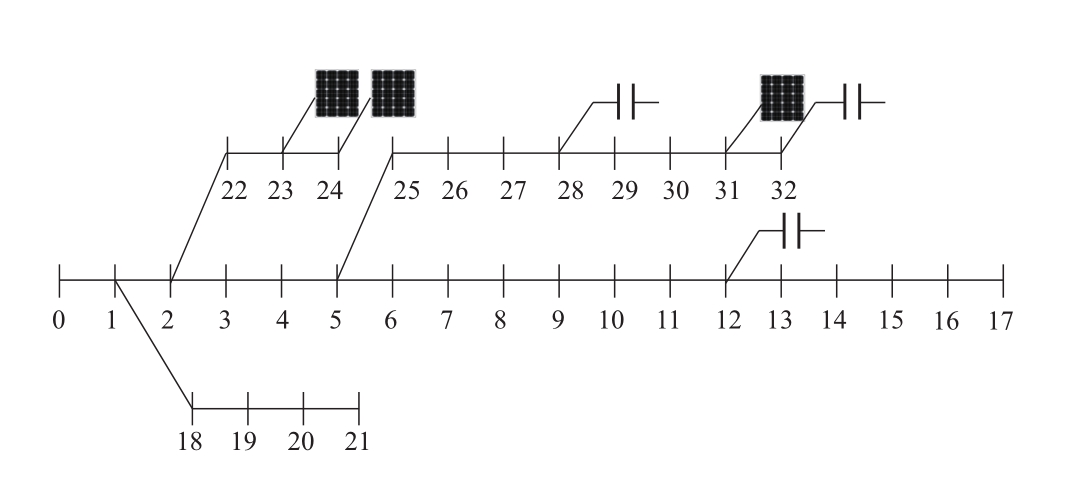
图2 33节点配电网算例系统
Fig. 2 33-bus distribution system
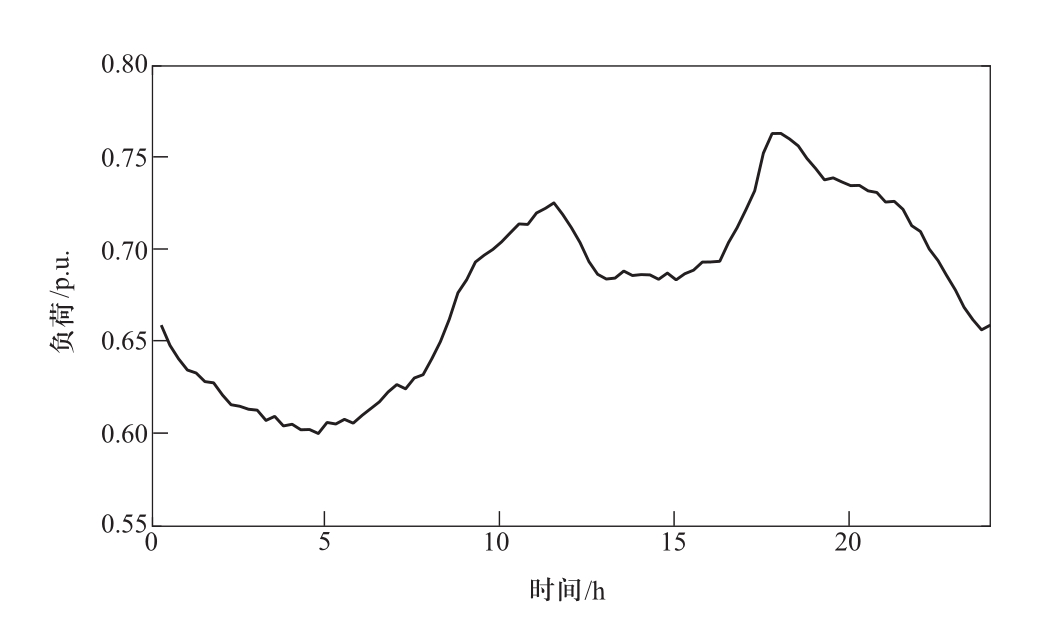
图3 系统日基础负荷曲线
Fig. 3 System daily base load profile
图4 光伏日前预测与实际出力
Fig. 4 Day-ahead predicted and actual solar power profile
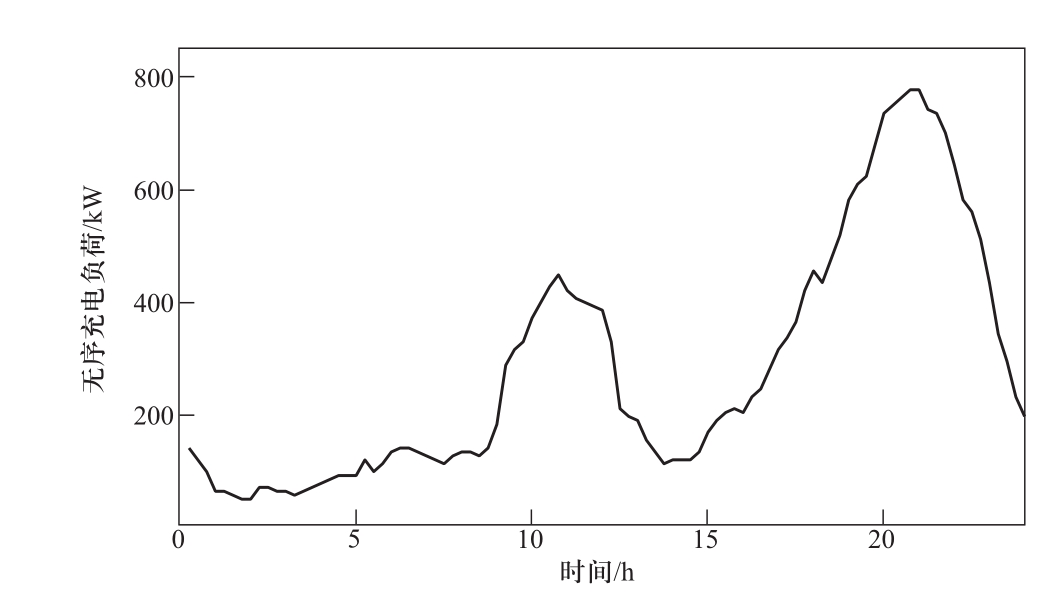
图5 电动汽车无序充电功率曲线
Fig. 5 Uncoordinated EV charging power profile
表1 分时电价参数设置
Table 1 Parameter settings of TOU electricity prices
3.2 算例结果
3.2.1 日前优化结果
图6给出了带有无功补偿的有序充电、仅有序充电、无序充电以及无电动汽车4种情况下的总有功负荷曲线。由图可见:电动汽车无序充电负荷会在峰电价时段进行集中充电,特别是晚高峰时段,不仅加重该时段电网的负荷压力,也导致总充电成本大大增加;有序充电策略可以有效实现充电负荷的转移,将峰电价时段的充电负荷转移至谷电价时段,在削减系统峰荷、减小峰谷差的同时节省了购电成本。是否引入无功补偿对于总有功负荷而言影响不大,因而两条曲线接近重合。电动汽车无序充电时总购电成本为48917.3元,其中充电成本为8560.0元,网损成本为1872.2元;而采用有序充电后,总购电成本为43586.5元,其中充电成本降为3563.0元,网损成本降为1138.8元。有序充电使得充电成本降低了58.4%,网损成本降低了39.2%。
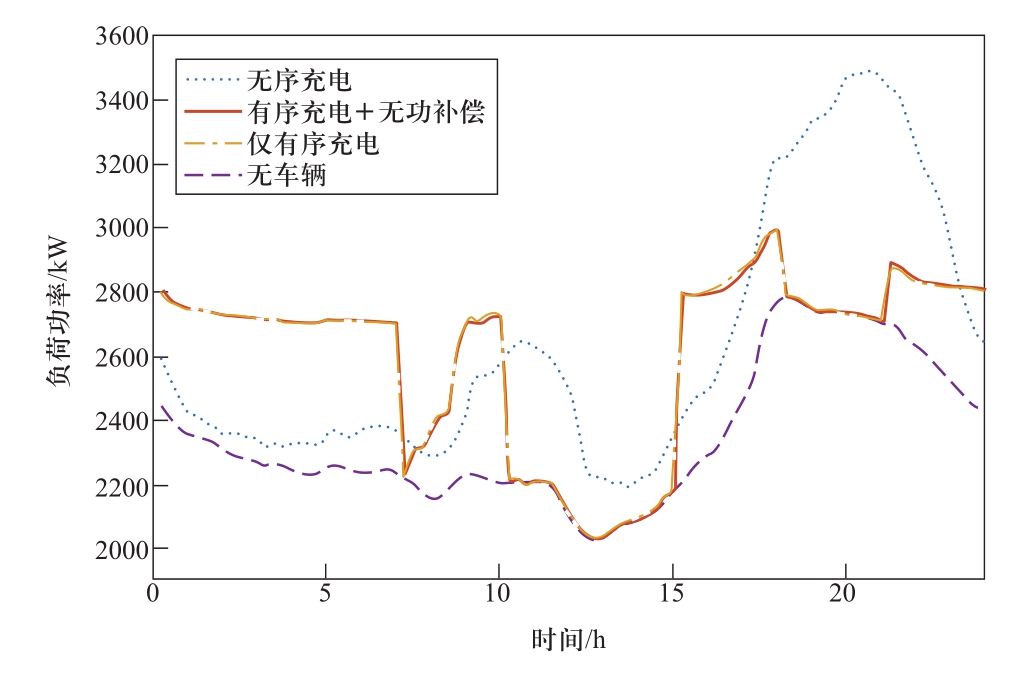
图6 不同场景的系统总有功负荷曲线
Fig. 3 Total active load power under different scenarios
图7 选取接入车辆总数最多的28号节点,给出了节点电动汽车充电功率曲线与无序充电曲线。分析后可以得知:有序充电可以减少充电峰荷,使节点充电负荷趋于平缓;充电尽可能选择在谷电价时段进行,当必须在峰电价时段进行充电时会尽可能减小不必要的充电功率。各节点处分档投切式补偿电容器的最优动作策略如图8所示。
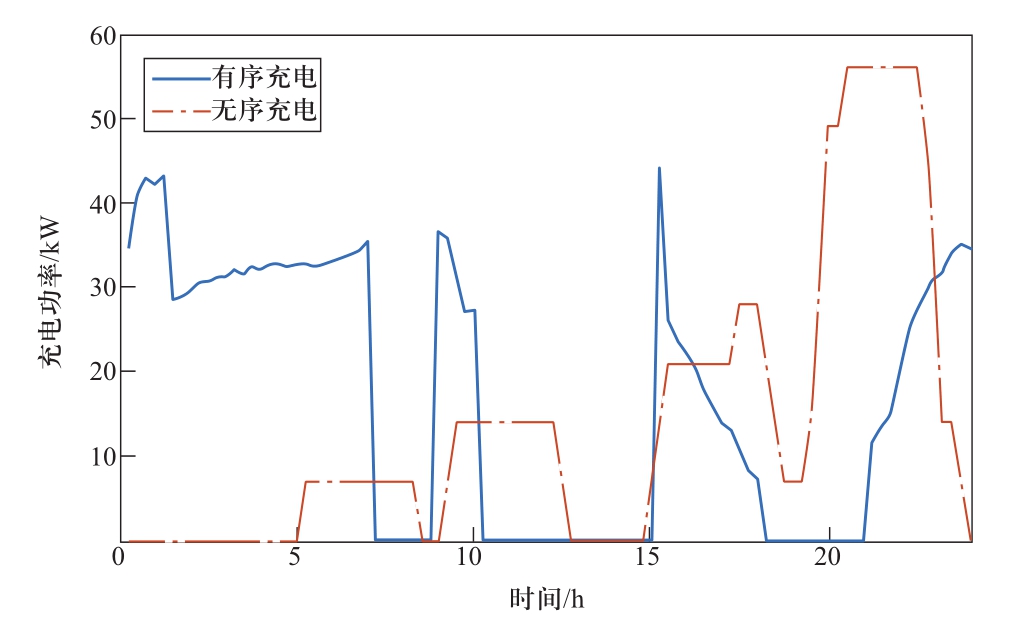
图7 节点28有序与无序充电负荷曲线
Fig. 7 Coordinated and uncoordinated EV charging power of Node 28
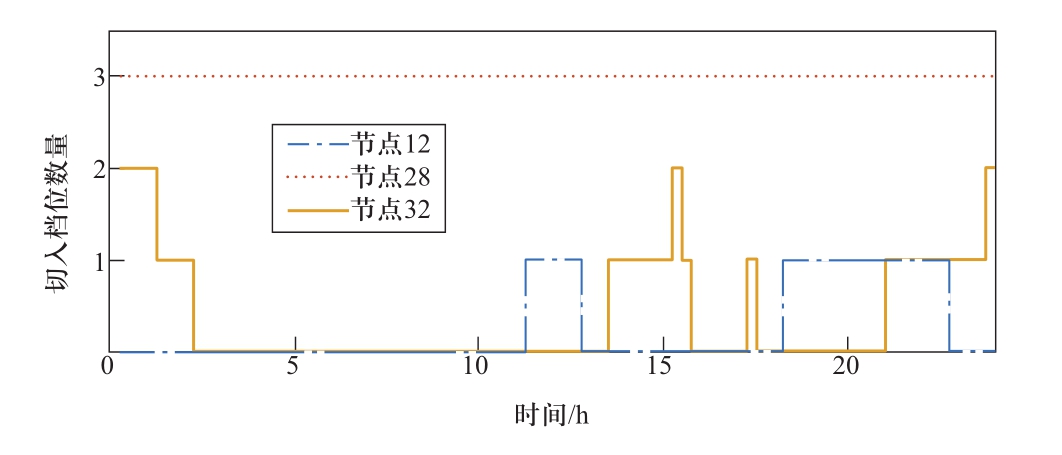
图8 补偿电容器最优动作策略
Fig. 8 Optimal action strategy of shunt capacitors
网损是配电网中需要考虑的重要指标,为此比较4种情况下的系统网损变化曲线,如图9所示。可以看到,无序的充电负荷将导致配电网网损增加,尤其是在电动汽车充电高峰时期,网损也会随之形成高峰。电动汽车有序充电可以通过平滑负荷曲线、减小系统峰谷差来降低网损;而在有序充电的基础上增加无功补偿则可进一步显著降低网损。在电动汽车渗透率为42.31%时,仅有序充电情况下配电网网损相比于无序充电情况下减少了8.87%,而引入无功补偿可进一步使网损减少21.87%。
选取距离根节点最远的17号节点进行电压水平变化情况的分析,几种情况下节点电压水平如图10所示。可以看到,电动汽车充电负荷的引入会使得配电网节点电压有所降低。在无序充电情况下,节点电压会在充电晚高峰时段出现急剧下降,电压越限可能性相对较大;而在有序充电策略下,节点电压水平将得到改善,节点电压波动得到有效抑制。在有序充电的基础上引入无功补偿则会整体提高节点电压水平,甚至可将电压幅值提高至基荷时水平以上,从而进一步增强了电网运行的安全性。
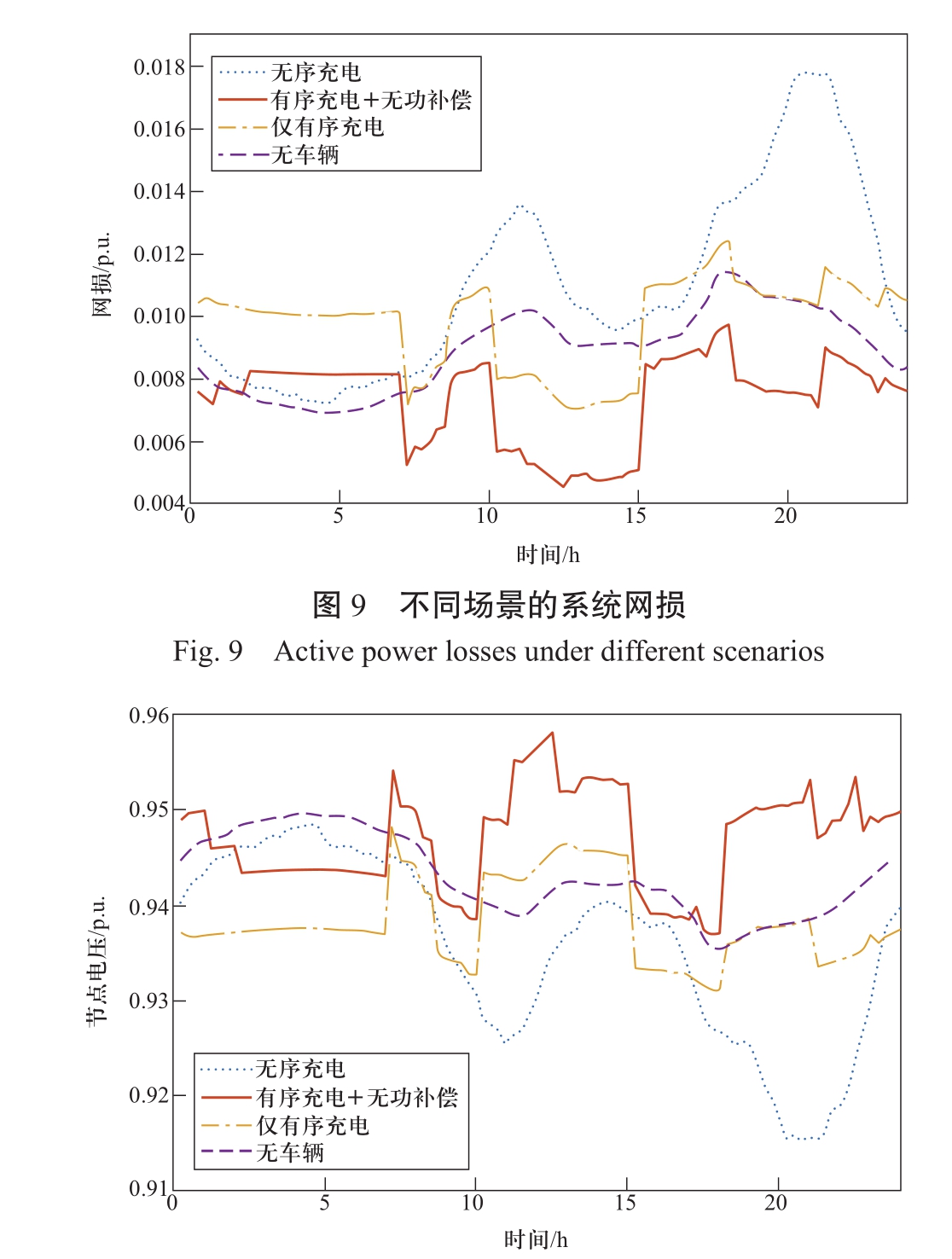
图10 不同场景下17号节点的电压变化曲线
Fig. 10 Voltage Curves of node 17 in different scenarios
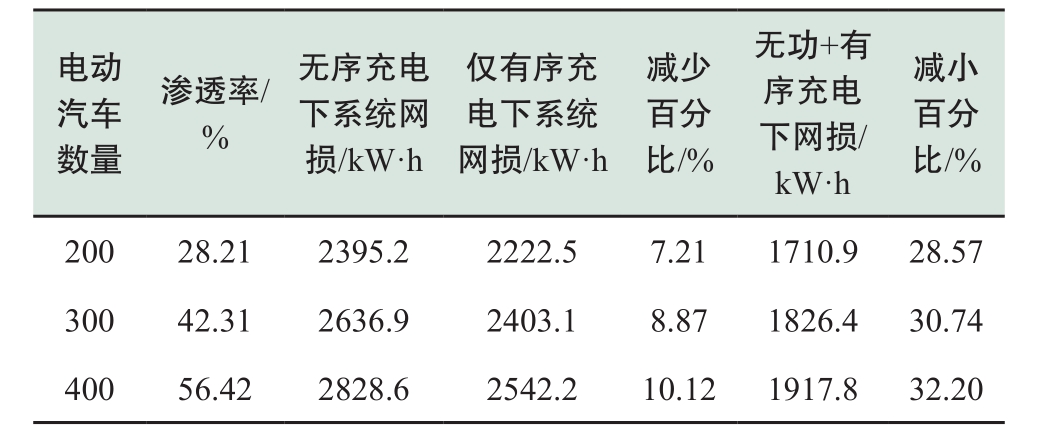
此外,为了进一步考察日前优化充电策略减少网损的效果与电动汽车数量的关系,对不同电动汽车渗透率水平下系统的网损进行了分析,结果如表2 所示。可以看到,随着电动汽车渗透率的提高,优化充电减小系统网损的比率也越来越大。当电动汽车渗透率达到56.42%时,每日可减少网损910.8 kW·h。因此随着电动汽车数量的进一步增加,上述优化充电策略将带来更加可观的经济效益。
表2 不同电动汽车渗透率下系统网损水平比较
Table 2 Power losses under different EV penetration levels
3.2.2 日内优化结果
日内优化修正后系统充电功率修正量曲线如图11所示。可以看到,在图4所示光伏出力存在负偏差的情况下,在峰电价时段光伏预测出力减少时充电负荷基本不进行调整,而是在平电价时段适当减小充电负荷,转移至谷电价时段。考虑出力预测偏差的情况下日前优化充电策略的购电成本共45432.8元,经日内修正后总购电成本降为43968.3元。
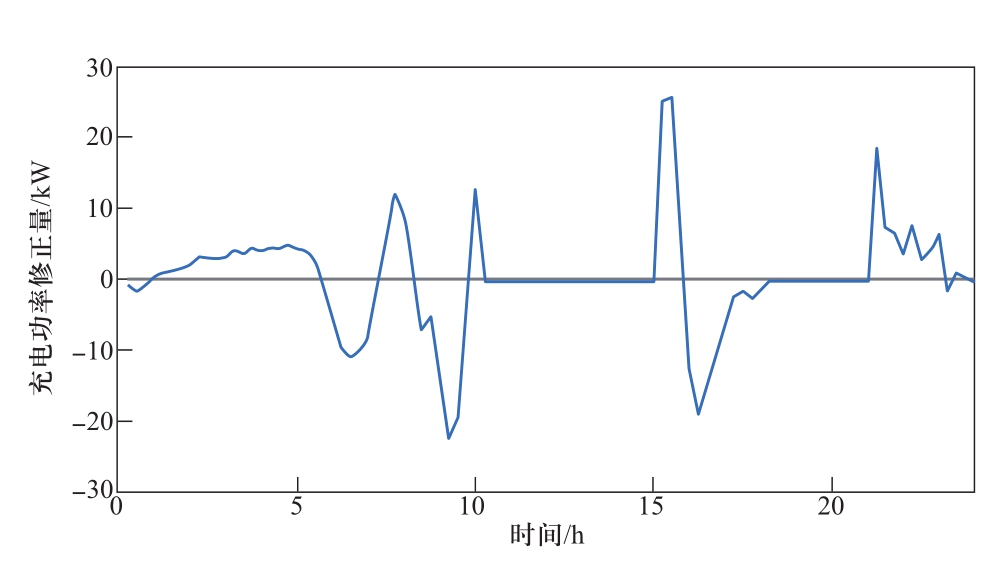
图11 日内优化充电功率修正量曲线
Fig. 11 EV Charging power corrections in intraday optimization
综上,日内滚动优化可以在实现在光伏预测出现偏差时修正电动汽车充电功率,以降低总购电成本。
4 结论
电动汽车以其灵活性为可以减小配电网负荷波动、降低运行成本提供了新的可能。本文提出了一种含电动汽车充电负荷、无功补偿装置与可再生能源的配电网两阶段优化策略,日前阶段以总购电成本最小为目标得到电动汽车最优充电策略与无功补偿装置动作策略,日内阶段以最小化购电成本为目标针对分布式能源出力偏差进行修正。通过对优化策略进行算例分析,得到如下结论。
1)以最小化购电成本为目标的电动汽车充电优化策略可以实现充电负荷向低电价时段转移,避开负荷高峰,实现削峰填谷,平抑负荷变化。
2)考虑无功补偿的电动汽车充电优化可以显著地降低配电网的网损。随着电动汽车渗透率的增长,优化充电的效果也逐渐提升。
3)电动汽车有序充电与无功补偿配合也可改善配电网节点电压,增强电网运行安全性。
在进一步的工作中,可对分布式能源出力与电动汽车充电负荷的不确定性和电动汽车反向放电(V2G)加以研究。
参考文献
[1] 张文亮,武斌,李武峰,等. 我国纯电动汽车的发展方向及能源供给模式的探讨[J]. 电网技术,2009,33(4):1-5.ZHANG Wenliang, WU Bin, LI Wufeng, et al. Discussion on development trend of battery electric vehicles in China and its energy supply mode [J]. Power System Technology, 2009,33(4):1-5(in Chinese).
[2] LUO Zhuowei, HU Zechun, SONG Yonghua, et al. Optimal coordination of plug-in electric vehicles in power grids with cost-benefit analysis—Part II: A case study in China[J]. IEEE Transactions on Power Systems, 2013, 28(4): 3556-3565.
[3] 中华人民共和国科学技术部. 科技部:中国新能源汽车全球占比一半[EB/OL]. http://www.most.gov.cn/ztzl/qgkjcxdhzkyzn/mtjj/201706/t20170607_133402.htm,2017.06.07/2017.06.29.
[4] 胡泽春,宋永华,徐智威,等. 电动汽车接入电网的影响与利用[J]. 中国电机工程学报,2012,32(4):1-10.HU Zechun, SONG Yonghua, XU Zhiwei, et al. Impacts and utilization of electric vehicles integration into power systems[J]. Proceedings of the CSEE, 2012, 32(4):1-10(in Chinese).
[5] 高赐威,张亮. 电动汽车充电对电网影响的综述[J]. 电网技术,2011,35(2):127-131.GAO Ciwei, ZHANG Liang. A survey of influence of electrics vehicle charging on power grid[J]. Power System Technology,2011, 35(2):127-131(in Chinese)
[6] 赵俊华,文福拴,杨爱民,等. 电动汽车对电力系统的影响及其调度与控制问题[J]. 电力系统自动化,2011,35(14):2-10.ZHAO Junhua, WEN Fushuan, YANG Aimin, et al. Impacts of electric vehicles on power systems as well as the associated dispatching and control problem[J]. Automation of Electric Power Systems, 2011, 35(14): 2-10(in Chinese).
[7] 李秋硕,肖湘宁,郭静,等. 电动汽车有序充电方法研究[J]. 电网技术,2012,36(12):32-38.LI Qiushuo, XIAO Xiangning, GUO Jing, et al. Research on scheme for ordered charging of electric vehicles[J]. Power System Technology, 2012, 36(12):32-38(in Chinese).
[8] 孙晓明,王玮,苏粟,等. 基于分时电价的电动汽车有序充电控制策略设计[J]. 电力系统自动化,2013,37(1):191-195.SUN Xiaoming, WANG Wei, SU Li, et al. Coordinated charging strategy for electric vehicles based on time-of-use price[J].Automation of Electric Power Systems, 2013, 37(1):191-195(in Chinese).
[9] 魏大钧,张承慧,孙波,等. 基于分时电价的电动汽车充放电多目标优化调度[J]. 电网技术,2014,38(11):2972-2977.WEI Dajun, ZHANG Chenghui, SUN Bo, et al. A time-of-use price based multi-objective optimal dispatching for charging and discharging of electric vehicles[J]. Power System Technology, 2014, 38(11):2972-2977(in Chinese).
[10] Sortomme E, Hindi M M, Macpherson S D J, et al. Coordinated Charging of Plug-In Hybrid Electric Vehicles to Minimize Distribution System Losses[J]. IEEE Transactions on Smart Grid, 2011, 2(1):198-205.
[11] 占恺峤,宋永华,胡泽春,等. 以降损为目标的电动汽车有序充电优化[J]. 中国电机工程学报,2012,32(31):11-18.ZHAN Kaiqiao, SONG Yonghua, HU Zechun, et al. Coordination of electric vehicle charging to minimize active power losses[J].Proceedings of the CSEE, 2012, 32(31):11-18(in Chinese).
[12] 王贵斌,赵俊华,文福拴,等. 配电系统中电动汽车与可再生能源的随机协同调度[J]. 电力系统自动化,2012,36(19):22-29.WANG Guibin, ZHAO Junhua, WEN Fushuan, et al. Stochastic optimizaition dispatching of plug-in hybrid electric vehicle in coordination with renewable generation in distribution systems[J]. Automation of Electric Power Systems, 2012,36(19):22-29(in Chinese).
[13] 张智晟,温令云,李国,等. 基于改进化学反应优化算法的电动汽车与可再生能源多目标协同调度[J]. 电网技术,2014,38(3):633-637.ZHANG Zhisheng, WEN Lingyun, LI Guo, et al. Multi-Objective coordinated scheduling of electric vehicles and renewable generation based on improved chemical reaction optimization algorithm[J]. Power System Technology, 2014,38(3):633-637(in Chinese).
[14] 张夏霖,杨健维,黄宇. 含电动汽车与可控负荷的光伏智能小区两阶段优化调度[J]. 电网技术,2016,40(9):2630-2637.ZHANG Xialin, YANG Jianwei, HUANG Yu. A two-stage dispatch optimization for electric vehicles and controllable load in PV intelligent community[J]. Power System Technology,2016, 40(9):2630-2637(in Chinese).
[15] GAN L, LI N, TOPCU U, et al. Exact convex relaxation of optimal power flow in radial networks[J]. IEEE Transactions on Automatic Control, 2013, 41(1):351-352.
[16] ZHENG W, WU W, ZHANG B, et al. A fully distributed reactive power optimization and control method for active distribution networks[J]. IEEE Transactions on Smart Grid, 2014,7(2):1021-1033.
[17] QIN M, CHAN K W, CHUNG C Y, et al. Optimal planning and operation of energy storage systems in radial networks for wind power integration with reserve support[J]. IET Generation,Transmission & Distribution, 2016, 10(8): 2019-2025.
[18] CUI H, LI F, FANG X, et al. Distribution network reconfiguration with aggregated electric vehicle charging strategy[C]//Power &Energy Society General Meeting, 2015 IEEE. IEEE, 2015: 1-5.
[19] IBM, “IBM ilog cplex optimazation studio 12.5”[EB/OL]. https://www.ibm.com/support/knowledgecenter/SSSA5P_12.6.3/ilog.odms.studio.help/Optimization_Studio/topics/COS_home.html, 2016.06.01/2017.06.29.
[20] 北京市发展和改革委员会. 北京市非居民峰谷分时销售电价表[EB/OL]. http://www.bjpc.gov.cn/cxfw/jgsfcx/jzjg/201208/t9779303.html, 2016.01.05/2017.07.05.
Two-stage Optimization of Distributed Network Operation Strategy with Electric Vehicle and Distributed Energy
DUAN Xiao-yu, HU Ze-chun, SONG Yong-hua, CHEN Hui-miao
(Department of Electrical Engineering, Tsinghua University, Haidian District, Beijing 100084, China)
Abstract: Coordinated charging of electric vehicles (EVs)can mitigate the load fluctuation of distributed network and decrease the operation cost. In this paper, based on the nodal charging load model, a two-stage optimization model of optimal operation strategy of distributed network containing electric vehicles, distributed energy and reactive power compensation is proposed. In day-ahead stage, a mixed integer second-order cone programming (MI-SOCP) model is formulated to minimize the total electricity purchase costs while considering distribution network security constraints. The rolling horizon optimization model is established in intraday stage to obtain the real-time charging strategy for the minimum electricity purchase costs as well. The case study results of a typical 33-bus system show that coordinated charging of EVs can effectively decrease the electricity purchase costs, and also reduce the active power losses and improve the nodal voltage profiles, which verifies the rationality and effectiveness of the proposed method.
Key words: electric vehicle; distributed generation; reactive power compensation; second-order cone programming; twostage optimization
Project Supported by National Natural Science Foundation of China (51477082) and National Basic Research Program of China(973 Program, 2013CB228202).
作者简介:

段小宇
段小宇(1994),男,博士研究生,主要从事智能电网、电动汽车、电力系统优化规划与运行等相关技术研究工作。
胡泽春(1979),男,博士,副教授,主要从事智能电网、电动汽车、储能应用、电力系统优化规划与运行等相关技术研究工作,E-mail:zechhu@tsinghua.edu.cn。
宋永华(1964),男,博士,教授,英国皇家工程院院士,主要从事智能电网和电力市场等相关技术研究工作。
陈慧妙(1993),男,硕士研究生,主要从事智能电网及电动汽车接入电网等相关技术研究工作。
(责任编辑 张鹏)
