0 引言
电力系统网架规模的扩大及运行方式的多样化,使电网运行控制的复杂性日益增加。近年来,对一系列重大停电事故的研究分析表明,依据系统的运行状态,及时准确地采取相应的控制措施,能有效提高电力系统抵御风险的能力[1-3]。
主动解列是电网安全稳定控制的重要手段,其依据系统实时运行状态和全局信息确定合理的解列断面,将系统分割成若干同步运行的子系统,能有效避免事故蔓延引发的大面积停电事故。选取最优的解列断面是主动解列的核心问题,主要从慢同调理论、图论以及智能算法三个方面展开研究[4-5]。
基于慢同调理论的方法,依据电力系统模式模态信息得到系统弱连接割集,并在考虑系统拓扑结构和功率平衡的基础上进行慢同调区域划分[6-7]。该方法能在不破坏各区域内部慢同调特性的基础上尽量维持各区域内功率平衡,但计算复杂度较高。为降低计算复杂度,有序二叉决策树[8]等方法从图论角度研究解列断面搜索取得了较好的成果,该类方法将电力系统视作带权图,将断面的搜索转化为在电力系统带权图中求取满足一定约束条件的割集[9]。为进一步突破复杂度的限制,文献[10-12]通过对搜索空间进行简化,进而确定最优的解列断面,但在网络化简时可能会丢失最优解。文献[13]则提出了一种适用于大规模电力系统,在发电机分群复杂的条件下快速确定解列断面的方法。针对上述研究发电机分群和断面搜索两阶段割裂的问题,文献[14]提出了同时计及发电机分群和孤岛功率平衡,更加灵活的单步方法。随着智能算法的发展,谱聚类[15-16]、蚁群[17-18]、粒子群[19]等智能算法被引入解列断面的搜索当中,通过建立相应的约束条件及目标函数模型求取最优的断面。文献[20]进一步将解列断面搜索转化为基于凸优化理论的求解过程,其与蚁群等智能算法相比具备更高的稳定性。
上述方法在最优解列断面选取方面取得了一定成果,但均是以最小不平衡功率或最小潮流冲击(被断开线路的有功潮流)为目标的单目标优化过程。随着新能源发电及直流输电的快速发展,新能源机组对电网的弱适应性及对调频的不利影响、直流对受端电网无功电压支撑能力的依赖性等问题,对电力系统的解列控制提出了更高要求。解列后的子系统必须具备更强的频率及电压支撑能力,从而有利于子系统的稳定运行和后续恢复。传统方法仅依据不平衡功率或潮流冲击选取解列断面,未能充分考虑上述因素给电网频率及电压稳定问题带来的不利影响及要求。
为应对电力系统特性的重要变化,少数研究对传统主动解列策略进行了改进。文献[21-22]提出了考虑柔性直流落点的断面搜索方法,通过使解列后子系统经柔直互联,从而减小了解列后的切机、切负荷量。文献[23]考虑线路传输的无功功率求取解列断面,但优先考虑的仍然是有功平衡问题。为同时考虑实际电网中的复杂因素,文献[24]提出了包含多种指标的交直流电网解列指标体系,但该方法依据权重以兼顾多种因素,指标权重的变化对断面搜索结果有重要影响。文献[25]考虑了系统惯性变化对发电机分群的影响,但解列断面的搜索仍然是基于最小潮流冲击。
针对上述问题,本文依据当前电网主动解列的原则,提出了考虑风电或直流输电等多因素的主动解列断面搜索方法,分别以风电并网的频率稳定问题及直流落点的电压支撑问题为例进行了仿真分析。仿真结果表明,该方法能有效提高解列后子系统稳定运行的能力,有利于孤岛的稳定控制及后续恢复。
1 主动解列的原则
主动解列的实质是依据电力系统的实时运行状态信息,以解列后系统的稳定性为目标,选取最优的解列断面,将系统分割成若干同步运行的子系统[5]。解列断面搜索则是在确定的约束条件基础上,依据相应的优化目标,在可选的解列断面集合中选取最优的解列断面,如图1所示,图中实心圆点代表发电机,空心圆点代表一般节点。
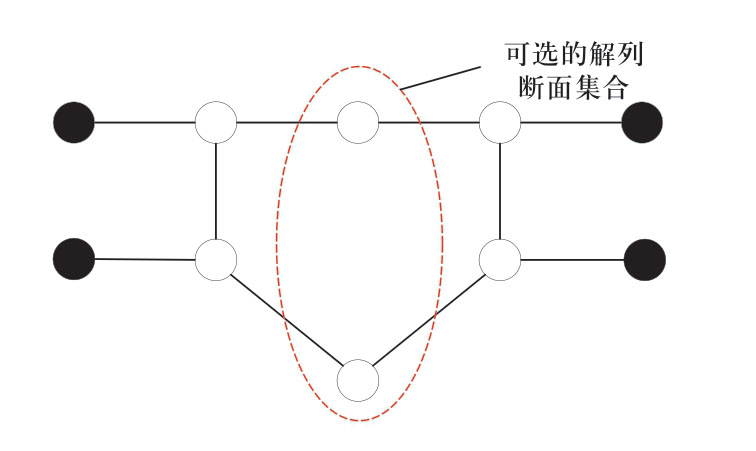
图1 可选的解列断面集合
Fig.1 Candidate resolution space of controlled islanding
由解列的实质可知,为提高解列后子系统稳定运行能力,利于后续稳定控制及恢复,解列断面的选取必须考虑以下稳定问题。
1)暂态稳定。基于实际电网的仿真研究表明,解列后同调性较差的子网可能会发生相继失稳[26],因此应避免解列操作对系统造成较大的暂态冲击。
2)频率稳定。解列后各子系统频率稳定性应较强,尤其对于风电并网区域,在受到功率扰动时,系统频率的波动应尽量小。
3)电压稳定。解列后子系统应具备较强的电压稳定性,尤其对于直流落点区域,为保证解列后直流的正常运行,交流系统应具备较好的无功电压支撑能力。
计及上述多方面问题,本文首先基于现有研究以潮流冲击表征解列对系统暂态稳定的影响,即以最小潮流冲击为目标搜索初始解列断面;然后从其邻域中寻找能提升解列后孤岛频率、电压稳定性的解作为最终的解列断面。从而在保证暂态稳定的基础上,提升解列后子系统稳定运行的能力。
2 计及多目标的解列策略
2.1 初始解列断面
基于图论方法求解初始解列断面,将电力系统视为带权无向图,边权值的计算如式(1)所示:

式中:Wij表示带权图边权值;Pij表示节点i、j联络线上输送功率的大小。
相关研究表明:以最小不平衡功率为目标尽可能地保证了解列后各区域内发电机出力与负荷需求的平衡,减少后续的切机、切负荷操作;最小潮流冲击则能有效减小潮流转移,降低解列操作对系统的冲击,有利于维持系统的暂态稳定性[5,27]。
因此本文以最小潮流冲击为目标,将解列断面的搜索转化为在电力系统带权图中求取满足一定约束条件的最小割,具体目标函数如式(2)所示:
式中,节点i、j分别属于区域V1、V2。其相应的约束条件如下所述。
1)机组同调性约束。当系统受到严重扰动引起发电机群失步,导致系统失稳需实施解列时,为保证解列后各局部电网的安全稳定运行,同调的发电机组必须处于同一区域,且非同调机组不能落在相同区域内:
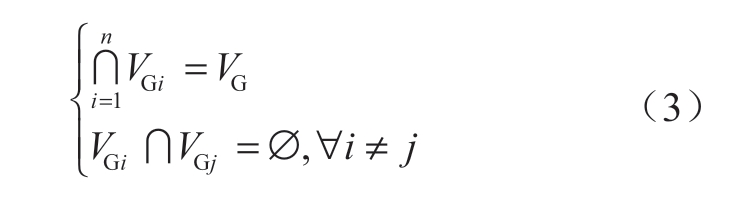
式中:VG表示发电机节点集合;n表示发电机分群数目。
2)节点连通性约束。为避免解列后出现孤立节点,同调机群中任意两台发电机之间应至少存在1条通路,且任意负荷节点应至少与1台发电机存在通路:

式中:VG、VL分别表示发电机节点和负荷节点;yij表示节点i、j间的连通路径。
最大流算法是图论中求取最小割的成熟方法,具有计算复杂度小、速度快的优势[28]。在电力系统带权无向图中,将两同调机群构成的子图分别视作等值源点和汇点,基于最大流算法可快速得到满足同调约束的最小割。因此本文采用该算法求取具有最小潮流冲击的解列断面。
2.2 初始解的邻域搜索空间
采用2.1节方法得到的解列断面仅以最小潮流冲击为目标,主要考虑的是系统暂态稳定问题,却忽略了解列后各子系统稳定运行特性,随着风电并网和直流投运这一问题更加不容忽视。为提升孤岛稳定运行能力、利于后续恢复,本文以该断面为初始解列断面,基于启发式变邻域搜索算法[10]调整最终的解列断面。
首先确定初始解的邻域搜索空间。定义与断面节点通过一条线路直接相连的节点为第1度节点,与第1度节点通过一条线路直接相连的节点为第2度节点。如图2所示,若初始断面为(A1-B1, A2-B2),则B3、B4为第1度节点,B5、B6、B7为第2度节点。若将线路A1-B1由邻近的B1-B3代替,可形成新的解列断面(A2-B2,B1-B3),以此类推,并依据2.1节所述约束条件去除不可行解,即可得到第1、2度节点构成的初始断面的邻域搜索空间。
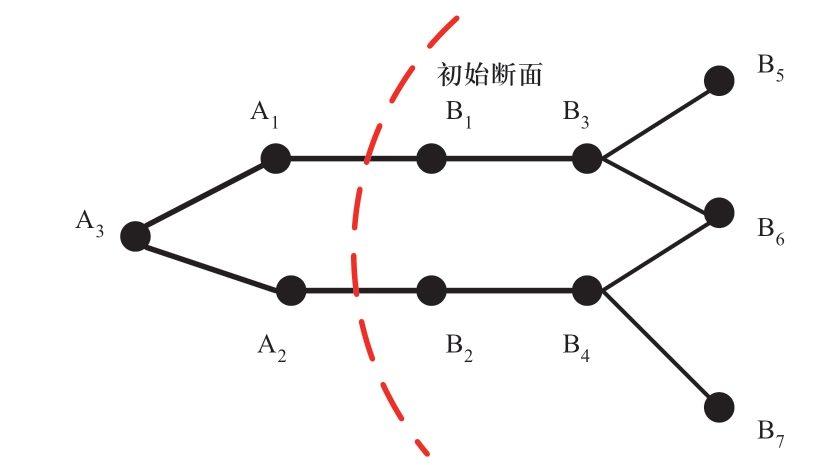
图2 邻域搜索空间
Fig.2 Neighborhood search space
2.3 最终的解列断面
在初始解列断面的邻域可行解集中,本文将潮流冲击偏差在20%之内视作与初始解列断面具有相近的潮流冲击。为计及风电和直流的影响、提升解列后孤岛稳定运行能力,则分别从以下角度考虑解列后子系统的频率稳定和电压稳定问题。
2.3.1 考虑风电渗透率的频率稳定
传统火力发电机的转速与系统频率耦合,当系统功率平衡受扰时,发电机电磁转矩变化以阻尼频率波动,发电机惯性时间常数越大,则系统受扰后频率越稳定。目前广泛使用的双馈风力发电机组,为实现最大功率点跟踪从而获得最大风能利用效率,其转速与系统频率解耦并依据风速变化实时调整。因此,风电机组与传统火电机组相比,不具备应对系统频率波动的惯性响应和调频能力,风电的并网相当于减小了系统整体的惯性时间常数,削弱了系统的频率稳定性[29]。
通常用风电渗透率来衡量系统对风电的消纳情况,其定义为风机容量占最大负荷的百分比,如式(5)所示[30]:
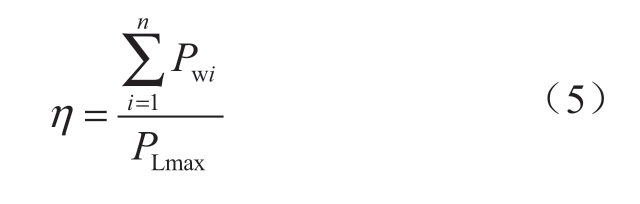
式中:η表示风电装机渗透率;PLmax表示系统最大负荷;Pw表示风机容量;n表示风机台数。
由上述分析可知,随着风电渗透率的增加,系统惯性响应能力逐渐减弱,受扰后的频率稳定性逐渐变差。而在风电并网系统,解列后风电的消纳将由原来的全网承担转变为局部电网消纳,进一步削弱了解列后子系统的频率调节能力。因此为保障解列后含风电子系统的频率稳定性,本文在火电机组有功备用充足的条件下,选取最终解列断面时使风电区域适当消纳更多负荷,提升火电机组出力,从而降低风电渗透率,提高子系统独立运行时的频率稳定性,如式(6)所示:
式中:PLN表示风电区域消纳的负荷;PL0表示初始解列断面条件下消纳的负荷;PGmax表示火电机组可用备用容量。
2.3.2 考虑多馈入短路比的电压稳定
在多馈入直流系统当中,解列后的子系统不可避免地包含直流落点,此时若仍然仅以线路交换功率为依据选取解列断面,可能会出现解列后多回直流落点于同一区域的极端情形,若孤岛对直流落点的支撑能力不足,则将不利于直流正常稳定运行。
通常用交直流系统容量的相对大小,即短路比指标衡量交直流系统间的相互作用强弱。对于多馈入直流系统,定义了多馈入短路比(multi-infeed short circuit ratio, MSCR),其近似表达式如式(7)所示[31]:

式中:Saci表示第i回直流换流母线短路容量;Pdeqi表示考虑其他直流影响后的第i回直流等值功率;Pdi、Pdj分别为第i、j回直流额定功率;Zij表示节点i、j的互阻抗;Zii表示节点i的自阻抗。
相关研究基于系统模型推导证明了MSCR具备衡量多馈入直流系统电压稳定性的基础,其在一定程度上反映了电网结构强度以及受端交流系统对直流落点的电压支撑能力。还通过仿真分析进一步指出,MSCR与直流系统换相失败情况关联密切,其值越大,交流系统电压支撑能力越强,则越有利于降低换相失败风险[32]。
因此,对于解列后子系统存在直流的情况,为保障解列后直流的正常运行,降低直流换相失败概率,减小对系统稳定运行的威胁,本文在选取最终解列断面时考虑使解列后子系统内各回直流具备较大的MSCR,如式(8)所示:
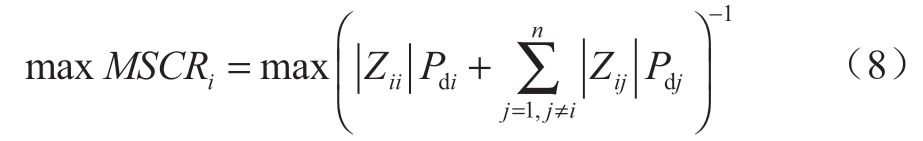
式中:MSCRi表示任一回直流多馈入短路比;Pdi、Pdj分别为第i、j回直流额定功率;Zij表示节点i、j的互阻抗;Zii表示节点i的自阻抗。
由式(7)可知,当直流功率保持不变时,MSCR仅与系统等值阻抗矩阵中直流落点的自阻抗和互阻抗有关。因此,为实现对MSCR的快速校验,本文基于支路追加法计算变化后的节点阻抗[33]。开断一条线路相当于追加一条阻抗为负的支路,而从已有的节点i接上阻抗为ziq的支路引出新节点q,则原p阶阻抗矩阵中对应网络原有部分的全部元素保持不变,新增元素如式(9)所示:
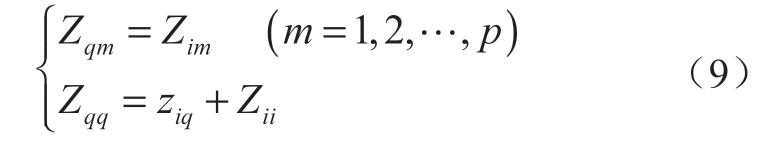
式中:Zqq、Zqm分别表示新增节点的自阻抗和互阻抗;Zii表示节点i的自阻抗;m表示原p阶矩阵对应网络的各节点。
2.4 解列策略流程
根据前文提出的提高解列后孤岛稳定特性、便于后续稳定控制和恢复的主动解列策略,图3描述了考虑风电或直流的解列策略流程,其主要步骤如下所述。
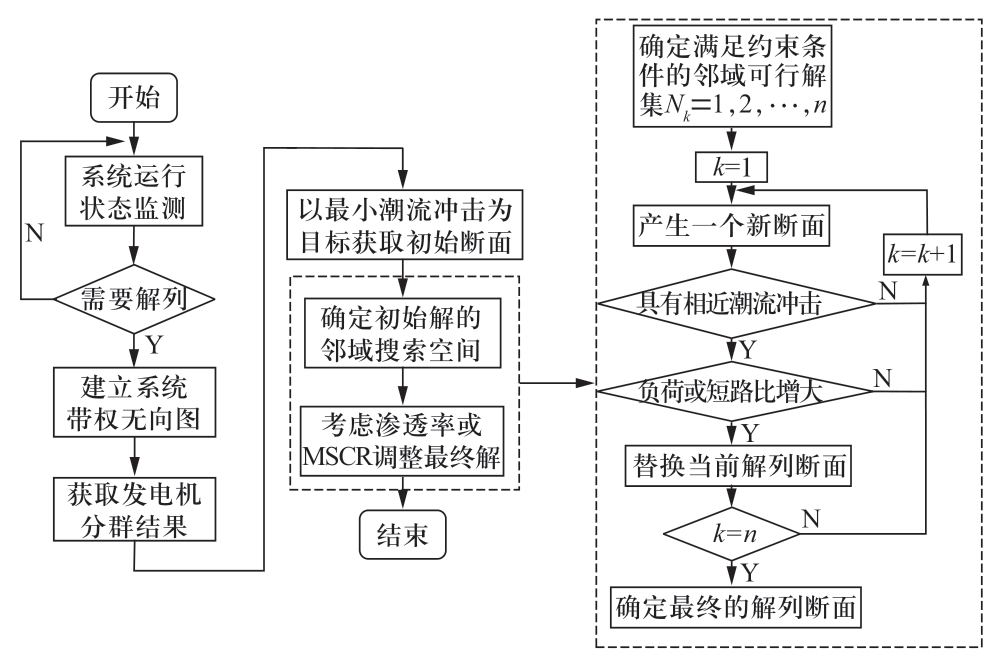
图3 解列策略流程
Fig.3 Flowchart of islanding strategy
1)根据故障前运行状态信息,以线路传输功率为边权值建立系统的带权无向图。
2)基于发电机同调性约束和节点连通性约束,以最小潮流冲击为目标搜索带权图的最小割,得到初始解列断面。
3)确定与断面节点相连的第1、2度节点,得到初始解列断面的邻域搜索空间。
4)从邻域可行解集中搜索具有与初始解列断面相近潮流冲击的且满足式(6)或式(8)的解列断面。
3 仿真分析
3.1 风电算例
使用中国电科院开发的PSD-BPA仿真系统,在新英格兰10机39节点系统中,将发电机30、37替换成具有相同出力的双馈风力发电机组成的风电场。假设故障使系统失稳,发电机分为两群,其中33~36、38为超前群。以最小潮流冲击为目标,可得到初始解列断面如图4方案1所示。此解列方案下,含风电的左侧区域风电渗透率为27%。
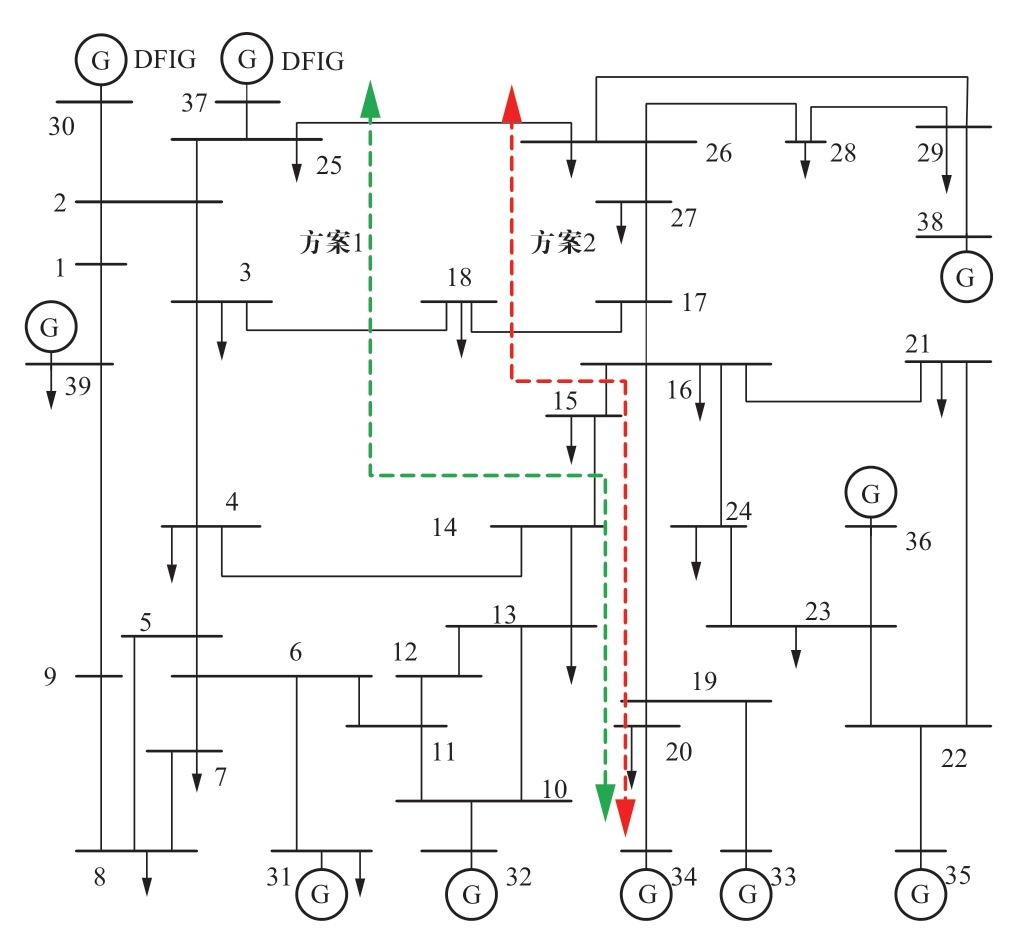
图4 考虑风电渗透率前后的解列策略
Fig.4 Islanding strategies before/after considering penetration of wind
确定初始解的邻域搜索空间如表1所示,由于发电机分群约束,此处仅考虑第1度节点空间。
在火电机组有功备用充足的条件下,根据同调性及连通性约束条件,从邻域可行解集中,基于式(6)选取如图4中方案2作为最终的解列断面。此时负荷节点15、18均纳入左侧区域,风电渗透率由27%下降至23%。
表1 邻域搜索空间
Table 1 Neighborhood search space

为对比不同解列方案下解列后孤岛的频率稳定性,在含风电的左侧子系统中,设置相同的功率扰动—发电机32切机400 MW,系统最低节点频率曲线分别如图5、图6所示。由其最低节点频率曲线可知,仅考虑潮流冲击解列后的子系统正常运行时的频率稳定性较差,在该功率扰动下系统的最低节点频率跌至49.42 Hz,而依据本文所提考虑风电渗透率的解列策略,在相同功率扰动下,系统的最低节点频率由49.42 Hz提升至49.55 Hz。

图5 方案1下频率仿真曲线
Fig.5 Frequency simulation curve of strategy 1
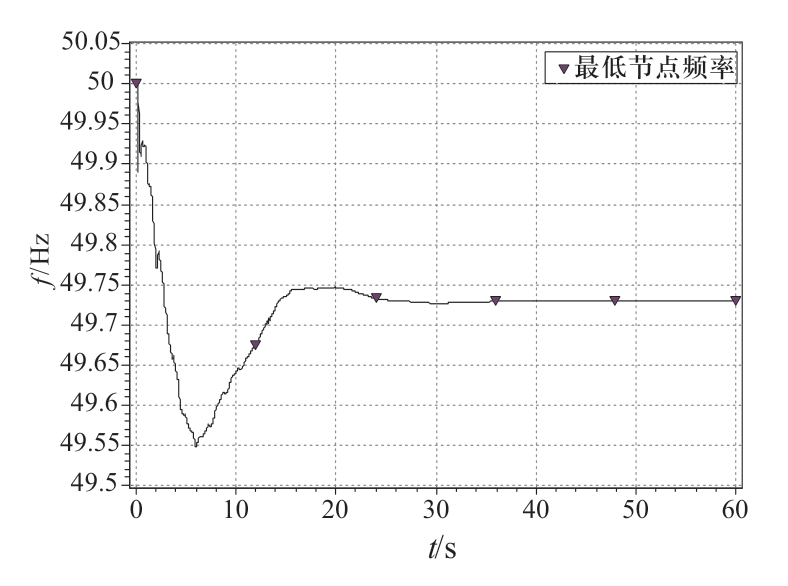
图6 方案2下频率仿真曲线
Fig.6 Frequency simulation curve of strategy 2
3.2 直流算例
使用中国电科院开发的PSD-BPA仿真系统,在10机39节点系统中馈入两回直流,直流落点分别为节点15和节点18,馈入功率分别为1000 MW和800 MW,如图7所示。
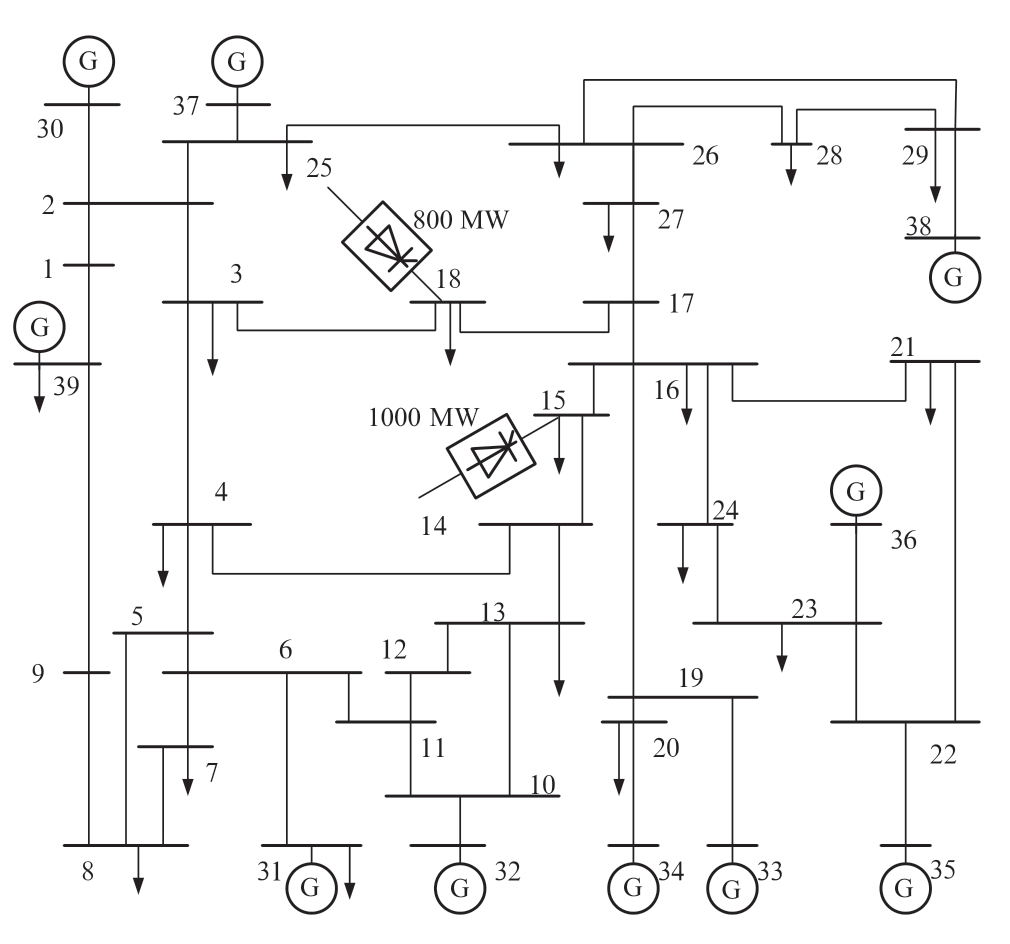
图7 10机39节点系统
Fig.7 10-generators 39-bus system
假设故障使系统失稳,发电机33~36、38为超前群。以最小潮流冲击为目标得到初始解列断面如图8方案1所示。若采取该解列方案后,则直流落点将全部划入右侧区域。采用本文所提策略,从其邻域可行解集中确定如图8方案2所示解列断面作为最终解。
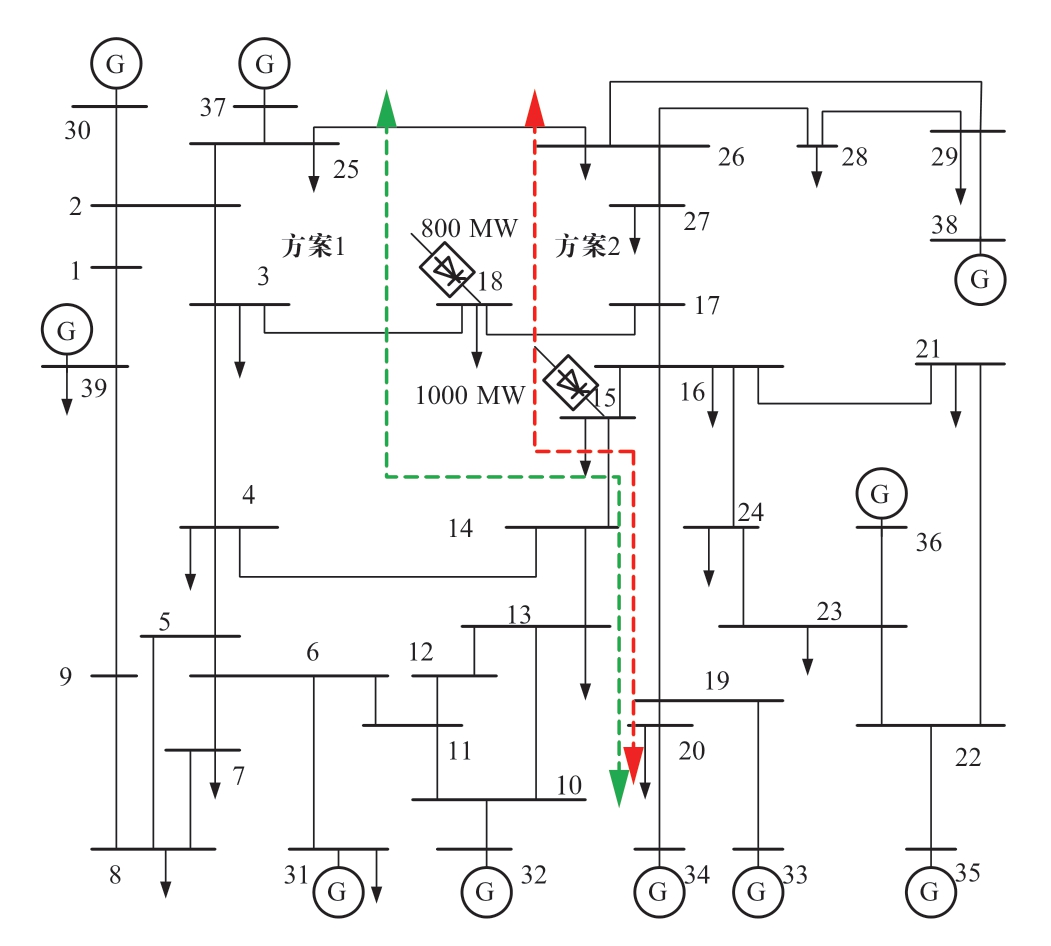
图8 考虑MSCR前后的解列策略
Fig.8 Islanding strategies before/after considering MSCR
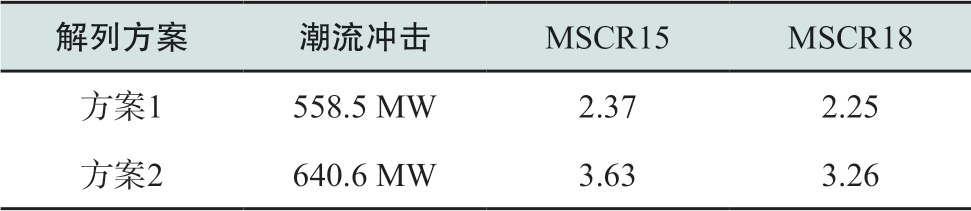
表2对比了不同解列方案下潮流冲击及多馈入短路比等指标的差异。以潮流冲击为目标得到的初始解列断面必然具有最小的潮流冲击558.5 MW,但两回直流均落点于弱交流系统。而考虑MSCR后与原解列方案相比,尽管有稍大的潮流冲击640.6 MW,但MSCR明显提高,两回直流均落点于强系统,有效提高了直流落点孤岛的运行稳定性。
表2 解列方案对比
Table 2 Comparison of islanding strategies
为对比两种解列方案下解列后系统的电压稳定性,在子系统中设置相同故障—母线26三相短路,15周波后故障消失,直流换流母线电压及熄弧角仿真曲线分别如图9、图10所示。由图9可知,依据初始解列断面,系统解列后两回直流落点于同一区域导致MSCR较小,受端交流系统对于直流落点的电压支撑能力较弱,在该故障下电压失去稳定。采取考虑MSCR的解列策略后,如图10所示,解列后的子系统正常运行时对直流落点的电压支撑能力较强,在相同故障扰动下避免了直流出现连续换相失败。
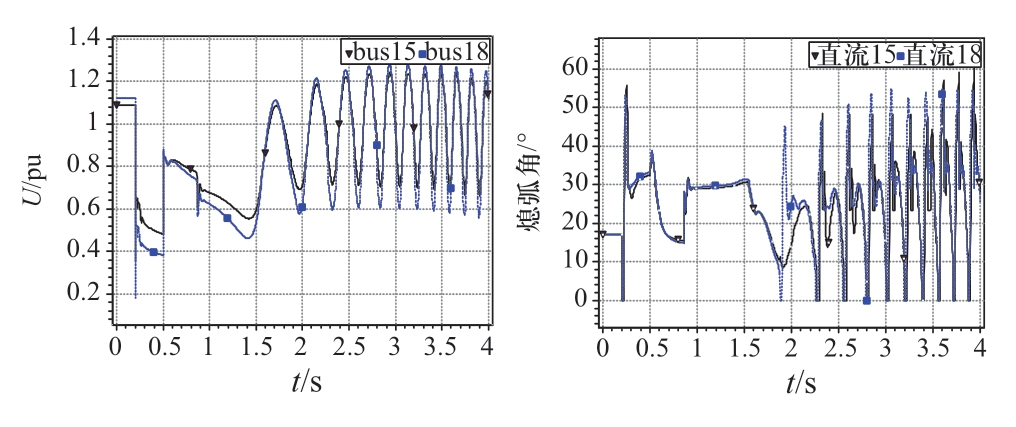
图9 方案1下仿真曲线
Fig.9 Simulation curves of strategy 1
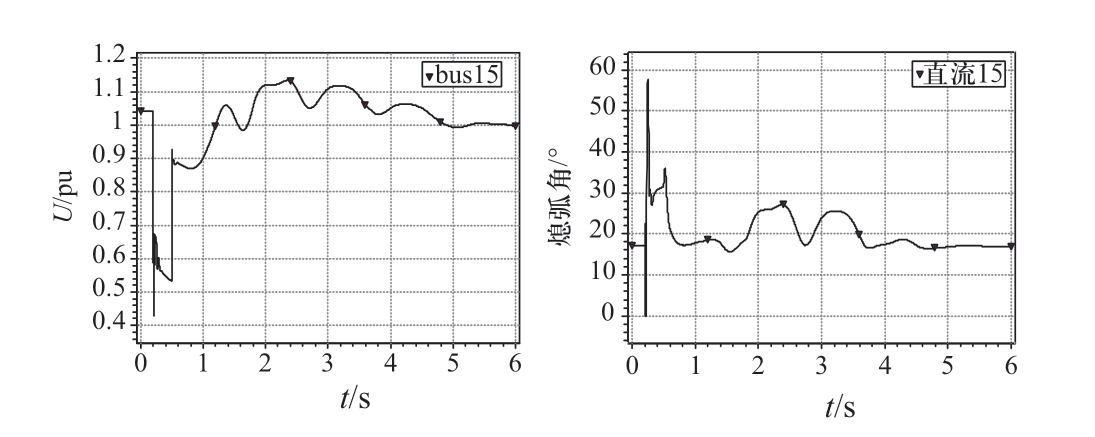
图10 方案2下仿真曲线
Fig.10 Simulation curves of strategy 2
3.3 讨论
由以上仿真结果可知,依据不同的解列方案解列后子系统稳定性差异较大。在火电机组备用充足的条件下,适当消纳负荷提升火电出力、降低风电渗透率,能有效提高系统运行的频率稳定性;而在直流落点区域考虑多馈入短路比选取解列断面,则有助于提升解列后子系统对直流的电压支撑能力。
对于大电网,在可选的方案内可能具有多个潮流交换差异不大的断面,此时依据影响系统稳定特性的其他因素选取最终的解列断面,对于提高解列后子系统的正常运行能力、利于后续稳定控制及恢复具有重要的意义。在实际应用当中,应当综合考虑暂态稳定、解列后系统频率和电压等多方面稳定特性,选取适应实际情况的最优解列断面。但由于现有研究未能明确潮流冲击指标与系统暂态稳定特性的联系,缺乏具体的暂态稳定裕度量化评价方法,且多目标问题的难点在于如何在多因素中取得平衡,本文暂时只分别单独考虑了风电或直流的情况,因此建立完善的同时计及多因素的解列断面搜索方法仍待进一步研究。
4 结语
在大量直流输电、新能源投运后,作为电力系统紧急控制手段之一的主动解列技术面临新问题和更高要求,即解列断面的选取应充分考虑解列后系统的频率、电压等多方面稳定问题。本文以解列后系统消纳风电的频率稳定及直流落点的电压支撑问题为例,提出了考虑解列后子系统渗透率、多馈入短路比等因素的主动解列策略。仿真分析表明,该方法以损失较小的潮流冲击指标为代价,能有效提高解列后孤岛运行时的频率稳定性和电压支撑能力,利于系统后续恢复。本文由此进一步指出,明确解列对系统暂态稳定的影响机理,建立完善的计及多因素的断面搜索模型是将来研究工作的重点。
参考文献
[1]汤涌,卜广全,易俊.印度“7.30”、“7.31”大停电事故分析及启示[J].中国电机工程学报,2012,32(25):167-174.Tang Yong, Bu Guangquan, Yi Jun.Analysis and lessons of the blackout in Indian power grid on July 30 and 31,2012[J].Proceedings of the CSEE, 2012, 32(25): 167-174(in Chinese).
[2]易俊,卜广全,郭强,等.巴西“3·21”大停电事故分析及对中国电网的启示[J].电力系统自动化,2019,43(2):1-9.Yi Jun, Bu Guangquan, Guo Qiang, et al.Analysis on blackout in Brazilian power grid on March 21, 2018 and its enlightenment to power grid in China[J].Automation of Electric Power Systems, 2019, 43(2): 1-9(in Chinese).
[3]Bo Zhiqian, Lin Xiangning, Wang Qingping, et al.Developments of power system protection and control[J].Protection and Control of Modern Power Systems, 2016, 1(1): 1-8.
[4]刘福锁,方勇杰,吴雪莲,等.基于相位角的失步解列判据在复杂场景下的适应性及对策[J].电力系统自动化,2015,39(16):71-75.Liu Fusuo, Fang Yongjie, Wu Xuelian, et al.Adaptability and countermeasures of splitting criterion based on phase angle in complex scenarios[J].Automation of Electric Power Systems, 2015, 39(16): 71-75(in Chinese).
[5]方勇杰,刘福锁,李碧君.关于大电网失步解列控制研究的综述[J].中国电机工程学报,2017,37(18):5256-5265.Fang Yongjie, Liu Fusuo, Li Bijun.A review of out-of-step oscillation islanding control of large scale power systems[J].Proceedings of the CSEE, 2017, 37(18): 5256-5265(in Chinese).
[6]倪敬敏,沈沉,陈乾.基于慢同调的自适应主动解列控制(一):理论基础探究[J].中国电机工程学报,2014,34(25):4374-4384.Ni Jingmin, Shen Chen, Chen Qian.Adaptive controlled islanding based on slow coherency-part I: research on the theoretical basis[J].Proceedings of the CSEE, 2014, 34(25): 4374-4384(in Chinese).
[7]Yang B, Vittal V, Heydt G T.Slow-coherency-based controlled islanding-a demonstration of the approach on the August 14, 2003 blackout scenario[J].IEEE Transactions on Power Systems, 2006, 21(4): 1840-1847.
[8]Sun K, Zhang D Z, Lu Q.Splitting strategies for islanding operation of large-scale power systems using OBDD-based methods[J].IEEE Transactions on Power Systems, 2003, 18(2): 912-923.
[9]Ding L, Gonzalez L, Peter W, et al.Two-step spectral clustering controlled islanding algorithm[J].IEEE Transactions on Power Systems, 2013, 28(1): 75-84.
[10]宋洪磊,吴俊勇,郝亮亮.考虑同调约束的电力系统主动解列断面的搜索方法[J].电力系统自动化,2014,38(14):49-54.Song Honglei, Wu Junyong, Hao Liangliang.A searching method for power system controlled islanding surfaces considering coherency constraint[J].Automation of Electric Power Systems, 2014, 38(14): 49-54(in Chinese).
[11]王乙斐,唐飞,刘涤尘,等.基于Dijkstra算法的最优解列断面快速搜索方法[J].电力自动化设备,2015,35(4):126-131.Wang Yifei, Tang Fei, Liu Dichen, et al.Quick search of optimal splitting surface based on Dijkstra algorithm[J].Electric Power Automation Equipment, 2015, 35(4): 126-131(in Chinese).
[12]Tang Y, Li F, Zheng C Y, et al.PMU measurement-based intelligent strategy for power system controlled islanding[J].Energies, 2018, 11(1): 143.
[13]Kyriacou A, Demetriou P, Panayiotou C, et al.Controlled islanding solution for large-scale power systems[J].IEEE Transactions on Power Systems, 2018, 33(2): 1591-1602.
[14]Liu Z P, Clark A, Bushnell L, et al.Controlled islanding via weak sub-modularity[J].IEEE Transactions on Power Systems, 2019, 34(3): 1858-1868.
[15]杨健,唐飞,廖清芬,等.基于半监督谱聚类的主动解列最优断面搜索[J].电网技术,2015,39(1):242-249.Yang Jian, Tang Fei, Liao Qingfen, et al.An optimal controlled partitioning scheme based on semi-supervised spectral clustering algorithm[J].Power System Technology, 2015, 39(1): 242-249(in Chinese).
[16]Esmaeilian A, Kezunovic M.Prevention of power grid blackouts using intentional islanding scheme[J].IEEE Transactions on Industry Applications, 2017, 53(1): 622-629.
[17]Aghamohammadi M R, Shahmohammadi A.Intentional islanding using a new algorithm based on ant search mechanism[J].International Journal of Electrical Power and Energy Systems, 2012, 35(1): 138-147.
[18]王乙斐,唐飞,廖清芬,等.带连通性约束的蚁群优化算法主动解列断面求解策略[J].电力系统及其自动化学报,2016,28(9):56-62.Wang Yifei, Tang Fei, Liao Qingfen, et al.Controlled splitting surface searching strategy based on ant colony optimization algorithm under connective constraints[J].Proceedings of the CSU-EPSA, 2016, 28(9): 56-62(in Chinese).
[19]Li L, Liu W, Cartes D A, et al.Slow coherency and angle modulated particle swarm optimization based islanding of large-scale power systems[J].Advanced Engineering Informatics, 2009, 23(1): 45-56.
[20]贾骏,谢天喜,陈舒,等.基于凸优化理论的电力系统主动解列最优断面搜索研究[J].中国电机工程学报,2018,38(1):168-177.Jia Jun, Xie Tianxi, Chen Shu, et al.Controlled islanding method of power system based on convex optimization theory[J].Proceedings of the CSEE, 2018, 38(1): 168-177(in Chinese).
[21]Imhof M, Valgaev O, Andersson G.Controlled islanding using VSC-HVDC links to reduce load shedding[C]//IEEE Eindhoven PowerTech, 2015.
[22]王振浩,张明译,杜虹锦,等.考虑柔性直流落点约束的最优主动解列断面搜索算法[J].电工技术学报,2017,32(17):57-66.Wang Zhenhao, Zhang Mingyi, Du Hongjin, et al.A searching algorithm for optimal controlled islanding surfaces considering VSC-HVDC terminal constraint[J].Transactions of China Electrotechnical Society, 2017, 32(17): 57-66(in Chinese).
[23]贾骏,谢天喜,唐飞,等.考虑无功功率的大电网主动解列最优断面搜索策略[J].电工技术学报,2017,32(S1):68-74.Jia Jun, Xie Tianxi, Tang Fei, et al.Study on an optimal partition scheme considering reactive power in large power grid[J].Transactions of China Electrotechnical Society, 2017, 32(S1): 68-74 (in Chinese).
[24]罗钢,乔煌煌,沈沉,等.基于贪心算法的自适应解列断面自动搜索方法:(一)解列指标体系与算法设计[J].电力系统自动化,2018,42(19):112-117.Luo Gang, Qiao Huanghuang, Shen Chen, et al.Greedy algorithm based automatic searching method for controlled islanding surface of power system part one index system of islanding control and design of algorithm[J].Automation of Electric Power Systems, 2018, 42(19): 112-117(in Chinese).
[25]Ding L, Ma Z, Wall P, et al.Graph spectra based controlled islanding for low inertia power systems[J].IEEE Transactions on Power Delivery, 2017, 32(1): 302-309.
[26]李碧君,刘福锁,吴雪莲,等.解列后局部电网功角首摆失稳问题研究[J].电力系统保护与控制,2017,45(12):22-28.Li Bijun, Liu Fusuo, Wu Xuelian, et al.A study on the first swing of angle instability in the local power network after splitting[J].Power System Protection and Control, 2017, 45(12): 22-28(in Chinese).
[27]程敏,杨文涛,文福拴,等.电力系统主动解列断面搜索方法与孤岛调整策略[J].电力系统自动化,2017,41(19):37-45.Cheng Min, Yang Wentao, Wen Fushuan, et al.Controlled splitting sections search method and islanding adjustment strategy for power system[J].Automation of Electric Power Systems, 2017, 41(19): 37-45(in Chinese).
[28]Wang C C.Pruning network coding traffic by network coding: a new class of max-flow algorithms[J].IEEE Transactions on Information Theory, 2010, 56(4): 1909-1929.
[29]李军徽,冯喜超,严干贵,等.高风电渗透率下的电力系统调频研究综述[J].电力系统保护与控制,2018,46(2):163-170.Li Junhui, Feng Xichao, Yan Gangui, et al.Survey on frequency regulation technology in high wind penetration power system[J].Power System Protection and Control, 2018, 46(2): 163-170(in Chinese).
[30]刘建平,吴锡昌,王旭斌,等.考虑频率约束的孤网风电渗透率极限评估[J].电网与清洁能源,2015,31(11):93-100.Liu Jianping, Wu Xichang, Wang Xubin, et al.An assessment of wind power penetrations limited with frequency constraint in an isolated system[J].Power System and Clean Energy, 2015, 31(11): 93-100(in Chinese).
[31]林伟芳,汤涌,卜广全.多馈入交直流系统短路比的定义和应用[J].中国电机工程学报,2008,28(31):1-8.Lin Weifang, Tang Yong, Bu Guangquan.Definition and application of short circuit ratio for multi-infeed AC/DC power systems[J].Proceedings of the CSEE, 2008, 28(31): 1-8(in Chinese).
[32]刘建,李兴源,傅孝韬,等.多馈入短路比及多馈入交互作用因子与换相失败的关系[J].电网技术,2009,33(12):20-25.Liu Jian, Li Xingyuan, Fu Xiaotao, et al.Relationship of multiinfeed short circuit ratio and multi-infeed interaction factor with commutation failure[J].Power System Technology, 2009, 33(12): 20-25(in Chinese).
[33]何仰赞,温增银.电力系统分析[M].武汉:华中科技大学出版社,2002:85-88.He Yangzan, Wen Zengyin.Analysis of power systems[M].Wuhan:Huazhong University of Science & Technology Press, 2002: 85-88(in Chinese).
Controlled Islanding Strategy Considering Multiple Factors
TANG Yi1, ZHENG Chenyi1, XIAO Jinyu2, HOU Jinming2
(1.School of Electrical Engineering, Southeast University, Nanjing 210096, Jiangsu Province, China;2.Global Energy Interconnection Development and Cooperation Organization, Xicheng District, Beijing 100031, China)
Abstract: Determining the optimal surface considering the stability of power system after splitting is the core problem of controlled islanding.However, the problem is seen as a single objective optimization process according to current research methods, which is not able to guarantee the stability required by current power systems due to the development of renewable energy and high voltage direct current (HVDC).Therefore, a controlled islanding strategy considering multiple factors is proposed in this paper.Firstly, initial islanding surface with minimum power-flow disruption is obtained based on single-objective optimization.Secondly, candidate islanding strategies with similar power-flow disruption are searched in neighborhood search space of the initial surface.Finally, the final splitting surface considering wind penetration and multiinfeed short circuit ratio is determined.The strategy verified by the simulation in New England 39-bus system can effectively improve the stable operation ability of islands after splitting, which is beneficial to subsequent control and recovery.
Keywords: power systems; islanding strategy; wind power; DC transmission
National Key Research and Development Program of China (2018YFB0904500); National Natural Science Foundation of China (NSFC) (51577030); Science and Technology Foundation of SGCC (Research on Control Forms of Power Electronics Dominated Power Systems, GEIGC-E-[2018]026).
文章编号:2096-5125 (2019) 04-0393-08
中图分类号:TM712
文献标志码:A
DOI:10.19705/j.cnki.issn2096-5125.2019.04.010
基金项目:国家重点研发计划(2018YFB0904500);国家自然科学基金(51577030);国家电网公司科技项目(电力电子化大电网控制形态研究,GEIGC-E-[2018]026)。
收稿日期:2018-10-16;修回日期:2019-02-25。

汤奕
作者简介:
汤奕(1977),男,副教授,博士生导师,研究方向为电力系统稳定分析与控制,电网信息物理系统等,E-mail:tangyi@seu.edu.cn。
郑晨一(1994),男,博士研究生,研究方向为电力系统稳定分析与控制,E-mail:220162328@seu.edu.cn。
(责任编辑 李锡)
