0 引言
近年来,自然灾害、网络攻击等导致的电力系统停电事故频发。2019年3月7日,网络攻击引起委内瑞拉全国性大面积停电,影响人群接近3000万。2019年3月21日,中国江苏省化工厂特大爆炸事故导致变电站主变停运以及若干条线路和配变停运,损失负荷2.9 万kW,对电力系统造成了严重的破坏。极端事件导致的频发停电事故对智能电网的建设提出了新的挑战。基于此,学术界与工业界共同提出了电力系统“韧性”的概念。韧性(resilience)被定义为“预防和适应环境变化、承受扰动以及快速恢复的能力”[1]。极端事件可能损毁基础设施,导致输电网无法及时为配电网送电,配电网可以利用本地可调度类电动汽车为关键负荷紧急供电,从而缩短停电时间,提升配电网韧性。目前,随着车用电池性能的不断提升以及V2G技术的日益成熟,电动汽车作为分布式储能单元在调节地区电网峰谷、调频、平抑分布式电源扰动、作为应急电源等方面展现了巨大的潜能[2]。大量研究与试验表明,将电动汽车与电网智能地结合起来,利用电动汽车的储能系统为电网服务是可行的[3]。电动汽车充电站作为电动汽车与电网的接口,其合理的布点方案有利于提升极端情况下配电网关键负荷恢复能力,从而提升配电网韧性。
目前对于电动汽车充电站的规划方法,按侧重对象可分为三类—侧重考虑交通网需求、侧重考虑电网需求、综合考虑交通网和电网需求的充电站规划方法。文献[4]假设电动汽车充电需求均匀分布在目标区域内,以此简化对电网需求的考虑。侧重考虑电网需求的文献[5]建立了考虑充电站布点优化的配电网规划模型,在满足规划区域传统负荷增长和充电需求等诸多条件下,通过优化区域充电需求在充电站备选站址间的分配,有效降低配电网的投资与运行成本。由于充电站的布点对交通系统和电网均会产生影响且同时受限于两个系统的运行情况,如交通网的车流分布以及电网的供电情况等,因此综合考虑交通网和电网需求的充电站规划成为目前很多学者的主要研究方向。文献[6]提出了一种多目标协同规划策略,解决耦合配电网和电动汽车充电系统的最优规划问题。模型以最小化年度总投资成本和网损、且最大化年度充电车流量为优化目标,并应用基于用户均衡的交通分配模型求解每个时刻线路上的车流量。文献[7]提出了一种同时考虑电动汽车行驶范围及充电需求的混合整数二阶锥规划模型,将电网与交通网的约束都考虑在内,应用已有优化求解器即可进行求解。文献[8]将经济效益作为充电站规划的唯一目标,提出了用净现值和生命周期成本来确定充电站位置和容量的方法,并考虑电网电压功率与交通服务半径、服务数量等相关约束。相关文献多将投资成本和经济效益作为充电站优化布点的目标,兼顾车流量以及电网运行约束等问题,尚未有文章在充电站布点规划中考虑利用电动汽车提升电网韧性这一因素。
在中国,随着政策引导和相关技术的不断进步,电动汽车进入了大规模发展阶段[9],很多城市采用了电动公交车、电动巴士以及电动出租车等,这些电动汽车调度灵活,为在极端情况下作为应急电源提供了可能[10-11]。基于车辆运营特性的考虑[12],本文仅考虑电动公交车和电动企业班车两类可调度类电动汽车的充电站布点问题。文章提出了一种兼顾交通网最小充电距离以及配电网最大关键负荷恢复的电动汽车充电站布点模型,在满足可调度电动汽车充电需求的前提下,进一步提升系统在极端情况下的恢复能力,从而提升配电网韧性。
1 问题描述
在正常情况下,电动公交车和电动企业班车具有固定的起点和终点,本文用一对始发站和终点站(origin and destination, OD)代表一类可调度电动车。由于电动公交车和企业班车具有服务性质,一般情况下,在其行驶过程中不充电,回到代表公交总站或公司的起点或终点时才会进行充电及相关维护。假设对于每一类可调度电动车,每日的发车计划已知(包括发车数量和时间),从而可得到每天各个时间段的充电需求以及充满电的闲置电动车数量。对于交通网中的电动汽车,充电站布点在需要满足充电需求的基础上,与起点或终点的行驶距离越小越好,即充电越便利越好。
另外,假设极端事件引发大停电后,在输电网无法及时为配电网送电的情况下,闲置的且带有电量的电动公交车和电动企业班车能够被快速调度至附近的充电站,作为电源通过配电网线路为配电网内关键负荷供电。在充电站布点时,需要考虑充电站附近应有停放闲置电动车的始发站或终点站,且与充电站距离越近越好,这样在极端事件发生后才能够迅速调度至充电站,这与交通网中充电站布点的目标是一致的。此外,由于没有大电网支撑,充电站的位置即是配电网中的电源位置,合理的布点方案需要考虑配电网故障后恢复过程中的各类运行约束是否能够满足。另外,极端事件可能发生在一天中的不同时刻,该时刻对应的闲置电动车数目(即可用发电资源)也不尽相同,合理的布点方案能够综合考虑各个时刻下恢复情况,最大化恢复效果。
综上,充电站布点方案,需充分考虑可调度电动汽车运营特性及充电习惯,既要满足日常情况下电动汽车从始发站或终点站去充电的便利性,又要实现在极端情况下各停电时刻场景恢复效果的最大化,即韧性提升的最大化。本文提出综合考虑配电网韧性和充电便利性的充电站布点模型,将在下一章节对具体布点模型进行介绍。
2 充电站布点模型
本文将充电站布点模型划分为考虑电网韧性部分和考虑充电便利性部分2个子模型分别阐述,最后将2个子模型的目标分配相应权重进行整合得到整体的充电站布点模型。
2.1 考虑配电网韧性的布点模型
由于极端事件可能在一天中的任意时刻发生,假设任意时刻发生极端事件的概率相同。根据极端事件发生的时刻,定义不同的停电场景s。配电网部分布点模型的主要目标是最大化所有场景下加权恢复负荷数目,用以最大化恢复能力;次要目标是最小化所有场景下所有节点与参考节点电压差,以优化各个恢复策略下系统的电压分布。决策变量是各个候选位置是否建设充电站。考虑的约束条件包括充电站布点数目约束,以及各个场景下的潮流约束、电压约束、拓扑约束和充电站节点向电网注入功率约束。具体的目标函数和约束条件如下。
2.1.1 目标函数
考虑配电网韧性的布点模型的目标函数如下:
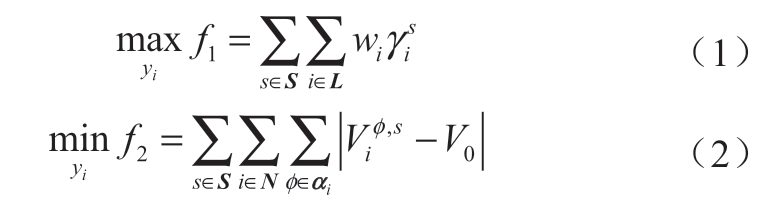
式中:yi为0-1决策变量,表示充电站候选节点上是否建设充电站,若建设该值为1,反之为0;S、N、L和αi分别为所有场景、配电网所有节点、所有负荷和节点i的所有相构成的集合;wi为负荷i的权重系数,该值越大代表负荷越为重要;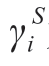 为负荷i在场景s的恢复状态,负荷恢复则
为负荷i在场景s的恢复状态,负荷恢复则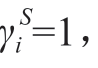 反之为0;,s iVφ为节点i的第φ相在场景s的电压幅值的平方,V0为参考节点的电压幅值的平方,电压幅值均为标幺值,本文取V0=1 pu。
反之为0;,s iVφ为节点i的第φ相在场景s的电压幅值的平方,V0为参考节点的电压幅值的平方,电压幅值均为标幺值,本文取V0=1 pu。
式(1)表示最大化所有场景下加权负荷恢复数目,式(2)表示最小化所有场景下所有节点电压与参考节点电压差。为了平衡这2个目标,首先将2个目标函数分别进行归一化处理,得到归一化的目标函数(3)和(4)。其中主要目标的基准值为当所有负荷恢复状态都为1时的主要目标函数值,次要目标的基准值为绝对值内的值为Vmax-Vmin时次要目标函数的值,其中Vmax和Vmin分别为节点电压幅值的允许的最大值和最小值。
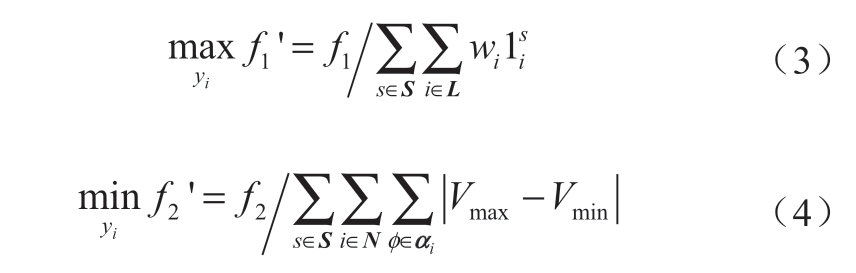
通过权重系数λ将二者结合,如式(5)所示。由于目标(2)为次要目标,因此 λ<0.5。
2.1.2 约束条件
需要考虑的约束条件包括充电站布点数目约束、每个停电场景下的潮流约束、充电站节点向电网注入功率约束、电压约束和辐射状拓扑约束,具体如下:
1)充电站布点数目约束
式中:K代表所有充电站候选节点构成的集合;p代表由于资金等原因计划拟建设充电站的数目。
2)潮流约束
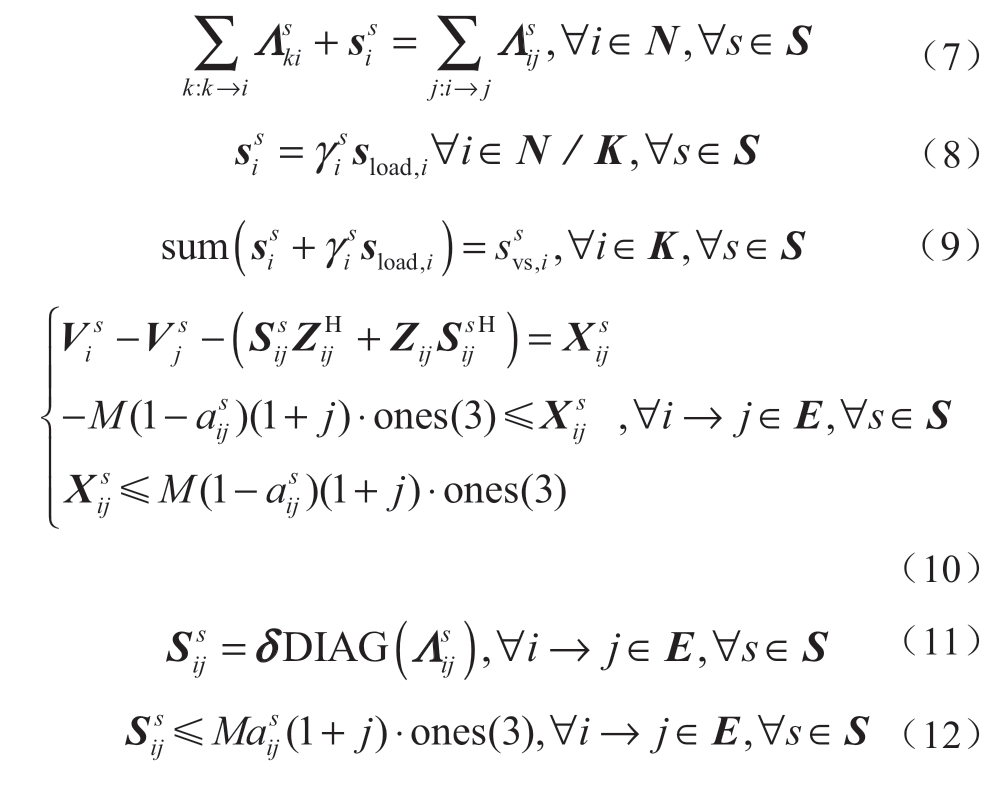
式中:E代表所有配电线路构成的集合; 为0-1变量,表示线路i→j在场景s下是否恢复;
为0-1变量,表示线路i→j在场景s下是否恢复;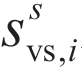 为复数变量,代表充电站候选节点i在场景s下向配电网注入的功率;
为复数变量,代表充电站候选节点i在场景s下向配电网注入的功率;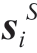 和
和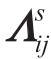 为向量变量,分别代表节点i在场景s下的三相节点注入功率、线路i→j在场景s下的三相功率;
为向量变量,分别代表节点i在场景s下的三相节点注入功率、线路i→j在场景s下的三相功率;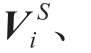
 代表矩阵变量,其中
代表矩阵变量,其中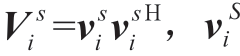 代表节点i在场景s下三相电压构成的复数向量,
代表节点i在场景s下三相电压构成的复数向量,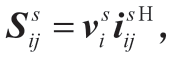 其中
其中 代表线路i→j在场景s下的三相电流构成的复数向量,
代表线路i→j在场景s下的三相电流构成的复数向量,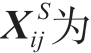 中间矩阵变量;M、sload,i、δ和ones(3)均为已知量,其中M为一值很大的正实数,sload,i为节点i上三相负荷功率需求构成的复数向量,ones(3)是维度为3、所有元素均为1的方阵。δ为常数矩阵,且
中间矩阵变量;M、sload,i、δ和ones(3)均为已知量,其中M为一值很大的正实数,sload,i为节点i上三相负荷功率需求构成的复数向量,ones(3)是维度为3、所有元素均为1的方阵。δ为常数矩阵,且
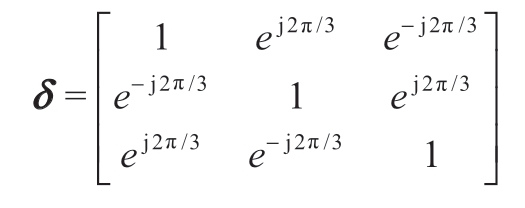
潮流约束参考了文献[13]中的三相不对称线性潮流模型,忽略了线路损耗,并在其模型基础上,建立了本文中考虑拓扑变化的潮流约束模型。其中,式(7)表示节点功率平衡约束;式(8)和式(9)分别表示节点i属于充电站候选节点以及不属于候选节点,节点注入功率的表达式;式(10)为线路两端电压矩阵的关系,在线路连接状态时第一行的等式成立,是由欧姆定律和功率定义式得来,中间变量的引入是为了表示当线路i→j相连时,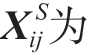 0矩阵,等式成立,反之则对
0矩阵,等式成立,反之则对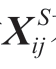 不做约束;式(11)表示矩阵变量
不做约束;式(11)表示矩阵变量 和向量变量
和向量变量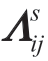 的代数关系,其中DIAG(·)表示返回以括号中向量为对角线元素、其他元素为0的方阵;式(12)表示若线路i→j相连,则对矩阵变量SijS不做约束,不相连则为0矩阵。
的代数关系,其中DIAG(·)表示返回以括号中向量为对角线元素、其他元素为0的方阵;式(12)表示若线路i→j相连,则对矩阵变量SijS不做约束,不相连则为0矩阵。
3)充电站节点注入功率约束

式中: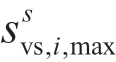 为充电站候选节点i在场景s下能向电网注入的最大功率值;
为充电站候选节点i在场景s下能向电网注入的最大功率值; 为在场景s下所有充电站可向电网注入的最大功率值。
为在场景s下所有充电站可向电网注入的最大功率值。
对于每个不同的停电场景s,所有起始站和终点站的闲置电动车数目不同,因此极端事件后总的发电资源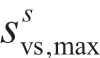 是不同的;并且为了更快发挥电动车的作用,电动车会被就近调度,各个充电站备选点在不同场景下能为系统提供的发电资源
是不同的;并且为了更快发挥电动车的作用,电动车会被就近调度,各个充电站备选点在不同场景下能为系统提供的发电资源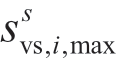 亦有所区别,本文中对于某一充电站候选节点i,其
亦有所区别,本文中对于某一充电站候选节点i,其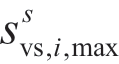 是根据其行驶距离某一范围内的起始站和终点站所有闲置车辆数确定的。由于恢复中使用的是闲置的已充好电的可调度电动车,剩余电量充足,持续放电时间较长,因此此处并未考虑电量约束。
是根据其行驶距离某一范围内的起始站和终点站所有闲置车辆数确定的。由于恢复中使用的是闲置的已充好电的可调度电动车,剩余电量充足,持续放电时间较长,因此此处并未考虑电量约束。
4)电压约束
式(15)表示所有节点各相电压幅值需要维持在某一范围内,本文取电压幅值在[0.95,1.05]之间。式中的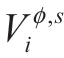 为矩阵变量
为矩阵变量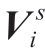 的对角线元素。
的对角线元素。
5)辐射状拓扑约束
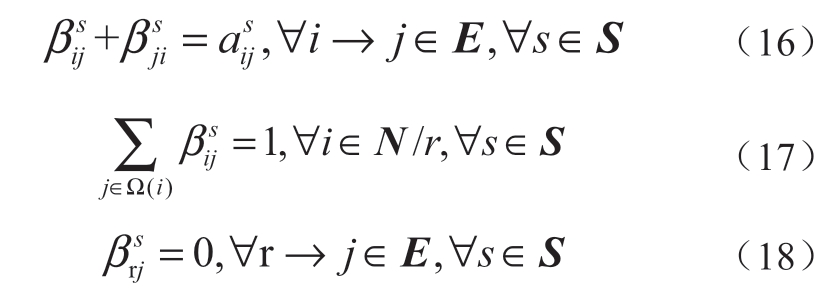
式中:Ω(i)代表与节点i相连的所有节点构成的集合;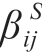 为辅助变量,代表节点j是否为节点i的父节点,如果是则为1,否则为0;
为辅助变量,代表节点j是否为节点i的父节点,如果是则为1,否则为0;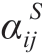 与式(10)中含义相同,表示线路i→j在场景s下是否恢复;r表示根节点编号。
与式(10)中含义相同,表示线路i→j在场景s下是否恢复;r表示根节点编号。
式 (16) — 式(18)为生成树约束,基于图论确保网络的辐射状[14]。
2.2 考虑充电便利性的布点模型
考虑充电便利性的布点模型主要考虑电动车正常运营情况下,充电站需要满足各类电动车回到起始站或终点站后去充电的便利性,由于公交车与班车日发车次数差异较大,发车次数可反映起始站/终点站的充电需求,因此考虑将起始站/终点站的日发车次数作为其充电距离的权重系数,以充电站到所有起始站和终点站的加权距离最小为目标,约束条件为充电站数目,模型如下:
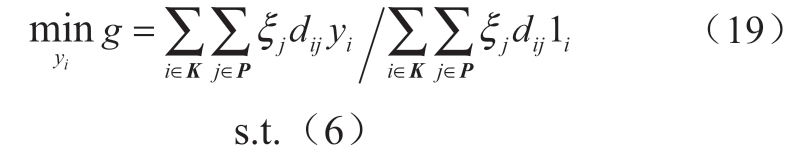
式中:P为交通网中所有起始站和终点站节点构成的集合;ξj为起始站/终点站j的日发车次数;dij表示充电站候选位置i与起始站/终点站j最短行驶距离,由交通网拓扑决定。
式(19)中分子含义为充电站到所有起始站/终点站加权总距离最小,除以分母对目标函数进行归一化,该目标能够综合考虑各类可调度电动车的充电需求,满足其充电的便利性。
2.3 综合配电网-交通网需求的充电站布点模型
整合以上2个子模型,得到综合考虑配电网韧性和充电便利性的充电站布点模型如下:

式(20)中,ρ为目标权重值,可由用户自定义,用以平衡充电便利性目标与电网韧性目标的重要程度。该优化模型为混合整数线性规划模型,可以利用成熟的优化求解器(如mosek)有效求解。
3 算例分析
3.1 算例介绍
本文采用一个21节点的交通网络与33节点的配电网相耦合的算例,其中配电网为三相不平衡配电网,具体负荷与线路参数详见文献[15],电压等级为110 kV。交通网络结构如图1所示[16],所有交通节点均为充电站候选节点。配电网结构如图2所示,配电网中的关键负荷在图中进行了标记,一级负荷权重设置为100,二级负荷权重为10,普通负荷权重为0.2。两个网络节点的耦合关系详见表1。对于交通网络,假定有6类电动公交车、3类A公司班车以及3类B公司班车,其中公司A设置在节点21,公司B设置在节点14。对于在同一OD对上的同一类电动车,认为车辆在白天发车时间段内有固定数量的车在行驶中,行驶中的车辆不可被调用,其余闲置车辆可以被紧急调用;并认为在距离充电站15 km之内的电动汽车可以在紧急情况下被调度至充电站进行供电。表2给出交通网线路情况及日发车次数,表3给出公交车的车辆运营时间、发车次数、车辆数以及运营时间闲置车辆数,表4给出电动班车的相关信息。本文将每天24 h划分为24种场景,每种场景对应不同的车辆运营情况,详见表5。根据运营情况,可将24个场景组合划分为7种场景(A~G),且各场景在一天中出现的比重分别为7/24,1/24,5/24,1/24,8/24,1/24,1/24。本算例中充电站数目p=6。
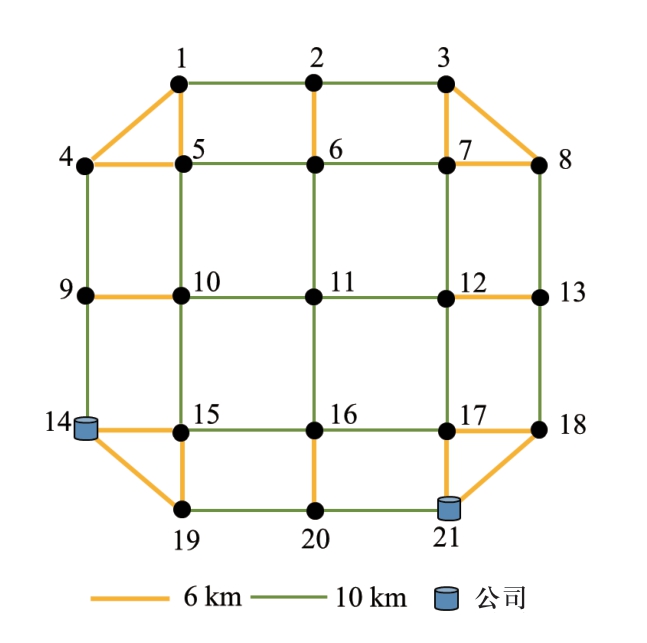
图1 交通21节点网络图
Fig.1 A 21-node transportation network
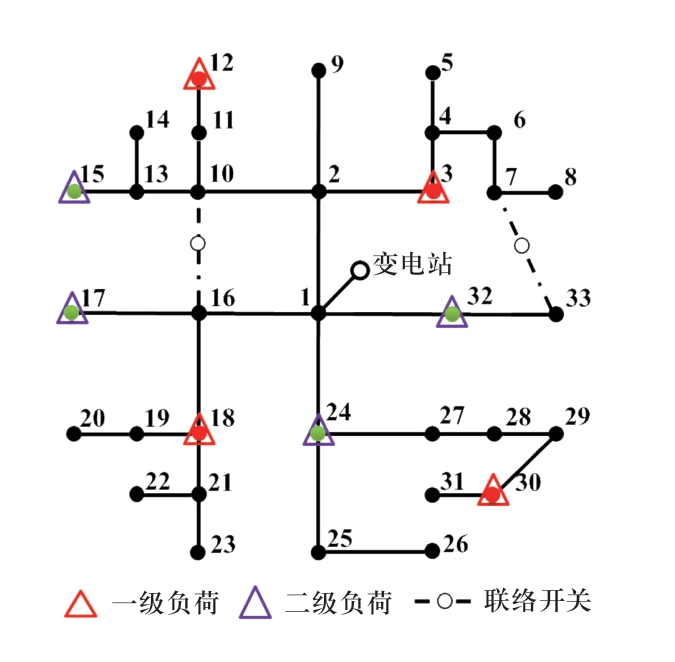
图2 110 kV配电网线路图
Fig.2 A 110 kV distribution network
表1 交通—配电网节点耦合情况
Table 1 Coupling nodes in transportation & distribution network
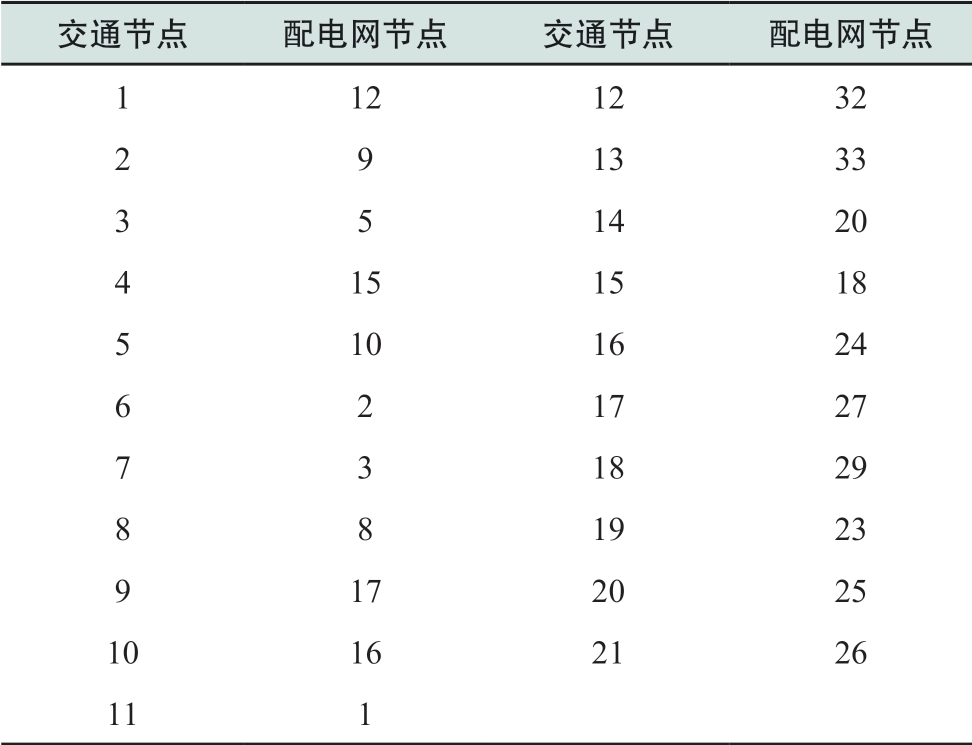
表2 交通网线路情况及日发车次数
Table 2 OD pairs and flows in transportation network
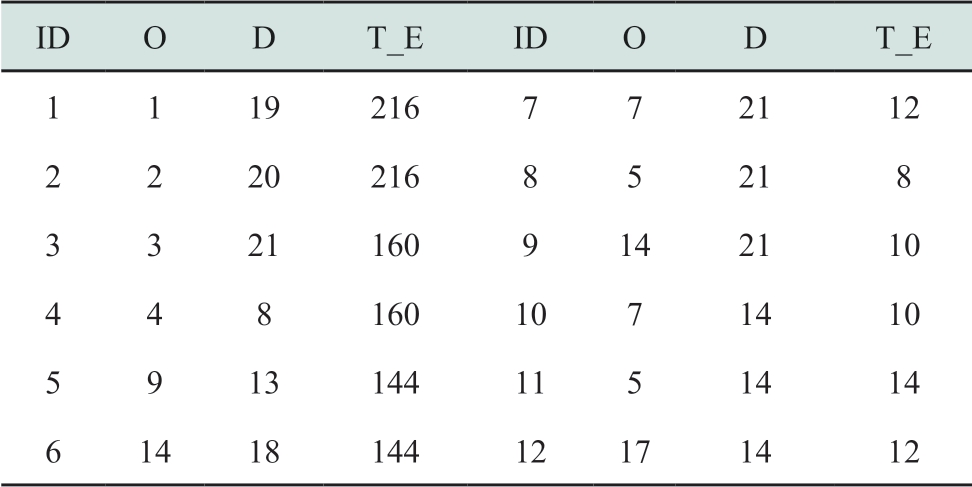
注:ID:线路编号,O:线路起点,D:线路终点,T_E:日发车次数(双向)。
表3 公交车运营情况
Table 3 Operation of electric buses
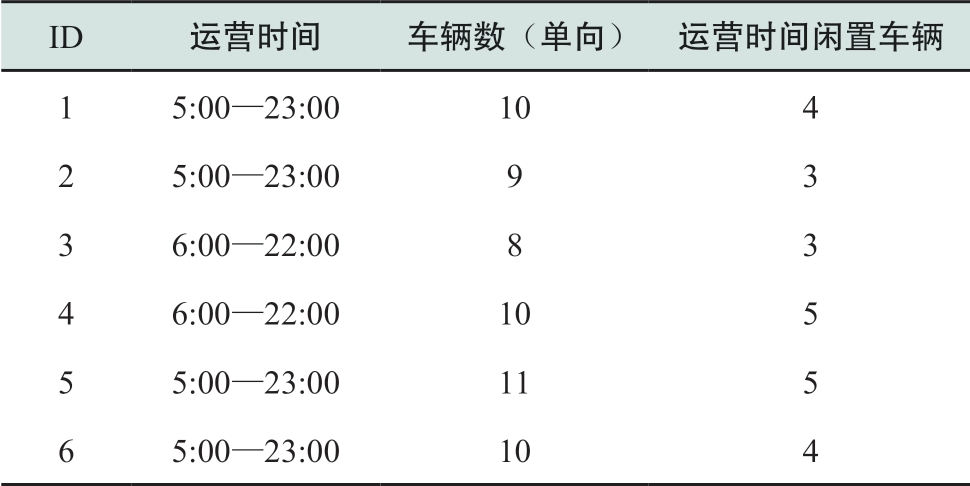
表4 企业班车运营情况
Table 4 Operation of electric shuttle buses
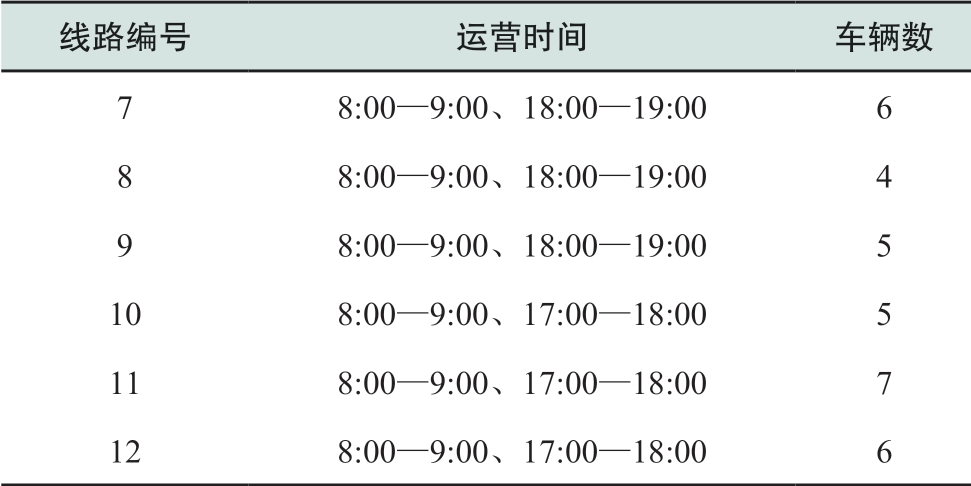
表5 不同场景车辆运营情况
Table 5 Operation of vehicles in different time during a day

续表

3.2 基础算例结果分析
设置电网2个目标中的权重值λ为e-5,即以负荷恢复最大化为主要目标。此外,综合目标的权重值ρ为0.5,即配电网韧性提升目标与充电便利性目标权重相同。将该算例情况视为基础算例。应用本文提出的综合交通网—配电网需求的充电站布点模型对算例进行建模和求解。模型采用mosek求解器进行迅速求解,基础算例有21245个标量变量,966个整数变量以及14470个约束条件,优化求解得出充电站布点位于节点1、11、14、18、19和21,如图3所示。
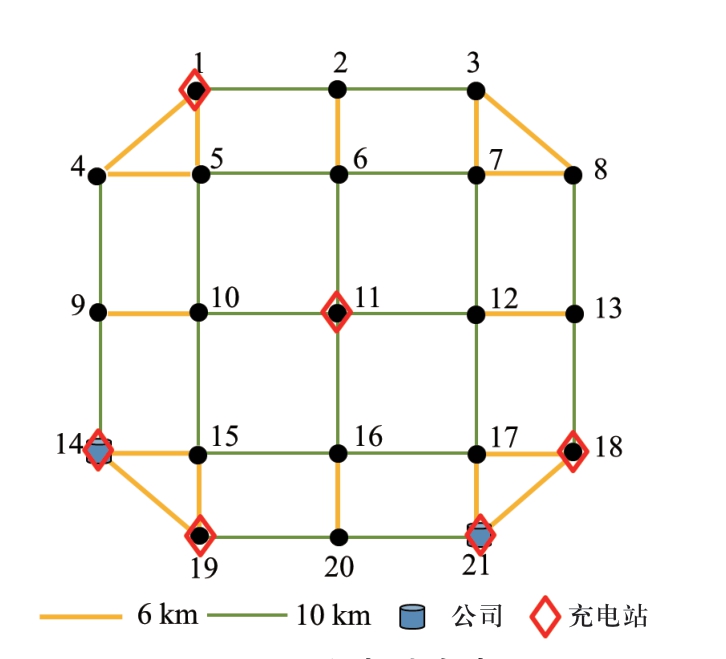
图3 充电站布点
Fig.3 Location of charging stations
表6给出A~G场景下的故障负荷恢复情况,可以看出由于不同场景下可调度的闲置电动车数目不同,可为配电网提供的发电容量不同,因此负荷恢复情况也不尽相同。此外,所有场景下的所有节点中电压幅值最大值为1.048,最小值为0.951,满足电压约束。此时交通网的12条线路上电动汽车的充电距离分别为0、10、0、6、10、0、0、0、0、0、0、0。在不同场景下,恢复策略优化出的网络拓扑是不同的。图4中给出了优化后A场景下配电网的辐射状拓扑结构图。
表6 A~G场景负荷恢复情况
Table 6 Restoration of loads in cases A~G
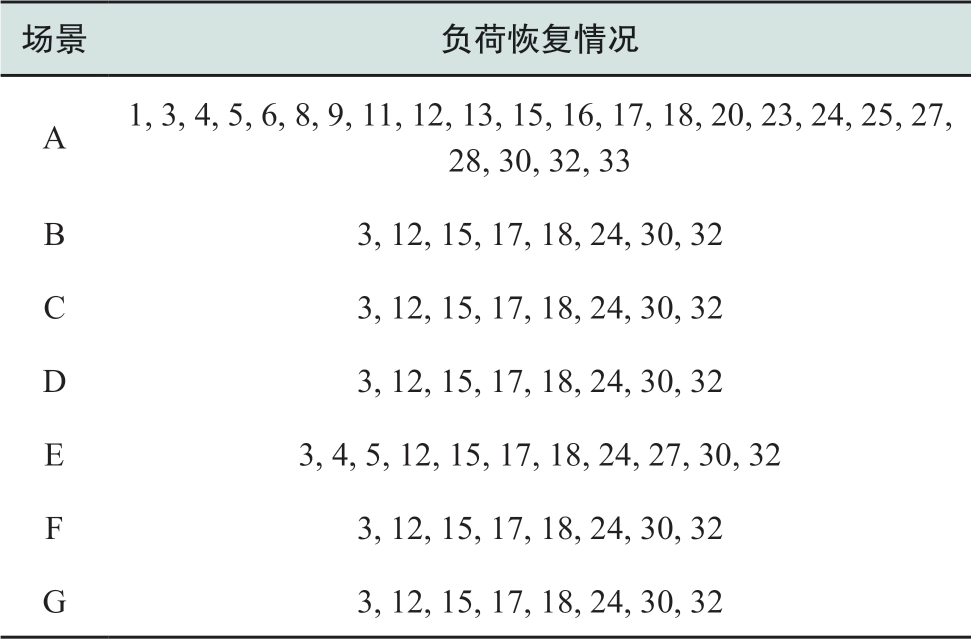
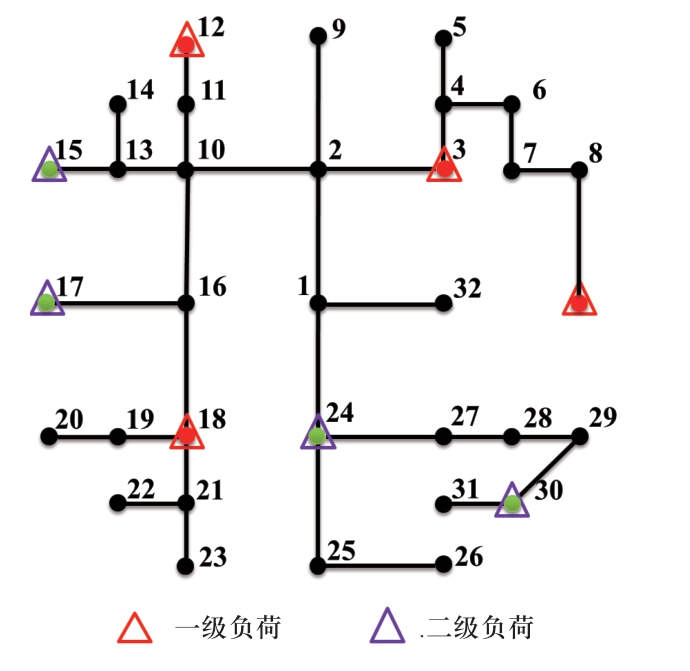
图4 场景A配电网拓扑结构
Fig.4 Topology of distribution system under scenario A
由数据分析可知,该布点方案中1点对应的配电网节点接有重要负荷,14和21附近的起始站和终点站的分布较为密集。此外,布点方案分布较为均匀,各个起始站/终到站可方便地到附近充电站充电,且各个场景下恢复后的电压分布较为合理,无过电压或欠电压现象。因此,本文提出的充电站布点方法能够计及所有约束,得到兼顾最大化交通网的充电便利性以及配电网韧性的充电站布点方案。
3.3 不同权重取值情况下对比分析
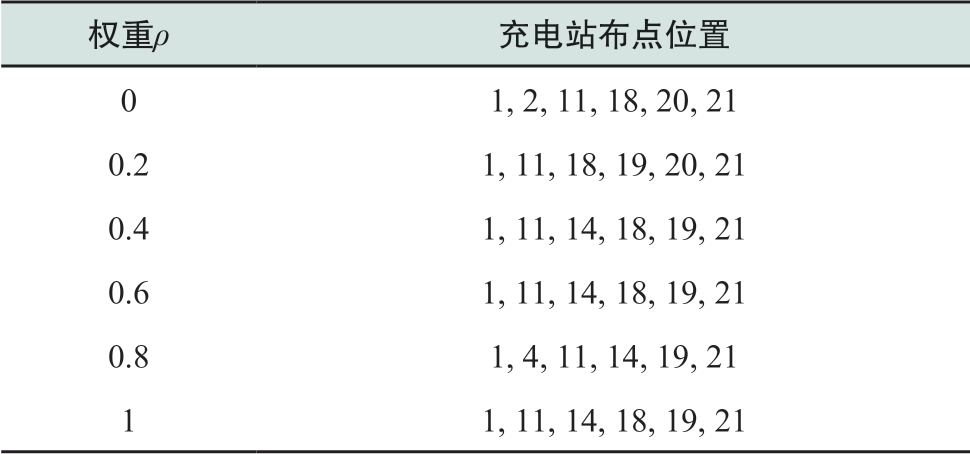
在由3.1节给出的系统信息基础上,分别设置不同的综合目标权重系数ρ为0、0.2、0.4、0.6、0.8、1,得到如表7所示的不同权重下的充电站具体布点位置。6种不同权重系数情况下的优化求解时间依次为0.84 s,0.84 s,0.73 s,0.78 s,0.86 s,0.69 s。
ρ=0时,充电站布点的整体目标仅考虑电网韧性提升,该布点方案是所有方案中可最大化提升配电网韧性的方案;ρ=1时,充电站布点目标仅考虑充电便利性,相应的布点方案能够使得交通网电动汽车充电最为便利。其他权重值的求解目标兼顾最小化交通网充电行驶距离与电网的最大化恢复负荷。在实际应用中,决策者可以根据偏好以及专家知识对权重进行选择。另外,观察不同权重下的充电站布点位置,可以发现1、11、21等节点出现频率较高,是由于该三点附近均接有重要负荷,且是电动车起点和终点分布较为密集的区域,意味着这3个充电站候选位置对于电网韧性提升和充电便利性均有重要意义,此结论可以为其他规划数目下的充电站布点提供一定参考。
表7 不同权重系数ρ下的充电站布点情况
Table 7 Locations of charging stations with different ρ
4 结论
本文基于可调度类电动汽车可作为移动电源在极端情况下为配电网馈电的特点,在充电站规划阶段综合考虑了正常情况下电动汽车充电需求及便利性,极端情况下电动汽车通过充电站为配电网中关键负荷进行供电恢复,提出了一种最小化加权充电距离与最大化配电网韧性的充电站布点混合整数线性规划模型。在算例测试部分,针对交通网与配电网耦合系统,利用本文提出的方法得到了满足各项约束、综合最大化电动车充电便利性与电网韧性的充电站布点位置;此外,综合对比了布点模型目标中不同权重系数下的布点方案,探讨了在相应布点方案下故障恢复与电动汽车充电距离的具体情况,为决策者根据需求确定多目标权重值提供了建议。
参考文献
[1]Office of the Press Secretary, The White House, United States.Presidential Policy Directive 21: Critical infrastructure security and resilience [EB/OL].[2017-1-7].
[2]C.Gouveia, C.L.Moreira, J.A.P.Lopes, et al.Microgrid service restoration: the role of plugged-in electric vehicles[J].IEEE Industrial Electronics Magazine, 2013, 7(04): 26-41.
[3]梁伟,靳小龙,穆云飞,等.含微网及电动汽车的主动配电网供电恢复策略[J].电力系统及其自动化学报,2014,26(6):1-9.Liang Wei, Jin Xiaolong, Mu Yunfei, et al.Service restoration method to active distribution network with microgrids and electric vehicles[J].Proceedings of the CSU-EPSA, 2014, 26(6): 1-9 (in Chinese).
[4]Payam Sadeghi Barzani, Abbas Rajabi Ghahnavieh, Hosein Kazemi Karegar.Optimal fast charging station placing and sizing[J].Applied Energy, 2014, 125: 289-299.
[5]杜爱虎,胡泽春,宋永华,等.考虑电动汽车充电站布局优化的配电网规划[J].电网技术,2011,35(11):35-42.Du Aihu, Hu Zechun, Song Yonghua, et al.Distribution network planning considering layout optimization of electric vehicle charging stations[J].Power System Technology, 2011, 35(11): 35-42 (in Chinese).
[6]Yao Weifeng, Zhao Junhua, Wen Fushuan, et al.A multiobjective collaborative planning strategy for integrated power distribution and electric vehicle charging systems[J].IEEE Transactions on Power Systems, 2014, 29(04): 1811-1821.
[7]Zhang Hongcai, Moura Scott J, Hu Zechun, et al.A secondorder cone programming model for planning PEV fast-charging stations[J].IEEE Transactions on Power Systems, 2018, 33(3): 2763-2777.
[8]Huang Xiaoqing, Chen Jie, Yang Hang, et al.Economic planning approach for electric vehicle charging stations integrating traffic and power grid constraints[J].IET Generation, Transmission & Distribution, 2018, 12(17): 3925-3934.
[9]张文亮,武斌,李武峰,等.我国纯电动汽车的发展方向及能源供给模式的探讨[J].电网技术,2009,33(04):1-5.Zhang Wenliang, Wu Bin, Li Wufeng, et al.Discussion on development trend of battery electric vehicles in China and its energy supply mode[J].Power System Technology, 2009, 33(04): 1-5 (in Chinese).
[10]韩海英.V2G参与电网调峰和调频控制策略研究[D].北京:北京交通大学,2011.
[11]刘晓飞,张千帆,崔淑梅.电动汽车V2G技术综述[J].电工技术学报,2012,27(2):121-127.Liu Xiaofei, Zhang Qianfan, Cui Shumei.Review of electric vehicle V2G technology[J].Transactions of China Electrotechnical Society, 2012, 27(2): 121-127 (in Chinese).
[12]王旻.潍坊市区电动汽车充电桩(站)规划研究[D].济南:山东大学,2015.
[13]Lingwen Gan, Steven H.Low.Convex relaxations and linear approximation for optimal power flow in multiphase radial networks[C]// Power Systems Computation Conference(PSCC), Wrocław, Poland, 2014.
[14]Wang Ying, Xu Yin, He Jinghan, et al.Coordinating multiple sources for service restoration to enhance resilience of distribution systems[J].Accepted by Transactions on Smart Grid.DOI 10.1109/TSG.2019.2891515.
[15]Xu Yin, Wang Ying, He Jinghan, et al.Resilience-oriented distribution system restoration considering mobile emergency resource dispatch in transportation system[J].Accepted by IEEE Access.DOI 10.1109/ACCESS.2019.2921017.
[16]Wei Wei, Mei Shengwei, Wu Lei, et al.Robust operation of distribution networks coupled with urban transportation infrastructures[J].IEEE Transactions on Power Systems, 2017, 32(3): 2118-2130.
Placement of Charging Stations for Electric Vehicles Considering Distribution System Resilience and Charging Convenience
SU Mingyu, XU Yin, WANG Ying, HE Jinghan
(School of Electrical Engineering, Beijing Jiaotong University, Haidian District, Beijing 100044, China)
Abstract: As a distributed mobile energy storage unit, electric vehicles can be dispatched to charging stations as an emergency power supply to restore critical loads in the distribution network after extreme events, thus enhancing resilience of the distribution network.Therefore, it is necessary to study the reasonable locating scheme of charging stations so as to give full play to their role for resilience enhancement.This paper focuses on the location of charging stations for dispatchable electric vehicles.The charging station placement problem considering both resilience of distribution network and charging convenience is formulated as a mixed-integer linear program model(MILP).The objective is maximizing the restoration of weighted critical loads under various scenarios, minimizing the voltage amplitude difference, and minimizing the charging distance of the traffic network.The constraints include number of charging stations constraints, distribution system operation constraints and charging stations output power constraints.The proposed MILP can be solved with the off-the-shelf optimization solvers.Finally, the effectiveness of the proposed charging station placement method is verified by case studies.
Keywords: charging station placement; resilience; electric vehicles; distribution network
National Natural Science Foundation of China (51807004).
文章编号:2096-5125 (2019) 04-0341-08
中图分类号:TM72;U469.72
文献标志码:A
DOI:10.19705/j.cnki.issn2096-5125.2019.04.004
基金项目:国家自然科学基金资助项目(51807004)。
收稿日期:2019-05-09;修回日期:2019-06-05。

苏明玉
作者简介:
苏明玉(1995),女,硕士研究生,研究方向为配电网故障恢复,E-mail:17121491@bjtu.edu.cn。
许寅(1986),男,教授、博士生导师,研究方向为配电网故障恢复与韧性、电力系统暂态建模与仿真,E-mail:xuyin@bjtu.edu.cn。
(责任编辑 张宇)