0 引言
温室气体排放引起的全球变暖是一个世界性问题,CO2作为主要的温室气体,占温室气体总排放的70%以上[1]。为缓解全球变暖威胁,CO2减排成为电力系统可持续发展不可逆转的趋势。在化石燃料中,天然气是一种优质、高效、清洁的低碳能源[2],这些优点推动了燃气轮机装机量日益提高。同时,以互联网思维和能源互联网技术改造传统电力系统,促进电力系统转型,是支持构建现代能源系统的关键步骤。电-气综合能源系统作为能源互联网的重要组成部分,通过燃气轮机将电力系统和天然气系统耦合,催生了电-气综合能源系统低碳经济调度问题的研究 热潮。
针对电-气综合能源系统的运行优化问题,各国学者已有较多研究。文献[3-4]利用燃气轮机耦合电力网络和天然气网络,较早研究了天然气网络与电力网络联合最优潮流问题。文献[5]构建了区域电-气综合能源系统稳态分析模型,并且利用此模型探究了天然气系统网络状态变化对综合能源系统的影响。文献[6-8]从不同研究角度入手,利用交替方向乘子法(ADMM)实现了电-气综合能源系统的分布式协同运行。其中,文献[6]对有无协调算子的电-气综合最优潮流问题展开研究;文献[7]比较了基于Gauss-Seidel串行迭代和Proximal-Jacobian并行迭代的两种ADMM计算模式的优劣性;文献[8]计及二阶锥规划和ADMM,进一步提高了分散式电-气综合能源系统最优能量流的计算效率。
同时,已有部分电-气综合能源系统研究考虑了碳排放的影响。文献[9]总结了低碳技术在综合能源系统中的研究现状和研究框架。文献[10]建立了基于碳交易机制的电-气综合能源系统低碳经济调度模型,但是并没有考虑燃气发电以外的天然气系统运行成本,易导致天然气系统运行的次最优。文献[11]通过计及阶梯型碳交易机制和外购能源成本,实现了综合能源系统的低碳经济调度,并分析了电转气技术和燃气轮机容量变化对调度结果影响,但没有提及求解速度。文献[12]提出一种新的协同的方法对电-气综合能源系统进行扩建规划,解决了电-气综合能源系统复杂性和风险增加、系统整体可靠性评估等问题。文献[13]构建了计及碳交易成本的多区域综合能源系统分散调度模型,相应提出了一种分散式求解方法,该方法偏重于结构上的划分,由于采用ADMM求解,使得求解时间增加。文献[14]提出了碳捕集系统和电转气技术的灵活运行策略,并通过碳税惩罚实现电-气综合能源系统的低碳经济运行,但求解速度未知。
电-气综合能源系统低碳经济调度是一个高维、多时段优化问题,特别是多时段联合优化大大降低了模型的收敛速度。粒计算是一种通用的结构化问题求解方法,其核心思想是采用合适的粒化方法将研究的复杂问题转化为等价的简单结构化问题,进一步应用优化算法实现结构化问题的快速求解[15]。该方法已经应用于多个领域,如时间序列的贝叶斯分析[16]、腹部器官检测[17]、信号粒度建模[18]、复杂网络分析[19]、电力系统潮流计算[20]和电力系统优化调度[21]等。
本文对计及碳交易机制和时段粒化的电-气综合能源系统低碳经济调度问题展开研究。首先,以燃气轮机耦合的电-气综合能源系统为研究对象,构建了考虑碳交易机制的低碳经济调度模型;然后,提出了一种计及时段粒化的适用于大型电-气综合能源系统快速求解策略,该策略包括基于改进k-means聚类的时段粒度划分,粗粒度的调度优化和调度结果的粒度细化3个阶段;最后,采用电力39节点和天然气20节点的电-气综合能源系统进行算例分析,验证了构建模型与时段粒化方法的可行性和有效性。
1 电-气综合能源系统低碳经济调度模型
传统的能源系统仅限于电力、天然气等单一的能源形式,无法发挥能源之间的互补优势和协同效益。电-气综合能源系统通过燃气轮机把电力网络和天然气网络耦合在一起,提高能源的利用率,保证电-气综合能源系统经济性整体最优。本文所研究的电-气综合能源系统如图1所示,包括燃气轮机耦合环节、天然气网络、电力网络、燃煤机组以及负荷侧的电力负荷和天然气负荷。其中,燃气轮机是电力网络和天然气网络的纽带,在电力系统中可以视作电源,而在天然气网络中则被看成是天然气负荷。
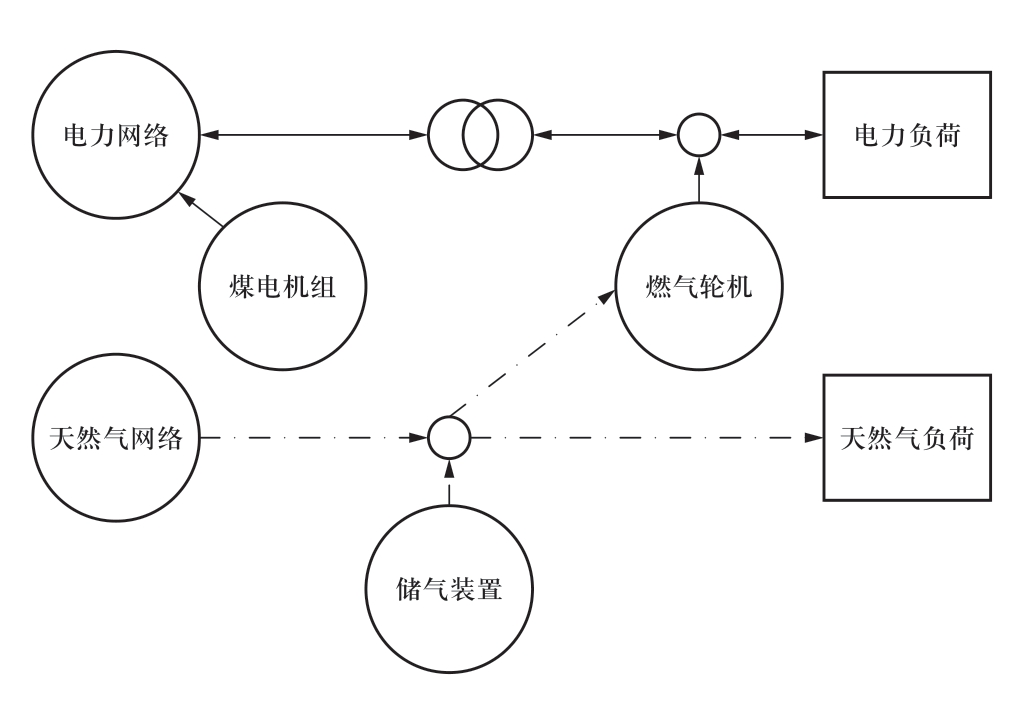
图1 电-气综合能源系统
Fig.1 Integrated electricity and natural gas systems
1.1 目标函数
考虑电-气综合能源系统的运行成本与碳交易成本,对应目标函数如下:
式中:F为电-气综合能源系统低碳经济调度的总成本,$;F1为电力系统的经济运行成本,$;F2为天然气系统的经济运行成本,$。F3为系统的环境成本,$。本文中计价单位为美元($)。
1.1.1 经济调度成本
电-气综合能源系统的经济调度成本包括电力系统中非燃气机组的能源消耗成本,天然气系统的气井生产成本和储气装置运营成本,可表示为式 (2) 和 (3)[14]:

式中:T为总调度段刻;Nf 、Nw和Ns分别为非燃气火电机组、天然气气井和天然气储气装置的个数;Qwt和Qst分别为t时刻天然气气井w的供气量和储存装置s的供气量,Mm3;ai、bi和ci为发电机的燃料成本系数,单位分别为$/MW2、$/MW和$;wρ和sρ为气井的生产成本系数和储气装置的运营成本系数,$/Mm3。
1.1.2 碳交易成本
碳交易是一种通过确立合法的碳排放权,并允许此类权利进行交易和出售来减少碳排放的交易机制。当排放源实际排放的CO2总量超过分配额度时,就需要购买碳排放额度;当排放源实际排放的CO2总量低于分配额度时,富余的碳排放额度可以用于出售获利[22-23]。不考虑在生产、运输等过程中产生的碳排放量,仅计及化石燃料机组碳排放的碳交易成本可表示为:
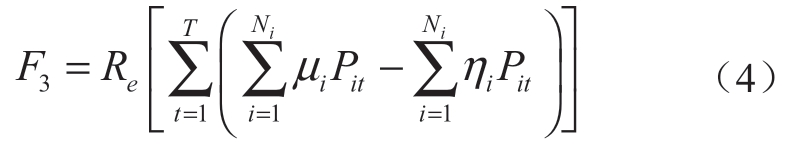
式中:Ni为化石燃料发电机数量;Re为单位碳排放的交易价格,$/t;iμ为发电机i单位有功出力的碳排放强度,m3/MWh;iη为发电机i单位有功出力碳排放配额,m3/MWh。
1.2 约束条件
1.2.1 电力系统约束
1)功率平衡约束

式中:ND为节点负荷总数量;Pit和Pdt分别为t时刻发电机i的输出功率和节点负荷d大小,MW。
2)机组的功率输出约束
式中:Pimin和Pimax为发电机i的最小输出功率和最大输出功率,MW。
3)爬坡约束
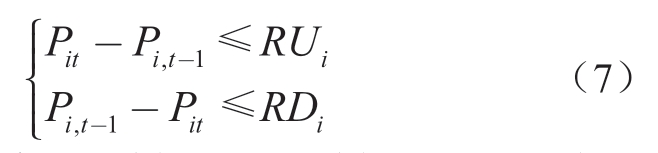
式中:Pit和Pi,t-1分别为t时刻和t-1时刻发电机i的输出功率,MW;RUi和RDi分别为发电机i的上爬坡率和下爬坡率,MW/15 min。
4)旋转备用约束
式中:SRt为t时刻发电机i的旋转备用容量,MW。5)线路传输功率约束
式中:PLit为t时刻线路i的传输功率,MW;PLimin和PLimax分别为线路i传输功率的下限和上限,MW。
为了降低本文数学模型的复杂程度,本文采用直流潮流的计算模型。
1.2.2 天然气系统约束
1)节点供需约束平衡
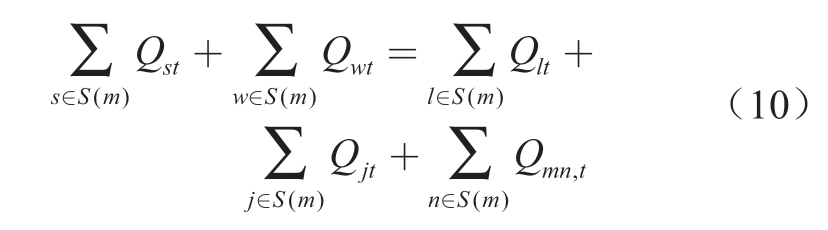
式中:S(m)为连接到天然气节点m的元件集合;Qlt为t时刻天然气负荷l的负荷量,Mm3;Qjt为t时刻燃气轮机j的天然气消耗量,Mm3;Qmn,t为t时刻节点m到n的天然气管道流量,Mm3。
2)传输管道的天然气流量模型
式中:Cmn,t为天然气管道特征常数,Mm3/bar;Pmt和Pnt分别为t时刻节点m和节点n的气压,bar。
式(11)和式(19)为非线性方程,故提出的模型为混合整数非线性规划问题,传统算法难以得到最优解。混合整数线性规划(MILP)技术可以解决高达数十万个变量的问题,并有许多相关的商业优化软件工具,如CPLEX。因此,本文采用分段线性化技术[24-25]来近似拟定调度模型中的非线性方程。
3)节点压力约束
式中:pn,min和pn,max分别为节点n承受压力的下限和上限,bar。
4)气井供气量约束
式中:Qw,min和Qw,max为气井供气量的下限和上限,Mm3。
5)储气装置约束
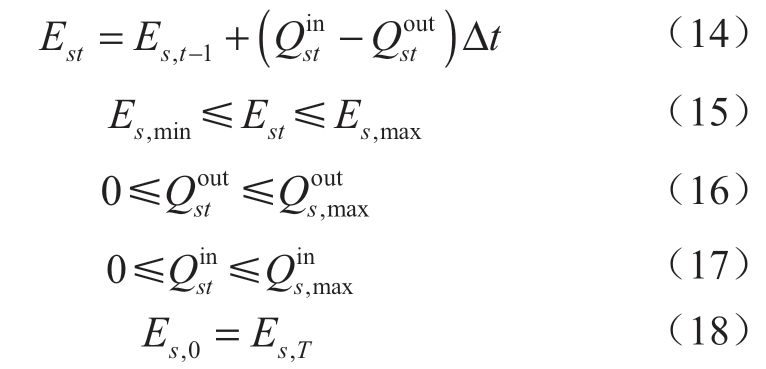
式中:Est为t时刻储气装置s的储气量,Mm3;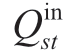 和
和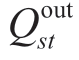 分别为t时刻储气装置s的进气量和出气量,Mm3/15 min;Es,min和Es,max分别为储气装置s的储气量下限和上限,Mm3;
分别为t时刻储气装置s的进气量和出气量,Mm3/15 min;Es,min和Es,max分别为储气装置s的储气量下限和上限,Mm3; 分别为储气装置s进气量的上限和出气量的上限,Mm3/15 min。Es,0和Es,T分别为储气装置s初始时刻的储气量和调度结束时刻的储气量,Mm3。
分别为储气装置s进气量的上限和出气量的上限,Mm3/15 min。Es,0和Es,T分别为储气装置s初始时刻的储气量和调度结束时刻的储气量,Mm3。
6)电力系统和天然气系统的耦合约束
本文中,电力和天然气系统通过燃气轮机耦合,其数学模型表示如下[3,10]:
式中:Qjt为t时刻燃气轮机 j消耗的天然气的量,Mm3;Pit为t时刻燃机轮机j的有功出力,MW;K1j、K2j和K3j为燃气轮机 j的热量系数,单位分别是Mm3/MW2、Mm3/MW和Mm3。
2 计及时段粒化的快速求解策略
2.1 时段粒化的理论描述
面对复杂的、难于准确把握的问题,人们通常不是采用系统的、精确的方法去追求问题的最佳解,而是通过逐步尝试的办法达到有限的、合理的目标,也就是取得所谓足够满意的解[26]。粒计算是一种由粗到细、不断求精的方法。通过对优化时段粒化,可以降低电-气综合能源系统低碳调度模型的维数,在满足一定精度的情况下加速模型求解速度。电-气综合能源系统低碳调度模型的时段粒化理论可描述为图2所示。
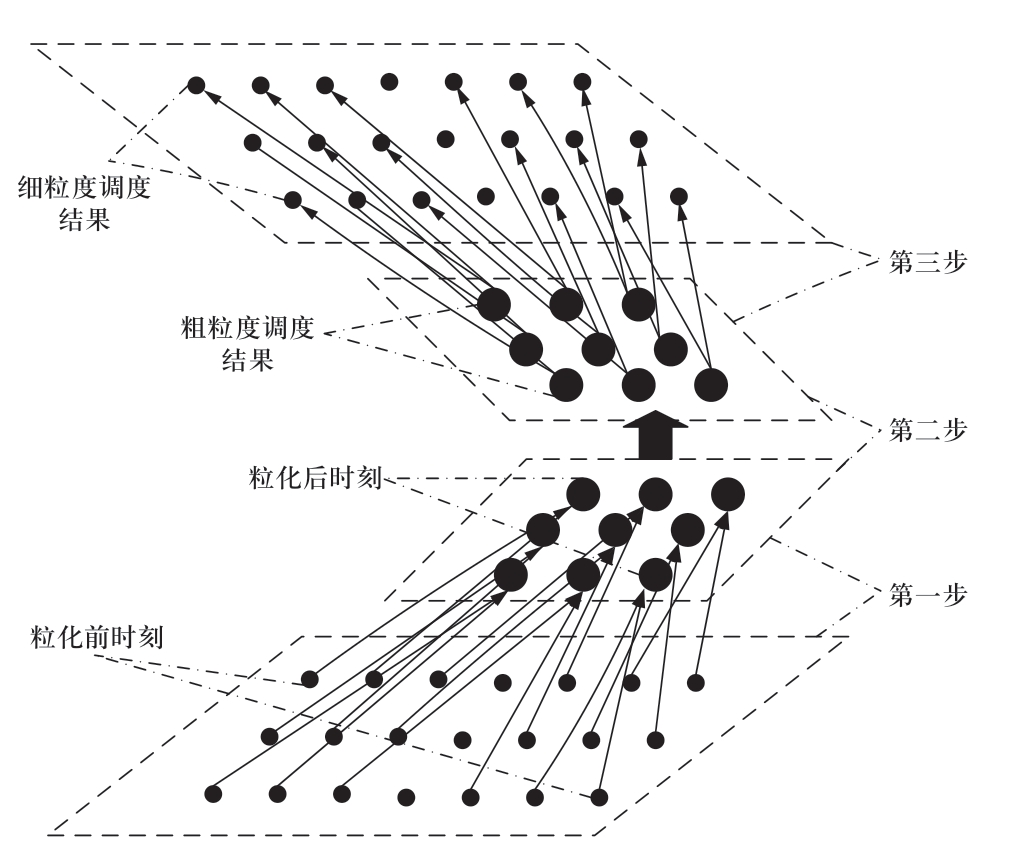
图2 时段粒化示意图
Fig.2 Sketch diagram of time interval granularity
根据粒化的电-气综合能源系统低碳调度周期,将优化时段粒化为:电-气综合能源系统运行时段粒子1、电-气综合能源系统运行时段粒子2、……、电-气综合能源系统运行时段粒子p,这些粒子构成了系统的粗粒度优化时段。
由公式 (20)和 (21)可知,时段粒化后,原电-气综合能源系统低碳优化调度模型的决策变量Xb降维为Xa,整个优化周期由原来的96个时段变为p个时段![]()
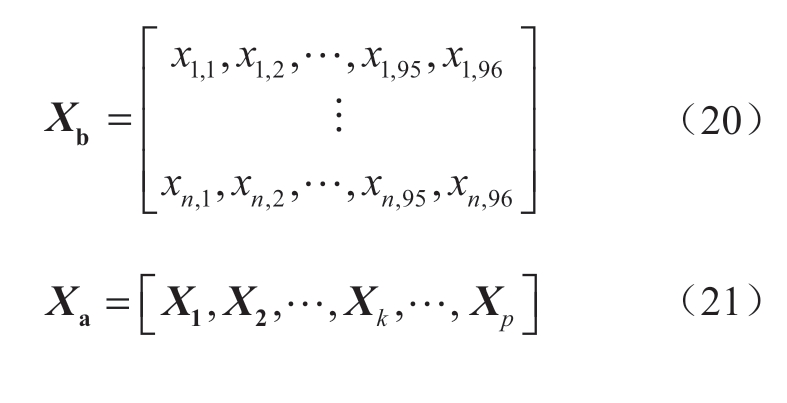
2.2 基于改进的k-means聚类粒度划分算法
粒计算主要包括粒化和粒的计算这两个步骤。为实现电-气综合能源系统低碳经济调度模型的时段粒化,本文结合k-means聚类算法的思想,设计了基于改进k-means聚类的粒度划分算法。该算法的基本思想是:在保证时间连续性的情况下,使得粒化为同一个粒子的决策变量之间的距离最小,从而最大程度保证精度。
因为k-means聚类对初始聚类点比较敏感,所以先通过最小距离的方法进行粗聚类,从而选出较好的初始聚类点。具体算法过程如下:
1)通过最短距离法[27]得到一个粗聚类结果。
2)计算每一簇粗聚类结果的中心,得到一组优化的k-means聚类的初始聚类中心![]()
3)通过小波分解把负荷数据分解成多尺度的数据集。
4)针对每个数据集中的样本xi,计算它到K个聚类中心的距离,并将其分到距离最小的聚类中心所对应的类中。
5)针对每个类别ci,重新计算它的聚类中心![]() (即属于该类所有样本的质心)。
(即属于该类所有样本的质心)。
6)重复第4)和5),直到聚类中心的位置不再变化,时段粒化结束。
7)把同一粒子决策变量求取的平均值,作为粒化后粒子的决策变量。
2.3 粗粒度的调度优化和调度结果的粒度细化
为了实现粒化后粒的求解,本文利用CPLEX求得在粒化后的决策变量Xa的条件下的调度结果。然后,为得到粒化前电-气综合能源系统的调度结果,需要把粒化后的调度结果进行粒度细化,细分准则如下:
1)在粗粒度划分时,如果一个时段单独成为一个粒子,则此时的粗粒度调度结果作为此时段的最后结果。
2)在粗粒度划分时,如果连续的几个时段成为一个粒子,那么把此时的粗粒度的调度结果作为这几个时段的最后结果。
计及时段粒化的模型求解流程如图3所示。
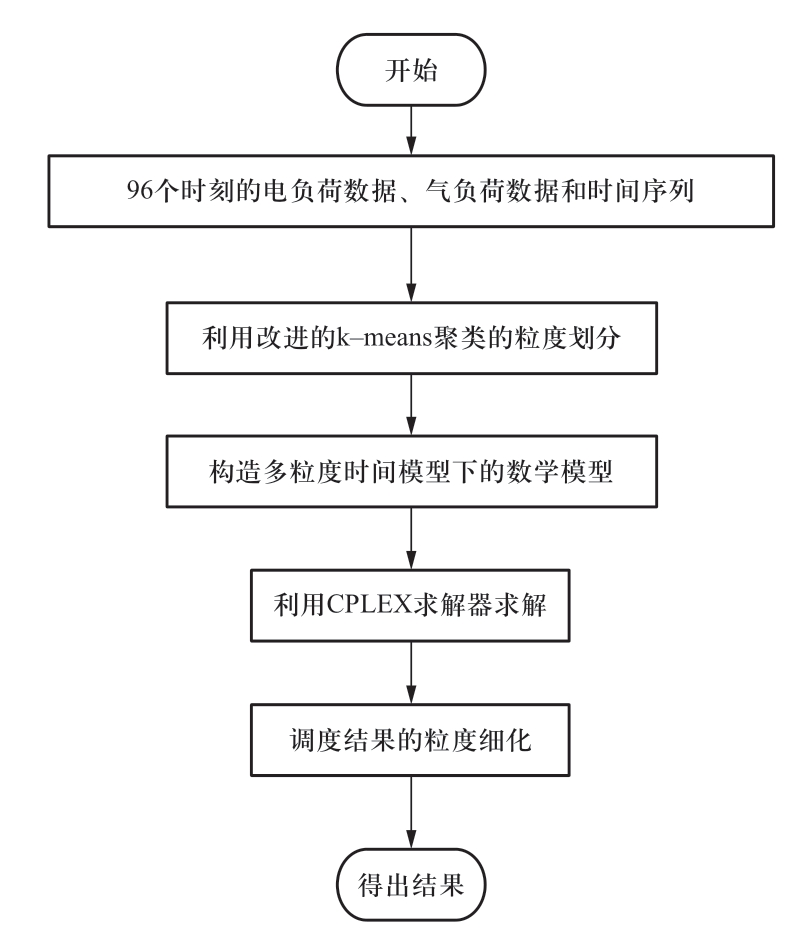
图3 求解流程图
Fig.3 Flowchart of solution procedure
3 算例分析
3.1 算例参数设置
本文采用IEEE 39节点电力系统和比利时20节点天然气系统进行算例分析,网络结构如图4所示。所有程序都在MATLAB 2014a平台上进行编码和测试,采用的商业求解器的版本为CPLEX 12.6,并且在具有Intel(R) Xeon(R) CPU E5-2620 v3(2.4 GHz)和64 GB RAM内存的PC上进行仿真分析。
电力系统中,G1、G7和G8是燃气轮机,它们分别连接到天然气节点5、14和2,其他的发电机均为燃煤发电机。天然气系统中,GW1和GW2为2个气源点,S1—S4为4个储气装置,C1—C3为压缩机,L1—L7为天然气负荷。
电-气综合能源系统的相关参数详见附录A,燃煤火电机组参数如表A1所示,电力系统线路参数如表A2所示,天然气网络管道参数如表A3所示,天然气网络节点参数如表A4所示,天然气网络气源点参数如表A5所示,天然气系统中燃气轮机参数如表A6所示。发电机单位有功出力的碳排放分配额为300 m3/MW,碳交易价格为82499.97 $/Mm3。算例中电气网络为电力系统主网的调度,电力负荷波动较平稳,调度周期的基础电力负荷预测曲线和天然气负荷预测曲线见附录B,如图B1所示。
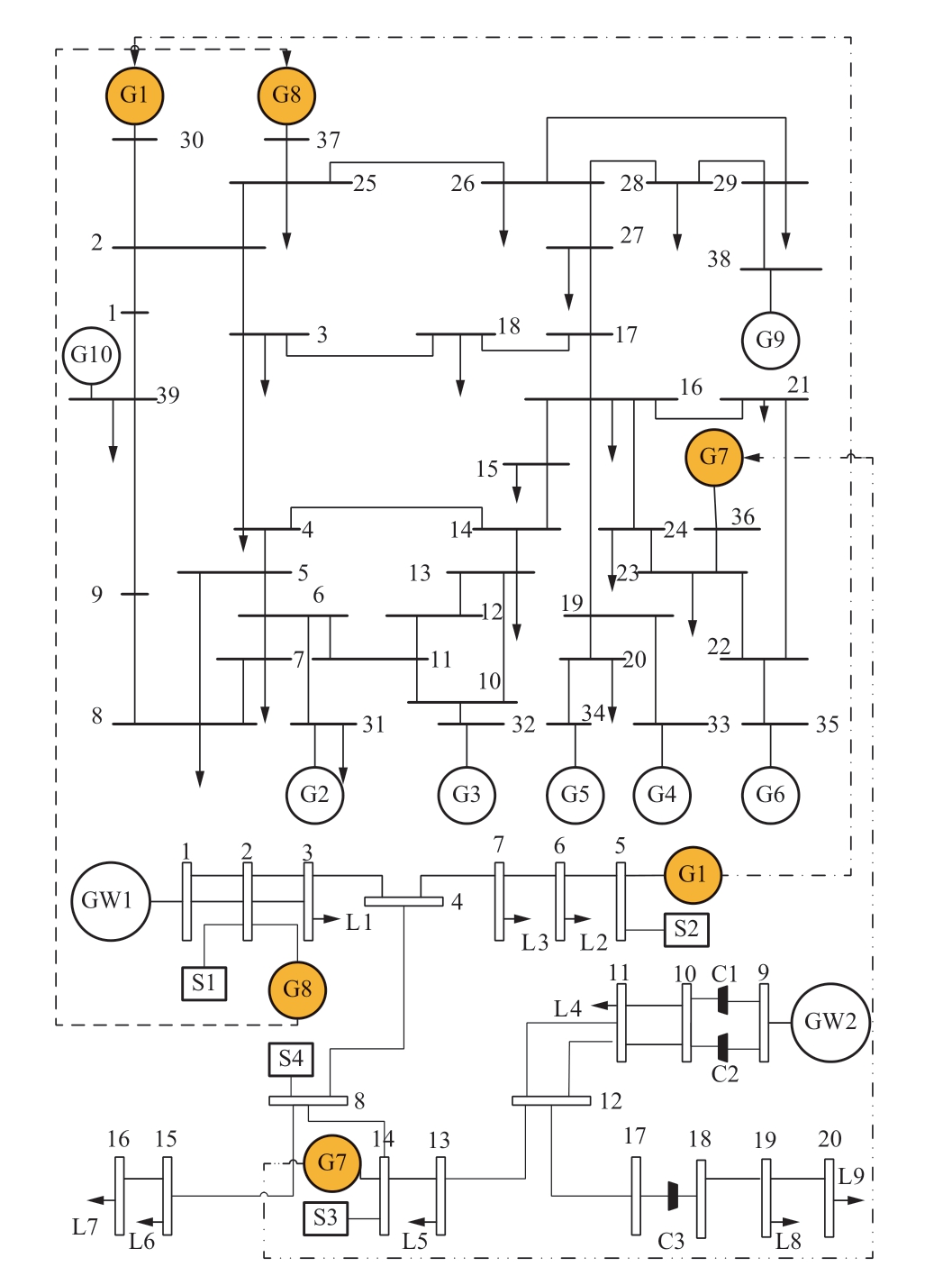
图4 39节点电力系统和20节点天然气系统
Fig.4 39-bus power system and 20-node natural gas system
3.2 算例结果
为了验证本文所提出模型和求解策略的有效性,设定4种模式并采用CPLEX求解器进行求解。4种模式如下:
模式一:如文献[2],仅考虑电力系统的能源消耗成本。
模式二:考虑电-气综合能源系统的总成本。
模式三:模式一条件下,引入本文提出的时段粒化求解策略,粒子数目分别为48个和72个。
模式四:模式二条件下,引入本文提出的时段粒化求解策略,粒子数目分别为48个和72个。
在模式一与模式二2种模式下,各台化石燃料发电机组的全天总出力的对比结果和各台燃气轮机的全天各个时刻出力对比结果分别如图5和图6所示。
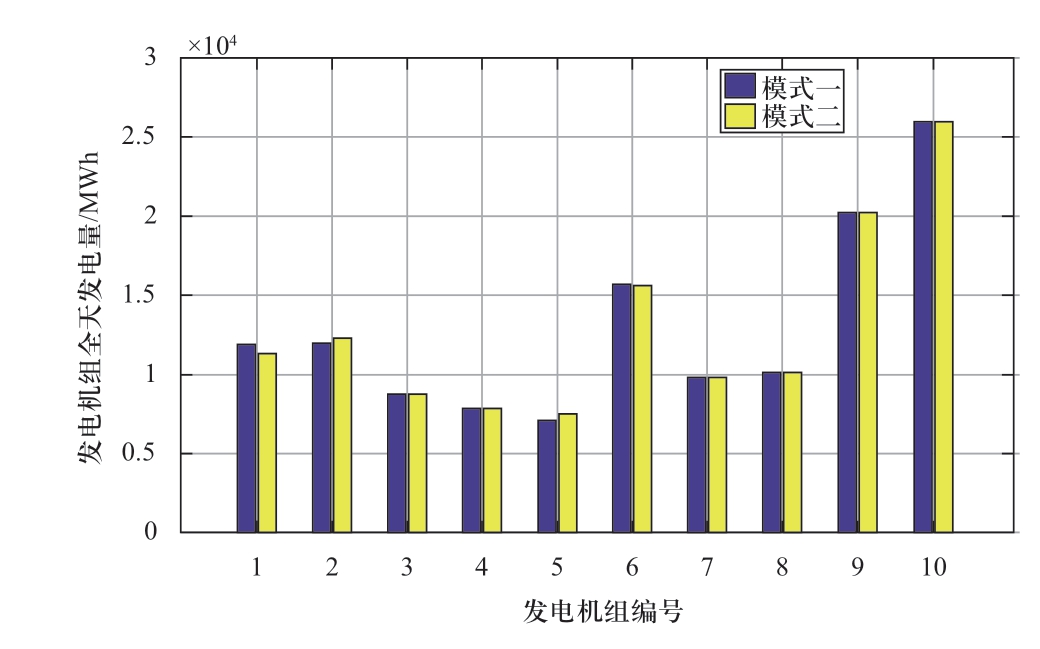
图5 模式一、模式二下各发电机组全天发电量
Fig.5 Full-day generation capacity of generating units under mode 1 and mode 2
由图5可知,由于模式一中没有考虑天然气网络约束,仅仅追求电力系统的能源成本和碳交易成本最优,导致燃气轮机G1的全天总发电量明显增加,相应的燃煤发电机G2和G5的全天总发电量有所减少,其他发电机变化幅度不大。
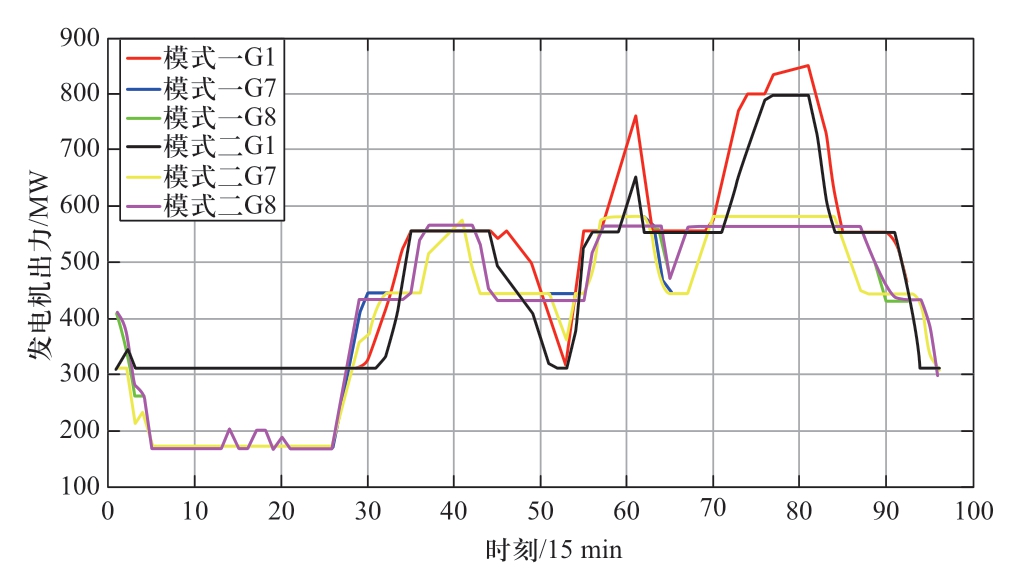
图6 模式一、模式二下燃气轮机的各个时刻出力
Fig.6 Gas turbine output at all times under mode 1 and mode 2
由图6可知,在电力负荷峰值时段54~63时刻和69~85时刻,燃气轮机G1的输出功率上升明显,而其他燃气轮机出力变化幅度不大。但是在其他时刻,所有燃气轮机的有功出力在2个模式下变化不是很明显。由此可见,在不考虑天然气网络约束的条件下,单纯地追求电力系统成本最优,电力负荷的增加会导致燃气轮机的有功出力增大,导致天然气系统运行的次最优。因此,单纯地考虑电力系统或者天然气系统单一运行均不能保证电-气综合能源系统整体最优,容易导致天然气系统运行的次最优,证明了本文提出电-气综合能源系统数学模型的有效性。
为了验证提出计及时段粒化求解策略的有效性,不同模式下的调度结果对比如表1所示。
表1 不同模式下调度结果对比
Table 1 Comparison of scheduling results under different modes
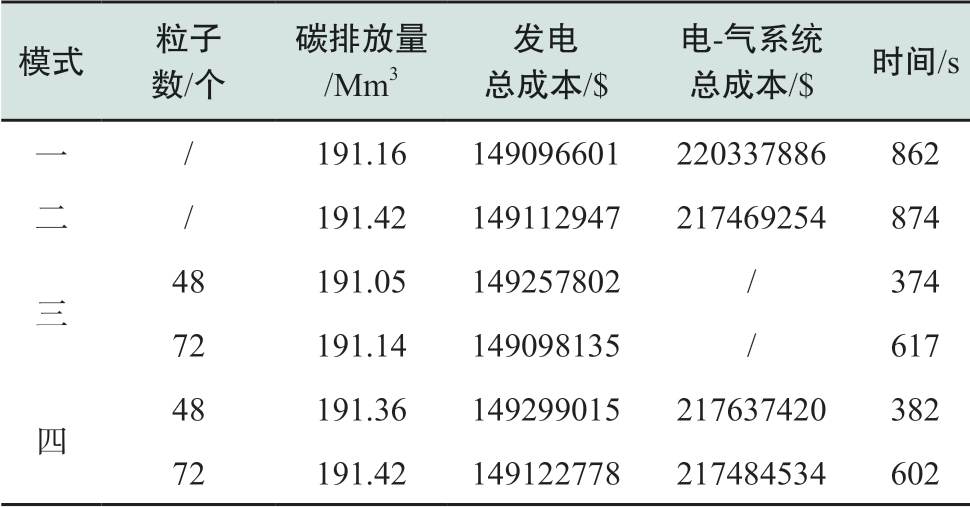
通过分析表1可知,在考虑天然气网络的成本时,由于燃气轮机出力有所下降,所以导致碳排放量有所上升,由原来的191.16 Mm3上升到191.42 Mm3,增加了0.26 Mm3,发电总成本也增加了$16346。但是,在模式一下电-气综合能源系统总成本为$220337886,而模式二下电-气综合能源系统总成本为$217469254,模式一较模式二成本增加$2868632,增加了1.3%。因此进一步证明考虑天然气网络成本的必要性。
模式三和模式四考虑了碳交易机制和时段粒化求解策略,调度结果如表2所示。
表2 模式三和模式四调度结果对比
Table 2 Comparison of scheduling results of mode 3 and mode 4

模式三中,当粒子数为48时,求解时间由原来的862 s降低到374 s,求解速度提高了56.84%,但是碳排放量的相对误差仅为-0.058%,发电的总成本相对误差为0.11%;当粒子数为72时,求解时间由原来的862 s降低到617 s,求解速度提高了28.42%,此时的求解精度更为准确,碳排放量的相对误差为-0.01%,发电总成本的相对误差仅为0.0010%。因此,本文提出的时段粒化求解策略,在牺牲可忽略的精度情况下,可以大幅度提高电力系统低碳经济调度模型的求解速度。
模式四中,当粒子数为48时,求解时间由原来的874 s降低到374 s,求解速度提高了57.21%,但是发电总成本相对误差为0.12%,电-气综合能源系统总成本相对误差为0.077%;当粒子数为72时,粒化结果详见附录A中表A7所示。其中,求解时间由原来的874 s降低到602 s,求解速度提高了31.12%,此时的求解精度更准确,发电总成本相对误差为0.0066%,电-气综合能源系统的总成本相对误差为0.0070%。因此,提出的时段粒化求解策略同样适用于电-气综合能源系统低碳经济调度模型。此外,粒子个数对最后的调度结果有一定影响。粒子数越多,最后结果精度越高,但是求解的时间会相应增加。
模式二和模式四下,各台发电机组的全天总出力情况和各个气井全天总供气量结果分别如图7和图8所示。
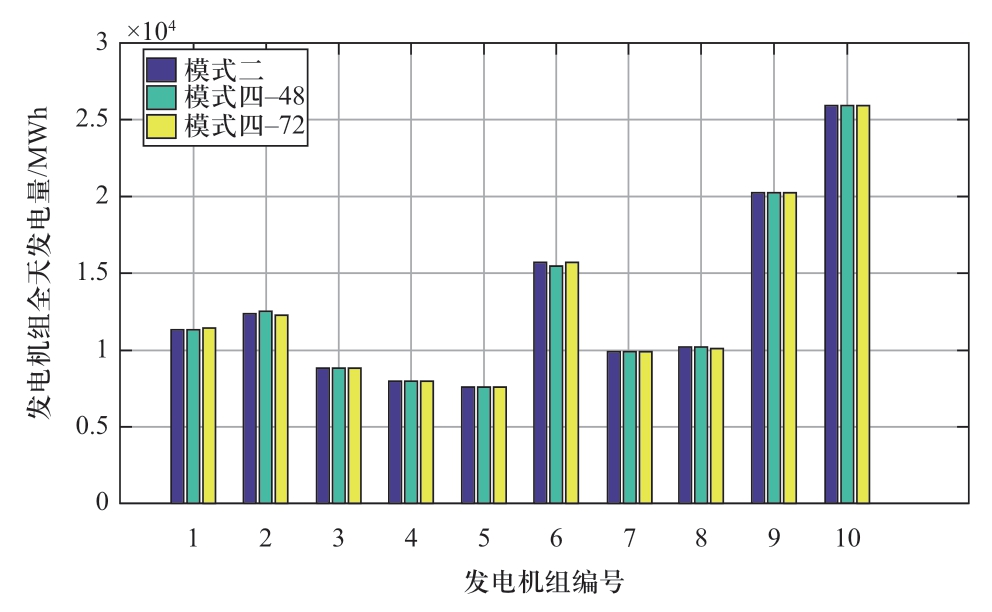
图7 不同模式各发电机组全天发电量
Fig.7 Full-day generation capacity of generating units in different modes
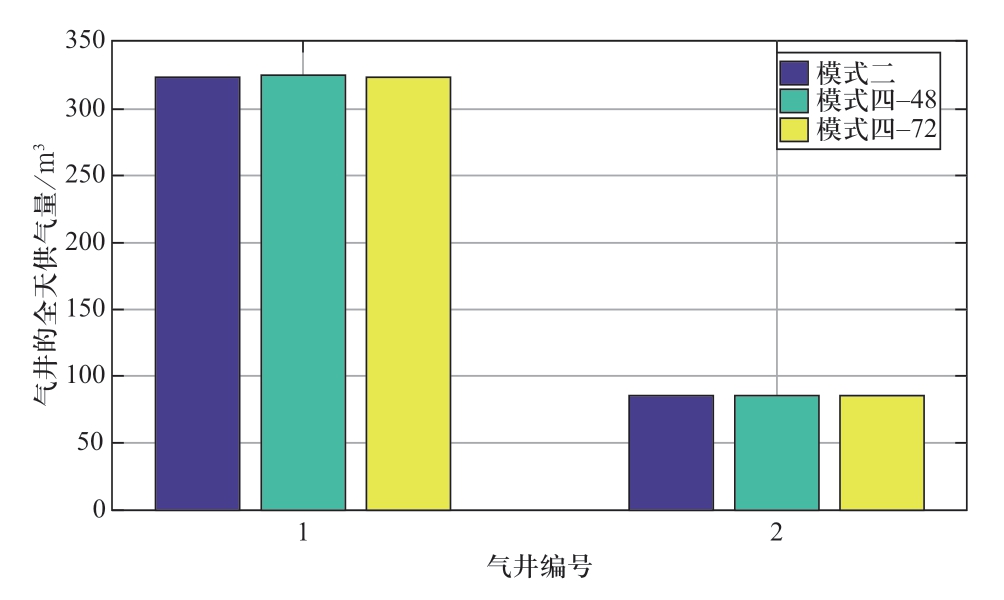
图8 不同模式下各个天然气气井全天供气量对比
Fig.8 Comparisons of full-day gas supply amounts for natural gas wells under different modes
分析图7和图8可以发现,考虑时段粒化求解策略后,发电机全天出力情况和气井的全天气流量变化幅度不大。电力系统以G2发电机为例,模式二下全天的输出功率为12240 MWh,模式四下48个粒子时全天的输出功率为12386 MWh,模式四下72个粒子时全天的输出功率为12215 MWh;天然气系统以气井1为例,模式二下全天的输出功率为323.48 Mm3,模式四下48个粒子时全天的输出功率为325.05 Mm3,模式四下72个粒子时全天的输出功率为323.69 Mm3。与模式二仿真结果相比,模式四中粒子数为72时仿真结果更加接近。通过分析结果可得,时段粒化求解策略对发电机全天出力和气井的全天气流量影响不大。
3.3 不同粒子数对调度结果的影响
通过3.2节可知,时段粒子数目与调度的最后结果有一定的关系。为了进一步探究粒子数目对调度结果的影响,本节对粒子数目从48到80的模型进行仿真分析。其中,求解时间与粒子个数的关系如图9所示,调度结果相对误差的绝对值与粒子数目的关系如图10所示。

图9 粒子数目与求解时间关系
Fig.9 Relationship between the number of particles and the solution time
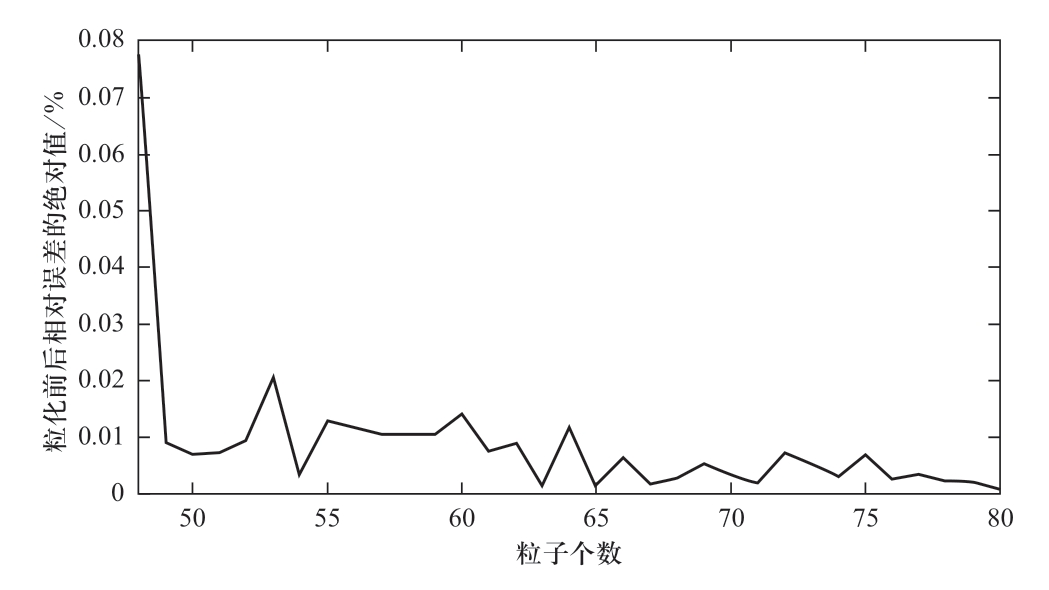
图10 粒子数目与结果相对误差关系
Fig.10 Relationship between the relative error of scheduling results and the number of particles
由图9可知,随着粒子数目的增加,求解的时间会增加,但是相应的最后调度结果的求解精度会提高。由图10可知,粒子数目较少时,由于不能准确反映实际情况,导致时段粒化前后调度结果相对误差的绝对值波动性较大。当粒子数达到65时,随着粒子数的增加,相对误差的波动性较小,且小于0.01%,已经达到相当准确的水平。因此调度人员可以根据对精度的要求恰当地选取粒子数,最后达到求解时间与求解精度的双赢。
4 结论
本文构建了基于碳交易机制的电-气综合能源系统的低碳经济调度模型,提出了考虑时段粒化的快速求解策略,通过仿真分析验证了提出模型和求解策略,得到结论如下:
1)仅考虑发电机能源成本的电-气综合能源系统模型,易导致天然气系统运行的次最优,而同时计及电力系统成本和天然气系统成本的低碳经济调度模型则更加合理。
2)提出的计及时段粒化求解策略,可以在兼顾求解精度的同时,显著提高模型求解速度。
3)计及时段粒化的求解策略中,粒子数目的选择对调度结果有一定的影响。随着粒子数目的增加,求解时间会相应增加,最后调度结果的求解精度也会相应提高。为兼顾求解精度与求解速度,调度人员可以根据实际情况需求与调度经验,选取合适的 粒子数。
4)时段粒化求解策略适用性较广,可同时适用于电力系统低碳经济调度和电-气综合能源系统低碳经济调度,也适用于其他的综合能源系统。
在下一步工作中,将寻求不同的粒化方法,提升提出方法的适用性,同时增加数学模型的复杂性,例如考虑机组组合模型、考虑天然气网络的动态特性等,探究快速求解策略在更加复杂的数学模型中的实用性。
附录 A
表A1 燃煤火电机组参数
Table A1 Parameters of coal-fired generators
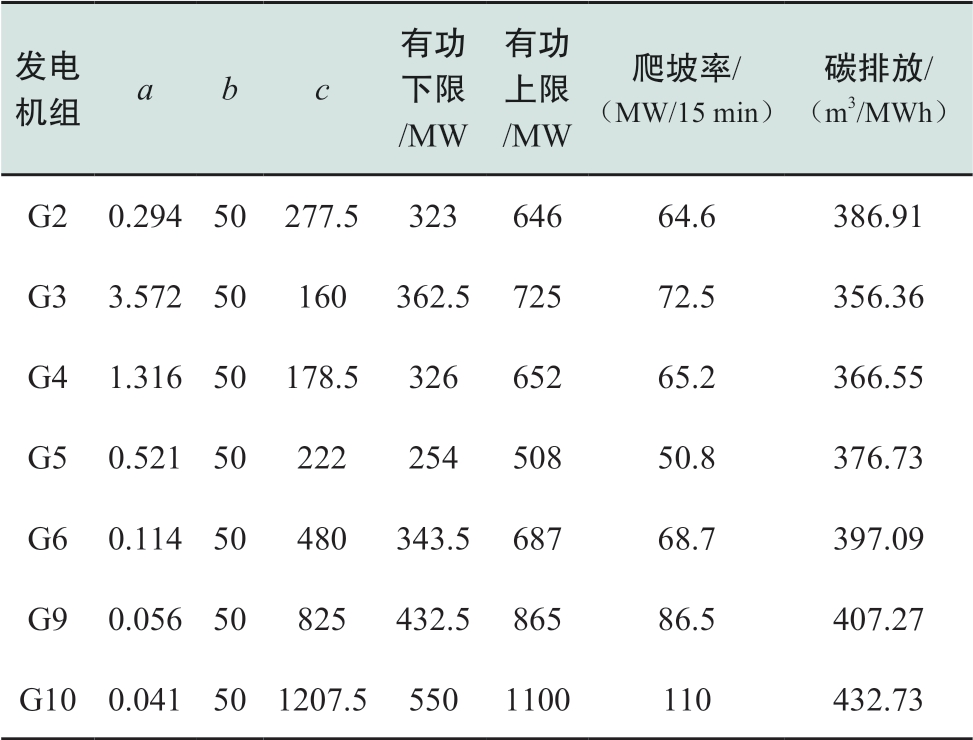
注:a单位:$/MW2,b单位:$/MW,c单位:$。
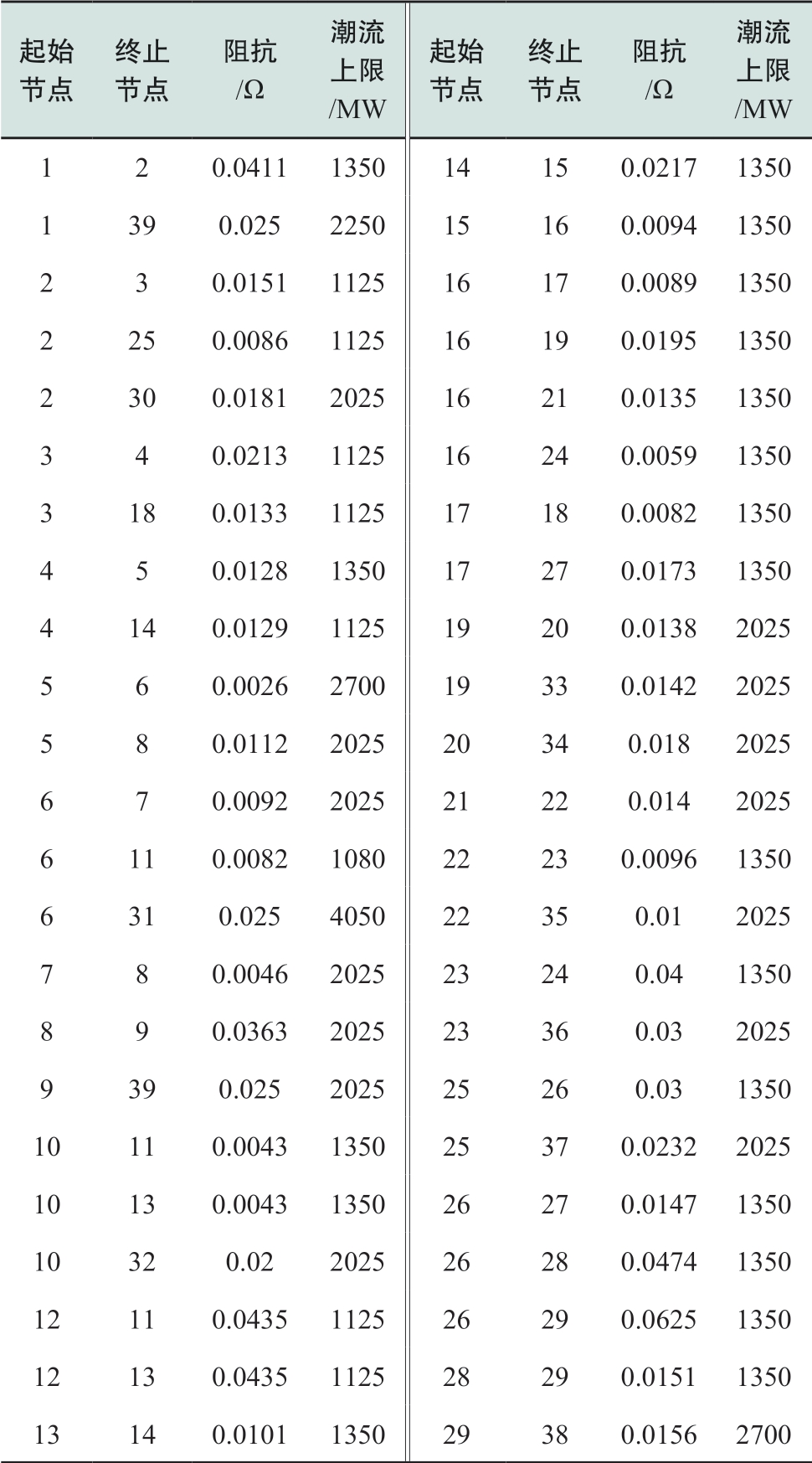
表A2 电力系统线路参数
Table A2 Line parameters of power system
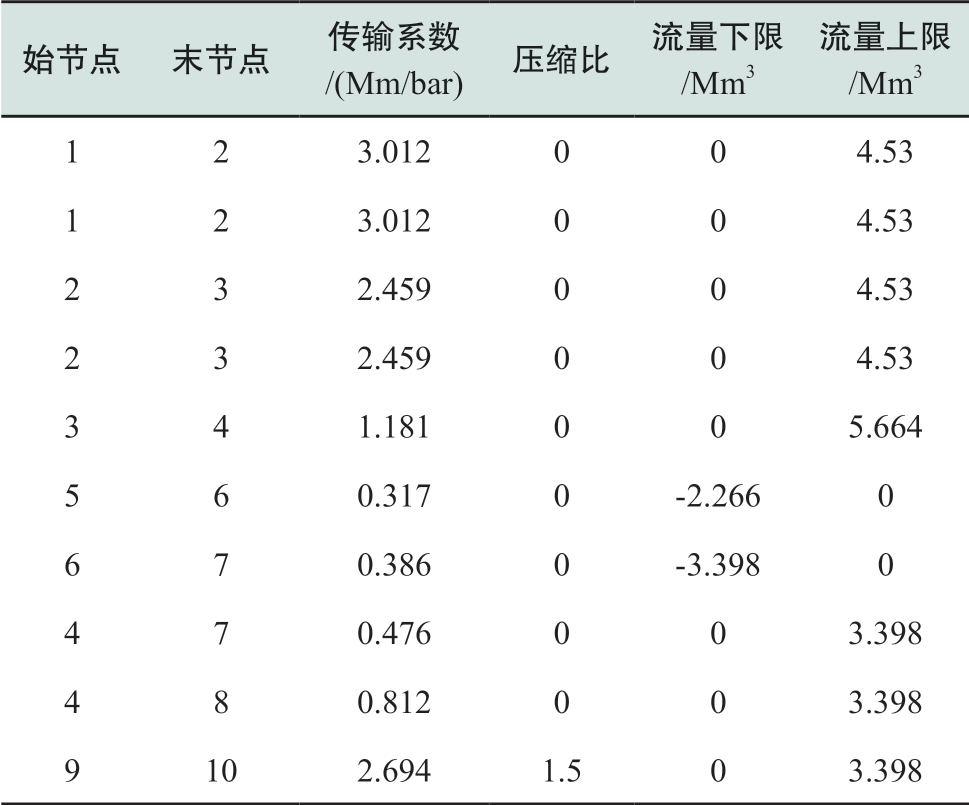
表A3 天然网络管道参数
Table A3 Pipwline parameters of natural gas network
续表
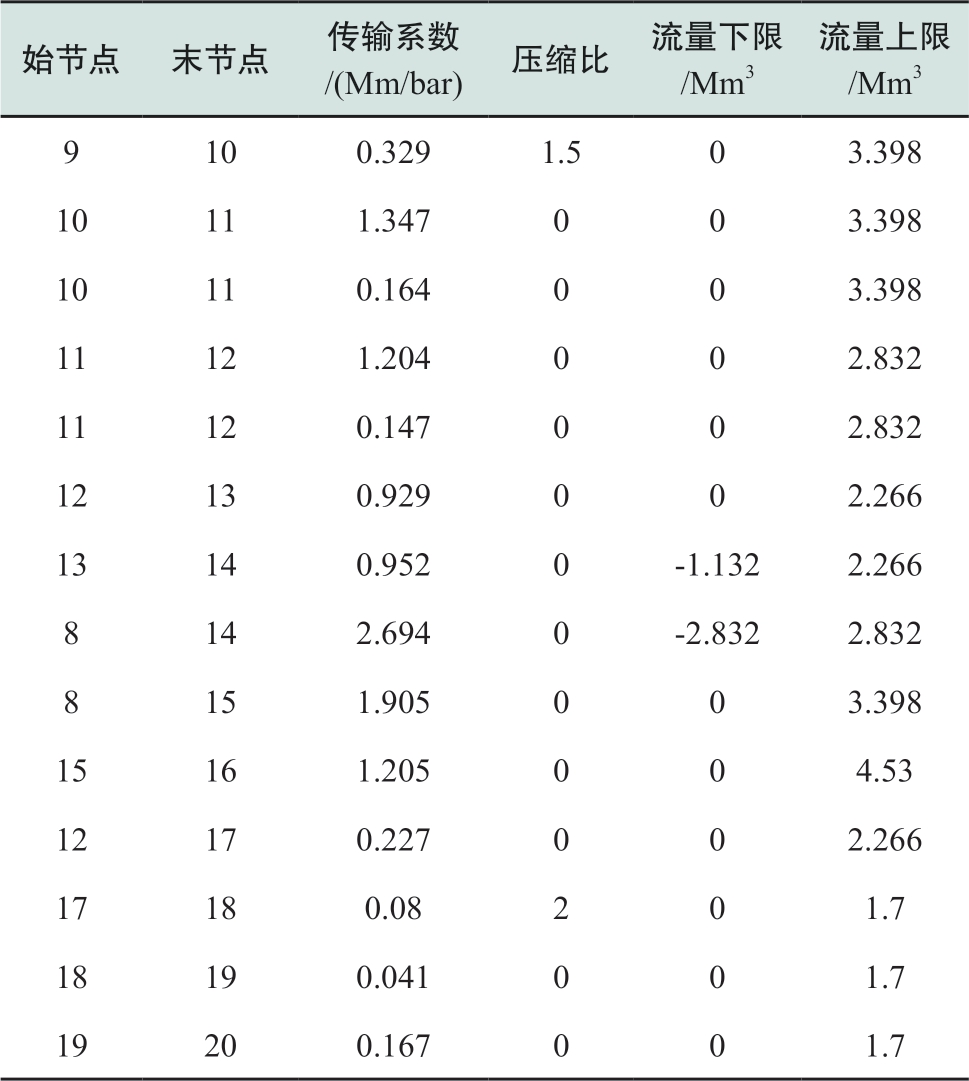
表A4 天然气网络节点参数
Table A4 Network node parameters of natural gas network

表A5 天然气网络气源点参数
Table A5 Parameters of gas production and storage point of natural gas network
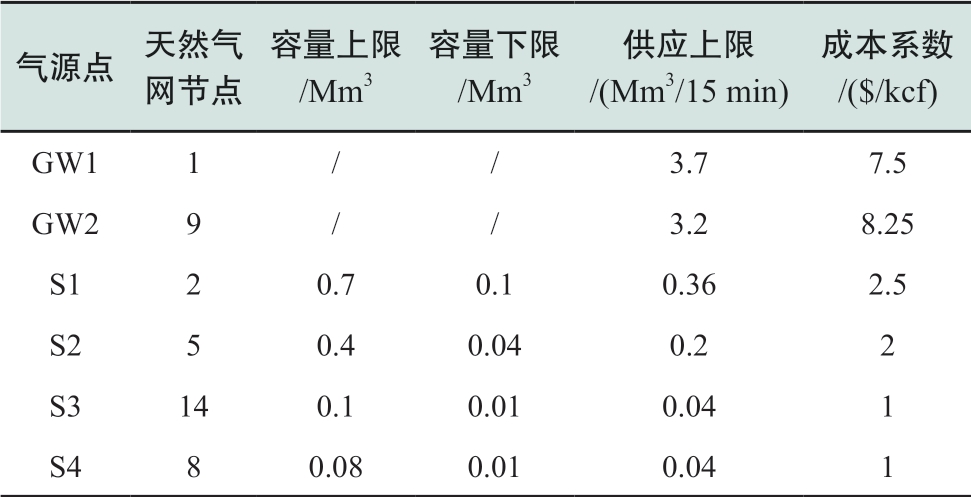
注:1 kcf=28.317 m3。
表A6 燃气轮机组参数
Table A6 Parameters of gas-fired generators
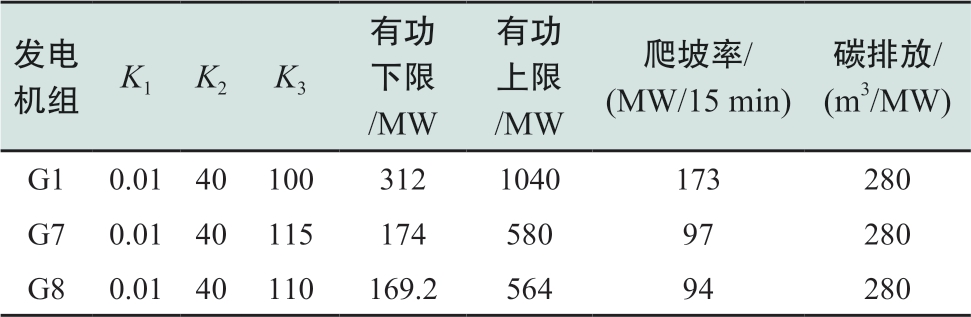
注:K1单位:m3/MW2,K2单位:m3/MW,K3单位:m3。
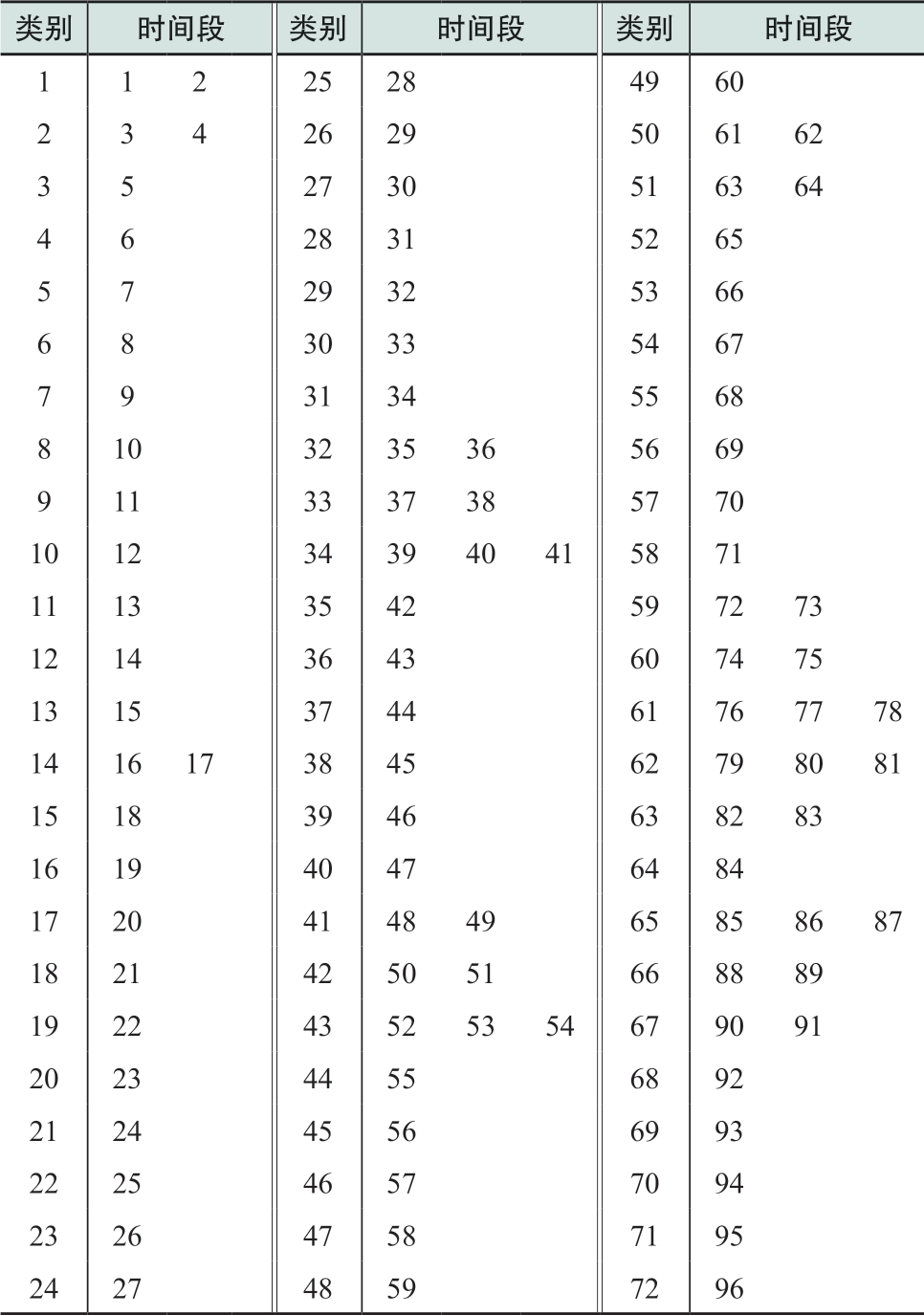
表A7 聚类结果
Table A7 Clustering results
附录 B
图B1 电负荷与气负荷的预测值
Fig.B1 Prediction value of electric load and gas load
参考文献
[1]Saboori H, Hemmati R.Considering carbon capture and storage in electricity generation expansion planning.IEEE Transactions on Sustainable Energy, 2016, 7(4):1371-1378.
[2]国家发展和改革委员会发展规划司.天然气发展“十三五”规划[EB/OL].北京:中华人民共和国国家发展和改革委员会,2017,[2017-06-07].http://www.ndrc.gov.cn/fzgggz/fzgh/ghwb/gjjgh/201706/W020170607564599576985.pdf.
[3]An S, Li Q, Gedra T W.Natural gas and electricity optimal power flow[C].Transmission and Distribution Conference and Exposition, 2003 IEEE PES, 138-143.
[4]Unsihuay C, Lima J W M, Souza A C Z D .Modeling the integrated natural gas and electricity optimal power flow[J].IEEE Power Engineering Society General Meeting, 2007, 1:1-7.
[5]王伟亮,王丹,贾宏杰,等.考虑天然气网络状态的电力-天然气区域综合能源系统稳态分析[J].中国电机工程学报,2017,37(5):1293-1305.Wang Weiliang, Wang Dan, Jia Hongjie, et al.Steady state analysis of electricity-gas regional integrated energy system with consideration of NGS network status[J].2017, 37(5): 1293-1305(in Chinese).
[6]Wen Y, Qu X, Li W, et al.Synergistic operation of electricity and natural gas networks via ADMM[J].IEEE Transactions on Smart Grid, 2018, 9(5): 4555-4565.
[7]瞿小斌,文云峰,叶希,等.基于串行和并行ADMM算法的电-气能量流分布式协同优化[J].电力系统自动化,2017,41(4):12-19.Qu Xiaobin, Wen Yunfeng, Ye Xi, et al.Distributed optimization of electric-gas integrated energy flow using serial and parallel iterative modes for alternating direction method of multipliers[J].Automation of Electric Power Systems, 2017, 41(4):12-19(in Chinese).
[8]He Y, Yan M, Shahidehpour M, et al.Decentralized optimization of multi-area electricity-natural gas flows based on cone reformulation[J].IEEE Transactions on Power Systems, 2018, 33(4): 4531-4542.
[9]程耀华,张宁,康重庆,等.低碳多能源系统的研究框架及展望[J].中国电机工程学报,2017,37(14):4060-4069+4285.Cheng Yaohua, Zhang Ning, Kang Chongqing, et al.Research framework and prospects of low-carbon multiple energy systems[J].Proceedings of the CSEE, 2017, 37(14): 4060-4069+4285(in Chinese).
[10]卫志农,张思德,孙国强,等.基于碳交易机制的电-气互联综合能源系统低碳经济运行[J].电力系统自动化,2016,40(15):9-16.Wei Zhinong, Zhang Side, Sun Guoqiang, et al.Carbon trading based low-carbon economic operation for integrated electricity and natural gas energy system[J].Automation of Electric Power Systems, 2016, 40(15): 9-16(in Chinese).
[11]秦婷,刘怀东,王锦桥,等.基于碳交易的电—热—气综合能源系统低碳经济调度[J].电力系统自动化,2018,42(14):8-13+22.Qin Ting, Liu Huaidong, Wang Jinqiao, et al.Carbon trading based low-carbon economic dispatch for integrated electricityheat-gas energy system[J].Automation of Electric Power Systems, 2018, 42(14): 8-13+22(in Chinese).
[12]Qiu J, Dong Z Y, Zhao J H, et al.Low carbon oriented expansion planning of integrated gas and power systems[J].IEEE Transactions on Power Systems, 2015, 30(2):1035-1046.
[13]Qu K, Yu T, Huang L, et al.Decentralized optimal multienergy flow of large-scale integrated energy systems in a carbon trading market[J].Energy, 2018, 149: 779-791.
[14]He L, Lu Z, Zhang J, et al.Low-carbon economic dispatch for electricity and natural gas systems considering carbon capture systems and power-to-gas[J].Applied Energy, 2018, 224: 357-370.
[15]Y.Y.Yao, Perspectives of granular computing[C].Proc.IEEE Int.Conf.Granul.Comput., Jul.2005, 1: 85-99.
[16]O.Hryniewicz, K.Kaczmarek, Bayesian analysis of time series using granular computing approach[J].Applied Soft Computing, 2016, 47: 644-652.
[17]J.Juszczyk, E.Pietka, B.Pyciński, Granular computing in model based abdominal organs detection[J].Computerized Medical Imaging and Graphics, 2015, 46: 121-130.
[18]A.Gacek, Granular modelling of signals: A framework of granular computing[J].Information Sciences, 2013, 221: 1-11.
[19]L.Zhang, F.G.He, Y.P.Zhang, et al, A new algorithm for optimal path f inding in complex networks based on the quotient space[J].Fund.Inf., 2009, 93(4): 459-469.
[20]Li X, Fang L, Lu Z, et al.A line flow granular computing approach for economic dispatch with line constraints[J].IEEE Transactions on Power Systems, 2017, 32(6): 4832-4842.
[21]张鹏,张旭涵,张铭洋.粒计算在电力系统优化调度中的应用探索[J].东北电力技术,2016,37(1):27-29.Zhang Peng, Zhang Xuhan, Zhang Mingyang.Application on granular computing in optimal dispatch of power system[J].Northeast Electric Power Technology, 2016, 37(1): 27-29(in Chinese).
[22]卢志刚,杨宇,耿丽君,等.基于Benders分解法的电热综合能源系统低碳经济调度[J].中国电机工程学报,2018,38(7):1922-1934+2208.Lu Zhigang, Yang Yu, Geng Lijun, et al.Low-carbon economic dispatch of the integrated electrical and heating systems based on Benders decomposition[J].Proceedings of the CSEE, 2018, 38(7): 1922-1934+2208(in Chinese).
[23]王信,袁方.碳排放权交易中的排放权分配和价格管理[J]. 金融发展评论,2010(11):48-57.Wang Xin, Yuan Fang.Carbon emission allocation and price management in emission trading scheme[J].Financial Development Comment, 2010(11): 48-57(in Chinese).
[24]Correa-Posada CM, Sánchez-Martin P.Integrated power and natural gas model for energy adequacy in short-term operation[J].IEEE Transactions on Power Systems, 2015, 30(6): 3347-3355.
[25]胡源,别朝红,李更丰,等.天然气网络和电源、电网联合规划的方法研究[J].中国电机工程学报,2017,37(1):45-54.Hu Yuan, Bie Zhaohong, Li Gengfeng, et al.Integrated planning of natural gas network and composite power system[J].Proceedings of the CSEE, 2017, 37(1): 45-54(in Chinese).
[26]张燕平,张铃,吴涛.不同粒度世界的描述法—商空间法[J].计算机学报,2004,27(3):328-333.Zhang Yanping, Zhang Ling, Wu Tao.A description method of different granularity world-quotient space method[J].Chinese Journal of Computers, 2004, 27(3): 328-333(in Chinese).
[27]谢中华.MATLAB统计分析与应用:40个案例分析[M].北京:北京航空航天大学出版社,2010:319-322.Xie Zhonghua.Statistical analysis and application of MATLAB: an analysis of 40 cases[M].Beijing: Beihang University Press, 2010: 319-322(in Chinese).
Low-carbon Economic Dispatch of Integrated Electricity and Natural Gas Systems Considering Period Granulation
LU Zhigang, LIU Haoran, HE Liangce
(Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province, Yanshan University,Qinhuangdao 066004, Hebei Province, China)
Abstract: The increasing installed capacity of gas turbines has promoted the research on the joint dispatch of integrated electricity and natural gas energy systems.To reduce carbon emission and improve the convergence speed, this paper proposes a low-carbon economic dispatch strategy for integrated electricity and natural gas energy systems that considers the granulation of time periods.Firstly, the low-carbon scheduling model of the integrated electricity and natural gas energy systems is established under the carbon trading mechanism.Secondly, a fast solving strategy, i.e.the granulation of time periods, is proposed.This strategy uses the improved k-means clustering method to granulate the 96 scheduling periods, which can accelerate the convergence speed of the presented model.Finally, the simulation is carried out on the 39-bus power system and 20-node natural gas system, and the simulation results have verified the feasibility and effectiveness of the proposed model and the solution strategy.
Keywords: granulation of time period; integrated electricity and natural gas systems; carbon trading; rapid solution; low-carbon
National Natural Science Foundation of China (61873225, 61374098); National Natural Science Foundation of Hebei Province (F2016203507); Provincial Graduate Innovation Assistant Project 2018 (023000307).
文章编号:2096-5125 (2019) 03-0266-11
中图分类号:TM73
文献标志码:A
DOI:10.19705/j.cnki.issn2096-5125.2019.03.008
基金项目:国家自然科学基金(61873225,61374098);河北省自然科学基金京津冀合作专项项目(F2016203507);2018年省级研究生创新助手项目(023000307)。
收稿日期:2019-02-26;修回日期:2019-04-14。

卢志刚
作者简介:
卢志刚(1963),男,教授,博士生导师,主要从事电力系统经济运行与分析研究,本文通讯作者,E-mail:zhglu@ysu.edu.cn。
刘浩然(1993),男,硕士,研究方向为电力系统经济调度,电-气综合能源系统低碳经济调度,E-mail:975057599@qq.com。
(责任编辑 李锡)