0 引言
中国幅员辽阔,而且资源分布不均衡,直流输电工程送端一般位于火电或水电资源丰富的地区,其中一些地区交流电网较为薄弱,为典型的直流输电连接于弱交流系统的接线方式。弱系统对直流输电的影响,目前的研究主要集中在无功设备过剩引起的过电压以及故障后恢复特性上,而对控制保护本身的影响研究不多。
由于变压器励磁涌流或和应涌流引起50 Hz保护动作的问题已有不少文献进行过研究[1-5],目前工程中对此问题也有较为深刻的认识并采取了一些措施,例如采用断路器选相分合闸装置或回路中串入合闸电阻等,实际应用效果也令人满意。但是,实际运行中发现如果是由于交流系统弱原因引起的50 Hz分量,本质上是电压谐波,上述针对励磁涌流的措施仍然不能奏效。例如某双回直流在系统调试期间送端交流系统为弱系统,发生了多次50 Hz 保护动作的事例[4],其中有一次励磁涌流并不大,但是由于交流电网薄弱,仍然在直流侧产生了较大的50 Hz谐波。由于该直流有4个极,有一个以上极在运行同时进行另一个极的换流变充电是常规操作,因此如何避免充电时50 Hz保护误动是一个急需解决的问题。同样连接于弱交流系统的国网青藏直流工程,在现场也发生了交流电网主变充电引起谐波保护误动的事例[8-9]。
目前针对弱交流系统下50 Hz保护的分析文献较少,本文在直流现场问题的分析基础上,从保护定值优化和保护逻辑优化两个方面对弱交流系统条件下50 Hz保护的优化措施进行了研究,并通过RTDS仿真试验,对保护逻辑优化方案进行了验证,试验结果表明该方案可以准确区分直流电流中的50 Hz分量是由于交流系统原因产生还是直流系统原因产生,优化后的50 Hz保护可以有效避免弱系统情况下换流变或邻近变压器充电引起的误动。
150 Hz保护动作事例分析
1.150 Hz保护原理和定值
50 Hz保护主要是作为换相失败、阀触发回路故障或阀体故障的后备保护[1],其动作方程为:
式中:IdN为阀厅低压侧互感器测量值,IdN_50为IdN的50 Hz分量值,保护动作策略分报警、切换、降功率和跳闸,除报警段外各段动作定值相同,但动作延时不同。
50 Hz保护的定值主要考虑与换相失败、阀区故障主保护配合,由于多种故障会引起50 Hz分量增大,一般动作段时间取的较大,以避免多极停运。
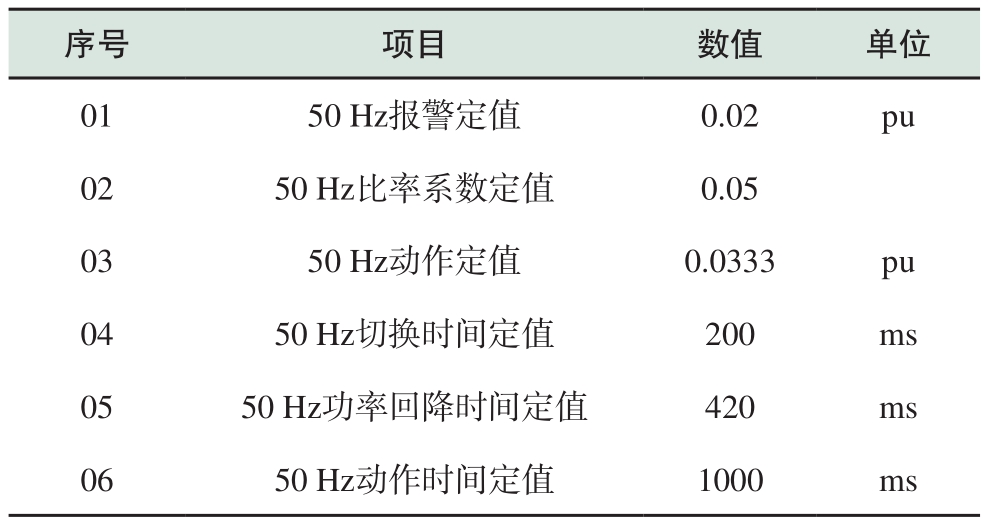
直流50 Hz保护的定值如表1所示,其中动作定值已经参考文献[3]的建议从0.02提高到了0.0333。
表1 直流50 Hz保护定值
Table 1 50 Hz protection settings
1.2 现场动作情况分析
2014年4月14日、5月19日和6月2日该直流分别发生了50 Hz保护动作的事例,其中6月2日为甲线极1直流双极运行,乙线极2换流变首次充电,保护动作波形如图1和图2所示(以甲线极1为例),运行电流为960 A,额定电流为3200 A,50 Hz保护动作门槛计算值为:960×0.05+0.0333×3200=154.5 A。

图1 整流侧50 Hz保护动作波形图
Fig.1 Diagram for 50 Hz protection waveform of rectifier-side
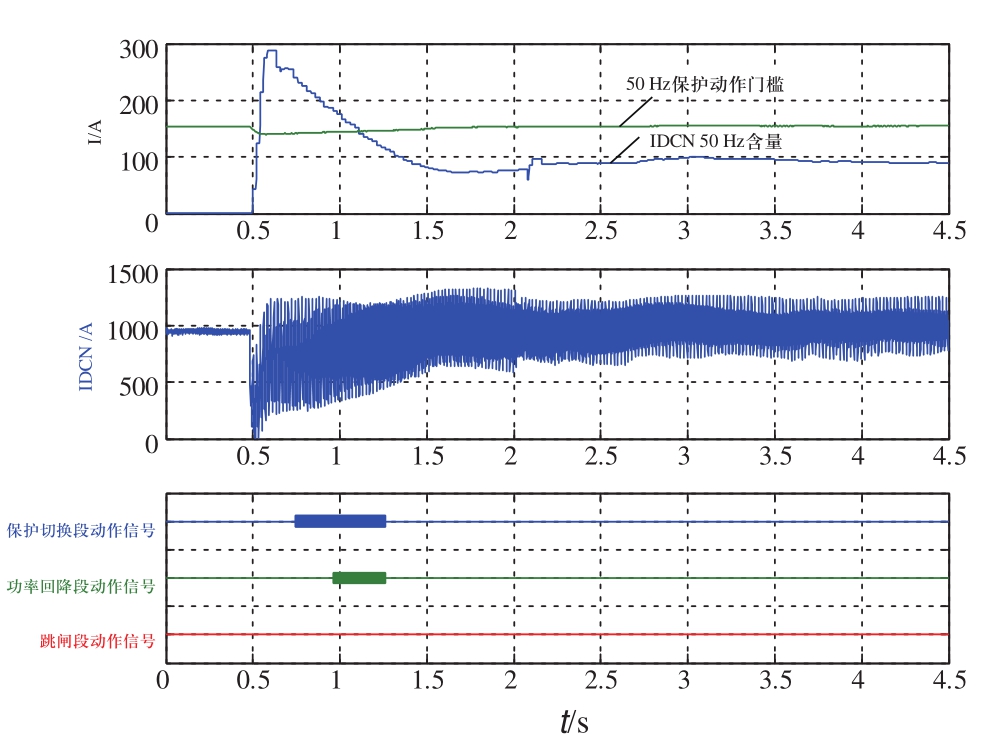
图2 逆变侧50 Hz保护动作波形图
Fig.2 Diagram for 50 Hz protection waveform of inverter-side
从波形可以看出,整流侧直流电流中50 Hz分量峰值略高于100 A,未达到定值,因此保护没有动作。
而逆变侧直流电流中50 Hz分量峰值将近300 A,已经超过保护定值,因此保护正确动作。首先是切换段动作,极控正确进行了切换,然后是功率回降段动作,由于当前功率正好是0.3 pu,实际未进行降功率。
1.3 现场动作原因分析
该直流送端交流系统较弱,联网运行时短路电流约为12 kA,系统调试期间电厂开机不足,短路电流小于7 kA[4]。3次事例均在系统调试期间发生,保护动作情况类似,但起因有所不同,4月14日为站内换流变首次充电,选相合闸装置参数未配置完善,充电时励磁涌流很大。5月19日为邻近电厂主变充电,造成站内交流电压畸变严重。6月2日也是站内换流变首次充电,当时选相合闸装置的参数已经配置完善,励磁涌流只有600多A,但由于交流电网薄弱,站内交流电压畸变严重,仍然在直流侧造成较大的50 Hz谐波。
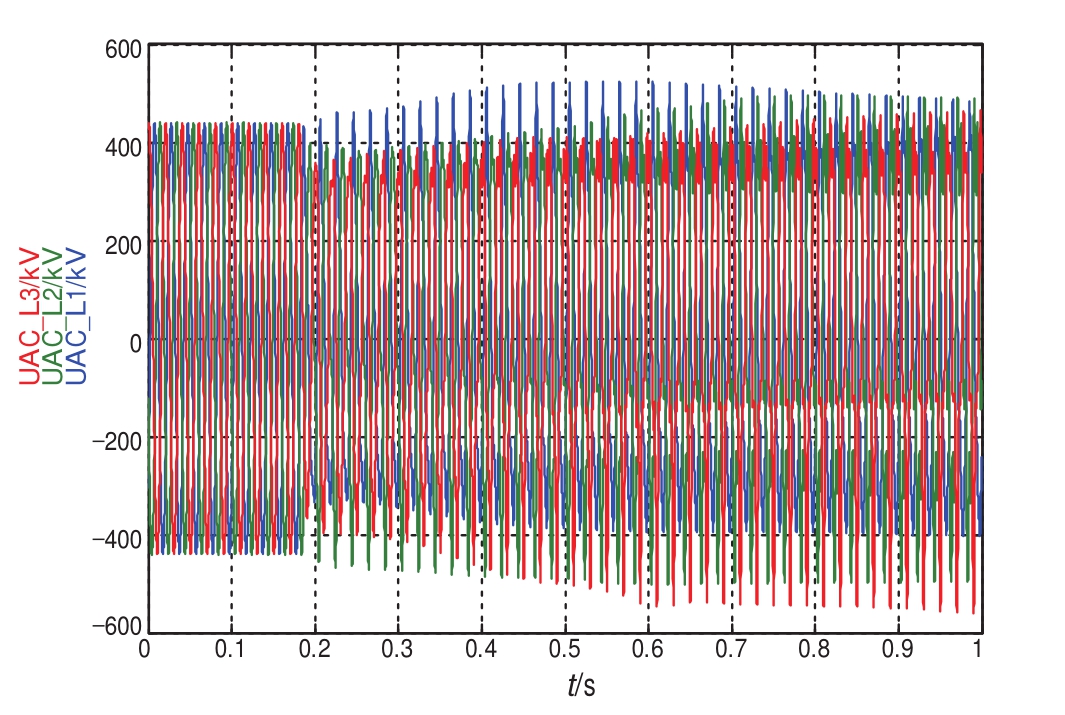
图3 乙线极2充电时甲极1UAC波形
Fig.3 Diagram for AC Voltage(UAC)waveform while transformer energizing
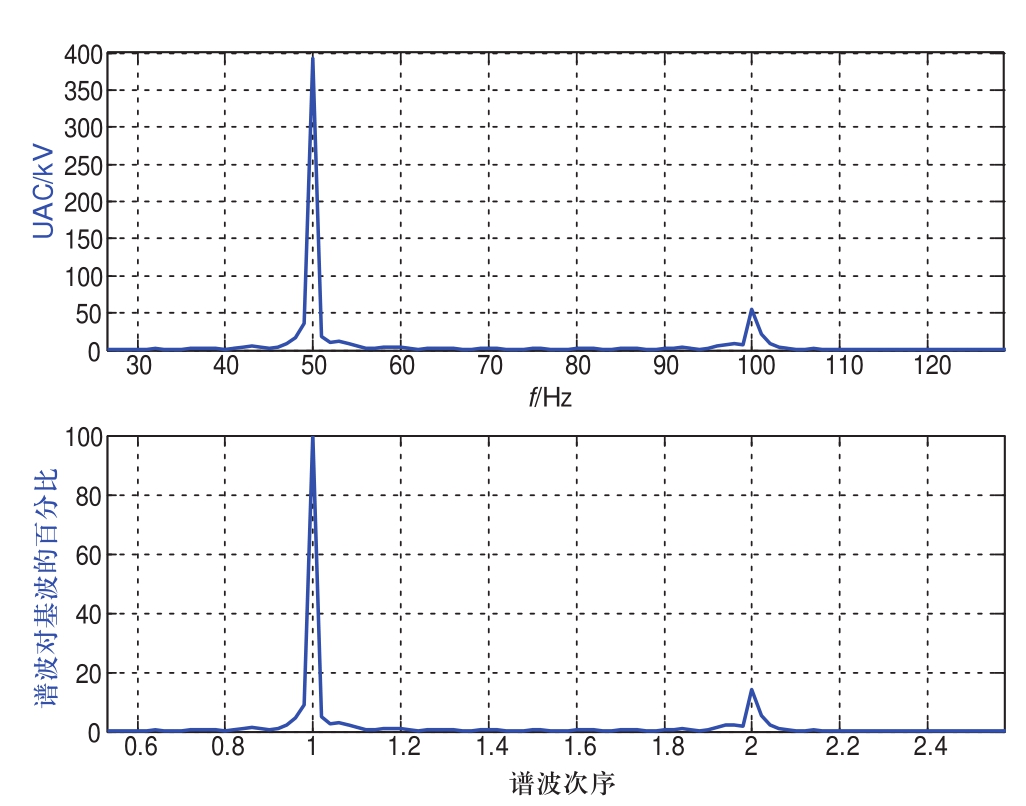
图4 乙线极2充电时甲线极1UAC频谱分析波形
Fig.4 Diagram for AC Voltage(UAC)spectral analysis waveform while transformer energizing
图3为6月2日乙线极2充电时甲极1的UAC波形,可知充电后交流电压畸变严重,选取畸变最严重的A相进行频谱分析,如图4所示,可知交流电网UAC中二次谐波占比高达14%。
从以上3次动作事例可以看出,站内换流变或邻近变压器充电时,可能会造成直流侧出现50 Hz分量,特别是当交流电网比较薄弱时,即使励磁涌流不是很大,但由于交流电压畸变严重,也会出现50 Hz分量。文献[7]通过分析,认为短路比(SCR)为5是换流变空投的交流系统强度边界,小于5时应关注空投引起的50 Hz分量的影响。
另外从事例中也可以看到一个有意思的现象,整流侧连接于弱交流系统且进行换流变充电,但50 Hz保护未动作,而逆变侧并非连接于弱系统且未有任何操作,反而50 Hz保护动作,这是由于直流线路对50 Hz分量具有放大作用[3][6],即经过直流线路放大后,对站检测到的50 Hz分量反而比本站大,因此本站50 Hz保护未达到动作定值,而对站50 Hz分量超过保护定值而动作。
2 保护定值优化
根据50 Hz保护原理,保护定值优化的方向有2个:一是提高动作定值,二是延长动作时间。
动作定值的选取主要从以下方面进行综合考虑的:
1)最小功率运行时发生触发系统或阀体故障,50 Hz保护能够动作保护设备。
2)大功率运行发生触发系统或阀体故障时,能快速降低功率(功率回降段动作),尽快减小阀承受的应力。
3)缓解电网遭受的冲击(先降功率再闭锁)。
4)考虑直流线路对该分量值的放大现象(即非故障站该分量值大于故障站)。
由于必须满足上述第1个条件,即最小功率运行情况下50 Hz保护必须确保具有灵敏性,因此动作定值方面优化空间不大,文献[3]建议从0.02提高到了0.0333,该直流在已经做过优化的前提下,仍然发生了误动。
动作时间的选取主要考虑以下方面:
1)考虑躲过充电暂态过程的影响,由于影响励磁涌流的因素很多,此暂态过程持续多长时间只能根据经验做一个估算,如有条件可根据现场获取的实际波形做回放,然后再留出一定裕度,此时间记为t1。
2)校核一次设备耐受谐波的能力,包括换流阀、平波电抗器、直流滤波器、交流滤波器等,能够在直流系统中引入50 Hz分量的情况很多,不论是交流系统原因,还是直流侧发生故障原因,校核一次设备能承受谐波的最大能力,此时间记为t2。
3)考虑与交流保护配合,交流系统故障或异常时,一般优先让交流保护自行处理,直流保护维持不变,因此可考虑与交流保护的后备保护配合,此时间记为t3。
综合以上3个方面,时间定值的优化区间为:![]() 以该直流定值优化为例,通过现场充电励磁涌流分析及波形回放,确定躲过充电暂态过程至少需要1.5 s,即t1=1.5 s;经过校核,一次设备耐受谐波能力较强,t2>5 s;交流保护的后备保护动作时间约2.3 s,即t3=2.3 s,综合考虑以上因素,最终确定保护动作延时优化为3 s。
以该直流定值优化为例,通过现场充电励磁涌流分析及波形回放,确定躲过充电暂态过程至少需要1.5 s,即t1=1.5 s;经过校核,一次设备耐受谐波能力较强,t2>5 s;交流保护的后备保护动作时间约2.3 s,即t3=2.3 s,综合考虑以上因素,最终确定保护动作延时优化为3 s。
3 保护逻辑优化
50 Hz保护主要是作为换相失败、触发系统或阀体故障故障的后备保护,其保护范围在直流侧;对于交流故障或变压器充电引起的直流侧50 Hz分量,故障都是在交流侧,实际上不属于50 Hz保护范围,现有的50 Hz保护原理仅通过检测直流侧50 Hz谐波含量来实现,无法有效区分故障是发生在交流侧还是直流侧。
通过对现场换流变充电波形的分析可知,充电后交流系统电压畸变严重,进行频谱分析可知除了基波外,还有二次、三次、四次谐波且以二次谐波为主,二次谐波含量占比高达10%以上,见图4所示,而直流侧50 Hz分量正是由交流侧的正序二次谐波经过换流阀换相而产生。另一方面,当发生直流侧故障时,交流电压几乎没有影响,即使是在逆变侧丢脉冲故障并且造成换相失败,交流电压也仅仅是略有变化,二次谐波含量很小。
因此本文提出一种50 Hz保护优化方案,通过交流电压的二次谐波正序含量的大小来区分产生50 Hz的来源是在交流侧还是在直流侧,大量的仿真试验和数据分析表明,由于变压器充电引起50 Hz保护动作时,交流电压的二次谐波正序含量超过3%,而其他直流侧故障引起50 Hz保护动作时,交流电压的二次谐波正序含量不到1%,因此该优化方案采用3%作为门槛值,当二次谐波正序含量超过3%时,说明直流侧的50 Hz分量是交流系统原因产生,短时闭锁50 Hz保护,同时将闭锁信号发送给对站,对站收到该闭锁信号后也将50 Hz保护短时闭锁。优化逻辑如图5所示。
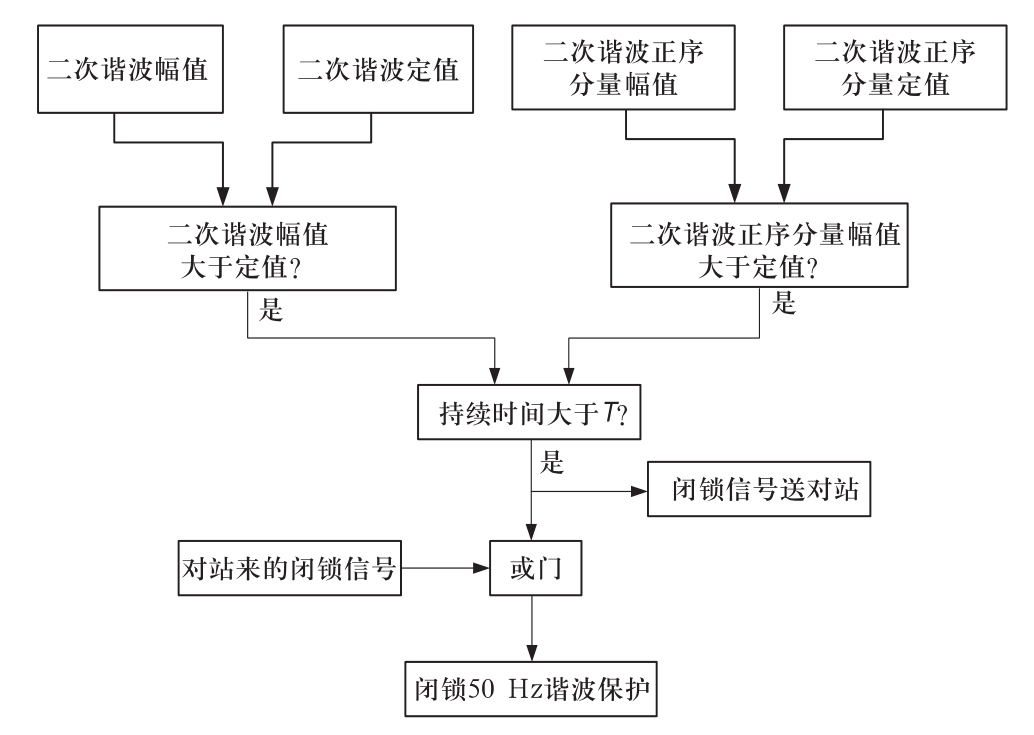
图5 50Hz优化逻辑框图
Fig.5 Diagram for logical block diagram of optimization
以上50 Hz保护优化方案,以交流电压的正序二次谐波含量为特征,交流系统越是薄弱,换流变空投产生的正序二次谐波分量越大[7],越容易满足优化使能条件,优化效果越好,而未优化之前50 Hz保护则越容易误动。反过来,如果交流系统强大,正序二次谐波含量小,则优化措施不会起作用,不影响原有50 Hz保护性能,因此该优化方案可应用于普遍情况。它的一个缺点是需要通过站间通信将本站的判断结果送给对站,由于50 Hz保护本身为后备保护,动作延时较长,因此站间通信的延时可以忽略。但如果出现站间通讯故障,则对站无法获知本站的情况,而直流线路对50 Hz的放大作用,将使得对站50 Hz保护动作,即相当于在站间通讯故障的情况下本优化方案不能起到作用。考虑到现在直流工程基本上对站间通信都是双通道配置,出现站间通信故障的概率较低,本优化方案仍然具有积极作用。
4 RTDS仿真分析
为验证保护逻辑优化的正确性,本文在直流模型上做了RTDS仿真试验,试验均在最小方式下进行。分以下4类:①各种工况下整流侧和逆变侧丢脉冲故障,试验的目的在于确保对50 Hz逻辑优化后,不影响50 Hz保护原有的直流侧保护性能;②50 Hz保护预先退出,各种工况下丢脉冲故障,试验的目的在于确保即使由于某种原因(例如交流电压二次谐波正序含量门槛选择不恰当等)使得优化后的50 Hz保护暂时未起作用,在丢脉冲故障时仍有保护可以动作;③各种工况下整流侧和逆变侧交流系统故障,试验的目的在于确保对50 Hz逻辑优化后,不影响交流故障时直流保护的整体性能;④现场充电波形回放试验,试验目的在于确保逻辑优化后能正确避免50 Hz保护误动。
1)最小功率下(320 A)整流侧丢脉冲,逆变侧50 Hz保护先于整流侧正确动作,波形如图6所示。
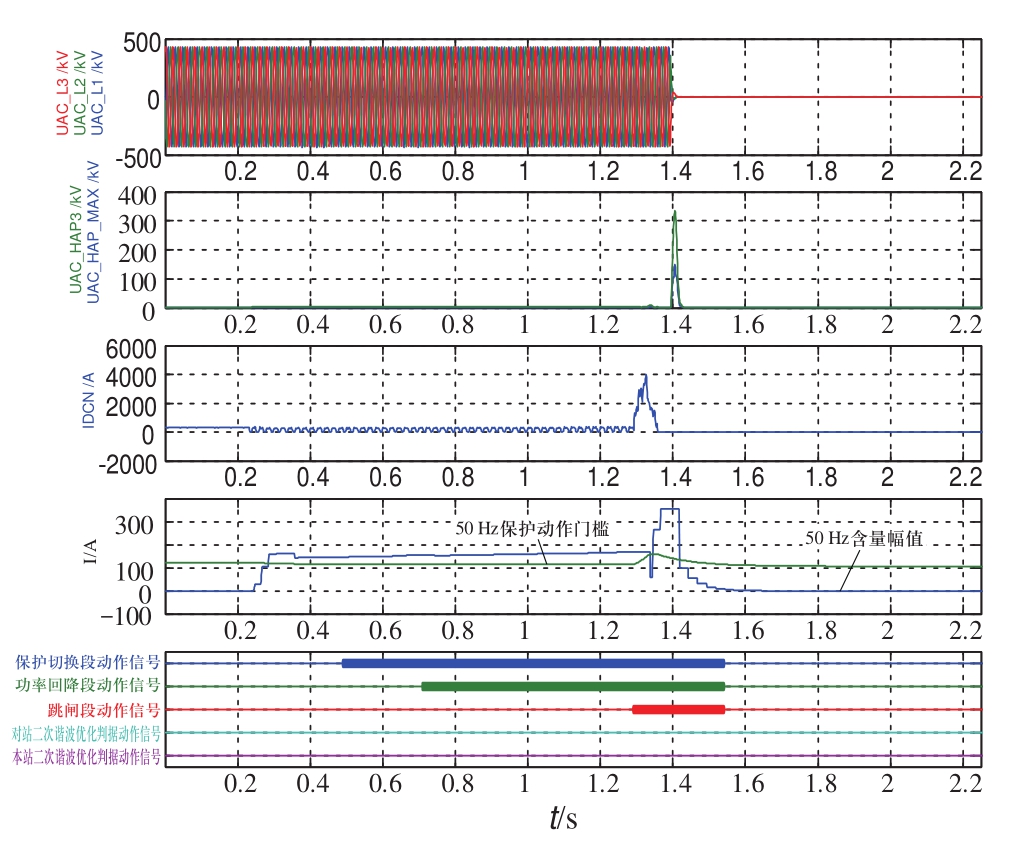
图6 最小功率整流侧丢脉冲
Fig.6 Misfile fault in rectifier-side with minimum power
2)最小功率下(320 A)逆变侧丢脉冲,逆变侧50 Hz保护正确动作,波形如图7所示。
3)50 Hz保护预先退出、最小功率(320 A)整流侧丢脉冲,IDCN的50 Hz及100 Hz分量均超过整定值,但由于50 Hz保护已退出,故只有100 Hz保护动作。交流电压中正序二次谐波含量很小,波形如图8所示。
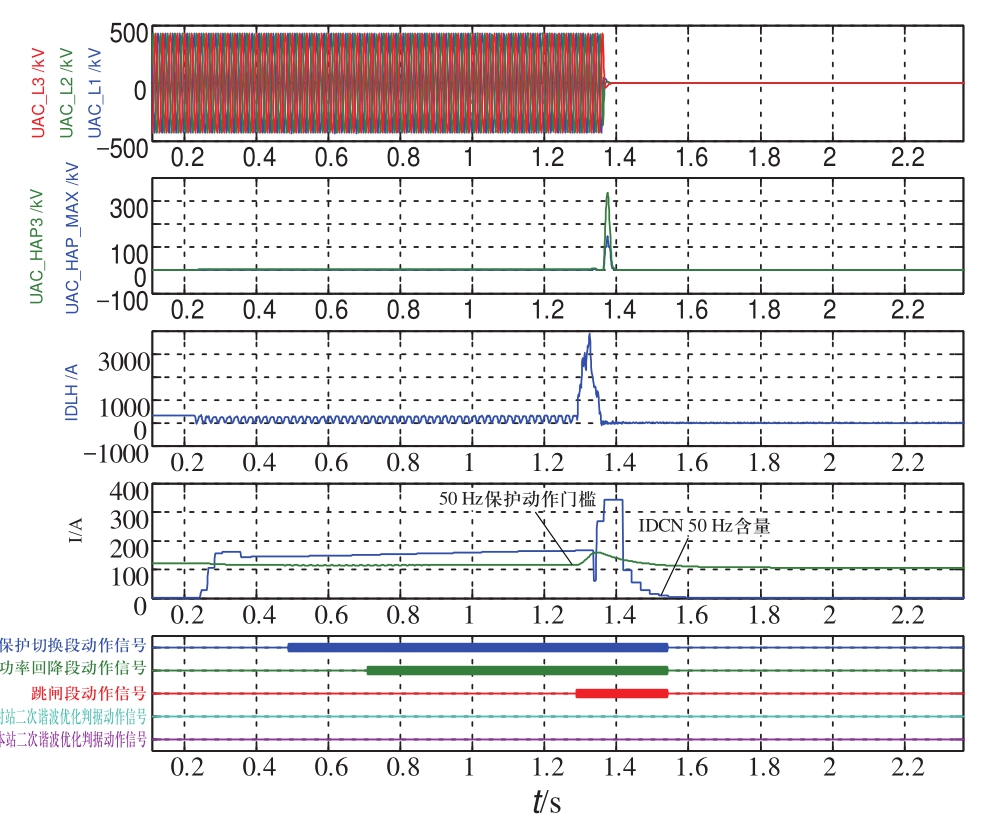
图7 最小功率逆变侧丢脉冲
Fig.7 Misfile fault in inverter -side with minimum power

图8 最小功率整流侧丢脉冲(50 Hz保护预先退出)
Fig.8 Misfile fault in rectifier-side with minimum power while 50 Hz protection quit in advance
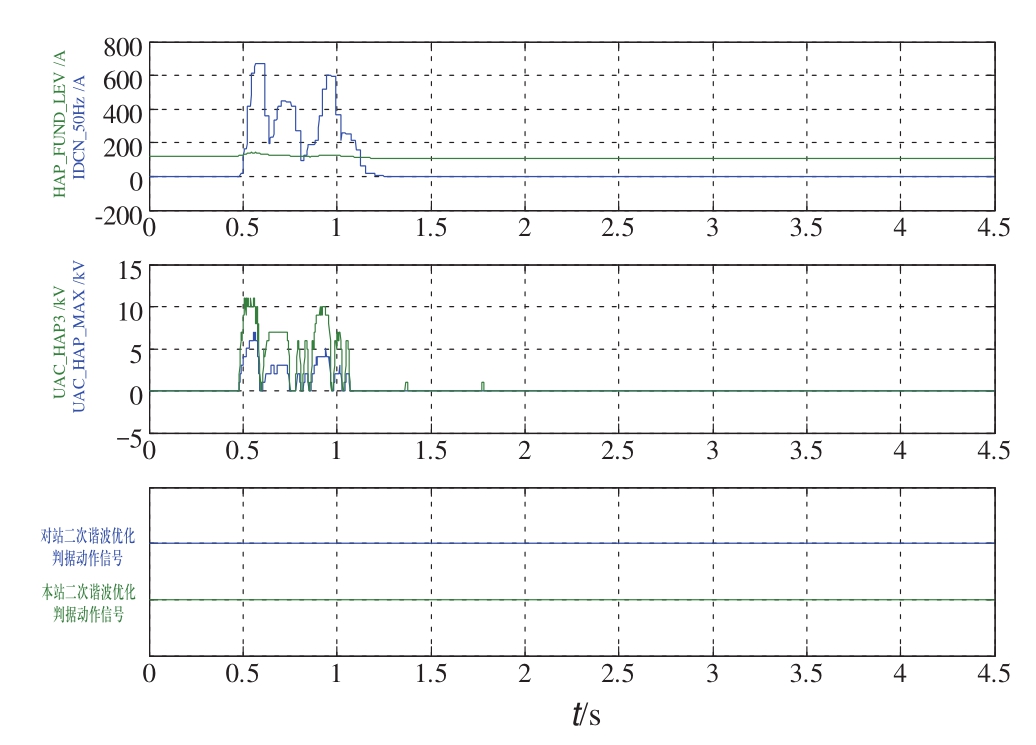
图9 最小功率逆变侧丢脉冲(50 Hz保护预先退出)
Fig.9 Misfile fault in inverter-side with minimum power while 50 Hz protection quit in advance
4)50 Hz保护预先退出、最小功率(320 A)逆变侧丢脉冲,两站的50 Hz分量均短时超过定值,逆变侧换相失败保护(87CFP)动作跳闸,交流电压中正序二次谐波含量很小,波形如图9所示。
5)最大功率(1600 MW),整流侧单相接地故障,整流侧交流低电压保护(27AC)动作跳闸,两站的50 Hz分量均未超过定值,交流电压中正序二次谐波含量很小,波形如图10所示。
6)最大功率(1600 MW),逆变侧单相接地故障,逆变侧换相失败保护(87CFP)动作跳闸,交流电压中正序二次谐波含量很小,波形如图11所示。
7)最小功率下(320 A)充电波形回放,在整流侧用现场充电波形回放,逆变侧50 Hz含量超过定值门槛,但由于优化后的辅助判据起作用,功率回降段和跳闸段优化后均不动作,波形如图12所示。
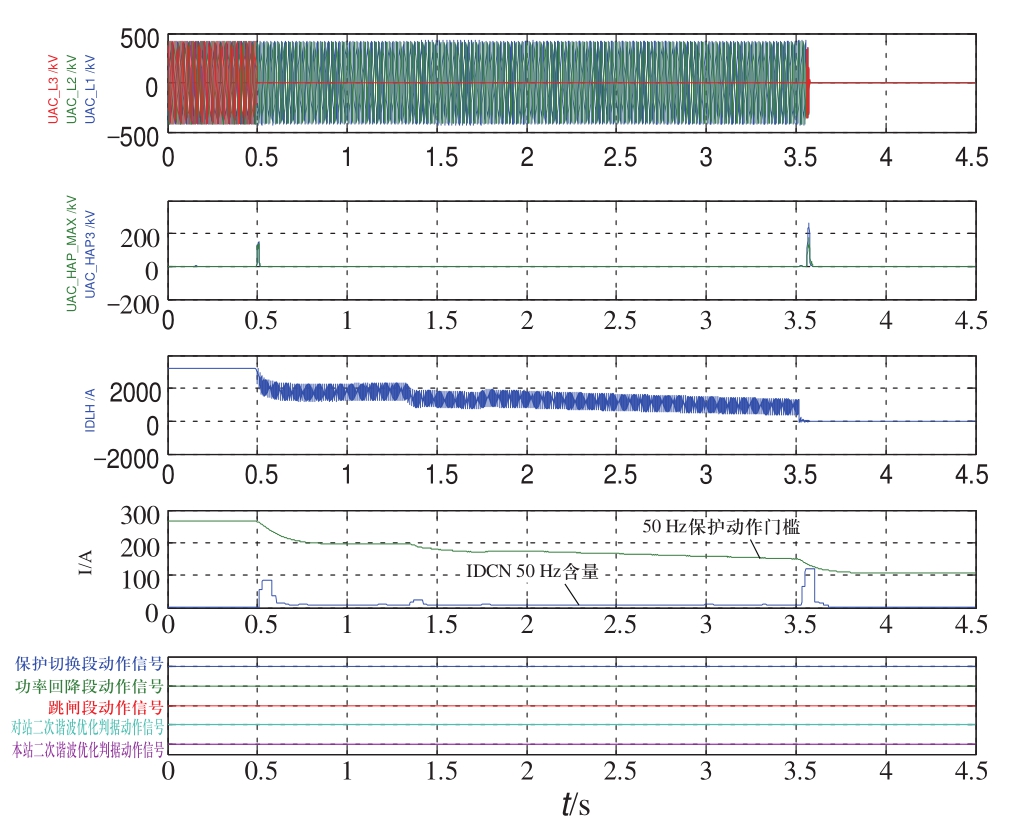
图10 最大功率整流侧交流故障
Fig.10 AC fault in rectifier-side with maximum power
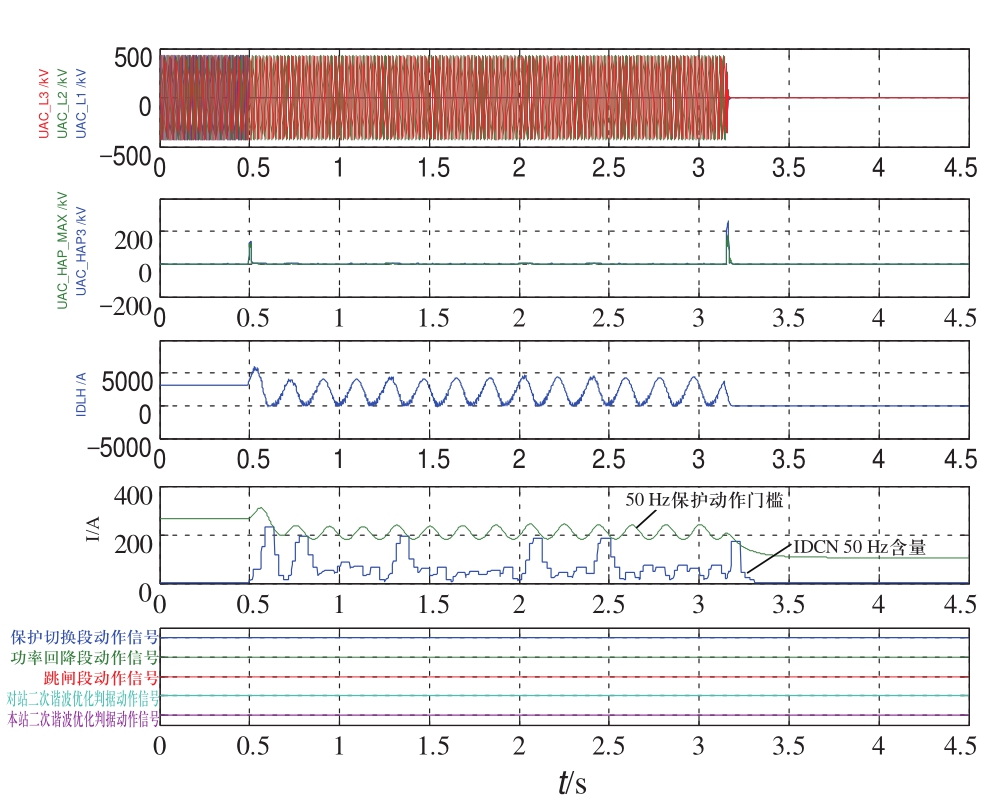
图11 最大功率逆变侧交流故障
Fig.11 AC fault ininverter-side with maximum power

图12 最小功率整流侧充电波形回放
Fig.12 Backplay wave for energizing a no-load transformer in rectifier-side with minimum power
以上RTDS仿真试验结果表明:
1)50 Hz保护优化后,整流侧和逆变侧丢脉冲故障时50 Hz保护能正确动作。
2)50 Hz保护优化后,考虑到最不利情况,50 Hz保护被优化判据闭锁同时发生丢脉冲故障,仍有其他原理保护可以正确动作。
3)50 Hz保护优化后,整流侧和逆变侧发生交流故障,直流保护整体性能没有发生改变。当整流侧或逆变侧发生交流系统故障时,在直流侧检测到的50 Hz含量较少,不会达到50 Hz保护的动作门槛和延时。另外故障时交流电压中正序二次谐波含量也很小,50 Hz保护的优化判据不会满足,因此对50 Hz保护优化后,不会对交流系统故障造成不良影响。
4)50 Hz保护优化后,可以准确识别由于交流系统原因造成直流侧出现50 Hz分量的情况,50 Hz保护不再受到变压器充电暂态过程的影响。
5 结论
本文根据弱交流系统情况下现场经常出现的换流变充电或邻近变压器充电引起50 Hz保护误动的现象,从保护定值优化和保护逻辑优化2个方面进行了研究,可得到以下结论:
1)定值优化措施。本文提出为了保证在最小功率下保护的灵敏性,动作定值优化空间不大,可对时间定值进行优化并提出了选取的原则,时间定值的选取需综合考虑躲过充电暂态过程、一次设备耐受谐波的能力,以及与交流保护的配合3方面因素。该优化措施适用于不方便大量修改控制保护逻辑的场合,例如在运直流工程。该双回直流采用本方法优化后,历经多次站内或站外充电操作,包括有一个以上极运行的同时对另一个极充电,至今未再发生50 Hz保护误动事件。
2)逻辑优化措施。本文提出了一种优化判据,通过检测交流电压中二次谐波正序分量大小,可以准确区分直流电流中的50 Hz分量是由于交流系统原因产生还是直流系统原因产生,如果是交流系统原因产生,则短时间内闭锁50 Hz保护。该优化措施适用于有条件进行控制保护功能测试的场合,例如新建直流工程。青藏直流采用本方法优化后,至今未再发生50 Hz保护误动事件。
以上2种优化措施均可以有效避免弱交流系统换流变或邻近变压器充电引起的50 Hz保护误动,对其他在运或新建的与弱交流系统相连的直流输电工程均有借鉴意义。
参考文献
[1] 傅闯,饶宏,黎小林.交直流混合电网中直流50 Hz和100 Hz保护研究[J].电力系统自动化,2008,32(12):57-60.Fu Chuang, Rao Hong, Li Xiaolin.HVDC 50 Hz and 100 Hz protection of AC/DC hybrid transmission system [J].Automation of Electric Power Systems, 2008, 32(12): 57-60(in Chinese).
[2] 杨汾艳,朱韬析,丁晓兵,等.考虑涌流影响的直流线路50 Hz分量机理性研究[J].高电压技术,2015,41(10):3363-3371.Yang Fenyan, Zhu Taoxi, Ding Xiaobing, et al.Research on 50 Hz component in HVDC transmission lines considering the influence of inrush current [J].High Voltage Engineering,2015.41(10): 3363-3371(in Chinese).
[3] 张建锋,柏传军,许训炜,等.变压器励磁对直流输电系统基波保护的影响[J].南方电网技术,2012,6(6):23-26.Zhang Jianfeng, Bai Chuanjun, Xu Xunwei, et al.The influence of transformer excitation on the fundamental harmonics protection of HVDC systems[J].Southern Power System Technology, 2012, 6(6): 23-26(in Chinese).
[4] 樊丽娟,黄莹,徐迪臻,等.送端励磁涌流对溪洛渡直流 50 Hz保护的影响[J].南方电网技术,2015,9(6):34-38.Fan Lijuan, Huang Ying, Xu Dizhen, et al.Impact of magnetizing inrush current at sending end on 50 Hz protection of xiluodu HVDC transmission project[J].Southern Power System Technology, 2015, 9(6): 34-38(in Chinese).
[5] 陈聪,李晓华,张冬怡,等.变压器涌流对直流 50 Hz 保护的影响机理与对策[J].广东电力.2017,30(9):91-96.Chen Cong, Li Xiaohua, Zhang Dongyi, et al.Influencing Mechanism and Countermeasures of Transformer Inrush current on DC 50 Hz protection [J].Guangdong Electric Power, 2017, 30(9): 91-96(in Chinese).
[6] 李晓华,吴立珠,丁晓兵,等.基于直流线路参数的50 Hz谐波放大评估方法[J].电力系统自动化,2018,42(6):146-151.Li Xiaohua, Wu Lizhu, Ding Xiaobing, et al.Evaluation method of 50 Hz harmonic amplification based on DC line parameter[J].Automation of Electric Power Systems, 2018,42(6): 146-151(in Chinese).
[7] 吴立珠,李晓华,张冬怡,等.励磁涌流下直流50 Hz谐波运行特性分析及应用[J].电气自动化,2017,39(5):60-64.Wu Lizhu, Li Xiaohua, Zhang Dongyi, et al.Operating characteristic analysis and application of DC 50 Hz harmonic under the influence of magnetizing Inrush Current[J].Electrical Automation, 2017, 39(5): 60-64(in Chinese).
[8] 种芝艺,粟小华,刘宝宏.西北电网主变充电引起青藏直流闭锁的原因分析及对策[J],电力建设,2013,34(3):88-91.Chong Zhiyi, Su Xiaohua, Liu Baohong.Analysis and countermeasures of Qinghai-Tibet DC blocking caused by main transformer charging in Northwest Power Grid[J].Electric Power Construction, 2013, 34(3): 88-91(in Chinese).
[9] 吉程,文俊,刘宝宏,等.青藏直流联网工程直流谐波保护研究[J].现代电力,2016,33(1):74-79.Ji Cheng, Wen Jun, Liu Baohong, et al.Research on DC Harmonic Protection in Qinghai-Tibet HVDC Project[J].Modern Electric Power, 2016, 33(1): 74-79(in Chinese).
Optimization for 50 Hz Protection in HVDC Connected With Weak AC System
XU Bin, HUANG Jinjun, WANG Yangzheng, CHEN Le, LU Jiang
(Nanjing NR Electric Co., Ltd., Nanjing 211106, Jiangsu Province, China)
Abstract: As an example of several misactions of 50 Hz protection while converter transformer or transformer nearby the convert station being energized which connected to weak AC system, the reasons of 50 Hz protection action are analyzed and two optimization methods are discussed in this paper, one is modificating predetermined setting values and the principles are proposed, the other is optimization of protect logic and simulationtests are carried out by RTDS.The test result shows the optimization is effective.Two optimization proposed in this paper can be used both for HVDC projects in operation or new HVDC projects.
Keywords: HVDC; 50 Hz protection; inrush current;optimization
文章编号:2096-5125 (2019)01-0093-07
中图分类号:TM 862
文献标志码:A
DOI:10.19705/j.cnki.issn2096-5125.2019.01.012
收稿日期:2018-06-19;
修回日期:2018-07-25。
作者简介:

徐斌
徐斌(1977),男,硕士,高级工程师,主要研究方向为高压直流输电控制和保护,E-mail:xubin1@nrec.com。
黄金军(1986),男,硕士,工程师,主要研究方向为高压直流输电控制和保护。
王杨正(1984),男,硕士,工程师,主要研究方向为高压直流输电控制和保护。
(责任编辑 张鹏)
