0 引言
柔性直流输电(voltage source converter based HVDC, VSC-HVDC)技术具备有功和无功独立控制、控制模式灵活多变、可向无源系统供电等优点[1-2],在新能源并网、交流电网异步互联等场合有着广阔的应用前景[3-4]。近年来欧洲在建、拟建柔直工程10余项,中国也拟于2020年投运张北四端柔直工程,局部形成了柔直互联多交流电网的形态。
在柔直网络的“隔离”下,异步互联同步子系统拥有各自的频率[5-6],任何一个子系统电网发生频率偏移时,其余系统无法获知其频率变化,从而提供惯性支撑或参与频率调整[7]。当柔直输送功率所占同步电网容量的比例较高时,该电网的惯性大幅减弱,调频能力下降。因此,有必要研究柔直互联多区域协同调频策略,使不同区域系统具备相互支援的能力,以维持频率稳定和保证频率质量。
文献[8]和[9]提出利用换流站远程通信的方法,实现送端电网和柔直电网协同参与受端电网调频。但该方法具有一定的延时,且存在可靠性和稳定性问题。在不采用通信的情况下,可利用换流站的附加下垂控制来实现信号传递。文献[10]-[12]提出了风电经柔直并网的换流站间协调策略,受端换流站通过直流电压-频率下垂方式传递受端电网频率变化信息。送端换流站接收到直流电压偏差信号后,通过频率-直流电压下垂方式改变其交流侧频率,从而使风电场参与调频。文献[13]提出了柔直换流站的辅助调频控制策略,通过调整直流电压使线路电容和送端风电场共同参与受端电网的频率调整。文献[14]设计了换流站附加下垂控制的控制器结构,并设置了控制器动作的上下限值。文献[15]提出了基于附加控制的风电场柔性直流并网与传统直流外送的源网协同调频控制策略,并设计了同步发电机、风电场和直流电网参与调频的时序。
上述文献均基于两端直流系统案例,以直流电压偏差作为换流站间的传递信号,实现多区域协同调频。但是,在风电集群接入的柔直电网中,风电功率正常波动也会引起直流电压偏差,导致风电集群侧换流站难以区分检测到的直流电压偏差信号究竟来源于受端电网频率偏移还是风电功率波动。这样带来的问题是:即使受端电网频率处于正常状态,风电集群侧换流站也会因风电功率波动引起的直流电压偏差而启动下垂控制,从而导致其所连风电集群在无需调频时频繁地调整出力。因此,有必要通过一定的方式区分电网频率偏移与风电功率波动这两种场景,排除风电功率波动引起的直流电压偏差干扰。
针对上述问题,本文提出基于直流电压偏差及其特征量的柔直互联多区域协同调频策略,分别提取由电网频率偏移和风电功率波动引起的直流电压偏差特征量,并基于二者的差异设置风电集群侧换流站启动下垂控制的判据,从而排除风电功率波动为调频带来的干扰。
1 柔直互联多区域协同调频过程
本节以某四端柔直互联多区域互联系统为例,介绍协同调频过程。如图1所示,VSC1和VSC2分别与风电集群1和风电集群2相连;VSC3与受端电网相连;VSC4与调节端电网相连,负责整个柔直电网的功率平衡。VSC1和VSC2采用定交流母线电压频率(VF)控制,为新能源集群提供运行电压与频率;VSC3交流侧采用定功率(PQ)控制;VSC4作为定直流电压控制站,采用定直流母线电压(UdQ)控制,起到缓冲柔直网络不平衡功率作用。
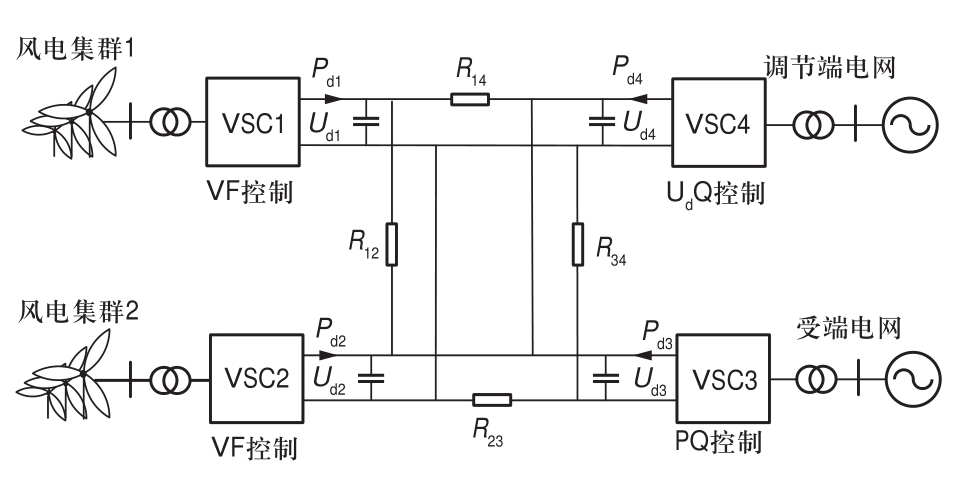
图1 四端柔直电网结构示意图
Fig.1 Configuration of four-terminal VSC-HVDC grid
在区域协同调频模式下,当VSC3所连受端电网频率发生偏移时,VSC1和VSC2所连风电集群通过柔直电网参与受端电网的频率调整。在不采用通信的情况下,各个换流站需要采用下垂控制并相互间协调配合才能实现多区域协同调频,各换流站的下垂控制策略如下。
1.1 风电集群侧换流站
风电集群侧换流站VSC1和VSC2采用fw-Ud下垂控制。以VSC1为例,当检测到直流电压偏差ΔUd1后,根据设定的fw-Ud下垂调整其交流侧频率指令fw1,即
式中:fw10和fw1分别为VSC1调整前和调整后的交流侧频率;k1为下垂系数;Ud10和Ud1分别为变化前和变化后的直流电压。
1.2 受端电网侧换流站
受端电网侧换流站VSC3采用P-f下垂控制,当检测到交流频率偏差Δf后,根据设定的P-f下垂调整其有功功率指令Pd3,即
式中:Pd30和Pd3分别为VSC3调整前和调整后的有功功率;k3为下垂系数;f0和f 分别为变化前和变化后的交流频率。
1.3 调节端电网侧换流站
调节端电网侧VSC4作为定直流电压控制站,与调节端电网相连,自动调整其有功功率维持整个柔直电网功率平衡,无需采用下垂控制。为避免调节端电网过多承担调频时送端电网不平衡功率、保证换流器容量裕度,可通过设定合理的k1~k3保证P4在调频过程中只分担直流网损增量。
根据上述换流站间协调过程,风电集群经柔直电网参与受端电网频率调整的过程如下:
1)VSC3所连受端电网受到扰动而发生频率偏移Δf超过阈值,根据设定的P-f下垂调整其有功功率指令Pd3。
2)VSC3的有功功率Pd3发生改变后,柔直电网的潮流重新分布,VSC1和VSC2的直流电压Ud1和Ud2以及VSC4的有功功率Pd4随之发生改变。
3)VSC1和VSC2检测到直流电压偏差ΔUd后,根据设定的fw-Ud下垂调整其交流侧频率指令fw。
4)VSC1和VSC2所连风电集群检测到频率偏差信号Δfw后,增加或减少输出功率以参与受端电网的频率调整。
风电机组的辅助控制策略分为功率减载控制和转子动能控制2种方式。功率减载控制方式下,风电机组提前预留了一定的备用容量供调频使用,但减载运行降低了风电场的经济性,所留容量不宜太多,且无法在短时间内提供大额虚拟惯性。对于运行在最大风能跟踪模式(MPPT)下的风电机组,可采用转子动能控制,在辅助调频控制器的作用下实现转子动能与电磁功率之间相互转换,从而增加或减少输出的电磁功率,起到短时间内提供大量虚拟惯性、提高频率最低点的作用,但是由于没有额外的机械功率输入,不能起到长期频率支撑、降低一次调频静差的作用。在实际运行中,需要二者互补,提高整体调频性能。两种模式的风电机组控制策略、风电机组与VSC策略和参数之间必须协调,才能收到较好的调频效果,否则还可能给系统带来二次频率跌落。已有研究[16-18]讨论了相关改进策略方法,限于篇幅,此处不赘述。
上述过程只涉及到电磁功率的调整,故能够在很短的时间内完成,整个调频过程可用图2来描述。
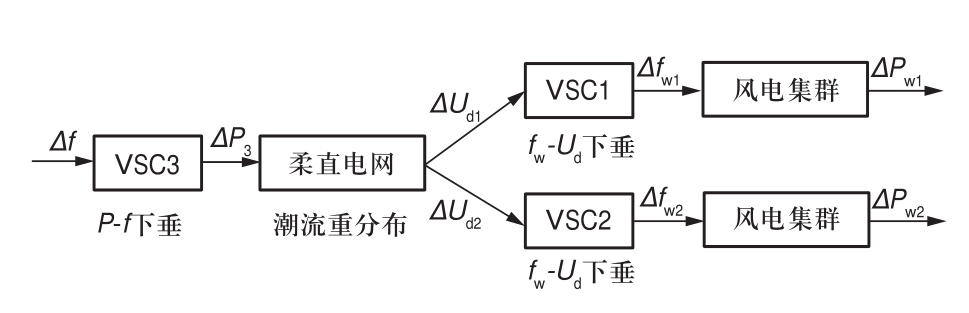
图2 风电集群经柔直电网参与受端电网调频的过程
Fig.2 Process of wind power participating in the frequency regulation of receiving grid through VSC-HVDC
2 直流电压偏差分析
由前述分析可知,风电集群侧换流站VSC1和VSC2需通过检测直流电压偏差信号ΔUd来判断VSC3所连受端电网的频率是否发生偏移,以及是否通过下垂控制改变其交流侧频率。因此,有必要对直流电压偏差信号的来源进行分析。对于图1所示的四端柔直电网,潮流方程如下:
式中:Pdi和Udi分别为第i个换流站的有功功率和直流电压;Yij为网络导纳矩阵Y中的元素,由直流线路参数决定。
将式(3)改写为如下矩阵形式:

由式(4)可得到各换流站的直流电压计算公式

式中zij为网络阻抗矩阵Z(即Y-1)中的元素。又,
以VSC1为例,其直流电压Ud1的表达式为
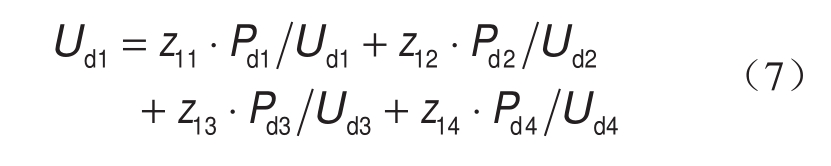
在式(6)中,Pd1和Pd2由注入VSC1和VSC2的风电功率决定,Pd3由VSC3的有功指令决定。因此,风电功率波动或VSC3的有功指令改变均会引起Ud1改变,并忽略直流网损增量。通常情况下,直流电压的变化范围较小,故可将式(6)中等号右侧的电压项近似视作恒定值。当风电集群的出力发生波动或VSC3的有功功率发生变化时,VSC1检测到的直流电压偏差![]() 为
为
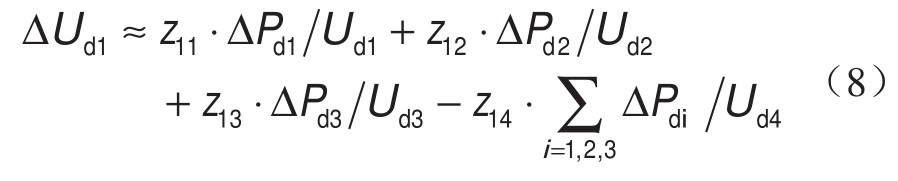
根据式(2),VSC3的有功功率Pd3与受端电网的频率f之间成下垂关系,将式(2)代入式(7)可得
式中:mp1 =z11/Ud1- z14/Ud4;mp2 =z12/Ud2- z14/Ud4;mf =k3(z13/Ud3- z14/Ud4),称为灵敏度,由直流电网参数和下垂系数决定。
在式(8)中,可认为直流电压偏差 包含两个分量:一个是由风电功率波动引起的分量
包含两个分量:一个是由风电功率波动引起的分量 ,另一个是由电网频率偏移引起的分量
,另一个是由电网频率偏移引起的分量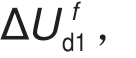 即
即
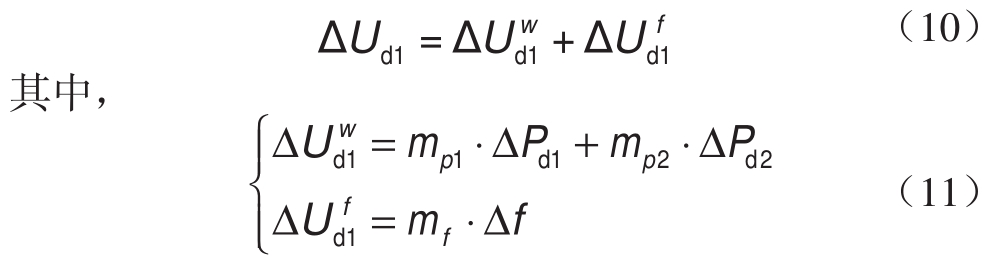
由此可见,对于风电集群侧换流站而言,若只通过检测直流电压偏差,则无法判断该偏差信号究竟来源于受端电网频率偏移还是风电功率波动。这样带来的问题是即使受端电网频率处于正常状态,换流站也会因风电功率波动引起的直流电压偏差而启动下垂控制,从而导致其所连风电集群在无需调频时频繁调整出力。因此,有必要通过一定的方式区分电网频率偏移与风电功率波动这两种场景,排除风电功率波动引起的直流电压偏差干扰。
为解决上述问题,可分别提取由电网频率偏移与风电功率波动引起的直流电压偏差的特征量,并基于它们之间的差异设置风电集群侧换流站启动下垂控制的判据,从而排除风电功率波动为调频带来的干扰。
3 直流电压偏差的特征分析
一次调频的持续时间较短,通常在几十秒内就能完成,故只需选取几十秒内的电网频率偏移和风电功率波动情况进行分析。下文基于实际录波数据恢复的风功率与频率波动变化曲线,分析二者引起的直流电压偏差特征。
3.1 原始曲线的获取
以VSC1为例,当受端电网因功率扰动而发生频率偏移,经过柔直电网的传递后,VSC1能够检测到直流电压Ud1的变化。图3给出了30 s内的电网频率变化曲线以及它所引起的直流电压变化曲线。由图可见,t=12 s时,电网频率f发生跌落,直流电压Ud1也随之发生骤降。

图3 电网频率和直流电压变化曲线示例
Fig.3 Examples of frequency and DC voltage
当风电功率波动时,VSC1也能检测到直流电压Ud1的变化。图4给出了30 s内的风电功率变化曲线以及它所引起的直流电压变化曲线。由图可见,t=10 s前,风电功率几乎无变化;t=10 s时,风电功率开始缓慢增大,Ud1也随之缓慢升高。
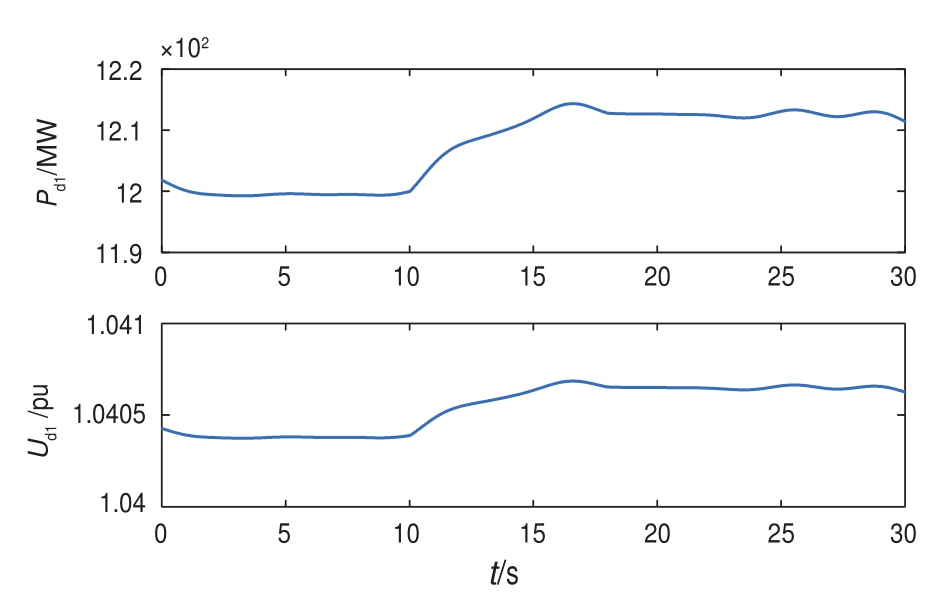
图4 风电功率和直流电压变化曲线示例
Fig.4 Examples of wind power and DC voltage
3.2 直流电压偏差的特征量提取
对上述两种场景引起的直流电压偏差进行特征量提取,根据常用的信号分析方法,可选取的特征量有:电压变化量、电压变化率和FFT频谱特征。
3.2.1 电压变化量ΔUd1
图5给出了电网频率变化和风电功率变化两种场景下,100 ms内直流电压变化量的分布统计情况。由图可见,风电功率波动引起ΔUd1的主要分布在±0.2×10-4 pu的范围内,而电网频率跌落引起的ΔUd1还分布在±0.2×10-4 pu的范围之外(主要由频率跌落瞬间引起)。因此,可将ΔUd1的绝对值大小作为区分两种场景的判据,设定直流电压变化量的阈值![]() 当
当![]() 时,认为由电网频率变化引起;当
时,认为由电网频率变化引起;当![]() 时,认为由风电功率变化引起。
时,认为由风电功率变化引起。
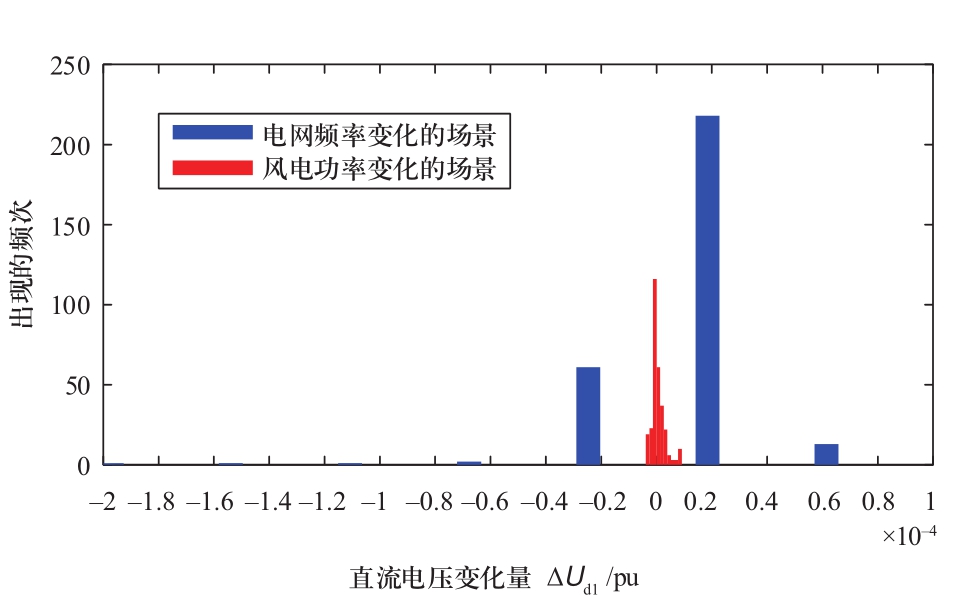
图5 直流电压变化量的分布统计
Fig.5 Distribution of DC voltage variation
值得注意的是,该判据中的阈值Uvariation = 0.2×10-4 pu是针对本文特定系统设定的。由式(8)可知,电网频率偏移和风电功率波动引起的直流电压偏差均与灵敏度参数有关,风电功率波动引起的直流电压偏差由直流线路参数决定,而电网频率偏移引起的直流电压偏差由直流线路参数和VSC3的下垂系数共同决定。因此,在实际工程中,需根据系统的实际参数以及风电功率波动和电网频率变化的实际情况,通过定量计算或仿真分析设定一个合适的阈值。
3.2.2 电压变化率dUd1/dt
图6给出了电网频率变化和风电功率变化两种场景下,直流电压变化率的时序曲线。由图可见,电网频率跌落瞬间引起的dUd1/dt约为风电功率波动引起的dUd1/dt的10倍,这是因为电网频率跌落的速度远大于风电功率波动的速度。因此,可将dUd1/dt的绝对值大小作为区分两种场景的判据,设定直流电压变化率的阈值Urate=2×10-3~3×10-3 (pu/s),当![]() 时,认为由电网频率变化引起;当
时,认为由电网频率变化引起;当![]() 时,认为由风电功率变化引起。
时,认为由风电功率变化引起。
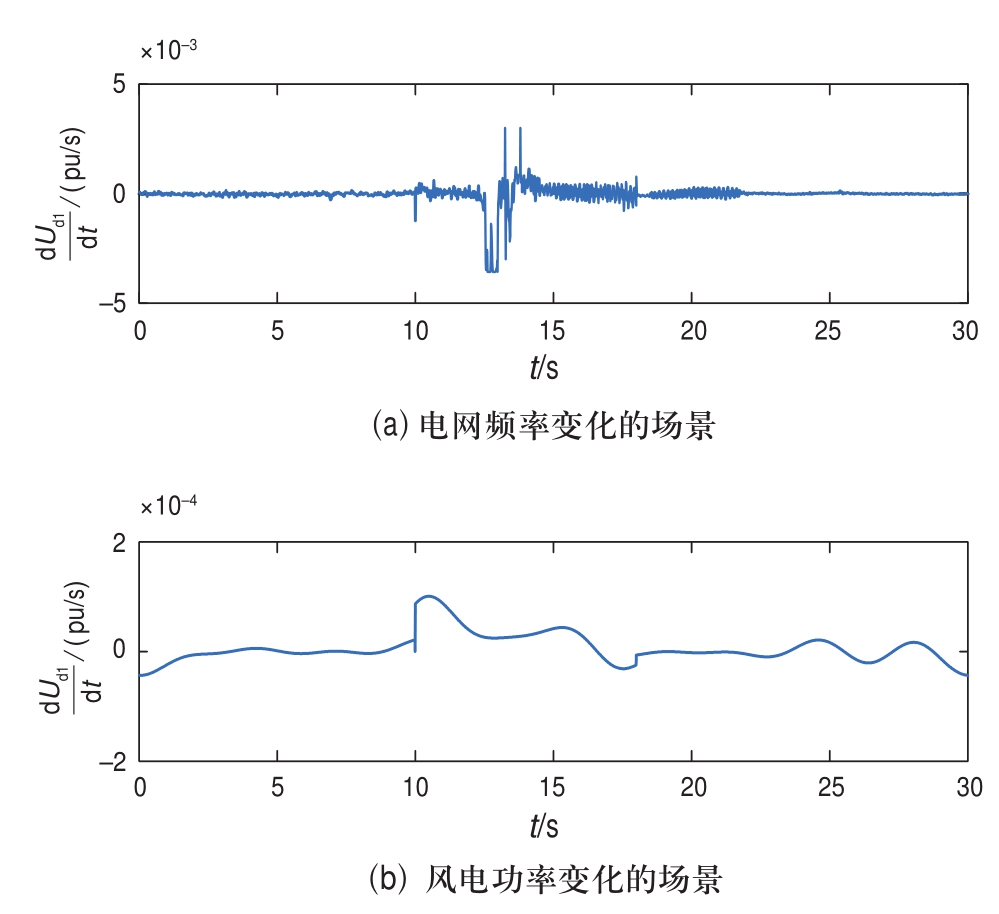
图6 直流电压变化率曲线
Fig.6 Curves of DC voltage change rate
3.2.3 FFT频谱特征
图7给出了电网频率变化和风电功率变化两种场景下,直流电压的FFT频谱分析结果。由图可见,风电功率波动引起的Ud1主要包含0.1 Hz以下的频率分量,而电网频率跌落引起的Ud1还包含了0.1~0.3 Hz频段的分量。因此,可用滤波器去除Ud1中0.1 Hz以下的低频分量,保留0.1~0.3 Hz频段的分量Ufilt,设定其最大幅值![]() 的阈值Am=0.1,当
的阈值Am=0.1,当![]() 时,认为由电网频率变化引起;当
时,认为由电网频率变化引起;当![]() 时,认为由风电功率变化引起。
时,认为由风电功率变化引起。
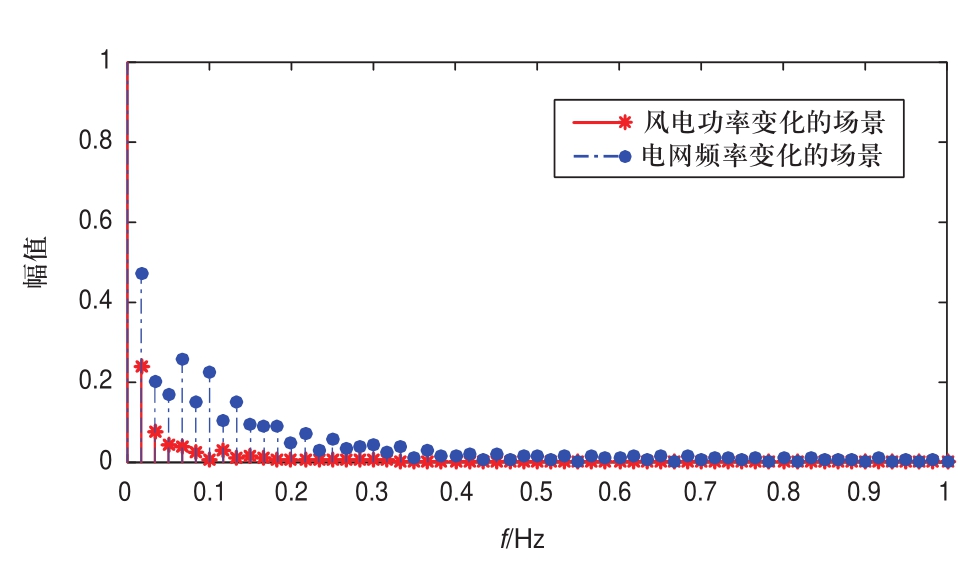
图7 直流电压的FFT频谱分析结果
Fig.7 FFT based spectrum analysis results of DC voltage
由此可见,电网频率偏移和风电功率波动引起的直流电压偏差特征量具有较为明显的差异,可用上述3个判据共同区分这两种场景。
3.3 风电功率突变引起的直流电压变化特征
由3.2节的分析可知,电网频率偏移与风电功率波动2种场景的直流电压偏差存在差异的主要原因是二者的变化速度和变化幅度不同。通常情况下风电功率变化较为缓慢、幅度较小,而电网频率跌落较为迅速、幅度较大,故根据上述3个判据能够较为容易地区分这两种场景。
但在实际运行中,风电功率有时也可能发生较大程度的突变,比如风速过大导致多台风电机组同时退出运行时,风电功率会在很短的时间内发生骤降。这种情况下,若仅根据上述3个直流电压特征量,则很难区分电网频率偏移和风电功率突变两种场景,故还需增加额外的判据。
以换流站VSC1为例,当风电功率发生突变时,VSC1可以检测到dPd1/dt与dUd1/dt同时增大;而当电网频率发生跌落时,VSC1只能检测到较大的dUd1/dt,不能检测到较大的dPd1/dt。因此,可额外增加一个功率变化率判据,以区分电网频率跌落和风电功率突变两种场景。当![]() 时,认为由风电功率突变引起;当
时,认为由风电功率突变引起;当![]() 且
且![]() 时,认为由电网频率偏移引起。此外,若是VSC2所连风电集群的功率发生突变,则VSC1也能检测到
时,认为由电网频率偏移引起。此外,若是VSC2所连风电集群的功率发生突变,则VSC1也能检测到![]() 并启动下垂控制使其所连风电集群调整出力。这种情况可以视作两个风电集群相互间进行功率支援,即VSC1所连风电集群通过调整出力来平衡VSC2所连风电集群的出力变化。
并启动下垂控制使其所连风电集群调整出力。这种情况可以视作两个风电集群相互间进行功率支援,即VSC1所连风电集群通过调整出力来平衡VSC2所连风电集群的出力变化。
4 风电集群侧换流站启动下垂控制的判据
风电集群侧换流站在检测到直流电压偏差信号后,需要根据直流电压偏差特征量和功率特征量判断信号来源,以确定是否启动下垂控制改变其交流侧的频率。风电场侧换流站启动下垂控制的判据总结如图8所示。
根据图8,换流站需要经过4个判据后才能确定是否启动下垂控制。首先检测直流电压变化量ΔUd1,若![]() 则认为换流站正常运行或风电功率正常波动,不足以引起直流电压大幅变化;若
则认为换流站正常运行或风电功率正常波动,不足以引起直流电压大幅变化;若![]() 则检测直流电压变化率dUd1/dt。若
则检测直流电压变化率dUd1/dt。若![]() 则认为风电功率正常波动,虽然引起直流电压变化量较大,但无需启动下垂控制;若
则认为风电功率正常波动,虽然引起直流电压变化量较大,但无需启动下垂控制;若![]() 则判断功率变化率dPd1/dt。若
则判断功率变化率dPd1/dt。若![]() 则认为由风电功率突变引起,无需启动下垂控制;若
则认为由风电功率突变引起,无需启动下垂控制;若![]() 则继续判断滤波后的分量是否满足
则继续判断滤波后的分量是否满足![]() 成立,则认为由电网频率偏移引起,换流站启动下垂控制。
成立,则认为由电网频率偏移引起,换流站启动下垂控制。
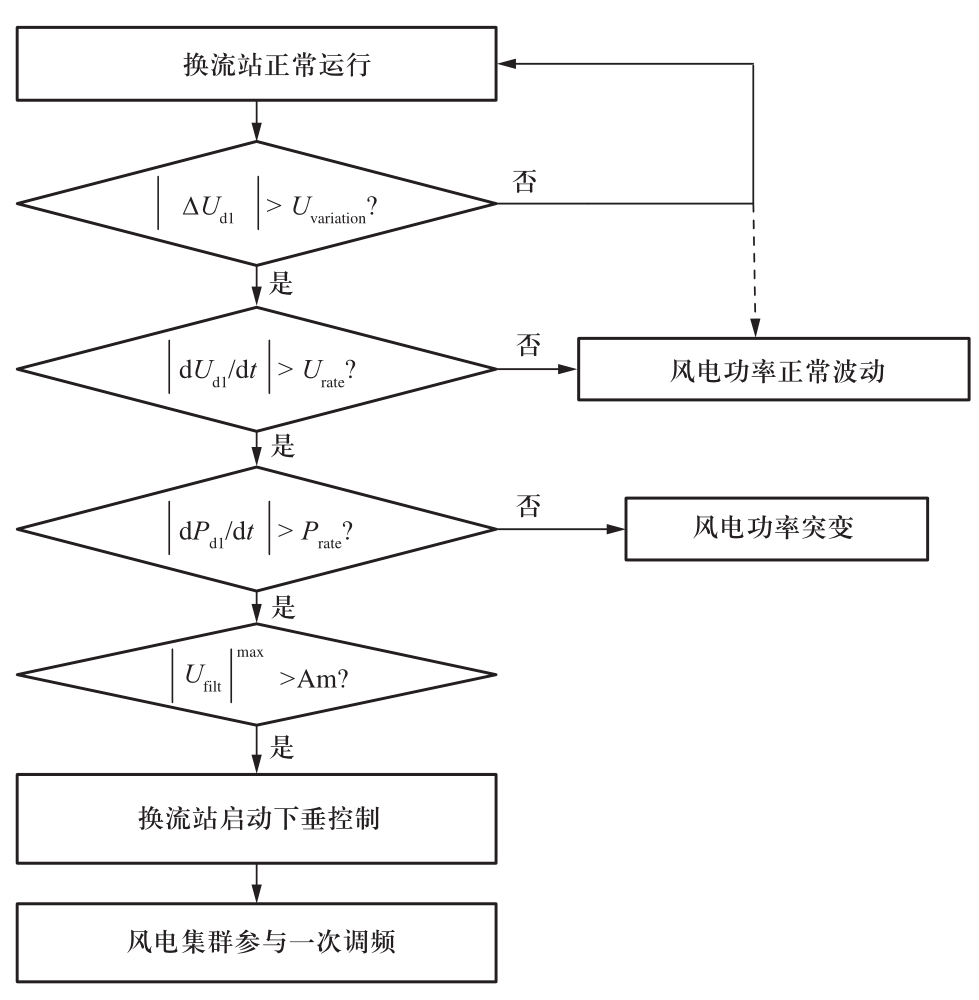
图8 风电经柔直参与一次调频启动的流程图
Fig.8 Flow chart of involving wind power via VSC-HVDC in primary frequency response
由此可见,风电集群并非在所有情况下都参与调频,只有当电网频率偏移所引起的直流电压偏差满足上述判据时才参与一次调频。
5 仿真结果
本文利用MATLAB/Simulink搭建了图1所示的风电集群接入的四端柔直电网,额定直流电压为500 kV。各个换流站的主要参数如表1所示,各条直流线路的参数如表2所示。
表1 各个换流站主要参数
Table 1 Main parameters of converter stations

表2 各条直流线路的参数
Table 2 Parameters of DC transmission lines

5.1 直流电压偏差特征量分类结果
为了验证上文所提判据的有效性,对构造的算例,设置了50种不同的仿真场景。构造场景基于对某省级电网一年内较大频率事件的提取。对近年PMU频率数据和一个风电集群数据进行了分析,筛选出其中造成30 s内频率偏移大于0.05 Hz的场景共14次,10 min内风电波动超过0.1 pu的35次,又增加了一次风电一半切机(作为)的场景,共计50次。对有频率偏移同期的全网有功功率曲线记录,提取等比例有功突变量,以负荷突然增加或减少形式仿真;对风电波动,选取同时期风电输出功率曲线等比例放大。
对不同场景引起的直流电压偏差进行特征量提取,并将各自的特征量绘制到一个三维坐标图中,以电压变化量ΔUd为x轴,以电压变化率dUd/dt为y轴,以滤波后的频率分量最大幅值![]() 为z轴,得到了如图9所示的结果。
为z轴,得到了如图9所示的结果。
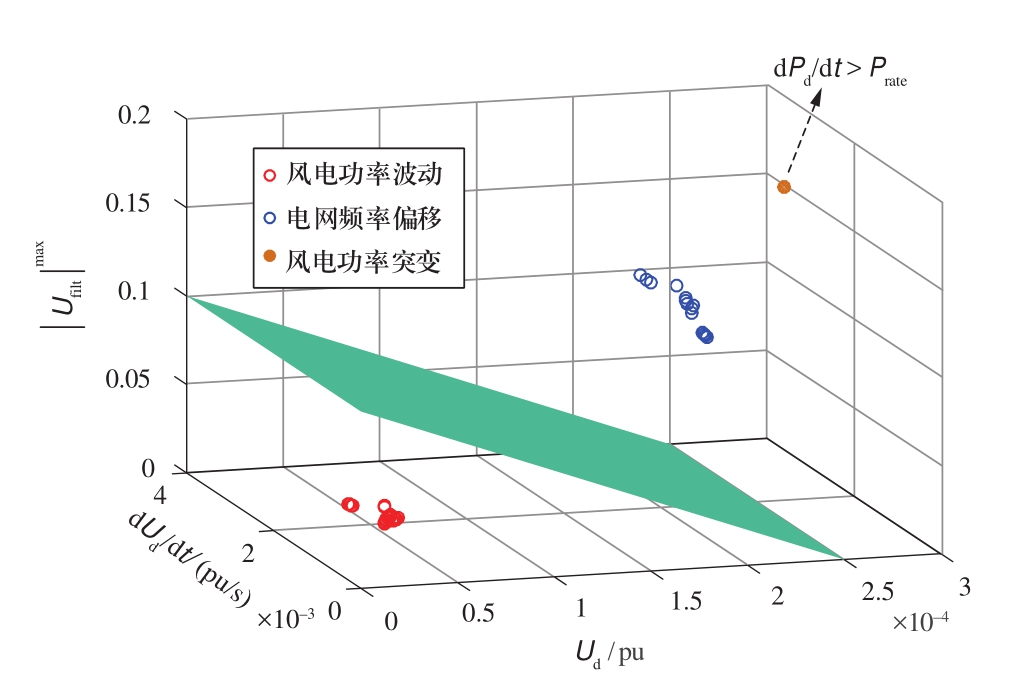
图9 直流电压偏差特征量分类结果
Fig.9 Classification results of DC voltage deviation characteristics
图9中,蓝色圆点代表电网频率偏移引起的直流电压偏差,红色圆点代表风电功率正常波动引起的直流电压偏差,橙色圆点代表风电功率突变引起的直流电压偏差。由图可见,蓝色圆点与红色圆点所处的三维空间位置相距较远,分别位于图中的绿色分割平面的两侧,说明了两种颜色的圆点属于两种不同的类别。因此,可认为电网频率偏移和风电功率正常波动引起的直流电压偏差特征量之间存在明显的差异,通过文中所提的判据能够较好地将二者区分开。此外,图中黄色圆点与蓝色圆点位于分割平面的同一侧,这说明仅通过直流电压偏差特征量无法区分电网频率偏移和风电功率突变的场景,故需要增加额外的功率特征量来进行区分。当![]() 时,认为由风电功率突变引起;当
时,认为由风电功率突变引起;当![]() 时,认为由电网频率偏移引起。
时,认为由电网频率偏移引起。
5.2 柔直互联多区域协同调频仿真
为验证文中的柔直互联多区域协同调频策略的有效性,对整个系统的调频过程进行了仿真。t=0时刻系统正常运行,四端换流站的有功功率分别为:Pd1=653.5 MW,Pd2=2500 MW,Pd3=2000 MW(吸收),Pd4=989.3 MW(吸收)。受端电网的负荷需求为3000 MW,常规同步机组出力为1000 MW。调节端电网的负荷需求为2000 MW,常规同步机组出力为1010.7 MW。t=5 s时,受端电网的负荷需求突然由3000 MW增加至3300 MW,电网频率发生跌落。经过柔直电网的传递,风电集群检测到交流频率偏差信号并参与调频。为了使仿真结果更为清晰和简化,假设只有风电集群1参与调频,并不考虑二次调频。其中,风电机组分为两组,分别提供功率减载控制和转子动能控制两种方式的辅助控制策略。功率减载控制方式下,风电机组提前预留了0.1 pu的备用容量供调频使用;最大风能跟踪模式(MPPT)下的风电机组采用转子动能控制。图10和图11分别给出了调频过程中各个换流站的有功功率和直流电压曲线。图12为备用总容量为0.1 pu.(总计65.35 MW)时各端电网的频率曲线。图13为不同备用容量下调节端电网频率曲线。
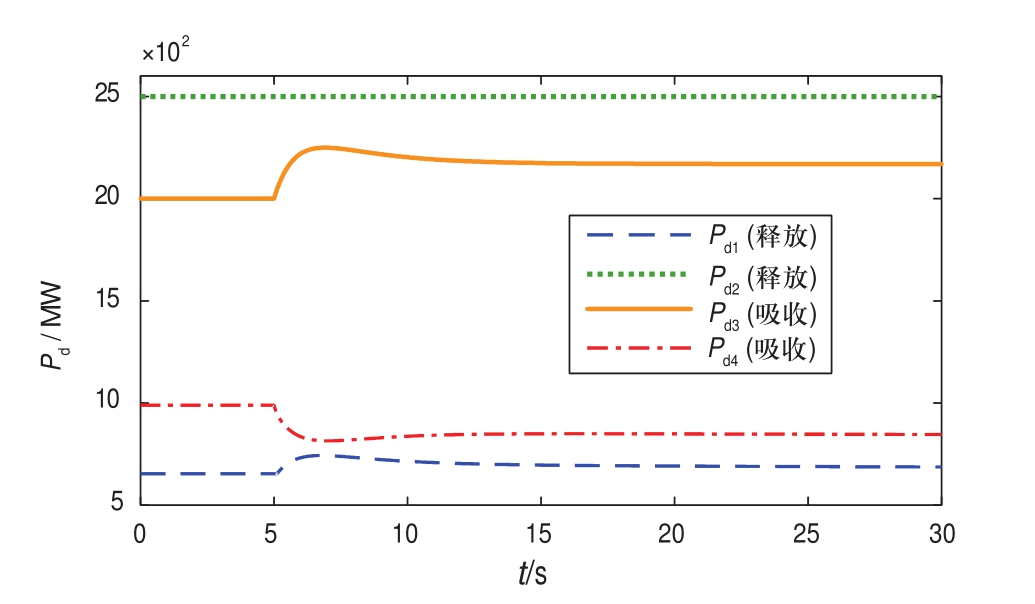
图10 各个换流站的有功功率曲线
Fig.10 Active power curves of converter stations
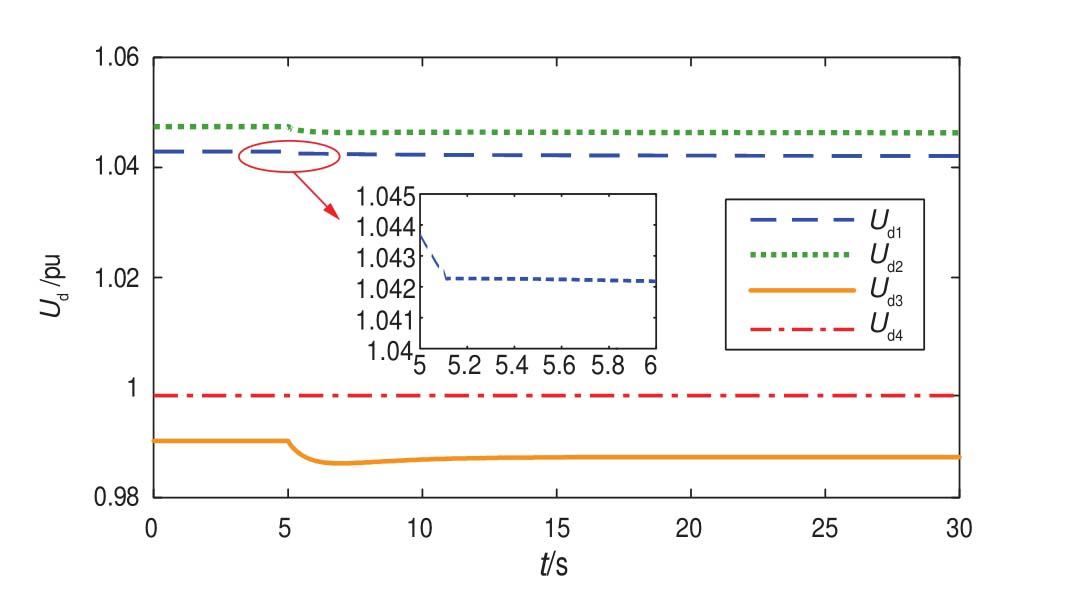
图11 各个换流站的直流曲线
Fig.11 DC voltage curves of converter stations
由图10可见,t=5 s时,受端电网频率下降,VSC3通过下垂控制增大有功功率Pd3,引起柔直电网的潮流重新分布,VSC1的直流电压Ud1降低(见图11)。VSC1检测到直流电压偏差后,通过下垂控制调整交流侧频率;风电集群1检测到交流频率偏差后参与调频,VSC1的有功功率Pd1增加。由于VSC1和VSC3的有功功率发生变化,柔直电网中出现不平衡功率,故VSC4通过调整其有功功率Pd4使全网功率达到平衡。VSC4参与调频之前吸收的有功功率为989.3 MW,参与调频后吸收的有功功率有所减少。
图12给出了受端电网、调节端电网和风电集群侧的频率变化曲线。由图可见,受端电网的频率先下降后上升,15 s左右达到稳定;调节端电网的频率在t=5 s时发生跌落,因为VSC4为其提供的有功功率Pd4有所减少;风电集群侧频率在t=5 s时由50 Hz降低为49.96 Hz,原因是换流站在检测到直流电压偏差后通过下垂控制自发调整交流侧频率。
图13给出了不同备用容量下调节端电网频率曲线。可见随着减载备用容量的增加,对系统频率最低点、一次调频静差都有改善作用,但因为整体容量有限,对一次调频静差的改善作用不太明显。
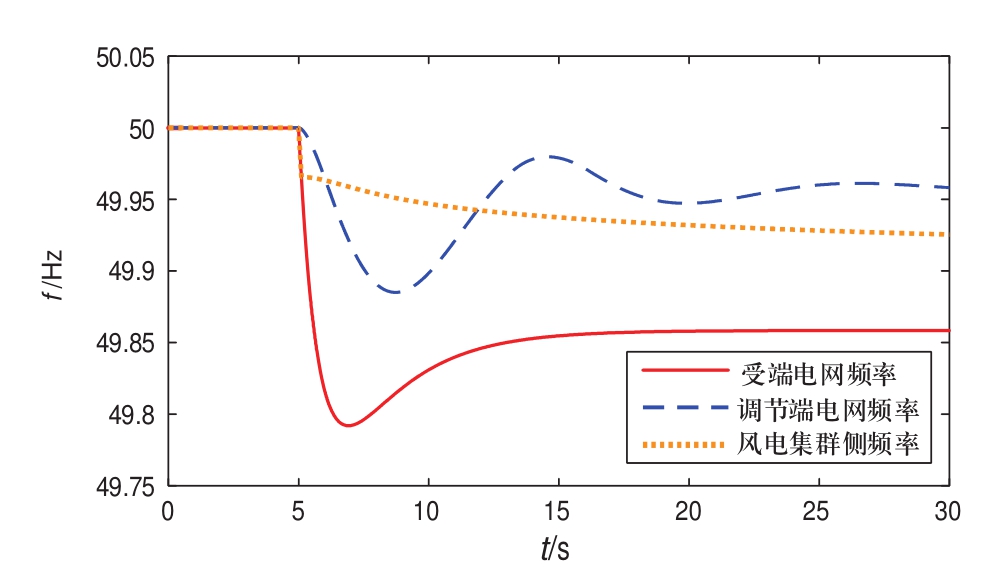
图12 各端电网的频率曲线
Fig.12 Frequency curves of each side grid
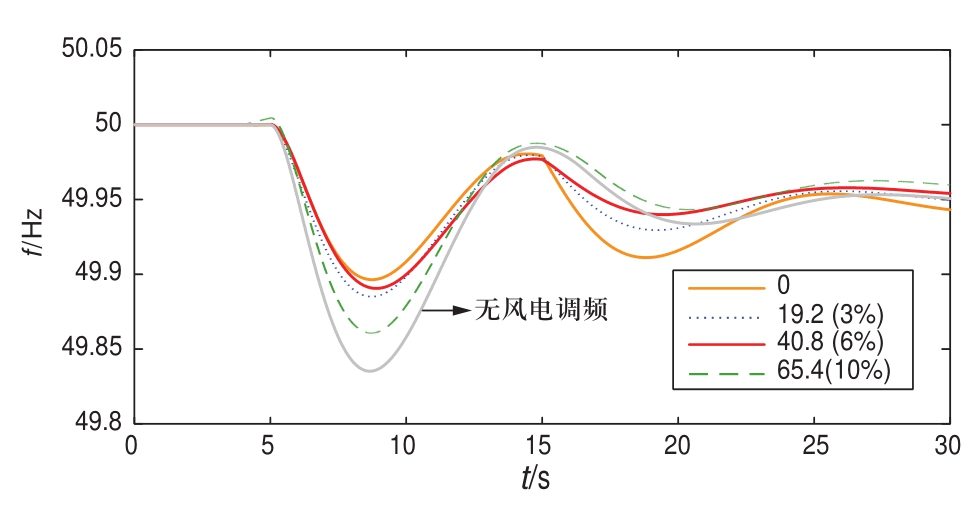
图13 不同减载备用率的调节端(VSC4)的频率
Fig.13 Frequency curves of VSC4 side grid under various deloading ratio
注:括号外数字表示减载备用容量,单位为MW;括号里表示减载备用占风电装机容量的比例。
6 结论
近年来,柔性直流输电技术在新能源并网、交流电网异步互联等场合发挥着愈加重要的作用。本文提出了基于直流电压偏差及其特征量的柔直互联多区域协同调频策略,论证了风电集群经柔直电网参与区域调频的可行性。主要研究结论如下:
1)建立了风电接入柔直互联多区域电网的协同调频模型,通过交流主网侧换流站采用交流频率—直流母线电压下垂控制,风电集群侧换流站采用直流母线电压—交流频率下垂控制,结合风电机组的调频减载控制和转子动能控制两种模式,实现多区域互联调频。仿真验证了方法可有效减少交流主网的最大频率偏差,缓解一次调频静差。
2)提出了被柔直隔离的多异步交流电网协同调频中的频率调整信号判别方法。针对风电功率正常波动引起直流电压变化而带来的干扰问题,提出了包含电压变化量、电压变化率和滤波后的电压分量幅值3个特征量,并基于二者的差异设置了风电集群侧换流站启动下垂控制的判据。此外还考虑了风电功率突变的场景,引入了功率变化率判据。仿真结果表明,电网频率偏移和风电功率波动引起的直流电压偏差特征量具有较为明显的差异,采用所提策略能够较好地区分这两种场景。
诚然,目前中国交流主网电网还是相当强健、惯量充裕的,还没有考虑柔直接入风电参与频率支援的场景。但就长远看来,高比例新能源接入、直流输送容量增加,系统惯性减小已成基本趋势,提升风电辅助调频能力,多区域互动提高全网频率性能将是未来发展的重要需求。本文所提方法对上述问题的解决提供一种技术思路。
参考文献
[1] Flourentzou N, Agelidis V G, Demetriades G D.VSC-based HVDC power transmission systems: an overview[J].IEEE Trans on Power Electronics, 2009, 24(3): 592-602.
[2] 王锡凡,卫晓辉,宁联辉,等.海上风电并网与输送方案比较[J].中国电机工程学报,2014,34(31):5459-5466.Wang Xifan, Wei Xiaohui, Ning Lianhui, et al.Integration techniques and transmission schemes for off-shore wind farms[J].Proceedings of the CSEE, 2014, 34(31): 5459-5466(in Chinese).
[3] 潘垣,尹项根,胡家兵,等.基于柔直电网的西部风光能源集中开发与外送[J].电网技术,2016,40(12):3621-3629.Pan Yuan, Yin Xianggen, Hu Jiabing, et al.Centralized exploitation and large-scale delivery of wind and solar energies in west china based on flexible DC grid[J].Power System Technology, 2016, 40(12): 3621-3629(in Chinese).
[4] Wang W, Li Y, Cao Y, et al.Adaptive droop control of MTDC system for frequency support and power sharing[J].IEEE Trans on Power Systems, 2018, 33(2): 1264-1274.
[5] 刘天琪,陶艳,李保宏.风电场经MMC-MTDC系统并网的几个关键问题[J].电网技术,2017,41(10):3251-3260.Liu Tianqi, Tao Yan, Li Baohong.Critical problems of wind farm integration via MMC-MTDC system[J].Power System Technology, 2017, 41(10): 3251-3260(in Chinese).
[6] 付媛,王毅,张祥宇,等.基于多端直流联网的风电功率协调控制[J].高电压技术,2014,40(2):611-619.Fu Yuan, Wang Yi, Zhang Xiangyu, et al.Coordinated control of wind power in multi-terminal DC transmission system[J].High Voltage Engineering, 2014, 40(2): 611-619(in Chinese).
[7] Wang W, Li Y, Cao Y, et al.Adaptive droop control of MTDC system for frequency support and power sharing[J].IEEE Trans on Power Systems, 2017, 33(2):1264-1274.
[8] Miao Z, Fan L, Osborn D, et al.Wind farms with HVDC delivery in inertial response and primary frequency control[J].IEEE Trans on Energy Conversion, 2010, 25(4): 1171-1178.
[9] Castro L M, Acha E.On the provision of frequency regulation in low inertia AC grids using HVDC systems[J].IEEE Trans on Smart Grid, 2016, 7(6): 2680-2690.
[10] Phulpin Y.Communication-free inertia and frequency control for wind generators connected by an HVDC-link[J].IEEE Trans on Power Systems, 2012, 27(1): 1136–1137.
[11] Pipelzadeh Y, Chaudhuri B, Green T C.Inertial response from remote offshore wind farms connected through VSC-HVDC links: A communication-less scheme[C]// Power and Energy Society General Meeting.San Diego, CA: IEEE, 2012: 1-6.
[12] 李宇骏,杨勇,李颖毅,等.提高电力系统惯性水平的风电场和VSC-HVDC协同控制策略[J].中国电机工程学报,2014,34(34):6021-6031.Li Yujun, Yang Yong, Li Yingyi, et al.Coordinated control of wind farms and VSC-HVDC to improve inertia level of power system[J].Proceedings of the CSEE, 2014, 34(34): 6021-6031(in Chinese).
[13] Liu H, Chen Z.Contribution of VSC-HVDC to frequency regulation of power systems with offshore wind generation[J].IEEE Trans on Energy Conversion, 2015, 30(3): 918-926.
[14] 朱瑞可,王渝红,李兴源,等.用于VSC-HVDC互联系统的附加频率控制策略[J].电力系统自动化,2014,38(16):81-87.Zhu Ruike, Wang Yuhong, Li Xingyuan, et al.An additional frequency control strategy for interconnected[J].Automation of Power Systems, 2014, 38(16): 81-87(in Chinese).
[15] 曾雪洋,刘天琪,王顺亮,等.风电场柔性直流并网与传统直流外送的源网协调控制策略[J].电网技术,2017,41(5):1390-1398.Zeng Xueyang, Liu Tianqi, Wang Shunliang, et al.A coordinated source-grid control strategy for wind farm integration with VSCHVDC and transmission with LCC-HVDC[J].Power System Technology, 2017, 41(5): 1390-1398(in Chinese).
[16] 刘巨,姚伟,文劲宇,等.大规模风电参与系统频率调整的技术展望[J].电网技术,2014,38(3):638-646.Liu Ju, Yao Wei, Wen Jingyu, et al.Prospect of technology for large- scale wind farm participating into power grid frequency regulation[J].Power System Technology, 2014, 38(3): 638-646(in Chinese).
[17] 赵嘉兴,高伟,上官明霞,等.风电参与电力系统调频综述[J].电力系统保护与控制,2017,45(21):157-169.Zhao Jiaxing, Gao Wei, Shangguan Mingxia, et al.Review on frequency regulation technology of power grid by wind farm[J].Power System Protection and Control, 2017, 45(21):157-169(in Chinese).
[18] 丁磊,尹善耀,王同晓,等.结合超速备用和模拟惯性的双馈风机频率控制策略[J].电网技术,2015,39(09):2385-2391.Ding Lei, Yin Shanyao, Wang Tongxiao, et al.Integrated frequency control strategy of DFIGs based on virtual inertia and over-speed control[J].Power System Technology, 2015,39(09): 2385-2391(in Chinese).
Coordinated Frequency Regulation for Multiple Systems Connected by VSC-HVDC With Wind Power Cluster
CUI Yang1, ZHANG Yangfan1, WANG Xiaosheng1, LIU Jingbo1, WU Linlin1, QIAO Ying2
(1.State Grid Jibei Electric Power Research Institute, Xicheng District, Beijing 100045, China;(2.State Key Lab of Control and Simulation of Power Systems and Generation Equipment, Dept.of Electrical Engineering,Tsinghua University, Haidian District, Beijing 100084, China)
Abstract: Due to the decoupling of frequency, how to coordinated frequency control among interconnected systems has attracted much attention.The frequency deviation signal is usually transferred via DC voltage in droop control mode in the pre-existing research.However, the DC voltage deviation also contains the components from wind power injection variation.If we neglect that, the system may change states frequently without the indeed frequency deviation.To solve the problem, this paper proposes a control strategy based on identify characteristics for DC voltage deviation caused by power system frequency or wind power variation.The characteristics includes voltage decrement, voltage drop rate, and peak value after being filtered.Based on dispersion, we set starting criteria of frequency coordinated control, and apply case study to show the validation.
Keywords: VSC-HVDC; multi-system interconnection; coordinated frequency regulation; DC voltage deviation; droop control
Science and Technology of SGCC ‘Study on Operation& Maintenance Key Technology of Demonstration Project in Zhangjiakou Renewable Energy Zone’(52018K170028).
文章编号:2096-5125 (2019)01-0053-09
中图分类号:TM721
文献标志码:A
DOI:10.19705/j.cnki.issn2096-5125.2019.01.007
基金项目:国家电网公司科技项目“张家口可再生能源示范区重大科技示范工程运维关键技术研究”(52018K170028)。
收稿日期:2018-10-18;
修回日期:2018-12-18。
作者简介:

崔阳
崔阳(1990),男,硕士,工程师,研究方向为新能源电站运行优化控制,E-mail:cy01583@163.com。
张扬帆(1987),男,硕士,工程师,研究方向为新能源电站运行优化控制,E-mail:zhangyangfanhit@163.com。
王晓声(1990),男,硕士,工程师,研究方向为新能源电站运行优化控制,E-mail:wangxs07@163.com。
刘京波(1986),男,硕士,高级工程师,研究方向为新能源电站运行优化控制,E-m a i l:liujingbo-520@163.com。
吴林林(1986),男,硕士,高级工程师,研究方向为新能源电站运行优化控制,E-mail:wulin226@163.com。
乔颖(1981),女,博士,副教授,通信作者,研究方向为新能源并网运行,E-mail: qiaoying@tsinghua.edu.cn。
(责任编辑 张鹏)