0 Introduction

With the advancement of global carbon peaking and carbon neutrality goals and the transformation of energy structures,the efficient utilization of distributed renewable energy has become a core issue in power system development[1].As an autonomous power system integrating distributed generation,energy storage devices,loads,and control systems,microgrids can flexibly switch between grid-connected and islanded modes,serving as a key technological means to enhance power supply reliability and facilitate the integration of renewable energy[2].However,the optimal dispatch of microgrids inherently constitutes a complex,high-dimensional,nonlinear,and multiconstrained optimization problem.Its core challenge lies in synergistically optimizing conflicting economic and environmental objectives—namely,achieving the comprehensive minimization of operational costs and environmental pollution control costs—while simultaneously meeting load demands [3–5].

To address this challenge,scholars worldwide have proposed various optimization methods,primarily categorized into traditional mathematical programming approaches and intelligent optimization algorithms.Traditional mathematical programming methods,such as Mixed-Integer Linear Programming (MILP) and Nonlinear Programming (NLP),demonstrate significant effectiveness under specific models due to their rigorous mathematical foundations and guarantees of optimal solutions.For instan ce,the novel automated adversarial deep learning unsupervised anomaly detection method EvoAAE [6].However,these methods typically require extensive linearization or convex approximation of real-world systems.When handling highly nonlinear device characteristics and complex objective functions,modeling errors may occur,and computational complexity increases dramatically as system scale expands.

In recent years,meta-heuristic algorithms such as particle swarm optimization (PSO),genetic algorithms (GA),grey wolf optimization(GWO),and binary particle swarm optimization (BPSO) [7]have been widely applied in microgrid optimization scheduling.These algorithms are favored for their low requirements on problem continuity and convexity,as well as their proficiency in global search.Reference[8]employs an improved gray wolf algorithm to solve the economic dispatch model for microgrids,achieving optimal daily power output while significantly reducing total operating costs.Reference [9]utilizes a vulture search algorithm to optimize operating costs,effectively enhancing the economic efficiency of microgrid systems.Reference [10]proposes an improved snake algorithm to balance economic and environmental costs,enabling peak shaving a nd valley filling for the main grid while reducing carbon emissions.

Meanwhile,new research trends have emerged in the field of microgrid optimization.On one hand,the research perspective has expanded from single power systems to integrated en ergy systems (IES),considering the coupled scheduling of multiple energy sources such as electricity,heat,cooling,and gas [11].On the other hand,new paradigms like distributed optimization and predefined-time convergence control have been proposed to address the bottlenecks of centralized computation and enhance the reliability of the optimization process.For instance,references [12,13]proposed a distributed predefined-time economic scheduling method.By designing a novel smoothing reconstruction penalty function,they achieved predefined-time convergence of the system state,offering new insights into optimizing algorithm convergence performance.These cu tting-edge studies have significantly enriched the scope of microgrid optimization while also imposing higher demands on algorithm convergence speed and solution set quality.

To address the aforementioned issues,this paper proposes a Multi-Objective Particle Swarm Optimization with Multi-Strategy (IMOPSO) for solving microgrid optimization dispatch models that balance economic and environmental considerations.The main contributions of this work are as follows:

Algorithmic Innovation: Systematically integrates four strategies—Logistic chaotic mapping,adaptive inertial weighting,adaptive grid with congestion mechanism,and fuzzy evaluation—into the MOPSO framework.This significantly enhances the algorithm’s performance in convergence speed,escaping local optima,and solution set diversity.

Model Construction: Developed a multi-objective optimization model for grid-connected microgrids incorporating PV,wind power,micro-gas turbines,diesel generators,and batteries,with refined modeling of generation costs and pollutant treatment expenses.

Comprehensive Validation: IMOPSO was comprehensively compared with the Multi-Objective Grey Wolf Optimization (MOGWO),Multi-Objective Ant Colony Optimization (MOACO),standard MOPSO,and the authoritative NSGA-II algorithm across multiple dimensions.The superio rity and robustness of the proposed algorithm were validated in terms of total cost,Pareto frontier quality,and statistical significance.

1 Microgrid system model

The microgrid system is employed which contains photovoltaic (PV),wind turbine (WT),micro gas turbine(MT),diesel generator (DG) and battery (BT) [14]and its topology is shown in Fig.1.

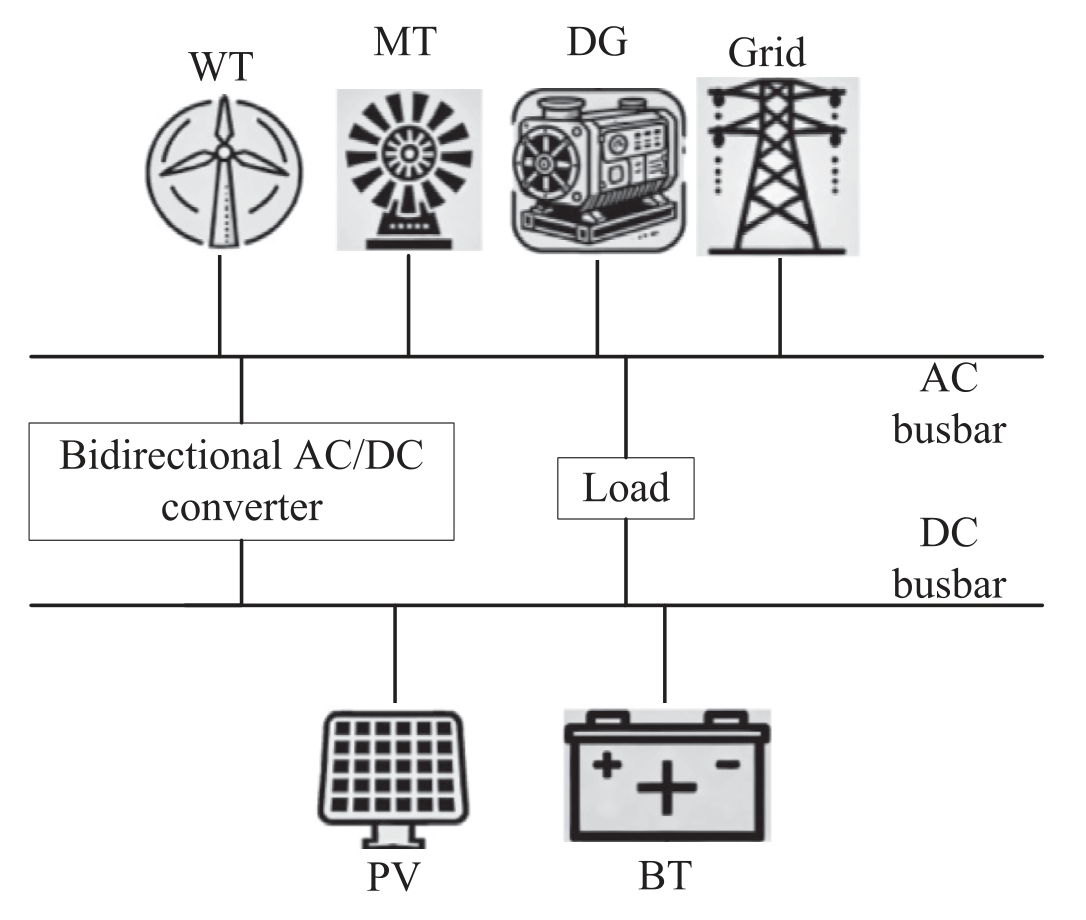
Fig.1.Microgrid topology diag ram.

It illustrates the grid-connected AC microgrid topology adopted in this research.The microgrid employs an AC busbar as the common connection point for the main grid and most AC loads and AC power sources (such as MT and DE),serving as the hub for energy collection,distribution,and transmission throughout the system.Concurrently,the system incorporates a DC busbar to connect DC sources and loads,including photovoltaic panels and batteries.AC/DC bidirectional converters are connected between the DC bus and AC bus.Their core function is to decouple AC and DC power sources while enabling bidirectional energy flow between the DC and AC sides.This hybrid AC/DC structure efficiently and flexibly accommodates distributed power sources and energy storage units with varying characteristics,representing a typical architecture for modern microgrids.

1.1 PV and WT generation modeling

Both PV and WT power generation are clean and renewable energy sources[15],and the power of PV varies with light intensity and temperature as:

where: ηPV is the conversion efficiency of PV,in simplified analysis,the decisive influence of light intensity on output power is typically the primary consideration,and it is assumed that conversion efficiency remains stable under certain conditions; S is the area of photovoltaic panels;δ is the light intensity;PPV is the pwer of PV.

WT is a renewable energy technology that utilizes wind energy to be converted into electricity [16].This model treats the wind farm as an aggregated power generation unit whose output is based on macro-scale wind speed forecast data.To simplify model complexity,the wake effect constraints between turbines within the wind farm are not currently considered,which may lead to an optimistic estimate of the actual available power of the wind farm.The output power of WT is:

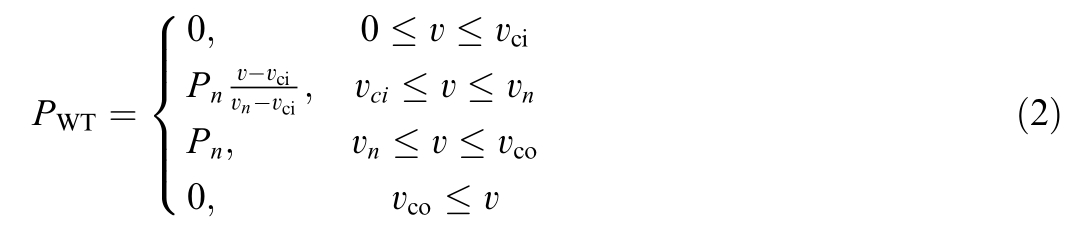
where: v ci,v n,vco is the fan’s cut-in air speed,rated air speed,and cut-out air speed; Pn is the rated power of the WT.

1.2 MT generation model

MT is a small,efficient and fast response gas turbine engine [17]with the equation of the relationship between power gen eration efficiency and operating power:

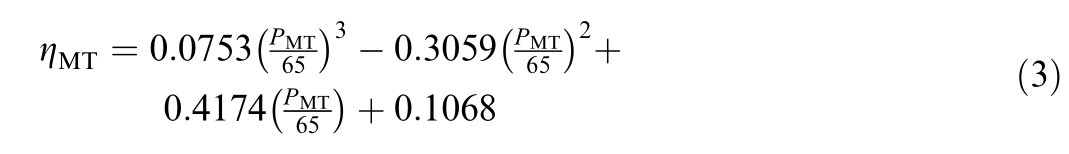
where: ηMT is the MT generation efficiency;PMT is the MT operating power.

1.3 DG mathematical model

DG is one of the main engine power sources in conventional power systems and has the adv antage of high reliability and very mature operation and maintenance technology [18].In a microgrid,DG can effectively bridge the energy gap when the power supply capacity of other distributed power so urces cannot meet the demand.Its combustion cost is:

where: α,β,γ is the combustion cost factor;PDG is the DG output power.

1.4 BT charge and discharge model

As an energy buffer device for microgrids,BTs play an important role in enhancing the safety and stability of microgrid operation.The charge state of a BT determines the switching of its operating mode,and is the ratio of the current stored power of the BT to its maximum power storage capacity,usually expressed as a percentage.It reflects the remaining charge of the battery,which helps to determine the usage of the battery and the remaining working time,and is calculated by the formula:

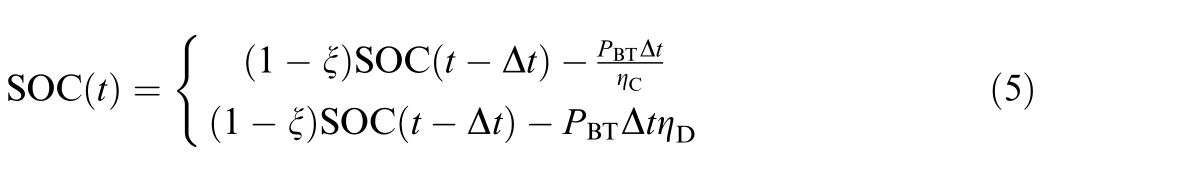
where: S OC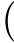t is the state of charge at the time of BT;ξis the internal loss rate;PBT is the charging and discharging power at the BT moment;ηC,ηD is the charging and discharging efficiency,This formula automatically covers both charging (PBT <0) and discharging (PBT >0) conditions based on the sign of the power value,while accounting for energy conversion efficiency during charging and discharging processes.

2 Microgrid optimal dispatch model

2.1 Objective function

After a detailed analysis of the output of each distributed power source in the system,the focus is on the minimum cost of generation (covering fuel costs,O&M costs and power exchange costs) and environmental costs during the optimization cycle of the microgrid [19].

1) Grid-connected microgrid power generation costs

The cost of microgrid power generation consists of fuel costs,operation and maintenance costs,and power interaction costs.

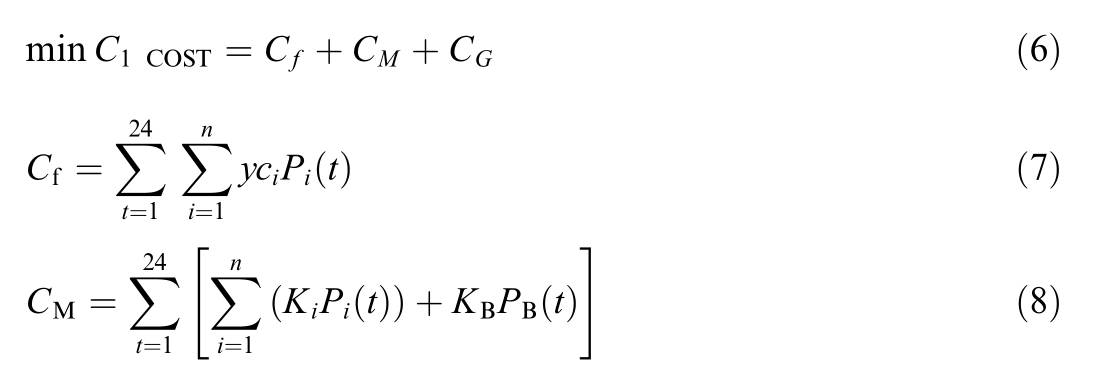
2) Environmental pollutant treatment costs

The pollutants that may be generated by grid-connected microgrids during operation mainly include CO2,SO2,NOx,etc.[20],and the cost of environmental pollutant managem ent is calculated by the formula.

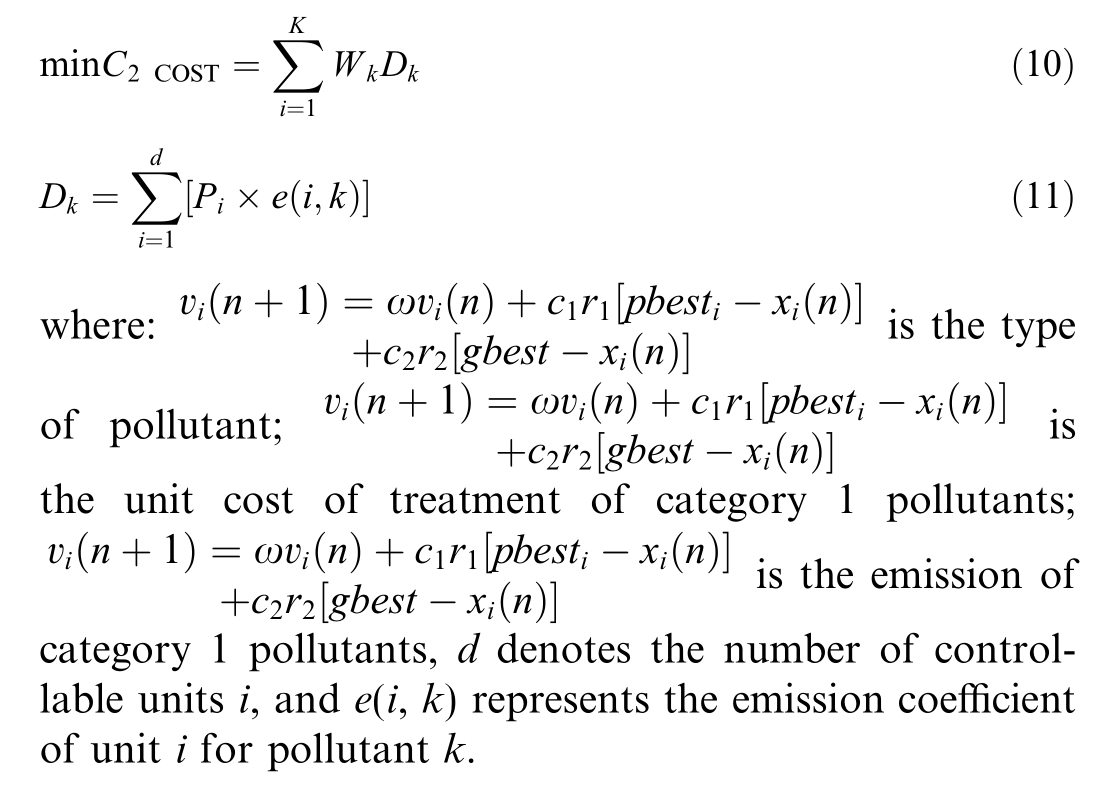
2.2 Restrictive condition

1) Load power demand balance constraints

where: PL is the microgrid demand load power.

2) Controllable unit handling constraints

where:  are the maximum and minimum values of the output power of the controllable unit;Piup, Pidown are the maximum and minimum values of the climb rate of the controllable unit.

3) Grid interaction constr aints

where:  are the minimum and maximum values of the grid interaction power,respectively.

4) Battery storage con straints

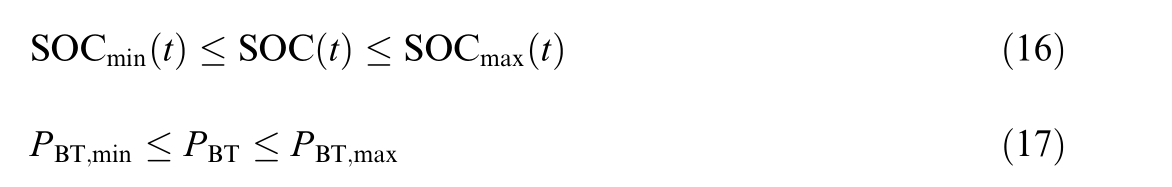
where: SOCmax t,SOCmin t is the upper and lower limits of battery capacity,is the upper and lower limits of battery power.

3 Multi-strategy improved MOP SO algorithm

3.1 MOPSO algorithm

In practical engineering applications,multiple optimization objectives are often faced,and there are often conflicts between these objectives.To address the above problems,researchers proposed a multi-objective oriented particle swarm optimization algorithm to cope with the optimization challenges of such complex systems [21,22].The multi-objective particle swarm algorithm inherits the core advantages of the classical particle swarm framework,while retaining its features of compact parameter space,simple algorithmic architecture,strong scalability and effi-cient convergence ability [23].The velocity and position upda te equations are:

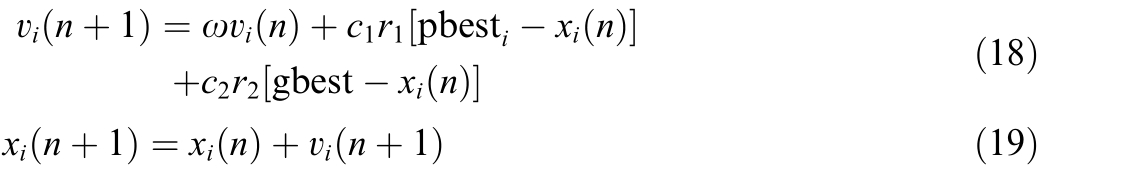
where: n is the number of iterations;ωis the inertia weight;c 1,c2 is the acceleration constant; r 1,r2 is a random number with the value in the range of [0,1];pbesti is the individual through the optimal position;gbest is the optimal position of the whole group.

3.2 IMOPSO algorithm

3.2.1 Logistic chaotic mapping

The core feature of chaos theory is the extreme sensitivity of its system evolution to initial conditions.By introducing the chaos mechanism into the design of optimization algorithms,its nonlinear dynamics can be effectively utilized to construct diversified search strategies,and this perturbation mechanism based on the chaotic mapping not only enhances the algorithm’s traversal ability in the solution space,but also maintains the population diversity by continuously generating the differentiated search patterns,thus significantly improving the probability of the algorithm breaking through the local extremum constraints to achieve the reliable search for the globally optimal solution[24].Logistic mapping is used to generate pseudo-random numbers,which can achieve better traversal,autocorrelation and inter-correlation,the initial number of populations is 100,and the location pair is shown in Fig.2.

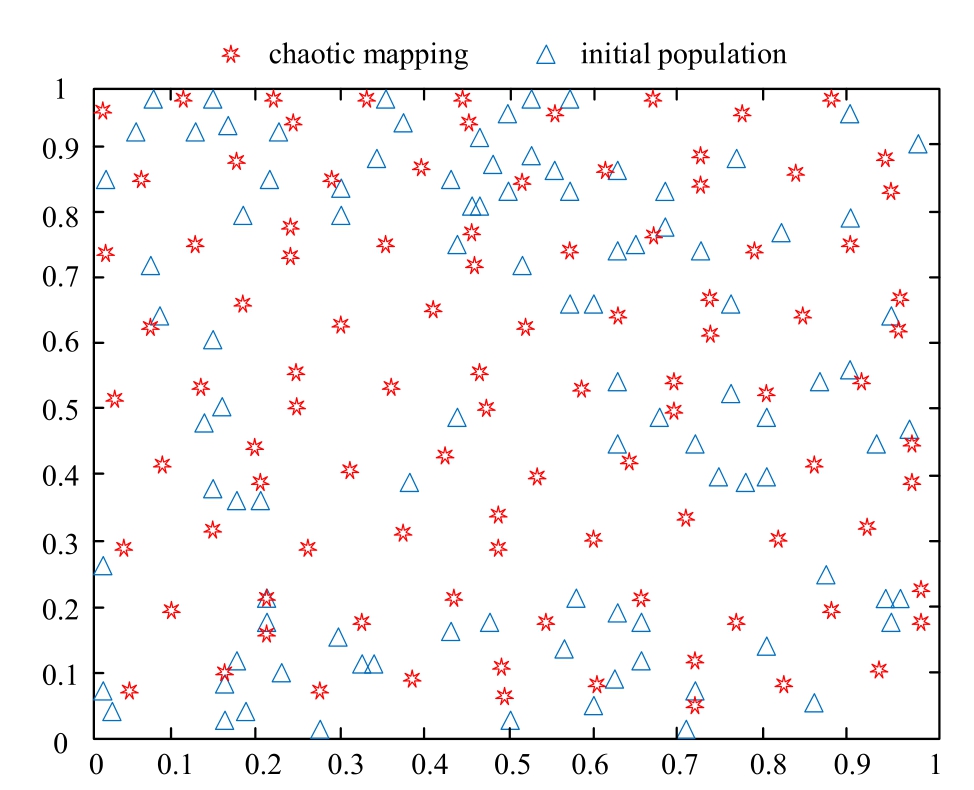
Fig.2.Comparison chart of particle position distribution.

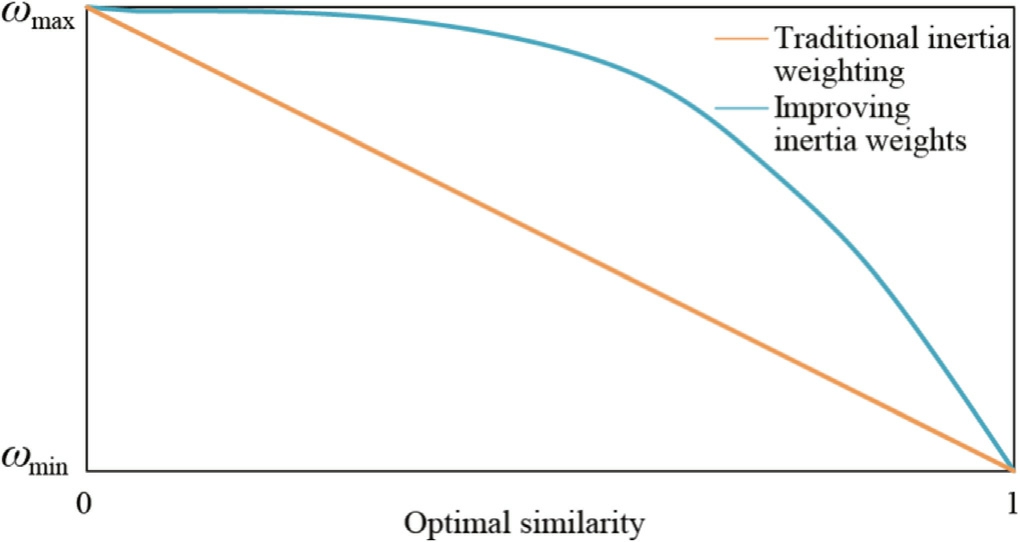
Fig.3.Inertia weight curve graph.

The mathematical expression of Logistic chaotic mapping is:

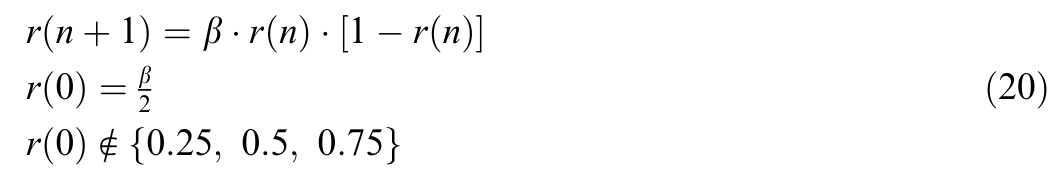
where: r n is the state value after several iterations;β is the control parameter of the system,take β 4;then the expression of the chaos operator is:

3.2.2 Adaptive adjustment of inertia weights

Aiming at the shortcomings of the traditional inertia weight adjustment strategy,which usually adopts linear or nonlinear decreasing mode to adjust the parameters and fails to effectively utilize the information of individual particle state,we propose the dynamic adjustment mechanism of inertia weight based on the correlation of optimal solution: through real-time calculation of the similarity index of each particle with the current global optimal solution,we construct the self-adaptive mapping relationship between the inertia weight and the particle state,so as to achieve the intelligent regulation of parameter values.Before the implementation of the optimal similarity calculation,it is necessary to implement the standardized preprocessing of the multi-dimensional positional parameters of the particles to eliminate the difference in the scale,so as to ensure that the parameters of each dimension are comparable.This processing unifies the parameters with different scales to the same order of magnitude through mathematical transformation to avoid the parameter weight imbalance problem caused by the scale difference.Counting the original matrix M=[M1, M2,, Md]and the normalized matrix N=[N1, N2,, Nd],i.e.N=[O1, O2,, On],the processing method is:

where: is the inertia weight of the ith particle;ωmax,ωmin are the maximum and minimum values of the inertia weight respectively.

This improved strategy compared with the traditional inertia weights,in the beginning of the iteration phase,showing a gradually decreasing trend,to ensure that the convergence coefficient can be maintained in a period of time a very high value,thus ensuring the algorithm’s global optimization ability;in the iterative process,the convergence coefficient is gradually reduced to a very small range,in order to avoid the loss of the optimal solution due to the large step size that occurs during the search process.

3.2.3 Adaptive mesh segmentation and congestion mechanisms

In some cases,the distribution of particles may be biased towards certain regions,resulting in an insuffi-ciently balanced search.In order to improve this problem,adaptive grid partitioning is introduced into multiobjective optimization,with the aim of dynamically adjusting the size of the grid and the partitioning strategy according to the current distribution of the population,and improving the adaptability of the algorithm in complex environments.In the initial stage,the objective space can be divided into larger grids to reduce the computational overhead;and as the search proceeds,the distribution of the particle population guides the refinement of the grid,making the search more focused on the potentially good solution regions in the objective space.

For a two-dimensional target space,the process of dividing the grid can be simplifeid to a grid within a twodimensional space.The target space is divided into n n small regions,denoted as Gi,j,where i,j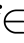{1,2,,n} denote the horizontal and vertical coordinates of the target space.Each small region Gi,j corresponds to a grid.The density of the grid indicates the distribution of particles in the region,and a smaller density of external archived optimal solutions means that the algorithm is more capable in performing global search,and the obtained so lutions can be more evenly and widely distributed.The density of a certain grid Gi,j is defined as the ratio of the number of particles in the region to the area of the grid for:

where: Ni j is the number of particles in the grid area;Δx,Δyare the unit division lengths in the x-axis and y-axis in the target space,respectively.

Under the multi-objective optimization scenario,the construction mechanism of the non-dominated solution set is fundamentally different from the updating strategy of the global optimal solution in the standard PSO algorithm,which is mainly reflected in the evaluation dimension and selection criteria of the solution space.In order to overcome the maintenance problem of the nondominated solution set,the adaptive external archiving strategy is designed to realize the diversity maintenance of the Pareto front through the dynamic density threshold regulation,which significantly improves the distribution breadth of the solution set.The specific updating method is as follows: adopt the non-dominated access criterion,only when the candidate solution can dominate at least one of the existing solutions in the archive can it be entered into the archive,otherwise,the solution set retention mechanism is triggered to ensure the Pareto-optimality of the archived solution set.Using the crowding distance threshold method,when the archive capacity reaches the preset upper limit,the solution individuals in the region with the highest distribution density in the target space are preferentially removed to maintain the uniformity of the frontier distribution.The formula for calculating the crowding distance of particles is as follows:

where: Cimax, Cimax, Cimax are three consecutive indivi duals;Cimax, Cimin are the objective function values for the maximum and minimum of all individuals in the external archive.

The non-dominated solution set screened based on the dynamic congestion regulation strategy can effectively balance the distribution density of solution individuals,and circumvent the tendency of discrete distribution while suppressing the overconcentration of frontier solutions,so as to enhance the diversity level of the population in the process of multi-objective optimization.

3.2.4 Fuzzy integrated evaluation

Based on the feasible solution set of Pareto frontier,a decision model combining fuzzy affiliation function and entropy weight method is constructed to realize the selection of optimal compromise scheme under multiattribute constraints.Breaking through the traditional constraints in the design of the decision-making process,we adopt the self-organized mapping technology of the frontier solution set to complete the optimal scheme extraction without the assignment of target weights by manual intervention.Define the affiliation function of the ith objective in the kth scheduling scheme as:

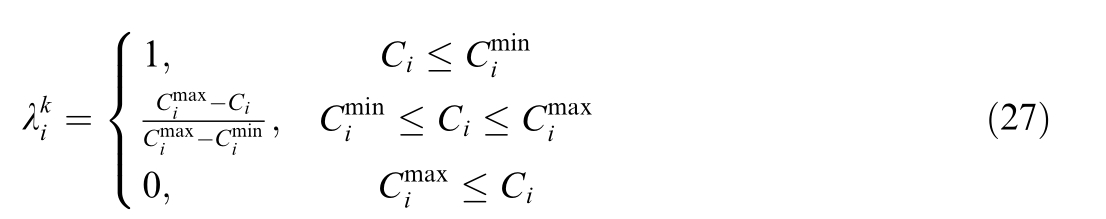
where:  is the minimum value of the ith objective function;is the maximum value of the ith objective function.

The affiliation function exhibits a strictly monotonic increasing property in this goal dimension,and its quantized value domain is positively correlated with the goal attainment.Next,for the kth candidate scheduling plan,its normalized affiliation function value is calculated based on (28).

where: L is the number of candidate decision options.

The design of the fuzzy affiliation function enables the quantification of the values of each objective function into a well-defined degree of affiliation,which in turn provides an evaluation of the relative superiority of each option.

3.3 Algorithm optimization process

Based on the established multi-objective optimization operation model of microgrid that takes into account the economy and environmental protection,the solution process of MOPSO algorithm improved by combining multiple strategies is shown in Fig.4.

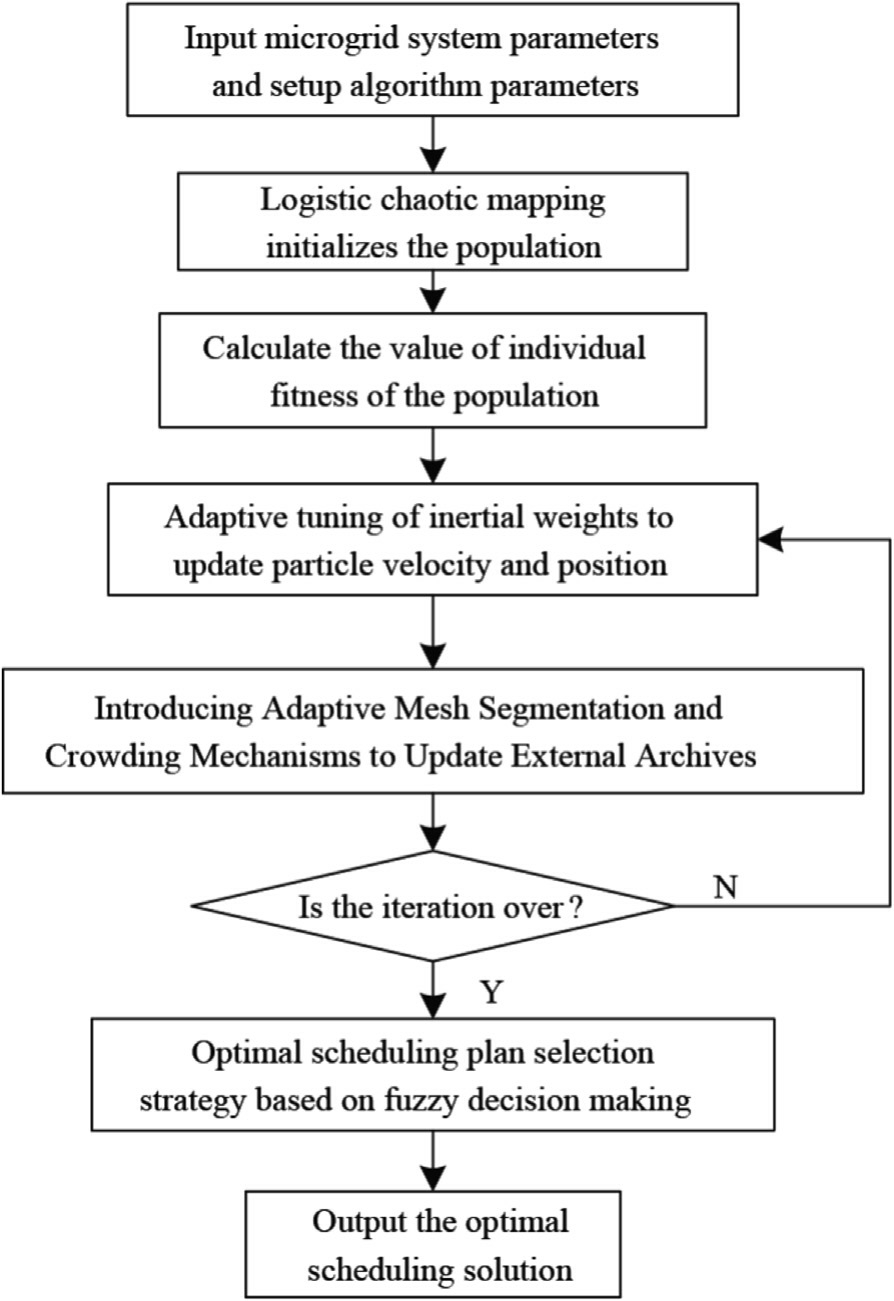
Fig.4.Algorithm flow.

Step 1: initialization stage.Firstly,input the microgrid parameters and set the core parameters of the algorithm.Logistic chaotic mapping is used to generate the initial particle swarm,which produces a uniformly distributed initial solution set in the solution space.

Step 2: iterative optimization phase.Calculate the fitness value of each particle and establish the mapping relationship between the particle and the target space.Guide the particles to move towards the Pareto front through the historical optimum and global optimum.

Step 3: archive maintenance phase.Prioritize the retention of high-quality solutions in sparse regions by calculating the grid congestion index.

Step 4: decision and output phase.After the iteration is completed,construct the fuzzy affiliation function to normalize the Pareto frontier solution set,select the optimal compromise from the non-dominated solution set,and output the best scheduling scheme.

4 Calculus analysis

4.1 MG basic data

A grid-connected microgrid system is used as a background for verification and analysis based on the power load forecast information and renewable energy processing data of a microgrid in central China.The scheduling period is set to be 24 h,and the load,wind,and PV output forecasts are shown in Fig.5,the output power limit and operation and maintenance cost of each dist ributed power source in the microgrid are shown in Table 1,the purchase price and sale price of electricity are shown in Table 2,and the pollutant treatment cost parame ters are shown in Table 3.

Table 1 Micropower supply parameter.

Table 2 Prices of electricity purchased and sold.

Table 3 Pollutant parameters.

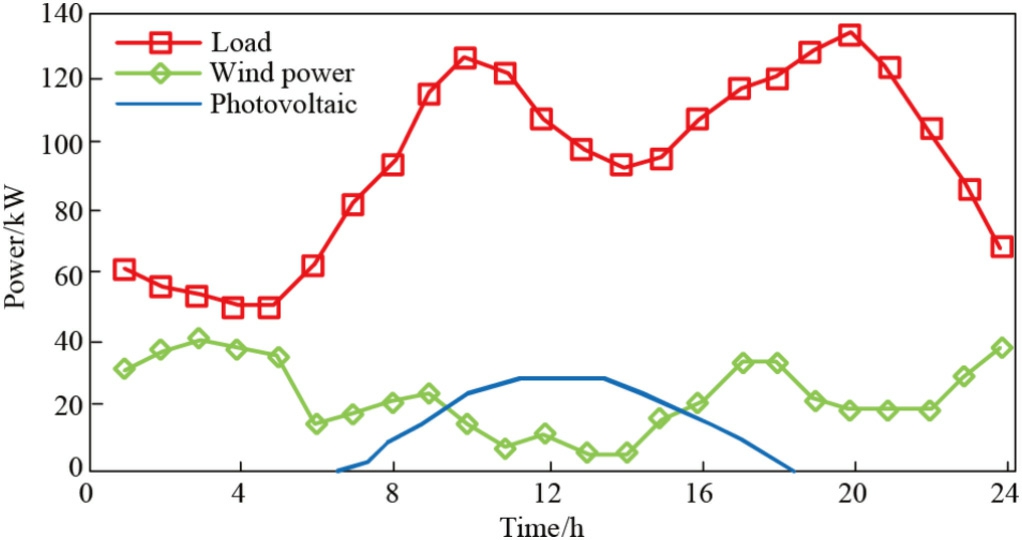
Fig.5.WT,PV output and load forecast curve.

4.2 Simulation analysis

Based on the coupling characteristics of energyenvironment system,we construct a parameter configuration system (group size=100,archive capacity=100,iteration number=300) to realize the Pareto frontier of microgrid economic cost and environmental governance expenditure through intelligent optimization algorithm.Figs.6 and 7 show the Pareto frontier results of the simulation runs of MOPSO and IMOPSO,respectively,from which it can be seen that the distribution of data points within the archive library of IMOPSO is more decentralized,reflecting the algorithm’s exploration of the diversity of the solution set.

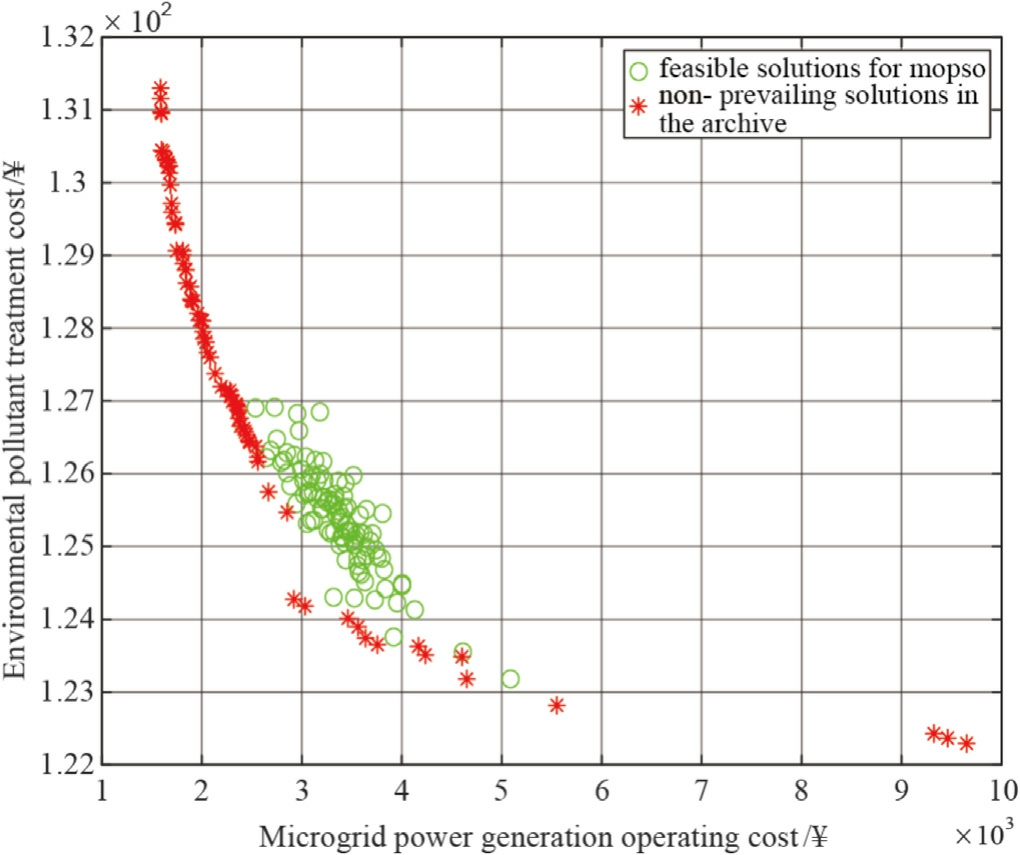
Fig.6.MOPSO pareto frontier.

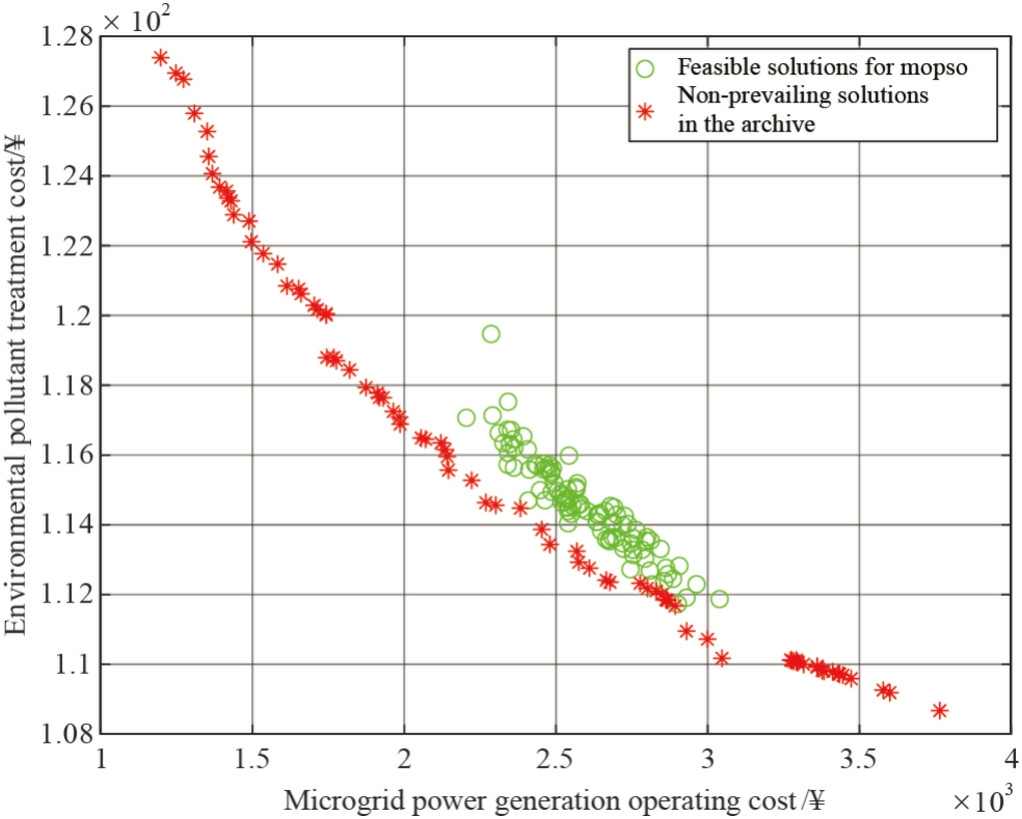
Fig.7.IMOPSO pareto frontier.

The power balance of each distributed power source is shown in Fig.8,the photovoltaic power generation is fully utilized at 1015 h,and the battery is in full power at 1922 h,effectively sharing the load of the diesel generator and the gas turbine,and the battery is recharged at the time of the low electricity price,effectively shaving the peak and filling the valley.The battery storage system plays a dynamic compensation role in the microgrid architecture,smoothing out the load peak-to-valley difference through the energy time-shifting strategy,significantly improving the transient stability of the grid and enhancing the fault ride-through capability.

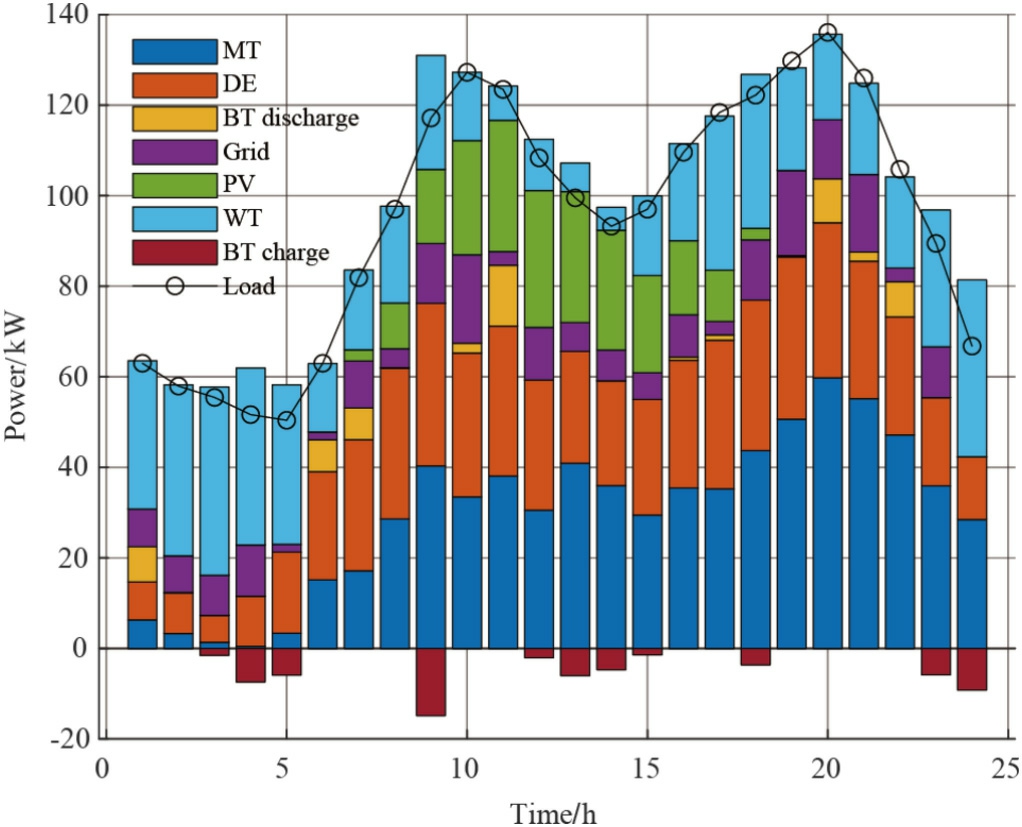
Fig.8.Distributed power balance diagram.

The distributed power output is shown in Fig.9,and the introduction of the storage battery provides an effective flexible regulation unit for microgrid operation,which can not only alleviate the power supply tension during peak hours,but also significantly enhance the operational reliability and system resilience of the system.

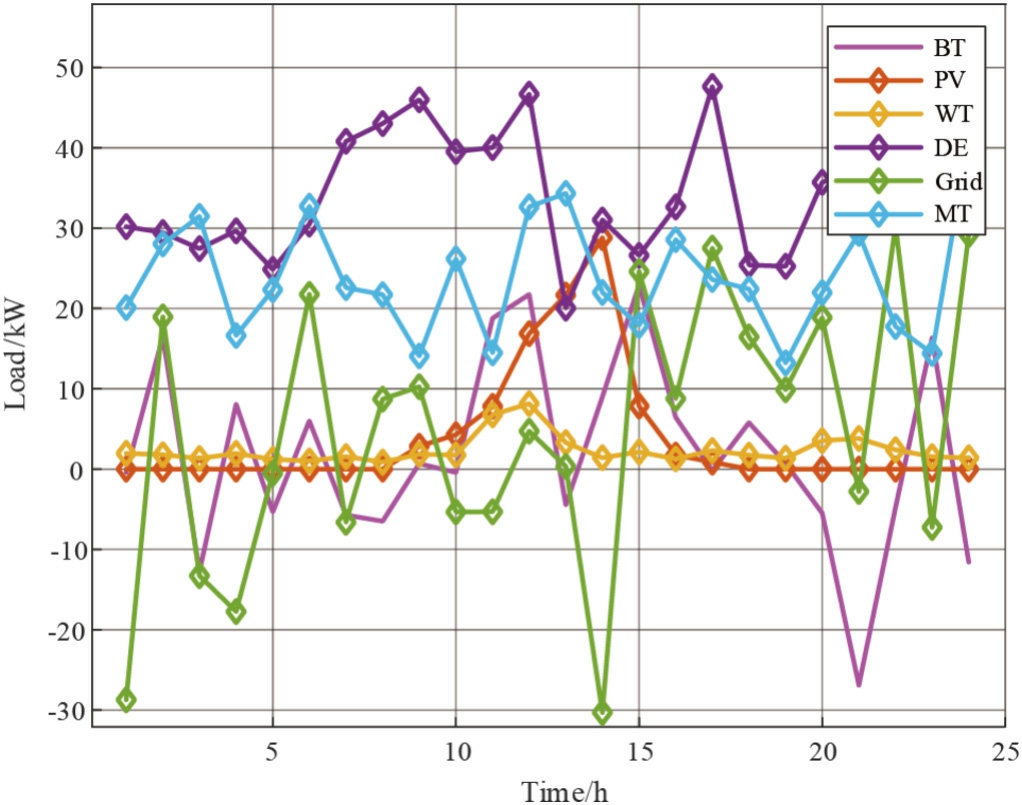
Fig.9.Distributed power output map by distributed power source.

In addition,the energy storage system adopts the tarifftime response strategy,which improves the economy while achieving the synergistic optimization of carbon emission reduction benefits.In the case that wind and light energy cannot meet the load requirements,if the energy storage device has power,the storage device will supply power to the system;when the storage battery does not have enough power,power can be purchased from the grid.

This study evaluates the performance of the improved IMOPSO algorithm in comparison with three traditional multi-objective optimization methods,namely multiobjective gray wolf optimization (MOGWO),multiobjective ant colony optimization (MOACO) and MOPSO.Objective optimization (MOACO),multi-objective ant colony optimization (MOPSO),and MOACO were compared and evaluated,and all the algorithms used uniformly set operation parameters.As shown in Fig.10,by comparing the convergence curves of the three algorithms,it can be found that the IMOPSO algorithm shows faster convergence characteristics,and its convergence speed is significantly better than that of the other compared algorithms.

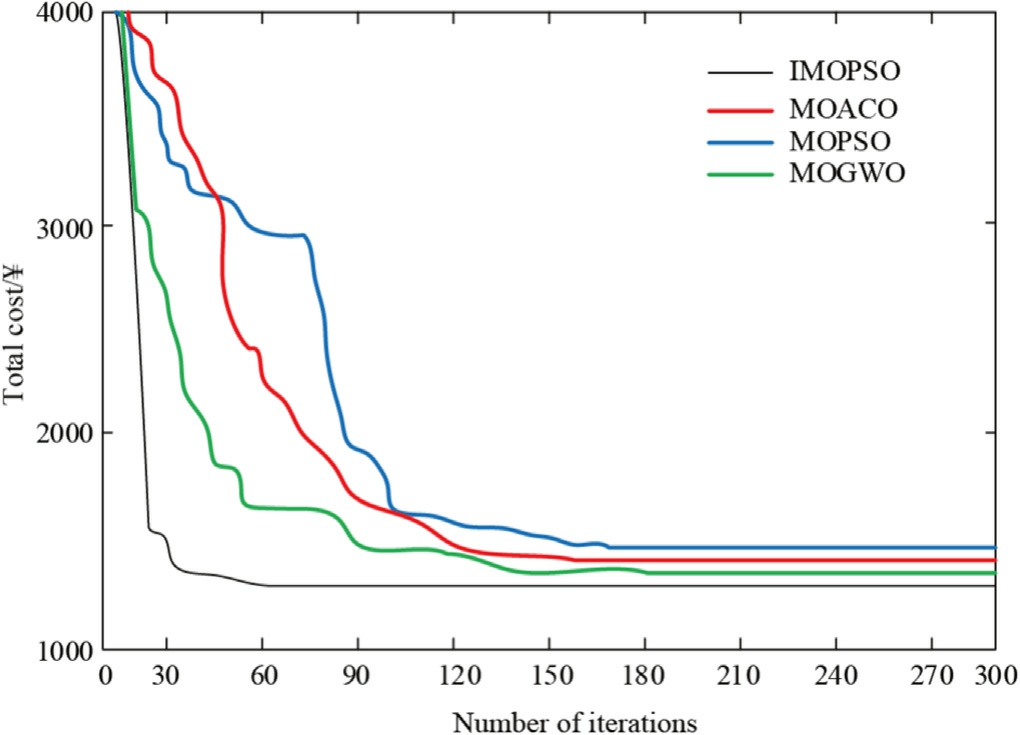
Fig.10.Comparison of the iterative curves of total operating costs.

Table 4 demonstrates the cost comparison data under different algorithms.The experimental data show that the proposed algorithm achieves a reduction of 3.15%,8.34%,and 10.27% in total cost compared to MOGWO,MOACO,and MOPSO,respectively;a reduction of 3.31%,8.72%,and 10.66% in power generation and maintenance cost,respectively;and a reduction of 1.61%,4.39%,and 6.18% in pollution control cost,respectively In terms of pollution control cost,the reduction is 1.61%,4.39% and 6.18% respectively.These data fully prove that the IMOPSO algorithm shows stronger global search capability in the optimization process,and can effectively avoid the local optimal trap,thus obtaining more ideal economic optimization results.

Table 4 Cost of fees for different algorithms.

5 Conclusion

For the multi-objective optimal scheduling problem of microgrid,IMOPSO algorithm is proposed for solving the system optimization model,and the superiority of the improved algorithm in terms of convergence speed,distribution of the solution set,and constraints processing capability is verified by building a multi-objective optimization model that includes the operating cost and pollutant emission control cost,and the optimization strategy for the microgrid operating cost is optimized for the economic benefits through the improvement of energy effi-ciency.The proposed method shows the superiority ofthe algorithm and the proposed operation strategy on simulation results,which verifies the engineering practicability of the proposed method.

CRediT authorship contribution statement

Yang Xue: Supervision,Methodology.Shiwei Liang: Writing– review &editing,Writing– original draft.Fengwei Qian: Project administration. Jinyi Tang: Validation,Investigation.

Declaration of competing interest

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Fengwei Qian is currently employed by Shanghai Solar Energy Engineering Technology Research Center.The other au thors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

This work was supported by the “Science and Technology Innovation Action Plan” project of Shanghai in 2021 program (21DZ1207502).

References

[1]H.Karimi,S.Jadid,S.Hasanzadeh,A stochastic tri-stage energy management for multi-energy systems considering electrical,thermal,and ice energy storage systems,J.Storage Mater.55(2022).

[2]Y.Yu,J.Wu,G.Sun,et al.,Event-triggered secondary frequency control of isolated microgrid based on fixed time consensus algorithm,J.Shandong Univ.Sci.Technol.(Nat.Sci.Ed.) 43 (2)(2024).

[3]C.Qin,Z.Ma,H.Chen,et al.,research on the optimal operation of new microgrids under the dual carbon goals,Electr.Measur.Instrum.62 (3) (2025) 46–53.

[4]H.Karimi,M.Monemi Bidgoli,S.Jadid,Optimal electrical,heating,cooling,and water management of integrated multi-energy systems considering demand-side management,Electr.Pow.Syst.Res.220 (2023).

[5]H.Huang,X.Wen,M.Niu,et al.,Multi-objective path planning of autonomous underwater vehicles driven by manta ray foraging,J.Marine Sci.Eng.12 (1) (2024) 88.

[6]G.-Q.Zeng,Y.-W.Yang,K.-D.Lu,G.-G.Geng,J.Weng,Evolutionary adversarial autoencoder for unsupervised anomaly detection of industrial internet of things,IEEE Trans.Reliab.74(3) (2025) 3454–3468.

[7]K.-D.Lu,Y.-W.Yang,G.-Q.Zeng,C.Peng,G.-G.Geng,J.Weng,BPSO-AHDL-IDS: binary particle swarm optimizationbased automated hybrid deep learning model for intrusion detection of internet of things,IEEE Trans.Autom.Sci.Eng.22(2025) 15859–15877.

[8]H.-X.Yang,H.-H.Kuang,Z.-L.Li,et al.,Optimal economic dispatch of microgrid based on improved grey wolf optimization algorithm,Acta Energiae Solaris Sinica (2025) 1–9.

[9]Z.-M.Li,N.-E.Wang,Economic optimization operation strategies for microgrids based on energy storage batteries and diesel generators,J.Lanzhou Univ.Technol.51 (04) (2025) 72–80.

[10]H.-Y.Li,H.-B.Xu,L.Zhang,et al.,Research on low-carbon economic optimization scheduling of hybrid energy microgrid group based on improved snake algorithm under time-of-use electricity price,J.Solar Energy 46 (03) (2025) 132–140.

[11]Y.Xu,H.Wang,Optimal scheduling of microgrid based on the improved grey wolf algorithm,Comput.Simu-lation 40 (03) (2023)96–102.

[12]Y.-W.Wang,Y.Zhang,X.-K.Liu,X.Chen,Distributed predefined-time optimization and control for multi-bus DC microgrid,IEEE Trans.Power Syst.39 (4) (2024) 5769–5779.

[13]Y.Zhang,Y.-W.Wang,J.-W.Xiao,X.-K.Liu,Distributed predefined-time optimal economic dispatch for microgrids,Automatica 169 (2024).

[14]J.Lai,X.Wen,Q.Zhang,et al.,Optimal allocation of DC microgrid capacity based on improved sparrow search algorithm,J.Solar Energy 44 (8) (2023) 157–163.

[15]X.Hao,M.Zhao,L.Pei,et al.,Scheduling decision optimization of wind/solar/hydrogen storage highway microgrid based on the improved Pareto algorithm,J.Traffic Transp.Eng.24(4)(2024)71–82.

[16]B.Sun,G.Zhao,J.Li,et al.,Research on multi-objective microgrid optimal scheduling based on improved bird swarm algorithm,Smart Power 52 (6) (2024) 46–53.

[17]J.Chen,X.Wang,W.Li,et al.,Research on Optimal Scheduling of Microgrid Using the Improved Northern Goshawk Algorithm Journal of Chongqing University of Technology(Natural Science)38 (1) (2024) 281–289.

[18]F.Li,X.Wei,Y.Chen,et al.,Optimal scheduling of microgrid based on the improved cuckoo algorithm,Control.Eng.31 (11)(2024) 1963–1971.

[19]R.Sun,Z.Yuan,W.Wang,et al.,Dynamic reactive power optimization method for active distribution networks with solidstate transformers when source load fluctuates,Renew.Energy 42(07) (2024) 937–945.

[20]X.H.Xie,H.J.Yang,B.Wang,et al.,Optimal day-ahead scheduling strategy of microgrid considering regional pollution and potential load curtailment,Global Energ.Int.(2024)749–760.

[21]Q.Ye,W.Wang,Z.Wang,Review of multi-objective particle swarm optimization algorithm and its application research,J.Zhejiang Univ.(Eng.Sci.) 58 (06) (2024) 1107–1120,+1232.

[22]Y.C.Duan,P.Li,J.Xia,Prediction and scheduling of multi-energy microgrid based on BiGRU self-attention mechanism and LQPSO,Global Energy Int.(2024) 347–361.

[23]H.Qin,L.Chen,H.Tang,et al.,Cement Raw Material Ratio Optimization Based on System Identification and Improvement of Multi-objective Particle Swarm Optimization Algorithm Control Engineering (2025) 1–10.

[24]L.Zhang,H.Guo,H.L.Yao,Research on microgrid optimization based on the improved bat algorithm,Power Grid Clean Energ.37(4) (2021) 122–126.

Received 15 June 2025;revised 30 October 2025;accepted 3 November 2025

Peer review under the responsibility of Global Energy Interconnection Group Co.Ltd.

* Corresponding author.

E-mail addresses: xueyang@shiep.edu.cn (Y.Xue),1596030028@qq.com (S.Liang),qianfengwei@126.com (F.Qian),1050057594@qq.com(J.Tang).

https://doi.org/10.1016/j.gloei.2025.11.001

2096-5117/© 2025 Global Energy Interconnection Group Co.Ltd.Publishing services by Elsevier B.V.on behalf of KeAi Communications Co.Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Yang Xue received his Doctor’s degree from Beijing Institute of Technology in 2003.He works at the School of Automation Engineering of Shanghai University of Electric Power as an associate professor.His research interests include intelligent control,new energy power generation,microgrids and robots.