0 Introduction
With the rapid growth in distributed renewable energy generation in microgrids and the rising number of electric vehicles (EVs),source load uncertainty in microgrids has been further exacerbated.The challenge of ensuring users’electricity supply while maintaining the stable operation of microgrids has emerged as a critical research focus,attracting widespread scholarly attention [1–3].
At present,optimal microgrid operation can be achieved through methods such as empirical,probabilistic model-based,and classical scenario-based methods [4].In particular,the empirical method selects typical days based on historical expert experience [5,6].The probabilistic method generates source load scenarios by combining the statistical experience or probability distributions of historical data with different sampling techniques [7,8].Meanwhile,the classical scenario-based method,rooted in a style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">In the formulation of microgrid operation strategies,traditional optimization constructs mathematical models based on practical engineering practices,simplifies and processes these models through mathematical techniques,and ultimately solves problems using optimization algorithms.These approaches include mixed-integer programming,nonlinear programming,and dynamic programming.Meanwhile,the solution methods encompass Lagrangian relaxation,the branch-and-bound method,Newton’s method,and intelligent algorithms.Ref.[13]established a bi-level optimization model to minimize the carbon emissions and operational costs of the system.Ref.[14]developed an optimal scheduling model considering carbon capture and power-to-gas technologies.However,the aforementioned methods suffer from slow solution convergence owing to the dimensions of complex systems and convergence failure due to the requirements of scenarios with real-time constraints [15].
style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">Ref.[28]designed an energy management system(EMS) for hybrid electric vehicles (HEV),utilizing the twin delayed DDPG (TD3) algorithm to improve the agent training efficiency and reduce the fuel consumption of HEVs.Ref.[29]utilized the TD3 algorithm to address power system operation safety problems and validated the method’s effectiveness and applicability in actual power system operation scenarios.Training results revealed that the algorithm still exhibited slow convergence induced by the random sampling of data and required a large number of iterations.Ref.[30]proposed an energy management strategy based on the TD3 algorithm with prioritized experience replay (PER-TD3).By utilizing the prioritized experience sampling method,the training process of TD3 was accelerated,and superior economic performance was attained.Ref.[31]proposed a sum-tree (ST) data structure-based TD3 algorithm to address the low-carbon economic dispatch of an IES.
Based on the existing TD3 algorithm,this study uses the ST data structure [32]to store and sample historical experience data and implements prioritized experience replay(PER),thereby improving the training efficiency and performance of the TD3 algorithm.First,an MDP model was constructed for the intraday real-time scheduling scenarios of microgrids.Subsequently,typical scenarios were generated using GPR,and a decision-making interaction mechanism was established to train the agent’s decisionmaking capability.During the training process,priorities were set based on value calculations of data updates.Next,by leveraging both the data itself and its priorities stored in the ST data structure,a hierarchical sampling method was employed to ensure the coverage of samples with “high,”“medium,” and “low” priorities,thereby enhancing the training efficiency.Finally,simulations were conducted to validate the effectiveness of the proposed method in microgrid intraday scheduling.Comparisons with different a lgorithms further demonstrated improvements in training efficiency and reductions in scheduling costs.
The main contributions of this study are summarized as follows:
To address microgrid generation-load uncertainties across different time scales,a GPR model based on the Bayesian framework is proposed.This model constructs confidence intervals using the mean and variance of historical generation-load data,enabling the generation of scenarios with the required degree of uncertainty.
Considering the slow solution speed of the traditional mixed-integer linear programming (MILP) method,this paper proposes an intraday real-time microgrid scheduling method based on DRL to rapidly generate unit dispatch schemes.Its advantage lies in the fact that the agent learns from a large number of historical generation-load scenarios during offline training,generating near-optimal strategies for real-time scheduling.
An improved PER-TD3 algorithm integrating an ST data structure is proposed.While reducing the update complexity,the algorithm parameters were adjusted through sensitivity analysis and ablation experiments.After ad justment,the algorithm fully explored and utilized high-value experience data,significantly improving the agent’s training efficiency and stability.
1 Scheduling model of microgrid considering source load uncertainties
1.1 Source–load uncertainty scenario generation method
GPR,leveraging a statistical approach to model historical data patterns,excels in handling nonlinear and highdimensional problems due to its inherent uncertainty quantification capability.

The GPR can be expressed as

Accordingly,the posterior distribution of the test set output vectorf  is
is
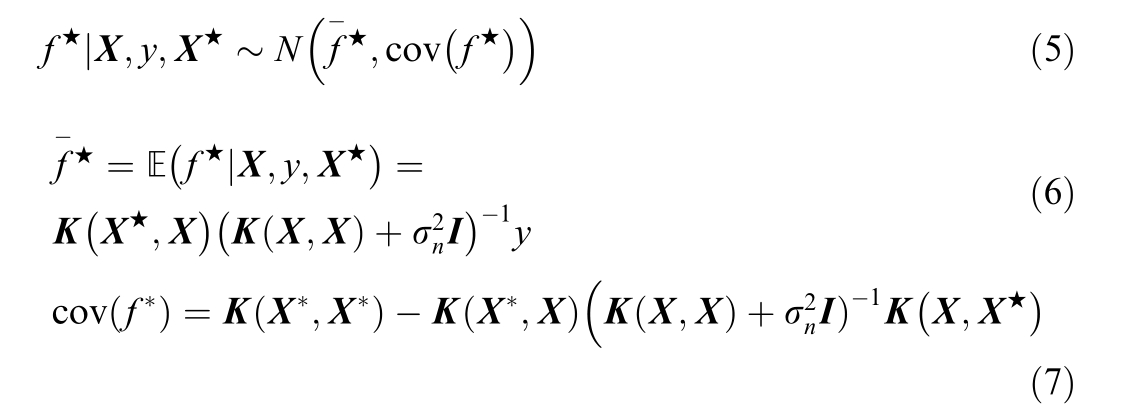
where ![]() denotes the inner expectation function,f★represents the expectation,and a confidence interval is constructed using the mean and variance to serve as the uncertain scenario.
denotes the inner expectation function,f★represents the expectation,and a confidence interval is constructed using the mean and variance to serve as the uncertain scenario.
The confidence interval with a confidence level of 1 α is:
α is:
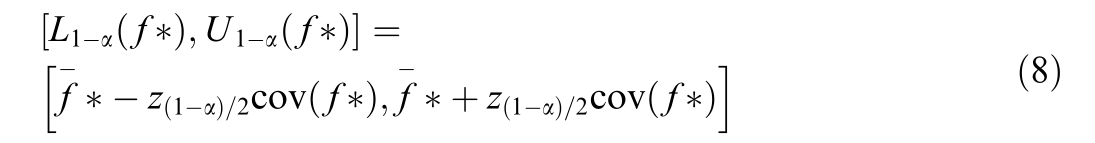
where ![]() denote the upper and lower bounds of the confidence interval,respectively,and
denote the upper and lower bounds of the confidence interval,respectively,and ![]() represents the quantile under the corresponding confidence level.
represents the quantile under the corresponding confidence level.
1.2 Objective function
The objective function of the microgrid intraday scheduling model is as follows:
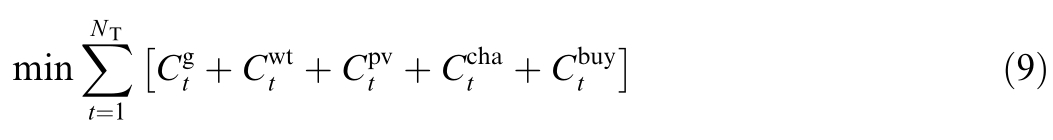

1.3 Constraints
Du ring the intra day scheduling,the constraints of micro grid operation are as follows:
1) Power balance equality constraint:
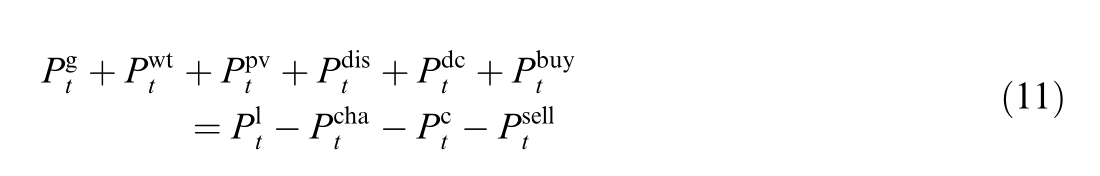
2) Generation output inequality constraints (upper/lower bounds):

3) The tie line power constraint:

4)The energy storage charging and discharging constraint:
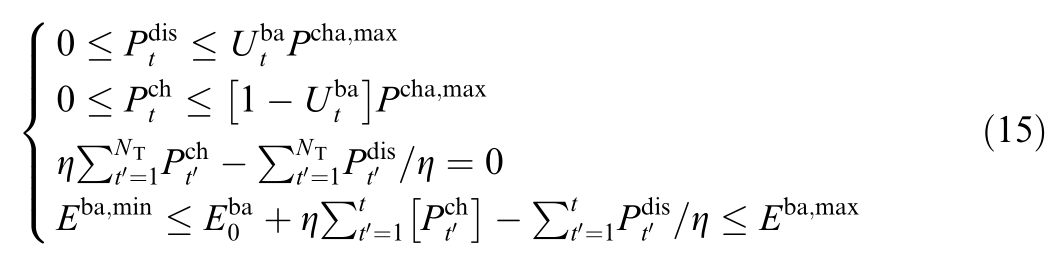
where ![]() denotes the energy storage charging/discharging status (1 represents charging,0 represents discharging);ηdenotes the charging/discharging efficiency;
denotes the energy storage charging/discharging status (1 represents charging,0 represents discharging);ηdenotes the charging/discharging efficiency;![]() denotes the storage capacity at the initial scheduling time;and
denotes the storage capacity at the initial scheduling time;and ![]() denote the maximum and minimum allowable remaining capacities of the storage during the scheduling process.
denote the maximum and minimum allowable remaining capacities of the storage during the scheduling process.
5) EV charging and dischar ging constraint:

2 Equivalent transformation of the microgrid scheduling model based on tailored TD3
2.1 Data preprocessing
To ensure the effective exploration of the agent and mitigate the negative impact of parameter order-of-magnitude differences on the agent’s training convergence results,all training data is normalized.The equation is:
where Xnormalized is the normalized result,X represents the pre-normalization value,and Xmin and Xmax are the minimum and maximum value in the sample sequence data,respectively.
2.2 Decision-making based on Markov process
In this study,the traditional microgrid model is transformed into a Markov process,whose basic components include ![]() where S represents the set of environmental states,A represents the set of agent actions,R denotes the reward for the agent,and γ represents the discount factor,which balances short-term and long-term rewards.Its environment,states,and actions are as follows:
where S represents the set of environmental states,A represents the set of agent actions,R denotes the reward for the agent,and γ represents the discount factor,which balances short-term and long-term rewards.Its environment,states,and actions are as follows:
1) Environment
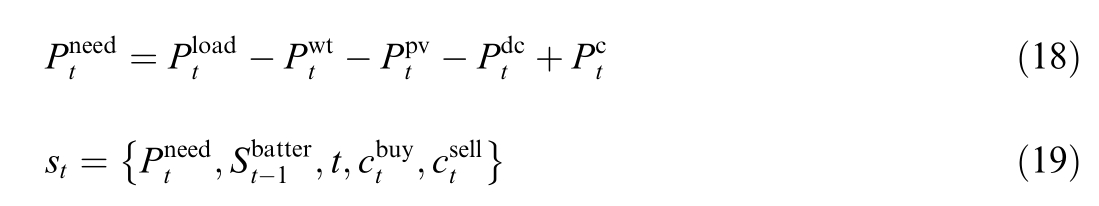
where st denotes the observed operatingstate provided by the environment to the agent;![]() is the power demand to be met at time t;and
is the power demand to be met at time t;and ![]() represents the state of charge(SOC) of the energy storage at the previous time step.
represents the state of charge(SOC) of the energy storage at the previous time step.
2) Action
3) Reward and penalty
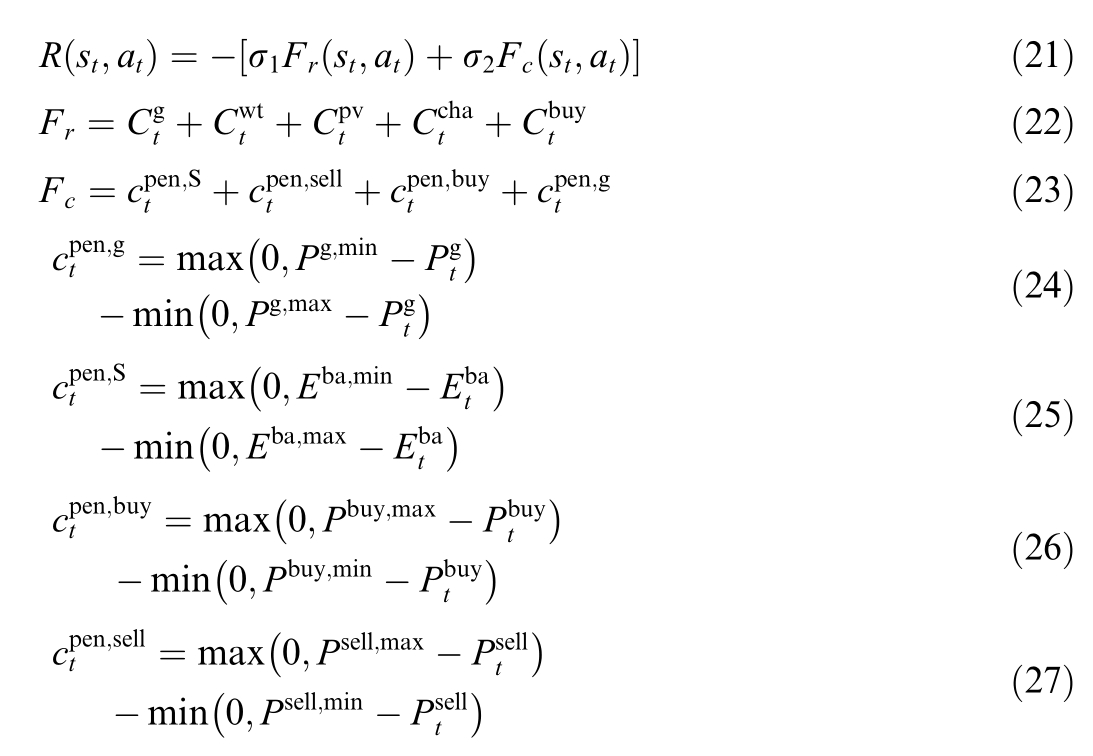
where σ1 denotes the scaling factor for the control costs;σ2 represents the scaling factor for the execution constraint penalties;F r and F ccan be represented as operational costs and constraint penalty values,respectively;![]()
![]() is the penalty for energy storage SOC out-ofbounds at time t;
is the penalty for energy storage SOC out-ofbounds at time t;![]() denote the penalties denotes the MT out-of-bounds violation penalty at time for the power grid power purchase and sale out-ofbounds at time t;and other constraints such as the output upper and lower bounds can be normalized using the Tanh function.
denote the penalties denotes the MT out-of-bounds violation penalty at time for the power grid power purchase and sale out-ofbounds at time t;and other constraints such as the output upper and lower bounds can be normalized using the Tanh function.
2.3 ST-PER-TD3 algorithm
The TD3 algorithm is an optimized improvement method for the deterministic policy method DDPG [33].Building on the DDPG,it introduces two independent critic networks to estimate the Q-values of the stateaction pairs,effectively reducing the overestimation of the action Q-values in the DDPG algorithm.The methodology of TD3 is as follows: First,to enhance the agent’s action exploration capability and smoothen the policy expectation during parameter updates,behavioral policy noise and target policy noise are separately added to the actor.Second,to mitigate overestimation,both the real and target networks of the critic employ twin networks.Finally,to improve the stability of the output policy,the parameters of the actor’s real network are updated with a delay only after the critic network has undergone multiple updates.However,TD3 performs random data sampling during training,which results in low training efficiency and slow reward convergence.As a tree-based data structure in computing,the ST’s logical architecture A aligns with TD3 s data storage and access requirements,and its integration into the algorithm can enhance the data processing efficiency.
This paper introduces the ST into the experience replay buffer,sets a priority indicator for experience data,and aims to achieve efficient PER and increase the utilization of high-update-value experience data,thereby improving the training efficiency of the agent.
In this report,the critic network employs the actionvalue function to compute the TD error:

where ρl and δdenote the sampling priority probability and corresponding TD error of the l th experience data,respectively,and υ is the weighting factor.
υ=0 corresponds to uniform sampling,and υ=1 corresponds to greedy strategy sampling.To reduce the discrepancy in sampling probability between data with larger δ and smaller δ,this report sets υ=0 6.Additionally,to avoid missing experience data with a very small TD error,new experience data are initialized as follows:
where δl0 denotes the TD error of the l th experience data when it is initially added to the experience replay buffer B,and δmax represents the maximum TD error within the experience replay buffer B,which aims to increase the sampling probability of experience data with very small TD errors.
The microgrid economic dispatch model based on the tailored TD3 method is shown in Fig.1.The specific training process of the agent is as follows:
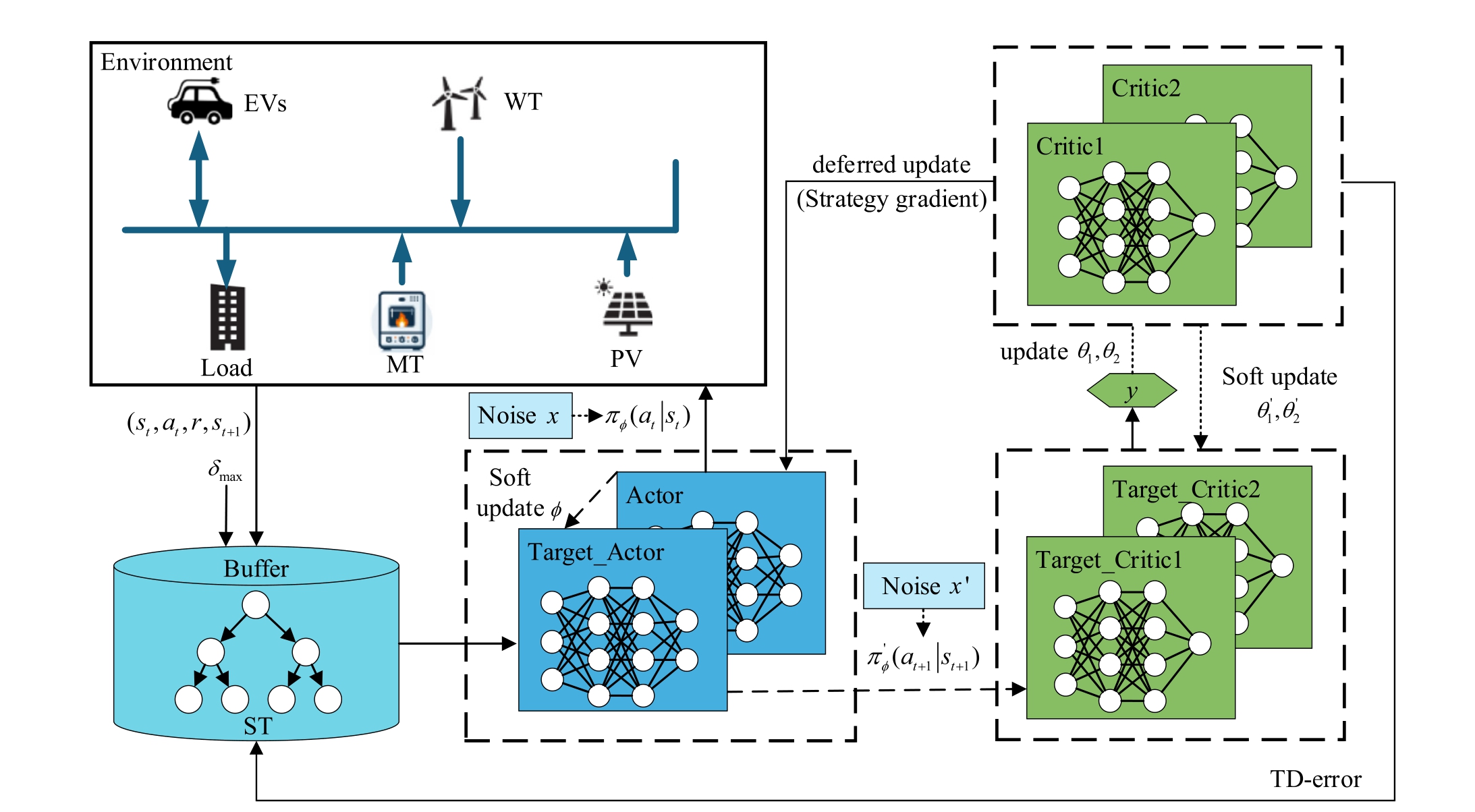
Fig.1.Tailored TD3 algorithm framework.
1) Initialize the parameters θ1,θ2,and φof the three real networks of critic1,critic2,and the actor network.Initialize the parameters of the three target networks with the same parameter values,namely![]()
2) Set the capacity of the experience replay buffer B and the number of training samples N.
3) Acquire and add experience data tuple s to B.
a) Randomly select an initial state s t from historical data.Under a noisy environment,πφselects an ac tion a t based on the state st:
b) In ter act with the environment using the action at,thereby obtaining the reward value rt and the next state s t 1,fo rm ing a data tuple
1,fo rm ing a data tuple![]()
c) Using the data’s TD error as its priority metric,the node values of the relevant nod esin the ST are updated accordingly.
d) Check the number of experience data entries in buffer B.If the number has not reached the set capacity limit,use the current st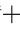 1 as the st in step 2,and repeat the above steps;otherwise,stop adding data and assign the largest δ in buffer B to the corresponding nodes of each data entry.
1 as the st in step 2,and repeat the above steps;otherwise,stop adding data and assign the largest δ in buffer B to the corresponding nodes of each data entry.
4) Sample N data entries from buffer B,and add a noise 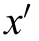 based on the target policy smoothing regularization to each data entry according to
based on the target policy smoothing regularization to each data entry according to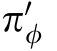 to obtain the target action at
to obtain the target action at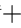 1 correspondingto st
1 correspondingto st 1:
1:
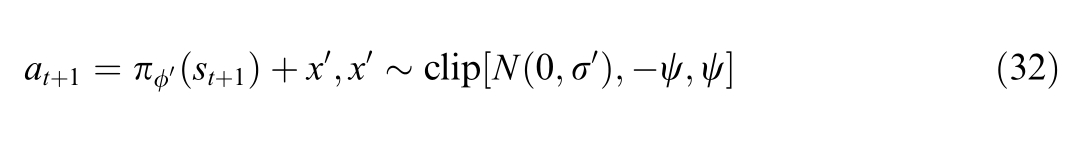
where ψdenotes the noise truncation value.
5) Record the obtained![]() and the observed reward
and the observed reward![]() then input them into the two critic target networks to compute the target value y t:
then input them into the two critic target networks to compute the target value y t:
6) Based on the gradient descent algorithm,we minimize the error between the target value and the observed value to thereby update the parameter s θof the two critic real networks.
7) Using a learning rate of τ1,compute the weighted average of the parameters of the real network and the target network to soft-update the parameters of the target network.
8) Recalculate the δof the data entry and update the nodevalues of its corresponding leaf node and relevantnodes in the ST.
9) After the critic network has been updated ford steps,the parameters φof the actor real network are sim ilarly updated using the gradient descent algorithm.
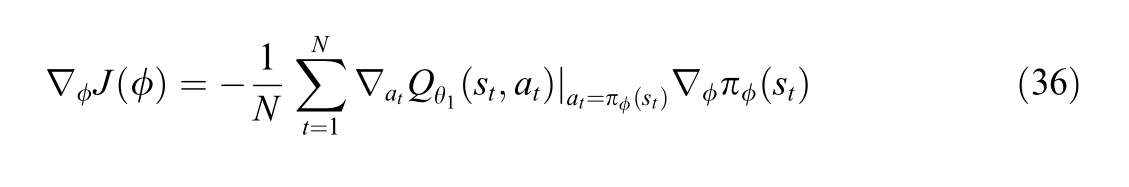
10) Use a learning rate of τ2 to soft-update the parameters of the actor target network.
Loop through steps (4) (9) and record the reward values until the number of rounds reaches the maximum.
3 Case studies
The simulation of new energy power generation,realtimeelectricity prices,and electric demand is conducted usingmonthly real-world data from an actual region in Zhejiang Province,China,with a sampling interval of 15 min.Since the selection of covariance functions has been extensively studied in existing literature [34],using the expert experience method [35],we selected a radial basisfunction (RBF) covariance function using the Python 3.10 soft ware.Eleven features were input into the model,specifically including month,day-of-week features,load values,wind speed,and surface radiation.The adaptive adjustment of GPR parameters was performed using the gp.fit()function from the scikit-learn library,and negative values were truncated.The single-day regression curve obtained from training,along with its 95% confidence region,was used to generate the uncertainty scenarios for intraday scheduling.
The input dimension of the DRL neural network is 7,corresponding to 7 state variables in the state space.The intermediate layers consist of 2 fully connected layers with 256 neurons each,and the rectified linear unit (ReLU) activation function was employed in these intermediate layers.The final output used the tanh activation function to map values to the range [ 1,1].The output layer has a dimension of 2,indicating 2 continuous actions in the action space.During training,the learning rates of the actor and critic networks were set to [α]and [β],respectively,with a decay rate of 0.99.The training configuration includes a sample library capacity of 20,000,a total of 100,000 training episodes,and 96 optimization steps per episode(each step spanning 15 min).Samples(200 in number)were collected from the critic network’s sample library every 480 episodes to update the actor network.The energy storage battery has a maximum capacity of 1000 kWh,with an initial SOC of 0.5.The first 1000 episodes were dedicated to storing environmental samples in the sample library.After the initial sample library reached 1000 entries,the reinforcement learning algorithm began to search for the optimal action policy.The parameters of the TD3 algorithm are listed in Table 1,those of generation and energy storage are provided in Table 2,and those of time-of-use electricity purchase and sale prices are shown in Table 3.
1,1].The output layer has a dimension of 2,indicating 2 continuous actions in the action space.During training,the learning rates of the actor and critic networks were set to [α]and [β],respectively,with a decay rate of 0.99.The training configuration includes a sample library capacity of 20,000,a total of 100,000 training episodes,and 96 optimization steps per episode(each step spanning 15 min).Samples(200 in number)were collected from the critic network’s sample library every 480 episodes to update the actor network.The energy storage battery has a maximum capacity of 1000 kWh,with an initial SOC of 0.5.The first 1000 episodes were dedicated to storing environmental samples in the sample library.After the initial sample library reached 1000 entries,the reinforcement learning algorithm began to search for the optimal action policy.The parameters of the TD3 algorithm are listed in Table 1,those of generation and energy storage are provided in Table 2,and those of time-of-use electricity purchase and sale prices are shown in Table 3.
Table 1 Hyperparameters of the deep reinforcement learning algorithm.
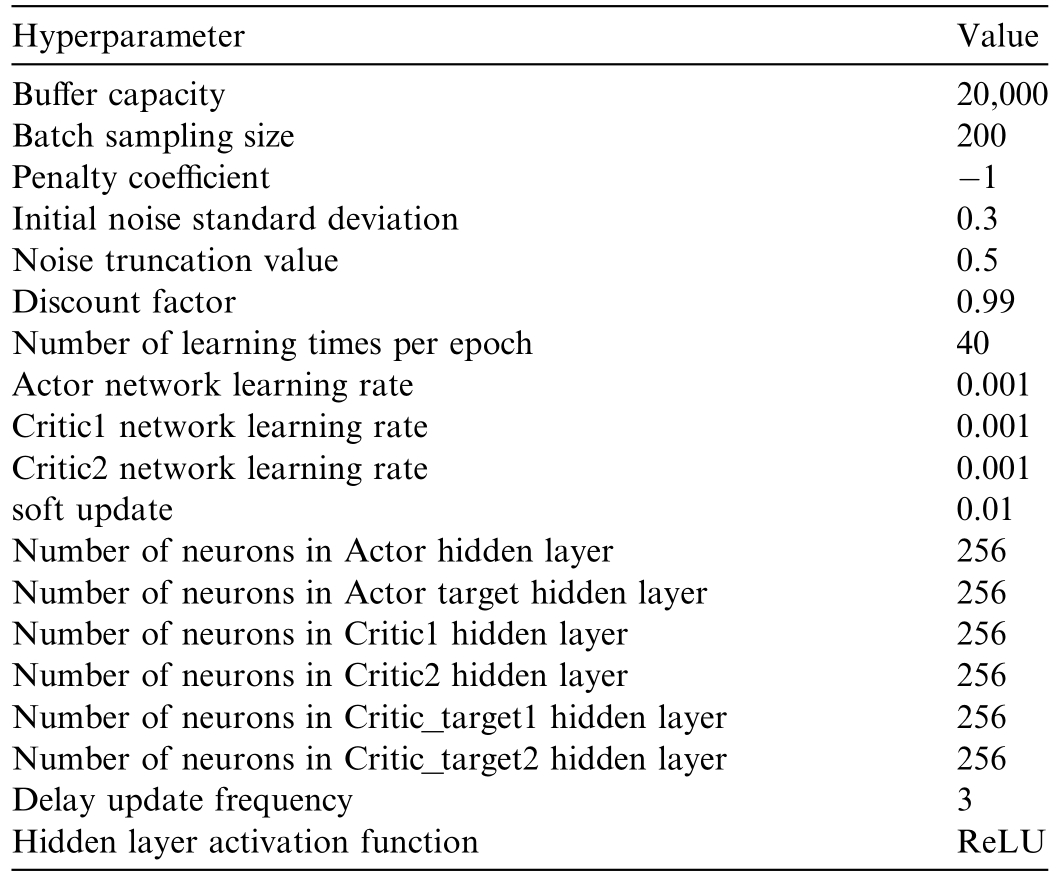
Table 2 Parameters of the distributed generator s and energy storage equipment.

Table 3 Time-of-use electricity price parameters.

Experiments were run on machines equipped with Intel(R) Xeon(R) E5-2666v3 CPU cores,32 GB memory,and NVIDIA GeForce GTX 1080.
All test cases were executed on identical hardware and within the same Python environment.Neural network models were trained using PyTorch 1.12.0 as the framework,wi th consistent neural network parameters.The computational results were compared with those of the following five algorithms:
B1: DDPG algori thm.
B2: TD3 algori thm.
B3: rank-based PER-TD3 algorithm.
B4: pure-greedy-based PER-TD3 algorithm.
B5: traditional robust scheduling method.
The description of rank-based and pure-greedy-based PER-TD3 algorithms can be found in Appendix A.
Notably,5 independent experiments were conducted for each sample,and we used 95% bootstrap percentile confidence intervals to describe the uncertainty in reward estimation [36].
During real-time operation,a 95% confidence interval of GPR is used to simulate the uncertainty of wind power output,photovoltaic power output,and demand (Fig.2).
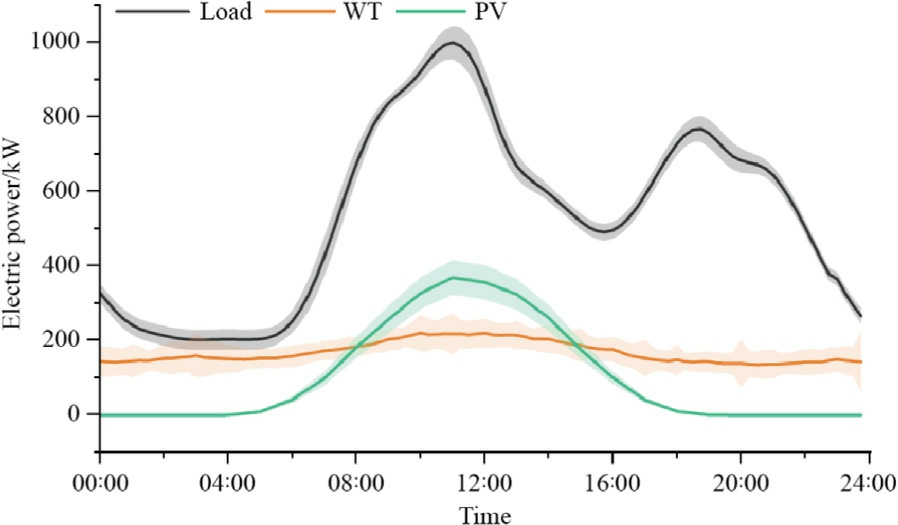
Fig.2.GPR curve and its 95% confidence interval.
The convergence of the reward cu rves is shown in Fig.3,which indicates that all baselines achieved their optimization objectives,after which the trained neural network models were saved for real-time scheduling.During training,B1,relying on a single critic network to evaluate action outcomes,is prone to overestimating Q-values,leading to significant fluctuations in reward values.B2 uses dual critic networks to estimate Q-values,which reduces reward fluctuations but results in slower convergence.B3 employs a rank-based prioritization sampling strategy,which discards the specific numerical values of TD errors.As a result,certain important transitions with low TD errors and lower ranking tend to be underestimated.For instance,during episodes 200–400,the algorithm occasion-ally failed to learn effective policies in certain training instances.B4 consistently replays the experience with the highest priority.While this approach accelerates convergence,it also leads to repeated sampling of high-error transitions.Consequently,samples with low TD errors—despite their potential importance—are rarely selected,resulting in slower convergence as reflected in the performance curve.As a conventional static robust optimization routine,B5 does not interact with the environment and thus produces no reward curve;instead,it yields a single worst-case solution by solving the min–max program off-line.The proposed ST-PER-TD3 algorithm achieves good convergence at the start of episodes and attains the optimal final cost.
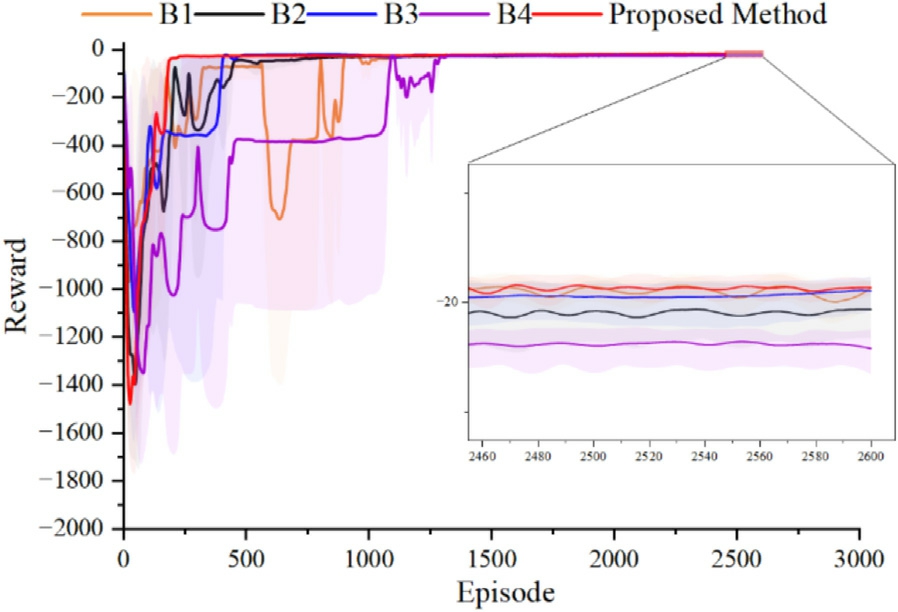
Fig.3.Reward curves of different algorithms.
The real-time scheduling results of different algorithms are shown in Fig.4,and Table 4 presents the comparison of the dispatching resul ts using different algorithms.
Table 4 Comparison of system operation average results by different methods.
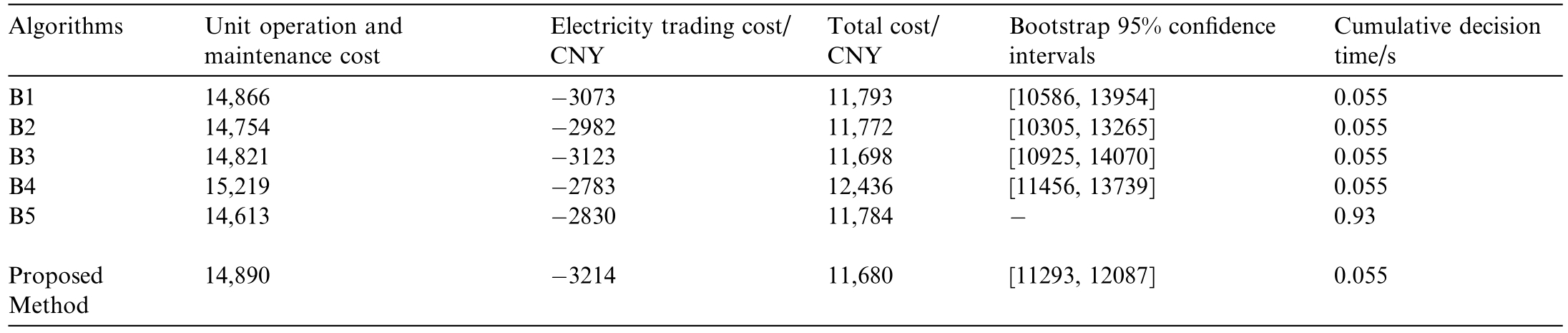
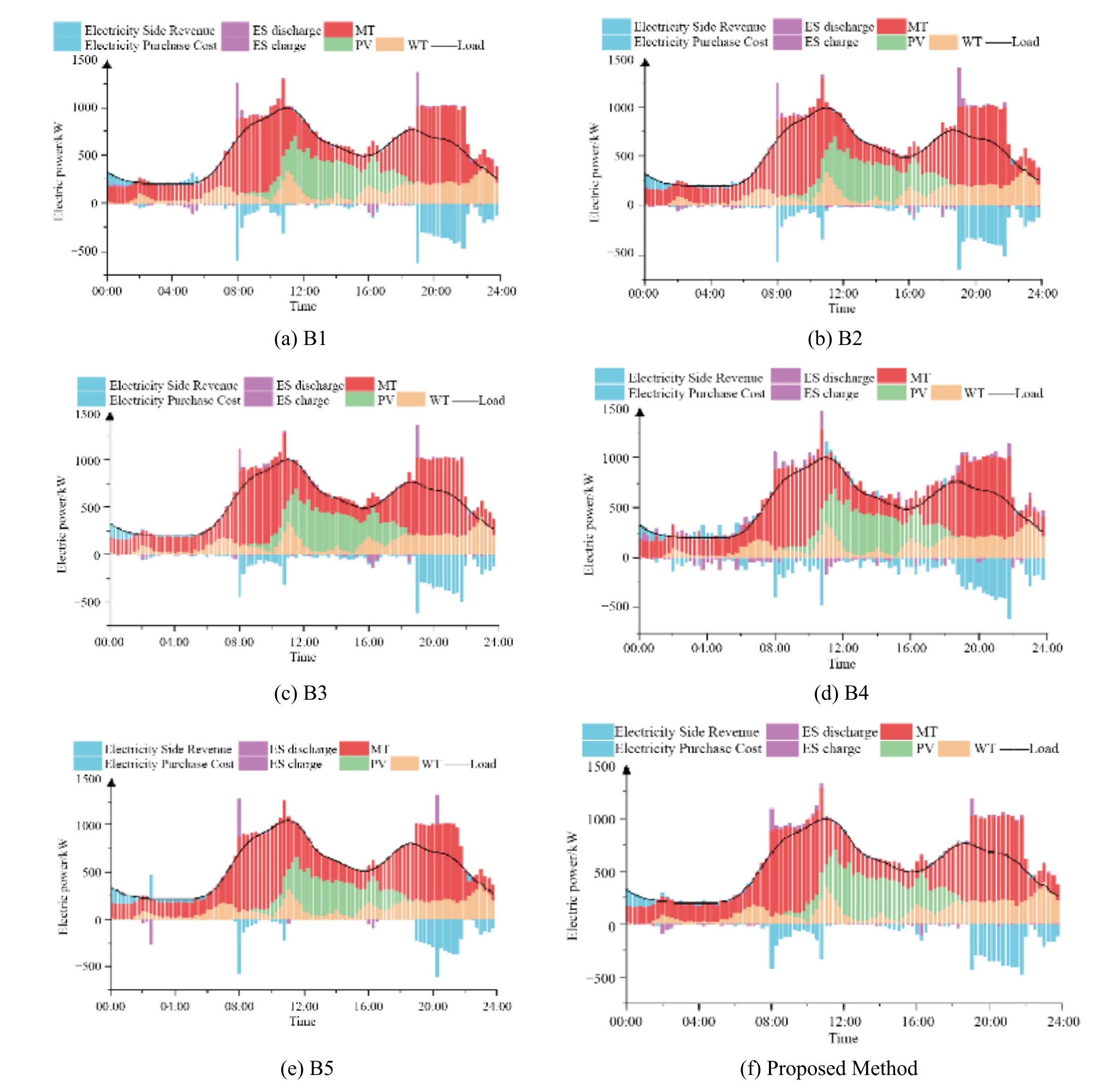
Fig.4.Power balance diagrams of scheduling strategies for various methods.
Fig.4 presents the results of different algorithms.The energy storage SOC values exhibit certain upward and downward fluctuations.This is a normal phenomenon.B1,B2,and B3 have similar real-time decisions within days,which can make better decisions for different moments.During intraday dispatching with B4,energy storage charging and discharging are frequently performed,resulting in higher unit operating costs and higher total costs.B5 offers a robust intraday optimal scheduling.The worst-case optimal solution is obtained by the Gurobi solver,and the decision-making speed is slow.The proposed algorithm achieves better results in electricity trading when the unit operation and maintenance cost is low,resulting in a lower intraday dispatching cost.
Table 4 demonstrates that the total cost of the proposed method,at 11,680 CNY,is the lowest and is 0.95%,0.78%,0.15%,6.08%,and 0.87% lower than that of B1,B2,B3,B4,and B5,respectively.The results indicate that the proposed ST-PER-TD3 algorithm generates superior strategies.Additionally,by screening key information using the TD error,the ST-PER-TD 3 algorithm effectively mitigates local convergence problems during training,with both the convergence speed and stability of its reward curve surpassing those of the other TD3 algorithms.It can therefore be concluded that the ST-PER-TD3 algorithm achieves a superior operating strategy.
Additionally,the solution time of the traditional robust optimization method is 0.93 s,whereas that of the trained ST-PER-TD3 algorithm is 0.055 s.The proposed ST-PERTD3 algorithm is approximately 17 times faster in solution speed than the traditional method.Compared with the TD3 algorithm,the ST-PER-TD3 algorithm achieves an improvement of approximately 2.42 times in convergence speed.
To investigate the impact of key parameters on the performance of the proposed ST-PER-TD3 algorithm,we employed the logarithmic spacing method,sampling uniformly within the range of [10–2,10–5 ].For each sampling point,five repeated experiments were conducted,and the smoothed reward values and their 95% bootstrap percentile confidence intervals were plotted.The learning rates of the actor and critic network test samples are![]()

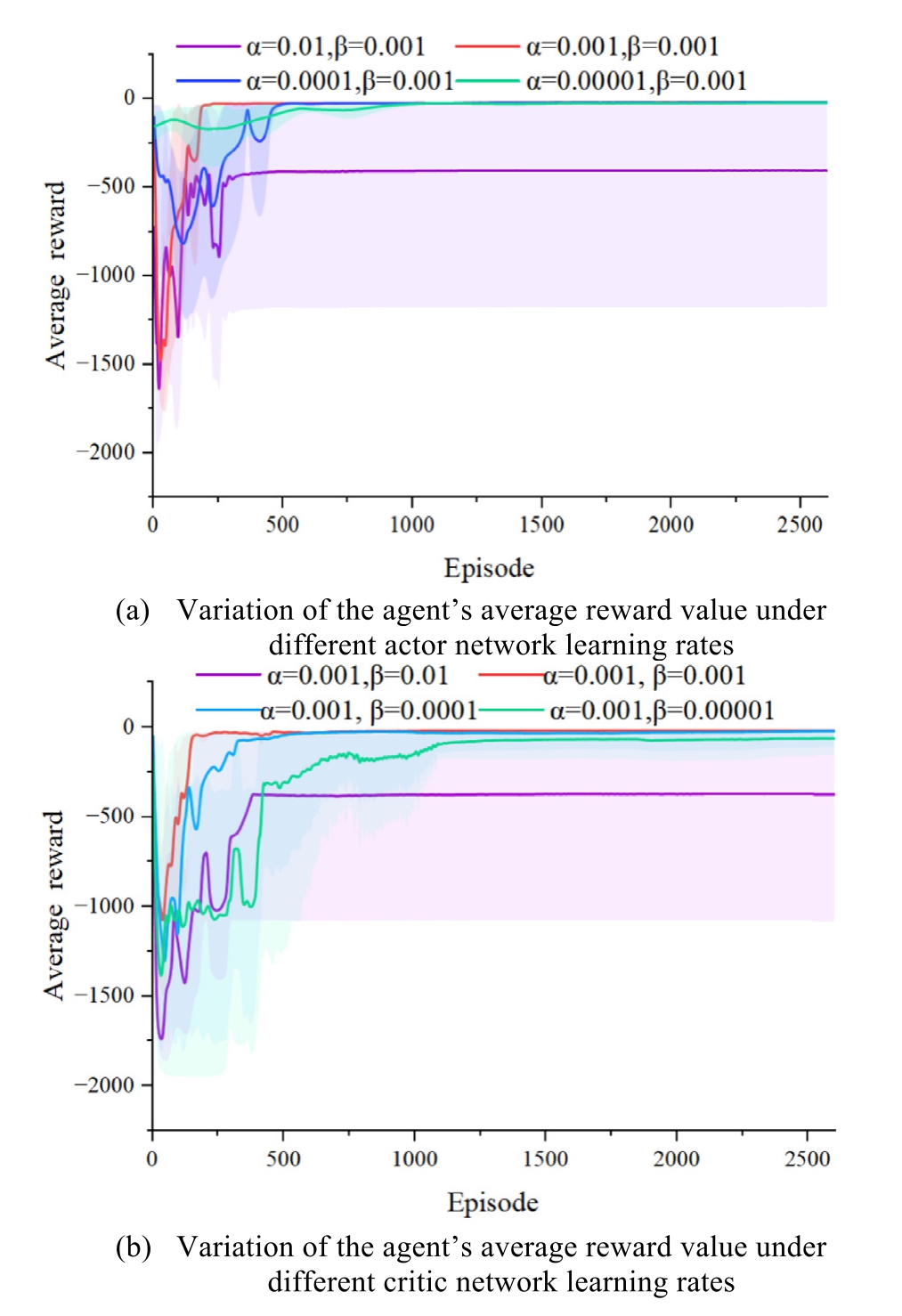
Fig.5.Variation of the agent’s average reward value under different parameter settings.
Meanwhile,to guide the agent to explore the environment extensively during the early training stage,avoid falling into local optima,and refine the policy during the middle-to-late training stages to enhance the stability of the policy,a noise decay strategy was adopted to dynamically adjust the noise magnitude.We selected different initial σ![]() to conduct ablation experiments,aiming to investigate the convergence performance of the agent under different noise levels.The σ was linearly decayed to 0.1 over 500 steps.
to conduct ablation experiments,aiming to investigate the convergence performance of the agent under different noise levels.The σ was linearly decayed to 0.1 over 500 steps.
Fig.6 shows the average training rewards of the agent and their 95% confdience intervals under different initial noise standard deviations.When there is no noise in the actions(i.e.,σ=0),the agent exhibits poor environmental exploration capability and converges slowly.When σ=0 1,the agent’s convergence speed accelerates.When σ was set to 0.2 or 0.3,the agent sufficiently explores the environment,and the reward curve achieves favorable convergence.However,σ=0 3resulted in more stable convergence performance.Therefore,this value was selected.
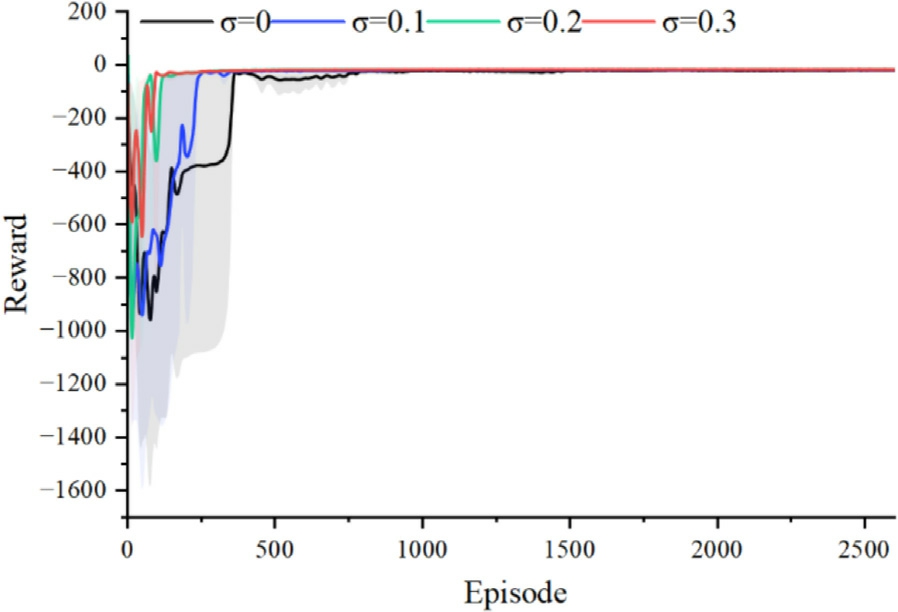
Fig.6.Variation of the agent’s average reward value under different initial noise values.
4 Conclusion
This study developed a DRL algorithm tailored for the intraday scheduling of microgrids under source load uncertainty.The optimal parameters of the ST-PERTD3 algorithm for microgrid intraday scheduling tasks were determined by accelerating the PER sampling process through the ST data structure and utilizing a proportional prioritization sampling strategy to select more valuable experiences for agent training.Case studies demonstrate that the proposed ST-PER-TD3 algorithm exhibits outstanding performance in both convergence speed and average intraday scheduling cost.In the future,we will study the robustness of the system under communication delay and errors between devices and attempt to extend it to multi-microgrid systems.
CRediT authorship contribution statement
Shenpeng Xiang: Writing– original draft,Formal analysis,Data curati on,Conceptualization. Mohan Lin: Writing– review &editing,Methodology,Formal analysis,Conceptualization.Zhe Chen: Supervision,Methodology,Funding acquisition.Pingliang Zeng: Writing– review &editing,Supe rvision,Resources. Xiangjin Wang: Supervision,Methodology,Data curation. Diyang Gong: Resources,Methodology.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Zhe Chen,Xiangjin Wang,and Diyang Gong are currently employed by Electric Power Research Institute of State Grid Zhejiang Electric Power Co.,Ltd.The other authors declare th at they have no known competing fniancial interests or personal relationships that could have appeared to infulence the work reported in this paper.
Acknowledgments
This work was supported in part by Science and Technology Project of State Grid Corporation of China (No.5400-202319829A-4-1-KJ).
Appendix A
The rank-based PER-TD3 algorithm defines the experience sampling probability based on the absolute value of the TD-error,with its formula as:
where υrepresents the weighting fact or;pi =1 ranki denotes the priority assigned to experience i,where ranki indicates the ranking of the ith experience among all experiences.
ranki denotes the priority assigned to experience i,where ranki indicates the ranking of the ith experience among all experiences.
The pure-greedy-based PER-TD3 algorithm consistently selects the current highe st-priority samples for replay.
References
[1]Multi-level optimal energy management strategy for a grid tied microgrid considering uncertainty in weather conditions and load,Sci.Rep.,(n.d.).https://www.nature.com/articles/s41598-024-59655-7 (accessed June 17,2025).
[2]EV and RE Uncertainty Analysis in Micro-Grids,IEEE Conference Publication,IEEE Xplore,(n.d.).https://ieeexplore.ieee.org/document/10474737 (accessed June 17,2025).
[3]S.Ray,A.M.Ali,T.Eshchanov,E.Khudoynazarov,Optimal energy management of the smart microgrid considering uncertainty of renewable energy sources and demand response programs,(2025).
[4]J.Zhang,Y.Cai,X.Tang,Y.Tan,Y.Cao,J.Li,Information gap decision theory-spectrum clustering typical scenario generation method considering source load uncertainty,J.Shanghai Jiao Tong Univ.(2023),https://doi.org/10.16183/j.cnki.jsjtu.2023.580.
[5]L.Li,W.Tang,M.Bai,et al.,Multi-objective locating and sizing of distributed generators based on time-sequence characteristics,Automat.Electr.Power Syst.37 (3) (2013) 58–63,https://doi.org/10.7500/AEPS201204046.
[6]M.Ding,J.Xie,X.Liu,W.Shi,The generation method and application of wind resources/load typical scenario set for evaluation of wind power grid integration,Proc.CSEE 36 (15)(2016) 4064–4071,https://doi.org/10.13334/j.0258-8013.pcsee.152854.
[7]L.Li,W.Tang,M.Bai,L.Zhang,T.Lu,Multi-objective locating and sizing of distributed generators based on time-sequence characteristics 58–63+128,Dianli Xitong Zidonghua/Automat.Electr.Power Syst.37 (2013),https://doi.org/10.7500/AEPS201204046.
[8]J.Li,Review of wind power scenario generation methods for optimal operation of renewable energy systems,Appl.Energy(2020).
[9]B.Bai,M.Han,J.Lin,et al.,Scenario reduction method of renewable energy including wind power and photovoltaic,Power Syst.Protect.Control 49 (15) (2021) 141–149.
[10]A.B.Krishna,A.R.Abhyankar,Time-coupled day-ahead wind power scenario generation: a combined regular vine copula and variance reduction method,Energy 265 (2023),https://doi.org/10.1016/j.energy.2022.126173 126173.
[11]P.Wang,L.Fan,Z.Cheng,A joint state of health and remaining useful life estimation approach for lithium-ion batteries based on health factor parameter,Proc.CSEE 42 (4) (2022) 1523–1533,https://doi.org/10.13334/j.0258-8013.pcsee.202368.
[12]J.A.Lin,S.Ament,M.Balandat,D.Eriksson,J.M.Hernández-Lobato,E.Bakshy,Scalable Gaussian processes with latent kronecker structure,(n.d.).
[13]B.Zhang,Y.Xia,X.Peng,Robust optimal dispatch strategy of integrated energy system considering CHP-P2G-CCS,Global Energy Interconnect.7 (2024) 14–24,https://doi.org/10.1016/j.gloei.2024.01.002.
[14]F.Tian,Y.Jia,H.Ren,Y.Bai,T.Huang,“Source-load” lowcarbon economic dispatch of integrated energy system considering carbon capture system,Power Syst.Technol.44 (9) (2020) 3346–3354,https://doi.org/10.13335/j.1000-3673.pst.2020.0728.
[15]P.Li,H.Zhong,H.Ma,J.Li,Y.Liu,J.Wang,Multi-timescale optimal dispatch of source-load-storage coordination in active distribution network based on deep reinforcement learning,Trans.China Electrotech.Soc.40 (5) (2025) 1487–1502.
[16]Y.Li,C.Yu,M.Shahidehpour,T.Yang,Z.Zeng,T.Chai,Deep reinforcement learning for smart grid operations: algorithms,applications,and prospects,Proc.IEEE 111 (2023) 1055–1096,https://doi.org/10.1109/JPROC.2023.3303358.
[17]J.Ding,C.Liu,Y.Zheng,Y.Zhang,Z.Yu,R.Li,H.Chen,J.Piao,H.Wang,J.Liu,Y.Li,Artificial intelligence for complex network: potential,methodology and application,arXiv (2024),https://doi.org/10.48550/arXiv.2402.16887.
[18]D.Zhang,X.Han,C.Deng,Review on the research and practice of deep learning and reinforcement learning in smart grids,CSEE J.Power Energy Syst 4 (2018).
[19]L.-L.Xiong,S.Mao,Y.Tang,K.Meng,Z.-Y.Dong,F.Qian,Reinforcement learning based integrated energy system management: a survey,Zidonghua Xuebao/Acta Automat.Sin.47 (2021) 2321–2340,https://doi.org/10.16383/j.aas.c210166.
[20]H.Zheng,Y.Jiang,J.Dai,Optimization of voltage regulation and loss reduction of offshore wind power transmission based on multi-agent Q-learning in uncertain environment,Zhongguo Dianji Gongcheng Xuebao/Proc.Chinese Soc.Electr.Eng.44(2024) 7995–8008,https://doi.org/10.13334/j.0258-8013.pcsee.230562.
[21]W.Lin,X.Wang,Q.Sun,Z.Liu,J.He,T.Pu,Dynamic dispatch of an integrated energy system based on deep reinforcement learning in an uncertain environment,Dianli Xitong Baohu Yu Kongzhi/Power Syst.Protect.Control 50(2022)50–60,https://doi.org/10.19783/j.cnki.pspc.211685.
[22]W.Luo,J.Zhang,Y.He,T.Gu,X.Nie,L.Fan,X.Yuan,B.Li,Optimal scheduling of regional integrated energy system based on advantage learning soft actor-critic algorithm and transfer learning,Dianwang Jishu/Power Syst.Technol.47 (2023) 1601–1611,https://doi.org/10.13335/j.1000-3673.pst.2022.1241.
[23]M.Chen,Y.Sun,Z.Xie,The multi-time-scale management optimization method for park integrated energy system based on the bi-layer deep reinforcement learning,Diangong Jishu Xuebao/Trans.China Electrotech.Soc.38 (2023) 1864–1881,https://doi.org/10.19595/j.cnki.1000-6753.tces.211879.
[24]S.Jiang,H.Gao,X.Wang,J.Liu,K.Zuo,Deep reinforcement learning based multi-level dynamic reconfiguration for urban distribution network: a cloud-edge collaboration architecture,Global Energy Interconnect.6 (2023) 1–14,https://doi.org/10.1016/j.gloei.2023.02.001.
[25]Q.-Y.Fan,M.Cai,B.Xu,An improved prioritized DDPG based on fractional-ord er learning scheme,IEEE Trans.Neural Netw.Learn.Syst.36 (2025) 6873–6882,https://doi.org/10.1109/TNNLS.2024.3395508.
[26]Real-time optimal power flow using twin delayed deep deterministic policy gradient algorithm,IEEE J.Mag.,IEEE Xplore,(n.d.).https://ieeexplore.ieee.org/document/9272783(accessed June 17,2025).
[27]J.Li,T.Yu,X.Zhang,F.Li,D.Lin,H.Zhu,Efficient experience replay based deep deterministic policy gradient for AGC dispatch in integrated energy system,Appl.Energy 285 (2021),https://doi.org/10.1016/j.apenergy.2020.116386.
[28]O.Yazar,S.Coskun,L.Li,F.Zhang,C.Huang,Actor-critic TD3-based deep reinforcement learning for energy management strategy of HEV,in: 2023 5th International Congress on Human-Computer Interaction,Optimization and Robotic Applications(HORA),2023,pp.1–6,https://doi.org/10.1109/HORA58378.2023.10156727.
[29]X.Gu,T.Liu,S.Li,T.Wang,X.Yang,Active power correction control of power grid based on improved twin delayed deep deterministic policy gradient algorithm,Diangong Jishu Xuebao/Trans.China Electrotech.Soc.38 (2023) 2162–2177,https://doi.org/10.19595/j.cnki.1000-6753.tces.221073.
[30]B.Zhang,Y.Zou,X.Zhang,G.Du,W.Sun,W.Sun,Energy management strategy based on TD3-PER for hybrid electric tracked vehicle,Qiche Gongcheng/Automot.Eng.44 (2022)1400–1409,https://doi.org/10.19562/j.chinasae.qcgc.2022.09.011.
[31]G.Qiu,H.He,K.Liu,S.Luo,C.He,F.Shen,Low-carbon economic dispatch of integrated energy system based on improved TD3 algorithm,Electr.Power Sci.Eng.39 (10) (2023) 52–62.
[32]T.Schaul,J.Quan,I.Antonoglou,D.Silver,Prioritized experience replay,arXiv (2016),https://doi.org/10.48550/arXiv.1511.05952.
[33]S.Fujimoto,H.van Hoof,D.Meger,Addressing function approximation error in actor-critic methods,arXiv (2018),https://doi.org/10.48550/arXiv.1802.09477.
[34]C.Lyu,X.Liu,L.Mihaylova,Review of recent advances in Gaussian process regression methods,(n.d.).
[35]N.Huang,B.Qi,Z.Liu,G.Cai,E.Xing,Probabilistic short-term load forecasting using Gaussian process regression with area grey incidence decision making,Dianli Xitong Zidonghua/Automat.Electr.Power Syst.42 (2018) 64–71,https://doi.org/10.7500/AEPS20180118008.
[36]A.Patterson,S.Neumann,M.White,A.White,Empirical design in reinforcement learning,(n.d.).
Received 18 June 2025;revised 6 September 2025;accepted 11 October 2025
Peer review under the responsibility of Global Energy Interconnection Group Co.Ltd.
* Corresponding authors.
E-mail addresses: spxiang@hdu.edu.cn (S.Xiang),mohan_lin@hdu.edu.cn (M.Lin),zchen331@163.com (Z.Chen),plzeng@hotmail.com (P.Zeng),hfwangxj@126.com (X.Wang),diyang915@outlook.com (D.Gong).
https://doi.org/10.1016/j.gloei.2025.10.003
2096-5117/© 2025 Global Energy Interconnection Group Co.Ltd.Publishing services by Elsevier B.V.on behalf of KeAi Communications Co.Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Shenpeng Xiang received the B.S.degree from the Department of Mechanical and Electrical Engineering,City University of Wuhan,Wuhan,China,in 2022.He is working towards M.S degree at Electrical Engineering with Hangzhou Dianzi University,Hangzhou,China.His research interests include the application of artificial intelligence methods in microgrid scheduling.
