0 Introduction

Modern power systems experience power imbalances from fluctuations in renewable energy generation or uncertain variations in load demand, leading to frequency and voltage deviations from their standard values [1-3].These deviations must be corrected promptly to ensure smart grid stability.Conventionally, primary controls are performed on the generation side to restore the power balance and stabilize the frequency and voltage [4].

However, these primary controls rely on synchronous generators or large transformers, resulting in high economic costs and environmental pollution [5,6].Furthermore, the inherent mechanical constraints result in long response times.Therefore, the load resources on the demand side must be effectively managed to support primary frequency and voltage regulation [7].

In the late 1970s, [8] proposed the concept of demandside contribution as a supplement or a replacement for conventional ancillary services.In particular, with the increasing presence of smart loads in grids, load resource management (LRM) technologies that can participate in the primary control are eagerly awaited [9,10].Reference[11] introduced a load modulation strategy based on virtual inertia for primary frequency regulation.Researchers argue that responsive loads have considerable potential to provide primary control [7,12].For instance, household appliances can adjust their load patterns to help alleviate power imbalances [13,14].A primary voltage control approach using heat-pump water heaters was advocated in[15]to avoid voltage rise in photovoltaic systems.Based on model predictive control, air-conditioning loads act as voltage/frequency response sources in [16].

Moreover, as mentioned in [17] and [18], LRM should be performed with minimal impact on end-user performance.To this end,[13]presented a decentralized demand response approach for primary frequency regulation through direct load control, without affecting consumer comfort.Reference [19] proposed a non-disruptive loadside control method for frequency regulation based on peer-to-peer communication.Drawing upon a novel mathematical concept—network dynamics as optimization algorithms, reference [20] developed optimal load control(OLC), a ‘‘ubiquitous continuous fast-acting distributed primary frequency load control” that seeks to minimize the overall disutility.Reference [21] further developed the OLC by selecting more appropriate gains for each controller rather than employing the same values.However,these load management paradigms were designed for primary frequency control and did not address voltage issues[22].

Recent studies have identified several critical deficiencies in load participation in primary control: ‘‘some researchers neglect the impact on user comfort; some approaches use the same control parameters for load resources in different locations; limited literature explores the capacity of smart loads to support both frequency and voltage.”

To address these drawbacks, an LRM framework to handle power imbalances promptly has been designed.The LRM method supports primary frequency and voltage regulation.Additionally, this study demonstrates that integrating LRM with network dynamics minimizes the established disutility function caused by load participation[23].In the previous work[24],the control effects of LRM under various disutility functions were studied,and all the load controllers had similar gain settings.However, as mentioned, it is not optimal to adopt the same controller gains for all load resources [25].For better response performance, the parameter settings for each load controller must be optimized, considering the frequency/voltage nadir, frequency/voltage steady-state error, and total load control effort.The non-dominated sorting genetic algorithm-II is a widely recognized and well-established multiobjective optimization algorithm that has been successfully applied in various fields,including power systems and engineering[26].Therefore,the LRM was subjected to an NSGA-II based multi-objective optimization procedure for gain tuning.

This study primarily contributes to optimizing the utilization of load resources to enhance the stability of frequency and voltage in a way that minimizes disutility.The network dynamic model and LRM framework are established in Section 1, serving as the foundation for the subsequent analysis and design.To obtain better frequency and voltage response performances, multiple related goals are proposed, and the NSGA-II-based gain-tuning procedure for LRM is presented in Section 2.A case study is presented in Section 3, and the significant conclusions of the study are presented in Section 4.

1 Network model and local LRM framework

1.1 Network dynamic model

The power network is expressed as a graph with （N，ε）.The vertex set N represents the bus vectors, and edge set ε(ε ⊆N ×N) indicates the power transmission lines [21].（N，ε） is assumed to be a directed graph; therefore, if e=（i，j）∈ε, it implies （j，i）∉ε.Cje are the elements of the incidence matrix of the power transmission network.

The generator bus G and load bus L form the set N,where G ∪L=N.A bus j ∈G has loads and a generator that can provide power,whereas a bus j ∈L has only loads but no generator.The dynamics of the power network model can be written as(2)-(4)[23],and all variables indicate their deviations in this study.

1.2 LRM framework

To address the power disturbance injected into the bus j ∈N and thereby ensure frequency and voltage stability,controllable loads pj and qj in (3) and (4) are anticipated to make adjustments that effectively rebalance power with minimal aggregate disutility of loads.Here, LRM framework is proposed in a manner that minimizes the established disutility to utilities and users.Therefore, a general form of the aggregated disutility function is formulated as in (7a), comprising cpj（pj）, cqj（qj）, ^p2j/2Dj, and^q2j/2DjL.cpj（pj） and cqj（qj） are cost functions caused by the active/reactive controllable load pj and qj,respectively,which might be a goal that considers the mechanical attributes of smart appliances, utility scheduling policies, or customer comfort levels.^p2j/2Dj and^q2j/2DjL are two fixed items that indicate the costs of the frequency/voltagesensitive but uncontrollable-load ^pj :=Djωj and^qj :=DjLV j, respectively.Moreover, (7b) represents the power balance constraint.

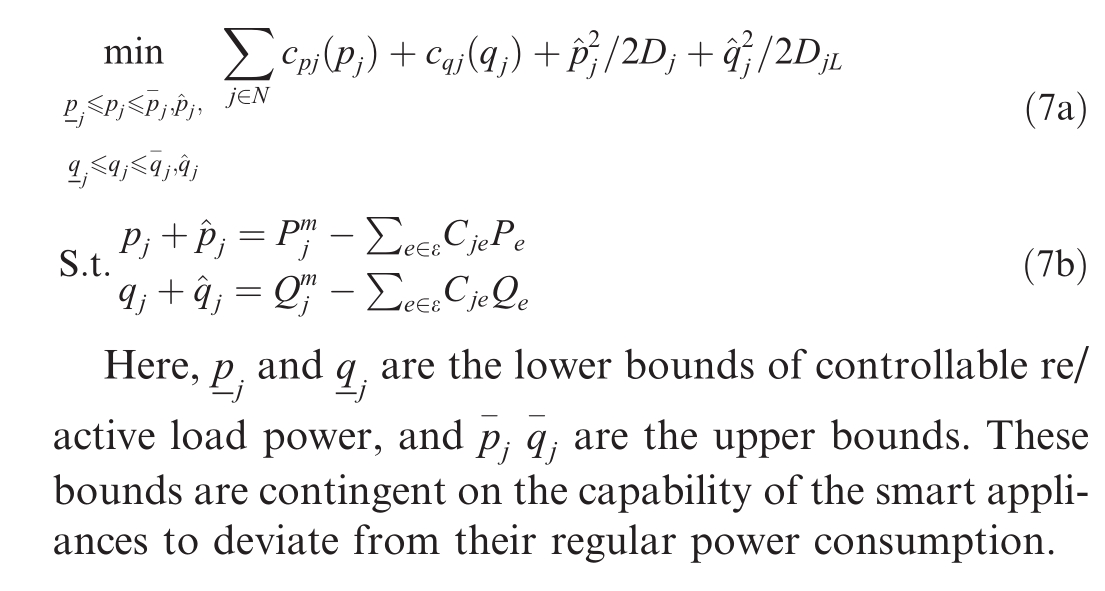
and the minimization function Φj（vj，λj） is obtained under the following optimality conditions:

where γj ＞0 and κj ＞0 are the step sizes.

Eqs.(10) and (11) present the optimization algorithms used to solve the dual problem.Next, the design variables vj and λj are replaced with ωj and V j.The step sizes are set to γj =1/Hj and κj =1/Kj.Subsequently, the optimality conditions in (9) become (12)-(15), and (10) and (11)become (16) and (17), respectively.

2 NSGA-II-based optimal LRM

This section provides an illustrative instance of a load controller design and proposes an optimization procedure based on NSGA-II to determine the parameter settings.

2.1 Illustrative instance of controller design for smart load resources

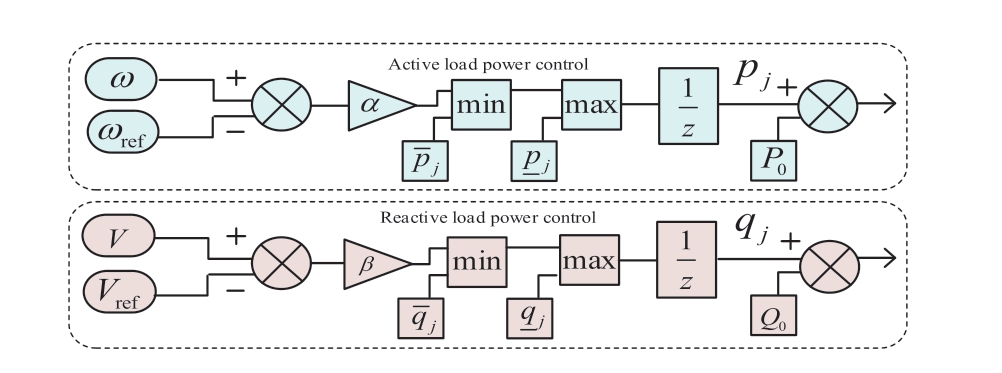
Fig.1.Local controller design scheme for controllable load resources.

In Fig.1, ωref and V ref are the references for the frequency and voltage, respectively, and P0 and Q0 are the nominal powers of the controllable loads.When the frequency or voltage deviation exceeds the dead zone, local load controllers are triggered to assist in restoring them to acceptable ranges.

The relevant frequency indicators are represented in Fig.2.The frequency nadir, ω（Tnadir）, is a critical metric that reflects the frequency condition of the system.If it drops below a specific threshold, it can result in a frequency collapse.For the power system to operate safely and stably,it is crucial to implement effective primary regulation that can alleviate frequency drops caused by power disturbances, ensuring that the system complies with the constraint for ω（Tnadir）.ω（Tsteady） represents the steadystate value of frequency, while Tsteady indicates the point in time when the frequency returns to a new steady-state value.Moreover, the curve of voltage response can be characterized by similar metrics.

According to the theorems, the control parameters α and β have positive numbers, and their values have no impact on system stability [23].However, the control actions vary with α and β.It is evident that assigning identical gain values to all load controllers is not optimal.These parameters can be further systematically optimized to improve the frequency and voltage response performance.

2.2 NSGA-II-based optimization procedure for parameter settings

The parameter optimization procedure for the LRM was formulated to attain the following goals: improving the frequency and voltage nadirs, minimizing the steadystate error of the frequency and voltage, and reducing the total load shedding throughout the process.Hence,the objective function vector F→for parameter optimization comprises the following five components:

f1 and f2 aim to improve the frequency and voltage nadirs, respectively.

Here, ωref and V ref are the frequency and voltage references, respectively.ω（Tnadir） and V（Tnadir） are the frequency and voltage nadirs, respectively.

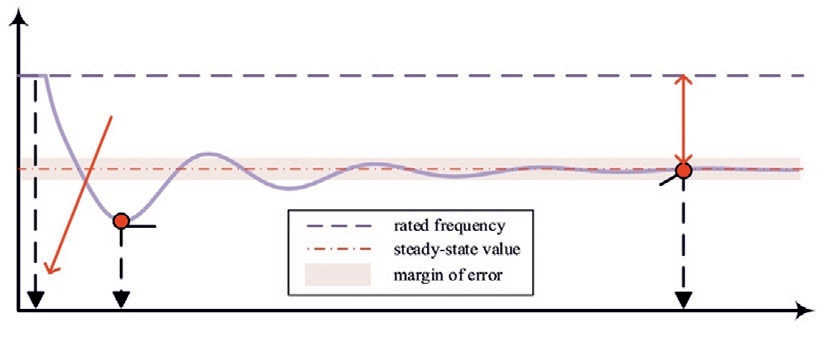
Fig.2.Illustration of the frequency response curve.

f3 and f4 aim to minimize the frequency and voltage steady-state errors, respectively.

Here, ω（Tsteady） is the steady-state frequency value, and V（Tsteady） is the steady-state voltage value.

f5 aims to reduce the load control effort.f5 :

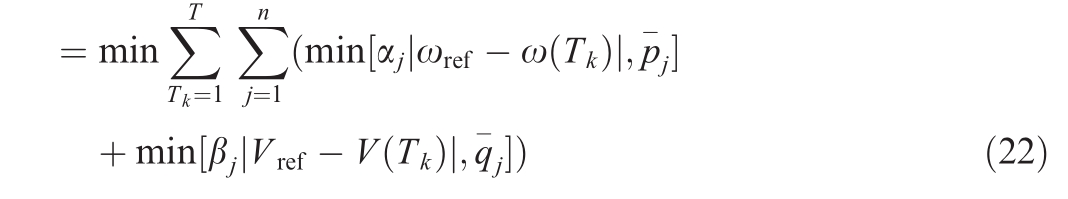
Here, Tk is the kth sampling time, and j is the jth controllable load.

As shown in Fig.3, the control gains α and β used in LRM are optimized using the NSGA-II algorithm, which is particularly suitable for problems with multiple conflicting objectives and provides a range of trade-offsolutions for decision-making.

The steps in Fig.3 are explained as follows:

Population initialization:The population size(pop=n),maximum generation, and other relevant parameters involved in the NSGA-II algorithm are set.The initial control gain population is randomly selected from a feasible area, which varies depending on specific practical scenarios.

Fig.3.Optimization flow chart for load control parameters based on NASA-II algorithm.

Non-dominated sorting and crowding calculation: Calculate the counts of the dominating and dominated individuals for each individual.Select the non-dominant individuals, and search for a new non-dominant set from the remaining population.This process is repeated until the entire population is sorted based on non-domination.To perform further order selection among individuals with the same rank of non-dominated sorting (same front surface), each individual’s crowding distance (CD) is calculated for each objective.A higher CD signifies a more uniform distribution of the calculation results in the target space, ensuring population diversity.

Here, i represents the ith individual, m represents the mth objective, and l represents the number of individuals on the front surface.

Genetic operation:Genetic operations involve simulated binary crossover and polynomial mutation.

a) Simulated binary crossover: x1j（t） and x2j（t） are parents, and 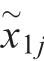（t） and 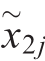（t） are their offspring.

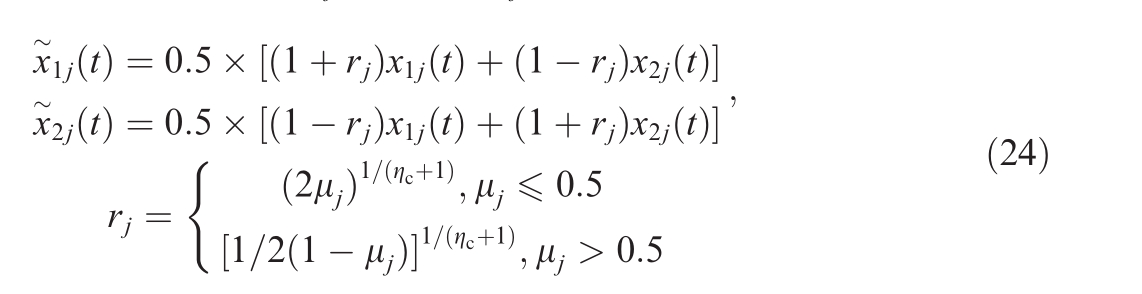
Here, μj is a random number within the range of 0-1, and ηc is the crossover distribution index(the empirical value is between 1 and 20).

b) Polynomial mutation: x～j（t）is the offspring of its parent xj（t）.

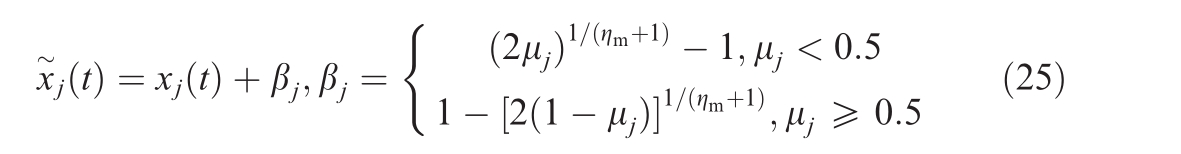
Here, μj is a random number between zero and one, and ηm is the crossover distribution index (the empirical value is between 1 and 20).

Merger of parents and offspring: The total population size of the parents and offspring is approximately 2n after the genetic operation.

Elitist strategy:Perform non-dominated sorting and CD calculations on the merged population.Select the top n individuals as new parents.By introducing an elitist strategy,the parent population is combined with its offspring to compete and produce the next-generation population.

Optimal solution selection: The operator can select a single solution from the Pareto-optimal set based on the preference for each objective in different practical scenarios.Considering the computational and communication pressures in modern power systems, the optimized load control parameters can be stored in a lookup table and utilized as a criterion for online selection by local controllers.

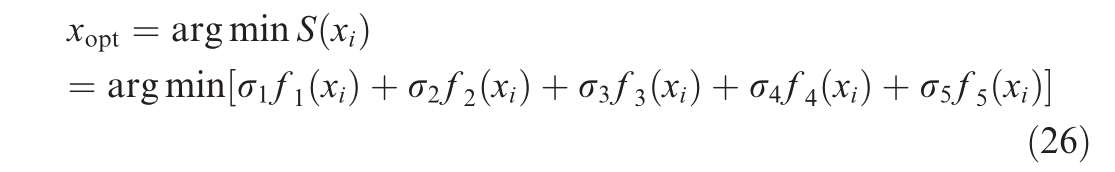
Here, σ1,...,σ5 represent the preference degree for each objective,xi is a solution from the Pareto-optimal solution set, and xopt is the optimal single solution.

The general framework of NSGA-II-based load resource management is illustrated in Fig.4,which clarifies how the demand side participates in the primary regulation.

As shown in Fig.4,smart loads sense the frequency and voltage through local meters and select the optimal control parameters online, enabling a faster and more effective response to frequency and voltage fluctuations.

3 Simulation results

3.1 Simscape power system model

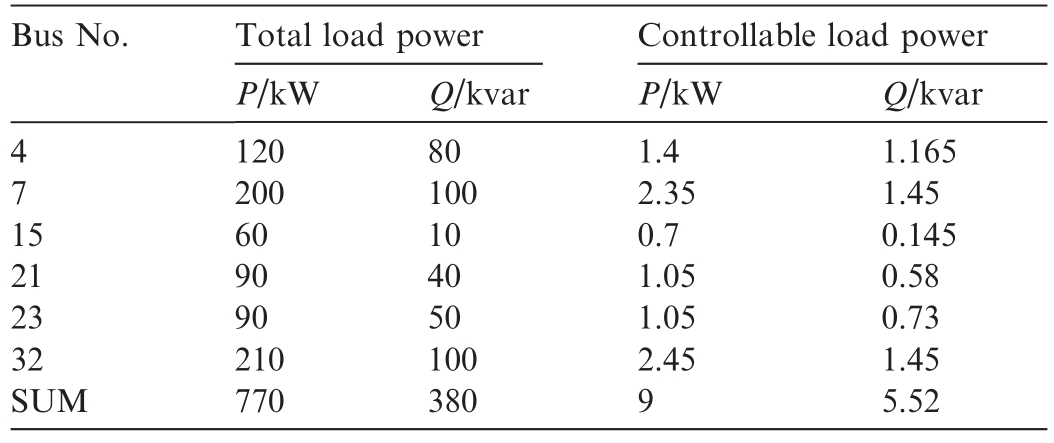
As depicted in Fig.5,the SPS model comprises a generator bus, 32 load buses, and 32 branches.The bus voltage reference was 12.66 kV, and the total load was 3715 + j2300 kVA.Among the 32 load buses, six load buses (indicated by blue circles) were chosen as controllable buses, and four buses (marked with purple circles)were considered disturbed buses.Smart load buses have both controllable and noncontrollable resources.Table 1 lists the primary regulation capacities of the controllable load buses.In the SPS model, controllable load resources are depicted by employing three-phase parallel RLC loads,whereas the noncontrollable load resources are represented using three-phase three-wire dynamic loads.

Moreover, once the total power usage of the disturbed buses undergoes an abrupt change, the predefined disutility of the regulation process is minimized under our LRM framework, as shown in Fig.6.

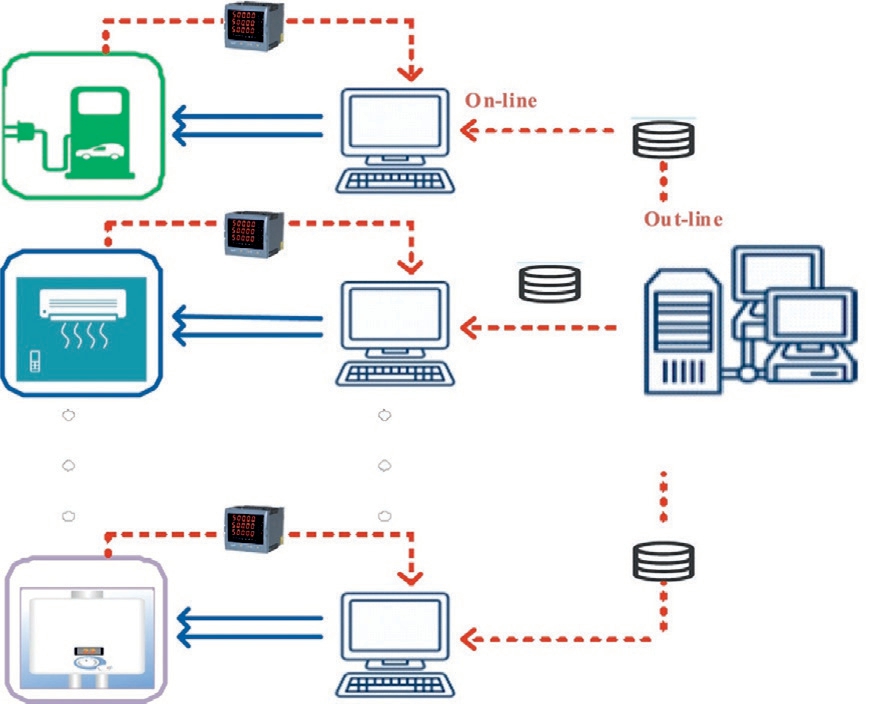
Fig.4.NSGA-II-based load side control for smart loads.

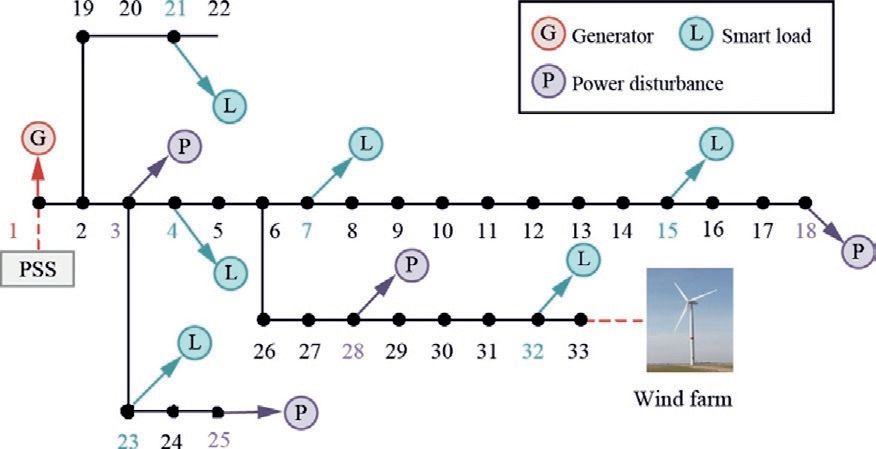
Fig.5.SPS model of the improved IEEE 33-bus test system.

Table 1
Primary regulation capacity of controllable load buses.

3.2 NSGA-II-based LRM vs.LRM vs.OLC

This section discusses the effectiveness of the proposed NSGA-II-based LRM method under load variations.

The NSGA-II-based LRM, LRM, and conventional OLC2 The OLC method was proposed to enable load participation in primary frequency control by Zhao et al.Detailed information can be accessed in [22]. were simulated and compared in terms of frequency/voltage nadir and steady-state values.

Load variation:at t=4 s,the total power usage of disturb buses 3, 18, 25, and 28 experiences a sudden increase of 12 kW, 4 kvar (1.26 pu).

The controllable loads were set with identical parameter settings in LRM and conventional OLC.In the NSGA-IIbased LRM, the gain parameters were optimized in the feasible regions.The feasible regions for the gain parameters of each load controller are set to α ∈[30 pu， 70 pu]and β ∈[15 pu， 25 pu].The initial population size was 40 (randomly generated within the feasible regions), the maximum number of generations was 50, the crossover distribution index was 10, and the mutation distribution index was 10.

Figs.7 and 8 depict the cross sections of the 2D and 3D Pareto fronts of the 5-dimensional Pareto-front, respectively.Table 2 presents the optimal solutions determined by different degrees of preference.

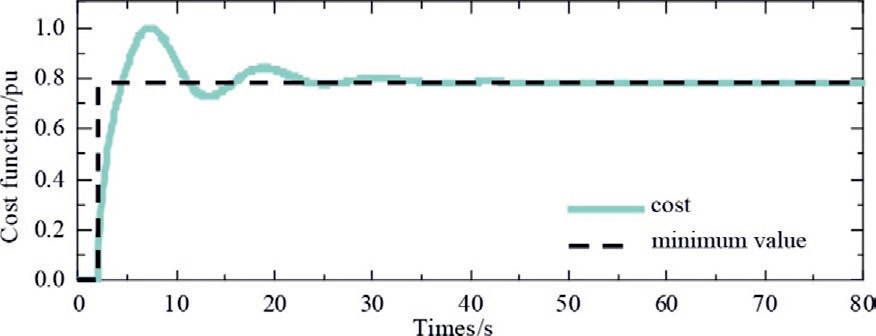
Fig.6.Cost function trajectory of LRM.

Fig.7, Fig.8, and Table 2 show that the values of the objective functions vary with preference degrees.For instance, when the importance percentage of the first objective decreases from 25 % to 15 %, the simulation result for the frequency nadir decreases from 49.8735 to 49.8634 Hz.

Furthermore, a comparative study was conducted to observe the differences in frequency/voltage dynamic response during LRM among the proposed NSGA-IIbased LRM,LRM,and traditional OLC.The corresponding conclusions are presented in Fig.9 and Fig.10.The NSGA-II-based LRM is simulated under the fifth preference degree with （σ1 =σ2 =σ3 =σ4 =σ5）=20%given in Table 2.Additionally, the parameter settings of the local load controllers are provided in Table 3.

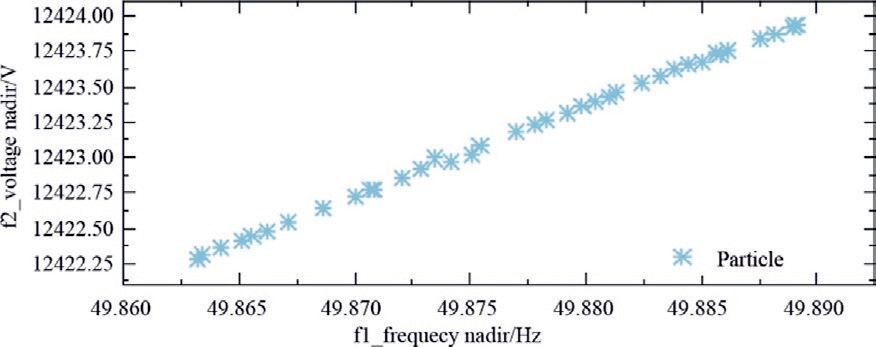
Fig.7.2D cross-sections of the 5-dimensional Pareto-front.

Fig.9 shows that LRM and traditional OLC provide similar benefits for primary frequency control.

However, as shown in Fig.10, the LRM method outperforms the traditional OLC method in terms of voltage regulation because it can suppress the voltage nadir by 21 % and reduce the steady-state error by approximately 24 %.This is because traditional OLC overlook the capability of load management to regulate voltage.

Moreover, the data analysis of the performance indices in Table 4 demonstrates that the proposed NSGA-II-based LRM method exhibits a better transient performance in terms of system frequency and voltage.This improvement was achieved by applying a systematic gain-tuning procedure to the LRM framework.

3.3 Coordination with other devices

This section discusses the coordination between the NSGA-II-based LRM and the other devices enabled in the system to handle load variations.

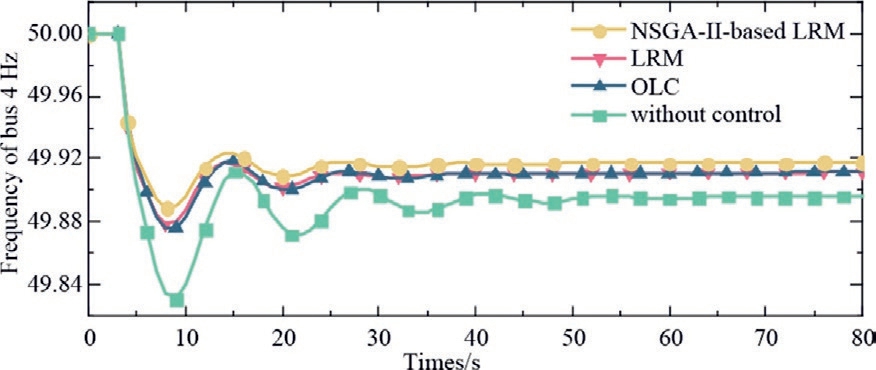
Fig.9.Frequency responses on bus 4 using different methods.

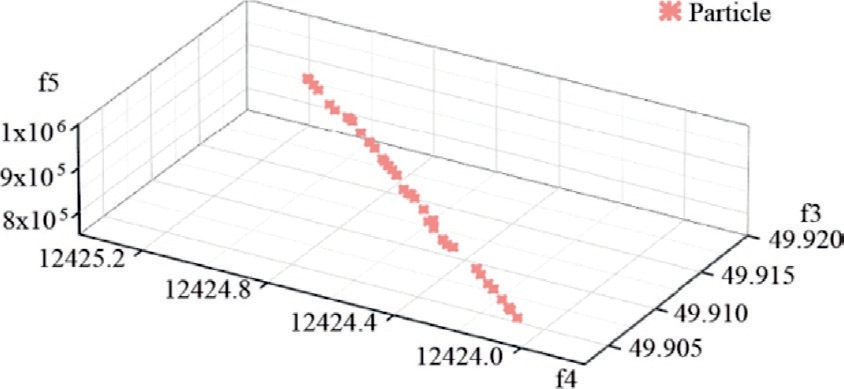
Fig.8.3D cross-sections of the 5-dimensional Pareto-front with NSGAII optimization.

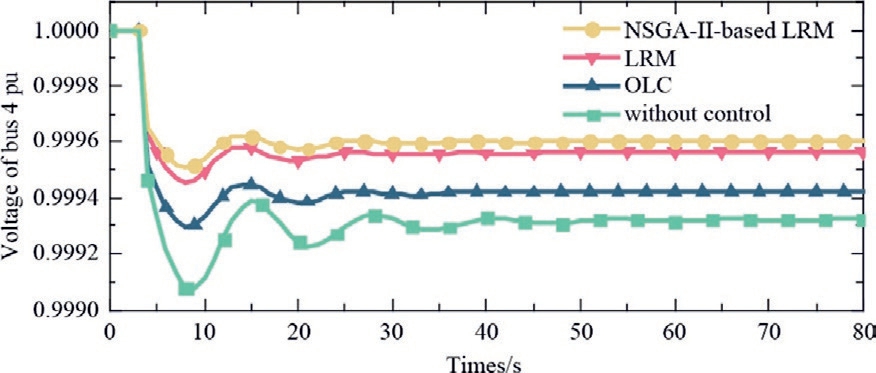
Fig.10.Voltage dynamics on bus 4 using different methods.

Table 2
Particle index selections based on different preference degrees.

Table 3
Load control parameter settings.

Table 4
Data analysis of the performance indices.

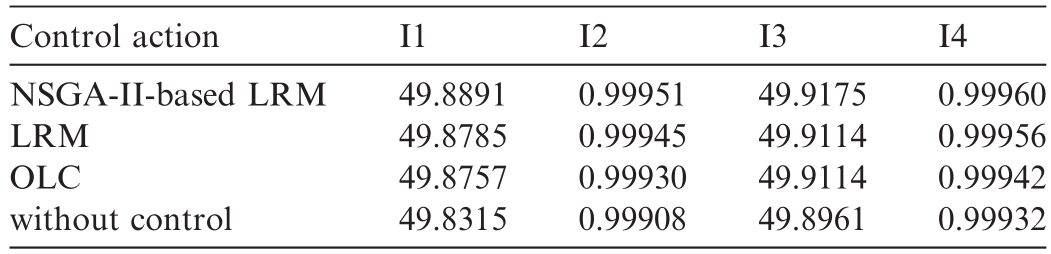
aPerformance index identification: I1-Frequency nadir (Hz); I2-Voltage nadir (pu); I3-Frequency steady state value (Hz); I4-Voltage steady state value (pu).

Scenario 1: Coordination with TG

In this scenario, compared to relying solely on turbinegovernor (TG) control action, incorporating LRM increases the frequency and voltage nadirs and the corresponding steady-state values and shortens the settling time.LRM helps mitigate frequency fluctuations and voltage drops.Furthermore,the effectiveness of the NSGA-IIbased LRM using was evacuated using the optimal parameter settings presented in Table 3.As shown in Fig.11,the NSGA-II-based parameter optimization procedure for the LRM suppressed the frequency nadir by 7.97 % and the steady-state error by 6.89 %.Moreover, the voltage nadir was suppressed by 10.91%,and the steady-state error was reduced by 9.09%.Therefore,in the‘‘TG”scenario,utilizing LRM with the systematic gain tuning procedure can further enhance the frequency and voltage dynamic performances.

Scenario 2: Coordination with PSS

A power system stabilizer (PSS) is a widely used generation-side stabilization mechanism.Applying PSS significantly suppresses the frequency and voltage fluctuations.

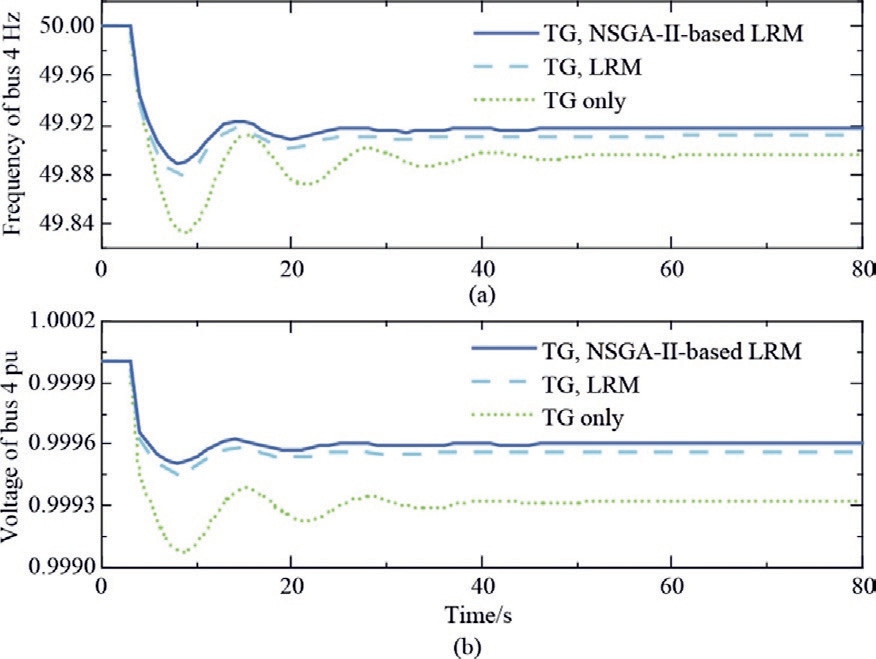
Fig.11.Response performances with the coordination of TG.

Fig.12(a)and(b)show a comparison of responses with different control strategies, namely, the PSS-controller only, PSS-controller with LRM, and PSS-controller with NSGA-II-based LRM (with the parameter settings presented in Table 5).For instance,the plots demonstrate that when PSS operates with LRM,deeper frequency and voltage support is achieved.

Moreover, after the NSGA-II-based parameter optimization procedure for LRM, the frequency nadir was suppressed by 7.03 %, and the steady-state error was reduced by 6.64 %.Similarly, the voltage nadir was suppressed by 8.33 %, and the steady-state error was reduced by 9.09 %.Therefore, in the ‘‘PSS” scenario, the best results, characterized by reduced overshoot and higher steady-state values, are achieved by PSS along with NSGA-II-based LRM.

3.4 NSGA-II-based LRM against the fluctuations of wind power production

A wind turbine (1.5 MW) was added to the SPS model shown in Fig.5 to assess the validity of the NSGA-IIbased LRM in the presence of intermittent renewable energy generation.

Power output fluctuation: the wind power production on bus 33 experiences a sudden decrease at t=14 s as the wind speed declines (Fig.13).

In this scenario,the parameter settings of the local load controllers were optimized using the NSGA-II-based procedure,as presented in Table 6.The dynamic responses of frequency and voltage, including their transient and steady-state behaviors, were explored.

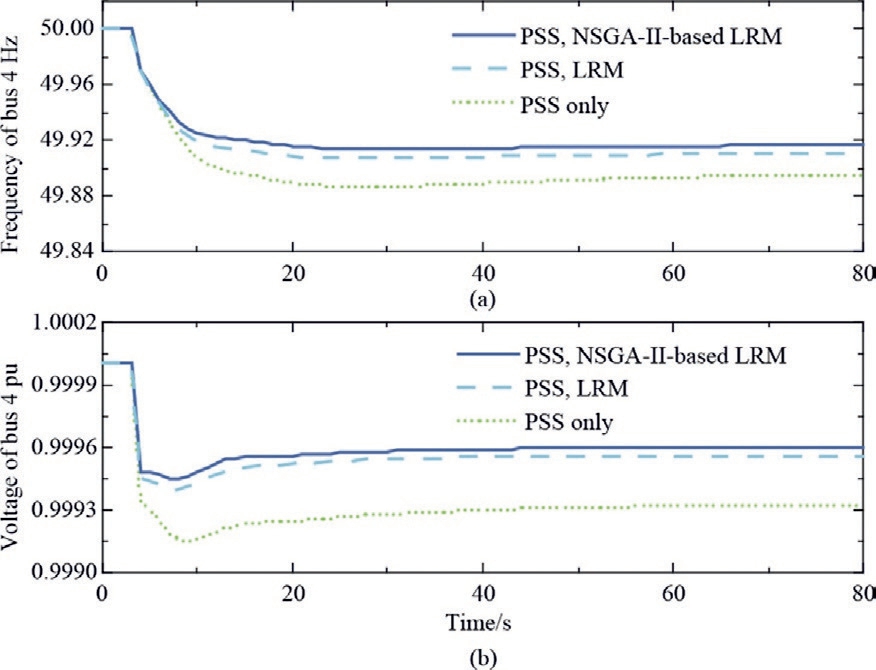
Fig.12.Response performances with the coordination of PSS.

Table 5
Load control parameter settings.

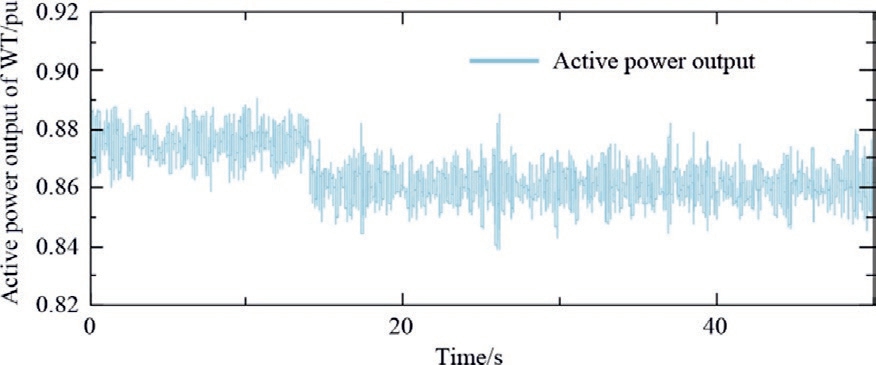
Fig.13.Power output fluctuation of WT on bus 33.

Table 6
Load control parameter settings.

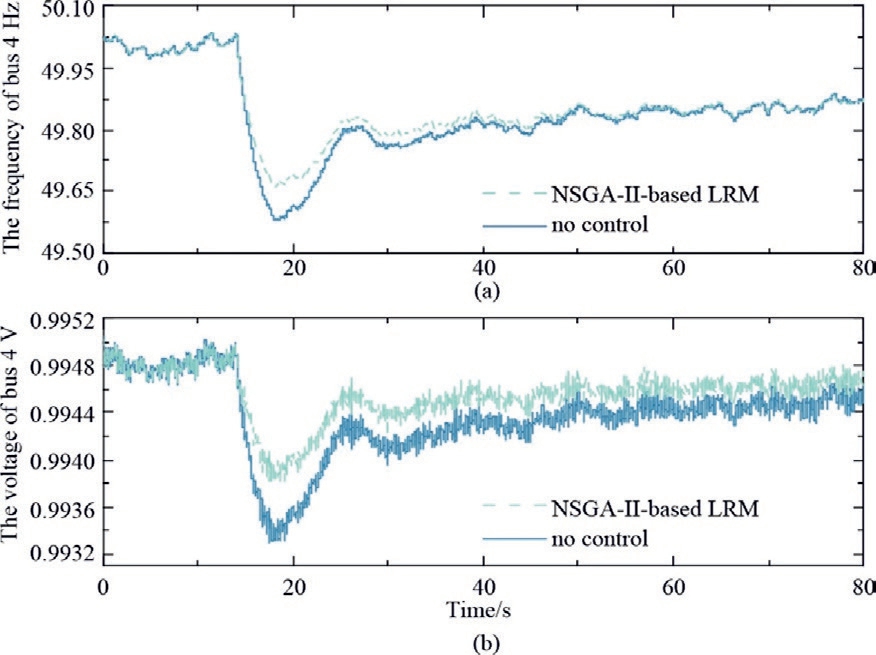
Fig.14.Frequency and voltage dynamics affected by fluctuations in wind power.

According to Fig.14(a)and(b),the frequency and voltage nadirs are suppressed, and the voltage steady-state error is significantly improved using the NSGA-II-based LRM.Hence, adopting the proposed LRM in power systems with high penetration of renewable energy generation is significantly effective.

Fig.15.Dynamic load variations (%) by the NSGA-II-based LRM.

Fig.15 illustrates the altered controllable load patterns through the NSGA-II-based LRM in response to wind power output fluctuations.The proposed approach showed that all controllable load resources reduced their power consumption from standard levels.This indicates that even amid wind power variations, load resources can provide primary reserve power.The subfigures in Fig.15 demonstrate that the reduction in power consumption varies for controllable load resources at different locations, depending on the capacity of the intelligent responsive devices at each bus.A greater reduction in load power consumption signifies a higher potential for providing primary reserve power.

4 Conclusion

This paper proposes an LRM framework for participating in primary frequency and voltage regulations as a provision of ancillary services.Through local sensing of frequency and voltage,smart loads effectively support primary control with minimal disutility,thereby ensuring reliable system operations.Under the assumptions established for the disutility function, the proposed load control was derived by computing the inverse of its derivative,thereby allowing for precise load adjustments.Furthermore, integrating the network dynamics with the proposed LRM demonstrates a primal-dual optimization algorithm that adaptively addresses the disutility function.

The control performance of the LRM was further enhanced using an NSGA-II-based parameter optimization procedure.The NSGA-II-based LRM helps improve the frequency and voltage nadirs, minimizes the steadystate errors in frequency and voltage,and reduces the total load shedding.The simulation results demonstrated an improvement in the frequency and voltage response curves when the parameter settings for the load controllers were systematically optimized.

In real power systems, the adoption of the proposed approach is contingent on the availability of a certain number of smart meters and responsive load resources.In future, these challenges can be progressively addressed with the rapid advancement of smart grids.Moreover,more efficient multi-objective optimization algorithms or distributed optimization methods can be explored to enhance the ability to achieve real-time responses in large-scale systems.

CRediT authorship contribution statement

Yaxin Wang: Writing - original draft, Validation,Methodology,Investigation,Formal analysis,Conceptualization. Zhihang Zhu: Validation, Resources, Investigation, Conceptualization. Zhihong Yu: Validation,Supervision, Resources, Conceptualization. Zigan Wang:Validation, Software, Resources.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: YaxinWang, ZhihongYu and ZiganWang are currently employed by China Electric Power Research Institute.

Acknowledgments

The authors would like to thank the support of State Grid Corporation of China Project:Research on key technologies of automatic generation of typical power grid operation modes and automatic calculation of section stability limits (5100-202355420A-3-2-ZN).

References

[1]Y.Li, X.H.Qin,Y.N.Chi,et al., Study on requirement of control and stability with renewable energy generation grid integration,in:Proceedings of 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP),2019 in Xi’an, China, 2019, pp.26-30.

[2]Y.L.Chen,D.L.Qi,H.X.Hui,et al.,Self-triggered coordination of distributed renewable generators for frequency restoration in islanded microgrids: a low communication and computation strategy, Adv.Appl.Energy 10 (2023) 100128.

[3]Y.L.Chen, K.W.Lao, D.L.Qi, et al., Distributed self-triggered control for frequency restoration and active power sharing in islanded microgrids, IEEE Trans.Ind.Inf.19 (10) (2023) 10635-10646.

[4]W.Yang, F.Reis, Y.Z.Xu, et al., Study on the demand and requirements of renewable energy primary frequency control, in:Proceedings of 2019 Chinese Control and Decision Conference(CCDC), 2019 in Nanchang, China, 2019, pp.5804-5808.

[5]Z.Lan, J.Kuang, K.Yang, et al., Near-zero carbon coordinated control of renewable energy considering environmental costs, in:Proceedings of 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), 2021 in Taiyuan, China, 2021,pp.2113-2118.

[6]Y.Q.Yin,X.X.Sun,T.Li,et al.,Research on power grid auxiliary frequency regulation technology based on electrolytic aluminum high-energy load regulation, in: Proceedings of 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES), 2022 in Beijing, China, 2022, pp.1701-1707.

[7]D.Chakravorty, B.Chaudhuri, S.Y.R.Hui, Rapid frequency response from smart loads in Great Britain power system, IEEE Trans.Smart Grid 8 (5) (2017) 2160-2169.

[8]F.C.Schweppe, R.D.Tabors, J.L.Kirtley, et al., Homeostatic utility control, IEEE Trans.Power Syst.PAS-99 (3) (2007) 1151-1163.

[9]G.De Carne, G.Buticchi, M.Liserre, et al., Real-time primary frequency regulation using load power control by smart transformers, in: Proceedings of 2020 IEEE Power & Energy Society General Meeting (PESGM), 2020 in Montreal, QC,Canada, IEEE, 2020, p.1.

[10]D.Chakravorty, Z.Akhtar, B.Chaudhuri, et al., Comparison of primary frequency control using two smart load types, in:Proceedings of 2016 IEEE Power and Energy Society General Meeting (PESGM), 2016 in Boston, MA, USA, 2016, pp.1-5.

[11]A.Delavari I.Kamwa, Virtual inertia-based load modulation for power system primary frequency regulation, in: Proceedings of 2017 IEEE Power & Energy Society General Meeting, 2017 in Chicago, IL, USA, 2017, pp.1-5.

[12]S.Ali Pourmousavi, M.H.Nehrir, Real-time central demand response for primary frequency regulation in microgrids, IEEE Trans.Smart Grid 3 (4) (2012) 1988-1996.

[13]W.Mendieta, C.A.Can˜izares, Primary frequency control in isolated microgrids using thermostatically controllable loads,IEEE Trans.Smart Grid 12 (1) (2021) 93-105.

[14]X.Zhou,C.Wei,J.F.Dai,et al.,Research on the strategy of largescale electric vehicles participating in primary frequency modulation based on model predictive control, in: Proceedings of 2022 China Automation Congress(CAC),2022 in Xiamen,China,2022, pp.4469-4475.

[15]A.L.M.Mufaris, S.Kawachi, J.Baba, Voltage control using coordinated control of Heat Pump Water Heaters with large penetration of photovoltaic systems, in: Proceedings of 2013 3rd International Conference on Electric Power and Energy Conversion Systems, 2013 in Istanbul, 2013, pp.1-6.

[16]X.Z.Yang, X.Lyu, Y.W.Jia, et al., Flexible air conditioning loads as voltage/frequency-responsive sources in microgrid, in:Proceedings of 2020 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), 2020 in Weihai, 2020, pp.1739-1744.

[17]M.Hajiakbari Fini, M.E.Hamedani Golshan, Frequency control using loads and generators capacity in power systems with a high penetration of renewables, Electr.Pow.Syst.Res.166 (2019) 43-51.

[18]M.H.Fini, M.E.H.Golshan, J.R.Marti, Reducing the effect of participation of loads in primary frequency control on the device life-time and customer convenience, in: Proceedings of 2019 IEEE Power & Energy Society General Meeting (PESGM), 2019 in Atlanta, GA, USA, IEEE, 2019, pp.1-5.

[19]T.Liu,D.J.Hill,C.C.Zhang,Non-disruptive load-side control for frequency regulation in power systems, IEEE Trans.Smart Grid 7(4) (2016) 2142-2153.

[20]C.H.Zhao, U.Topcu, N.Li, et al., Design and stability of loadside primary frequency control in power systems, IEEE Trans.Autom.Control 59 (5) (2014) 1177-1189.

[21]A.Delavari, I.Kamwa, Improved optimal decentralized load modulation for power system primary frequency regulation, IEEE Trans.Power Syst.33 (1) (2018) 1013-1025.

[22]J.J.Zhao, D.Y.Shi, D.Zhou, et al., Load shedding control strategy for power system based on the system frequency and voltage stability(Apr 2018), in: Proceedings of 2018 China International Conference on Electricity Distribution (CICED),2018 in Tianjin, 2018, pp.1352-1355.

[23]Y.X.Wang,D.L.Qi,J.L.Zhang,et al.,Novel optimal load control for power system frequency and voltage regulation, J.Mod Power Syst.Clean Energy 11 (6) (2023) 1746-1755.

[24]Y.X.Wang, D.L.Qi, X.B.Wang, et al., Forward engineering of local load control for primary frequency and voltage regulation,Electr.Pow.Syst.Res.223 (2023) 109472.

[25]K.Kalsi, M.A.Elizondo, J.Lian, et al., Loads as a resource:Frequency responsive demand,2014.Pacific Northwest Nat.Lab.,Richland, WA, USA, Tech.Rep.PNNL-23764, 2014.

[26]K.Deb, A.Pratap, S.Agarwal, et al., A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Trans.Evol.Comput.6 (2) (2002) 182-197.

[27]P.Samadi,A.H.Mohsenian-Rad,R.Schober,et al.,Optimal realtime pricing algorithm based on utility maximization for smart grid, in: Proceedings of 2010 First IEEE International Conference on Smart Grid Communications.Gaithersburg, MD, USA, 2010,pp.415-420.

[28]N.Li, L.J.Chen, S.H.Low, Optimal demand response based on utility maximization in power networks, in: Proceedings of 2011 IEEE Power and Energy Society General Meeting, Detroit, MI,USA, 2011, pp.1-8.

Received 12 August 2024;revised 5 December 2024; accepted 25 January 2025

* Corresponding author.

E-mail addresses: 15269639282@163.com (Y.Wang),1015207896@qq.com (Z.Zhu), ygyzhh@sohu.com (Z.Yu), wangzigan@epri.sgcc.com.cn (Z.Wang).

https://doi.org/10.1016/j.gloei.2025.01.005

2096-5117/© 2025 Global Energy Interconnection Group Co.Ltd.Publishing services by Elsevier B.V.on behalf of KeAi Communications Co.Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

Yaxin Wang received her Ph.D.degree in electrical engineering from Zhejiang University,Hangzhou, China, in 2024.Now she works in China Electric Power Research Institute.Her research interests include voltage and frequency optimization control in smart grids, and game theory-based distributed optimization with applications to power systems.

Zhihang Zhu received the B.E.degrees in Electrical Engineering from Zhejiang University,Hangzhou, China, in 2022.He is currently studing for the M.E.degree in Electrical Engineering from Zhejiang University.His research interests include computer vision, image processing and artificial neural network.

Zhihong Yu received the Ph.D.degree in electrical engineering from the Harbin Institute of Technology, China, in 2004.She is currently with the China Electric Power Research Institute (CEPRI).She is also a Principal Engineer with the Dynamic Security Assessment Studies Group.Her current research interests include power system stability simulation,analysis,and control , data mining and its engineering applications in power system.

Zigan Wang received his Master’s degree in Electrical Engineering from the University of Melbourne, Australia, in 2022.He is currently employed at China Electric Power Research Institute.His research interests include security and stability analysis of large-scale power grids and artificial intelligence applications in power systems.

(Editor Zedong Zhang)