0 Introduction

In recent years,the scale of new energy produced by wind and solar power systems has increased globally,contributing to the advantages of low cost,low carbon emissions,and renewability [1,2].However,owing to the large-scale integration of new energy,power systems require sufficient flexible resources to handle the inherent volatility and uncertainty of the new energy sources (i.e.,wind power and solar power) [3,4].Hydropower is a crucial flexible power source that can effectively suppress the output fluctuations of new energy sources and promote the electricity consumption [5,6].Therefore,it is essential to conduct capacity planning for hydro-wind-solar power systems (CPHPS) to facilitate the complementarity of flexible hydropower with variable wind-solar power.

CPHPS is one of the most important factors to be addressed in the rapid expansion of new energy sources.Ref.[7] focused on the impact of hydropower-photovoltaic coordination in water resource systems and optimized the size of a utility-scale photovoltaic plant through a costbenefit analysis.Ref.[8] proposed a two-level nested programming model to determine the optimal scale of the photovoltaic complementarity to the Naijili hydropower plant by considering the randomness of natural runoffs and photovoltaic outputs,which helps in maximizing the renewable energy consumption.Ref.[9] developed an analysis framework based on dynamic planning and evaluated the potential of the Akosombo hydropower plant in Ghana to support the grid integration of local new energy under different scenarios of power demand.However,these studies focused on the coordinated planning of hydropower and new energy at the plant level.Ref.[10] introduced a reliability evaluation method considering the impact of cascade hydraulic connections on hydropower regulation capacity and new energy consumption.This method uses the flexible regulation capacity of hydropower to evaluate its role in promoting the wind power consumption at a certain confidence level.The proposed model was successfully applied to the hydro-wind complementary planning in the Zambezi River.Ref.[11] considered the Swedish hydropower-dominated system as an example to evaluate the market value and income of wind power through the coordinated planning and operation of hydrowind systems in power markets.Ref.[12] presented a capacity planning model of large-scale hydro-windphotovoltaic power systems by considering the electricity transmission requirements and cascade hydropower comprehensive characteristics.It obtained the optimal wind and photovoltaic capacity configuration based on the complementary guarantee rate.Although these studies consider the cascade hydraulic connections,they do not sufficiently address the operational challenges of hydropower,such as the FZs of hydropower units.

The FZs of hydropower units are the vibration areas produced by the inertial and dynamic effects of the rotating machine parts during the operation of the hydropower unit.The FZ phenomenon is prevalent in the operation of hydropower units owing to continuous variations in the water flow,pressure,and flow state in the pipeline [13,14].Hydropower units must not be operated within the FZs since they are prone to violent vibrations that affect the stability of the unit structure and safe operation [15,16].Previous studies have focused on FZs in short-term hydropower generation scheduling [17-19],but did not sufficiently consider the impact of FZs on CPHPS.FZs typically account for a large proportion of the unit output range (e.g.,up to 60% or more).Therefore,it is essential to comprehensively consider FZs in CPHPS,which helps in enhancing the economy and feasibility of the planning scheme.

Based on the above analysis,this study proposes a capacity planning model for CPHPS that considers the influence of hydropower FZs.Firstly,the FZs of the hydropower units are converted into those of hydropower plants based on set theory to avoid unit commitment optimization during the calculations.Secondly,a mathematical model for the CPHPS is formulated,which couples the FZ constraints of hydropower plants with other operational constraints (e.g.,power balance constraints,new energy consumption limits,and hydropower generation functions) to minimize the investment and operational costs of the power system.Thirdly,dynamic programming with successive approximations (DPSA) is implemented to address the non-linearity and non-convexity of the proposed model.Lastly,case studies were conducted on a hydrowind-solar system in the Qingshui River to demonstrate the effectiveness of the proposed model.

1 Mathematical formulation of hydropower forbidden zones

The FZ is the output domain of the hydropower units during operation which damages the life cycle of the hydropower units.It must be avoided to ensure the safe operation of hydropower plants [20].Considering the widely used Francis turbine as an example,this type of hydropower turbine typically contains one or more FZs [21].Furthermore,the output range of the FZ varied dynamically with the water head.

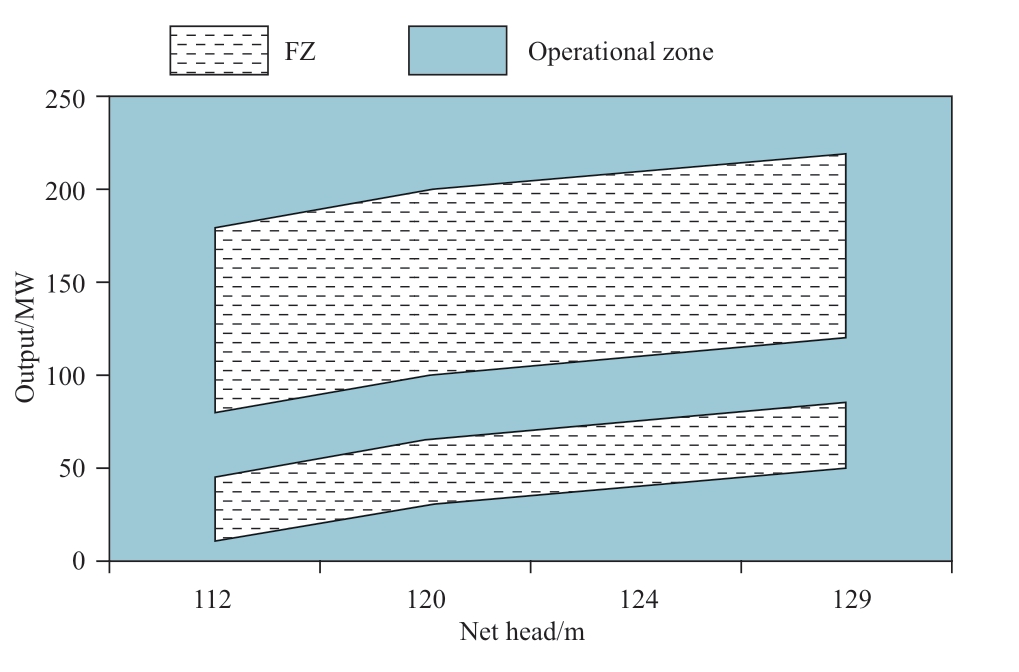
Fig.1 Sketch map of FZs of hydropower unit

Figure 1 illustrates the FZs of a vertical-shaft Francis hydropower turbine (nominal capacity of the unit is 250 MW).The unit has two FZs in the 112-129 m water head range,which account for more than half of the output space of the unit and can severely limit the hydropower regulation capacity.Therefore,it is crucial to consider the effect of FZs on the CPHPS when evaluating new energy capacities that can be complemented by hydropower.

The FZ is an inherent feature of the hydropower unit,due to which unit commitment is required when considering the hydropower unit as the object to participate in the CPHPS,which significantly increases the computational burden.Thus,this study presents an alternative solution which involves converting the FZs of hydropower units into those of hydropower plants.This enables the hydropower plant to participate in the optimization instead of the hydropower unit.In this way,unit commitment can be avoided,thereby simplifying the problem solving.

In this study,set operations based on set theory were implemented to transform the FZs between the hydropower plant and the hydropower unit.Figure 2 depicts the entire procedure,and the detailed steps are summarized as follows:

Step 1: Formulation of FZs of the hydropower unit.

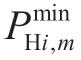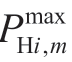For the unit,m,in plant,i,the lower and upper output limits are represented by  and (MW),respectively.The output domains of unit m and plant i can then be represented as follows:

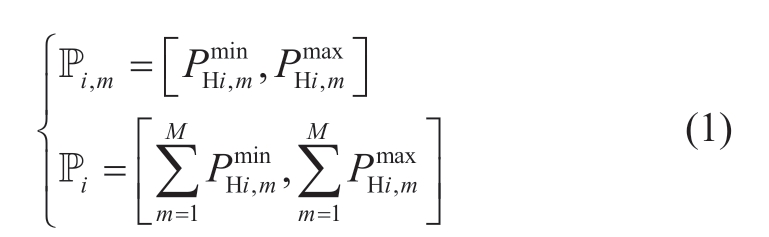
where M denotes the number of hydropower units in the hydropower plant,i.Pi and Pi,m represent the output domains of the plant,i,and unit,m,respectively.

Assuming that the water head,Hi,of the plant,i,is given,the FZ of the unit,m,is calculated using the union operation as follows:

where Vi,m denotes the FZ set of unit,m,in plant,i;VZi,m denotes the number of FZ subsets of unit,m,in plant,i;vz denotes the index of FZ;Hi denotes the given water head of plant,i(m);and 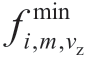(Hi) and 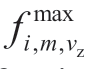(Hi) represent the lower and upper limits of FZ,vz,of unit,m,in plant,i,at the water head,Hi(MW).

Step 2: Formulation of feasible operational zones (OZs)of the hydropower unit.

Let Ri,m represent the set of OZs of unit,m,in the plant,i.Then,Ri,m is equal to the complement of Vi,m in Pi,m as follows:

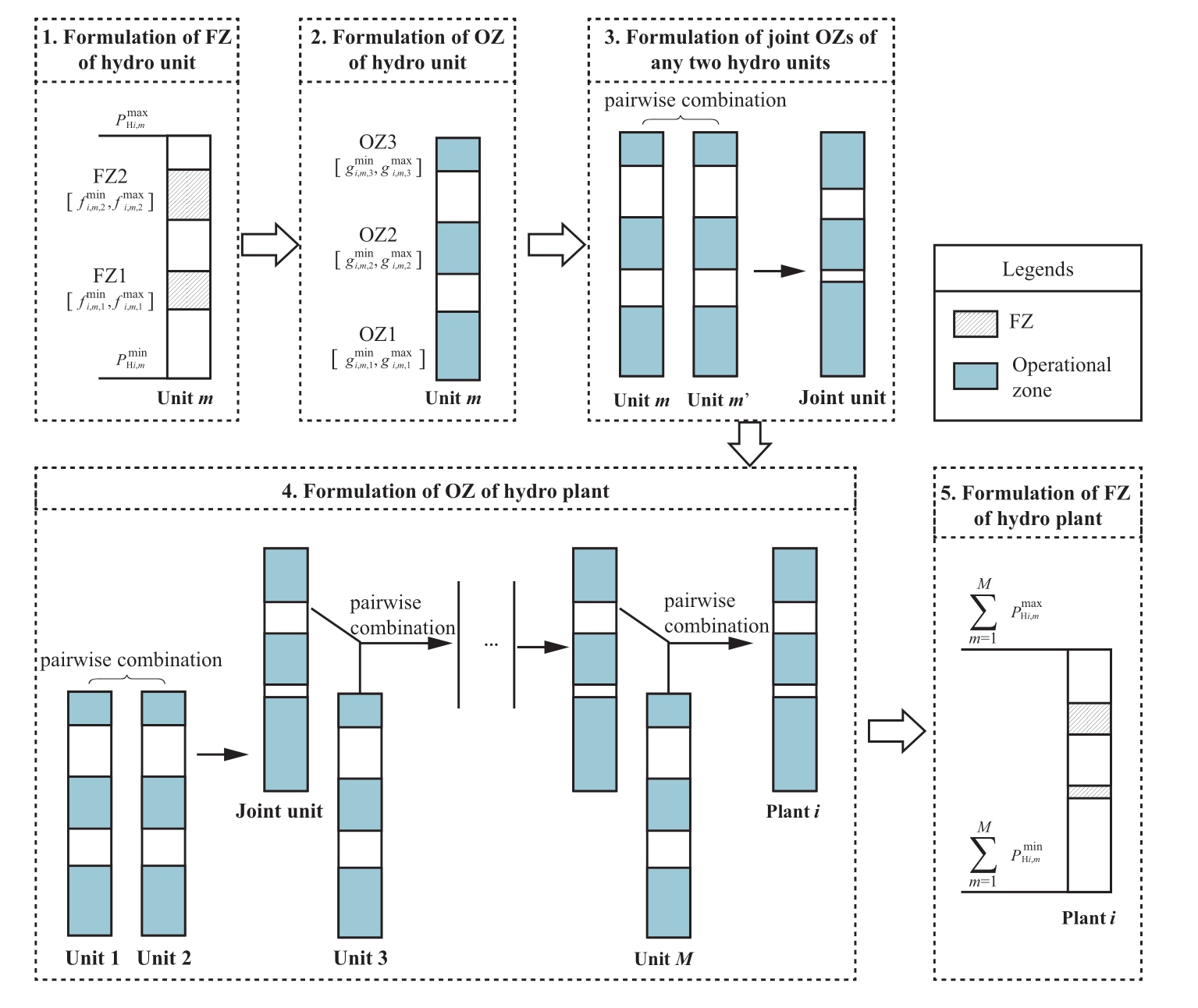
Fig.2 Modeling procedure of hydropower FZs

According to the rules of the complementary operation,Ri,m represents the union of a collection of discrete subsets that can be further converted into

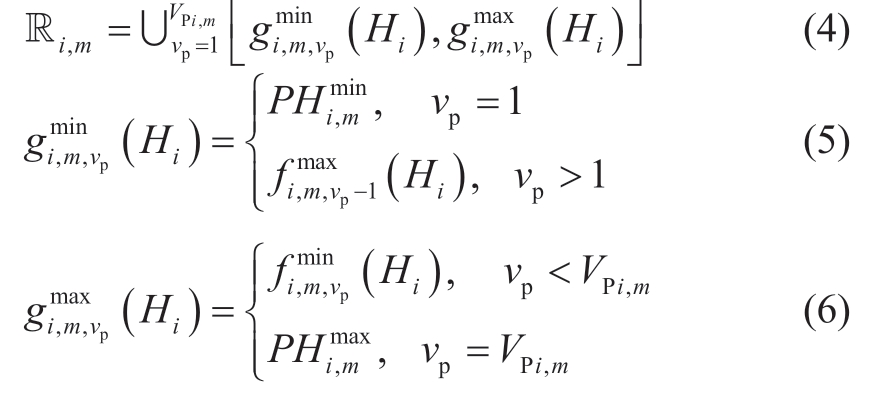
where vp denotes the index of OZ;VPi,m denotes the number of OZ subsets in Ri,m;and 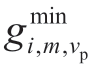(Hi) and(Hi) represent the lower and upper limits of the OZ of unit,m,in the plant,i,at the given head,Hi (MW),respectively.

Step 3: Formulation of joint OZs of any two hydropower units.

For any two units,m and m',in the plant,i,the joint OZs can be formulated using the union operation as follows:

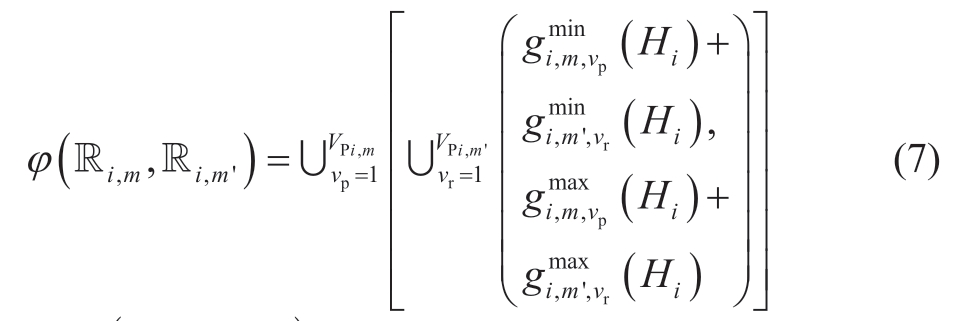
where φ(Ri,m,Ri ,m') represents the function combining the OZs of units,m and m'.

Step 4: Formulation of OZs of hydropower plant.

Assuming that all the hydropower units in the plant can be started,the OZs of the hydropower plant,i,can be obtained through pairwise iterations of the OZs of the hydropower units as follows:

where Ri denotes the set of OZs of the plant,i.In Eq.(8),a total of M -1 times of φ(·) function operations are required.

Step 5: Formulation of FZs of hydropower plant.

The FZ of the hydropower plant can be obtained through a complement operation as follows:

where Vi denotes the set of FZ of the hydropower plant,i.

Eq.(9) can be further expanded as follows:

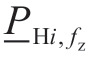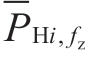where fz denotes the FZ index of hydropower plants,VZi denotes the number of FZs of plant,i,and  andrepresent the lower and upper limits of the FZ,fz,of the plant,i (MW),respectively.

Eq.(10) represents the FZs of the hydropower plant at a given head,Hi.The FZs of the hydropower plant under different water heads can be obtained by traversing all the water heads and repeating Steps 1-5.

Step 6: Operational constraints of FZs of hydropower plant.

At the head,Hi,the output of the hydropower plant,i,must satisfy the following constraints to avoid operation in the FZ domain:

where PHi denotes the output of the plant,i (MW).

2 Capacity planning model of hydro-windsolar power systems

To minimize the total cost of the system,the CPHPS optimizes the scale of the wind-solar power coordinated with hydropower by fully utilizing the hydropower flexibility and transmission lines [23].In the CPHPS,the hydro-windsolar electricity is bundled together to be integrated into the power grid and transmitted to the load center.Figure 3 depicts a sketch of the coordinated operation of the hydrowind-solar system.

A mathematical model for a CPHPS was developed,comprising various constraints,such as system-wide constraints,new energy constraints,and hydropower system constraints [24].In this model,the hydropower plants participating in the optimization have already been operated.A wind plant and solar plant will be built in the neighboring area of each hydropower plant.

Fig.3 Sketch map of coordinated operation of the hydro-wind-solar system

2.1 Objective function

The objective of the model is to minimize the total cost of the power system,including the investment and operation costs of the wind-solar power and the penalty costs of load shedding,as follows:

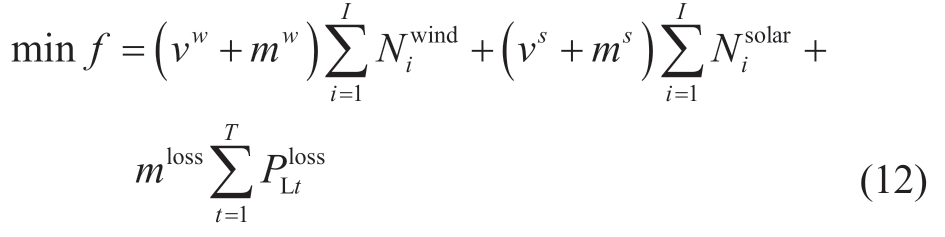
where vw and mw represent the annualized investment and operation costs per unit of the wind capacity (CNY/MW),respectively;vs and ms represent the annualized investment and operation costs per unit of the solar capacity (CNY/MW),respectively;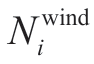 and  represent the planned capacity of wind power and solar power near hydropower plant i (MW),respectively;mloss denotes the penalty cost of load shedding (CNY/MW);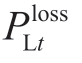 denotes the load curtailment at period,t (MW);and I denotes the number of hydropower plants.

Since each hydropower plant is integrated with one wind plant and one solar plant,they share the same plant index,i.

2.2 Constraints

2.2.1 System-wide operation constraints

1) Power balance constraints

where PWi,t and PVi,t represent the outputs injected into the power grid for the wind plant,i,and solar plant,i,at period,t (MW),respectively;and Dt denotes the system load demand at period,t (MW).

2) Transmission line operation constraints

where 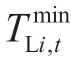and 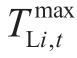represent the lower and upper limits of the transmission line capacity attached to the hydropower plant,i,at period,t (MW),respectively.

2.2.2 New energy operation constraints

1) Power output constraints

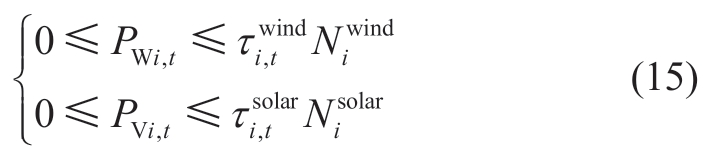
where 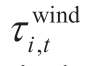 and 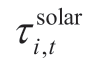 represent the theoretical outputs of the wind plant,i,and the solar plant,i,per unit of the installed capacity at period,t,respectively.

2) New energy consumption constraints

where δ denotes the minimal new energy consumption rate.

2.2.3 Hydropower system operation constraints

For cascade hydropower plants,the hydraulic connections between the adjacent reservoirs,FZ constraints,and other relevant operational constraints must be considered.

1) Cascade hydraulic connections

where 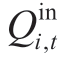 and Bi,t represent the total inflow and natural inflow of the plant,i,at period,t (m3/s),respectively,and 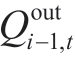denotes the outflow of the plant,i-1,at period,t (m3/s).The hydropower plant,i-1,is upstream of the hydropower plant,i,and the water travel time between the adjacent hydropower plants is ignored.

2) Water balance constraints

where Si,t denotes the storage of the plant,i,at period,t (m3),and Δt denotes the time duration of a period (h).

3) Water level constraints

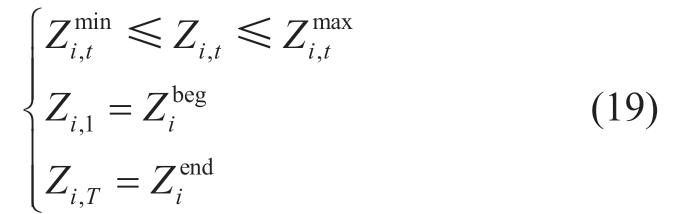
where Zi,t denotes the forebay water level of the plant i at period t (m);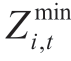 and 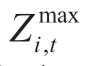 represent the minimal and maximal water levels of plant,i,at period,t (m),respectively; 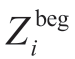and 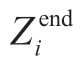 represent the initial and terminal water levels of the plant,i (m),respectively;and T denotes the number of time periods.

4) Relationships between forebay water level and storage

where ai,0,ai,1,ai,2,ai,3,and ai,4 denote the coefficients that depend on the storage characteristics of the hydropower plant,i.

5) Water discharge constraints

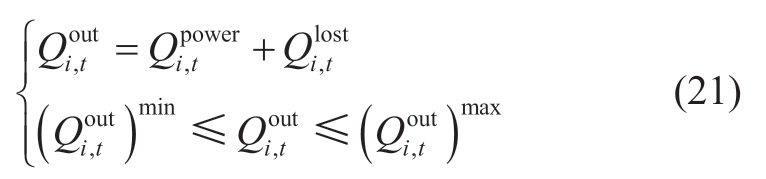
where 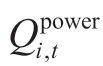 and 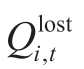 denotes the power release and spillage of the plant,i,at period,t (m3/s),respectively,andanddenote the minimum and maximum outflows of the plant,i,at period,t (m3/s),respectively.

6) Relationships between tailrace water level and discharge

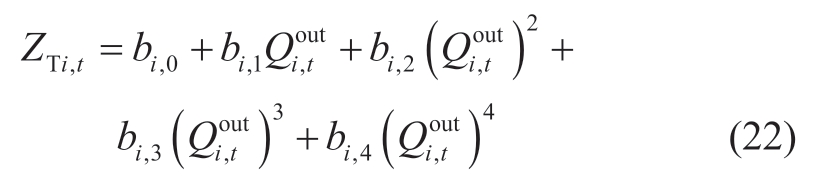
where bi,0,bi,1,bi,2,bi,3,and bi,4 denote the coefficients that depend on the outflow characteristics of the hydropower plant,i,and ZTi,t denotes the tailrace water level of the plant,i,at period,t (m).

7) Water head constraints

where Hi,t denotes the net water head of the plant,i,at period,t (m),and  denotes the head loss of the plant,i (m).

8) Hydropower generation functions

where PHi,t denotes the output of the plant,i,at period,t(MW),and ηi denotes the output coefficient of the plant,i.

9) Output constraints

where 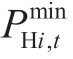and 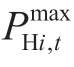represent the lower and upper output limits of the plant,i,at period,t (MW),respectively.

10) Electricity consumption constraintswhere Ei denotes the minimum electricity limit of the plant,i (MWh).

3 Solution methods

The CPHPS is a large-scale,non-convex,non-linear problem involving thousands of constraints and decision variables,making it difficult to obtain an optimal solution within a short period [25,26].

DPSA is an adaptation of dynamic programming (DP)that can effectively solve multidimensional optimization problems [27,28].Figure 4 presents the schematic diagram of DPSA.

The general steps of DPSA are summarized as follows.

1) Problem decomposition.The primal high-dimensional optimization problem is decomposed into a series of independent low-dimensional subproblems by relaxing the coupling constraints [29].

2) Sub-problem solving.In DP,the state and decision variables corresponding to the other sub-problems are considered to identical to those in the previous iteration,and only the state variables of the sub-problem to be optimized are discrete [30].The sub-problem is solved by traversing the state combinations of the subproblem to be optimized periodically [31,32].

3) Convergence judgment.We determine whether the convergence criteria are satisfied.If so,the calculation is stopped;otherwise,the variable corresponding to the relaxed constraints is updated and Step 2 is repeated.

The advantages of DPSA are as follows: 1) the multidimensional problem is split into several onedimensional sub-problems,which can significantly reduce the solution time;2) in the iteration of sub-problem solving,the local optimal solution is obtained by traversing the combinations of state variables.This avoids the approximation of non-linear and non-convex constraints and maintains the inherent properties of the CPHPS [33].

Therefore,DPSA was implemented to solve the CPHPS problem,the framework of which is summarized in Fig.5.The detailed steps are as follows:

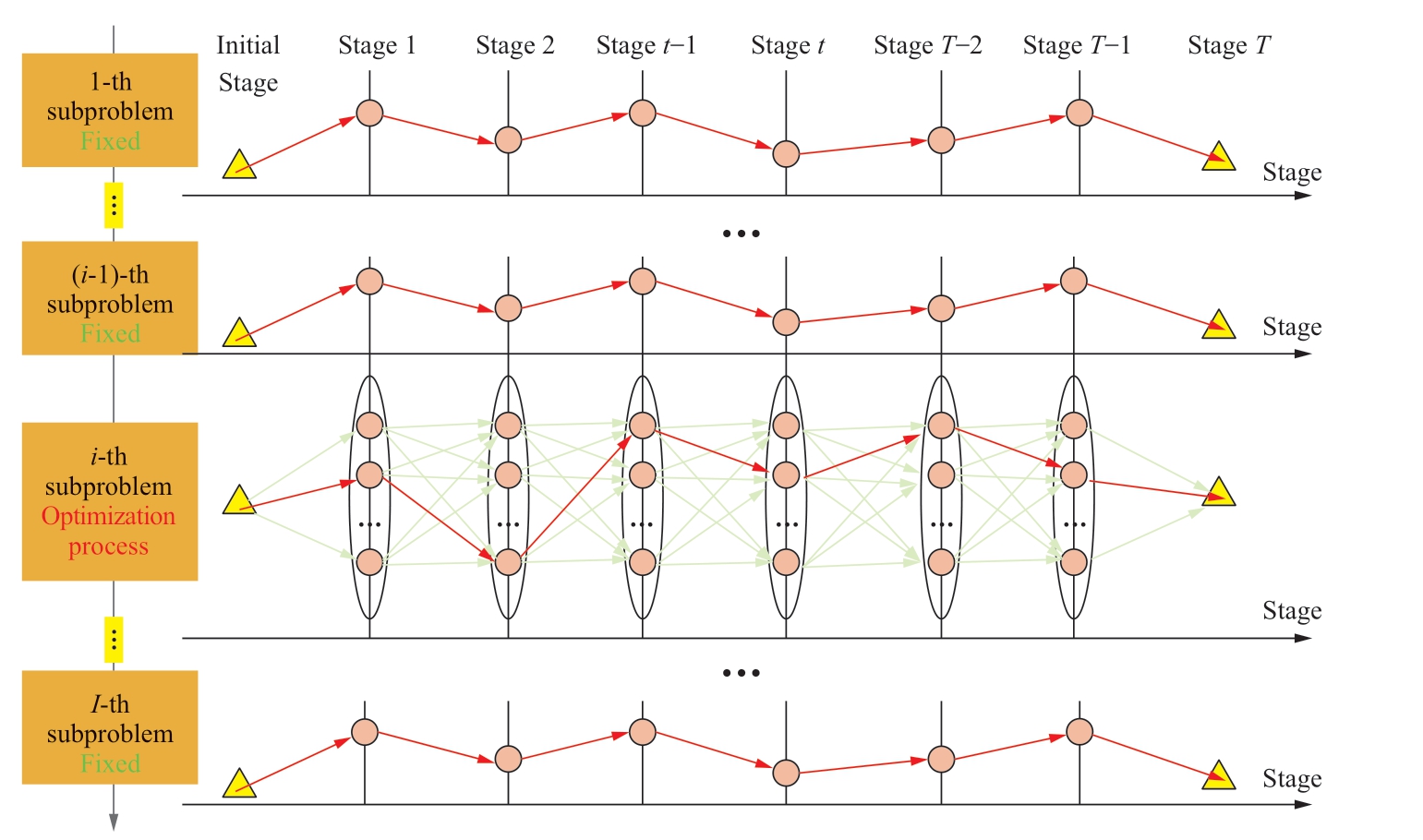
Fig.4 Schematic diagram of DPSA

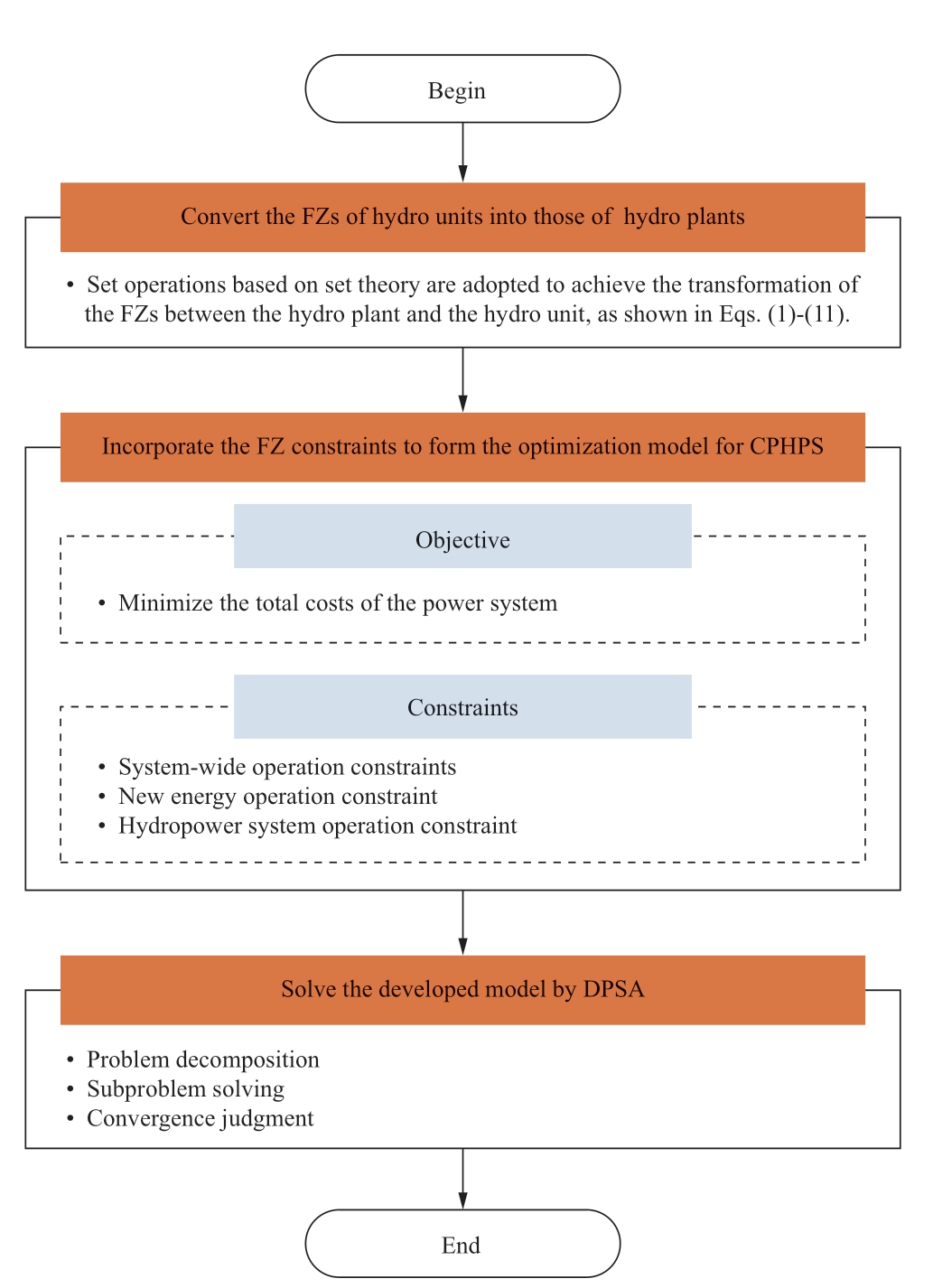
Fig.5 Solving procedures of DPSA for CPHPS

Step 1: The power balance constraints (Eq.(13)) and the cascade hydraulic connections (Eq.(17)) are decoupled to ensure that the original CPHPS problem is converted into I sub-problems [34].In the sub-problem i,the variables independent to the sub-problem i are fixed,which are equal to the values in the previous iteration.

The sub-problem is formulated as follows.

Objective:

Constraint: In addition to Eqs.(11),(14)-(15),and (18)-(26),the following constraints (Eqs.(28)-(30)) must be considered.

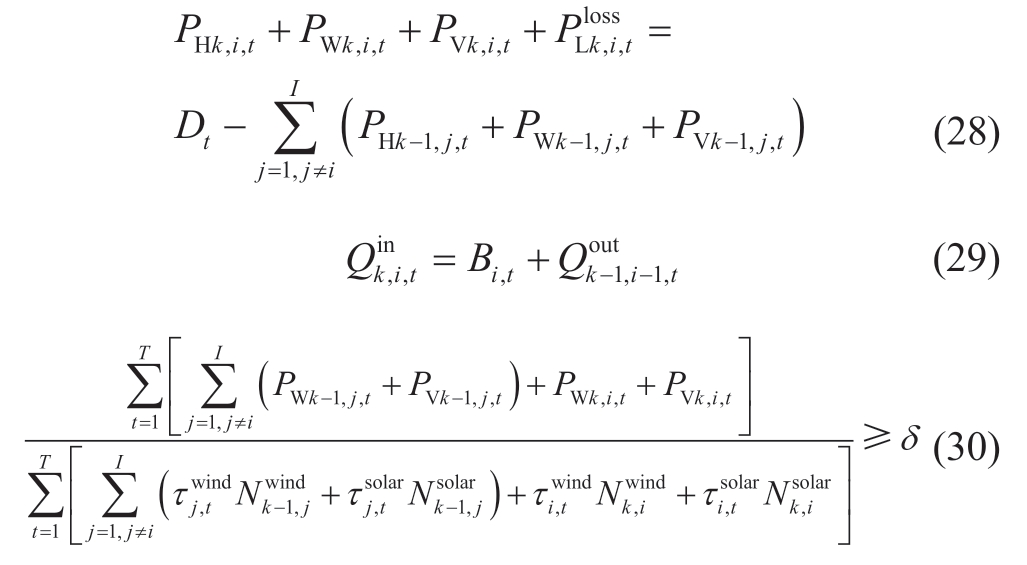
where PHk,i,t,PWk,i,t,and PVk,i,t are the outputs of the hydropower plant i,wind plant i,and solar plant i at period t at iteration k (MW),respectively;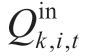 is the total inflow of the hydropower plant i at period t at iteration k (m3/s);and  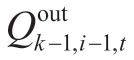is the outflow of hydropower plant i-1 at period t at iteration k-1 (m3/s).

Step 2: Set k=1.

By discretizing the state variable into several state combinations,the decision variables of the sub-problem can be determined through the DP,which is represented as:μk,i,t =[PHk,i,t,PWk,i,t,PVk,i,t].

In the state transition process of the DP,the capacities of the wind power and solar power are calculated as follows:

where and 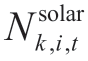represent the optimal wind and solar capacities of the sub-problem,i,at iteration,k,from period,0 to t (MW),respectively.

The objective is achieved by solving Eqs.(27) and (32),respectively.

Step 4: Δf≤Δfmax is set as the convergence criterion,whererepresents the objective difference between the previous two iterations.If convergence is achieved,the calculation is stopped;otherwise,we set k =k +1 and update the fixed variables in Eq.(28)-(30),according to the results,and repeat Step 3.

4 Case studies

Located in Guizhou,China,the Qingshui River has a total length of 134 km,a drop of 1005 m,and an average annual runoff of 40 m3/s.Hitherto,two hydropower plants have been built on the Qingshui River: Dahuashui and Geliqiao,as shown in Fig.6.The Qingshui River Basin has abundant wind and solar energy resources.There are significant exploitable amounts of wind and solar power within 200 km of the river;their capacities are 1.7 GW and 40 GW,respectively.The generation utilization hours for the wind and solar power were 2271 and 1138,respectively.The 8760-hour-time-series output characteristics of the wind and solar power were obtained through the statistical analysis of long-sequence meteorological data and served as the data input for the mode,as shown in Fig.7.

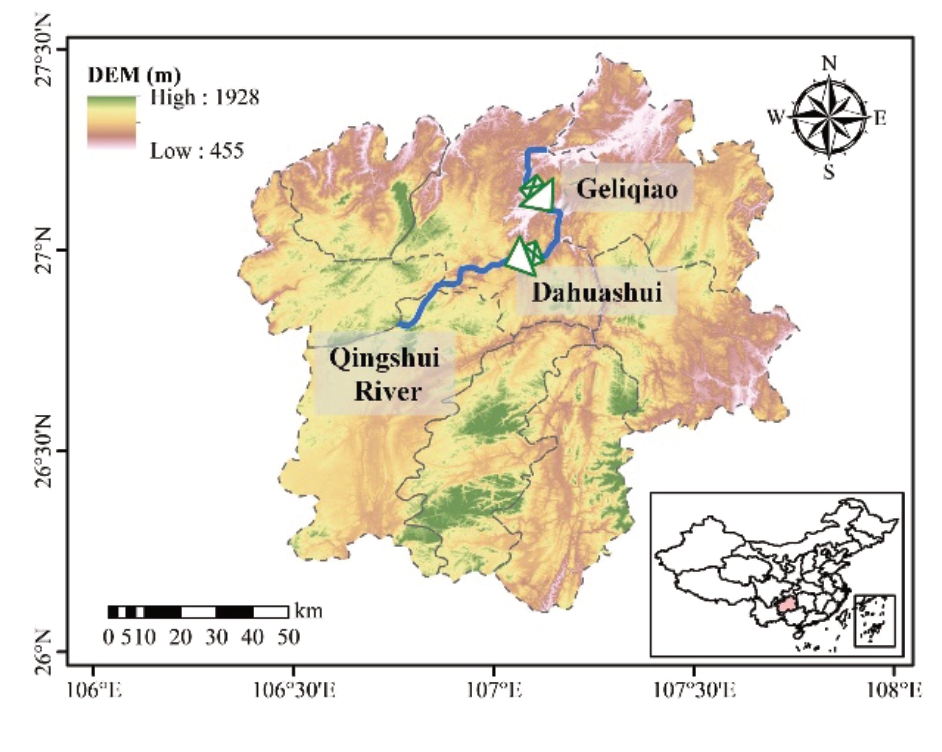
Fig.6 Location of the cascade hydropower system

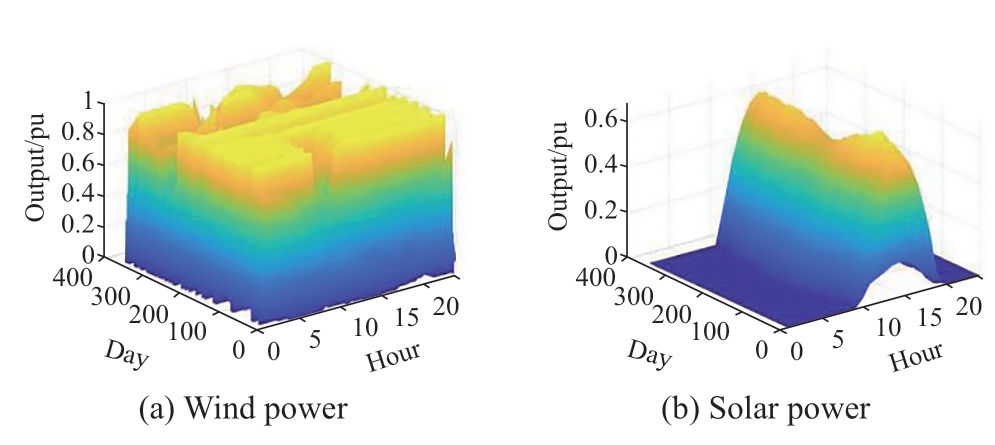
Fig.7 Generation characteristics of wind and solar power in Qingshui River Basin

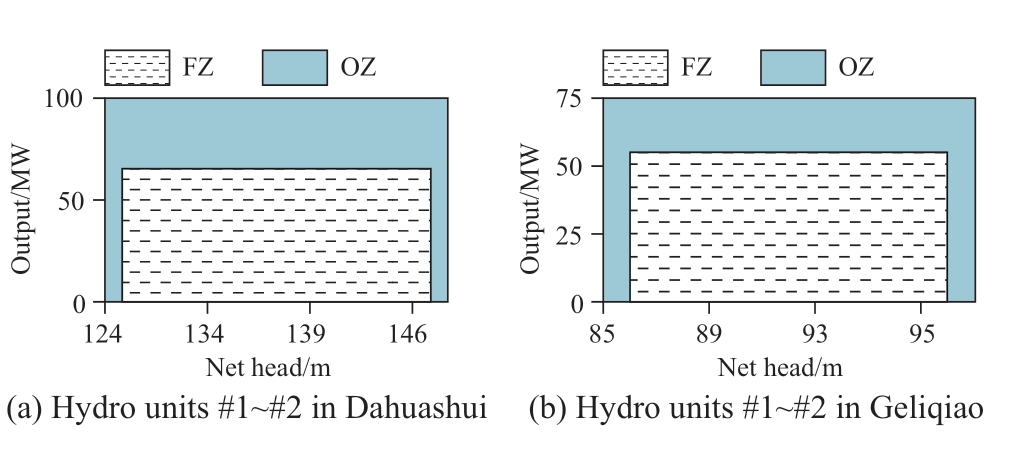
Fig.8 FZs of hydropower units

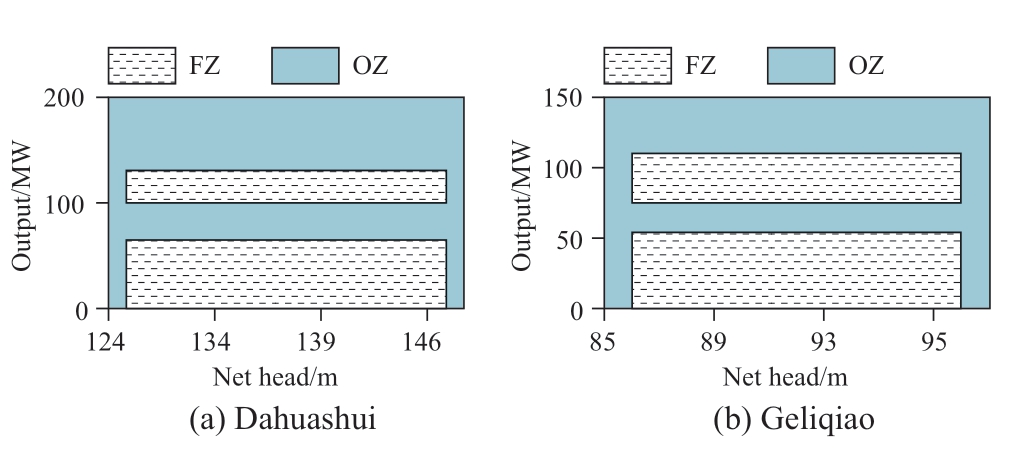
Fig.9 Converted FZs of the hydropower plants

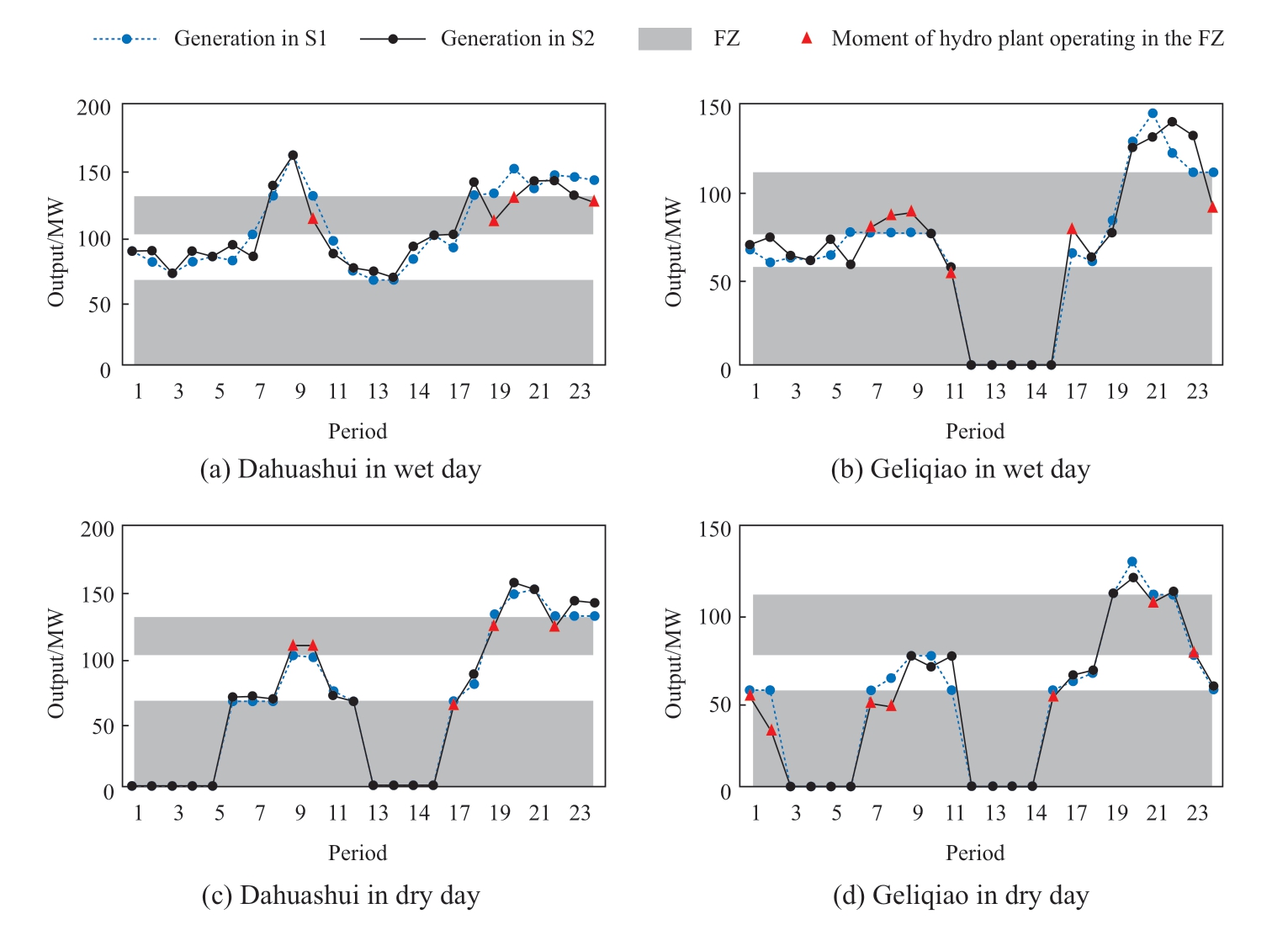
Fig.10 Hydropower output curves on typical wet and dry days under different scenarios

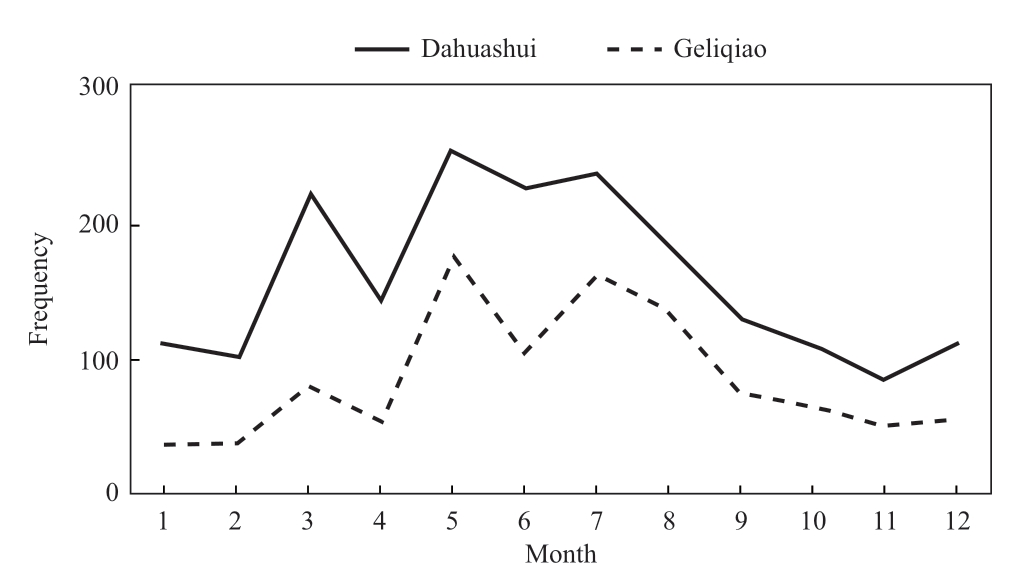
Fig.11 Operation frequencies of hydropower plants in the FZs

Fig.12 Monthly complement operations of hydro-wind-solar hybrid system

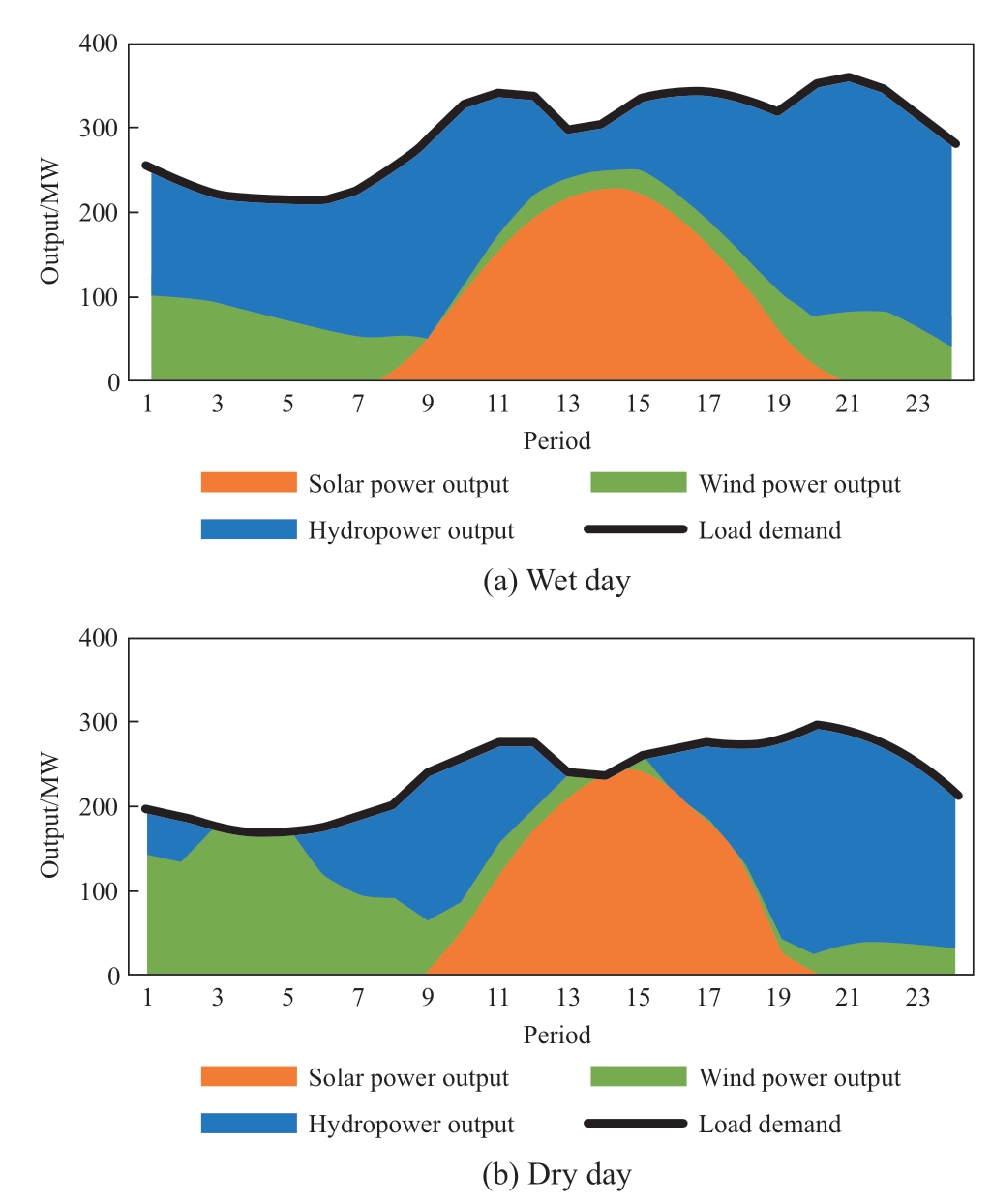
Fig.13 Operations of hydro-wind-solar hybrid system on typical wet and dry days

Case studies were conducted on the capacity planning of the hydro-wind-solar systems by selecting the Qingshui River Basin as the study area.Table 1 lists the basic parameters of the hydropower plants.Figure 8 depicts the FZs of the hydropower plants.

Table 1 Basic parameters of hydropower plants

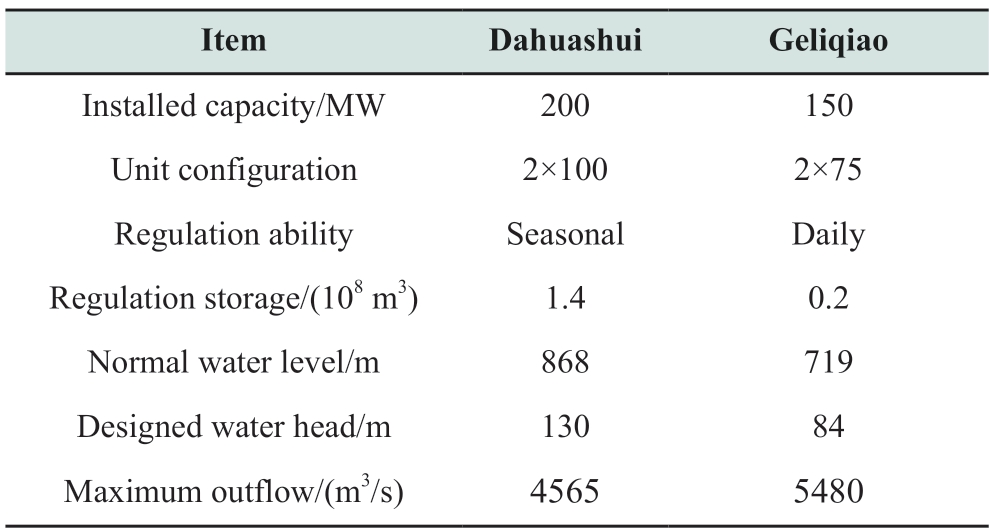
In the data input,the average annual natural inflows are adopted to represent the natural inflows of the hydropower plants.The average annual power generation is used to represent the lower limit of hydropower generation.The load demand is obtained from the historical data in 2019.Furthermore,the parameters,vw,mw,vs,and ms,are set to 6.5×106,4.15×104,3.6×106,and 4×104,respectively,based on the investment statistics of new energy projects in 2022.To achieve a penalty effect,the parameter,mloss,is set to a sufficiently large number,i.e.,1×108.The minimal new energy consumption rate,δ,is set to 0.9.The planning horizon of the model is 1 year with a time interval of 1 hour.

4.1 Analysis of forbidden zones transformation

Figure 9 depicts the FZs of the hydropower plants after transformation.The ratio of the converted FZs to the installed capacity of the hydropower plant decreased significantly when compared to the ratio of the unit FZs to the unit capacity.Table 2 lists the transformation results of the unit FZs for Dahuashui and Geliqiao under the designed water heads.In Dahuashui,there are two hydropower units that have the same FZ of (0,65) MW,accounting for 65%of the unit capacity.After the transformation,the FZs of the hydropower plant were (0,65)U(100,130) MW,accounting for 48% of the installed capacity.Geliqiao exhibits similar features.Before unit combination,the FZ of the unit accounted for 73% of its capacity.After combination,the FZ of the power plant accounted for 60% of its capacity.

Table 2 FZ transformation of hydropower plants under the designed water heads

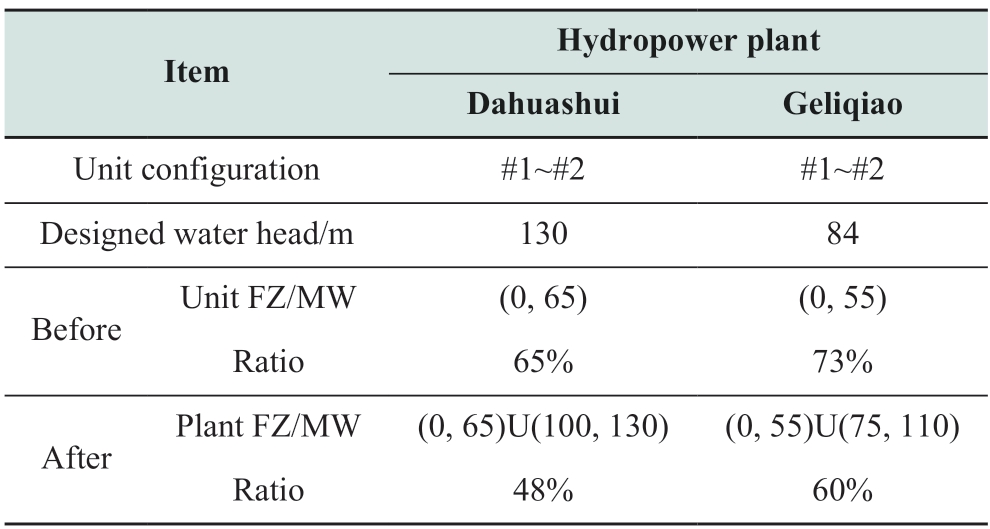
Based on the above analysis,the following conclusions can be drawn: 1) The FZ of the hydropower units significantly affects the range of the unit output regulation,with the FZ accounting for approximately 60% or more of the nominal capacity of the unit.2) The impact of the unit FZ on the power-plant output range can be reduced to a certain extent through unit combinations and FZ transformation.

4.2 Scenario setting

To analyze the impact of FZs on the CPHPS,the following three scenarios were set up:

S1: Solving the proposed CPHPS model while considering the FZ constraints.

S2: Solving the proposed CPHPS model while ignoring the FZs constraints.

S3: Optimizing the operations of the hybrid power systems are based on the planning results from S2 to maximize the energy consumption of the hydro-wind-solar system while considering the FZ constraints.

Based on the above scenario settings,we first analyzed the impact of the FZs on the scale of the wind and solar power,and optimized the capacity of the wind and solar power under S1 and S2.To analyze the impact of the FZs on the wind and solar energy consumption,S3 was added to compare the energy consumption under S1,S2,and S3.Subsequently,to analyze the impact of the FZs on the safety of the hydropower operations,the time periods of the hydropower plants falling into the FZs during operations under S1 and S2 were compared.Lastly,the complementary operation of the hydro-wind-solar power system was analyzed by using S1 as an example.

4.3 Analysis of wind-solar power scale

Table 3 depicts the wind-solar power capacity that the hydropower can support under S1 and S2.

Table 3 Impact of FZs on wind power and solar power scale

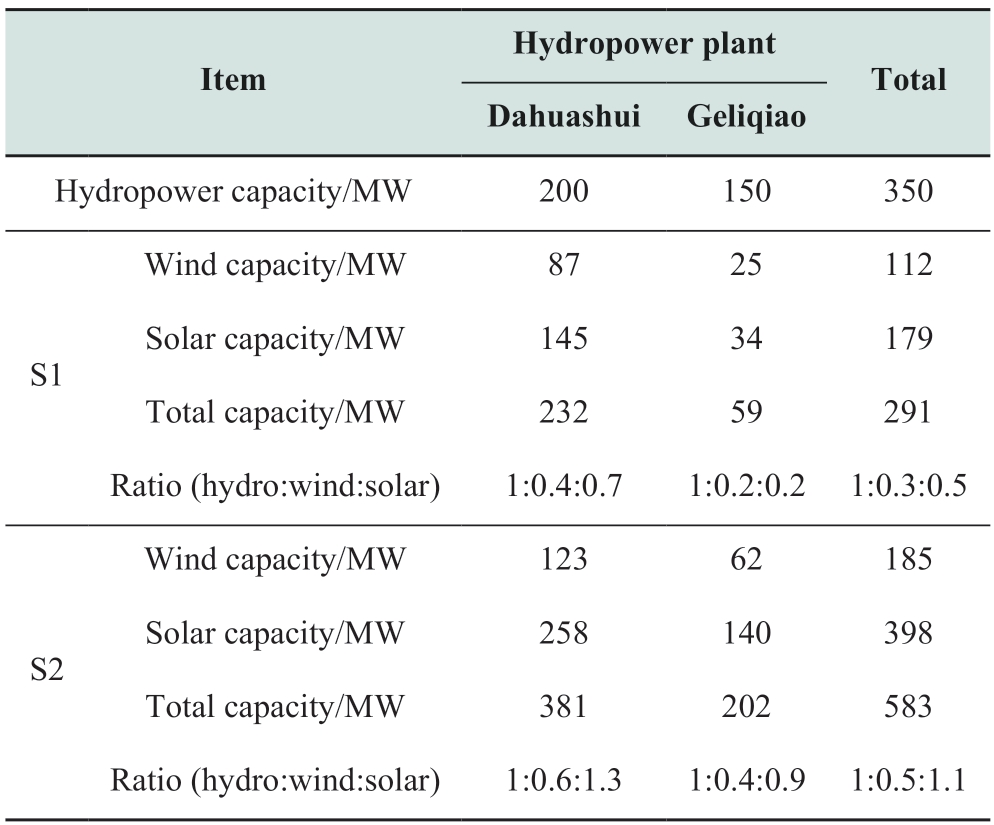
From the perspective of the new energy scale,the two hydropower plants supported 291 MW of new energy with the wind and solar power capacities of 112 MW and 179 MW,respectively,in S1.The ratio of the installed capacity of the hydropower,wind power,and solar power was approximately 1:0.3:0.5.In S2,the total installed capacity of the new energy source was 583 MW,which was twice that of S1.This is because the FZ constraints are not considered in S2,which exaggerates the regulation ability of hydropower,resulting in a larger scale of new energy being supported by the hydropower for grid integration.

From the perspective of the hydropower plants,the scale of the new energy that the hydropower can support varies significantly.It is positively correlated with the regulation ability of the hydropower plant and negatively correlated with the FZ ratio.The regulatory ability of Dahuashui was seasonal and better than that of Geliqiao.Consequently,the wind and solar power capacities that Dahuashui can compensate are 123 MW and 258 MW,respectively,in S2,which are larger than the corresponding new energy scales corresponding to Geliqiao.Moreover,the proportion of FZs in Dahuashui is lower than that in Geliqiao.Thus,the ratio of the installed capacity among the hydropower,wind power,and solar power in Dahuashui is 1:0.4:0.7,which is greater than that in Geliqiao.

4.4 Analysis of wind-solar energy consumption

Table 4 presents the consumption of the hydro-windsolar energy in different scenarios.It can be observed that the hydropower generation is 1070 GWh in all scenarios,which is equal to the lower limit of hydropower electricity.This indicates that hydropower primarily contributes to the capacity regulation and provides consumption room for new energy.

Table 4 Impact of FZs on the energy consumption of wind power and solar power

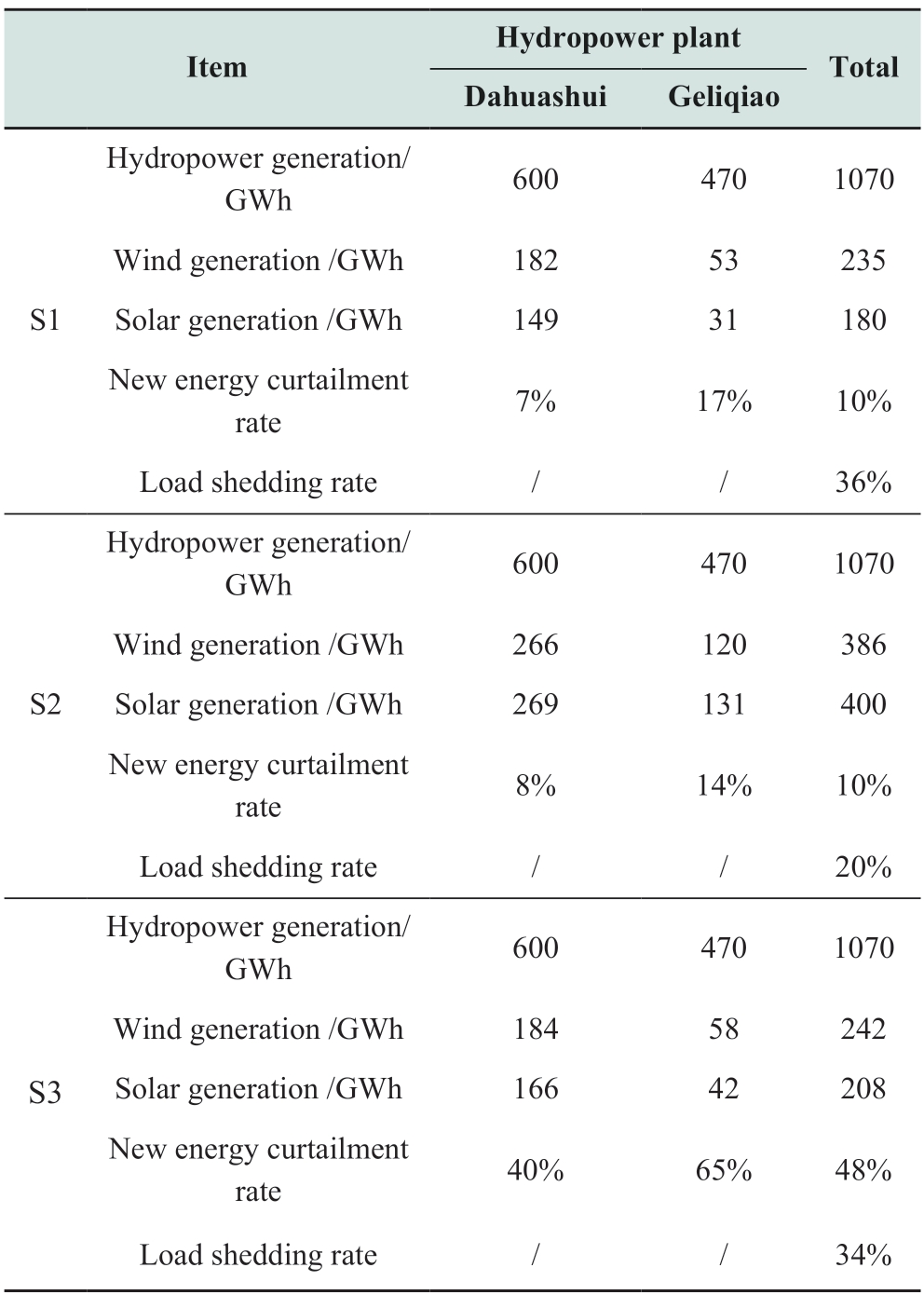
In S1 and S2,the curtailment rate of the new energy is equal to the upper limit of the curtailment rate of 10%.This is because the penalty cost for load shedding in the objective function is much higher than the investment and operational costs of the new energy.Therefore,in the optimization process,the system prioritizes increasing the capacity of the new energy and reducing the load shedding until the new energy becomes difficult to consume and reaches the maximum curtailment rate.Nonetheless,the generation of hydropower and new energy cannot satisfy the system energy demand,leading to the load-shedding rates of 36%and 20% in S1 and S2,respectively.

When compared to S2,S3 reduced the consumption of the new energy by 336 GWh,and the curtailment rate of the new energy increased from 10% to 48%.When compared to S1,S3 exhibits a new installed energy capacity increment of 292 MW and an actual increase in electricity consumption of 35 GWh.Consequently,the actual utilization rate of the incremental capacity of the new energy was only 8%,resulting in a large amount of electricity abandonment.

In summary,ignoring the FZ constraints results in a larger scale of new energy in the CPHPS.However,in the actual operation of the power systems,it is difficult to achieve incremental generation of new energy,leading to a high curtailment rate and damage to the system economy.

4.5 Analysis of forbidden zone avoidance

To analyze the FZ avoidance of the hydropower plants,the operation processes of Dahuashui and Geliqiao under S1 and S2 are presented on typical wet and dry days,respectively.

Figs.10(a) and 10(b) depict the output curves of the hydropower plants on a wet day.The FZ constraints were not considered in S2,and the periods of Dahuashui and Geliqiao falling into the FZ were four and six,respectively.These periods were primarily distributed between 7-11 AM and 5-8 PM.In these periods,the outputs of the hydropower plants were continuously ramped up/down to satisfy the system flexibility demand.Consequently,the hydropower plants operate in the FZ for multiple periods.In S1,all the power plants operate outside the FZs owing to the consideration of the FZ constraints in the model.

Figs.10(c) and 10(d) depict the output curves of the hydropower plants on a dry day.The hydropower had a lower load rate and stronger regulatory ability on dry days than on wet days.To satisfy the system flexibility requirements,the output of the hydropower plants was increased from 0 to a high output interval,and then decreased rapidly within a short period.During this process,the hydropower plant entered the FZs multiple times.Consequently,the Dahuashui and Geliqiao operations in the FZ were conducted for 5 and 7 times,respectively.Conversely,all the power plants operated outside the FZs in S1.

Figure 11 depicts the monthly distribution of the operating periods of each hydropower plant falling into the FZs under S2 throughout the year.In the 8760 periods throughout the year,the time periods of Dahuashui and Geliqiao operating in the FZs were 1893 and 1016,respectively,and the occurrence probabilities were 22% and 12%,respectively.These periods were primarily distributed during the wet season (June-September) and pre-flood months (March-May).

In summary,each hydropower plant operated outside the FZs throughout the planning horizon in S1 owing to the consideration of the FZ constraints.In S2,there is a certain probability that the hydropower plants will operate in the FZs,threatening their safe operation of hydropower plant because the FZ constraints are ignored.

4.6 Complement operations of hydro-wind-solar system

This section presents the monthly and hourly complementary operations of the hybrid power system to demonstrate the effectiveness of the proposed method.

4.6.1 Monthly complement operations

Figure 12 depicts the monthly operation process of the hydro-wind-solar system in S1.

In terms of seasonal complementarity,the hydropower output was concentrated during the flood season from May to October,accounting for 66% of the annual hydropower generation.The output trends of the wind and solar power were consistent,with the output valley in summer and the output peaks in spring and autumn,which effectively complemented the hydropower.

In terms of the monthly energy balance,the load shedding during the flood season was relatively small.From May to July,the system load demands were completely satisfied by the hydro-wind-solar complementary generation,and the wind and solar power curtailment occurred during this period.In spring and winter,the power shortage was significant,reaching a maximum of 77 GWh in November.

4.6.2 Hourly complement operations

Figure 13 depicts the hourly output process of the hydrowind-solar system on wet and dry days in the Qingshui River under S1.

On wet days,the hydropower load rate was relatively high(approximately 70 %) and contributed significantly to the electricity supply.At noon,the hydropower output was reduced to promote the solar energy consumption.At night,the solar power outputs turn to 0,and the wind power output is relatively high.The hydropower and wind power complement each other to satisfy the power balance of the system.The electricity consumption ratios of the hydropower,wind power,and solar power on wet days were 1:0.3:0.4.

On dry days,the load rate of the hydropower is low(approximately 30 %),and its regulation ability is strong.At noon,the solar power output reaches its maximum.Correspondingly,the hydropower adjusts its storage capacity to store water without generating electricity,reducing its output to zero and leaving room for the solar energy consumption.At night,the wind power is abundant and fluctuates significantly,while the hydropower is flexible in suppressing fluctuations in the wind power output.The electricity consumption ratios of the hydropower,wind power,and solar power on dry days was 1:0.5:0.6.

5 Conclusions

FZs are widely present in the operation processes of large and medium-sized hydropower plants in China.This affects the flexibility and safety of the hydropower operations,making the CPHPS crucial.This study presents a CPHPS model that considers the FZ constraints for hydro-wind-solar capacity planning.In the model,a mathematical formulation of the hydropower FZs was developed to achieve the transition of the FZs between the hydropower plant and hydropower unit based on set theory.Subsequently,the capacity-planning model is formulated considering the system-wide constraints,new energy constraints,and hydropower system constraints.Lastly,DPSA was implemented to solve the model.Case studies were then conducted on the Qingshui River,and the following conclusions were drawn:

1) The FZs significantly affect the flexibility of the hydropower units and plants.In Dahuashui and Geliqiao,the FZs of the hydropower units accounted for more than 60%of the capacity of the unit,and the FZs of the hydropower plants accounted for more than 40% of the installed capacity of the power plant after transformation.

2) The FZ constraints in the CPHPS were effectively improved the modeling accuracy of the hydropower flexibility,safety of hydropower operation,and utilization efficiency of new energy,which contributes to economical and feasible new energy capacity planning schemes.

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] Zhou P,Zhu X T,WU J,et al.(2023) Economic analysis of largescale rooftop photovoltaics considering carbon trading market.Electric Power Engineering Technology,42(6): 83-90

[2] Li J Y,Liu R J,Zhou C Y,et al.(2023) Technical analysis of China's energy security situation.Electric Power Engineering Technology,42(6): 249-255

[3] Ma C J,Sun Y Z,Peng D G,et al.(2023) Multivariate load forecasting for integrated energy system based on XGBoost-MTL.Electric Power Engineering Technology,42(5): 158-166

[4] Jiang W,Shan M,Deng Y F,et al.(2023) Optimization strategy for aggregating electric vehicles through VPP to participate in the carbon market.Electric Power Engineering Technology,42(4):13-22,47

[5] Dai J,Tian N J,Jiang Y G,et al.(2022) Collaborative maintenance scheduling and unit commitment for hydropower and thermal power systems considering cascade hydropower coupling.Electric Power Engineering Technology,41(3): 83-91

[6] Zhang Y,Cheng C T,Yang T T,et al.(2022) Assessment of climate change impacts on the hydro-wind-solar energy supply system.Renewable and Sustainable Energy Reviews,162:112480

[7] Ming B,Liu P,Guo S L,et al.(2017) Optimizing utility-scale photovoltaic power generation for integration into a hydropower reservoir by incorporating long-and short-term operational decisions.Applied Energy,204: 432-445

[8] Yuan W L,Liu Z,Su C G,et al.(2020) Photovoltaic capacity optimization of small and medium-sized hydro-photovoltaic hybrid energy systems considering multiple uncertainties.Journal of Cleaner Production,276: 124170

[9] Danso D K,François B,Hingray B,et al.(2021) Assessing hydropower flexibility for integrating solar and wind energy in West Africa using dynamic programming and sensitivity analysis.Illustration with the Akosombo Reservoir,Ghana.Journal of Cleaner Production,287: 125559

[10] Gebretsadik Y,Fant C,Strzepek K et al (2016) Optimized Reservoir operation model of regional wind and hydro power integration case study: Zambezi Basin and South Africa.Applied Energy,161: 574-582

[11] Hirth L (2016) The benefits of flexibility: The value of wind energy with hydropower.Applied Energy,181: 210-223

[12] Zhang Y S,Lian J J,Ma C,et al.(2020) Optimal sizing of the grid-connected hybrid system integrating hydropower,photovoltaic,and wind considering cascade reservoir connection and photovoltaic-wind complementarity.Journal of Cleaner Production,274: 123100

[13] Taktak R,D’Ambrosio C (2017) An overview on mathematical programming approaches for the deterministic unit commitment problem in hydro valleys.Energy Systems,8(1): 57-79

[14] Wang J W,Zhang Y C (2012) Short-term optimal operation of hydropower reservoirs with unit commitment and navigation.Journal of Water Resources Planning and Management,138(1):3-12

[15] Jia R,He M J,Zhang X Y,et al.(2022) Optimal operation of cascade hydro-wind-photovoltaic complementary generation system with vibration avoidance strategy.Applied Energy,324:119735

[16] Shen J J,Shen Q Q,Cheng C T,et al.(2020) Large-scale unit commitment for cascaded hydropower plants with hydraulic coupling and head-sensitive forbidden zones: Case of the xiluodu and xiangjiaba hydropower system.Journal of Water Resources Planning and Management,146(11): 05020023

[17] Cheng C T,Shen J J,Wu X Y (2012) Short-term scheduling for large-scale cascaded hydropower systems with multivibration zones of high head.Journal of Water Resources Planning and Management,138(3): 257-267

[18] Cheng C T,Wang J Y,Wu X Y (2016) Hydro unit commitment with a head-sensitive reservoir and multiple vibration zones using MILP.IEEE Transactions on Power Systems,31(6): 4842-4852

[19] Shang Y Z,Lu S B,Gong J G,et al.(2017) Improved genetic algorithm for economic load dispatch in hydropower plants and comprehensive performance comparison with dynamic programming method.Journal of Hydrology,554: 306-316

[20] Shen J J,Hu L,Cheng C T,et al.(2020) Automatic generation control of a large hydropower plant with head-sensitive forbidden and restricted zones.IET Renewable Power Generation,14(7):1113-1123

[21] Colonetti B,Finardi E,Borges Picarelli L (2021) Hydrothermal unit-commitment problem of a large-scale system with representation of forbidden zones.Energies,15(1): 39

[22] Li X,Li T J,Wei J H,et al.(2014) Hydro unit commitment via mixed integer linear programming: A case study of the Three Gorges Project,China.IEEE Transactions on Power Systems,29(3): 1232-1241

[23] Zhang J T,Cheng C T,Yu S,et al.(2021) Assessing the integration potential of new energy in river basin clean energy corridors considering energy-power coupled complementary operation modes249(7831): 114867

[24] Jin X Y,Liu B X,Liao S L et al (2022) Impacts of different wind and solar power penetrations on cascade hydroplants operation Renewable Energy,82(12): 227-244

[25] Feng Z K,Niu W J,Wang S,et al.(2018) Developing a successive linear programming model for head-sensitive hydropower system operation considering power shortage aspect.Energy,155: 252-261

[26] Zhao Z P,Cheng C T,Yan L Z (2021) An efficient and accurate Mixed-integer linear programming model for long-term operations of large-scale hydropower systems.IET Renewable Power Generation,15(6): 1178-1190

[27] Hajidavalloo M R,Shirazi F A,Mahjoob M J (2020) Performance of different optimal charging schemes in a solar charging station using dynamic programming.Optimal Control Applications and Methods,41(5): 1568-1583

[28] He Z Z,Wang C,Wang Y Q,et al.(2021) Dynamic programming with successive approximation and relaxation strategy for longterm joint power generation scheduling of large-scale hydropower station group.Energy,222: 119960

[29] Yan Z Y,Liao S L,Cheng C T,et al.(2021) Lagrangian relaxation based on improved proximal bundle method for shortterm hydrothermal scheduling.Sustainability,13(9): 4706

[30] Zhao T,Cai X M,Lei X H,et al.(2012) Improved dynamic programming for reservoir operation optimization with a concave objective function.Journal of Water Resources Planning and Management,138(6): 590-596

[31] Feng Z K,Niu W J,Cheng C T,et al.(2017) Hydropower system operation optimization by discrete differential dynamic programming based on orthogonal experiment design.Energy,126(3): 720-732

[32] Wu X Y,Cheng C T,Lund J R,et al.(2018) Stochastic dynamic programming for hydropower reservoir operations with multiple local optima[J].Journal of Hydrology,564: 712-722

[33] Yan Z,Liao S,Cheng C,et al.(2020) Long-term optimization of large-scale hydropower system operations based on decomposition-coordination.Journal of Water Resources Planning and Management,146(10): 04020078

[34] Li C L,Zhou J Z,Ouyang S,et al.(2014) Improved decomposition-coordination and discrete differential dynamic programming for optimization of large-scale hydropower system[J].Energy Conversion and Management,84(24): 363-373

Scan for more details

Received: 17 December 2023/Revised: 20 March 2024/Accepted: 2 April 2024/Published: 25 December 2024

Lu Zhang

luzhang11@outlook.com

Zhiyu Yan

zhiyu-yan@geidco.org

Fulong Song

songfulong@geidco.org

2096-5117/© 2024 Global Energy Interconnection Group Co.Ltd.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Zhiyu Yan received his PhD degree from Dalian University of Technology in Dalian,China.He is currently working at GEIDCO as a researcher.His research interests include multienergy coordination and renewable power generation modeling.

Lu Zhang received his Ph.D.from the Dalian University of Technology in Dalian,China.She is currently working with the China Three Gorges Corporation as a researcher.Her research interests include the optimization of the ecological operation of multi-reservoir systems.

Fulong Song received his MEng and BEng degrees from the Huazhong University of Science and Technology,Wuhan,China.He worked with GEIDCO as a division director.His research interests include power system planning,UHV transmission technology applications,and economic analyses of power systems.

(Editor Yu Zhang)