0 Introduction

Considering the critical need for reliability in power supply systems driven by rapid societal and economic advancements,the power sector is increasingly integrating renewable energy sources (RES) to address energy deficits and environmental concerns [1].However,this integration introduces greater complexity to the power system operations,enhancing the risk of outages and blackouts[2].Although infrequent,such blackouts have significant implications.For example,in 2018,a blackout in Brazil affected more than 2,000 cities,and about a quarter of the users in the country were affected,with a final loss of 21,735 MW [3].In June 2019,the failure of the Argentine power grid not only caused a nationwide power outage in Argentina but also affected the power grids of surrounding countries,such as Uruguay,Brazil,and Chile,resulting in a total loss of approximately 13,200 MW of load [4].During the 2019 blackout in the UK [5],traffic in important cities could not operate normally,and the ordinary lives of one million people were affected.In August 2020,a power outage occurred in the California power grid in the United States,affecting approximately 810,000 people were affected by the power outage [6].This study addresses these challenges by developing an advanced black start model for power systems.A black start is a critical process initiated during total blackouts,involving the selfstarting of generators with black-start capabilities and the sequential restart of other units.The proposed model aims to significantly improve the strategy and efficiency of this process.Recognizing the importance of the swift and effective restoration of post-outage power systems,the proposed model addresses the need for a more systematic and robust approach.

In power system restoration planning,it is imperative to establish a viable restoration strategy that encompasses generator restoration pathways for starting generators,energizing transmission lines,and restoring critical loads to stabilize power systems.Power plants equipped with black-start capabilities are crucial in supplying cranking power to non-black-start power plants,restoring vital loads,and reenergizing the necessary transmission lines.The power system restoration problem has been addressed by introducing an optimal scheduling method for black start (BS) units to assist non-BS units and ensure optimal transmission path selection for expedited restoration [7].Reference [8] presented an optimal search algorithm for determining the generator cranking plan.Reference [9]formulated a bi-level optimization problem to ascertain the optimal start-up sequence for generation units,employing a teaching-learning-based optimization algorithm at the upper level and a search path graph-based algorithm at the lower level.Reference [10] introduced a minimum-cost flow model-based energizing path optimization method,cast as a mixed-integer linear programming problem,to secure feasible restoration paths.In [11],an orthogonal genetic algorithm was implemented to optimize the restoration path;however,it focused solely on the generator cranking sequence.

Considering load restoration,Reference [12] introduced an advanced two-stage optimization approach for simultaneous network and load recovery.Reference [13]presented a dual-stage self-healing system restoration strategy to enhance power system resilience by considering key factors such as voltage balance,transmission loss,and generation cost.This strategy proposes schedules for load pick-up and transmission line charging in the initial phase,followed by continuous nonlinear optimization employing AC power flow and incorporating frequency constraints in the subsequent phase.Reference [14] proposed an adaptive restoration decision support system that determines optimal restoration actions in both the planning and realtime phases and can adapt to dynamically changing system conditions.Reference [15] addressed serial planning for a generator start-up sequence and introduced flexibility in reenergizing transmission lines by converting various constraints into mixed-integer linear constraints.In [16],Monte Carlo tree search (MCTS) and sparse autoencoder(SAE) methodologies were used to formulate a generator start-up algorithm,facilitating real-time decision-making.In[17],an information-theoretic co-clustering approach was proposed to address black-start decision-making challenges in the presence of incomplete information.Reference [18]introduced an optimal routing strategy based on the optimal AC power flow to restore elements affected by specific contingencies.A power system restoration plan considering load prioritization to maximize the restored load was presented in [19].Notably,most of these research endeavors concentrated primarily on traditional transmission system black-start planning without incorporating considerations for wind turbines (WT) and photovoltaic generators (PV).

With the development of renewable energy integration techniques,WT and PV can be considered flexible sources during the system restoration process.In [20],a decentralized multi-agent system approach was introduced to address the system restoration challenge by considering WT and PV.Reference [21] explored an optimization strategy for network reconfiguration to mitigate line overloads resulting from wind power uncertainty.The agent-based methodology proposed in[22] focuses on optimizing system reliability during restoration,with load balancing as a key constraint.In [23],a novel offline restoration-planning tool was developed to leverage wind energy to enhance grid resilience.A distributed strategy for the restoration of integrated transmission and distribution systems was presented in [24] without considering the potential support from energy storage systems in the restoration process.Power systems with numerous energy storage systems offer considerable potential for black-start services [25].Reference[26] introduced a microgrid-based load restoration model to bolster resilient urban power distribution systems,although it did not consider the generator restart procedure.

Although recent studies have begun to acknowledge the significance of energy storage systems (ESS) in power system restoration,there remains a substantial gap in research focusing on their role during black-start events.Existing literature has only partially explored the capabilities of ESS.In [27],a hierarchical planning model was developed to determine the optimal ESS configuration for black start operations.Reference [28] proposed a rolling optimization model integrating ESS with wind farms to enhance transmission network recovery and load restoration.However,these studies do not comprehensively explore ESS in the broader context of black-start scenarios.

This paper proposes a novel two-stage black-start model that incorporates energy storage systems and the integration of RES.In the first stage,the system restoration path model is crucial for forming a foundational network and determining the generator start-up sequence after a blackout.The Dijkstra algorithm was used to effectively identify the optimal restoration path for each generator,considering constraints such as generator start times.This approach streamlines the calculation of the power output at each time step,thereby ensuring high efficiency without the complexity of extensive computation.The second stage revolves around the load pick-up model,aiming to strategically maximize the load restored at every time step.This model is framed as a mixed-integer linear programming (MILP)problem that can be efficiently solved using commercially available optimization solvers.This facilitates a more effective restoration process and significantly enhances the computational efficiency of the model.

The remainder of this paper is organized as follows.Section II describes the proposed two-stage power system restoration model.Section III elaborates on the associated solution methodologies.Numerical case studies to validate the proposed model are presented in Section IV.Finally,Section V provides concluding remarks.

1 Power restoration model

The proposed model introduces a two-stage approach for power restoration,focusing on the sequence of generator start-up and load pick-up.This bifurcated methodology contrasts with integrated optimization strategies,providing enhanced flexibility and adaptability.The complexity of the optimization problem was reduced by segmenting the restoration process into two distinct stages,allowing for a more focused consideration of the unique objectives and constraints inherent to each stage.Consequently,this twostage framework facilitates greater adaptability to various scenarios,tailoring optimization efforts more effectively for each phase of the restoration process.

1.1 First stage: generator restoration

(1) Generator Output Characteristics

Depending on whether a unit has a black-start capability,generators are categorized into black-start generators (BS)and non-black-start generators (NBS).A BS has a selfenergized capability,whereas an NBS requires cranking power from an external power supply to restart.After the generators are started,their outputs are increasingly restricted to the maximum ramping rate until the maximum output is reached.The output characteristics of the BS and NBS generators are shown in Fig.1.The starting processes of the BS and NBS generators should satisfy the following constraints [29]:

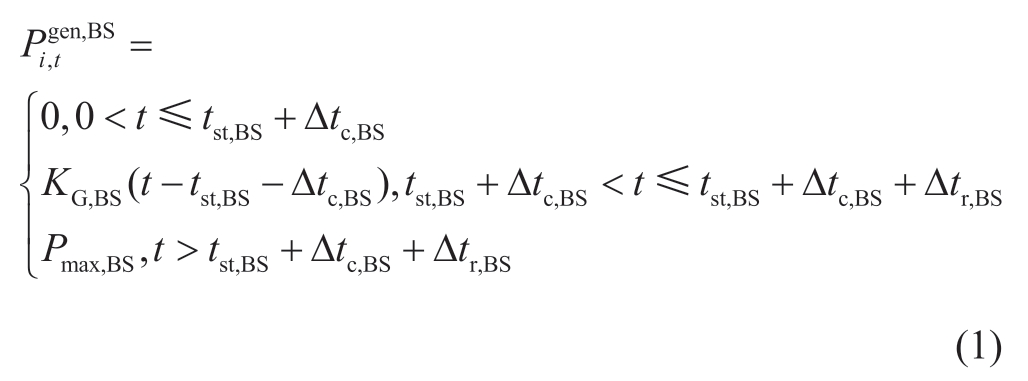
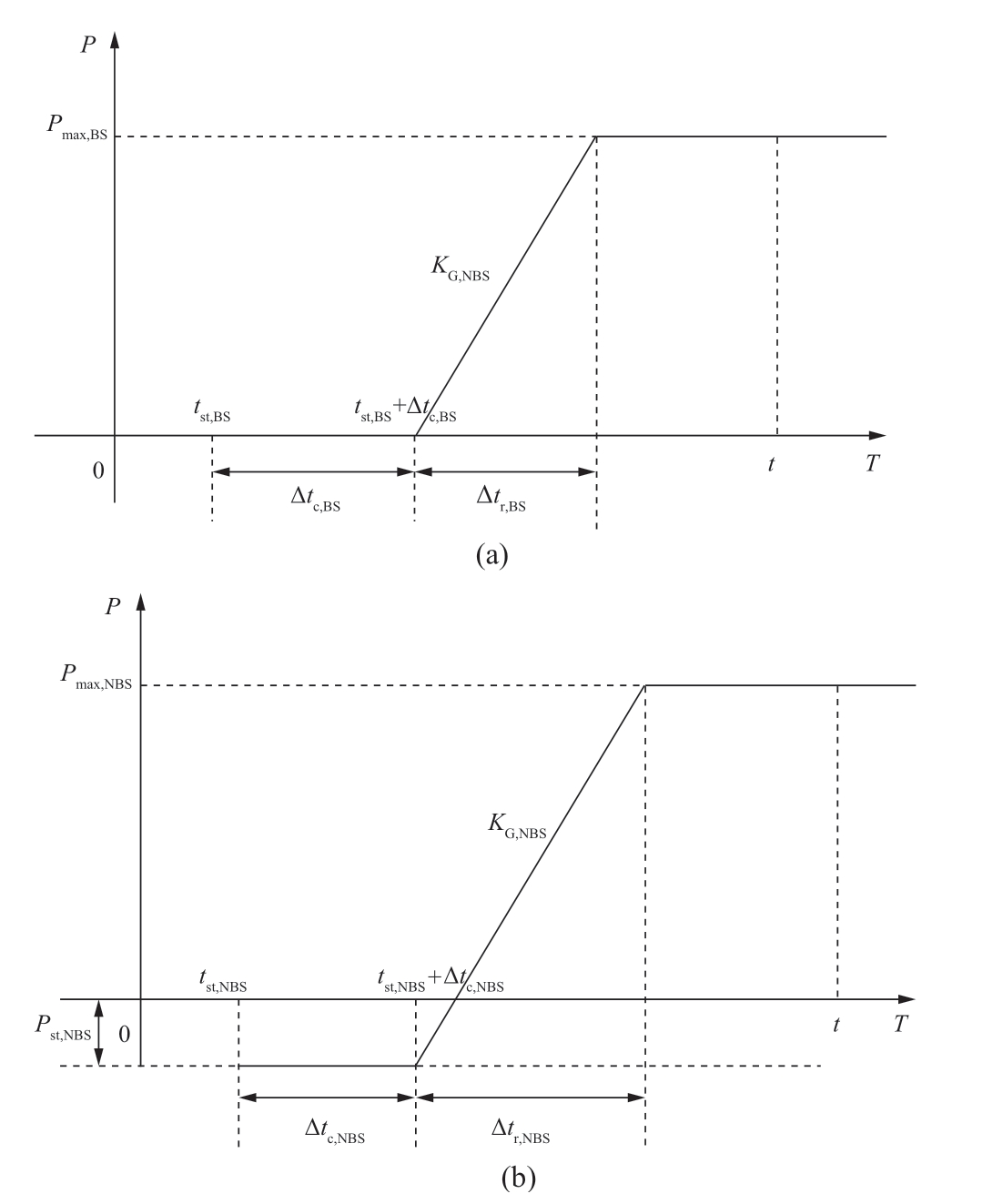
Fig.1 Start characteristic of (a) black-start generator and(b) non-black-start generator

Where tst,BS denotes the start time of the BS generator.The Δtc,BS is the self-start time before the BS generator is connected to the network.KG,BS is the ramp rate.Pmax,BS represents the maximum power of the BS generator.

NBS generators cannot self-start and depend on the start power Pst,NBS provided by other power sources.tst,NBS is the start time of the non-black-start generator when the generator is not cranked.Δtc,NBS is the self-start time.KG,BS is the ramp rate.Pmax,NBS represents the maximum power of the NBS generator.The difference between the BS and NBS generators is that the cranking power of the BS generator was 0.

(2) System Restoration Path Model

Determining the system restoration path model is essential for constructing a target configuration topology during the black start process.This model can achieve a generator restoration sequence and the corresponding restoration paths.The generator start-up permutation is set as the system restoration path model input h,whereas the output is the system restoration path V ={V1,V2,…,Vk,…,Vn},where Vk is a set that includes buses along the optimal restored path at the kth stage.The first bus on this path is one of the restored buses from the previous stages,and the last bus is the target generator in the present restoration stage.For example,V3={25,23,14,18}represents the optimal path at Stage 3,where bus 25 is the already restored bus to start,and bus 18 is the target NBS generator.

At each stage,Tstagek is defined as the time when the k-th stage is already restored.tst,i represents the start-up time of bus i.T is the total restoration time.The restoration time for each line is set at 2 min.The Tsi and T are determined after Tstagei is obtained.The Dijkstra algorithm is introduced to search for the system restoration path.It should follow the rules: a) The start bus in the first stage is a BS generator bus.b) Within each stage,the optimization objective of the algorithm is to identify the most efficient path connecting the start bus and the end bus.c) Only one NBS generator is considered the target bus in each stage.The constraints in each stage consist of the generator start time and state constraints,which are checked accordingly.

1) Generators start time constraint

The start time of the generator must fall within the prescribed range bounded by the minimum and maximum start times.

where,tmin,i and tmax,i are the minimum and maximum start time for generator i,respectively.

2) The generator state constraint

Upon activation,the generator remains operational throughout the restoration procedure.

where ui,t is a binary variable that signifies the operational state of the generator i.The variable takes a value of 1 if the generator begins and 0 otherwise.

After the restoration time of each bus in the system is obtained,the generator output at each time step can be calculated based on the generator output characteristics.Moreover,the line and bus states should be checked as follows.

3) Restoration line constraint

Following the restoration of the BS generators,the associated transmission lines can be reenergized.

where xl,t serves as a binary variable representing the status of line l,taking the value of 1 when line l begins and 0 otherwise.Ωline,BS denotes the set of lines connected directly to the BS generators.

Moreover,it is assumed that once the lines are reinstated,they will remain operational and will not experience any subsequent trips throughout the restoration phase,leading to the establishment of the associated constraint.

4) Restoration of non-black-start generator constraint

The restoration of NBS generators is contingent on the reestablishment of lines that are directly connected to them in prior time steps,which can be concisely expressed in the following mathematical formulation:

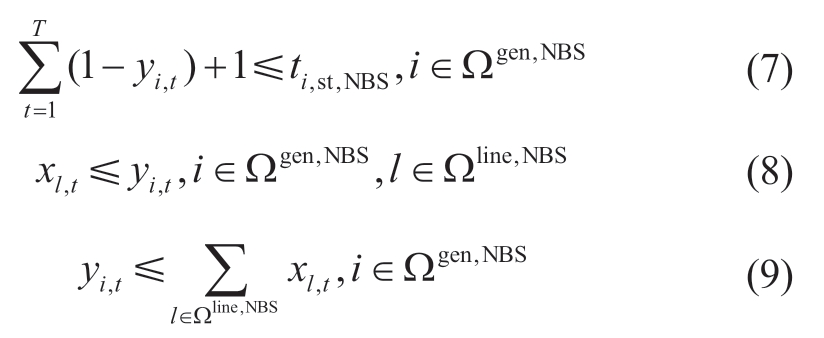
where yi,t is a binary variable that represents the state of the NBS generator,such that yi,t=1 if the non-black-start generator i begin to start,and yi,t=0 otherwise.Ωline,NBS denotes the set of lines connected to NBS generators.

The restoration of a given transmission line is contingent on the prior restoration of an adjacent line or its connection to a bus with inherent restoration capabilities,such as a bus linked to a black-start generator,RES,or ESSs.This stipulation is encapsulated in the following constraint formulation.

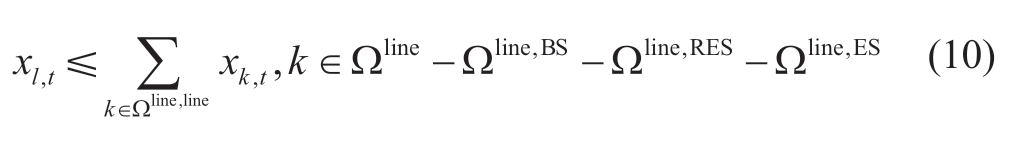
where Ωline denotes the set of total lines.Ωline,line is a set of lines directly interconnected to line l.

5) Restoration of bus constraint

where bi,t is a binary variable representing the status of bus i at time t.bi,t equals l if bus t is restored at time t and 0 otherwise.

1.2 Second stage: load pick-up model

(1) Objective function

Owing to the uncertain nature of wind speed and solar irradiance,RES outputs and load demands generally have stochastic and intermittent characteristics.These impact factors should be considered in the restoration process to support the stable and safe operation of the system.After establishing the skeleton network through the system restoration path model,the subsequent goal is load restoration,which the load-pickup model addresses.The primary objective of this model is to maximize the cumulative weighted restored load demand,which is defined as follows:

where Ωbus is the set of buses.

(2) Constraints

1) Load restoration constraint

If the bus i is restored,the load connected to the bus can be partially or fully restored according to the following formulation:

2) Energy storage system constraint

The ES system can improve the power restoration process,and its charge and discharge can be modeled as follows:

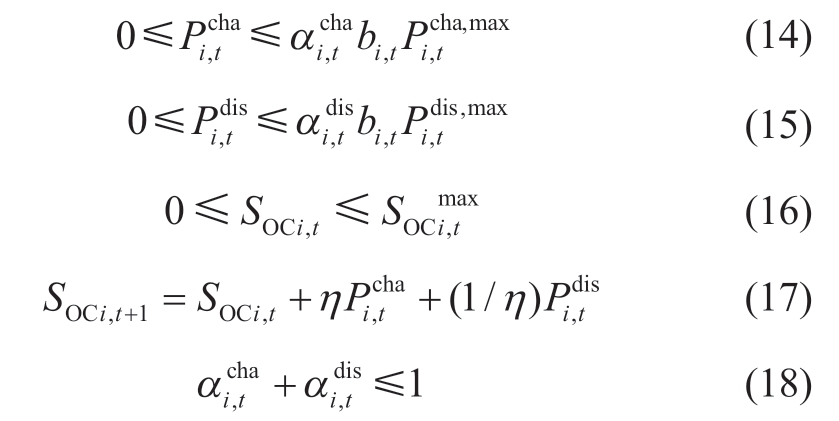
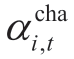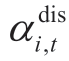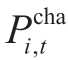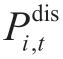where  and are binary variables indicating the charge and discharge states of the ES system.SOCi,t is the state-of-charge (SOC) of an ES system. and  are the charge and discharge power at bus i at time t,respectively,where η is the charge-discharge coefficient.

3) The power balance constraint

It is imperative to ensure adherence to the power balance constraints,as expressed in the following mathematical representation [30].

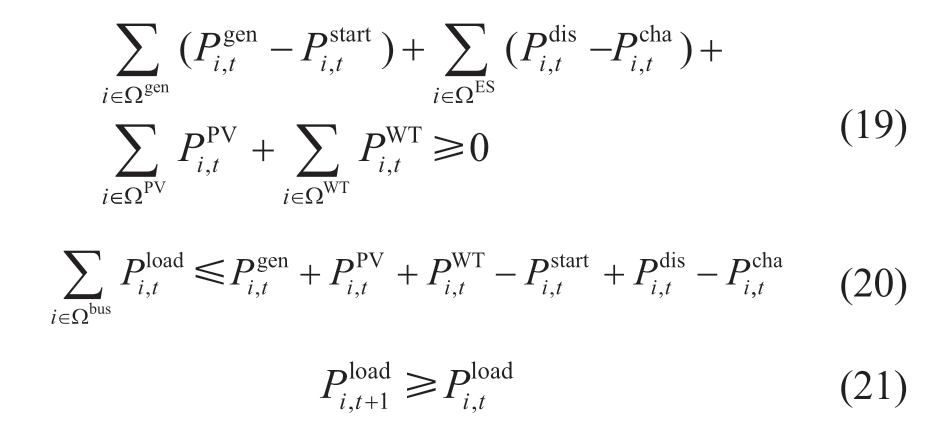
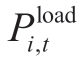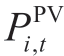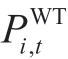where  is the pick-up load at node i at time-step t.Pl,t symbolizes the power flowing through line l.ΩES,ΩPV,and ΩWT were set to ES,PV,and WT,respectively.whereand  are the power outputs of the PV and WT,respectively.Eq.(19) ensures that the total generated power output is non-negative.Eq.(20) ensures that the power from the generators satisfies the restored load demand.Eq.(21) guarantees no load shedding for the restored loads.It should be noted that in constraints (19) and (20),the variable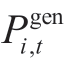is defined by the generator start time in conjunction with equations (1) and (2).This approach ensures that the capacity and ramping speed of each unit are comprehensively integrated and accounted for during restoration.

2 Solution

The black start procedure encompasses both system restoration and load pick-up models.The system restoration model was efficiently solved using the Dijkstra algorithm,as referenced in [31].The Dijkstra algorithm,an integral for identifying the minimal path between nodes in a graph,is initiated from the starting node and employs a greedy algorithm approach.It systematically explores the unvisited nodes adjacent to the node nearest the starting node,progressively extending its reach until it successfully connects to the terminal node.The Dijkstra algorithm plays a pivotal role in our model by effectively determining the optimal sequence for generator start-ups,thereby minimizing the restoration time,which is a critical factor in power system restoration scenarios.Notably,its computational efficiency is advantageous for large-scale power-system applications.Furthermore,the capability of the algorithm for the rapid recalculation of paths makes it well-suited for dynamic environments,supporting real-time decision-making essential in fluctuating operational conditions.This can be achieved through the following steps.

Step I.Initial node set S,which only contains the start node s;node set U,which contains all nodes except S;and distance set D,which contains the distance between the start node and all nodes.Calculate the distance between the start node and all the nodes in U.

Step II.Choose the smallest distance to the next node v.Add node v to set S and delete v from set U.Update set D.

Step III.Steps I and II are repeated until all nodes are traversed.The distance D represents the shortest path from each node to the initial node.

After implementing the Dijkstra algorithm,a generator cranking plan can be obtained by searching for the shortest restoration transmission lines.For example,the generator in bus 30 was set as the BS generator,and the others were NBS generators.If the generator start-up permutation is set to h={30,39,37,16,36,32,34,33,35},10 stages are set.At each stage,one generator was assumed to start.In the first stage,the generator on Bus 30 starts.At the second stage,the Dijkstra algorithm determines the restoration path from bus 30 to bus 39.Thus,Tstage1=0 and Tstage2 are the summations of all the transmission line restoration times in V30-39.In the third stage,the generator on bus 37 was expected to start.The same calculation process is followed,leading to path V2-37={2,25,37}.Tstage3 is equal to Tstage2 plus the sum of all transmission line restoration times in path V2-37.Finally,the Tsi was calculated for each bus at each time step.By combining the generator output character functions,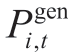for each generator at each time step can be obtained.Dijkstra’s algorithm defines the transmission line distance as the restoration time.These parameters were then used in the load-pick-up optimization model.Note that equations(3)-(11) complement Dijkstra’s algorithm by detailing the operational backdrop against which the algorithm output must be implemented.They ensure that the restoration paths identified by the Dijkstra algorithm are efficient in sequence and timing and feasible within the power system’s physical and operational realities.

The load pick-up model is formulated as a mixed-integer linear programming problem that is amenable to solutions using readily available optimization solvers.Thus,a global optimizer can be obtained directly.The energy storage system was applied only to the load pick-up model in this restoration model.

The proposed two-stage restoration approach is depicted in Fig.2,with specific details elaborated below.

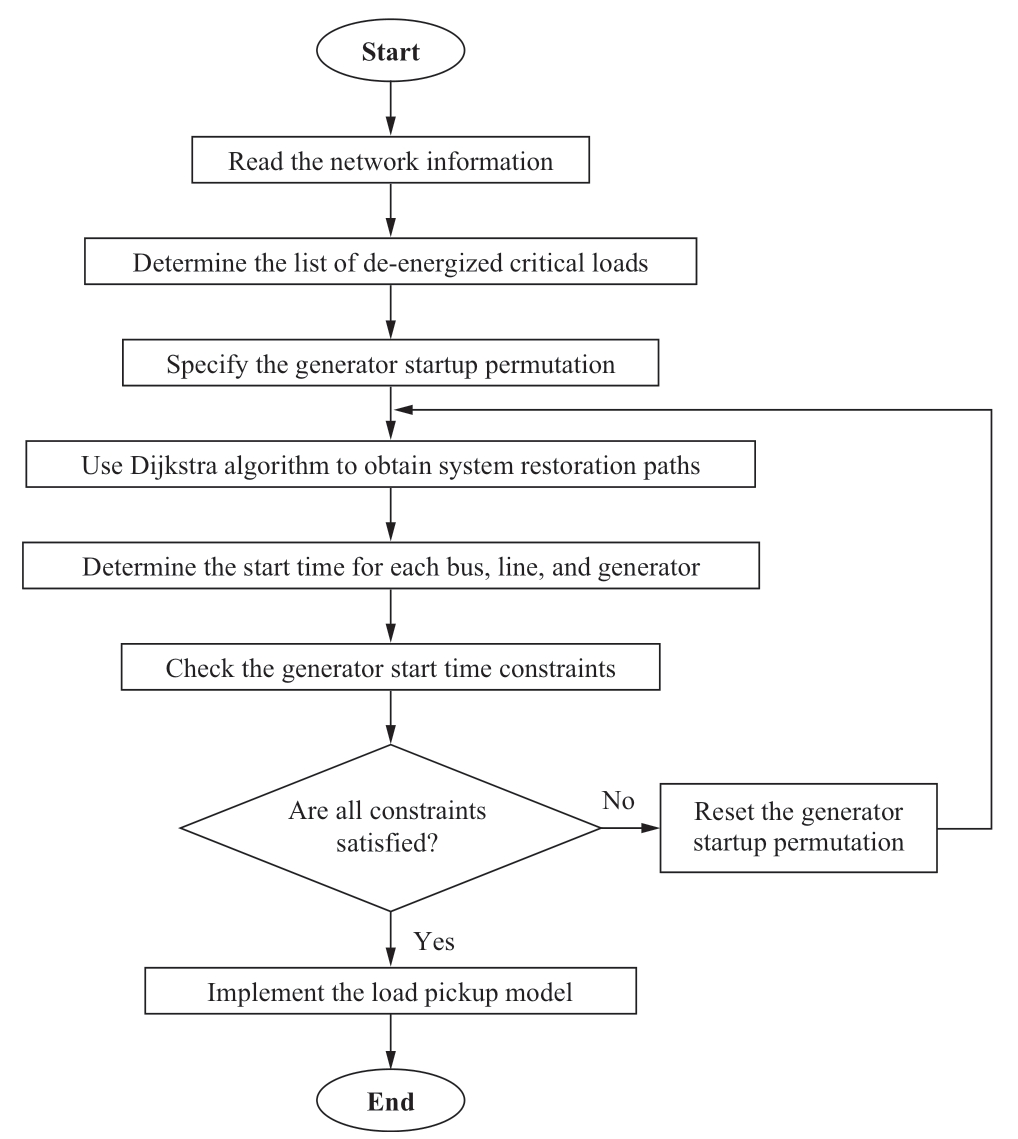
Fig.2 Two-stage power system restoration model

Step 1: Read the power system information,including the BS generator,NBS generator,and topology of the power system.

Step 2: Determine the list of deenergized critical loads for the specified number,capacity,and importance of the deenergized loads.

Step 3: Specify the generator start-up permutation.Because NBS generators closer to the BS generator are easier to restart,the distance between the BS and NBS generators is the most critical factor in determining the generator start-up permutation.

Step 4: Take the generator start-up permutation system restoration path model as input and use the Dijkstra algorithm to obtain the system restoration paths.

Step 5: Based on the obtained system restoration paths,the start times of the buses,transmission lines,and generators were calculated.

Step 6: The generator start-time constraints are checked.If not satisfied,reset the generator start-up permutation and proceed to Step 4;otherwise,proceed to the following steps:In this step,if the start time of an NBS generator is less than the calculated start time in Step 5,the generator queues slightly ahead.

Step 7: Implement the load pick-up model to obtain the restoration plan for critical loads.

In the load pick-up model,leveraging the MILP method ensures that the most critical loads are prioritized,enhancing the effectiveness of the restoration process in terms of meeting vital demands first.In addition,the MILP model is scalable and can be adapted to different power system sizes and configurations.This adaptability is essential for creating a model that is not only applicable to a wide range of realworld scenarios but also future-proof against evolving grid structures.

3 Case study

3.1 Parameter setting

For performance evaluation of the proposed model,this study utilizes a modified version of the IEEE 39-bus transmission system [32],incorporating a WT generator,a PV,and a BSS situated at buses 4,16,and 13,respectively.The schematic diagram of the modified IEEE 39-bus system is depicted in Fig.3.There are 10 traditional generators,including one BS generator at bus 30 and 9 NBS generators.The WT and PV generators are set as NBS generators.The power outputs of PV and WT are characterized in Fig.4.The choice to use 24-hour data profiles for WT and PV output modeling is rooted in the aim to capture a realistic yet manageable representation of daily generation patterns,which are constructed based on historical data,and include typical variability patterns observed in renewable energy generation.The typical outputs of PV and WT can be set according to the variability of daily renewable energy output.In this configuration,the PV and WT generators are assigned a fixed rated power of 600 MW each,and their outputs are considered non-dispatchable.Before initiating the restoration process,the system is presumed to be in a state of complete outage,meaning all lines and buses are disconnected and non-operational.The parameter η is set at 95%.The time step is set at 2 min.All computational algorithms relevant to this study are implemented using the Python programming language and executed on a PC outfitted with an Intel Core i5-7600 processor (3.5 GHz)and 16 GB of RAM.

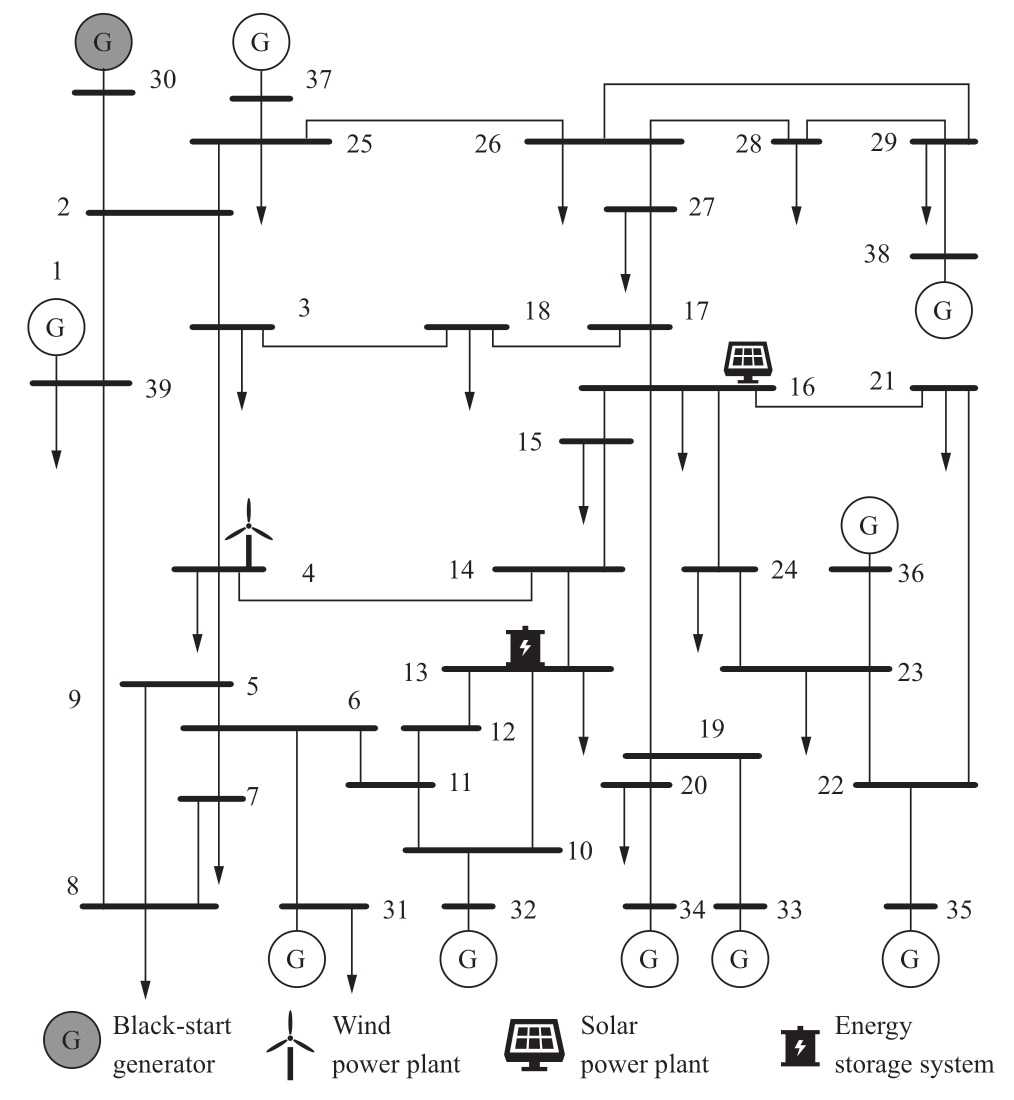
Fig.3 Schematic diagram of the modified IEEE 39-bus system

Fig.4 PV and WT active power output

3.2 Performance of the system restoration path model

The results of the restoration path listed in Table 1 allow us to investigate the performance of the system restoration path model.The start-up times for each node are listed in Table 2.The restoration paths for each generator are shown in Fig.5.From Tables 1 and 2,it can be observed that using the Dijkstra algorithm,the shortest restoration path for each generator can be obtained.This is also observed in Fig.5.The plan to crank the NBS generators was obtained through the selected paths of the transmission lines.Compared to the generator start-up sequences derived from the optimization program detailed in [33] and [15],the proposed restoration path and generator start-up sequence demonstrated a comparable recovery rate,even in scenarios incorporating PV and WT systems.Furthermore,the proposed Dijkstra algorithm offers a streamlined approach by eliminating the need to construct complex optimization models across various scenarios,thereby alleviating the computational load.Therefore,the proposed Dijkstra algorithm can effectively restore the sequence of the generators.

Table 1 Restoration path results of the revised IEEE 39-bus system

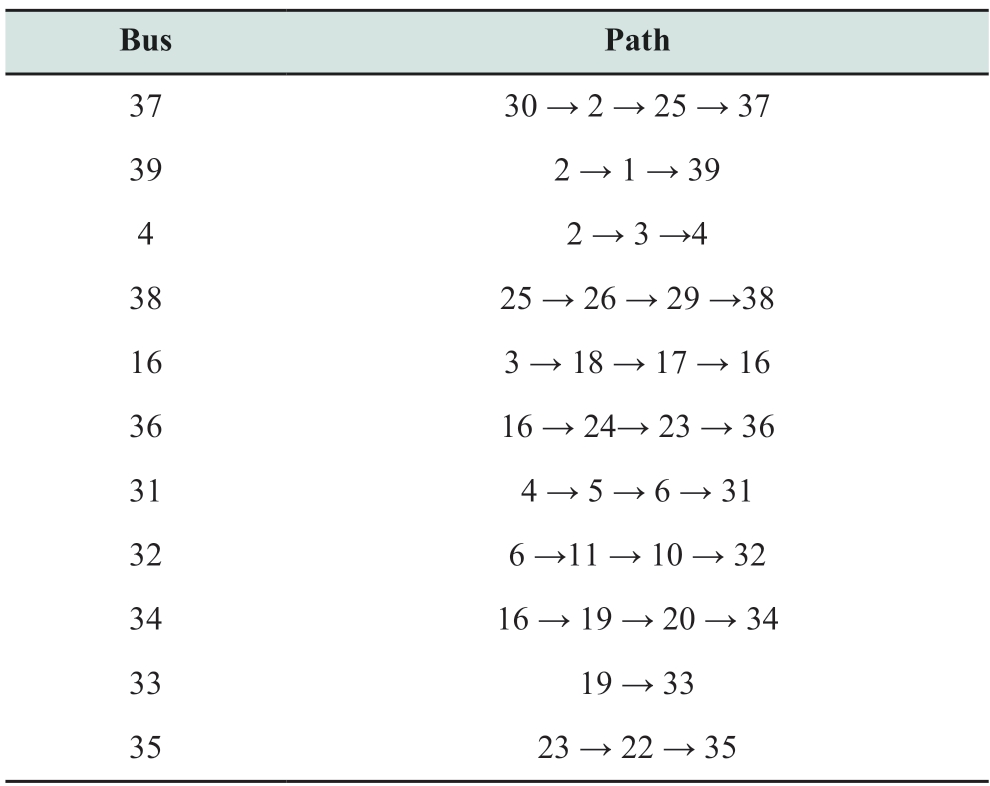
Table 2 Start-up times of each bus in the revised IEEE 39-bus system

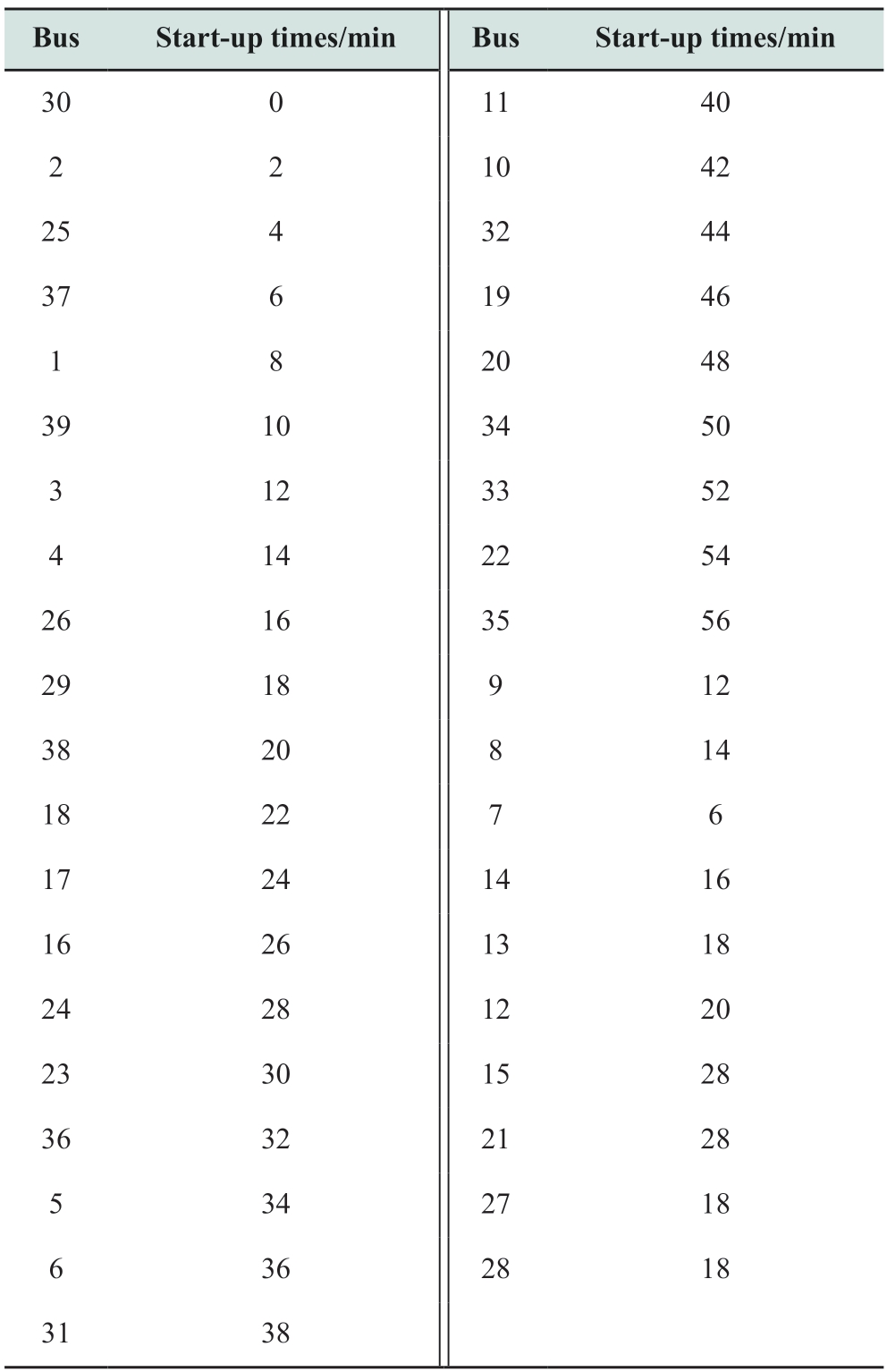
Fig.5 Restoration skeleton after a complete outage

Three distinct scenarios—Case I,II,and III—were established to assess the efficacy of the proposed loadpick-up model,corresponding to initiation times of 2:00,9:00,and 18:00,respectively.This approach is designed to scrutinize the performance of the model during various parts of the day—midnight,morning,and dusk—to account for the fluctuating power outputs from photovoltaic (PV)and wind turbine (WT) generators,as well as variations in the load demand characteristics during these periods.The energy storage system was initialized with the stateof-charge (SOC) set at 50%,and the charge/discharge efficiency coefficient,denoted by,was fixed at 0.95.The load demand coefficient multiplying IEEE 39 bus system standard load was defined for different load demand levels in different cases.The demand coefficients for Cases I,II,and III were set to 0.8,1,and 1.3 for Cases I,II,and III.The system restoration path model can be implemented for different cases because the generator restoration sequence is preset.

3.3 Performance of the load pick-up model

The SOC and charge/discharge power for the different cases are shown in Fig.6.This shows that the SOC curves are significantly different for different cases.This is because the PV power,WT power,and load demand profiles were significantly different in these cases.At midnight,there is no solar power but only WT power;thus,the SOC exhibits a decreasing trend during the restoration process.In the morning,the PV power increased over time such that the SOC was reduced at the beginning and increased at the final period of load recovery.There is a heavy load with less PV power at dusk than in the morning.Thus,the ES system stopped charging during the final period of the restoration process.Therefore,the ES can serve as a flexible resource to support the load restoration process with the participation of the PV and WT systems.

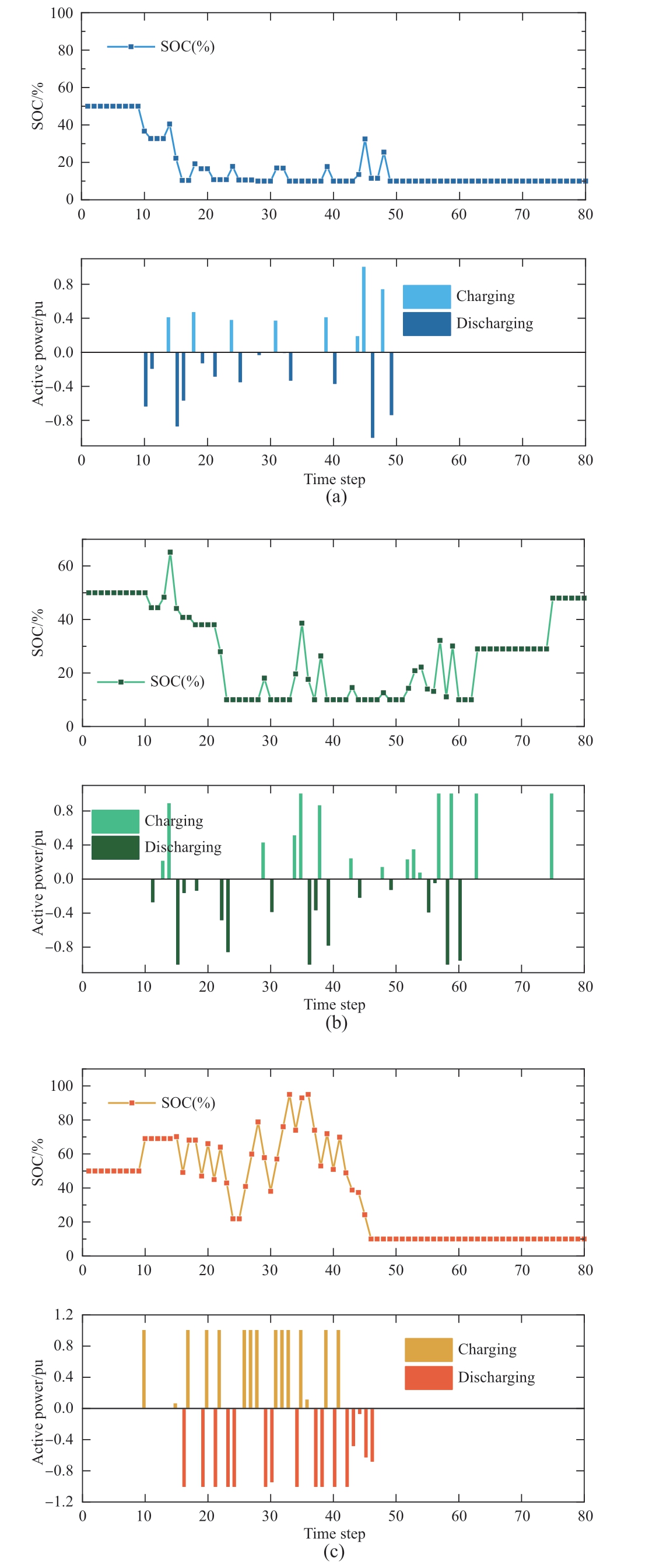
Fig.6 State-of-charge and charging/discharging power for (a) Case I,(b) Case II,and (c) Case III

The load-restoration speed intuitively can be represented by the overall load-restoration curves for the cases shown in Fig.7.Although Case III has limited PV power and heavy load demand,the restoration speed is the fastest.In bagasse,the WT power is redundant during the restoration process.This indicates that renewable power support can accelerate the load restoration process in terms of the economy and efficiency.The restoration in Case I was slower than that in Case II,which was due to the lack of PV power and limited WT power outputs at midnight,even with a light load demand.

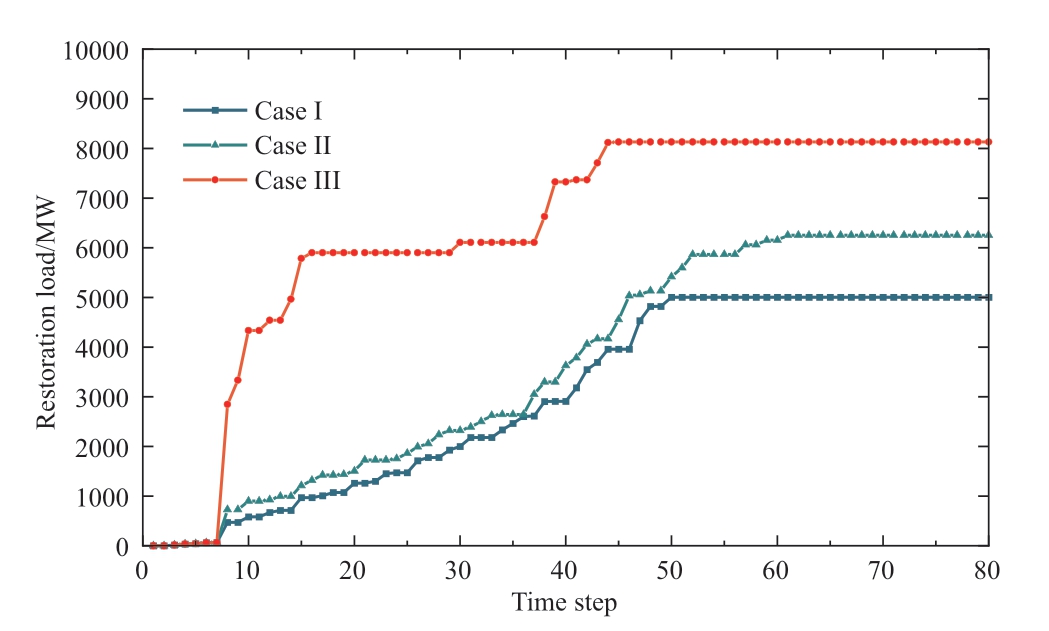
Fig.7 Overall load restoration curves in different cases

The load restoration process at each bus are illustrated more accurately in the restoration load curves for different cases depicted in Fig.8.This reveals that Case III achieved the quickest full-load restoration,whereas Case II experienced the most prolonged restoration period.This discrepancy in restoration speed is attributed to the constrained availability of PV and WT power resources in Case II.

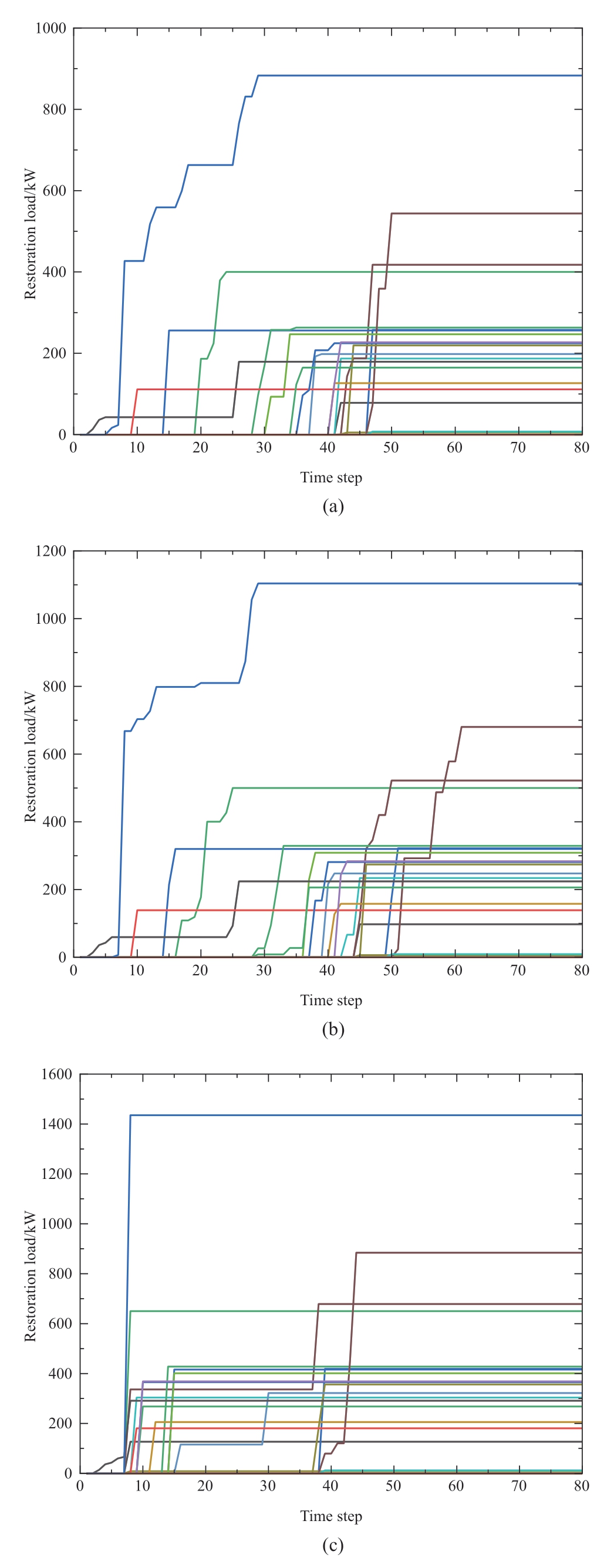
Fig.8 Restoration load curves in each bus for (a) Case I,(b) Case II,and (c) Case III,respectively

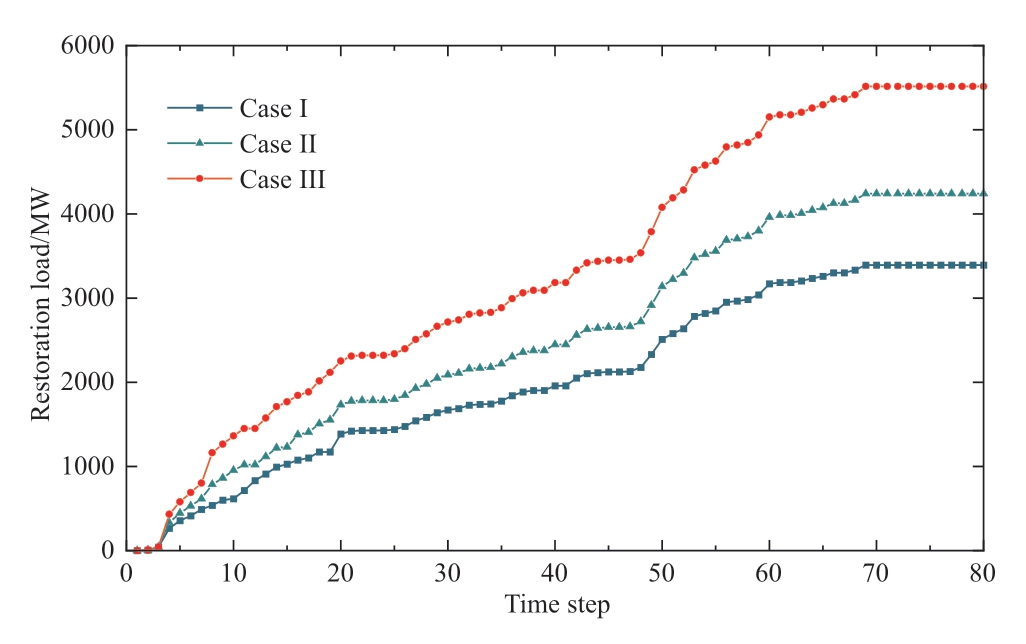
Fig.9 Overall load restoration curves in different cases in the IEEE 118-bus system

3.4 Application on large-scale system

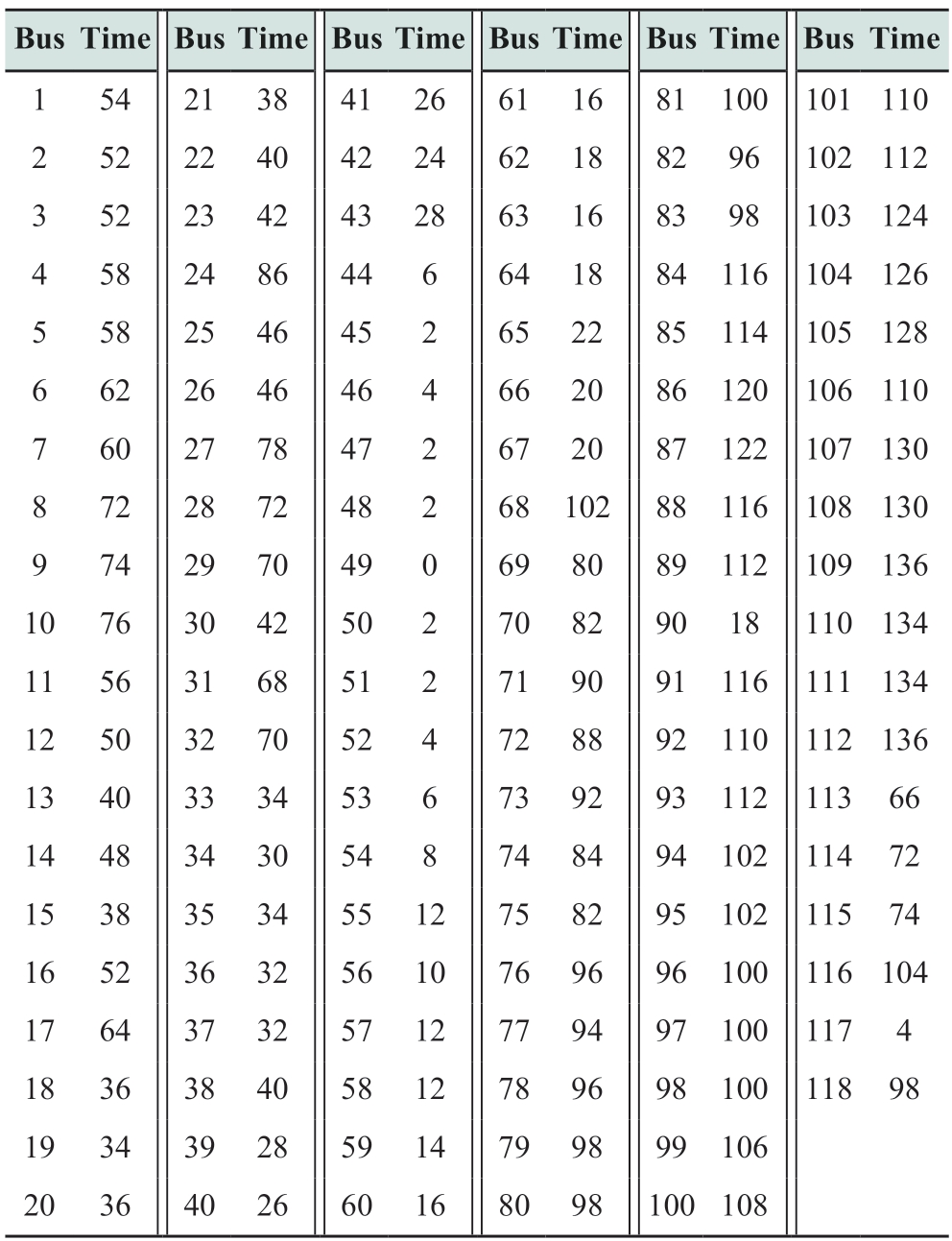
The efficacy of the proposed model in a large-scale power system was evaluated using an IEEE 118-bus transmission system [34].In this setup,the PV and WT generators were positioned at buses 96 and 44,respectively,whereas the energy storage system was located at bus 38.The restoration pathways for each generator are comprehensively detailed in Table 3,accounting for the 53 paths necessary for the complete restoration of all generators.The start-up times for each node are compiled in Table 4,illustrating the effectiveness of the model in managing large-scale system restorations.

Table 3 Restoration path results of the revised IEEE 118-bus system

Table 4 Start-up times of each bus in the revised IEEE 118-bus system

To verify the performance of the proposed load pick-up model,three cases,I,II,and III,with initiation times of 2:00,9:00,and 18:00,respectively,were also set for large-scale system studies.The energy storage system was initialized with the state-of-charge (SOC) set at 50%,and the charge/discharge efficiency coefficient,denoted by,was fixed at 0.95.The load demand coefficient multiplying IEEE 118 bus system standard load was defined for different load demand levels in different cases.The demand coefficients for Cases I,II,and III were set to 0.8,1,and 1.3 for Cases I,II,and III.

Figure 9 illustrates the load restoration velocities across the different scenarios,revealing that the restoration speeds were relatively similar in all three cases.In contrast to the placement of the WT generator in the IEEE 33-bus system,in the IEEE 118-bus system,the WT generator is positioned nearer the BS generator,enabling its restoration as early as the sixth time step,as indicated in Table 4.This proximity allows for more rapid system restoration,even during midnight black-start scenarios,with the aid of a WT generator.Consequently,renewable-energy generators are instrumental in expediting the restoration process for specific periods.

To provide a clearer understanding of the loadrestoration process for each bus,Fig.10 graphically displays the restoration load curves for each bus with loads across different scenarios.This illustration confirms that all the loads were restored within 80 time steps,thereby underscoring the effectiveness of the proposed load-pickup model in the context of large-scale system applications.

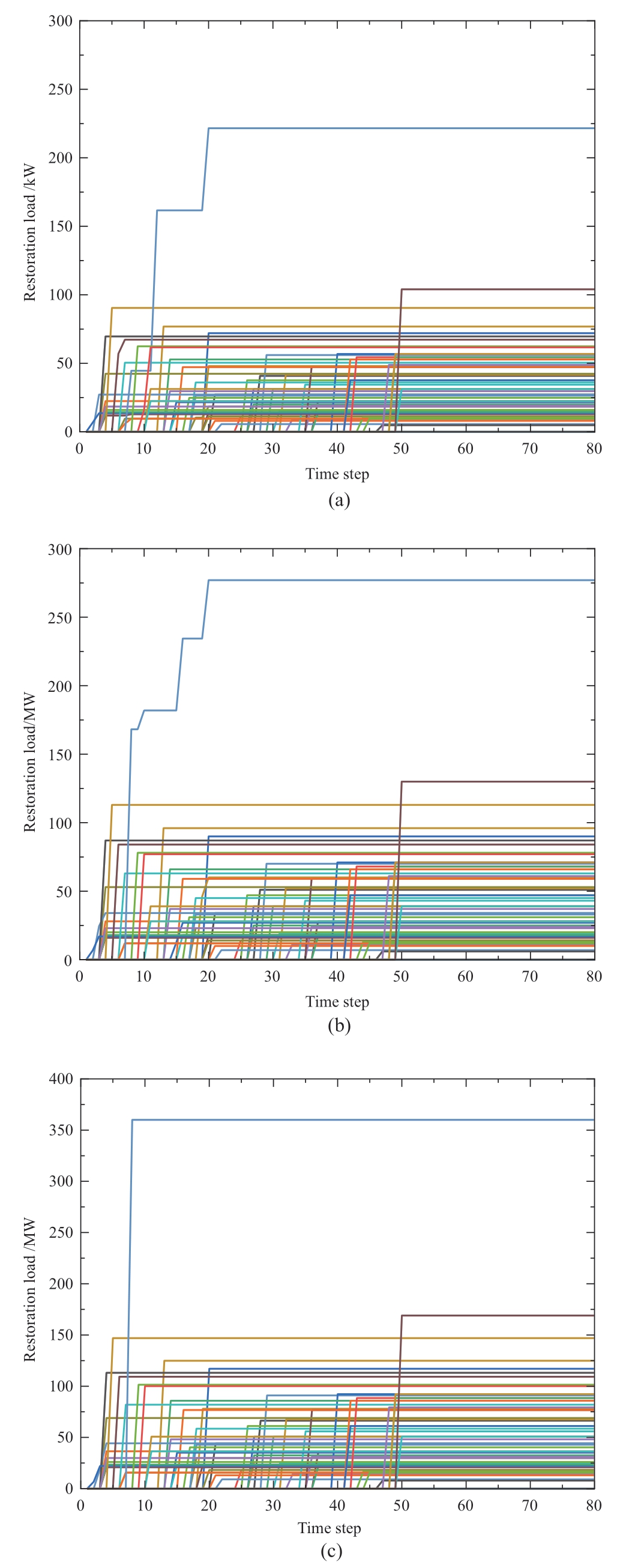
Fig.10 Restoration load curves in each bus in the IEEE 118-bus system for (a) Case I,(b) Case II,and (c) Case III,respectively

4 Conclusion

This study proposes a two-stage power system restoration model that considers energy storage,WT,and PV systems.In the first stage,the system restoration path model can effectively provide the sequences of the generator,bus,and lines while satisfying the constraints of the generator start time.In the second stage,as an MILP optimization program,the load pick-up model efficiently optimizes the load restoration sequence to obtain the maximum weighted load restoration for different complete outage times.In this MILP model,the energy storage system achieves charge and discharge flexibility to support PV and WT power accommodation and different restoration times under various renewable power and load demands.

Acknowledgement

This study was funded by the Science and Technology Project of the State Grid,Shanxi Electric Power Research Institute.(Project name: Research on equivalent inertia and frequency response characteristics of induction motors and applications of black-start scheme in power grids,project number: 52053022000 J).

Declaration of competing interest

The authors declare that they have no competing financial interests or personal relationships that may have influenced the work reported in this study.

References

[1] Zhang J,Gao X D,Wang T C et al.(2023) Evaluate the hosting capacity of PV in distribution network: considering PV curtailment constraints.Electric Power Engineering Technology,42(6): 14-21

[2] Yao J Z,Fu Q,Du W J,et al.(2023) Static voltage stability of photovoltaic grid-connected system based on eigenvalue index.Electric Power Engineering Technology,42(6): 32-41,140

[3] Zhou B W,Chen Q Y,Yang D S (2018) On the power system large-scale blackout in Brazil.Power Generation Technology,39(2): 97-105

[4] Yuan P,Zhang Q,Zhang T,et al.(2019) Analysis and enlightenment of the blackouts in Argentina and New York.2019 Chinese Automation Congress (CAC).Hangzhou,China.IEEE,:5879-5884

[5] Zhao Q,Qi X M,Hua M,et al.(2020) Review of the recent blackouts and the enlightenment.CIRED -Open Access Proceedings Journal,2020(1): 312-314

[6] Wang Y,Wu J C,Yi H Q (2021) Analysis on several blackouts caused by extreme weather and its enlightenment.IOP Conference Series: Earth and Environmental Science,766(1): 012020

[7] El-Zonkoly A M (2015) Renewable energy sources for complete optimal power system black-start restoration.IET Generation,Transmission &Distribution,9(6): 531-539

[8] Jiang Y Z,Chen S J,Liu C C,et al.(2017) Blackstart capability planning for power system restoration.International Journal of Electrical Power &Energy Systems,86: 127-137

[9] Ketabi A,Karimizadeh A,Shahidehpour M (2019) Optimal generation units start-up sequence during restoration of power system considering network reliability using bi-level optimization.International Journal of Electrical Power &Energy Systems,104: 772-783

[10] Li S Y,Gu X P,Zhou G Q,et al.(2019) Optimisation and comprehensive evaluation of alternative energising paths for power system restoration.IET Generation,Transmission &Distribution,13(10): 1923-1932

[11] Xie Y Y,Song K L,Wu Q W,et al.(2018) Orthogonal genetic algorithm based power system restoration path optimization.International Transactions on Electrical Energy Systems,28(12):e2630

[12] Liao S W,Yao W,Han X N,et al.(2019) An improved two-stage optimization for network and load recovery during power system restoration.Applied Energy,249: 265-275

[13] Pang K Y,Wang C Y,Wen F S,et al.(2020) Two-stage selfhealing restoration strategy considering operating performance.Journal of Energy Engineering,146(4): 04020036

[14] Golshani A,Sun W,Zhou Q,et al.(2017) Two-stage adaptive restoration decision support system for a self-healing power grid.IEEE Transactions on Industrial Informatics,13(6): 2802-2812

[15] Xie Y Y,Li D Z,Xu Y,et al.(2021) A MILP-based restoration planning method for generator start-up considering flexible reenergizing times of transmission lines.International Journal of Electrical Power &Energy Systems,124: 106357

[16] Sun R J,Liu Y T,Wang L (2019) An online generator start-up algorithm for transmission system self-healing based on MCTS and sparse autoencoder.IEEE Transactions on Power Systems,34(3): 2061-2070

[17] Leng Y J,Yue X,Lu Y Q,et al.(2021) Using informationtheoretic co-clustering for power system black-start decision making with incomplete information.Electric Power Components and Systems,49(6-7): 573-583

[18] Quinteros F,Carrión D,Jaramillo M (2022) Optimal power systems restoration based on energy quality and stability criteria[J].Energies,15(6): 2062

[19] Hou J,Xu Z,Dong Z Y,et al.(2013) Permutation-based power system restoration in smart grid considering load prioritization.Electric Power Components and Systems, 42(3-4): 361-371

[20] Pirzadi M,Ghadimi A A,Daeichian A (2021) Distributed multi-agent transmission system restoration using dynamic programming in an uncertain environment.Electric Power Systems Research,196: 107270

[21] Li S Y,Wang L Y,Gu X P,et al.(2022) Optimization of loopnetwork reconfiguration strategies to eliminate transmission line overloads in power system restoration process with wind power integration.International Journal of Electrical Power &Energy Systems.134: 107351

[22] Ren Y,Fan D M,Feng Q,et al.(2019) Agent-based restoration approach for reliability with load balancing on smart grids.Applied Energy,249: 46-57

[23] Golshani A,Sun W,Zhou Q,et al.(2019) Incorporating wind energy in power system restoration planning.IEEE Transactions on Smart Grid,10(1): 16-28

[24] Roofegari nejad R,Sun W,Golshani A (2019) Distributed restoration for integrated transmission and distribution systems with DERs.IEEE Transactions on Power Systems,34(6): 4964-4973

[25] Zhao Y Q,Zhang T T,Sun L,et al.(2022) Energy storage for black start services: A review.International Journal of Minerals,Metallurgy and Materials,29(4): 691-704

[26] Lin C F,Chen C,Liu F,et al.(2022) Dynamic MGs-based load restoration for resilient urban power distribution systems considering intermittent RESs and droop control,International Journal of Electrical Power &Energy Systems, 140: 107975

[27] Li C P,Zhang S N,Zhang J X,et al.(2018) Method for the energy storage configuration of wind power plants with energy storage systems used for black-start.Energies,11(12): 3394

[28] Sun L,Liu W J,Chung C Y,et al.(2022) Rolling optimization of transmission network recovery and load restoration considering hybrid wind-storage system and cold load pickup.International Journal of Electrical Power &Energy Systems,141: 108168

[29] Liang B M,Xu Y,Wen F S,et al.(2019) Fast path-oriented strategy for power system restoration.2019 Electric Power Quality and Supply Reliability Conference (PQ) &2019 Symposium on Electrical Engineering and Mechatronics (SEEM).Kärdla,Estonia.IEEE,: 1-8

[30] Gu X P,Zhou G Q,Li S Y,et al.(2019) Global optimisation model and algorithm for unit restarting sequence considering black-start zone partitioning.IET Generation,Transmission &Distribution,13(13): 2652-2663

[31] Salem I E,Mijwil M M,Abdulqader A W,et al.(2022) Flightschedule using Dijkstra’s algorithm with comparison of routes findings.International Journal of Electrical and Computer Engineering (IJECE),12(2): 1675

[32] Tricarico G,Azuara-Grande L S,Wagle R,et al.(2022) Security Constrained Unit Commitment and Economic Dispatch applied to the Modified IEEE 39-bus system Case.IECON 2022 -48th Annual Conference of the IEEE Industrial Electronics Society.Brussels,Belgium.IEEE,: 1-5

[33] Sun L,Lin Z Z,Xu Y,et al.(2019) Optimal skeleton-network restoration considering generator start-up sequence and load pickup.IEEE Transactions on Smart Grid,10(3): 3174-3185

[34] Peña I,Martinez-Anido C B,Hodge B M (2018) An extended IEEE 118-bus test system with high renewable penetration.IEEE Transactions on Power Systems,33(1): 281-289

Scan for more details

Received: 4 November 2023/Revised: 28 December 2023/Accepted: 10 March 2024/Published: 25 December 2024

Hong Yang

yanghongdky@sx.sgcc.com.cn

Wei Wang

604186127@ qq.com

Zhen Tang

tangzhen@sx.sgcc.com.cn

Zhihang Xue

xzh21@stu.xjtu.edu.cn

2096-5117/© 2024 Global Energy Interconnection Group Co.Ltd.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Hong Yang received her M.S.degree in engineering from Northeastern University.Currently she is a senior engineer in the State Grid Shanxi Electric Power Research Institute.Her research interest is power transmission technology.

Zhen Tang is now a professor level senior engineer in the State Grid Shanxi Electric Power Research Institute.He is mainly engaged in power system analysis and risk prevention and control.

Wei Wang is a master’s candidate.Currently he is engaged in distribution automation,distribution network inspection technology research in the State Grid Shanxi Electric Power Research Institute.

Zhihang Xue received his B.S.degree in electrical engineering from Jiangnan University,China,in 2023.Currently he is pursuing his master degree in electrical engineering at the School of Electrical Engineering,Xi’an Jiaotong University.His research interest is renewable power generation.

(Editor Yu Zhang)