0 Introduction

A microgrid is a power grid system involving renewable energy, various dispatchable distributed power generators,energy storage systems, and loads [1] with improved energy utilization.Considering the significance of economic and environmental factors, it is vital to ensure the optimal scheduling of microgrids.The power generation of a single microgrid is significantly affected by the external environment with uncertain instability.Thus, multimicrogrids (MMGs) are preferred for future comprehensive energy systems.

The primary aspect of MMG optimization is to use proper dispatching or scheduling schemes with multiple energy carriers for more complex needs and higher energy efficiency; thus, multi-energy complementarity can be realized with better flexibility and economy [2, 3].In [4],to facilitate pow er-sharing among multiple communities,a day-ahead operational dispatch approach was proposed for a multi-community system.In [5], a double-layer optimization method was developed for efficient scheduling of multi-energy microgrids.In [6], a piecewise linear approximation was used to construct the corresponding optimal scheduling model as an mixed integer linear programming (MILP) problem.Reference [7] established an MILP model to achieve optimal scheduling of multienergy microgrids in grid-connected and islanded modes.In [8], microgrid power generation was optimized by establishing a mixed-integer second-order cone problem.Reference [9] proposes an improved model predictive control (MPC) method to achieve effective and reliable management of grid-connected integrated energy systems.Further, in [10], an improved robust optimization method was proposed to realize the optimal operation of multienergy microgrids.Furthermore, [11] introduced stochastic optimization methods for the energy optimization of multienergy microgrids.However, most of these methods require a complex modeling process with high solution costs.In particular, for complex nonlinear scenarios, these methods may be unable to obtain multi-objective optimization solutions in real time.

Intelligent optimization algorithms are used to address this issue.For example, [12] performed scheduling optimization of a day-ahead multi-objective microgrid based on particle swarm optimization (PSO).Reference [13]realizes the load optimization of a microgrid according to the gravitational search and PSO algorithm.However, these methods use weights to convert a multi-objective problem into a single-objective problem.Although this can improve speed by reducing complexity, it is difficult to determine the co-efficient.Considering that the particle swarm optimization has a population-based structure and effective learning mechanism [14], several improvements based on PSO have been proposed.For example, [15] proposed a multi-objective PSO (MOPSO) algorithm to optimize the energy management of microgrid.For day-ahead demandside management optimization of a microgrid, an improved MOPSO with an index-based ring topology was proposed in[16].However, balancing the exploration and exploitation capacities of the algorithm while ensuring the diversity of solutions and the global search ability of the optimization algorithm is a topic that requires further study.

The second key aspect for microgrid operation is the effect of uncertainties arising from renewable energy sources such as solar and wind power on prediction and utilization.For example, because of intermittence and uncertainty, predicting solar power is a challenging task.Typical forecasting methods can be categorized into two types: physical and statistical.Physical methods depend on the establishment of a detailed and accurate physical model using meteorological data, photovoltaic component parameters, and geographic information; however, their robustness is relatively weak.Statistical methods that rely on historical data are particularly appropriate for shortterm prediction [17].However, the relationship between output values and historical data is often nonlinear in nature,and typical statistical methods cannot ensure prediction accuracy.Therefore, nonlinear prediction models based on artificial intelligence algorithms have been proposed.

Numerous artificial intelligence algorithms have been studied for solar power prediction, including machine learning and deep learning.These methods exhibited strong feature extraction and nonlinear mapping capabilities [18].For example, in [19], an ANN-based prediction model is proposed.In [20], an uncertainty forecasting framework based on an interpretable neural network (INN) and an improved evidential neural network (IENN) is proposed for the probabilistic forecasting of renewable energy and load.In [21], a wind power probabilistic forecasting framework based on an improved deep neural network (DeepNNPF) was proposed.Subsequently, [22] used a variety of machine learning methods, including random forest,to predict short-term solar power.Traditional machinelearning methods seldom consider time dependence;therefore, accurate prediction results cannot be obtained.Reference [23] summarized the use of machine learning approaches in solar power forecasting and concluded that a hybrid prediction model can further improve the forecast accuracy.Forecasting the solar power in a microgrid is a time-series forecasting problem.In contrast to regression prediction modeling, time-series analysis introduces the challenge of capturing complex sequence dependencies among input variables.To address this problem, recurrent neural networks (RNN) are typically used to handle the sequential data.For example, [24] proposed different methods based on long short-term memory (LSTM), gated recurrent unit (GRU), and CNN-LSTM for solar irradiance prediction.In [25], a hybrid LSTM model was proposed for predicting solar power.Reference [26] proposes a combined forecast method for solar power consisting of LSTM and autoregressive integrated moving average (ARIMA).In[27], LSTM and an attention mechanism were used for power prediction.However, the above-mentioned prediction models still have several parameters that need to be tuned manually; if the intelligent optimization algorithm used for tuning falls into a local optimum, it may not enhance the training accuracy of the prediction model.

Inspired by the aforementioned observations, this study provides a scheme for the solar power prediction and scheduling of multi-energy microgrid clusters.The flowchart is shown in Fig.1.

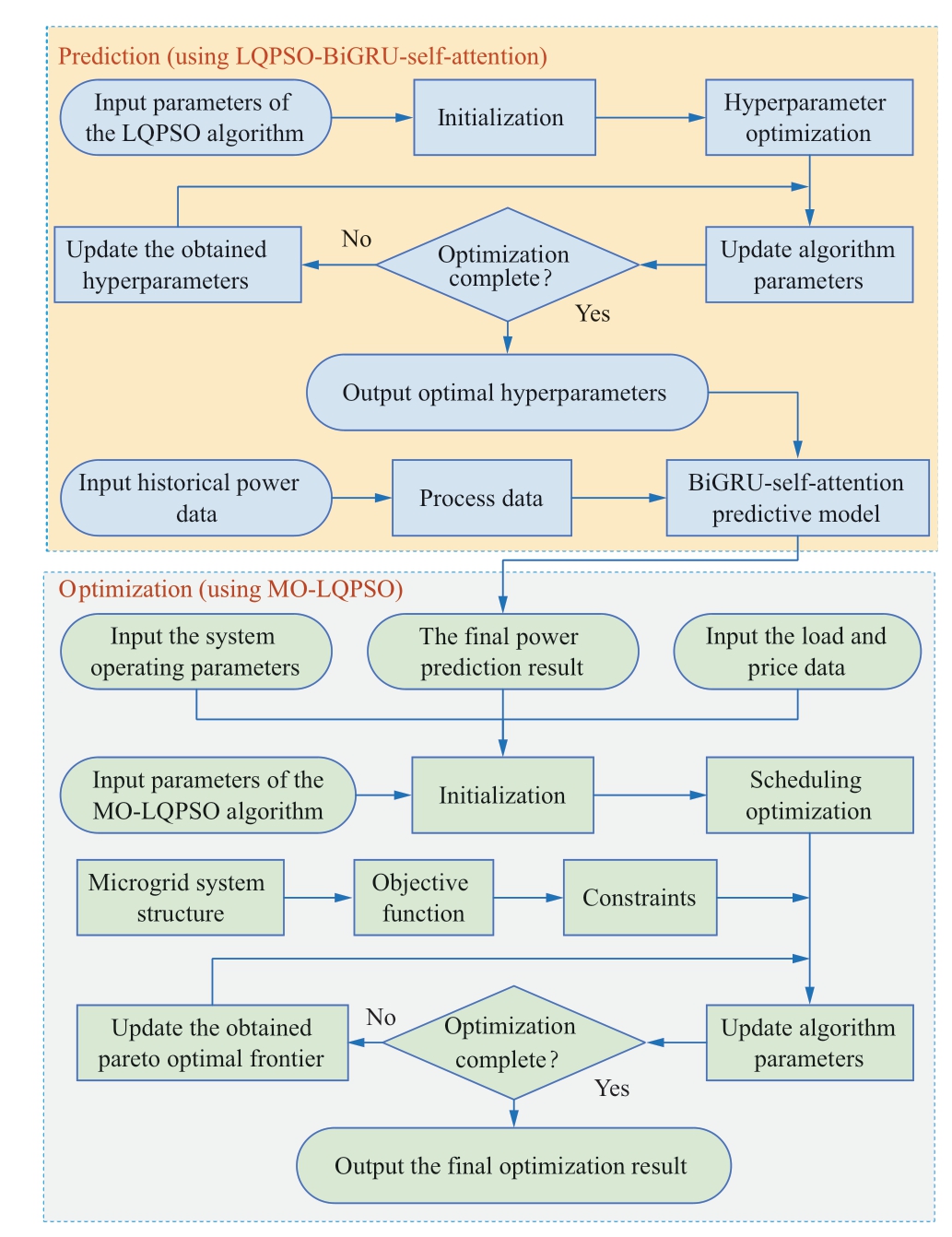
Fig.1 Flowchart of the scheme

First, a forecasting model based on the BiGRU network and a self-attention mechanism was constructed to realize solar power prediction.Subsequently, to enhance the accuracy of the prediction, a hybrid forecasting model,named as LQPSO-BiGRU-self-attention, was formulated to obtain the power prediction results and input them into the optimization model.Finally, a multi-objective optimal model of multi-energy microgrids is constructed, and a multi-objective LQPSO called MO-LQPSO is designed for the optimal scheduling of the microgrids system.The main contributions of this study are summarized as follows.

1) A hybrid model based on LQPSO, BiGRU, and a self-attention mechanism is proposed to predict solar power.This hybrid model provides more effective and accurate predictions.By blending the Lévy flight with quantum particle swarm optimization (QPSO), the global search performance of the algorithm is improved.This enables the prediction model to adjust the parameters adaptively based on the characteristics of different time-series data.

2) A day-ahead multi-objective optimization model was established, and a hybrid optimization approach called MO-LQPSO was proposed.The proposed method balances both exploration and exploitation abilities by designing an adaptive two-stage search mechanism such that the proposed algorithm can be applied to complex scenarios.

The remainder of this paper is organized as follows.Section 1 formulates the framework of the solar power forecasting model based on LQPSO and BiGRU selfattention.Section 2 describes the optimization model and the hybrid MO-LQPSO algorithm.In Section 3,the comparative simulations are presented to verify the proposed approach.Finally, the conclusions and discussion are presented in Section 4.

1 Solar power prediction based on LQPSO and BiGRU-self-attention model

1.1 QPSO algorithm

Sun et al.proposed quantum particle swarm optimization algorithm to improve the global optimization ability [28].The key principles of QPSO are as follows:

1.2 GRU network

The gated recurrent unit network simplifies the gate structure in LSTM by removing the memory unit, which provides a simpler calculation process and shorter training time while ensuring the forecast performance of LSTM.The GRU addresses the gradient disappearance problem of the LSTM with a faster convergence speed and higher accuracy close to that of the LSTM [29].Its structure is illustrated Fig.2.

A GRU network has two gates: a reset gate and an update gate.First, the update gate is defined as

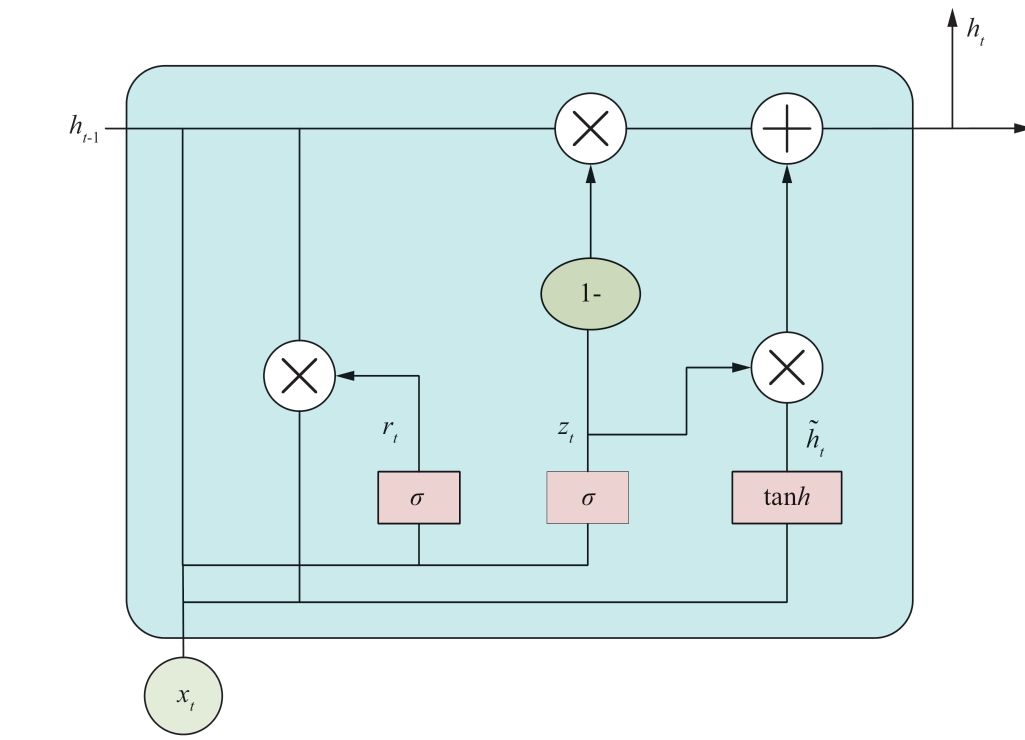
Fig.2 Structure of GRU network

where xt is the input vector at the current moment and ht-1 is the hidden state output at the previous moment.The hidden state within a neural network serves as a memory component that retains information from previous nodes that processed data.The update gate gating signal is between 0 and 1; the closer it is to 1, the more past information is retained.

The reset gate is defined as

The reset gate is used to regulate whether information is ignored from the previous time point.The current unit-state h～t controls the selective memory screening information as well as the current input.Finally, the current output ht is calculated as

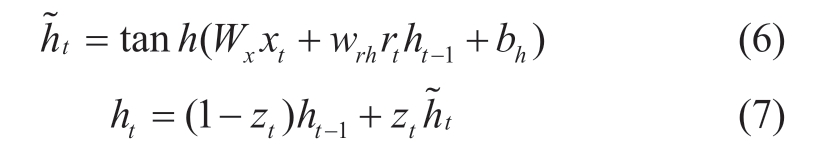
where W and b are the related weight matrix and bias vector,respectively.

1.3 Self-attention mechanism

Although the GRU performs well in processing long time-series data, it lacks the ability to distinguish information from different time steps.Therefore, it may ignore certain key information in the time series, which may impact the prediction results.Thus, a self-attention mechanism was introduced to highlight the influence of different nodes, thereby improving the performance of the model.

The self-attention mechanism was first proposed by Google and utilizes the query-key-value (QKV) approach as an effective modeling method [30].The self-attention mechanism maps the input features to three matrices:query matrix Q, key matrix K, and value matrix V.The dot products of Q and K are then calculated, and the resulting scores are scaled to determine the similarity between them.Next, the attention matrix is normalized and transformed into a probability distribution.

The self-attention mechanism focuses on significant characteristics of an input sequence.Therefore, the output is obtained by calculating the weighted sum of the attention and value matrices as follows:

where dK is a scaling factor that has the same dimension as the input vector.

1.4 Hybrid forecasting model based on LQPSO and BiGRU-self-attention

A hybrid forecasting model based on the LQPSO and BiGRU self-attention was proposed to predict the solar power of a microgrid using historical data.Determining the appropriate learning rate and number of hidden layer nodes is often challenging during model training.The learning rate significantly influenced the training effectiveness of the model, whereas the number of neurons in the hidden layer affected the model’s fitting capability.These parameters are typically determined based on experience and are uncertain, which can result in reduced model accuracy.Therefore, the QPSO intelligent optimization algorithm was used to optimize the hyperparameters to avoid manual tuning.The QPSO algorithm incorporates a Lévy flight strategy to expand the particle search space.By using the unique random walk mechanism of the Lévy flight,including the short-distance local search of most individuals and the long-distance global search of a few individuals,the global search ability is improved.The Lévy flight-based QPSO, named LQPSO, is described as:

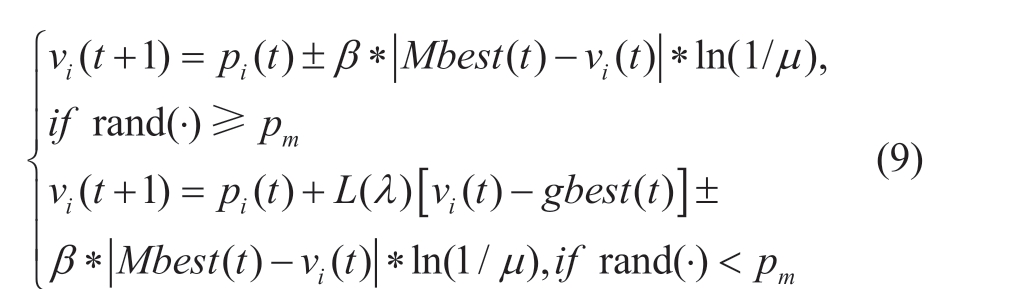
where rand()· is uniformly distributed between (0,1); pm can be used to adjust the exploration ability of particles, that is, to introduce the Lévy flight strategy with its probability to update the position, and help particles jump out of their current position; L( )λ is a random search path with a step size following the Lévy distribution; λ is a scale parameter with λ =β +1.

Thus,

where µ and v are random numbers that follow a normal distribution; µ∈N(0σ, µ2); ν∈N(0σ, ν2); the gamma function Γ(z) is introduced.The values of the standard deviations σµand σν are

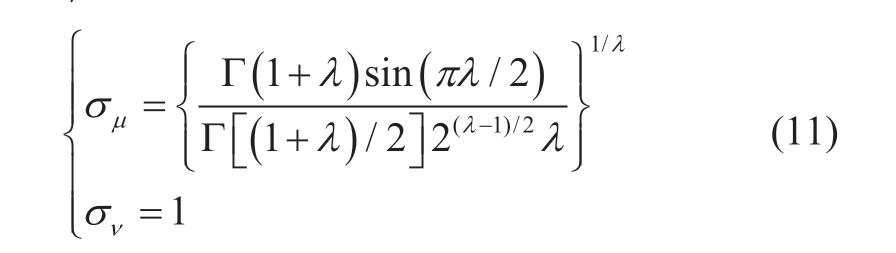
The BiGRU model was then used for the prediction.This model combines two unidirectional GRUs for the model output.The two GRUs are trained in opposite directions.The BiGRU output is:

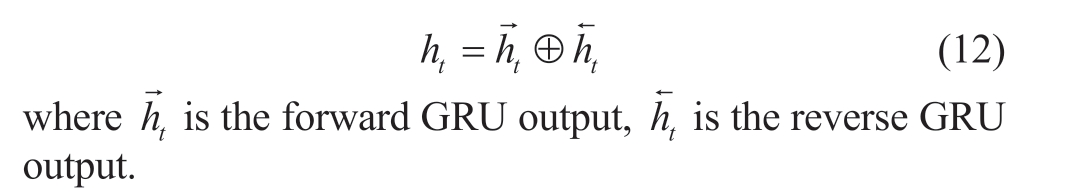
Next, the hidden state vector output of the BiGRU model was input into the self-attention mechanism, and the results reflected the effects of each node on the forecast results.Finally, the result was entered into the full connection layer to obtain the final forecast result.

Thus, we obtained a hybrid prediction model based on the LQPSO and BiGRU self-attention.A flowchart of this process is shown in Fig.3.

2 Optimal scheduling of multi-energy microgrids based on MO-LQPSO algorithm

2.1 Multi-energy microgrid cluster system structure

Three sub-microgrids involving photovoltaic (PV),electrolytic cell (EL), fuel cell (FC), wind turbine (WT),diesel generator (DE), battery energy storage system (ES),gas turbine (MT), and hydrogen storage tank (HS) were used to form a microgrid cluster for optimization.The system topology is illustrated in Fig.4.Sub-microgrid 1 included PV1, WT1, ES1, DE1, and MT1.Sub-microgrid 2 included PV2, WT2, ES2, FC2, and MT2.Submicrogrid 3 included PV3, WT3, EL3, HS3, and ES3.In Sub-microgrid 3, the hydrogen energy network acts as an energy supplier that converts excess electrical energy into hydrogen energy within the microgrid and satisfies the hydrogen energy load as much as possible, such as in hydrogen-energy vehicles.

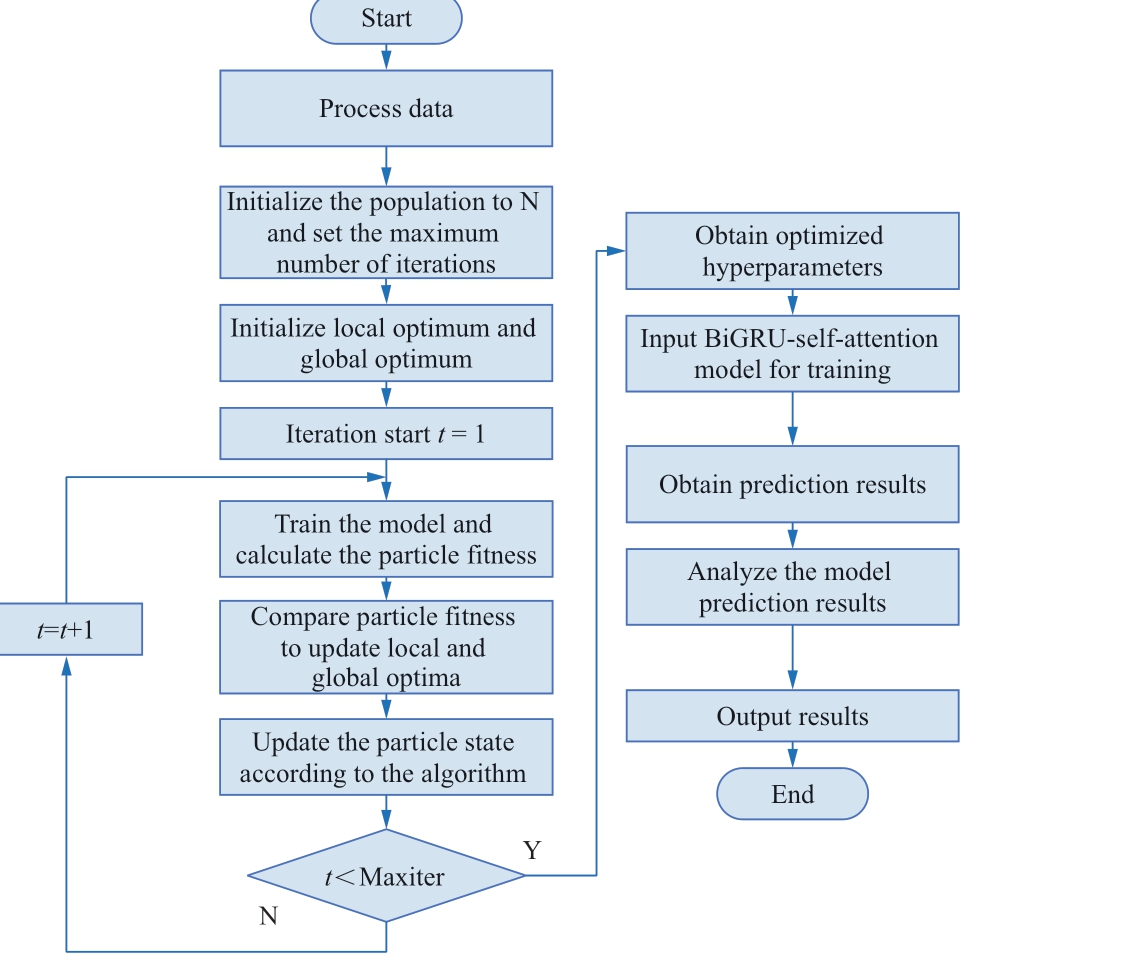
Fig.3 Flowchart of the hybrid prediction model based on LQPSO and BiGRU-self-attention

2.2 System modeling

2.2.1 Objective function

Considering the environmental cost of the objective function, a multi-objective optimal scheduling model was constructed.The economic cost of the microgrid should be minimized as follows:

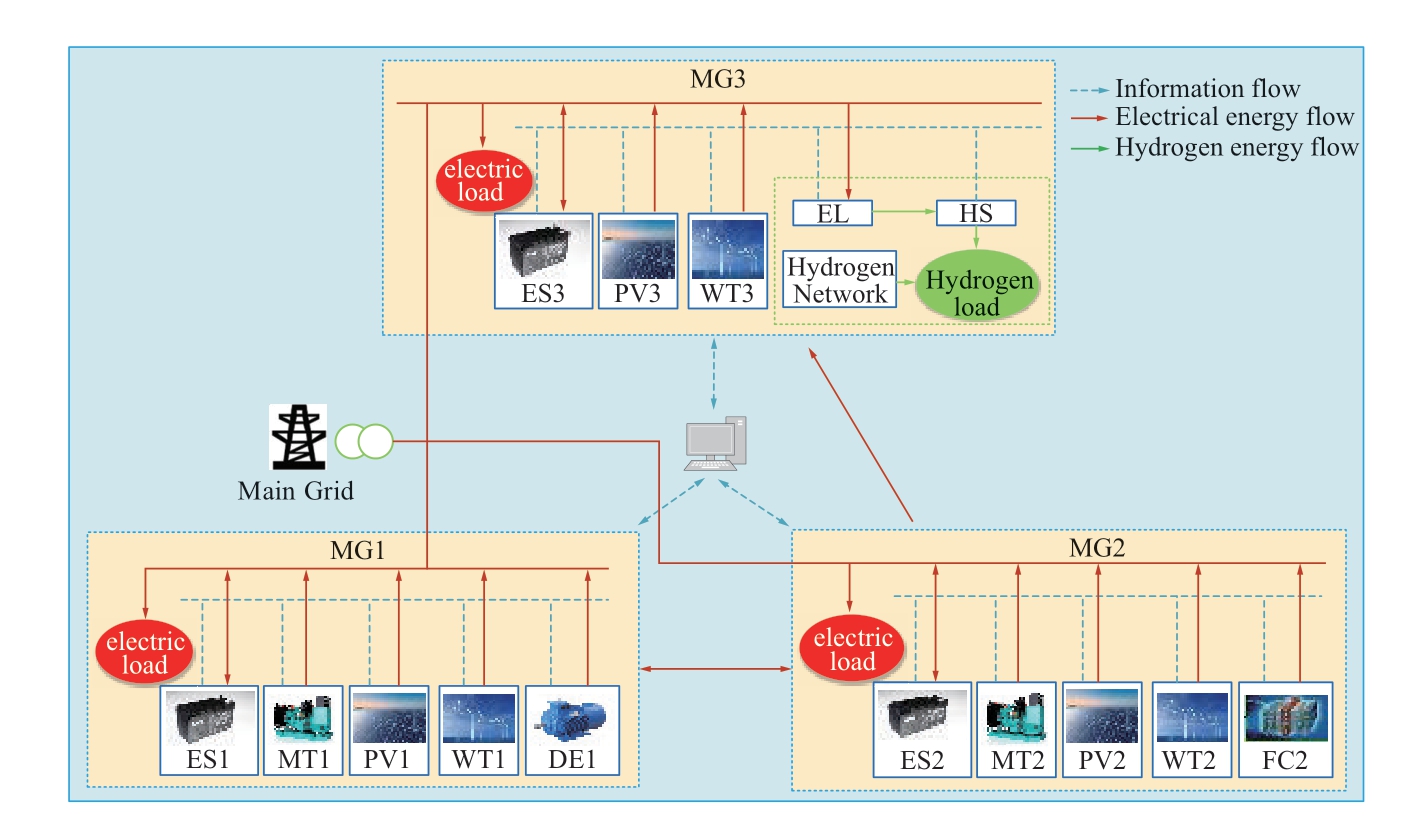
Fig.4 Structure of a three-microgrid cluster

Environmental cost specifically refers to the management cost of the total amount of pollutant gas emissions from distributed generators and energy storage systems, as well as the main grid.The environmental costs of microgrids are as follows:

where K is the type of pollutant gas emitted, γk is the treatment coefficient of the k-th pollutant gas, 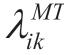, 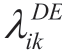and λik FC are the emission coefficients of the k-th pollutant gas emitted by the i-th distributed power generators, and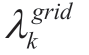is the emission coefficient of the k-th pollutant gas emitted by the main grid.

2.2.2 Constraints

The objective function of the model mainly includes the following constraints:

1) For battery energy storage systems,

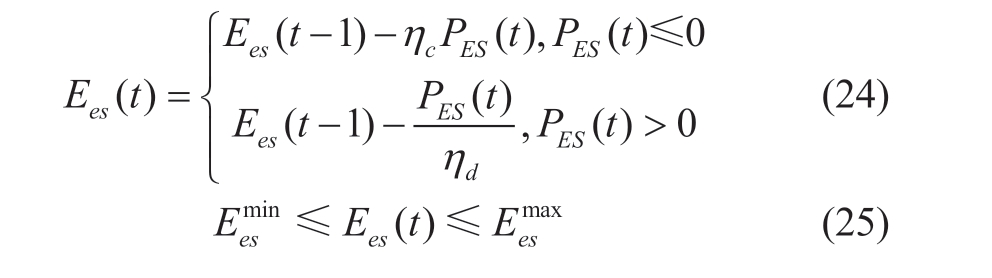
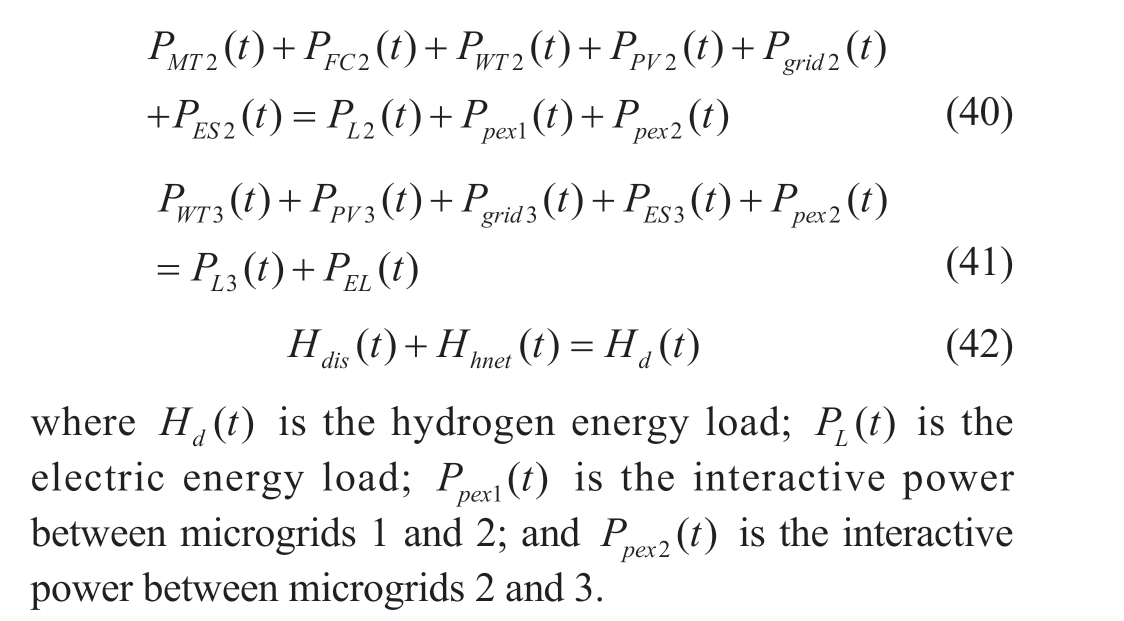
2.3 MO-LQPSO intelligent optimization algorithm

There are two key issues in extending the QPSO algorithm to multi-objective applications: the rapid decline in solution diversity and the inability to eliminate local optima.To enhance the diversity of solutions and strengthen the global search capacity while enhancing the ability to avoid local optima, a two-stage search strategy was proposed.

Exploration behavior involves accessing all new regions in the search space, and exploitation behavior involves accessing the neighborhood of known points in the search space.The two-stage search strategy uses a dynamic coefficient to achieve balance between exploration and exploitation.In the exploration phase, a wider solution space is searched to increase the diversity of solutions.In the exploitation phase, a global optimal solution is used to guide the convergence.The Lévy distribution is introduced to enhance the search capacity in the exploration stage,avoid the unexpected situation of premature convergence,and avoid falling into the local optimum.

Therefore, a two-stage adaptive multi-objective quantum PSO algorithm aided by a Lévy flight, called MO-LQPSO,was formulated.

2.3.1 Two-stage searching strategy

First, the dynamic coefficient β is used.During the exploration stage, a larger β value helps the particles explore a wider space.With increasing iterations, the particles access the second stage of searching (the exploitation stage),and the best solution around the local attractor is used to search near the optimal point, which ensures a global search ability.

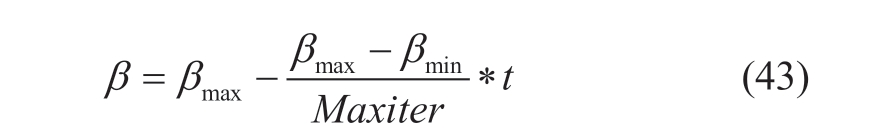
where β decreased linearly from βmax to βmin.t and Maxiter represent the current and maximum iterations,respectively.

A threshold γ was then introduced to determine whether the particles should execute the exploration or exploitation strategy.During β ≥γ , the particles should be explored rather than exploited.At this stage, to facilitate the particles to jump out of their current positions, the Lévy flight strategy was introduced, and the original formula was replaced with an improved formula using the probability pl.The learning strategies in the exploration stage are expressed as follows.

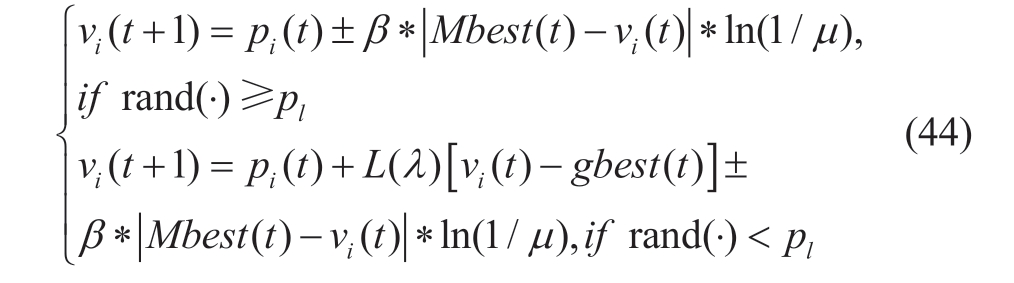
In the exploitation phase with β ＜γ , the particles should search around the optimal position to converge to the optimal position.At this stage, Mbest is replaced with the global best position gbest (t ) selected from the external archive.Similarly, to avoid local optima, the probability pl of Lévy flight variation is executed.The learning strategy of the exploitation phase is expressed as:

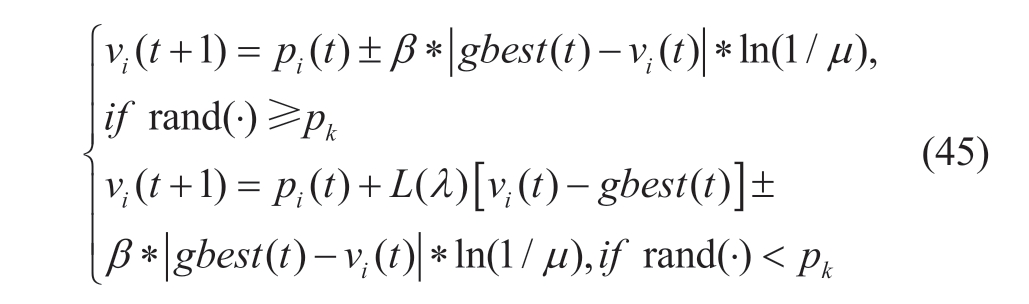
2.3.2 Multi-objective optimization strategy

For multi-objective optimization problems, Pareto dominance is introduced to select pbest t i( ).The elite external archive set Archive is used to save the nondominated solution set generated in the historical iteration of the population, and gbest(t) is selected from the current Archive.When the Archive is empty at the beginning of the algorithm, the non-dominated solutions in the population are directly added to the Archive.When the Archive is not empty, the new non-dominated solution generated must determine whether it should be added to the Archive, and whether the particles in the Archive need to be removed according to the dominance relationship with the solution in the Archive.

The crowding distance (CD) serves as a criterion for eliminating non-dominant solutions and is a measure of density for neighboring solutions and can be calculated as the Euclidean distance between adjacent individuals.

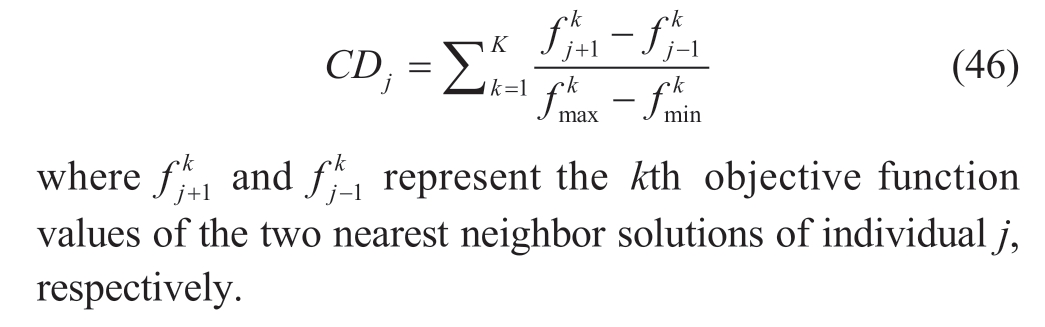
Simultaneously, the adaptive grid method and roulette wheel selection were used for the group optimal selection and archive updates.The adaptive grid method meshes the non-dominated particles in the Archive set in the target space.All individuals were divided into different grids,and the density of each grid was calculated.The smaller the density of the grid, the greater is the probability of the individual being selected.A grid with a low density, in which the particles are sparse, can better ensure the diversity of the final population.The steps are as follows:

1) By iterating through all the individuals in the set,we can determine the minimum and maximum values for each individual for every objective function.To ensure that the boundary particles could also be extended in the grid,the maximum and minimum values were slightly extended based on a certain proportion and the boundary of the grid was finally obtained.

2) The parameter of grid size was set as 9, so that the grid could be cut into 81 grids on average.

3) The individual grids were selected and the total number of individuals stored in these grids was calculated.

4) The selection probabilities of these grids were calculated from the number of individuals previously obtained.The fewer the number of individuals, the greater is the probability of being selected.The sum of the selection probabilities for all the grids was 1.

5) Based on the probability of the previous calculation,a grid was selected using the roulette-wheel selection approach, and the individuals in the grid were selected as the candidate set.In the candidate set, one individual was selected as the global optimal individual using the random selection method.

The flowchart of MO-LQPSO is shown in Fig.5.

The steps of the proposed MO-LQPSO algorithm are described as follows:

Step 1: Initialize the parameters, including the population size M, maximum iteration number Maxiter,maximum and minimum dynamic coefficients βmax and βmin, threshold γ, replacement probabilities pl, and pk.

Step 2: Population Initialization: Generate the position v according to the position range of the particle, evaluate the fitness of the particle, initialize pbest t i( ), and gbest (t );maintain and update Archive based on the initialized external archive set of the population.

Step 3: Sort the fitness values of all particles in Archive and determine the maximum and minimum fitness values.

Step 4: Update gbest (t ).

Step 5: According to the two-stage adaptive search strategy combined with the Lévy distribution, each particle is updated and iterated.

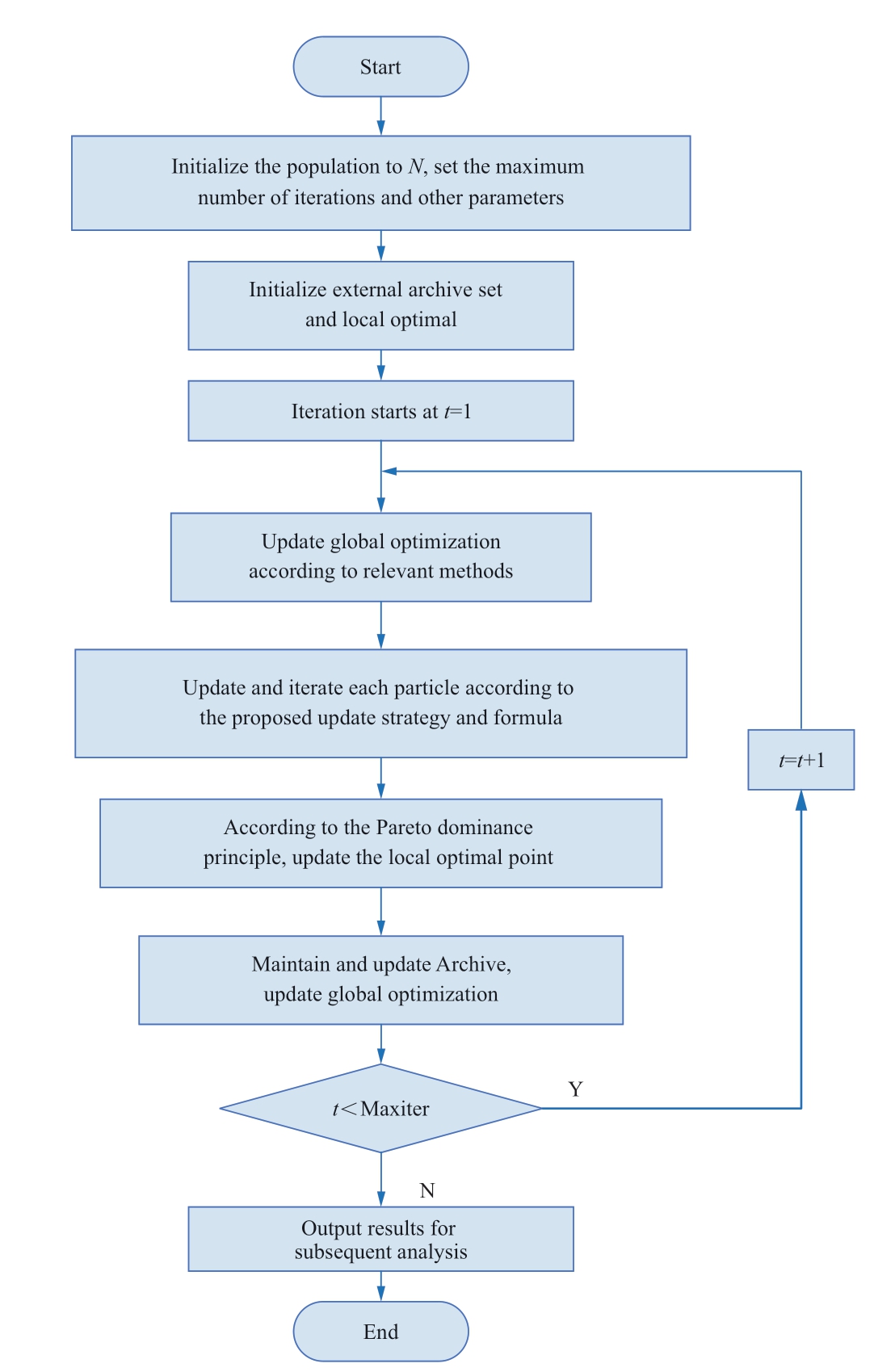
Fig.5 Flowchart of the MO-LQPSO algorithm

Step 7: Maintain and update Archive and maintain the number of members in Archive less than that in M.

Step 8: Let t =t +1.If the iteration termination condition is met, output the results in the final Archive and plot the Pareto optimal front; otherwise, go to Step 3.

The MO-LQPSO algorithm to optimize scheduling is shown in Algorithm 1.

3 Case studies and results

3.1 Solar power prediction using LQPSO and BiGRU-self-attention

The historical dataset of solar power was obtained from the Australian PV Institute (APVI) [31].The sampling interval was one hour.The dataset was split into training and test sets, with 70% of the data used for training and 30%used for testing.Subsequently, the data were processed with outliers and vacancy values, and the data were normalized as:

where yN represents the normalized solar power, ymin and ymax represent the minimum and maximum values.

Various evaluation metrics were used to assess the performance of the model and to measure the deviation between the predicted and actual values.The three selected evaluation indicators are the mean square error (MSE),mean absolute error (MAE), and root mean square error(RMSE), defined as follows.

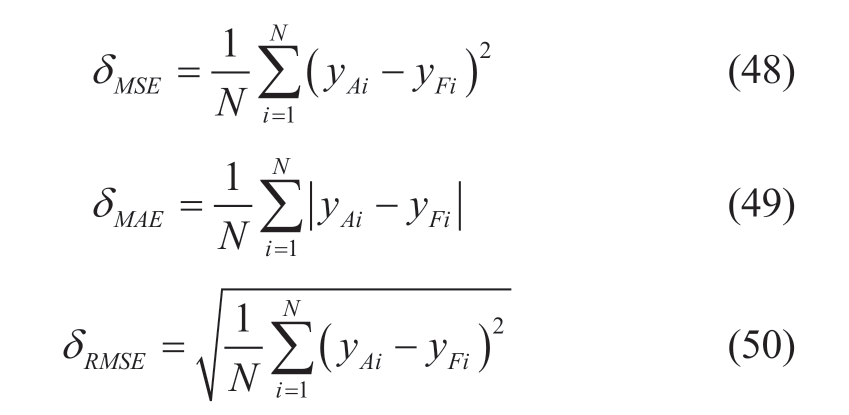
where yAi represents actual data, yFi represents forecast data, and N represents the sample number.

The maximum iteration number of the LQPSO algorithm was set to 20, the population number was set to 15, and the dimension was three.That is, the optimized hyperparameters were the node number in the hidden layer,learning rate, and maximum number of iterations.

Simulations were executed on a laptop equipped with Python 3.11, 64-bit operating system, 16 GB memory, and Intel Core i9-13900HX CPU.The optimization iteration results of the algorithm are shown in Fig.6.

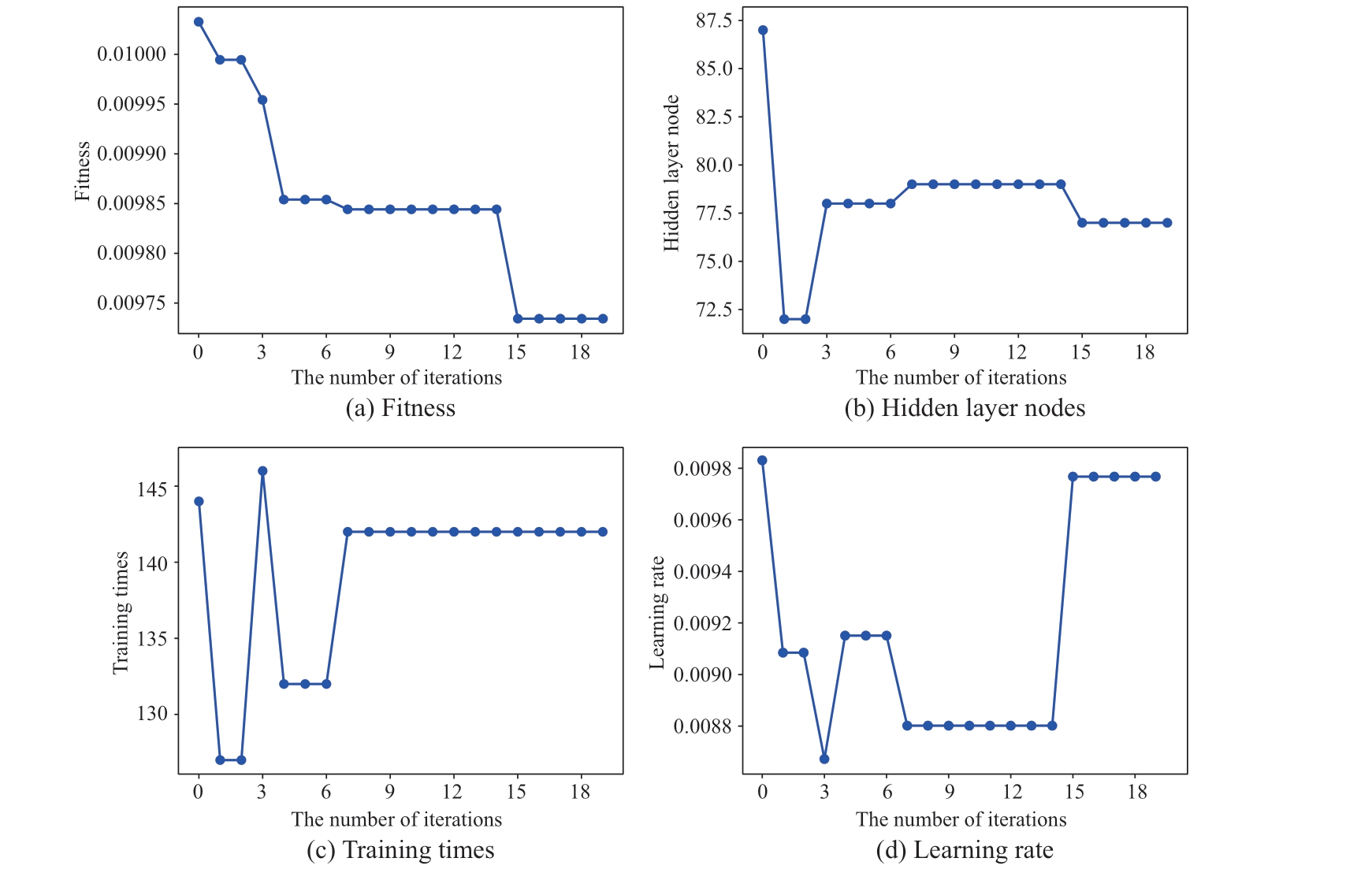
Fig.6 Iterative process of optimization algorithm

As shown in Fig.6, the fitness remained unchanged after a few iterations.That is, the hyperparameters can be obtained with very limited iterations.The optimized hyperparameters, namely, the learning rate of 0.0098,maximum iteration number of 142, and node number in the hidden layer of 77, were input into the model for the final training.The output power for the next 24 h was predicted one day in advance.The training process is shown in Fig.7,and the final training loss was 0.0129.

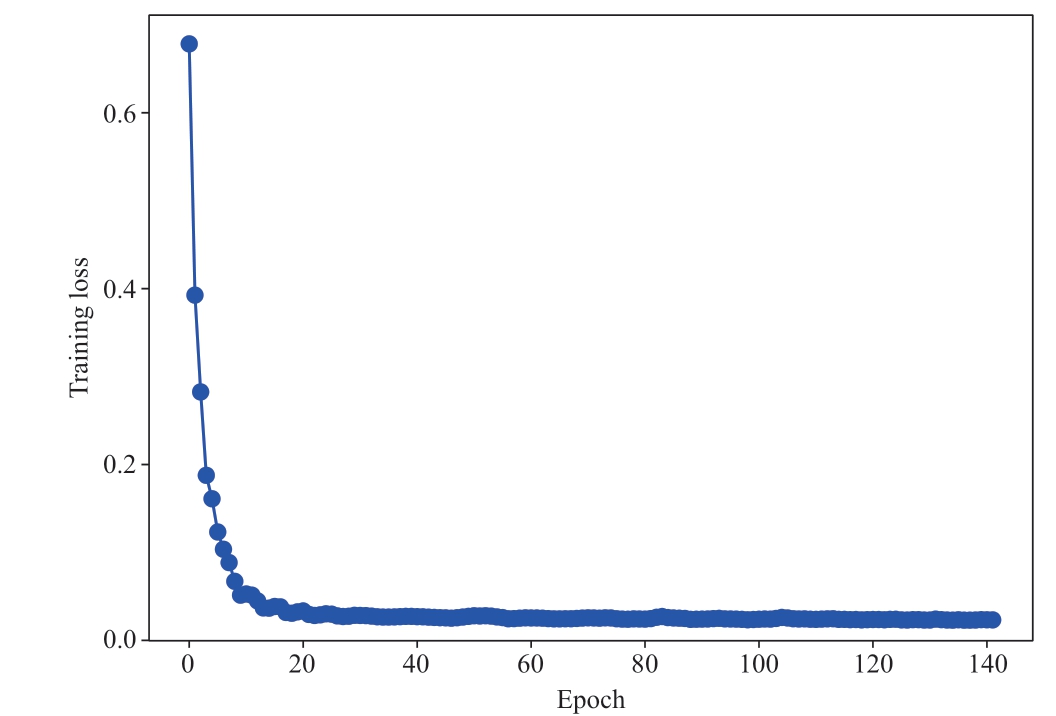
Fig.7 Training process of the model

The prediction results are presented in Fig.8.The model was evaluated using a test set.The results show that MSE,RMSE and MAE were 0.0104, 0.1018, and 0.0514, respectively.

The model was compared with GRU and BiGRU models to prove its effectiveness and superiority.The results are summarized in Table 1.

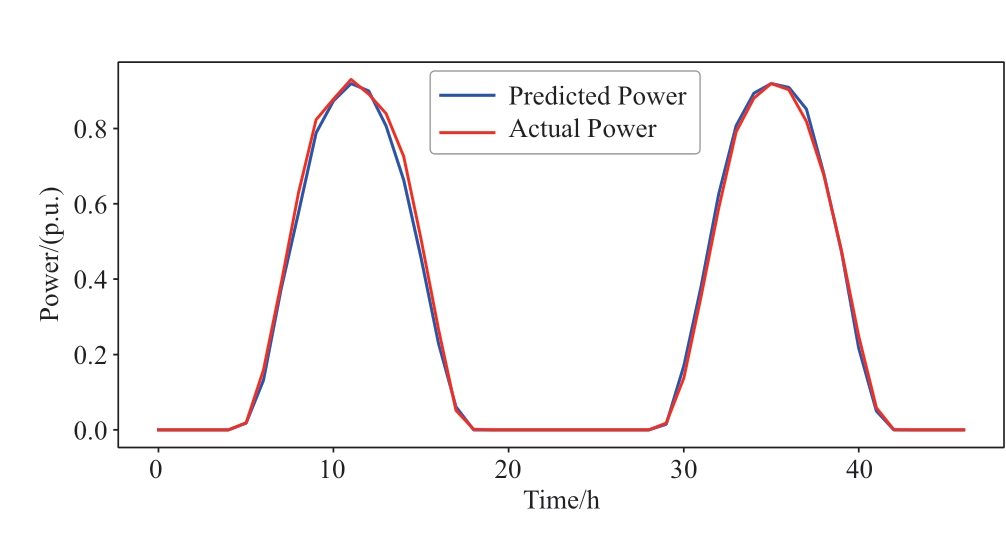
Fig.8 Prediction results of the LQPSO-BiGRU-selfattention model

Table 1 Comparison results of different models

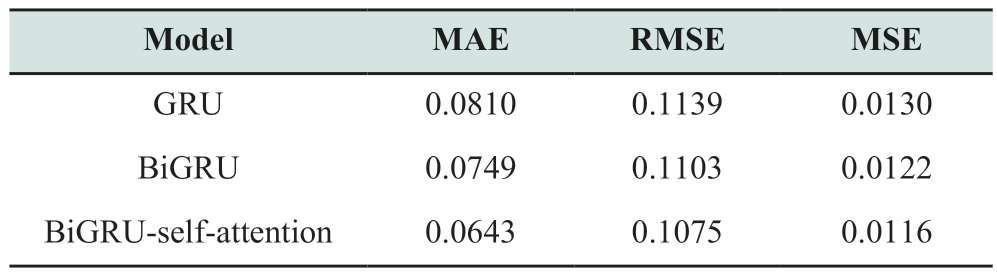
The forecasting results for the different models are shown in Fig.9.From Table 1 and Fig.9, the BiGRU selfattention model achieved the best performance.The MAE of BiGRU-self-attention was 0.0643, which was 20.6% and 14.2% lower than those of GRU and BiGRU, respectively.The MSE of BiGRU-self-attention was 0.0116, which was 10.8% and 4.9% lower than those of GRU and BiGRU,respectively.

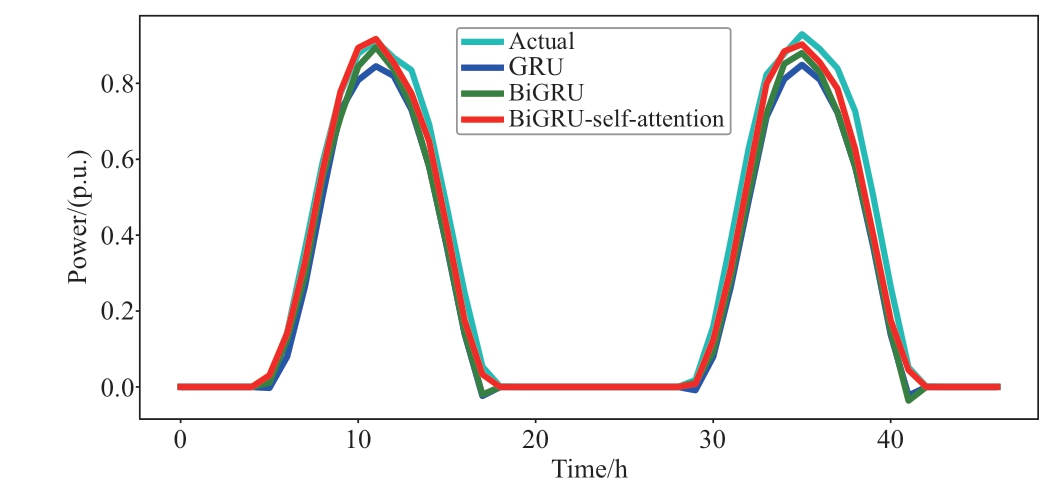
Fig.9 Power prediction results of different models

In addition, the model was compared with the BiLSTM self-attention model, and the forecasting results of the two models are shown in Fig.10.It can be observed that the MAE of BiLSTM-self-attention was 0.0722, which was 12.3% higher than that of BiGRU-self-attention.The MSE of BiLSTM-self-attention was 0.0123, which was 6% higher than that of BiGRU-self-attention.The results show that the BiGRU self-attention model ensures an improved prediction performance.

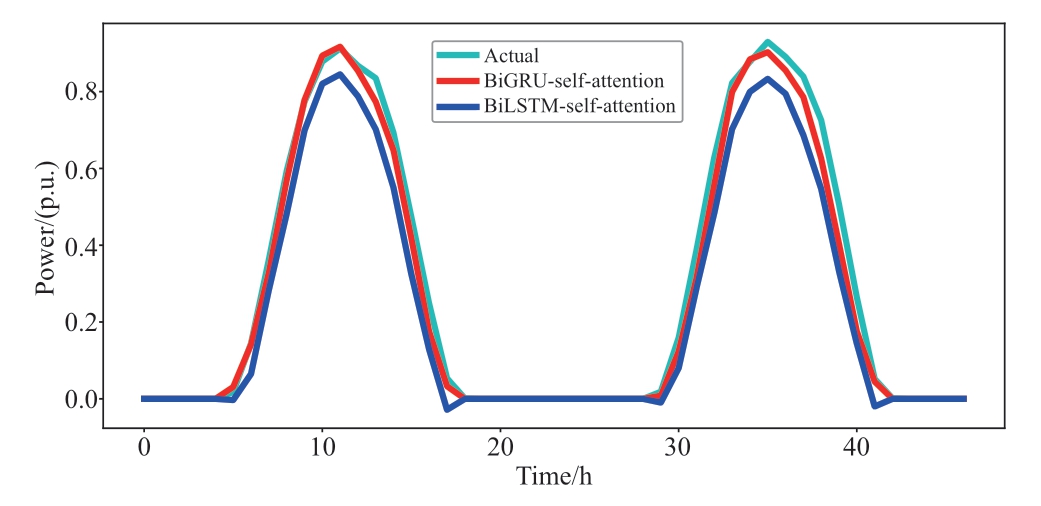
Fig.10 Power prediction results of two models

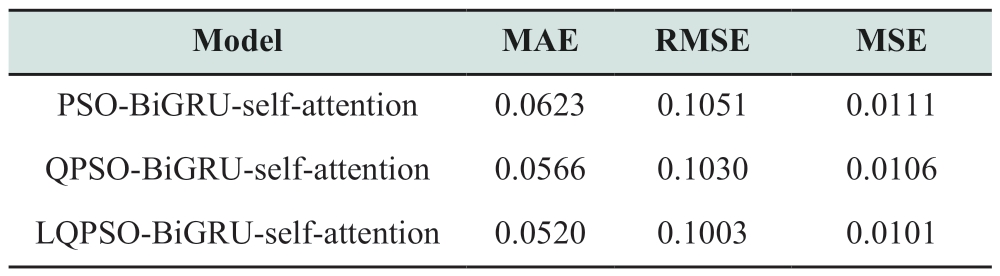
Next, BiGRU self-attention was used as the basic prediction model, and the PSO, QPSO, and LQPSO algorithms were used to optimize the hyperparameters of the model to verify the effectiveness and superiority of the proposed hybrid forecast model based on LQPSO and BiGRU self-attention.The results are summarized in Table 2.

Table 2 Comparison results of different combined models

The forecast results for different hybrid models are shown in Fig.11.The results show that ensuring prediction performance using a single prediction method is not satisfactory.The hybrid model based on LQPSO and BiGRU self-attention achieved the best performance.The MAE of LQPSO-BiGRU-self-attention method decreased by 16.5% and 8.1%, respectively, when compared with PSO-BiGRU-self-attention and QPSO-BiGRU-selfattention methods.The MSE is decreased by 9.0% and 4.7%, respectively, when compared with PSO-BiGRU-selfattention and QPSO-BiGRU-self-attention methods.

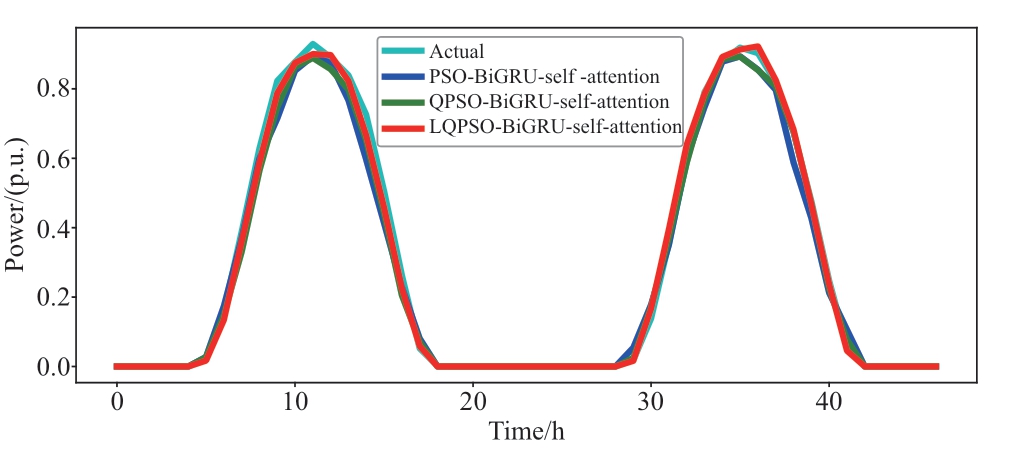
Fig.11 Prediction results of different hybrid models

3.2 Microgrid scheduling optimization results

To validate the effectiveness of the proposed algorithm,simulations were conducted on a system that included three sub-MGs, as shown in Fig.4.The system parameters were set according to existing researches [32-34], and some information was obtained from the U.S.DOE [35].

First, the proposed MO-LQPSO algorithm was compared with the conventional method.As the established model was nonlinear, the solver could not solve it.Therefore, the model was simplified and transformed into a MILP problem.Finally, the commercial solver CPLEX was used to solve the problem, and the comparison results are presented in Table 5.The results show that the proposed algorithm exhibits a better performance and can be applied to different scenarios more flexibly.

Table 3 Operating parameters of the system

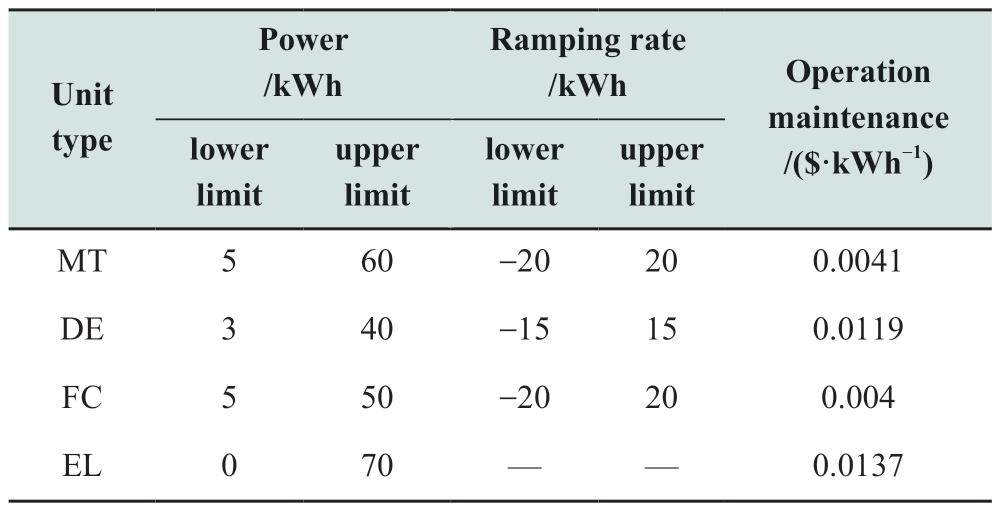
Table 4 Pollutant emission coefficients

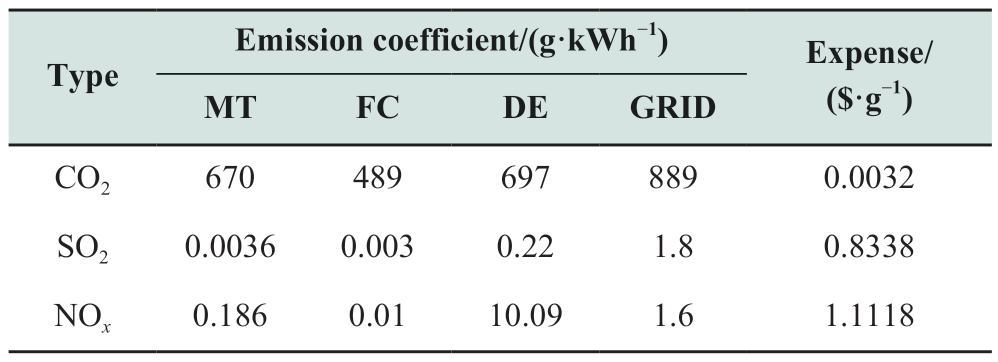
Table 5 Comparison results

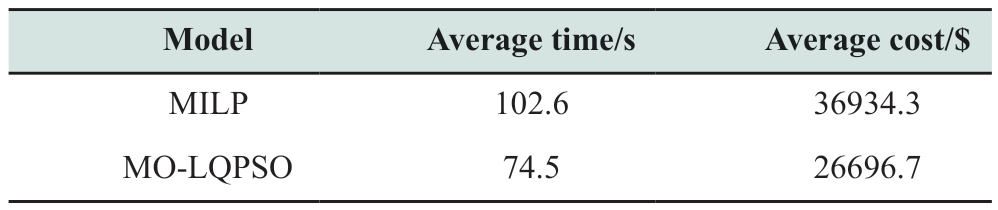
All experiments were performed under the same experimental conditions using MATLAB 2022a.The maximum number of iterations and the population size were set to 200.First, the performance of the proposed MO-LQPSO algorithm was verified, and the final experimental results are presented in Table 6 and Table 6,Fig.12 and Fig.13.

Table 6 Comparison results of different algorithms

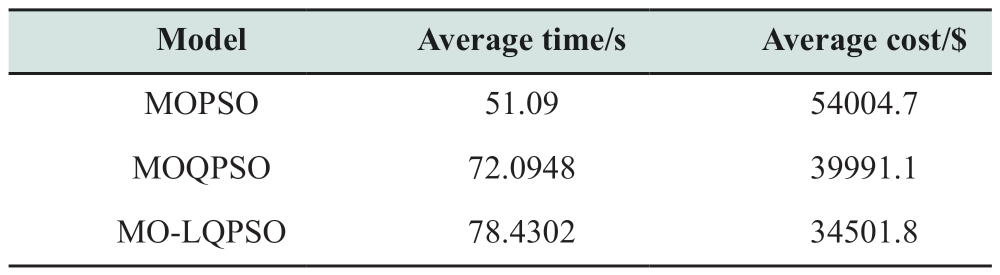
The results indicate that the MO-LQPSO algorithm achieves the best performance without significantly increasing running time.The cost is the smallest, which is 36.1% and 13.6% lower than those of MOPSO and MOQPSO, respectively.The MO-LQPSO algorithm obtained a more comprehensive Pareto front, demonstrating its effectiveness and superiority.

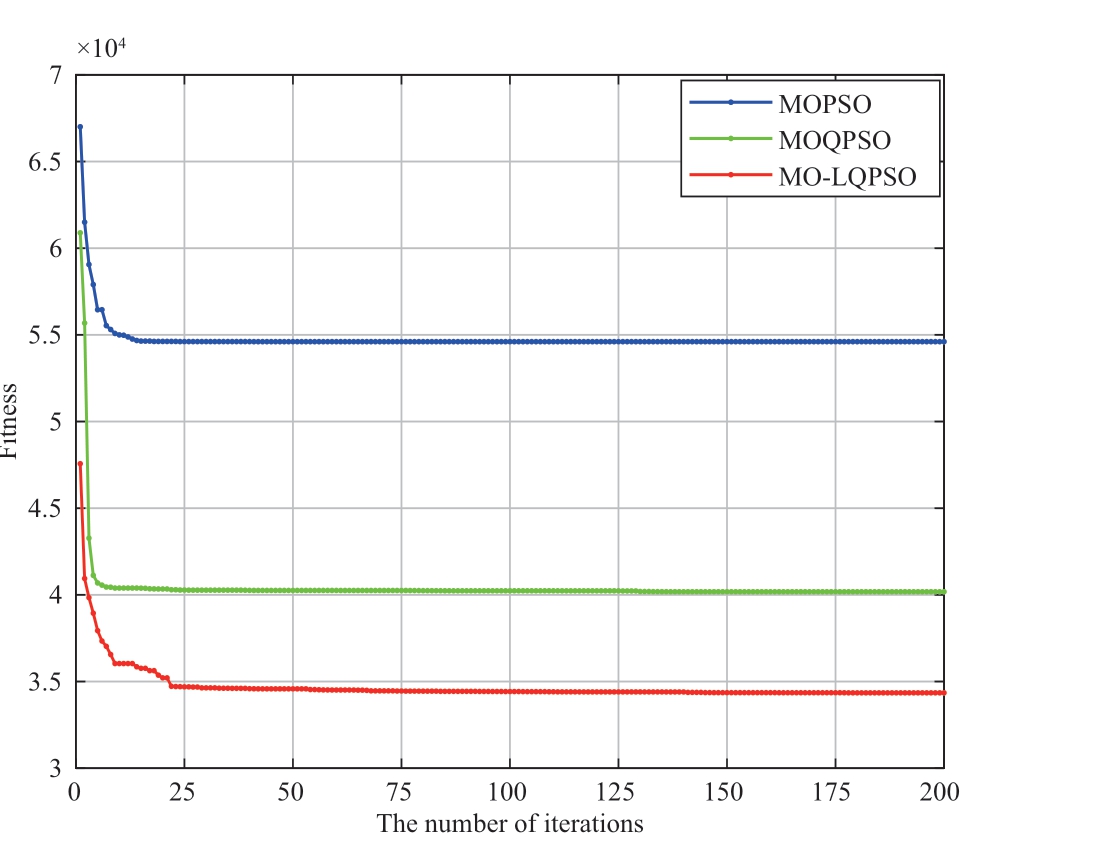
Fig.12 Iterative process of different algorithms

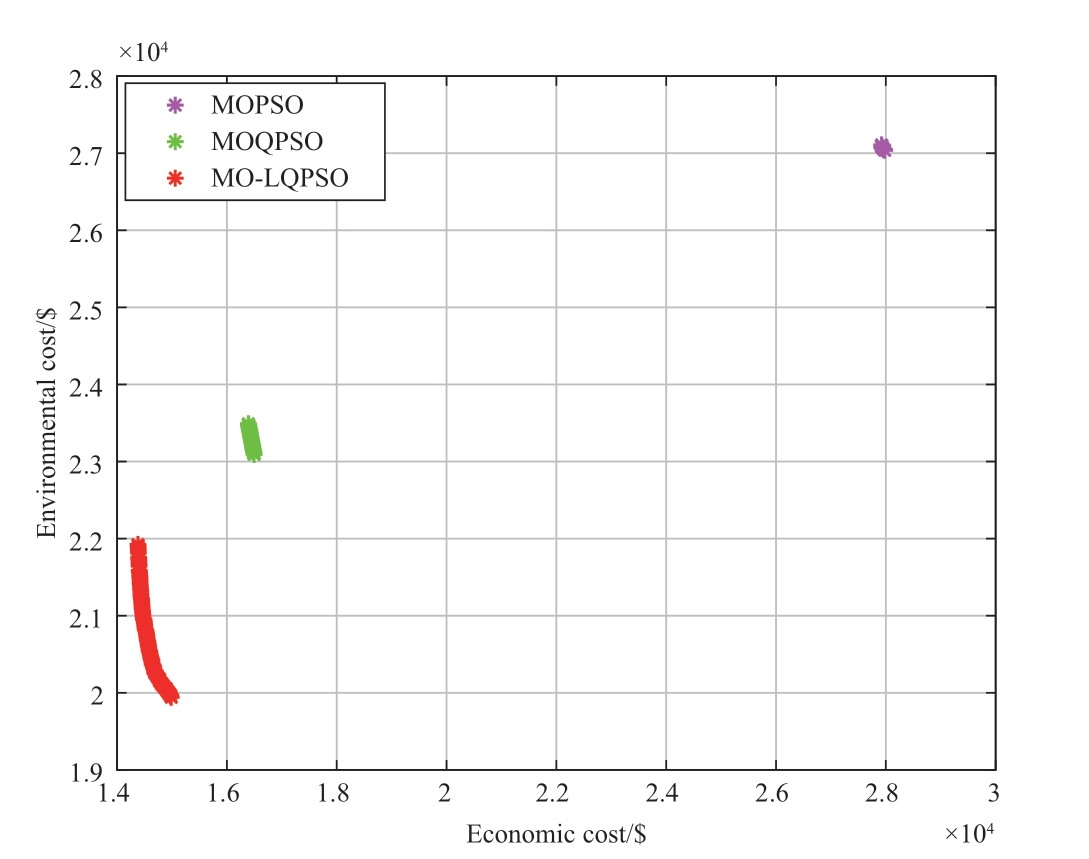
Fig.13 Pareto optimal frontiers obtained by different algorithms

Finally, the proposed algorithm is implemented in a multi-energy microgrid cluster involving hydrogen energy,as described in Section 3.The iterative results are shown in Fig.14 and Fig.15.

The results show that the MO-LQPSO algorithm can rapidly obtain optimization results and ensure the diversity of the obtained results.From the Pareto solution set, it can be observed that the algorithm considers the environmental and economic costs well and can formulate a solution selection strategy according to specific operational requirements.Environmental and economic factors were regarded as equally important,and the solution with the lowest total cost was selected in the Pareto-optimal frontier.The final results of the environmental and economic multi-objective optimization scheduling are shown in Fig.16 and Fig.17.

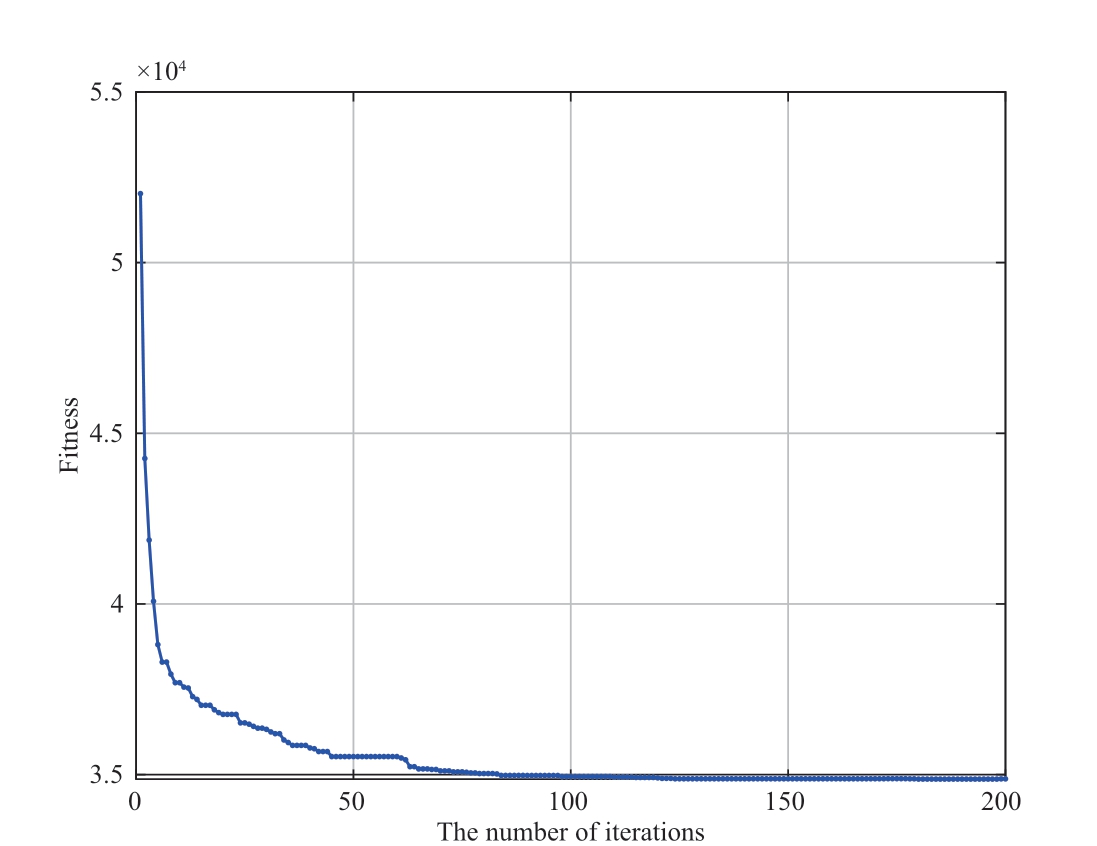
Fig.14 Optimization iteration process of the MO-LQPSO

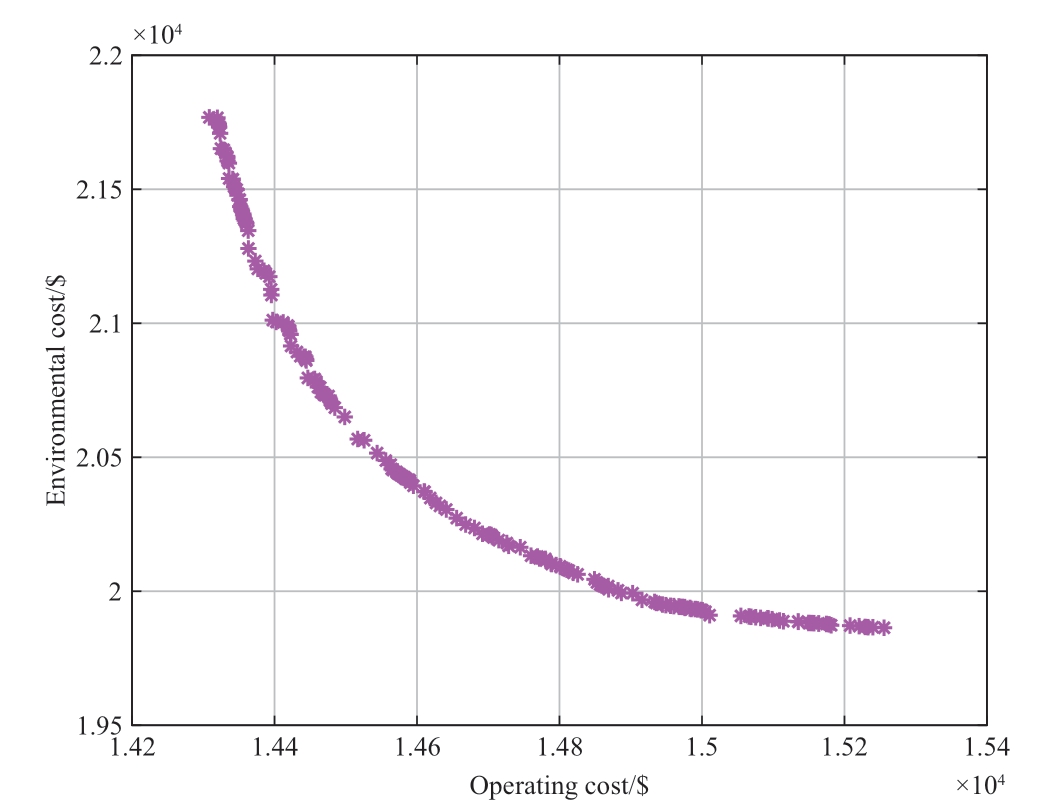
Fig.15 Pareto optimal frontier obtained with the MO-LQPSO

Because of the different electricity prices between the different microgrids and the main grid, Microgrid #1 with a lower electricity price transmits excess power to Microgrid#2 with a higher electricity price as much as possible in most time periods, and then sells the spare power to the main grid.Microgrid #3 had a higher cost of purchasing electricity and received as much electricity as possible from Microgrid #2.

At the peak of power consumption at noon, the output of dispatchable units, such as the fuel cell, reached a peak,whereas at the peak of the power load at night, the output of the MT reached its peak.

The ES is charged in the early morning hours, which consumes part of the excess electricity, whereas the diesel generators ensure energy balance as much as possible throughout the day.

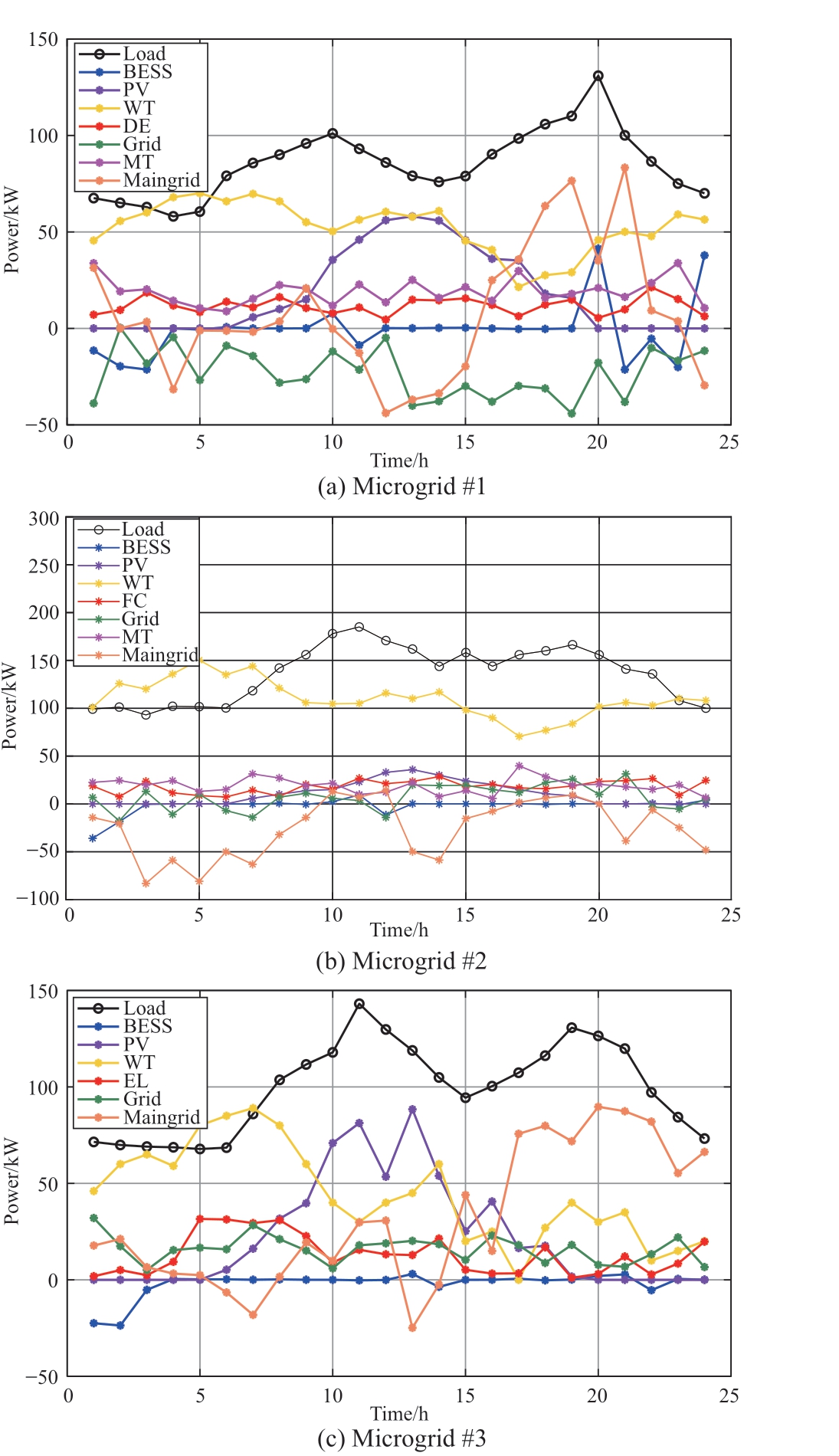
Fig.16 Optimization scheduling results for the microgrids

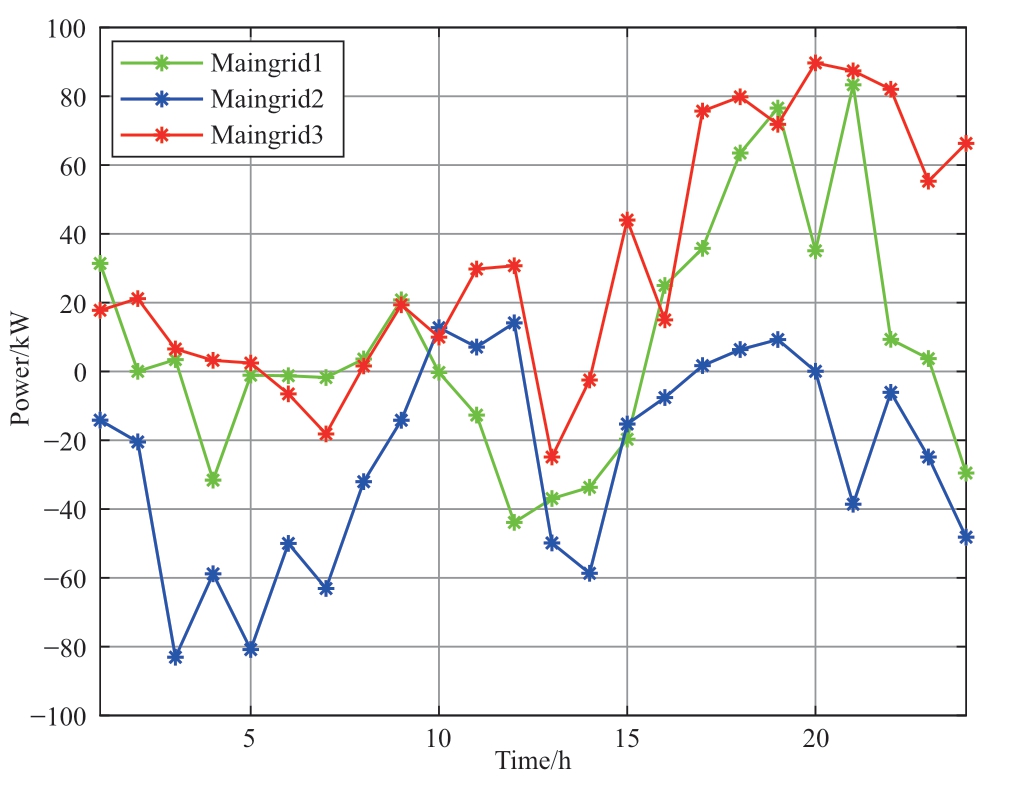
Fig.17 Optimization results of main network interaction

Fig.18 shows that the hydrogen energy load is provided as much as possible to satisfy the power load in Microgrid#3, which alleviates the pressure on the hydrogen energy network.That is, coordinated and optimized utilization of microgrids can be realized.

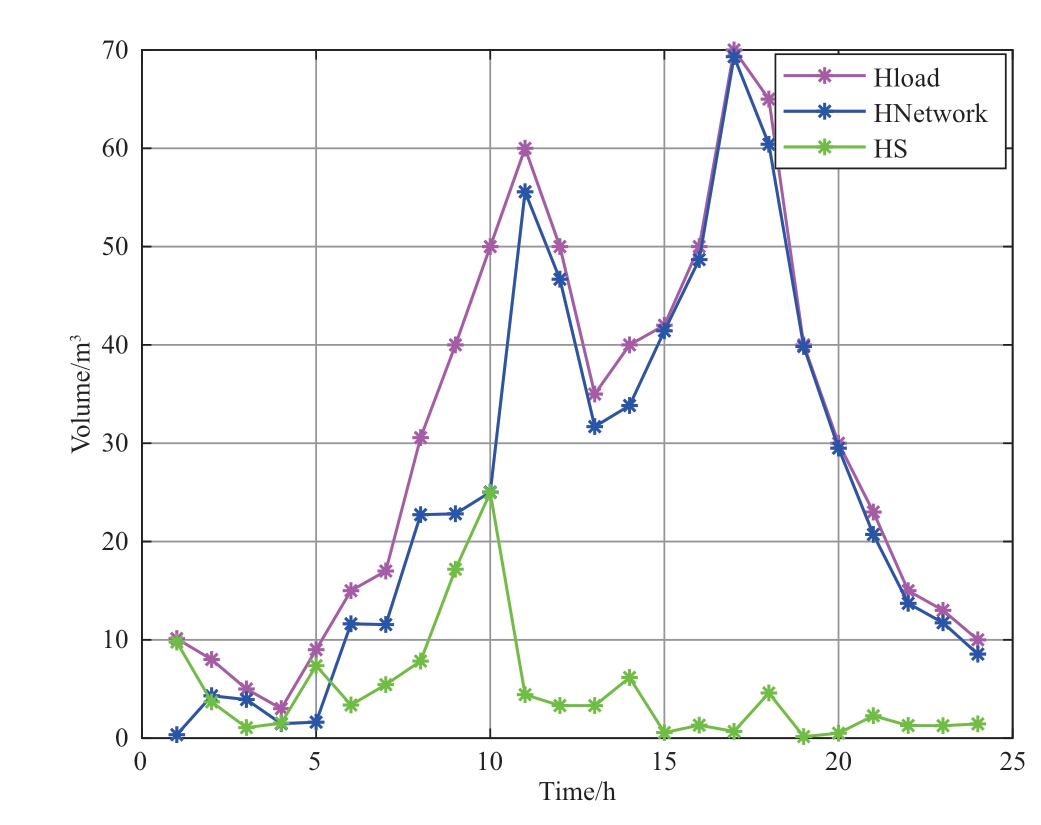
Fig.18 Optimization results of hydrogen energy in Microgrid 3

4 Conclusion

This study proposed a hybrid approach by blending LQPSO with the BiGRU self-attention mechanism.This method was used for solar power prediction by adaptively tuning the hyperparameters of the model while effectively addressing the uncertainty of renewable energies and ensuring reliable operation of the microgrid system.

Subsequently, a multi-objective optimization model for multi-energy microgrids was constructed.A two-stage optimization algorithm based on MO-LQPSO was proposed to realize the comprehensive optimization scheduling of the system.This algorithm ensures a better search performance and balances the global and local search abilities of the algorithm.

Future study can include weather conditions using the numerical weather prediction (NWP).In addition, the system model can be improved to adapt to more complex application scenarios.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant 51977004,and the Beijing Natural Science Foundation under Grant 4212042.

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1]Gao K, Wang T, Han C, et al.(2021) A review of optimization of microgrid operation.Energies, 14(10): 2842

[2]Chen C, Li Y, Qiu W, et al.(2022) Cooperative-game-based dayahead scheduling of local integrated energy systems with shared energy storage.IEEE Transactions on Sustainable Energy, 13(4):1994-2011

[3]Zhou S, Han Y, Mahmoud K, Darwish M, et al.(2023) A novel unified planning model for distributed generation and electric vehicle charging station considering multi-uncertainties and battery degradation.Applied Energy, 348: 121566

[4]Siqin Z, Niu D, Li M, et al.(2022) Distributionally robust dispatching of multi-community integrated energy system considering energy sharing and profit allocation.Applied Energy,321: 119202

[5]Liu L, Yao X, Qi X, et al.(2023) Low-carbon economy configuration strategy of electro-thermal hybrid shared energy storage in multiple multi-energy microgrids considering power to gas and carbon capture system.Journal of Cleaner Production,428: 139366

[6]Tian L, Cheng L, Guo J, et al.(2020) System modeling and optimal dispatching of multi-energy microgrid with energy storage.Journal of Modern Power Systems and Clean Energy,8(5): 809-819

[7]Li Z, Xu Y (2018) Optimal coordinated energy dispatch of a multi-energy microgrid in grid-connected and islanded modes.Applied Energy, 210: 974-986

[8]Shaghaghi-shahr G, Sedighizadeh M, Aghamohammadi M, et al.(2020) Optimal generation scheduling in microgrids using mixed-integer second-order cone programming.Engineering Optimization, 52(12): 2164-2192

[9]Wu L, Yin X, Pan L, et al.(2023) Distributed economic predictive control of integrated energy systems for enhanced synergy and grid response: A decomposition and cooperation strategy.Applied Energy, 349: 121627

[10]Chen T, Cao Y, Qing X, et al.(2022) Multi-energy microgrid robust energy management with a novel decision-making strategy.Energy, 239: 121840

[11]Zou Y, Xu Y, Zhang C (2023) A risk-averse adaptive stochastic optimization method for transactive energy management of a multi-energy microgrid.IEEE Transactions on Sustainable Energy, 14(3): 1599-1611

[12]Hou S, Fujimura S (2023) Day-ahead multi-objective microgrid dispatch optimization based on demand side management via particle swarm optimization.IEEE Transactions on Electrical and Electronic Engineering, 18(1): 25-37

[13]Zhang X, Wang Z, Lu Z (2022) Multi-objective load dispatch for microgrid with electric vehicles using modified gravitational search and particle swarm optimization algorithm.Applied Energy, 306: 118018

[14]Cheng S, Lu H, Lei X, et al.(2018) A quarter century of particle swarm optimization.Complex & Intelligent Systems, 4: 227-239

[15]Anh H P H, Kien C V (2020) Optimal energy management of microgrid using advanced multi-objective particle swarm optimization.Engineering Computations, 37(6): 2085-2110

[16]Hou S, Gebreyesus G D, Fujimura S (2024) Day-ahead multimodal demand side management in microgrid via two-stage improved ring-topology particle swarm optimization.Expert Systems with Applications, 238: 122135

[17]Zou W, Li C, Chen P (2019) An inter type-2 FCR algorithm based T-S fuzzy model for short-term wind power interval prediction.IEEE Transactions on Industrial Informatics, 15(9):4934-4943

[18]Wang H, Liu Y, Zhou B, et al.(2020) Taxonomy research of artificial intelligence for deterministic solar power forecasting.Energy Conversion and Management, 214: 112909

[19]Wang S, Zhang Y, Zhang C, et al.(2020) Improved artificial neural network method for predicting photovoltaic output performance.Global Energy Interconnection, 3(6): 553-561

[20]Wang Q, Pan L, Liu Z, et al.(2024) Interpretable uncertainty forecasting framework for robust configuration of energy storage in a virtual power plant.Journal of Energy Storage, 84: 110800

[21]Wang Q, Pan L, Wang H, et al.(2022) Short-term wind power probabilistic forecasting using a new neural computing approach:GMC-DeepNN-PF.Applied Soft Computing, 126: 109247

[22]Munawar U, Wang Z (2020) A framework of using machine learning approaches for short-term solar power forecasting.Journal of Electrical Engineering & Technology, 15: 561-569

[23]Zhang W, Li Q, He Q (2022) Application of machine learning methods in photovoltaic output power prediction: A review.Journal of Renewable and Sustainable Energy, 14(2)

[24]Azizi N, Yaghoubirad M, Farajollahi M, et al.(2023) Deep learning based long-term global solar irradiance and temperature forecasting using time series with multi-step multivariate output.Renewable Energy, 206: 135-147

[25]Wen L, Zhou K, Yang S, Lu X (2019) Optimal load dispatch of community microgrid with deep learning based solar power and load forecasting.Energy, 171: 1053-1065

[26]Jiang Y, Zheng L, Ding X (2021) Ultra-short-term prediction of photovoltaic output based on an LSTM-ARMA combined model driven by EEMD.Journal of Renewable and Sustainable Energy,13(4)

[27]Shang Y, Shang Y, Yu H, et al.(2021) Achieving efficient and adaptable dispatching for vehicle-to-grid using distributed edge computing and attention-based LSTM.IEEE Transactions on Industrial Informatics, 18(10): 6915-6926

[28]Sun J, Fang W, Wu X, et al.(2011) QoS multicast routing using a quantum-behaved particle swarm optimization algorithm.Engineering Applications of Artificial Intelligence, 24(1): 123-131

[29]Li D, Sun G, Miao S, et al.(2022) A short-term electric load forecast method based on improved sequence-to-sequence GRU with adaptive temporal dependence.International Journal of Electrical Power & Energy Systems, 137: 107627

[30]Vaswani A, Shazeer N, Parmar N, et al.(2017) Attention is all you need.Advances in Neural Information Processing Systems, 30

[31]Solar Power History Data (2023) Australian PV Institute.http://apvi.org.au/ (accessed 19 Jun 2023)

[32]Fang X, Dong W, Wang Y, et al.(2022) Multiple time-scale energy management strategy for a hydrogen-based multi-energy microgrid.Applied Energy, 328: 120195

[33]Pashaei H, Nojavan S, Nourollahi R, et al.(2019) Optimal economic-emission performance of fuel cell/CHP/storage based microgrid.International Journal of Hydrogen Energy, 44(13):6896-6908

[34]Zhang D, Zhu H, Zhang H, et al.(2021) Multi-objective optimization for smart integrated energy system considering demand responses and dynamic prices.IEEE Transactions on Smart Grid, 13(2): 1100-1112

[35]Power Data for Integration Studies (2023) U.S.Department of Energy.https://energy.gov/eere/ (accessed 29 Sept 2023)

Scan for more details

Received: 6 February 2024/Revised: 30 March 2024/Accepted: 8 May 2024/Published: 25 June 2024

Peng Li

lipeng@bjtu.edu.cn

Yuchen Duan

duanyuch@163.com

Jing Xia

xiajingbeijing@126.com

2096-5117/© 2024 Global Energy Interconnection Group Co.Ltd.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co., Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/ ).

Biographies

Yuchen Duan received bachelor’s degree at Beijing Forestry University, Beijing, China, in 2021.He is working towards a master’s degree at Beijing Jiaotong University, Beijing, China.His research interests include modeling and optimization of multi-energy microgrid system and renewable energy forecasting.

Peng Li received the Ph.D.degree from Harbin Institute of Technology, Harbin, China,in 2009.He undertook postdoctoral research at Beijing Jiaotong University, China, from 2009 to 2011, and visiting research at University of Melbourne, Australia, from 2013 to 2014.He is with School of Automation and Intelligence,Beijing Jiaotong University, Beijing, China.His research interests include automatic control, renewable energies,and smart grids.

Jing Xia received the Ph.D.degree from North China Electric Power University, Beijing,China, in 2023.She worked at Goldwind Windenergy GmbH, Germany, from 2010 to 2011.She is with Goldwind Science &Technology Co., Ltd., Beijing, China.Her research interests include wind turbine design and power systems integration.

(Editor Zedong Zhang)