0 Introduction
Global decarbonization efforts have significantly boosted the widespread deployment of various renewable energy resources [1].However,the rapid proliferation of residential distributed energy resources (RDER) in distribution networks,especially energy storage systems (ESS),electric vehicles (EV),and controllable loads (CL),has exacerbated the difficulty in balancing electricity and challenged the secure operation of the grid [2,3].Virtual power plants(VPPs) have emerged as a new technique for coordinating demand-side RDER and have drawn significant attention from industry and academia [4].
VPPs typically optimize operational policies for aggregated resources based on power tariffs,thereby alleviating the operational burden on the grid.In traditional studies,determining the optimal scheduling strategies for VPPs entails solving sophisticated optimization problems that are nonconvex and NP-hard.However,operations research-based VPP scheduling methods,such as semidefinite programs [5],second-order cone programs[6],stochastic optimization [7],robust optimization [8],and heuristic algorithms [9],rely heavily on accurate parameters and intact physical models.However,these assumptions are generally impractical in actual distribution networks.Furthermore,these methods require powerful computational platforms and often struggle to provide feasible solutions within a limited timeframe,particularly for large-scale power plants with numerous control variables and operational constraints.
With the rapid development of artificial intelligence,model-free reinforcement learning (RL) has been widely used in various scenarios.At present,classical discreteaction RL algorithms include [10],DQN [11],and Dueling DQN [12],and continuous-action RL algorithms include DDPG [13],TRPO [14],PPO [15],and SAC [16].The sampling efficiency is improved by proposing a modelbased RL algorithm called MBPO [17].Online interaction is difficult in some scenarios,such as user feedback systems;thus,CQL has been proposed to learn from offline data [18].The problem of sparse rewards is solved by developing a goal-oriented RL algorithm HER [19] to improve the utilization rate of the “failure” experience through hindsight experience replay.
Extensive research has been conducted on deep reinforcement learning (DRL)-based VPP scheduling schemes to counteract the shortcomings of the former model-driven approaches.These methods guide agents in learning economically oriented scheduling strategies by interacting with VPP simulators.Well-trained policies can be directly deployed into a VPP energy management system without solving complex optimization models,enabling timely decision-making for VPPs.Ref [20] employed Q-learning to determine the optimal bidding strategy for a VPP.Ref [21] employed a double deep Q-Network to control the VPP and track target load profiles.Ref [22]utilized a deep Q-Network to adaptively determine the optimal DR pricing strategy for a VPP.Ref [23] applied the DDPG to solve the VPP pricing problem.Ref [24]optimal coordination for microgrids owned virtual power plants via Twin Delayed DDPG (TD3).Ref [25] efficiently decompose the frequency regulation requests issued by a power system superior to DER aggregators via SAC.
Although significant progress has been made in research on VPP scheduling using deep reinforcement learning,several unresolved challenges still require further investigation.First,these studies typically focused solely on VPP schedules in the real-time market with limited attention to the day-ahead market.Limited by a strong uncertainty endowment,RES are more inclined to participate in realtime markets,increasing intra-day trading demand.The difference in clearing results between the real-time and day-ahead markets increases,which raises intra-day price volatility [26].In situations where real-time power tariffs fluctuate sharply,this may result in higher purchase costs.Coordinating day-ahead and real-time markets enables the better management of consumption risks.Therefore,developing day-ahead schedules is necessary.
On the other hand,they incorporate inequality constraints in the VPP scheduling problem as a penalty term into the reward function;however,determining a proper penalty coefficient is difficult for reward-driven DRL.Even with a large penalty coefficient,it is difficult to guarantee that the constraints are satisfied strictly.Moreover,a centralized controlled VPP structure was used in these studies.Once a new RDER is integrated into a VPP,a welltrained DRL model requires retraining,which impedes the plug-and-play and scalability.A fully distributed virtual power plant (FDVPP) allows RDER agents to make independent decisions and participate in the power market[27].The power of the RDER is generally small,and there is almost no cooperative competition between them;therefore,in this study,we used the FDVPP structure to improve the scalability of the residential virtual power plant (RVPP).
We propose a novel GRU-CSAC learning-enabled scheduling method for the VPP to address these challenges.The primary contributions of this study are as follows.
1) A novel RVPP scheduling method that leverages the GRU-integrated DRL algorithm is proposed to guide the RVPP in participating effectively in the day-ahead market(DAM) and real-time balancing market (RBM),thereby reducing electricity purchase costs and consumption risks.
2) To avoid violating the constraints during training,the Lagrangian relaxation technique guarantees introduced to transform the constrained Markov decision process(CMDP) into an unconstrained optimization problem,which guarantees that the constraints are strictly satisfied without determining the penalty coefficients.
3) To enhance the scalability of the CSAC-based RVPP scheduling approach,we designed a fully distributed scheduling architecture that enables plug-and-play of the RDER.
The remainder of this paper is organized as follows.Section 1 presents the formulation of the model-based RVPP scheduling model.Section 2 establishes the Markovdecision-process-based RVPP scheduling model,and Section 3 presents the GRU-CSAC-based RVPP scheduling method.The numerical simulation is described in detail in section 4.Finally,Section 5 presents conclusions and outlines future work.
Global decarbonization efforts have significantly boosted the widespread deployment of various renewable energy resources [1].However,the rapid proliferation of residential distributed energy resources (RDER) in distribution networks,especially energy storage systems (ESS),electric vehicles (EV),and controllable loads (CL),has exacerbated the difficulty in balancing electricity and challenged the secure operation of the grid [2,3].Virtual power plants(VPPs) have emerged as a new technique for coordinating demand-side RDER and have drawn significant attention from industry and academia [4].
VPPs typically optimize operational policies for aggregated resources based on power tariffs,thereby alleviating the operational burden on the grid.In traditional studies,determining the optimal scheduling strategies for VPPs entails solving sophisticated optimization problems that are nonconvex and NP-hard.However,operations research-based VPP scheduling methods,such as semidefinite programs [5],second-order cone programs[6],stochastic optimization [7],robust optimization [8],and heuristic algorithms [9],rely heavily on accurate parameters and intact physical models.However,these assumptions are generally impractical in actual distribution networks.Furthermore,these methods require powerful computational platforms and often struggle to provide feasible solutions within a limited timeframe,particularly for large-scale power plants with numerous control variables and operational constraints.
With the rapid development of artificial intelligence,model-free reinforcement learning (RL) has been widely used in various scenarios.At present,classical discreteaction RL algorithms include [10],DQN [11],and Dueling DQN [12],and continuous-action RL algorithms include DDPG [13],TRPO [14],PPO [15],and SAC [16].The sampling efficiency is improved by proposing a modelbased RL algorithm called MBPO [17].Online interaction is difficult in some scenarios,such as user feedback systems;thus,CQL has been proposed to learn from offline data [18].The problem of sparse rewards is solved by developing a goal-oriented RL algorithm HER [19] to improve the utilization rate of the “failure” experience through hindsight experience replay.
Extensive research has been conducted on deep reinforcement learning (DRL)-based VPP scheduling schemes to counteract the shortcomings of the former model-driven approaches.These methods guide agents in learning economically oriented scheduling strategies by interacting with VPP simulators.Well-trained policies can be directly deployed into a VPP energy management system without solving complex optimization models,enabling timely decision-making for VPPs.Ref [20] employed Q-learning to determine the optimal bidding strategy for a VPP.Ref [21] employed a double deep Q-Network to control the VPP and track target load profiles.Ref [22]utilized a deep Q-Network to adaptively determine the optimal DR pricing strategy for a VPP.Ref [23] applied the DDPG to solve the VPP pricing problem.Ref [24]optimal coordination for microgrids owned virtual power plants via Twin Delayed DDPG (TD3).Ref [25] efficiently decompose the frequency regulation requests issued by a power system superior to DER aggregators via SAC.
Although significant progress has been made in research on VPP scheduling using deep reinforcement learning,several unresolved challenges still require further investigation.First,these studies typically focused solely on VPP schedules in the real-time market with limited attention to the day-ahead market.Limited by a strong uncertainty endowment,RES are more inclined to participate in realtime markets,increasing intra-day trading demand.The difference in clearing results between the real-time and day-ahead markets increases,which raises intra-day price volatility [26].In situations where real-time power tariffs fluctuate sharply,this may result in higher purchase costs.Coordinating day-ahead and real-time markets enables the better management of consumption risks.Therefore,developing day-ahead schedules is necessary.
On the other hand,they incorporate inequality constraints in the VPP scheduling problem as a penalty term into the reward function;however,determining a proper penalty coefficient is difficult for reward-driven DRL.Even with a large penalty coefficient,it is difficult to guarantee that the constraints are satisfied strictly.Moreover,a centralized controlled VPP structure was used in these studies.Once a new RDER is integrated into a VPP,a welltrained DRL model requires retraining,which impedes the plug-and-play and scalability.A fully distributed virtual power plant (FDVPP) allows RDER agents to make independent decisions and participate in the power market[27].The power of the RDER is generally small,and there is almost no cooperative competition between them;therefore,in this study,we used the FDVPP structure to improve the scalability of the residential virtual power plant (RVPP).
We propose a novel GRU-CSAC learning-enabled scheduling method for the VPP to address these challenges.The primary contributions of this study are as follows.
1) A novel RVPP scheduling method that leverages the GRU-integrated DRL algorithm is proposed to guide the RVPP in participating effectively in the day-ahead market(DAM) and real-time balancing market (RBM),thereby reducing electricity purchase costs and consumption risks.
2) To avoid violating the constraints during training,the Lagrangian relaxation technique guarantees introduced to transform the constrained Markov decision process(CMDP) into an unconstrained optimization problem,which guarantees that the constraints are strictly satisfied without determining the penalty coefficients.
3) To enhance the scalability of the CSAC-based RVPP scheduling approach,we designed a fully distributed scheduling architecture that enables plug-and-play of the RDER.
The remainder of this paper is organized as follows.Section 1 presents the formulation of the model-based RVPP scheduling model.Section 2 establishes the Markovdecision-process-based RVPP scheduling model,and Section 3 presents the GRU-CSAC-based RVPP scheduling method.The numerical simulation is described in detail in section 4.Finally,Section 5 presents conclusions and outlines future work.
1 Problem formulation
The RVPP comprises four categories of RDERs,namely,ESS,EV,air conditioner (AC),and electric water heater (EWH),within the RVPP framework,as shown in Fig.1.The RVPP adopts the structure of the FDVPP and assumes that there is no cooperation or competition among the RDERs.An individual controller regulated each RDER,and its next-day operating schedules were reported to the RVPP cloud platform.The RVPP delivers power tariff signals to customers and aggregates their power plans to engage in the DAM and RBM.
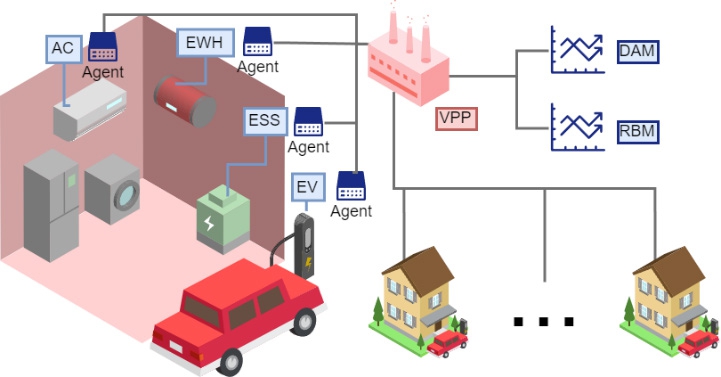
Fig.1 Decentralized RVPP model
The RVPP comprises four categories of RDERs,namely,ESS,EV,air conditioner (AC),and electric water heater (EWH),within the RVPP framework,as shown in Fig.1.The RVPP adopts the structure of the FDVPP and assumes that there is no cooperation or competition among the RDERs.An individual controller regulated each RDER,and its next-day operating schedules were reported to the RVPP cloud platform.The RVPP delivers power tariff signals to customers and aggregates their power plans to engage in the DAM and RBM.

Fig.1 Decentralized RVPP model
1.1 Market
It is not feasible for many residential loads with small capacities to participate directly in the electricity market[28].The RVPP serves as a bridge between these two entities.The RVPP scheduling problem in this study aims to minimize the total purchasing costs from the upstream grid during the DAM and RBM.The optimization problem for the RVPP is formulated as follows:
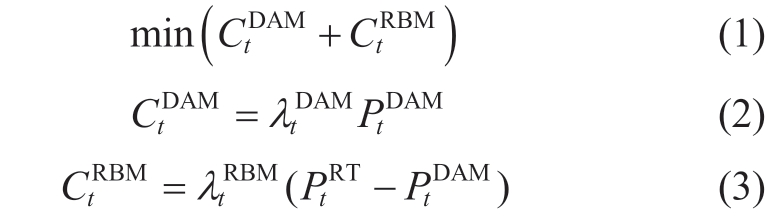
where 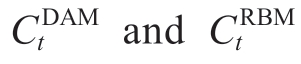 denote the purchasing costs in DAM and RBM,respectively.
denote the purchasing costs in DAM and RBM,respectively.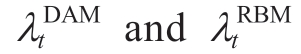 are the corresponding tariffs,respectively.
are the corresponding tariffs,respectively.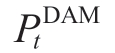 represents the electricity demand reported by RDER to RVPP in DAM,while
represents the electricity demand reported by RDER to RVPP in DAM,while 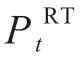 is the electricity demand in RBM.In this problem,the RVPP is treated as a price taker,allowing simultaneous participation in the DAM and RBM.Here,our focus is solely on the scheduling strategies of RDER agents in the RVPP,disregarding grid constraints and market game processes.
is the electricity demand in RBM.In this problem,the RVPP is treated as a price taker,allowing simultaneous participation in the DAM and RBM.Here,our focus is solely on the scheduling strategies of RDER agents in the RVPP,disregarding grid constraints and market game processes.
It is not feasible for many residential loads with small capacities to participate directly in the electricity market[28].The RVPP serves as a bridge between these two entities.The RVPP scheduling problem in this study aims to minimize the total purchasing costs from the upstream grid during the DAM and RBM.The optimization problem for the RVPP is formulated as follows:
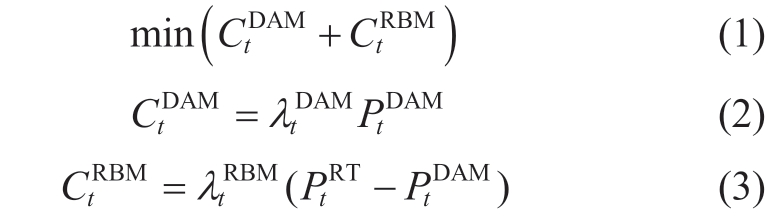
where ![]() denote the purchasing costs in DAM and RBM,respectively.
denote the purchasing costs in DAM and RBM,respectively.![]() are the corresponding tariffs,respectively.
are the corresponding tariffs,respectively.![]() represents the electricity demand reported by RDER to RVPP in DAM,while
represents the electricity demand reported by RDER to RVPP in DAM,while ![]() is the electricity demand in RBM.In this problem,the RVPP is treated as a price taker,allowing simultaneous participation in the DAM and RBM.Here,our focus is solely on the scheduling strategies of RDER agents in the RVPP,disregarding grid constraints and market game processes.
is the electricity demand in RBM.In this problem,the RVPP is treated as a price taker,allowing simultaneous participation in the DAM and RBM.Here,our focus is solely on the scheduling strategies of RDER agents in the RVPP,disregarding grid constraints and market game processes.
1.2 ESS model
Given the efficiency of the power conversion system(PCS),the relationship between the set power and actual power is as follows:

Given the efficiency of the power conversion system(PCS),the relationship between the set power and actual power is as follows:

1.3 EV model
The charging power and SOC of the EV should be subject to the following constraints.The vehicle-to-grid mode is not accounted for here.

The charging power and SOC of the EV should be subject to the following constraints.The vehicle-to-grid mode is not accounted for here.

1.4 EWH model
The thermal energy stored in the water tank is formulated as

where m and c are constants that represent the mass and specific heat capacity of water,respectively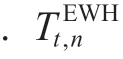 and
and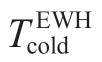 are the temperatures of the water in the tank and cold water,respectively [29].The cold water temperature is usually assumed to be 20 °C in engineering practice.
are the temperatures of the water in the tank and cold water,respectively [29].The cold water temperature is usually assumed to be 20 °C in engineering practice.
The updating process of thermal storage in the hot water tank is:
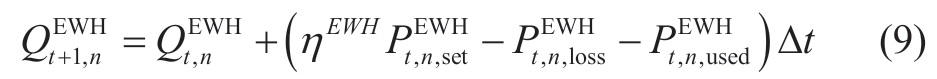
where 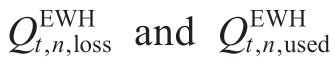 denote the dissipated thermal energy and the thermal energy used by residents,respectively
denote the dissipated thermal energy and the thermal energy used by residents,respectively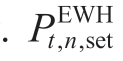 denotes the set boiling power of the nth EWH.
denotes the set boiling power of the nth EWH.
The thermal energy and EWH power should satisfy the following constraints:
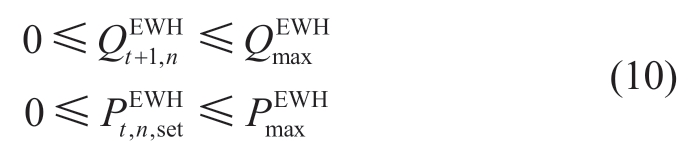
where 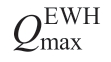 denotes the tank capacity
denotes the tank capacity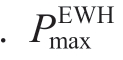 represents the maximum boiling power of the EWH.
represents the maximum boiling power of the EWH.
The thermal energy stored in the water tank is formulated as
where m and c are constants that represent the mass and specific heat capacity of water,respectively![]() and
and![]() are the temperatures of the water in the tank and cold water,respectively [29].The cold water temperature is usually assumed to be 20 °C in engineering practice.
are the temperatures of the water in the tank and cold water,respectively [29].The cold water temperature is usually assumed to be 20 °C in engineering practice.
The updating process of thermal storage in the hot water tank is:
where ![]() denote the dissipated thermal energy and the thermal energy used by residents,respectively
denote the dissipated thermal energy and the thermal energy used by residents,respectively![]() denotes the set boiling power of the nth EWH.
denotes the set boiling power of the nth EWH.
The thermal energy and EWH power should satisfy the following constraints:
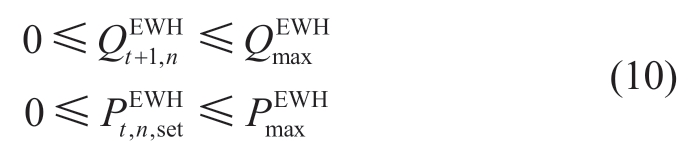
where ![]() denotes the tank capacity
denotes the tank capacity![]() represents the maximum boiling power of the EWH.
represents the maximum boiling power of the EWH.
1.5 AC model
Herein,we did not consider the thermodynamic equation and focused only on its reducibility [30].The reduced power when the AC receives the reduction command from the RVPP is formulated as
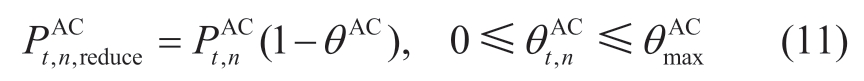
where 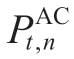 represents the power of the AC at time t,and the load reduction factor
represents the power of the AC at time t,and the load reduction factor 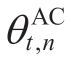 must be less than the maximum load reduction factor
must be less than the maximum load reduction factor 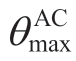 agreed upon by the user and VPP.
agreed upon by the user and VPP.
Herein,we did not consider the thermodynamic equation and focused only on its reducibility [30].The reduced power when the AC receives the reduction command from the RVPP is formulated as
where ![]() represents the power of the AC at time t,and the load reduction factor
represents the power of the AC at time t,and the load reduction factor ![]() must be less than the maximum load reduction factor
must be less than the maximum load reduction factor ![]() agreed upon by the user and VPP.
agreed upon by the user and VPP.
2 CMDP-based RVPP scheduling modeling
In our RVPP scheduling problem,the decision of each agent at any time slot is not connected to the previous RVPP historical states,which is compatible with Markovianity.Regardless of the decisions made by the agent,the RVPP transfers from the current state to the next state.In addition,all the agents operate in a fully distributed environment.The abovementioned individual points involve all components of the Markov decision process: agents,states,and actions.Moreover,the decisions of all the agents must fulfill their operational constraints.Thus,it is reasonable to formulate the RVPP scheduling problem as a CMDP with a discrete time series that is commonly defined by the following multivariate tuple:

where S is the set of states;A is the set of actions;R(s,a)is the reward function computed based on the states and actions;C(s,a) is the cost function;and P(s′|s,a)denotes the probabilistic transfer function already included in the model of the environment.The objective of the CMDP problem is to find the optimal policy π*,which is the policy that maximizes the long-term discount reward R(π) and satisfies the constraints of long-term discount cost Ci(π),formulated as
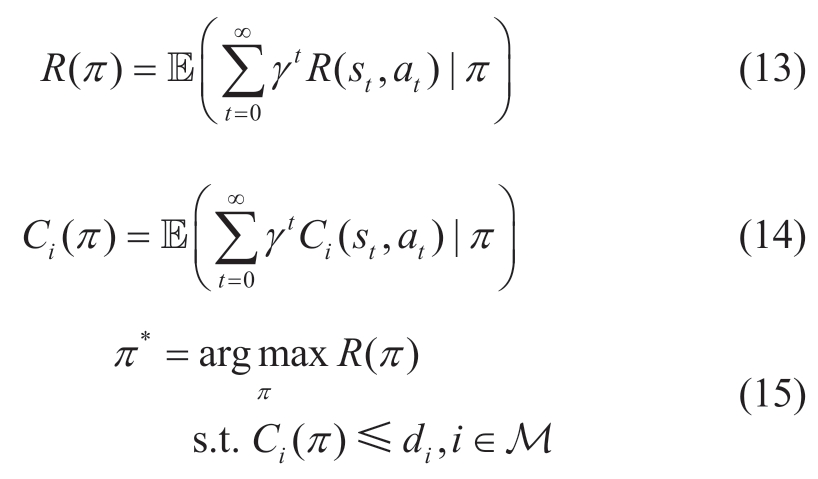
where M={1,2,...,m} denotes the number of constraints and γ∈[0,1) the discount factor.Detailed definitions of the elements of the CMDP-based RVPP scheduling problem are as follows.
State space: The state space of all the agents contains the DAM and RBM prices and the timestamp ts.In addition,the state space of the ESS contains the SOC and energy;the state space of the EWH contains the temperature of the water in the tank,the heat stored,and the heat consumed;the state space of the EV contains the SOC and energy;and the state space of the AC contains the user’s current set power and reduced power.
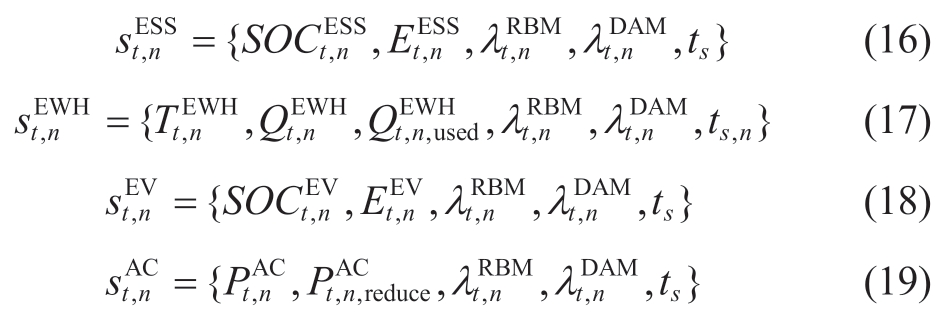
Action Space: The actions of the ESS,EWH,and EV are the set powers of the respective devices,whereas the action of the AC is the load reduction factor.Note that when the RVPP participates in the market,it multiplies the predicted and real-time power of the AC by a reduction factor.

Reward function: For residents,the purpose of joining the RVPP is to reduce electricity costs.All the agents use the following reward: revenue from selling electricity to the grid by the RVPP in the DAM and RBM.
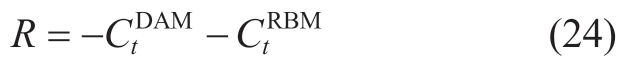
Cost function: The ESS may engage in ineffective actions such as frequent charge and discharge cycles when electricity prices remain constant.This behavior can result in wasteful degradation of the ESS lifespan.Therefore,we considered the lifetime discount cost of the ESS.
The relationship between the discharge depth of the electrochemical energy storage and cycle life is fitted in the form of a power function [31] and can be formulated as
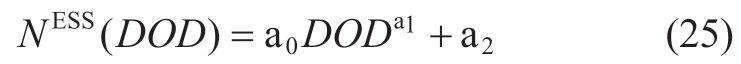
where DOD denotes the discharge depth of the battery,and NS(DOD)denotes the maximum number of cycles that the battery can undergo at a given discharge depth.a0,a1,and a2 represent the fitting parameters.
The cost of ESS life can be approximately calculated as

Economy is the main factor influencing industrial users’adjustment of electricity consumption strategies.However,unreasonable economic scheduling strategies for residential users can significantly affect their comfort and satisfaction[32].To ensure user satisfaction,we introduced a comfort penalty factor formulated as
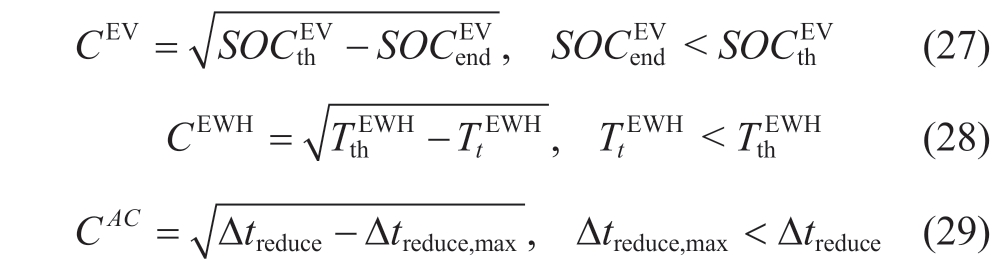
where 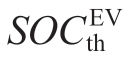 denotes the desired charging threshold for the EV owners.
denotes the desired charging threshold for the EV owners.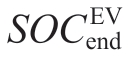 denotes the EV SOC at the end of charging.
denotes the EV SOC at the end of charging.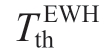 indicates the minimum hot water temperature desired by residents.Δtreduce denotes the reduction time of the AC load and Δtreduce,max is the upper limit that residents accept.
indicates the minimum hot water temperature desired by residents.Δtreduce denotes the reduction time of the AC load and Δtreduce,max is the upper limit that residents accept.
The reasons for adopting this form of the penalty function are to ensure that the gradient of the penalty will not be zero and that the gradient of the penalty becomes larger as it approaches the boundary.
The comfort cost associated with EV arises only when the owner enters the vehicle after charging is completed.Similarly,the comfort cost of EWH is incurred only when residents consume hot water,with a cost of zero during all other periods.
In our RVPP scheduling problem,the decision of each agent at any time slot is not connected to the previous RVPP historical states,which is compatible with Markovianity.Regardless of the decisions made by the agent,the RVPP transfers from the current state to the next state.In addition,all the agents operate in a fully distributed environment.The abovementioned individual points involve all components of the Markov decision process: agents,states,and actions.Moreover,the decisions of all the agents must fulfill their operational constraints.Thus,it is reasonable to formulate the RVPP scheduling problem as a CMDP with a discrete time series that is commonly defined by the following multivariate tuple:
where S is the set of states;A is the set of actions;R(s,a)is the reward function computed based on the states and actions;C(s,a) is the cost function;and P(s′|s,a)denotes the probabilistic transfer function already included in the model of the environment.The objective of the CMDP problem is to find the optimal policy π*,which is the policy that maximizes the long-term discount reward R(π) and satisfies the constraints of long-term discount cost Ci(π),formulated as
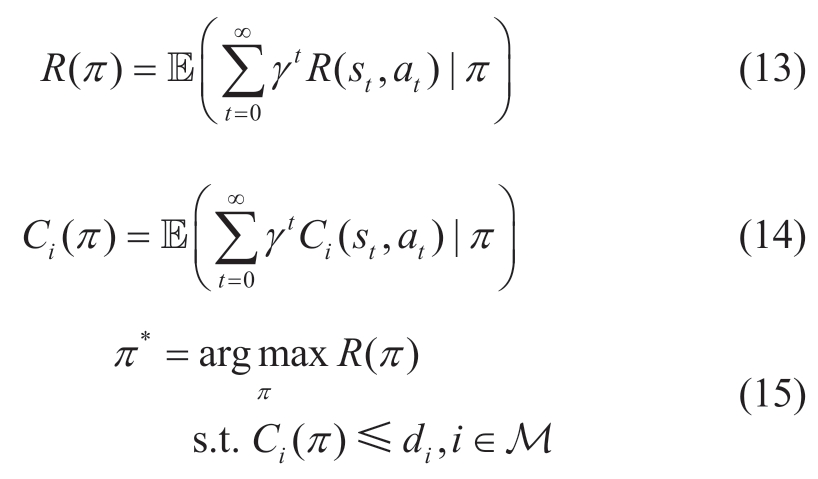
where M={1,2,...,m} denotes the number of constraints and γ∈[0,1) the discount factor.Detailed definitions of the elements of the CMDP-based RVPP scheduling problem are as follows.
State space: The state space of all the agents contains the DAM and RBM prices and the timestamp ts.In addition,the state space of the ESS contains the SOC and energy;the state space of the EWH contains the temperature of the water in the tank,the heat stored,and the heat consumed;the state space of the EV contains the SOC and energy;and the state space of the AC contains the user’s current set power and reduced power.
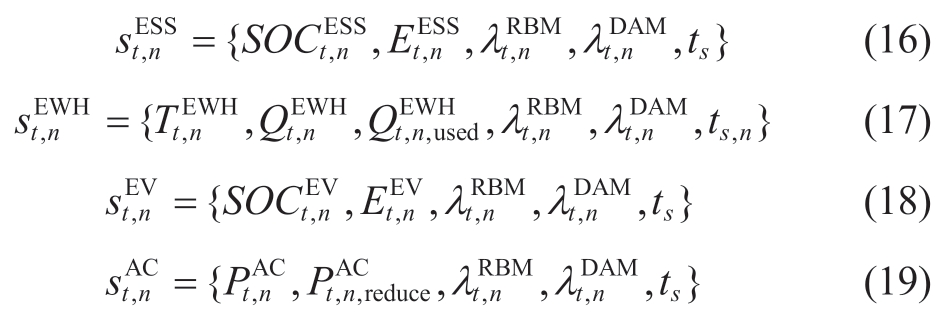
Action Space: The actions of the ESS,EWH,and EV are the set powers of the respective devices,whereas the action of the AC is the load reduction factor.Note that when the RVPP participates in the market,it multiplies the predicted and real-time power of the AC by a reduction factor.

Reward function: For residents,the purpose of joining the RVPP is to reduce electricity costs.All the agents use the following reward: revenue from selling electricity to the grid by the RVPP in the DAM and RBM.
Cost function: The ESS may engage in ineffective actions such as frequent charge and discharge cycles when electricity prices remain constant.This behavior can result in wasteful degradation of the ESS lifespan.Therefore,we considered the lifetime discount cost of the ESS.
The relationship between the discharge depth of the electrochemical energy storage and cycle life is fitted in the form of a power function [31] and can be formulated as
where DOD denotes the discharge depth of the battery,and NS(DOD)denotes the maximum number of cycles that the battery can undergo at a given discharge depth.a0,a1,and a2 represent the fitting parameters.
The cost of ESS life can be approximately calculated as

Economy is the main factor influencing industrial users’adjustment of electricity consumption strategies.However,unreasonable economic scheduling strategies for residential users can significantly affect their comfort and satisfaction[32].To ensure user satisfaction,we introduced a comfort penalty factor formulated as
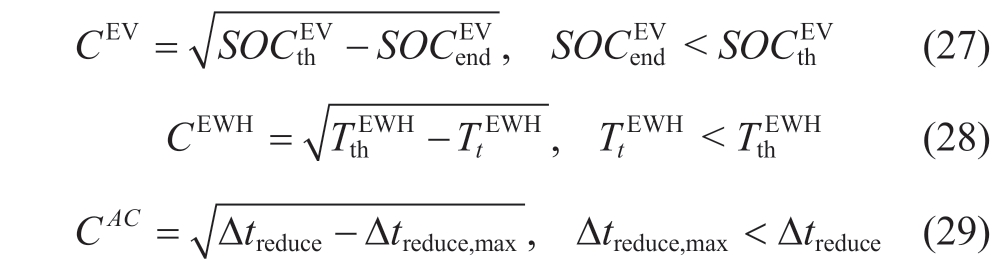
where ![]() denotes the desired charging threshold for the EV owners.
denotes the desired charging threshold for the EV owners.![]() denotes the EV SOC at the end of charging.
denotes the EV SOC at the end of charging.![]() indicates the minimum hot water temperature desired by residents.Δtreduce denotes the reduction time of the AC load and Δtreduce,max is the upper limit that residents accept.
indicates the minimum hot water temperature desired by residents.Δtreduce denotes the reduction time of the AC load and Δtreduce,max is the upper limit that residents accept.
The reasons for adopting this form of the penalty function are to ensure that the gradient of the penalty will not be zero and that the gradient of the penalty becomes larger as it approaches the boundary.
The comfort cost associated with EV arises only when the owner enters the vehicle after charging is completed.Similarly,the comfort cost of EWH is incurred only when residents consume hot water,with a cost of zero during all other periods.
3 GRU-CSAC-based RVPP scheduling method
The SAC algorithm is an off-policy approach that relies on the entropy framework.It is well known for its exceptional exploration capabilities,which allow the easy scalability of complex VPP scheduling problems.Furthermore,compared with algorithms such as DDPG and TD3,SAC eliminates the need for time-consuming manual hyperparameter tuning and exhibits higher levels of robustness [33].
The central concept of the SAC algorithm revolves around enhancing long-term rewards while maximizing randomness.This is achieved by incorporating entropy,which serves as a metric for evaluating the level of randomness of the algorithm.By integrating the entropy into a long-term reward,the algorithm is encouraged to actively increase its level of randomness.The entropy of scheduling policies at time t is denoted as
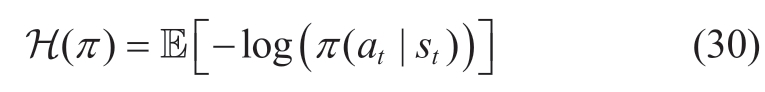
To guarantee the minimum level of randomness required by the algorithm,we incorporate the minimum entropy constraint:
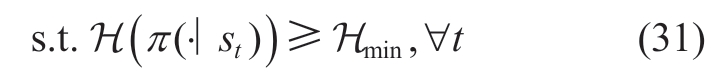
To solve the RVPP scheduling model based on the CMDP,we applied the Lagrangian relaxation technique to convert the problem into an unconstrained optimization problem.The transformed RVPP unconstrained scheduling problem is expressed as follows:
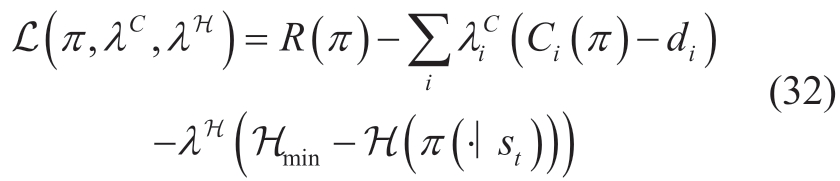
where  and λHare the Lagrangian coefficients of the constraints and entropy,respectively.λHis commonly known as a temperature hyperparameter[16],and for the purpose of this study,we interpreted it as a Lagrangian dual variable.The dual variables in constrained soft actor-critic (CSAC) dynamically adjust the relative importance of each constraint.
and λHare the Lagrangian coefficients of the constraints and entropy,respectively.λHis commonly known as a temperature hyperparameter[16],and for the purpose of this study,we interpreted it as a Lagrangian dual variable.The dual variables in constrained soft actor-critic (CSAC) dynamically adjust the relative importance of each constraint.
The objective function for solving the RVPP unconstrained scheduling problem is formulated as follows:
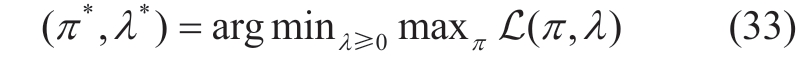
This equation represents the solution to maximize the Lagrangian function with respect to the policy π* and minimize the optimal Lagrangian coefficient λ*,where λ includes both λC andλH.We employed the primaldual optimization (PDO) method to iteratively update these parameters.The iterative formula is as follows:
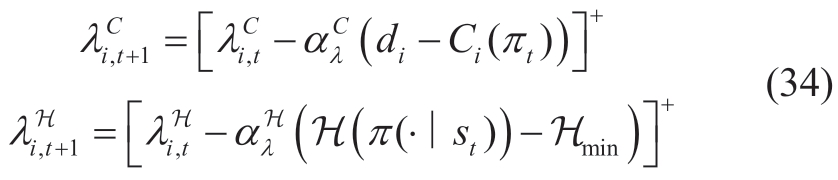
where 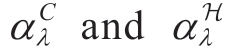 denote the learning rates for the corresponding parameters,respectively.They are multiplied by the partial derivatives of the Lagrangian function with respect to the dual variables and used for gradient descent.The notation [x]+=max{0,x} is used to enforce that the dual parameters remain non-negative.When updating
denote the learning rates for the corresponding parameters,respectively.They are multiplied by the partial derivatives of the Lagrangian function with respect to the dual variables and used for gradient descent.The notation [x]+=max{0,x} is used to enforce that the dual parameters remain non-negative.When updating 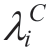 andλH,the policy π needs to be fixed.On the contrary,when updating the policy π,
andλH,the policy π needs to be fixed.On the contrary,when updating the policy π,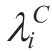 and λH need to be fixed.
and λH need to be fixed.

where y(rt,st+1) is the target in the root mean squared error,formulated as
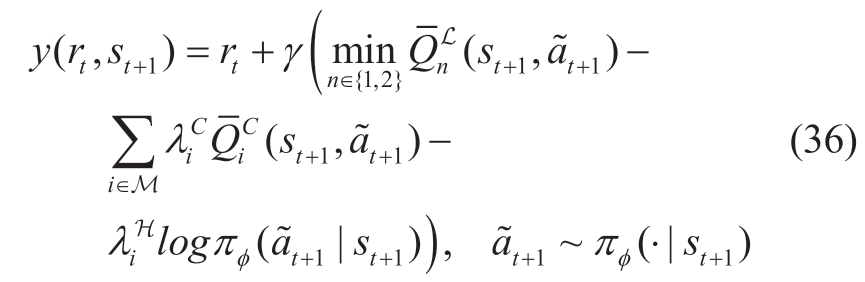
where 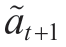 denotes the next action sampled from the policy based on the next state.Notably,during off-policy algorithm training,(st,at,rt,st+1)is typically randomly sampled from the replay buffer D to reduce the correlation between samples.To improve the learning efficiency and stability of the algorithm,we used the clipped double-Q trick,which takes a smaller Q-value between the two Q networks to reduce overestimation during the optimization process[34]
denotes the next action sampled from the policy based on the next state.Notably,during off-policy algorithm training,(st,at,rt,st+1)is typically randomly sampled from the replay buffer D to reduce the correlation between samples.To improve the learning efficiency and stability of the algorithm,we used the clipped double-Q trick,which takes a smaller Q-value between the two Q networks to reduce overestimation during the optimization process[34] are critical networks for estimating the long-term costs and target networks,respectively.We used the following mean squared error as the loss function to optimize the estimation of the long-term cost:
are critical networks for estimating the long-term costs and target networks,respectively.We used the following mean squared error as the loss function to optimize the estimation of the long-term cost:
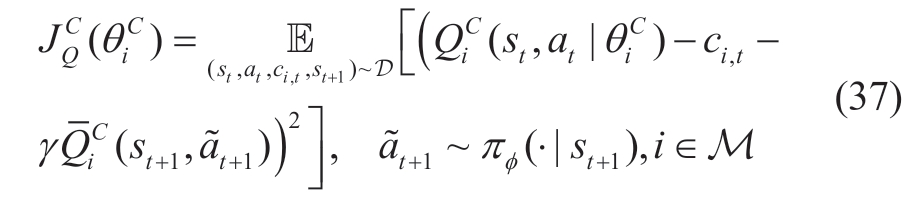
where π(s|φ) denotes the actor network of the SAC,which is a stochastic policy algorithm.It outputs a normal distribution with parameters µφ(s) andσφ(s).The output action values were sampled from this distribution using a reparameterization technique,enabling gradient computation and backpropagation.
A common practice for actions with a finite range is passing the sampled actions through a hyperbolic tangent or sigmoid function to ensure that the action values,such as the set powers of the EV and ESS,fall within the specified range.The sampling of actions is expressed as follows:
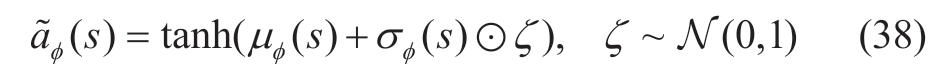
where ζ is a parameter-independent random variable that follows a standard normal distribution.
However,this makes it difficult for the agent to explore the boundary values.For scenarios that require high-frequency boundary actions,the effectiveness of the algorithm cannot be guaranteed.Our solution introduces a boundary action zone βb to ensure that RVPP agents can explore sufficient boundary values.
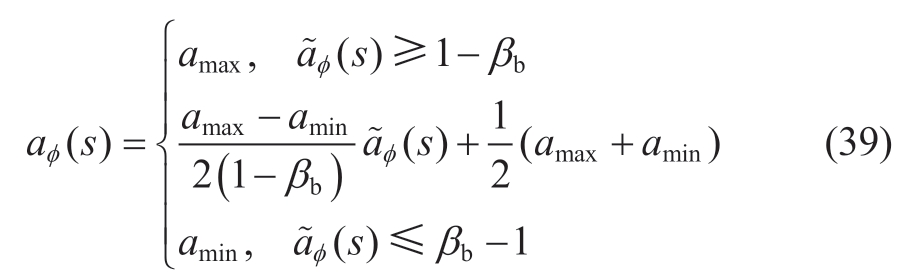
The agent optimizes its policy by minimizing the following objective:
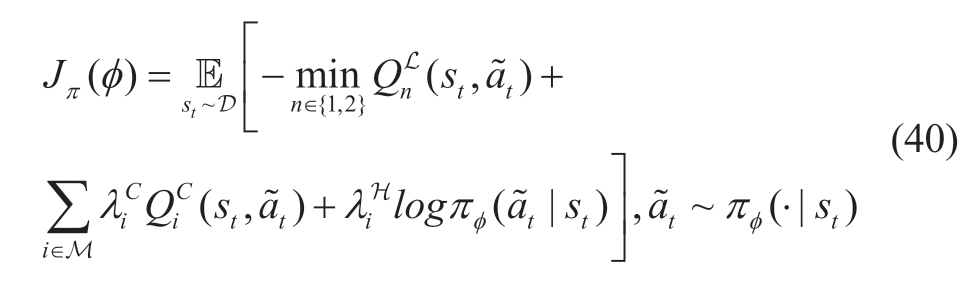
Unlike the original SAC algorithm,we consider the estimation of the long-term cost and include it in the optimization objective of the policy.This ensured that the algorithm adaptively adjusted the constraints.
Participation in both the DAM and RBM is paramount for VPPs.This paper presents a novel agent framework that facilitates day-ahead scheduling by leveraging Gated Recurrent Units (GRU) [35] to anticipate and construct a sequence of environmental states for the following day,as illustrated in Fig.2.
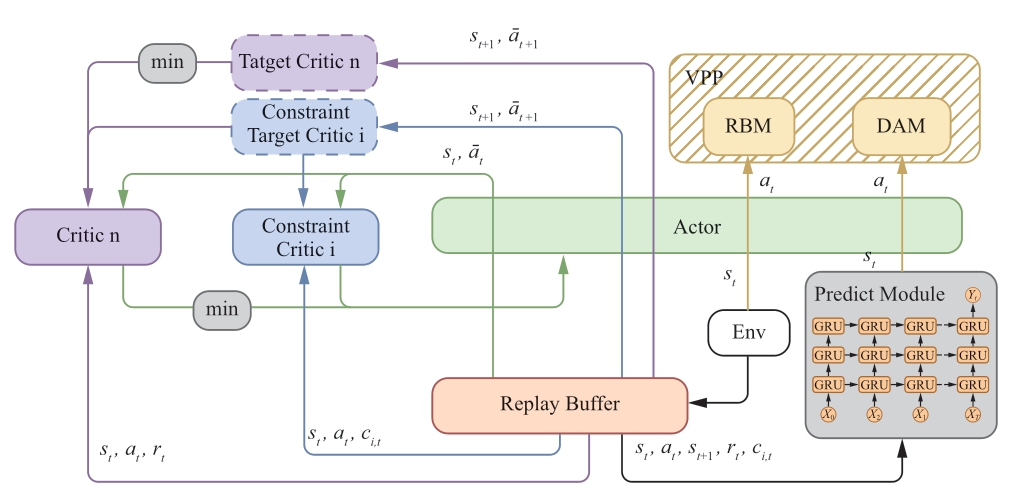
Fig.2 GRU-CSAC-based RVPP scheduling structure
By making informed decisions based on the predicted environment,the agent generates day-ahead power curves and participates in the DAM through RVPP aggregation.This framework enhances the overall efficiency and effectiveness of the RVPP when engaging in market mechanisms.
The RVPP acts as a price receiver and engages in realtime interaction with the RBM,effectively communicating the price to each agent.Agents,in turn,determine appropriate actions based on the current environmental state and price and subsequently transmit their actual actions back to the RVPP.The RVPP then collects subsequent actions from all the agents and submits the corresponding quoted quantity to the market.
The action trajectory of the agent was stored in the replay buffer.The blue part represents the update process for the constraint critic network,whereas the purple part signifies a similar update step for the critical network,considering only the minimum predicted Q-value from the target network.The parameter-update step for the actor is denoted in green.
Algorithm 1 describes the CSAC-GRU algorithm,and its flow is as follows:
1) Initialize the network parameters and the replay buffer.
2) During the action loop,the agents interact with RDER,and RVPP stores the experiential data in the replay buffer.
3) During the training loop,data are retrieved from the replay buffer,gradients are calculated,and backpropagation is performed.The target network is updated smoothly using Polyak averaging,which computes the updated parameters using the weighted sum of the target and online networks.
4) Update the dual parameters by PDO.
5) Predict the actions of the next-day Apre by GRU and the actor.The RVPP aggregates the actions of agents and participates in the DAM.The GRU net is then trained using the data in the replay buffer D.
As processes 2-5 are repeated,the rewards and costs tend to stabilize,and the strategies of RVPP agents tend to be optimal.


The SAC algorithm is an off-policy approach that relies on the entropy framework.It is well known for its exceptional exploration capabilities,which allow the easy scalability of complex VPP scheduling problems.Furthermore,compared with algorithms such as DDPG and TD3,SAC eliminates the need for time-consuming manual hyperparameter tuning and exhibits higher levels of robustness [33].
The central concept of the SAC algorithm revolves around enhancing long-term rewards while maximizing randomness.This is achieved by incorporating entropy,which serves as a metric for evaluating the level of randomness of the algorithm.By integrating the entropy into a long-term reward,the algorithm is encouraged to actively increase its level of randomness.The entropy of scheduling policies at time t is denoted as
To guarantee the minimum level of randomness required by the algorithm,we incorporate the minimum entropy constraint:
To solve the RVPP scheduling model based on the CMDP,we applied the Lagrangian relaxation technique to convert the problem into an unconstrained optimization problem.The transformed RVPP unconstrained scheduling problem is expressed as follows:
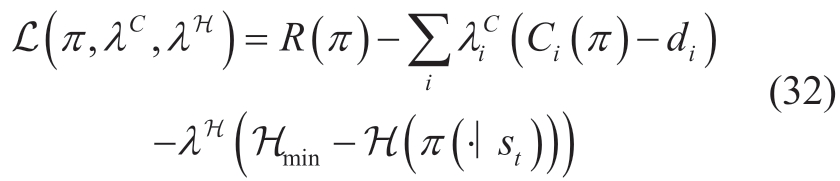
where ![]() and λHare the Lagrangian coefficients of the constraints and entropy,respectively.λHis commonly known as a temperature hyperparameter[16],and for the purpose of this study,we interpreted it as a Lagrangian dual variable.The dual variables in constrained soft actor-critic (CSAC) dynamically adjust the relative importance of each constraint.
and λHare the Lagrangian coefficients of the constraints and entropy,respectively.λHis commonly known as a temperature hyperparameter[16],and for the purpose of this study,we interpreted it as a Lagrangian dual variable.The dual variables in constrained soft actor-critic (CSAC) dynamically adjust the relative importance of each constraint.
The objective function for solving the RVPP unconstrained scheduling problem is formulated as follows:
This equation represents the solution to maximize the Lagrangian function with respect to the policy π* and minimize the optimal Lagrangian coefficient λ*,where λ includes both λC andλH.We employed the primaldual optimization (PDO) method to iteratively update these parameters.The iterative formula is as follows:
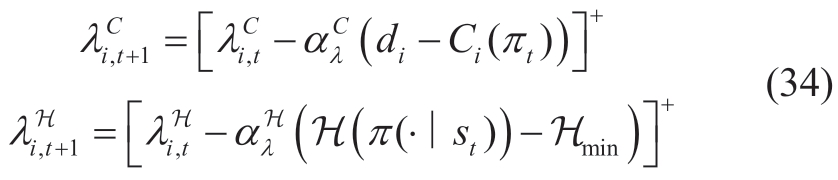
where ![]() denote the learning rates for the corresponding parameters,respectively.They are multiplied by the partial derivatives of the Lagrangian function with respect to the dual variables and used for gradient descent.The notation [x]+=max{0,x} is used to enforce that the dual parameters remain non-negative.When updating
denote the learning rates for the corresponding parameters,respectively.They are multiplied by the partial derivatives of the Lagrangian function with respect to the dual variables and used for gradient descent.The notation [x]+=max{0,x} is used to enforce that the dual parameters remain non-negative.When updating 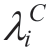 andλH,the policy π needs to be fixed.On the contrary,when updating the policy π,
andλH,the policy π needs to be fixed.On the contrary,when updating the policy π,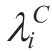 and λH need to be fixed.
and λH need to be fixed.

where y(rt,st+1) is the target in the root mean squared error,formulated as
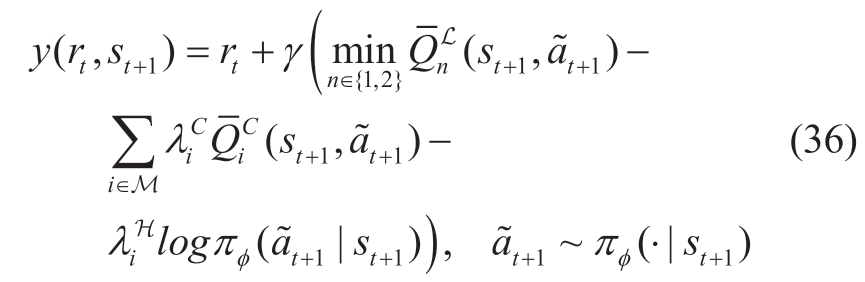
where 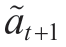 denotes the next action sampled from the policy based on the next state.Notably,during off-policy algorithm training,(st,at,rt,st+1)is typically randomly sampled from the replay buffer D to reduce the correlation between samples.To improve the learning efficiency and stability of the algorithm,we used the clipped double-Q trick,which takes a smaller Q-value between the two Q networks to reduce overestimation during the optimization process[34]
denotes the next action sampled from the policy based on the next state.Notably,during off-policy algorithm training,(st,at,rt,st+1)is typically randomly sampled from the replay buffer D to reduce the correlation between samples.To improve the learning efficiency and stability of the algorithm,we used the clipped double-Q trick,which takes a smaller Q-value between the two Q networks to reduce overestimation during the optimization process[34]![]() are critical networks for estimating the long-term costs and target networks,respectively.We used the following mean squared error as the loss function to optimize the estimation of the long-term cost:
are critical networks for estimating the long-term costs and target networks,respectively.We used the following mean squared error as the loss function to optimize the estimation of the long-term cost:
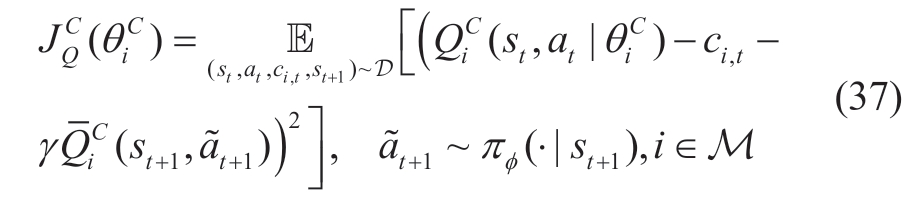
where π(s|φ) denotes the actor network of the SAC,which is a stochastic policy algorithm.It outputs a normal distribution with parameters µφ(s) andσφ(s).The output action values were sampled from this distribution using a reparameterization technique,enabling gradient computation and backpropagation.
A common practice for actions with a finite range is passing the sampled actions through a hyperbolic tangent or sigmoid function to ensure that the action values,such as the set powers of the EV and ESS,fall within the specified range.The sampling of actions is expressed as follows:
where ζ is a parameter-independent random variable that follows a standard normal distribution.
However,this makes it difficult for the agent to explore the boundary values.For scenarios that require high-frequency boundary actions,the effectiveness of the algorithm cannot be guaranteed.Our solution introduces a boundary action zone βb to ensure that RVPP agents can explore sufficient boundary values.
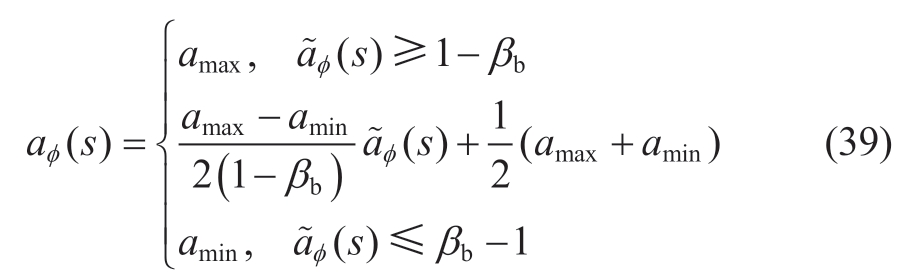
The agent optimizes its policy by minimizing the following objective:
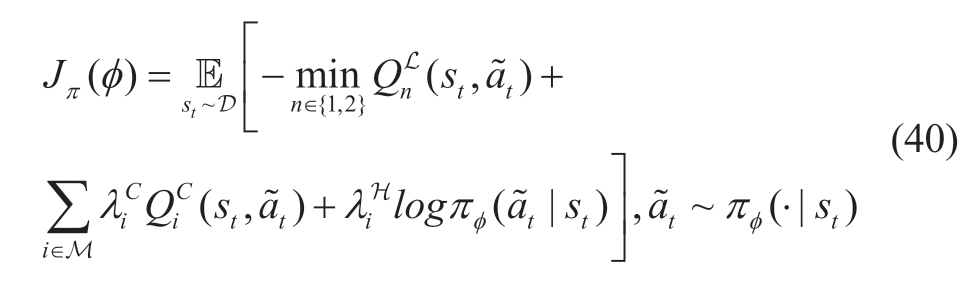
Unlike the original SAC algorithm,we consider the estimation of the long-term cost and include it in the optimization objective of the policy.This ensured that the algorithm adaptively adjusted the constraints.
Participation in both the DAM and RBM is paramount for VPPs.This paper presents a novel agent framework that facilitates day-ahead scheduling by leveraging Gated Recurrent Units (GRU) [35] to anticipate and construct a sequence of environmental states for the following day,as illustrated in Fig.2.

Fig.2 GRU-CSAC-based RVPP scheduling structure
By making informed decisions based on the predicted environment,the agent generates day-ahead power curves and participates in the DAM through RVPP aggregation.This framework enhances the overall efficiency and effectiveness of the RVPP when engaging in market mechanisms.
The RVPP acts as a price receiver and engages in realtime interaction with the RBM,effectively communicating the price to each agent.Agents,in turn,determine appropriate actions based on the current environmental state and price and subsequently transmit their actual actions back to the RVPP.The RVPP then collects subsequent actions from all the agents and submits the corresponding quoted quantity to the market.
The action trajectory of the agent was stored in the replay buffer.The blue part represents the update process for the constraint critic network,whereas the purple part signifies a similar update step for the critical network,considering only the minimum predicted Q-value from the target network.The parameter-update step for the actor is denoted in green.
Algorithm 1 describes the CSAC-GRU algorithm,and its flow is as follows:
1) Initialize the network parameters and the replay buffer.
2) During the action loop,the agents interact with RDER,and RVPP stores the experiential data in the replay buffer.
3) During the training loop,data are retrieved from the replay buffer,gradients are calculated,and backpropagation is performed.The target network is updated smoothly using Polyak averaging,which computes the updated parameters using the weighted sum of the target and online networks.
4) Update the dual parameters by PDO.
5) Predict the actions of the next-day Apre by GRU and the actor.The RVPP aggregates the actions of agents and participates in the DAM.The GRU net is then trained using the data in the replay buffer D.
As processes 2-5 are repeated,the rewards and costs tend to stabilize,and the strategies of RVPP agents tend to be optimal.


4 Numerical results
4.1 Experiment settings
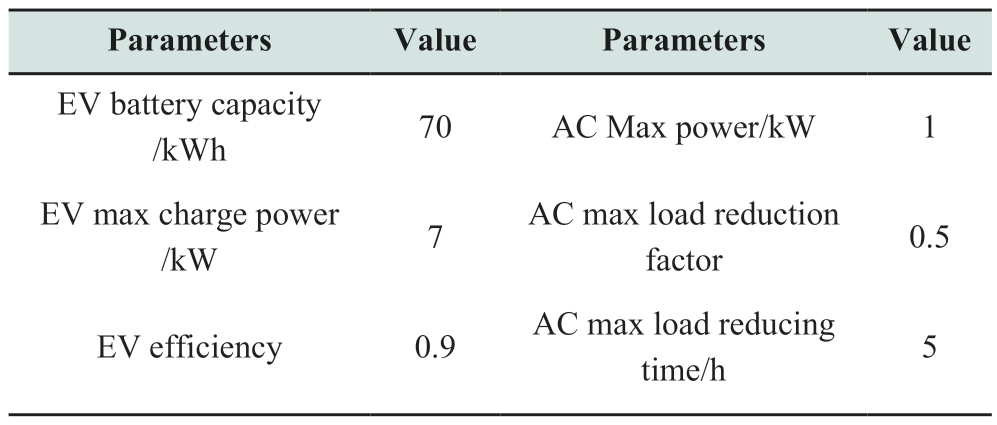
The experiment constructed an RVPP with 10 residences equipped with identical residential appliances.The specifications of the residential appliances are listed in Table 1.The experimental assumptions are as follows: The EV starts charging at 8 p.m.and departs from the residence at 8 a.m.;the power consumption of the EV during the daytime follows a beta distribution B(14.7,6.3).Residential water usage occurred during the following intervals: 7 a.m.,12 p.m.,and 7-10 p.m.Water consumption followed a beta distribution B(1.66,2.5).Assuming that all residences have an AC running continuously,the power consumption of the AC follows a beta distribution B(50.625,5.625).
Table 1 Parameters of household appliance
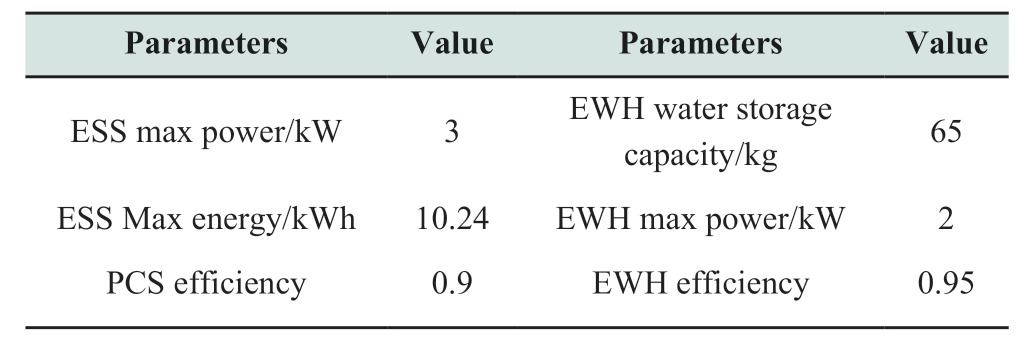
continue
The electricity price data we used were from the PJM hourly real-time price data for 2020.We obtained typical data for one week and scaled them to approximate the current market price.
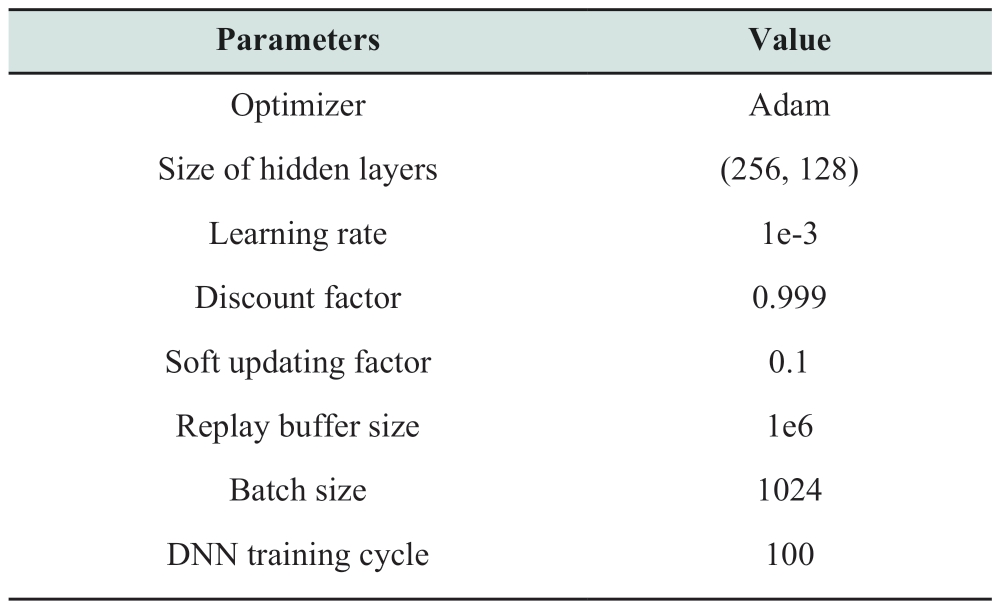
The experiment was conducted using a device equipped with an Intel i5 11400 CPU,NVIDIA RTX 4070 GPU,and 16GB of memory for training.The parameter configurations of the CSAC algorithm are listed in Table 2.
Table 2 GRU-CSAC algorithm hyperparameters
The experiment constructed an RVPP with 10 residences equipped with identical residential appliances.The specifications of the residential appliances are listed in Table 1.The experimental assumptions are as follows: The EV starts charging at 8 p.m.and departs from the residence at 8 a.m.;the power consumption of the EV during the daytime follows a beta distribution B(14.7,6.3).Residential water usage occurred during the following intervals: 7 a.m.,12 p.m.,and 7-10 p.m.Water consumption followed a beta distribution B(1.66,2.5).Assuming that all residences have an AC running continuously,the power consumption of the AC follows a beta distribution B(50.625,5.625).
Table 1 Parameters of household appliance

continue

The electricity price data we used were from the PJM hourly real-time price data for 2020.We obtained typical data for one week and scaled them to approximate the current market price.
The experiment was conducted using a device equipped with an Intel i5 11400 CPU,NVIDIA RTX 4070 GPU,and 16GB of memory for training.The parameter configurations of the CSAC algorithm are listed in Table 2.
Table 2 GRU-CSAC algorithm hyperparameters

4.2 Effectiveness analysis
The rewards,costs,and Lagrange coefficients λC during the training process of the GRU-CSAC algorithm for the four controlled devices are shown in Fig.3.The training phase comprised five distinct random seeds for ten users,encompassing a total of 10,000 steps,with each step consisting of 24 time slots.The blue area represents the span encompassing the highest and lowest values,and the dark line signifies the average value.
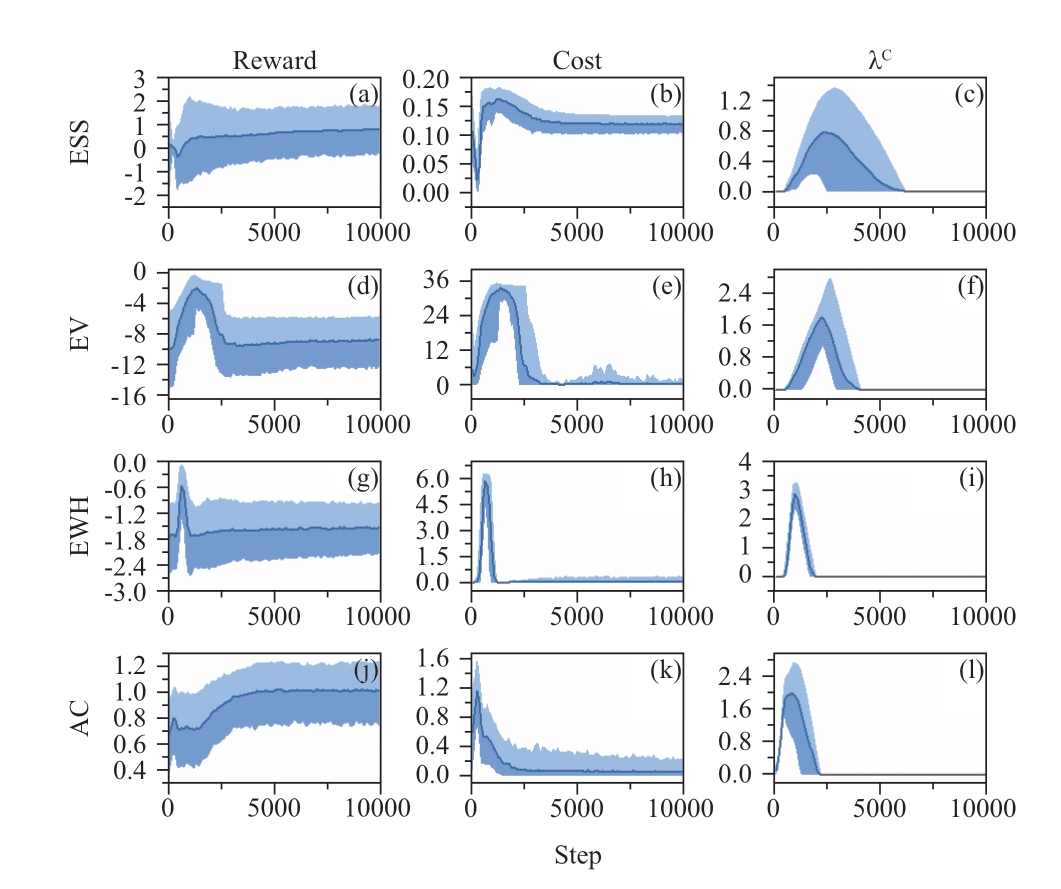
Fig.3 The process of 10,000 steps of training for different appliances,where (a)-(c) represent the rewards,costs,and Lagrangian coefficients of energy storage system (ESS);(d)-(f) represent the rewards,comfort costs,and Lagrangian coefficients of electric vehicle (EV);(g)-(i) represent the rewards,comfort costs,and λC of electric water heater (EWH);(j)-(l) represent the rewards,comfort costs,and Lagrangian coefficients of air conditioner (AC)
Fig.3 indicates that our GRU-CSAC algorithm reached a relatively stable state in approximately 5000 steps.The cost initially exhibits an increasing trend,indicating that the algorithm violates the constraints more frequently during the exploratory phase,leading to an increase inλC.Once the algorithm acquires the rules and reduces the frequency of constraint violations,the cost decreases,ultimately decreasing λC to zero.
An exception is the cost of the ESS,which shows a brief decline in the initial phase,indicating that the ESS strategy is to reduce its degradation.However,to attain higher rewards,the ESS must undergo charging and discharging,which rapidly increases the cost.Ultimately,the agent finds a balance between these two objectives.
In environments with low randomness,such as ESS and AC,rewards consistently demonstrate a discernible upward trend.Conversely,in the case of shiftable loads such as EV and EWH,where the total energy cannot be altered,the increasing trend of rewards is less pronounced.EWH and EV demonstrated a significant reward peak during the initial stage.This can be attributed to rewards reflecting the electricity consumption costs.During the exploration phase,the agent deliberately restricts the power of both the EV and EWH to effectively maximize the reward.However,the agent faces penalties that severely affect user comfort.Ultimately,the agent acquires a strategy to circumvent the penalties through training.
In conclusion,the CSAC has essentially learned a strategy that tends towards correctness within the constraints.The effectiveness of the proposed algorithm is demonstrated.
The rewards,costs,and Lagrange coefficients λC during the training process of the GRU-CSAC algorithm for the four controlled devices are shown in Fig.3.The training phase comprised five distinct random seeds for ten users,encompassing a total of 10,000 steps,with each step consisting of 24 time slots.The blue area represents the span encompassing the highest and lowest values,and the dark line signifies the average value.

Fig.3 The process of 10,000 steps of training for different appliances,where (a)-(c) represent the rewards,costs,and Lagrangian coefficients of energy storage system (ESS);(d)-(f) represent the rewards,comfort costs,and Lagrangian coefficients of electric vehicle (EV);(g)-(i) represent the rewards,comfort costs,and λC of electric water heater (EWH);(j)-(l) represent the rewards,comfort costs,and Lagrangian coefficients of air conditioner (AC)
Fig.3 indicates that our GRU-CSAC algorithm reached a relatively stable state in approximately 5000 steps.The cost initially exhibits an increasing trend,indicating that the algorithm violates the constraints more frequently during the exploratory phase,leading to an increase inλC.Once the algorithm acquires the rules and reduces the frequency of constraint violations,the cost decreases,ultimately decreasing λC to zero.
An exception is the cost of the ESS,which shows a brief decline in the initial phase,indicating that the ESS strategy is to reduce its degradation.However,to attain higher rewards,the ESS must undergo charging and discharging,which rapidly increases the cost.Ultimately,the agent finds a balance between these two objectives.
In environments with low randomness,such as ESS and AC,rewards consistently demonstrate a discernible upward trend.Conversely,in the case of shiftable loads such as EV and EWH,where the total energy cannot be altered,the increasing trend of rewards is less pronounced.EWH and EV demonstrated a significant reward peak during the initial stage.This can be attributed to rewards reflecting the electricity consumption costs.During the exploration phase,the agent deliberately restricts the power of both the EV and EWH to effectively maximize the reward.However,the agent faces penalties that severely affect user comfort.Ultimately,the agent acquires a strategy to circumvent the penalties through training.
In conclusion,the CSAC has essentially learned a strategy that tends towards correctness within the constraints.The effectiveness of the proposed algorithm is demonstrated.
4.3 Algorithm comparison
In the AC scenario and the CSAC,we employed the SAC,TD3,and DDPG algorithms to train the agents under identical parameters.Fig.4 (a) -(d) show the mean,upper,and lower values for the rewards of each algorithm,respectively.TD3 and DDPG,which rely on deterministic policies,demonstrated inadequate performance with significant reward fluctuations.The mean reward of the DDPG algorithm decreases.The CSAC and SAC algorithms,which are based on stochastic policies,perform better with almost identical mean rewards.
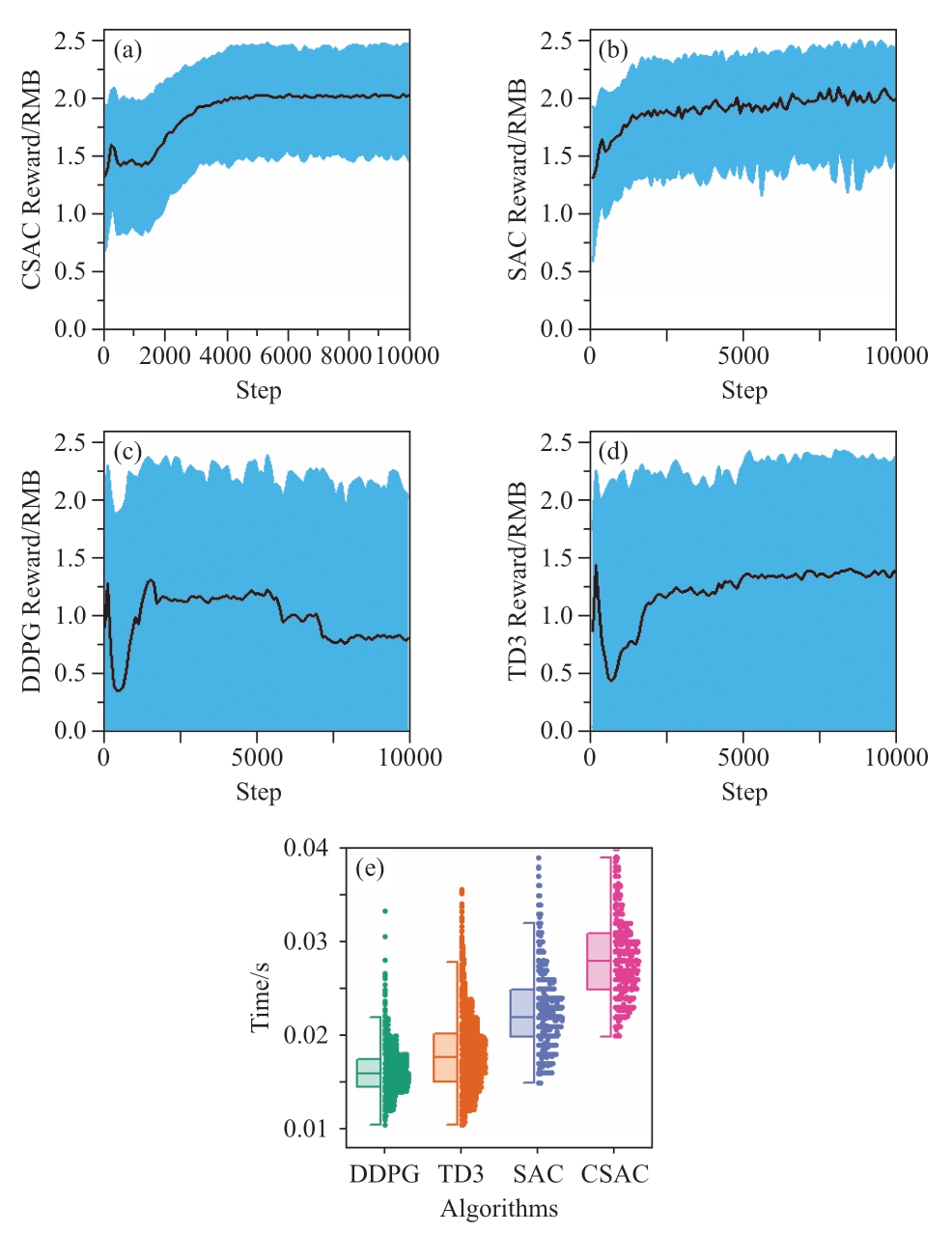
Fig.4 Rewards and single-step iteration time for CSAC,SAC,TD3,and DDPG algorithms
Employing a stochastic policy and maximum entropy framework enhances the exploration capabilities and training stability of the agents,thereby ensuring the effectiveness of their strategies.
Fig.4 (e) shows a box plot comparing the time required for single-step training across the aforementioned algorithms.The CSAC algorithm exhibited the longest training duration,which is attributed to the additional training of the network responsible for evaluating longterm discounted costs.The training time for CSAC was 1.75 times that of the DDPG algorithm.
Although the CSAC reward improvement rate in the early stages of training is not as rapid as that of SAC,it showcases remarkable adaptability when confronted with constraints.Fig.5 focuses on the cost during the training process of different algorithms.CSAC significantly suppressed the cost compared to the other algorithms,with the smallest fluctuation and strong stability.Compared to the proposed method,SAC’s performance in handling constrained problems was inferior,demonstrating the effectiveness of the Lagrangian relaxation technique in constrained reinforcement learning.
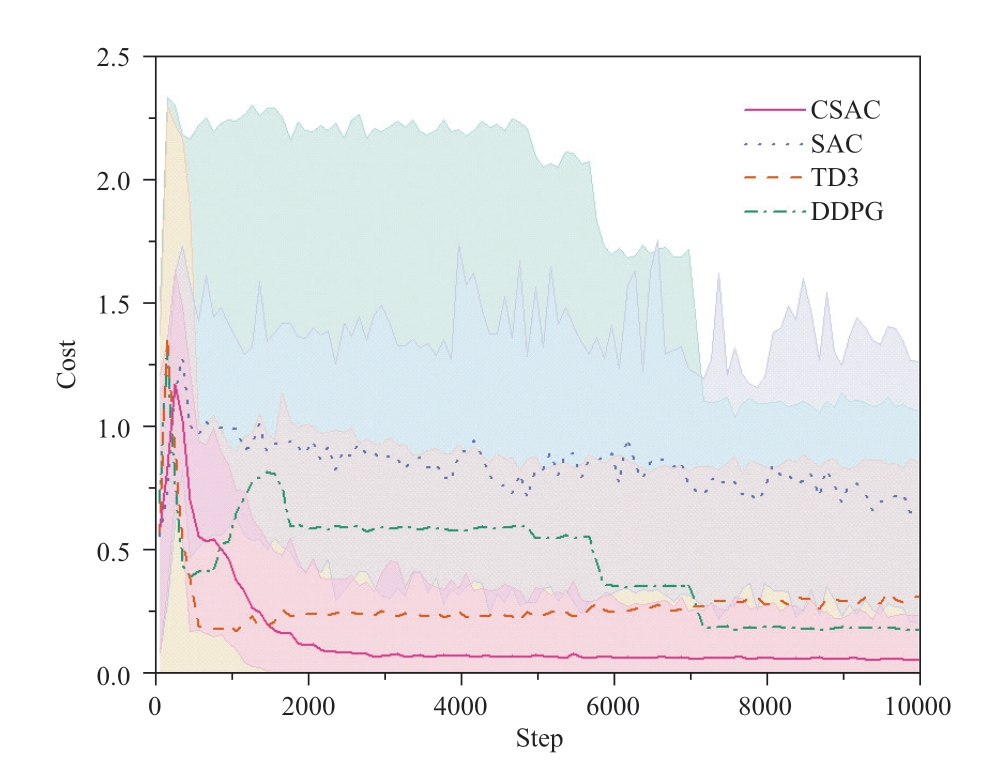
Fig.5 Cost for CSAC,SAC,TD3,and DDPG algorithms
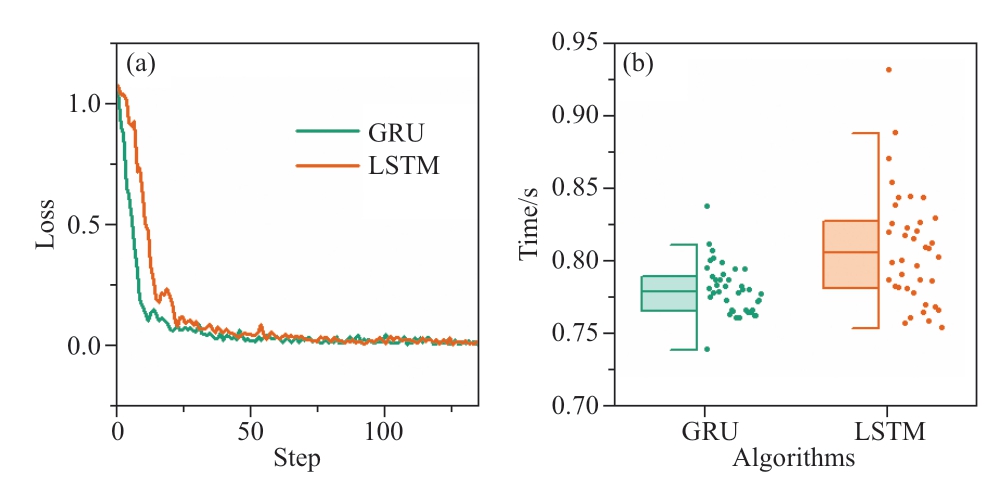
Fig.6 Loss and training time of GRU and LSTM
DDPG and TD3 exhibited lower mean costs than SAC,but their rewards remained significantly low.This is the primary reason for the high demand these algorithms place on the initial DNN parameters and hyperparameters.Hence,even within the same environment,different agents may generate divergent policies,leading to many agents failing to acquire effective strategies.
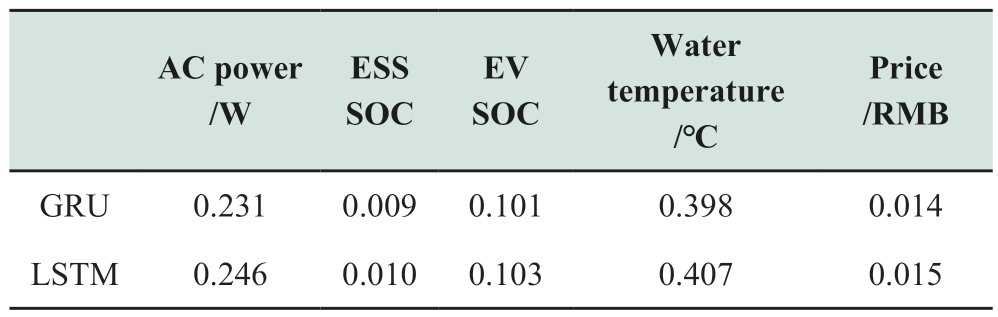
Our algorithm adopts the GRU to predict the next day’s status of devices and performs day-ahead scheduling based on this prediction.Table 3 compares the average prediction errors of the states of the GRU and LSTM algorithms.The networks used 140 days of data,70% for training and 30%for testing and evaluation.Because the data were normalized during training,the errors in the table were scaled by one standard deviation from the actual mean error.The results indicate that the GRU has a slight advantage in prediction error compared to the LSTM.We compare the performance of the two algorithms in Fig.3 and observe that the GRU has a faster loss reduction and a more advantageous training time than the LSTM.
Table 3 Average error of predicting different state variables using GRU and LSTM
In the AC scenario and the CSAC,we employed the SAC,TD3,and DDPG algorithms to train the agents under identical parameters.Fig.4 (a) -(d) show the mean,upper,and lower values for the rewards of each algorithm,respectively.TD3 and DDPG,which rely on deterministic policies,demonstrated inadequate performance with significant reward fluctuations.The mean reward of the DDPG algorithm decreases.The CSAC and SAC algorithms,which are based on stochastic policies,perform better with almost identical mean rewards.

Fig.4 Rewards and single-step iteration time for CSAC,SAC,TD3,and DDPG algorithms
Employing a stochastic policy and maximum entropy framework enhances the exploration capabilities and training stability of the agents,thereby ensuring the effectiveness of their strategies.
Fig.4 (e) shows a box plot comparing the time required for single-step training across the aforementioned algorithms.The CSAC algorithm exhibited the longest training duration,which is attributed to the additional training of the network responsible for evaluating longterm discounted costs.The training time for CSAC was 1.75 times that of the DDPG algorithm.
Although the CSAC reward improvement rate in the early stages of training is not as rapid as that of SAC,it showcases remarkable adaptability when confronted with constraints.Fig.5 focuses on the cost during the training process of different algorithms.CSAC significantly suppressed the cost compared to the other algorithms,with the smallest fluctuation and strong stability.Compared to the proposed method,SAC’s performance in handling constrained problems was inferior,demonstrating the effectiveness of the Lagrangian relaxation technique in constrained reinforcement learning.

Fig.5 Cost for CSAC,SAC,TD3,and DDPG algorithms

Fig.6 Loss and training time of GRU and LSTM
DDPG and TD3 exhibited lower mean costs than SAC,but their rewards remained significantly low.This is the primary reason for the high demand these algorithms place on the initial DNN parameters and hyperparameters.Hence,even within the same environment,different agents may generate divergent policies,leading to many agents failing to acquire effective strategies.
Our algorithm adopts the GRU to predict the next day’s status of devices and performs day-ahead scheduling based on this prediction.Table 3 compares the average prediction errors of the states of the GRU and LSTM algorithms.The networks used 140 days of data,70% for training and 30%for testing and evaluation.Because the data were normalized during training,the errors in the table were scaled by one standard deviation from the actual mean error.The results indicate that the GRU has a slight advantage in prediction error compared to the LSTM.We compare the performance of the two algorithms in Fig.3 and observe that the GRU has a faster loss reduction and a more advantageous training time than the LSTM.
Table 3 Average error of predicting different state variables using GRU and LSTM

4.4 VPP scheduling results
In the RVPP,each agent observes the predicted 24-hour states generated by the GRU and outputs their corresponding day-ahead decision curves.These curves were aggregated using the RVPP to participate in the DAM.In the intra-day scheduling phase,agents make hourly decisions.The RVPP consolidates these decision values and utilizes the difference from the day-ahead decisions as the purchasing quantity in the RBM.
The trading power curves of the various entities within the RVPP participating in the DAM and RBM are illustrated in Fig.7 using stacked bar and line graphs.Additionally,Table 4 provides the aggregated values for power consumption and electricity tariffs.The following observations were made:
Table 4 Power consumption and electricity tariff of RVPP
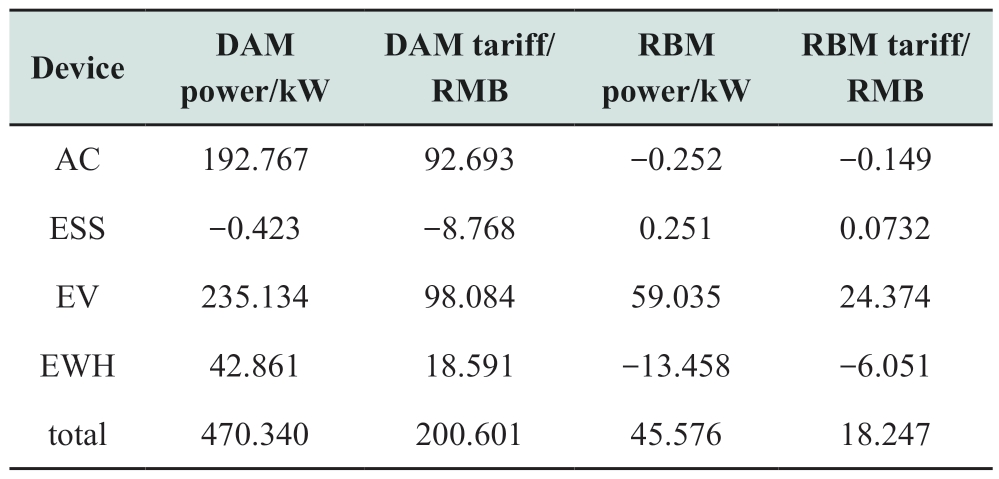
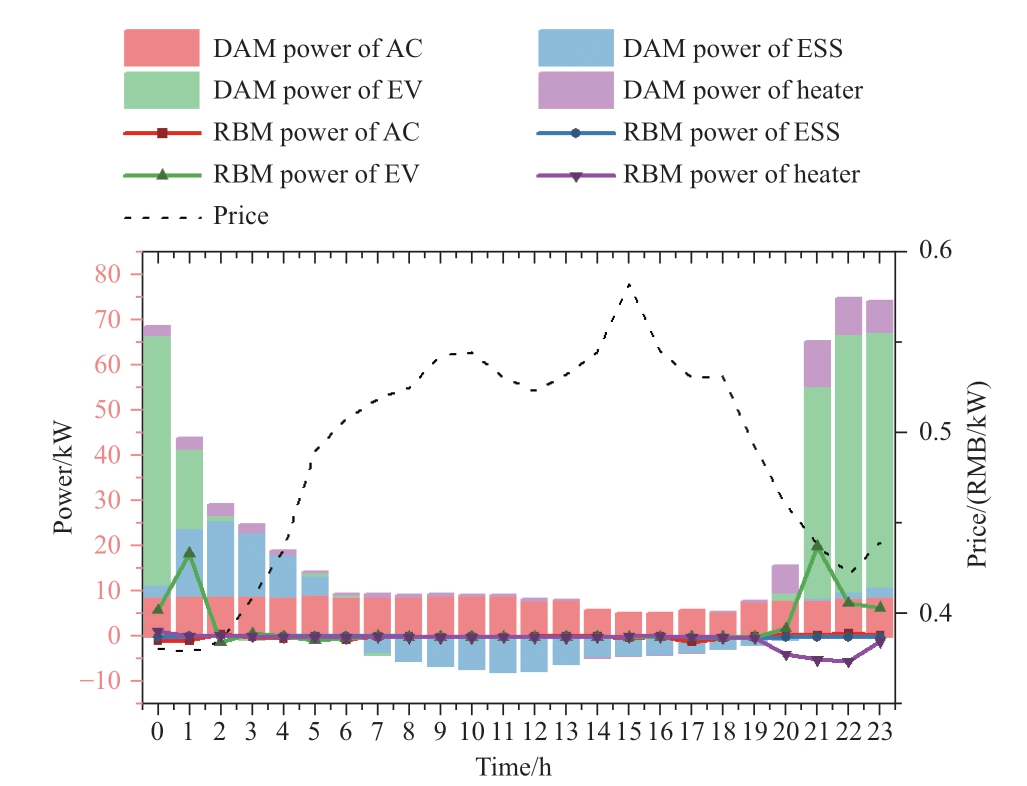
Fig.7 The trading power in DAM and RBM of the RVPP and price curves for RBM
1) Regarding the overall trend,the operational trend of all the entities in the RVPP was opposite to that of the electricity price.Power trading in the DAM is lower in the high-price range and higher in the low-price range.The proposed algorithm has shown significant effects in balancing the market supply and demand.
2) From a comprehensive standpoint of total power and electricity tariffs,our RVPP framework successfully decreased those in the RBM to merely 10%of the corresponding figures in the DAM.The proposed framework holds significant value for VPPs in mitigating high-risk trading within the RBM,primarily because of the favorable price advantages offered by the DAM compared with the RBM.
3) In the RBM trading curves,EV and EWH have the largest proportions,which are closely associated with environmental stochasticity.Forecasts always produce errors;deviations occur when hot water and EV power consumption do not match the forecasts.By contrast,ESS and AC,which are less affected by external stochasticity,produced a bias of approximately 0.In short,the stochasticity of the environment affects the prediction accuracy and final trading results,and the benefits of implementing our proposed method are more pronounced in scenarios characterized by regularity.
In the RVPP,each agent observes the predicted 24-hour states generated by the GRU and outputs their corresponding day-ahead decision curves.These curves were aggregated using the RVPP to participate in the DAM.In the intra-day scheduling phase,agents make hourly decisions.The RVPP consolidates these decision values and utilizes the difference from the day-ahead decisions as the purchasing quantity in the RBM.
The trading power curves of the various entities within the RVPP participating in the DAM and RBM are illustrated in Fig.7 using stacked bar and line graphs.Additionally,Table 4 provides the aggregated values for power consumption and electricity tariffs.The following observations were made:
Table 4 Power consumption and electricity tariff of RVPP


Fig.7 The trading power in DAM and RBM of the RVPP and price curves for RBM
1) Regarding the overall trend,the operational trend of all the entities in the RVPP was opposite to that of the electricity price.Power trading in the DAM is lower in the high-price range and higher in the low-price range.The proposed algorithm has shown significant effects in balancing the market supply and demand.
2) From a comprehensive standpoint of total power and electricity tariffs,our RVPP framework successfully decreased those in the RBM to merely 10%of the corresponding figures in the DAM.The proposed framework holds significant value for VPPs in mitigating high-risk trading within the RBM,primarily because of the favorable price advantages offered by the DAM compared with the RBM.
3) In the RBM trading curves,EV and EWH have the largest proportions,which are closely associated with environmental stochasticity.Forecasts always produce errors;deviations occur when hot water and EV power consumption do not match the forecasts.By contrast,ESS and AC,which are less affected by external stochasticity,produced a bias of approximately 0.In short,the stochasticity of the environment affects the prediction accuracy and final trading results,and the benefits of implementing our proposed method are more pronounced in scenarios characterized by regularity.
4.5 Analysis of CSAC strategy
We collected the action and state sequences from 10 residential agents for one week,along with the action strategy of one specific agent.The action strategy shows the mean and 50% confidence intervals of random decisions made by the CSAC agents.As the action strategy is the raw output of the agents’ neural networks,its values are in the range of [-1,1].
Fig.8 (a) shows the operational power of the ESS.These ESSs charge during low-priced intervals at night and sell them back to the grid in high-priced intervals to earn a pricedifference profit,which is more evident in the SOC curve in(b).Notably,the SOC range spans nearly the entire interval of [0,1],and the ESS has been effectively utilized.The action strategy in subplot (c) shows an even distribution of the action variance.This indicates that the agent maintains a strong exploration capability while achieving profits,thus showcasing the delicate balance between exploration and exploitation offered by the maximum entropy policy.
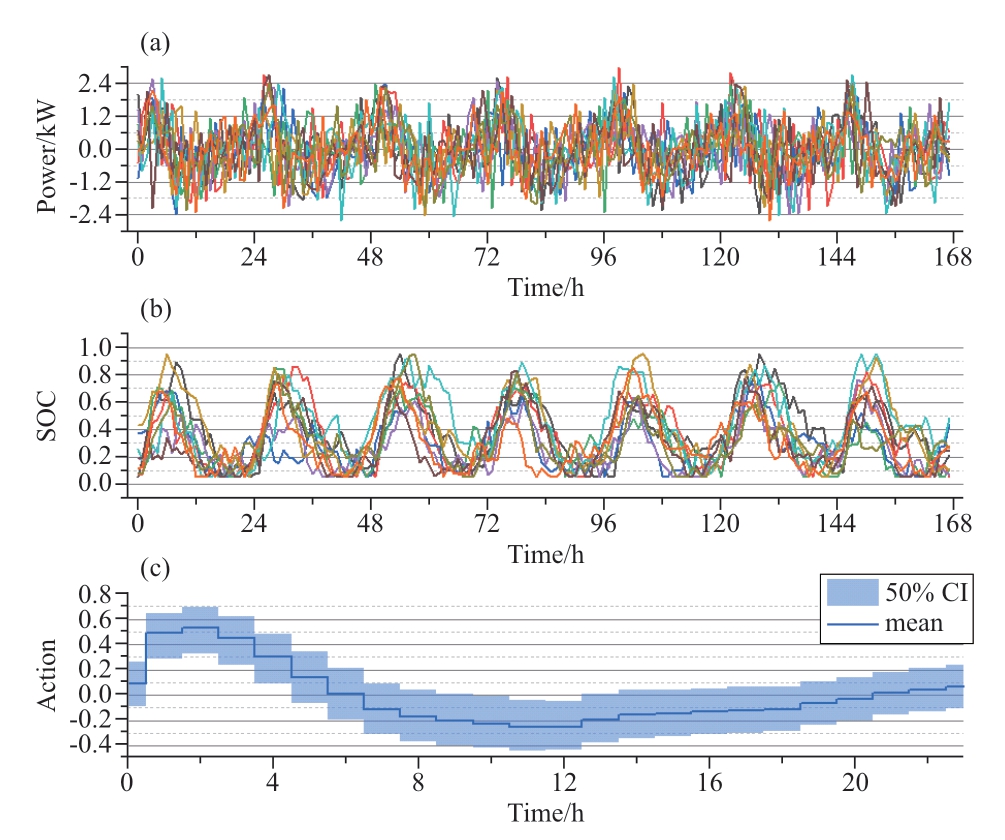
Fig.8 Power,SOC,and action strategy of ESS
As shown in Fig.9,the agent learns a strategy to charge the EVs after returning home and fully charges the SOC before the vehicle leaves in the morning.The agents adopt a decreasing-power strategy to charge the EVs.Although it does not completely shift the power peak to the period with the lowest prices,it still exhibits some capacity for load shifting compared to charging at full power throughout the entire duration.
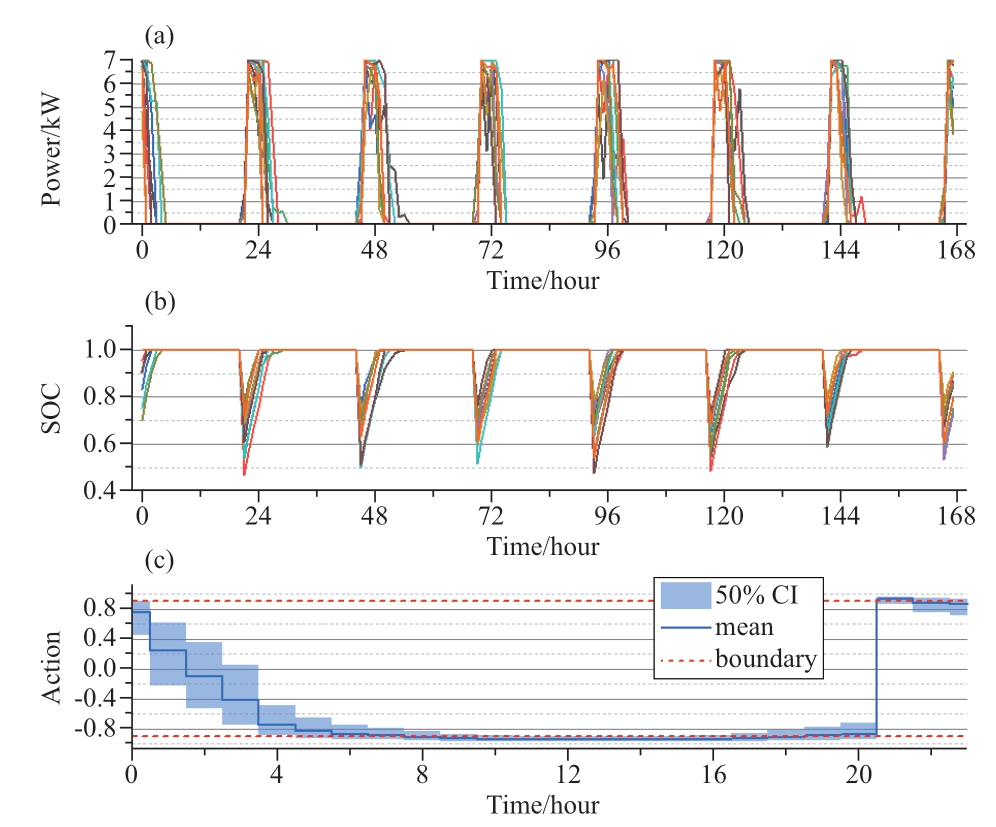
Fig.9 Power,SOC,and action strategy of EV
In Fig.10,subplot (a) shows that the peak power of the EWH occurs during the lowest-priced interval at midnight,whereas it operates at a low power level during the highpriced interval.(b) provides a clearer view of the loadshifting characteristics;The EWH is not immediately activated in response to the small amount of hot water consumption during the morning and noon.Instead,it waits until midnight,when prices are lower and demand is higher,to heat water at a high power level.This enables the reduction of electricity costs while ensuring that the water temperature remains above 50 ℃.
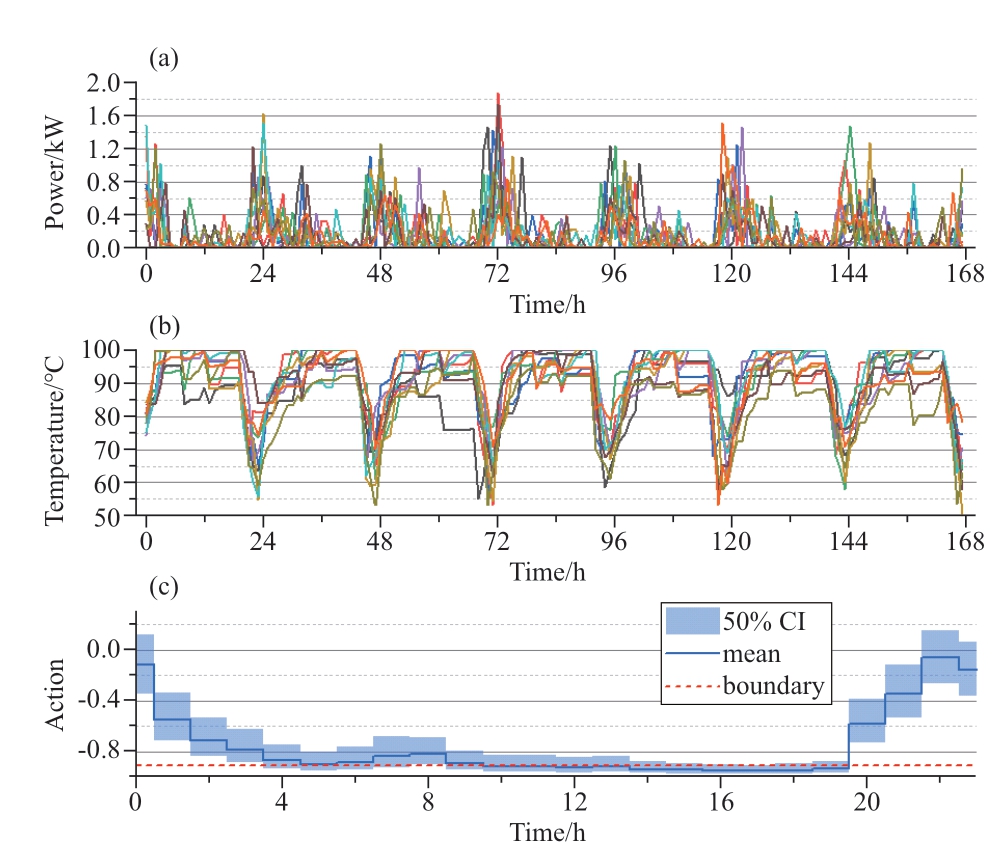
Fig.10 Power,water temperature,and action strategy of the EWH
Because the reduction factor of AC involves many boundary actions,we designed a wide boundary to ensure that the agents have a comprehensive exploration of the boundary actions.Owing to the nature of stochastic strategies,there is a diversity of load-reduction interval preferences among the various agents in Fig.11;however,a significant majority of agents opt to reduce loads during periods of high electricity prices.
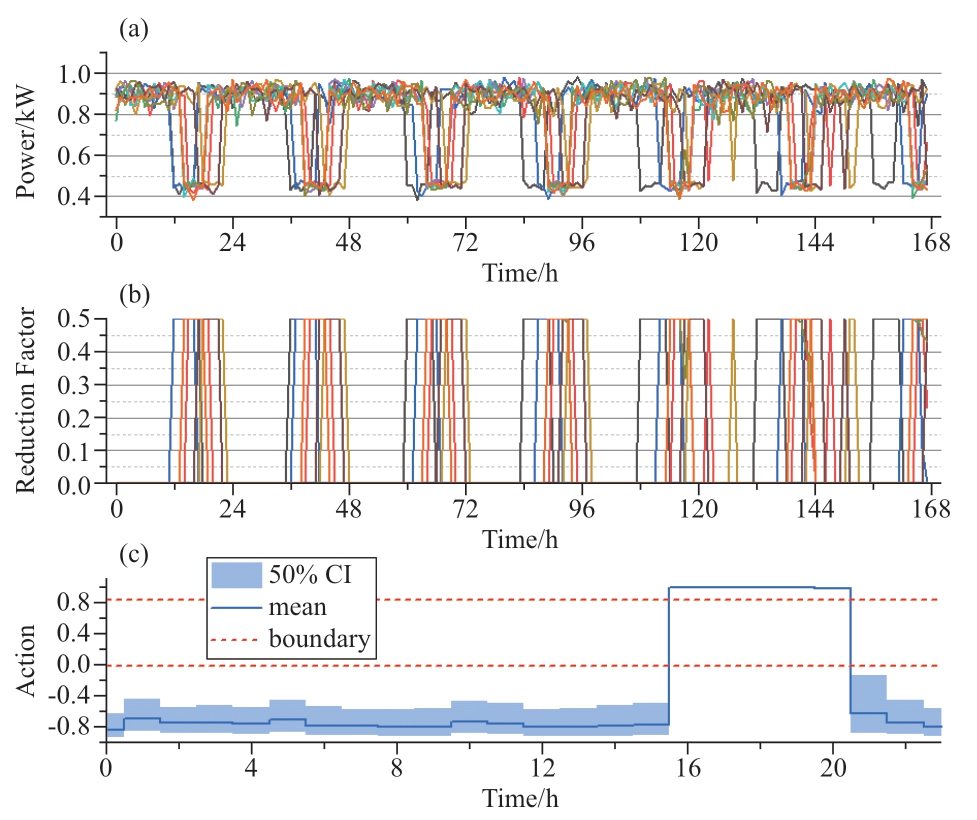
Fig.11 Power,reduction factor,and action strategy of the air conditioner
We collected the action and state sequences from 10 residential agents for one week,along with the action strategy of one specific agent.The action strategy shows the mean and 50% confidence intervals of random decisions made by the CSAC agents.As the action strategy is the raw output of the agents’ neural networks,its values are in the range of [-1,1].
Fig.8 (a) shows the operational power of the ESS.These ESSs charge during low-priced intervals at night and sell them back to the grid in high-priced intervals to earn a pricedifference profit,which is more evident in the SOC curve in(b).Notably,the SOC range spans nearly the entire interval of [0,1],and the ESS has been effectively utilized.The action strategy in subplot (c) shows an even distribution of the action variance.This indicates that the agent maintains a strong exploration capability while achieving profits,thus showcasing the delicate balance between exploration and exploitation offered by the maximum entropy policy.

Fig.8 Power,SOC,and action strategy of ESS
As shown in Fig.9,the agent learns a strategy to charge the EVs after returning home and fully charges the SOC before the vehicle leaves in the morning.The agents adopt a decreasing-power strategy to charge the EVs.Although it does not completely shift the power peak to the period with the lowest prices,it still exhibits some capacity for load shifting compared to charging at full power throughout the entire duration.

Fig.9 Power,SOC,and action strategy of EV
In Fig.10,subplot (a) shows that the peak power of the EWH occurs during the lowest-priced interval at midnight,whereas it operates at a low power level during the highpriced interval.(b) provides a clearer view of the loadshifting characteristics;The EWH is not immediately activated in response to the small amount of hot water consumption during the morning and noon.Instead,it waits until midnight,when prices are lower and demand is higher,to heat water at a high power level.This enables the reduction of electricity costs while ensuring that the water temperature remains above 50 ℃.

Fig.10 Power,water temperature,and action strategy of the EWH
Because the reduction factor of AC involves many boundary actions,we designed a wide boundary to ensure that the agents have a comprehensive exploration of the boundary actions.Owing to the nature of stochastic strategies,there is a diversity of load-reduction interval preferences among the various agents in Fig.11;however,a significant majority of agents opt to reduce loads during periods of high electricity prices.

Fig.11 Power,reduction factor,and action strategy of the air conditioner
5 Conclusions
A fully distributed scheduling strategy for RVPP based on the GRU-CSAC considering day-ahead predictions was proposed.By conducting simulations and training within a virtual RVPP environment,the following conclusions were drawn:
1) The proposed CSAC-based scheduling strategy demonstrates strong cost inhibition in comparison to other reinforcement learning algorithms,which enhances the adaptability of the VPP under constrained environments.
2) The integration of GRU and CSAC empowers distributed agents to perform day-ahead scheduling.In addition,the combination reduces the trading volume of the VPP in the RBM to approximately 10% in the DAM.
3) The proposed method effectively shifts peak loads to low-price intervals by responding to electricity price fluctuations.This alleviates the pressure on the supplydemand balance of the power grid and reduces electricity costs for residents.
Adversarial and cooperative scenarios among agents were not considered in this study.In future studies,a more in-depth investigation will be conducted on multi-energycoupled VPPs and their scheduling methods.
Acknowledgments
This study was supported by the Sichuan Science and Technology Program (grant number 2022YFG0123).
Declaration of Competing Interest
We declare that we have no conflict of interest.
References
[1] Shen B,Kahrl F,Satchwell A J (2021) Facilitating power grid decarbonization with distributed energy resources: Lessons from the united states.Annual Review of Environment and Resources,46: 349-375
[2] Bahloul M,Breathnach L,Cotter J,et al.(2022) Role of aggregator in coordinating residential virtual power plant in“StoreNet” : A pilot project case study.IEEE Transactions on Sustainable Energy,13(4): 2148-2158
[3] Liu Y,Ren P,Zhao J,et al.(2023) Real-time topology estimation for active distribution system using graph-bank tracking bayesian networks.IEEE Transactions on Industrial Informatics,19(4):6127-6137
[4] Rouzbahani H M,Karimipour H,Lei L (2021) A review on virtual power plant for energy management.Sustainable Energy Technologies and Assessments,47: 101370
[5] Tang Z,Hill D J,Liu T (2016) Fully distributed voltage control in subtransmission networks via virtual power plants.Proceedings of 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm).pp 193-198
[6] Babaei S,Zhao C,Fan L (2019) A name="ref7" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[7] Kardakos E G,Simoglou C K,Bakirtzis A G (2016) Optimal offering strategy of a virtual power plant: A stochastic bi-level approach.IEEE Transactions on Smart Grid,7(2): 794-806
[8] Fang F,Yu S,Xin X (2022) name="ref9" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[9] Gao H,Zhang F,Xiang Y,et al.(2023) Bounded rationality based multi-vpp trading in local energy markets: A dynamic game approach with different trading targets.CSEE Journal of Power and Energy Systems,9(1): 221-234
[10] Watkins C J C H,Dayan P (1992) Q-learning.Mach Learn,8:279-292
[11] Mnih V,Kavukcuoglu K,Silver D,et al.(2015) Human-level control through deep reinforcement learning.Nature,518(7540):529-533
[12] Wang Z,Schaul T,Hessel M,et al.(2016) Dueling network architectures for deep reinforcement learning.Proceedings of the 33rd International Conference on International Conference on Machine Learning (PMLR),New York,NY,USA,pp 1995-2003
[13] Lillicrap T P,Hunt J J,Pritzel A,et al.(2019) Continuous control with deep reinforcement learning.arXiv: 1509.02971
[14] Schulman J,Levine S,Moritz P,et al.(2015) Trust region policy optimization.Proceedings of 32nd International Conference on Machine Learning,Lile,France,6-11 Jul 2015,pp 1889-1897
[15] Schulman J,Wolski F,Dhariwal P,et al.(2017) Proximal policy optimization algorithms.arXiv: 1707.06347
[16] Haarnoja T,Zhou A,Hartikainen K,et al.(2019) Soft actor-critic algorithms and applications.arXiv:1812.05905
[17] Janner M,Fu J,Zhang M,et al.(2019) When to trust your model: Model-based policy optimization.Proceedings of 33rd Annual Conference on Neural Information Processing Systems,Vancouver,BC,Canada,8-14 Dec 2019,32
[18] Kumar A,Zhou A,Tucker G,et al.(2020) Conservative Q-learning for offline reinforcement learning.In: 34th Conference on Neural Information Processing Systems,6-12 Dec 2020,33:1179-1191
[19] Andrychowicz M,Wolski F,Ray A,et al.(2017) Hindsight experience replay.Proceedings of 31st Annual Conference on Neural Information Processing Systems,4-9 Dec 2017,pp 5049-5059
[20] Javareshk S M A N,Biyouki S A K,Darban S H (2019) Optimal bidding strategy of virtual power plants considering internal power market for distributed generation units.Proceedings of 2019 International Power System Conference (PSC).pp 250-255
[21] Zhou H,Wang F,Li Z,et al.(2021) Load tracking control strategy for virtual power plant via self-approaching optimization.Proceedings of the Chinese Society of Electrical Engineering,41:8334-8348
[22] Kuang Y,Wang X,Zhao H,et al.(2023) Model-free demand response scheduling strategy for virtual power plants considering risk attitude of consumers.CSEE Journal of Power and Energy Systems,9(2): 516-528
[23] Xu Z,Guo Y,Sun H,et al.(2023) Deep reinforcement learning for competitive DER pricing problem of virtual power plants.CSEE Journal of Power and Energy Systems,pp 1-12
[24] Liu X,Li S,Zhu J (2023) Optimal coordination for multiple network-constrained VPPs via multi-agent deep reinforcement learning.IEEE Transactions on Smart Grid,14: 3016-3031
[25] Yi Z,Xu Y,Wang X,et al.(2022) An improved two-stage deep reinforcement learning approach for regulation service disaggregation in a virtual power plant.IEEE Transactions on Smart Grid,13(4): 2844-2858
[26] Brijs T,De Jonghe C,Hobbs B F,et al.(2017) Interactions between the design of short-term electricity markets in the CWE region and power system flexibility.Applied Energy,195: 36-51
[27] Andersen P B,Poulsen B,Decker M,et al.(2008) Evaluation of a Generic Virtual Power Plant framework using service oriented architecture.Proceedings of 2008 IEEE 2nd International Power and Energy Conference.IEEE,Johor Bahru,Malaysia,pp 1212-1217
[28] Yi Z,Xu Y,Gu W,et al.(2020) A multi-time-scale economic scheduling strategy for virtual power plant based on deferrable loads aggregation and disaggregation.IEEE Transactions on Sustainable Energy,11(3): 1332-1346
[29] Fan D,Wang R,Qi H,et al.(2022) Edge intelligence enabled optimal scheduling with distributed price-responsive load for regenerative electric boilers.Frontiers in Energy Research,10:976294
[30] Zhu Z,Wang M,Xing Z,et al.(2023) Optimal configuration of power/thermal energy storage for a park-integrated energy system considering flexible load.Energies,16(18): 6424
[31] Duggal I,Venkatesh B (2015) Short-term scheduling of thermal generators and battery storage with depth of discharge-based cost model.IEEE Transactions on Power Systems,30(4): 2110-2118
[32] Liu R,Liu Y,Jing Z (2020) Impact of industrial virtual power plant on renewable energy integration.Global Energy Interconnection,3(6): 545-552
[33] Chen Y,Liu Y,Zhao J,et al.(2023) Physical-assisted multi-agent graph reinforcement learning enabled fast voltage regulation for PV-rich active distribution network.Applied Energy,351:121743
[34] Fujimoto S,Hoof H,Meger D (2018) Addressing Function Approximation Error in Actor-Critic Methods.Proceedings of the 35th International Conference on Machine Learning.PMLR,pp 1587-1596
[35] Cho K,Van Merrienboer B,Gulcehre C,et al.(2014) Learning phrase representations using RNN encoder-decoder for statistical machine translation.Proceedings of 2014 Conference on Empirical Methods in Natural Language Processing,Doha,Qatar,25-29 Oct 2014,pp 1724-1734

Scan for more details
Received:1 February 2024/Revised: 9 March 2024/Accepted:13 March 2024/Published: 25 April 2024
 Yongdong Chen
Yongdong Chen
chenyongdong@stu.scu.edu.cn
Xiaoyun Deng
dengxiaoyun@stu.scu.edu.cn
Dongchuan Fan
scu_fdc@stu.scu.edu.cn
Youbo Liu
liuyoubo@scu.edu.cn
Chao Ma
mac0472@sc.sgcc.com.cn
2096-5117/© 2024 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Biographies

Xiaoyun Deng received bachelor’s degree at Sichuan University,Chengdu,2021.He is working towards master’s Sichuan University,Chengdu.His research interests includes deep reinforcement learning,virtual power plant and edge intelligence.

Yongdong Chen received the B.S.degree in electrical engineering and automation from Chongqing Jiaotong University,Chongqing,China,in 2018,and the M.S.degree in electrical engineering from Xiangtan University,Xiangtan,Ching,in 2021.He is currently pursuing the Ph.D.degree in electrical engineering with Sichuan University,Chengdu,China.His research interests include operational control of active distribution networks and distributed resources optimization driven by edge intelligence.

Dongchuan Fan is currently pursuing the master’s degree in electrical engineering with Sichuan University.The main research directions are demand side management and artificial intelligence and their applications in power systems.

Youbo Liu graduated from Sichuan University,currently serves as a professor and doctoral supervisor at Sichuan University,and is a reserve for academic and technical leaders in Sichuan Province.He is mainly engaged in research in the fields of artificial intelligence in power systems,low-carbon electricity markets,distributed energy and energy storage,and active distribution networks.

Chao Ma received PhD degree at Sichuan University,Chengdu,2013.(He received master degree at Sichuan University,Chengdu,2009;bachelor degree at Sichuan University,Chengdu,2006).He is working in State Grid Sichuan Comprehensive Energy Service Co.Ltd,Chengdu.His research interests includes Now power system and Energy storage.
(Editor Yajun Zou)
A fully distributed scheduling strategy for RVPP based on the GRU-CSAC considering day-ahead predictions was proposed.By conducting simulations and training within a virtual RVPP environment,the following conclusions were drawn:
1) The proposed CSAC-based scheduling strategy demonstrates strong cost inhibition in comparison to other reinforcement learning algorithms,which enhances the adaptability of the VPP under constrained environments.
2) The integration of GRU and CSAC empowers distributed agents to perform day-ahead scheduling.In addition,the combination reduces the trading volume of the VPP in the RBM to approximately 10% in the DAM.
3) The proposed method effectively shifts peak loads to low-price intervals by responding to electricity price fluctuations.This alleviates the pressure on the supplydemand balance of the power grid and reduces electricity costs for residents.
Adversarial and cooperative scenarios among agents were not considered in this study.In future studies,a more in-depth investigation will be conducted on multi-energycoupled VPPs and their scheduling methods.
Acknowledgments
This study was supported by the Sichuan Science and Technology Program (grant number 2022YFG0123).
Declaration of Competing Interest
We declare that we have no conflict of interest.
References
[1] Shen B,Kahrl F,Satchwell A J (2021) Facilitating power grid decarbonization with distributed energy resources: Lessons from the united states.Annual Review of Environment and Resources,46: 349-375
[2] Bahloul M,Breathnach L,Cotter J,et al.(2022) Role of aggregator in coordinating residential virtual power plant in“StoreNet” : A pilot project case study.IEEE Transactions on Sustainable Energy,13(4): 2148-2158
[3] Liu Y,Ren P,Zhao J,et al.(2023) Real-time topology estimation for active distribution system using graph-bank tracking bayesian networks.IEEE Transactions on Industrial Informatics,19(4):6127-6137
[4] Rouzbahani H M,Karimipour H,Lei L (2021) A review on virtual power plant for energy management.Sustainable Energy Technologies and Assessments,47: 101370
[5] Tang Z,Hill D J,Liu T (2016) Fully distributed voltage control in subtransmission networks via virtual power plants.Proceedings of 2016 IEEE International Conference on Smart Grid Communications (SmartGridComm).pp 193-198
[6] Babaei S,Zhao C,Fan L (2019) A name="ref7" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[7] Kardakos E G,Simoglou C K,Bakirtzis A G (2016) Optimal offering strategy of a virtual power plant: A stochastic bi-level approach.IEEE Transactions on Smart Grid,7(2): 794-806
[8] Fang F,Yu S,Xin X (2022) name="ref9" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[9] Gao H,Zhang F,Xiang Y,et al.(2023) Bounded rationality based multi-vpp trading in local energy markets: A dynamic game approach with different trading targets.CSEE Journal of Power and Energy Systems,9(1): 221-234
[10] Watkins C J C H,Dayan P (1992) Q-learning.Mach Learn,8:279-292
[11] Mnih V,Kavukcuoglu K,Silver D,et al.(2015) Human-level control through deep reinforcement learning.Nature,518(7540):529-533
[12] Wang Z,Schaul T,Hessel M,et al.(2016) Dueling network architectures for deep reinforcement learning.Proceedings of the 33rd International Conference on International Conference on Machine Learning (PMLR),New York,NY,USA,pp 1995-2003
[13] Lillicrap T P,Hunt J J,Pritzel A,et al.(2019) Continuous control with deep reinforcement learning.arXiv: 1509.02971
[14] Schulman J,Levine S,Moritz P,et al.(2015) Trust region policy optimization.Proceedings of 32nd International Conference on Machine Learning,Lile,France,6-11 Jul 2015,pp 1889-1897
[15] Schulman J,Wolski F,Dhariwal P,et al.(2017) Proximal policy optimization algorithms.arXiv: 1707.06347
[16] Haarnoja T,Zhou A,Hartikainen K,et al.(2019) Soft actor-critic algorithms and applications.arXiv:1812.05905
[17] Janner M,Fu J,Zhang M,et al.(2019) When to trust your model: Model-based policy optimization.Proceedings of 33rd Annual Conference on Neural Information Processing Systems,Vancouver,BC,Canada,8-14 Dec 2019,32
[18] Kumar A,Zhou A,Tucker G,et al.(2020) Conservative Q-learning for offline reinforcement learning.In: 34th Conference on Neural Information Processing Systems,6-12 Dec 2020,33:1179-1191
[19] Andrychowicz M,Wolski F,Ray A,et al.(2017) Hindsight experience replay.Proceedings of 31st Annual Conference on Neural Information Processing Systems,4-9 Dec 2017,pp 5049-5059
[20] Javareshk S M A N,Biyouki S A K,Darban S H (2019) Optimal bidding strategy of virtual power plants considering internal power market for distributed generation units.Proceedings of 2019 International Power System Conference (PSC).pp 250-255
[21] Zhou H,Wang F,Li Z,et al.(2021) Load tracking control strategy for virtual power plant via self-approaching optimization.Proceedings of the Chinese Society of Electrical Engineering,41:8334-8348
[22] Kuang Y,Wang X,Zhao H,et al.(2023) Model-free demand response scheduling strategy for virtual power plants considering risk attitude of consumers.CSEE Journal of Power and Energy Systems,9(2): 516-528
[23] Xu Z,Guo Y,Sun H,et al.(2023) Deep reinforcement learning for competitive DER pricing problem of virtual power plants.CSEE Journal of Power and Energy Systems,pp 1-12
[24] Liu X,Li S,Zhu J (2023) Optimal coordination for multiple network-constrained VPPs via multi-agent deep reinforcement learning.IEEE Transactions on Smart Grid,14: 3016-3031
[25] Yi Z,Xu Y,Wang X,et al.(2022) An improved two-stage deep reinforcement learning approach for regulation service disaggregation in a virtual power plant.IEEE Transactions on Smart Grid,13(4): 2844-2858
[26] Brijs T,De Jonghe C,Hobbs B F,et al.(2017) Interactions between the design of short-term electricity markets in the CWE region and power system flexibility.Applied Energy,195: 36-51
[27] Andersen P B,Poulsen B,Decker M,et al.(2008) Evaluation of a Generic Virtual Power Plant framework using service oriented architecture.Proceedings of 2008 IEEE 2nd International Power and Energy Conference.IEEE,Johor Bahru,Malaysia,pp 1212-1217
[28] Yi Z,Xu Y,Gu W,et al.(2020) A multi-time-scale economic scheduling strategy for virtual power plant based on deferrable loads aggregation and disaggregation.IEEE Transactions on Sustainable Energy,11(3): 1332-1346
[29] Fan D,Wang R,Qi H,et al.(2022) Edge intelligence enabled optimal scheduling with distributed price-responsive load for regenerative electric boilers.Frontiers in Energy Research,10:976294
[30] Zhu Z,Wang M,Xing Z,et al.(2023) Optimal configuration of power/thermal energy storage for a park-integrated energy system considering flexible load.Energies,16(18): 6424
[31] Duggal I,Venkatesh B (2015) Short-term scheduling of thermal generators and battery storage with depth of discharge-based cost model.IEEE Transactions on Power Systems,30(4): 2110-2118
[32] Liu R,Liu Y,Jing Z (2020) Impact of industrial virtual power plant on renewable energy integration.Global Energy Interconnection,3(6): 545-552
[33] Chen Y,Liu Y,Zhao J,et al.(2023) Physical-assisted multi-agent graph reinforcement learning enabled fast voltage regulation for PV-rich active distribution network.Applied Energy,351:121743
[34] Fujimoto S,Hoof H,Meger D (2018) Addressing Function Approximation Error in Actor-Critic Methods.Proceedings of the 35th International Conference on Machine Learning.PMLR,pp 1587-1596
[35] Cho K,Van Merrienboer B,Gulcehre C,et al.(2014) Learning phrase representations using RNN encoder-decoder for statistical machine translation.Proceedings of 2014 Conference on Empirical Methods in Natural Language Processing,Doha,Qatar,25-29 Oct 2014,pp 1724-1734

Scan for more details
Received:1 February 2024/Revised: 9 March 2024/Accepted:13 March 2024/Published: 25 April 2024
 Yongdong Chen
Yongdong Chen
chenyongdong@stu.scu.edu.cn
Xiaoyun Deng
dengxiaoyun@stu.scu.edu.cn
Dongchuan Fan
scu_fdc@stu.scu.edu.cn
Youbo Liu
liuyoubo@scu.edu.cn
Chao Ma
mac0472@sc.sgcc.com.cn
2096-5117/© 2024 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Biographies

Xiaoyun Deng received bachelor’s degree at Sichuan University,Chengdu,2021.He is working towards master’s Sichuan University,Chengdu.His research interests includes deep reinforcement learning,virtual power plant and edge intelligence.

Yongdong Chen received the B.S.degree in electrical engineering and automation from Chongqing Jiaotong University,Chongqing,China,in 2018,and the M.S.degree in electrical engineering from Xiangtan University,Xiangtan,Ching,in 2021.He is currently pursuing the Ph.D.degree in electrical engineering with Sichuan University,Chengdu,China.His research interests include operational control of active distribution networks and distributed resources optimization driven by edge intelligence.

Dongchuan Fan is currently pursuing the master’s degree in electrical engineering with Sichuan University.The main research directions are demand side management and artificial intelligence and their applications in power systems.

Youbo Liu graduated from Sichuan University,currently serves as a professor and doctoral supervisor at Sichuan University,and is a reserve for academic and technical leaders in Sichuan Province.He is mainly engaged in research in the fields of artificial intelligence in power systems,low-carbon electricity markets,distributed energy and energy storage,and active distribution networks.

Chao Ma received PhD degree at Sichuan University,Chengdu,2013.(He received master degree at Sichuan University,Chengdu,2009;bachelor degree at Sichuan University,Chengdu,2006).He is working in State Grid Sichuan Comprehensive Energy Service Co.Ltd,Chengdu.His research interests includes Now power system and Energy storage.
(Editor Yajun Zou)
