0 Introduction

Under the background of “double carbon,” the power system is gradually transforming from high carbon to low carbon,which means that the new power system will consume a large amount of wind power in the future.From the power supply perspective,the proportion of renewable power will significantly increase,and the power structure will be optimized.Compared to a coal-fired generator with controllable output power,the output power of winddriven generators is controllable owing to the fluctuations,uncertainties,and anti-peak regulation characteristics of wind energy.

Therefore,the capacity of conventional generators that may be used for peak shaving must not only cope with the random fluctuation of load but also meet the power fluctuation of wind power.This forces decision-makers of the power grid to set aside more reserve generators to cope with situations in which electric power generators fail to meet the expected value.The power grid must bear the opportunity cost of the reservation generator,which increases the expenditure on daily operation maintenance.The tradeoff between risk reduction,wind power accommodation,and operational maintenance costs complicates decision-making.

Some scholars have tried to do much work on quantifying the uncertainties of wind power.Wind power is primarily determined by wind speed,and the wind speed probability distribution of a wind farm generally follows a two-parameter Weibull distribution.Using historical data and fitting methods,characteristic indicators that may reflect the distribution of wind energy resources,such as the average wind speed,average wind energy density,average effective wind energy density,and other parameters,may be derived,and then the output power of wind-driven generators [1,2].The Monte Carlo simulation method was used to characterize the probability distribution of the power output of wind-driven generators,that is,normal distribution.Combination curves of multiple power outputs of wind-driven generators were obtained,successfully simulating the uncertainty of wind power and correcting the shortcomings of the stochastic production simulation method [3,4].Fuzzy theory can also describe the uncertainty of the power output of winddriven generators,introduce constraints with trapezoidal or triangular fuzzy parameters,use confidence intervals to quantify risks,convert deterministic system constraints into fuzzy constraints,and better balance the risk and operation and maintenance costs [5-7].

Robustness is an operation optimization strategy that can help the system cope with various uncertain factors and has a particular anti-interference ability;it can also be understood as a conservative decision-making scheme [8,9].This study proposes a collaborative optimization model for source-network-load tripartite cooperation.It introduces an adjustable demand response load at the load side as a vital means of accommodating wind power.Owing to its fast response speed,it can track changes in the power output of wind-driven generators,thus reducing the adjustment pressure of conventional generators and eliminating the impact of the reverse peak regulation effect on the power grid owing to wind power.At the same time,to ensure that the cost is low,we reasonably arrange the sequence of generators connected to the grid end and select the connection sequence of the generator nodes with the best effect of consuming wind power.The C&CG algorithm was used to decompose the problem into min-max-min two-layer problems to obtain the solution.The inner layer contains max-min sub-problems that cannot be solved directly.Using the dual theory to process the constraints into a max-max problem is necessary.The original problem is transformed into a main problem and a subproblem with mixed-integer linear characteristics,and the twolevel problem is solved alternately.The solutions of the subproblem and main problem are used as the upper and lower bounds,respectively,and the upper and lower bounds constantly approach the final convergence.

Based on the improved IEEE30 system,this study starts from the three aspects of source,network,and load.It establishes an optimization model that considers the maximum amount of wind power consumption and the lowest system operating cost.The C&CG algorithm solved this problem,making the decision-making method economical and anti-interference.

1 Source-network-load cooperation mode

1.1 Output power characteristics of the generators

Using the measured data of wind-driven generators,the following phenomena were observed:wind speed generally fluctuates between zero and the rated value;the probability of the change rate of the output power of winddriven generators being less than 5%/10 min is as high as 93.9%,with a maximum change rate of 27.4%/10 min;and the probability of wind-driven generators exhibiting antipeak characteristics is 74.7% [10].The data from these studies indicate a mismatch between the output change rate of wind-driven generators and wind speed.The output of wind-driven generators also exhibits significant anti-peak characteristics.

1.2 Output characteristics of conventional generator

This study used thermal and nuclear power as conventional power sources.Operational restrictions exist when using nuclear energy,reflected in the inflexibility of nuclear power regulations.Nuclear-driven generators can participate in the peak-shaving task and frequently adjust the output power to track load changes.In that case,this may lead to a decrease in reliability (for example,the frequent action of power rods may increase the probability of fuel cladding damage).Therefore,to ensure the safe operation of nuclear-driven generators,changes in their output power are strictly limited.Therefore,nuclear-driven generators generally only bear the basic load and do not undertake peak-shaving tasks [11,12].Coal-fired generators are subjected to basic and peak loads.However,the capacity of coal-fired generators that may be used to participate in peakshaving tasks is generally within the range of 30% to 50% of the rated capacity,and the regulating capacity is not large and is also limited by the up-and-down power.The startup and shutdown times of coal-fired generators are related to the installed capacity and start-up status of the generator.In contrast,those of large-capacity generators are long and relatively inflexible.Coal-fired generators that provide reserving services are characterized by small capacity,rapid startup and shutdown,timely response,and a strong ability to track load changes;however,the depth of peak shaving is not large,and the operating costs are relatively high [13].

1.3 Source-network-load collaboration

When conventional and wind-driven generators are used as power sources,if the grid fully accepts wind power,the equivalent load curve of the electric load power minus wind power may exceed the lower limit of the output power of conventional generators (Fig.1),and some conventional generators are forced to shut down to accommodate wind power.

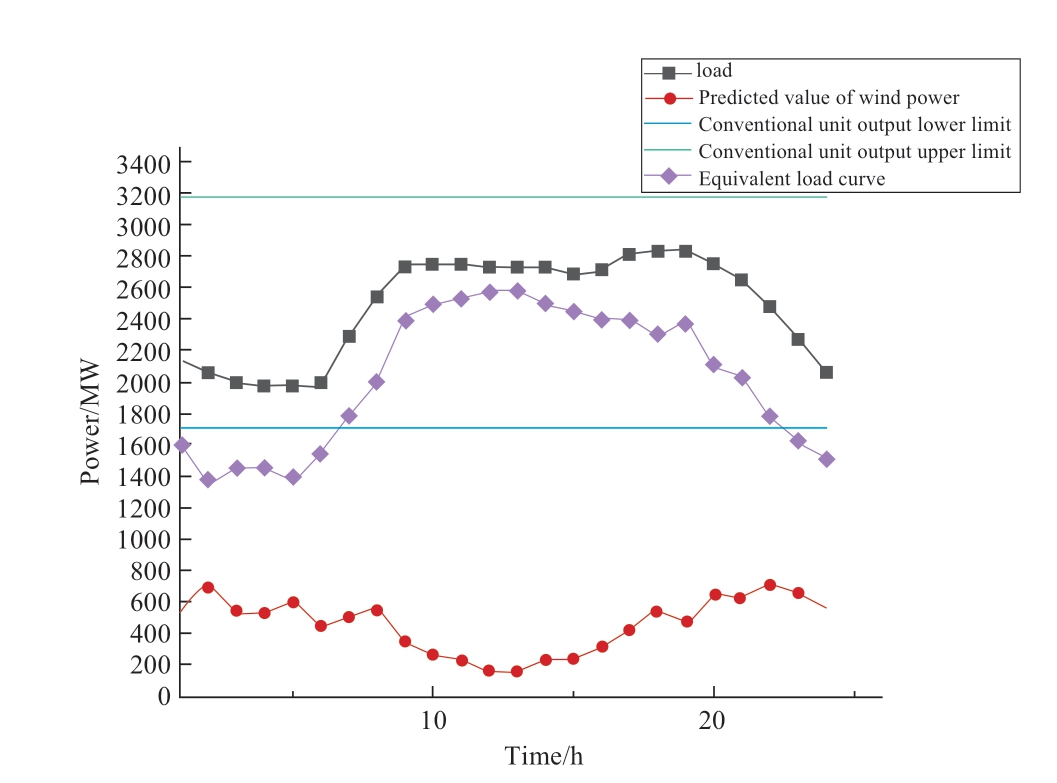
Fig.1 Equivalent load curve

When the equivalent load curve rises,the generator that is forced to shut down has a limit on the start and stop time,which may lead to a power shortage or a sudden increase in power supply costs due to calls to backup.Demand response load refers to the load that can flexibly adjust the power consumption plan to meet the total demand [14].The translatable load should have the characteristics of a stable distribution of the daily load curve,a slight difference of peak and valley load between day and night,and a fast response.Therefore,when the demand-response load is involved in the power regulation,cooperation with conventional generators may increase the regulation capacity of conventional generators.In the demand response,the power grid should compensate for the power accommodation of users with translatable load due to the comfort affected by changing the power accommodation plan.It should maximize the accommodation of wind power to ensure the power balance between the supply and demand of the power system.However,at the same time,it should also try to reduce the probability of forced outage of conventional generators to reduce the abandoned wind volume and the outage probability of conventional generators [15].

The accommodation of wind power is constrained and affected by the degree of source-network-load collaboration.This study proposes a cooperative optimization model for source network loads based on robust ideas to accommodate as much wind power as possible.The model includes source-source,source-load,and source-network interactions.The source-source interaction requires some conventional generators to track the changes in the load and output power of the generators with renewable energy to make adjustments to realize the complementarity of adjustable,high-carbon power supply and intermittent,lowcarbon power supply.The source-load interaction means that there are increasingly more loads on the user side that may participate in the unified dispatching of the power grid,such as the high energy consumption industrial load,which may be used as demand-side resources to respond quickly and participate in the balance of power supply and demand,which is an essential means to balance the output power of intermittent power sources.Traditional source-network collaboration only considers unit commitment;however,considering the sequence and location of the injected nodes of the generators is more suitable for the operation and control of the new power system.The essence of sourcenetwork-load collaborative optimization is an optimization mechanism that may maximize resource utilization [16].In this study,by optimizing the sequence of the injected nodes of the generators,including conventional generators and renewable energy generators,a two-stage robust optimization model and solution method were adopted to solve the optimization scheme in the scenario where the output power fluctuation of the wind-driven generators had the most significant impact on the power system in a specific scenario.

2 Source-network-load collaborative optimization model

Robust optimization is not a model for calculating the maximum probability distribution of the output power of the generators but a conservative optimization scheme.For an uncertain set of a given wind power,all the elements in the set must satisfy the rigid constraints of the power system.By setting the lower limit of the optimization objective function,the method of maximizing the minimum value of the objective function is adopted to ensure that the sensitivity of the power system to the disturbance of uncertain factors is reduced while ensuring that the economy or reliability will not significantly deteriorate owing to fluctuations in the output power of the wind-driven generator [17].

2.1 The objective functions

The power generation cost of a power system mainly includes the startup,shutdown,and operation costs of conventional generators.The objective function of the twostage robust optimization model is given as follows:

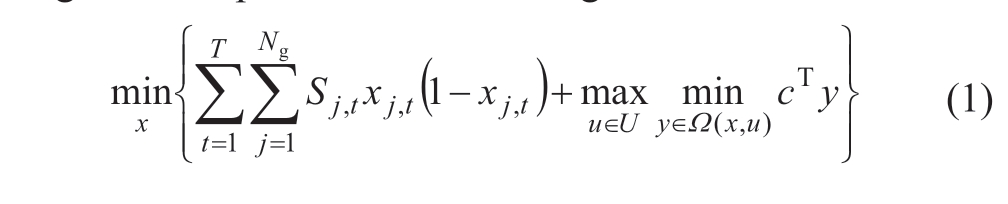
where u is the variable of the output power of the winddriven generator,U is the uncertainty set of the output power of the generators,c is the coefficient matrix of the operating cost,y is the optimization variable,Sj,t is the startup and shutdown cost of the jth generator,xj,t is a binary variable indicating the start-up and shutdown of the jth generator at the t time period,T is the operation period,and Ng is the generator number.

The objective function consists of two parts:start-up and shutdown costs and operation costs of conventional generators.The first part comprises the start-up and shutdown costs of coal-fired and gas-powered generators,and the second part comprises the dispatching costs of demand response load and the operating costs of coal-fired,gas-powered,and nuclear-driven generators (i.e.,fuel costs).

The optimization variable vector y is mathematically expressed as follows:

where Pg(t),PN(t)and Pw(t)respectively represent the output power of coal-fired,nuclear-driven,and winddriven generators at t time period;PDR(t)is the actual power accommodation of users participating in demand response at t time period;PDR1(t)and PDR2(t)is auxiliary variables related to PDR(t);PL(t)represents the load power at t time period.

(1)The dispatching cost of demand response load

The user load demand response must go through unified power grid dispatching,which will always incur expenses,forming the dispatching cost of the demand response load.The dispatching cost of demand response load mainly depends on the power of the user participating in demand response and the time required to schedule,which can be expressed mathematically as

where KDR is the unit dispatching cost of the user demand response,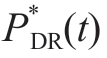is the power demand of users participating in demand response the t time period,and PDR(t)is the actual power accommodation of users participating in demand response the t time period.

Any deviation from the power accommodation plan requires compensation.Therefore,the absolute value term expresses the deviation between the actual and expected powers.To facilitate this solution,it is necessary to introduce auxiliary variables PDR1(t)and PDR2(t).By adding constraints,we can rewrite (2)as

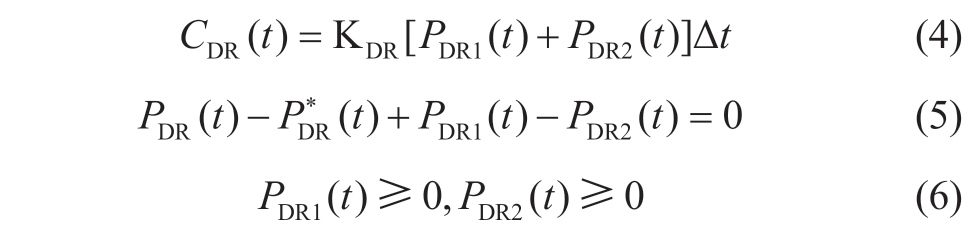
Equation (3),with an absolute value,may be linearized using auxiliary variables and Equations (4)–(6).

(2)The power generation cost of coal-fired generator

The generation cost of a coal-fired generator is considered a quadratic function of the output power of the coal-fired generator,which may be expressed mathematically as

where aj,bj,and cj are the coefficients of the generation cost of the coal-fired generator related to the secondary,primary,and constant terms,respectively,and Pg,j,t is the output power of the coal-fired generator.

Because the generation cost of a coal-fired generator is a quadratic function,it is necessary to perform piecewise linearization of the quadratic function in Equation (2)using N line sections to obtain the following primary function:

where ait is the startup and shutdown state variables of the ith coal-fired generator in the form of a startup binary at the t time period,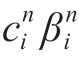is the slope and intercept of the linearized section of the ith coal-fired generator at the t time period,and ψit is an auxiliary variable.

The quadratic function may be divided into linear piecewise functions using auxiliary variables.

(3)The power generation cost of nuclear-driven generator

The power generation cost of nuclear-driven generators consists mainly of operational and fuel costs.Because nuclear-driven generators may not start or stop frequently,the operating cost is fixed.The fuel cost is related to the output power,which can be expressed as

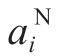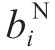where and  are the constant terms of the operation cost and the fuel factor of the ith nuclear-driven generator,respectively,and is the output power of the ith nucleardriven generator at t time period.

2.2 The constraint conditions

(1)Power balance constraints

To ensure power balance between the supply and demand of the power system,the following power balance constraints must be met:

where Pg, j(t),PN(t),and Pw(t)are the output power of the coal-fired,nuclear-driven,and wind-driven generator,and PL(t)is the load power during the time period t.

(2)Output constraint of wind-driven generator

Owing to the uncontrollability of the output power of a wind-driven generator,when the power supply exceeds demand,wind abandonment can quickly occur.Therefore,the lower limit of the output power of the wind-driven generator can be considered to be 0.The output power of a wind-driven generator should not exceed its maximum allowable value or less than its minimum allowable value.

where Pw,max(t)is the upper limit of the output power of wind-driven generator at t time period.

(3)The constraints of coal-fired generator

1)Output power constraints of coal-fired generator

The output power of the coal-fired generator should not be greater than its maximum allowable value and not less than its minimum allowable value.

where represent the maximum and minimum output powers of the coal-fired generator,respectively,which are limited by the minimum load and rated power,respectively.

2)The ramp rating power constraints of coal-fired generator

The ramp rating power of the coal-fired generator should not be greater than its allowable power value for an upward increase and not less than its allowable power value for a downward decrease.

where rd, j and ru, j are the power values allowed to increase and decrease downward for the jth coal-fired generator.

3)Minimum start-stop time constraints of coal-fired generators

The minimum startup and shutdown times of the coalfired generator depend on the shortest startup and shutdown times and the operational status of the coal-fired generator.

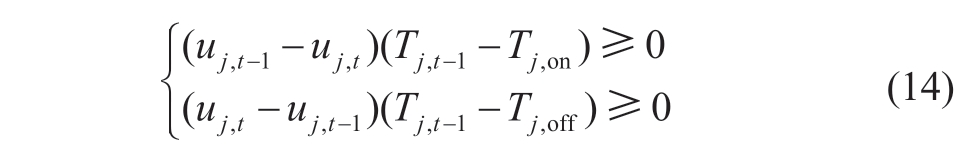
where Tj,on and Tj,off are the shortest starting and stopping times of the coal-fired generators,respectively,and uj,t represents the startup and shutdown statuses of the jth coalfired generator at the t time period.

(4)Reserve demand conditions of conventional generator

Under different scenarios,the power system has different demands for the rotating reserves.In general,neither winddriven nor nuclear-driven generators can undertake a rotating reservation.Therefore,all reserves were assumed to be coal-fired generators.In this case,the power system demand for the rotating reserve can be expressed as

where hp represents the demand for rotating reserve of the system,it takes 0.05 when only considering load reserving and 0.1 when considering load reserve and emergency reserve.ug, j(t)represents the startup and shutdown status of the jth coal-fired generator at t time period.

(5)Constraints of nuclear-driven generator

1)Linearization of the output power of a nuclear-driven generator

The output power of the nuclear-driven generator can be expressed using the following linearization formula:

whererepresent the upper and lower limit values of the output power of the nuclear-driven generator,ht and lm,t represent the 0-1 state variable of the high and low output power states of the nuclear-driven generator,and qm, j,t represents the 0-1 state variable of the power increase and decrease state of the coal-fired generator.

The peak-shaving power of nuclear-driven generators may be evenly divided into nd levels,and the power of the mth level is expressed as:

When the nuclear-driven generator is in the mth section,the lower section of the output power is.

By adjusting the location of the line segment to adjust the output power of the nuclear-driven generator to the peak load,the output power of the low-power section of the nuclear-driven generator can be changed indirectly.

The time required for nuclear-driven generators to increase or decrease their power is generally 1-3 hours.Assuming that the three variables of the power-up and-down states of the nuclear-driven generator are qm,1,qm,2,and qm,3,respectively,the power in the power-up and down sections may be expressed as

where j is the status label of power increase or decrease.

2)Output power constraints of nuclear-driven generator

Nuclear-driven generators may not operate in different states simultaneously;therefore,the operation marks of nuclear-driven generators must meet the following constraints:

Equation (20)is a nonlinear term and needs to be linearized.

3)Operational state constraints of nuclear-driven generators

Assuming that the output power of the nuclear-driven generator is increased or decreased for 3 h,the operating state of the nuclear-driven generator can be expressed by the following constraints:

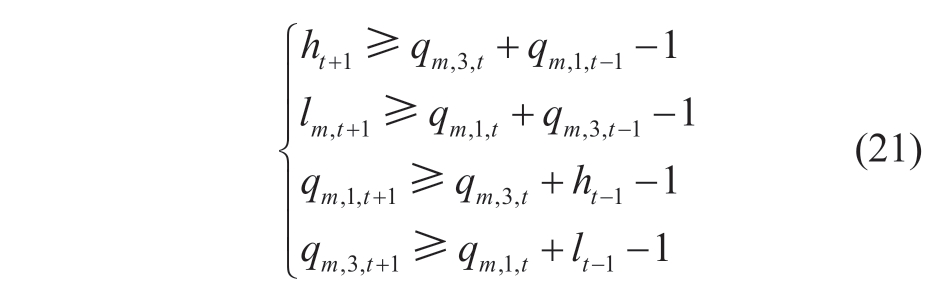
After Equation (20)is changed to Equation (21),mixed integer linear programming can be directly calculated.

(6)Transmission power constraints of the line

1)Transfer power constraints of the line

The transfer power of the line should not be greater than its maximum allowable value and not less than its minimum allowable value.

where Pl,max and Pl,min represent the maximum and minimum power the line is allowed to flow,respectively.When the minimum power is negative,it indicates that the power flow direction is in the opposite direction of the reference direction and Pl,t represents the power transferred by the jth line during time period t.

2)Transfer distribution factor matrix of power flow

Using the transfer distribution factor matrix,the G of the power flow obtained using Equation (22)can be rewritten as

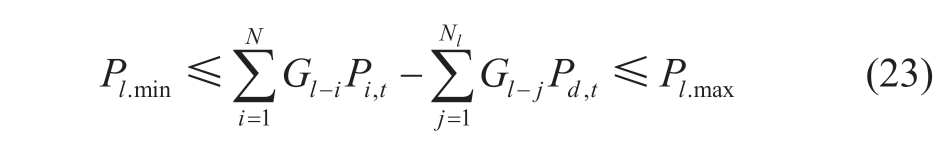
where G is called the factor matrix of transfer distribution,Gl-i represents the factor matrix of the lth branch affected by the injected power at the ith power node,N represents the number of power node in the network,Pi,t represents the power of the ith power node at t time period;Gl-j represents the factor matrix of the lth branch affected by the output power at the jth power node,Nl represents the number of load nodes in the network,and Pj,t represents the load power of the ith node at t time period.

The expression of the transfer distribution factor matrix G may be given:

where m and n represent the first and last nodes of the lth branch,respectively,xl is the impedance value of the lth branch and X is the inverse matrix of the node admittance matrix.

(7)Translatable load constraint

Translatable loads have uninterruptible and transferable operation properties.The following formulas can be used to characterize the operational characteristics of this type of load:The load participating in the demand response is connected to the network at the node j,and the power flow on the branch l decreases the Gl-i MW for a 1 MW reduction in the demand response load.Similarly,when the demand response load increases by 1 MW in a time period,the power flow on the branch l increases Gl-i by MW.Demand–response loads may change the power consumption behavior,change the power flow of the line,reduce the power of heavy-duty lines,and achieve peak shaving,peak shifting,and valley filling.The translatable load should satisfy the following constraints:

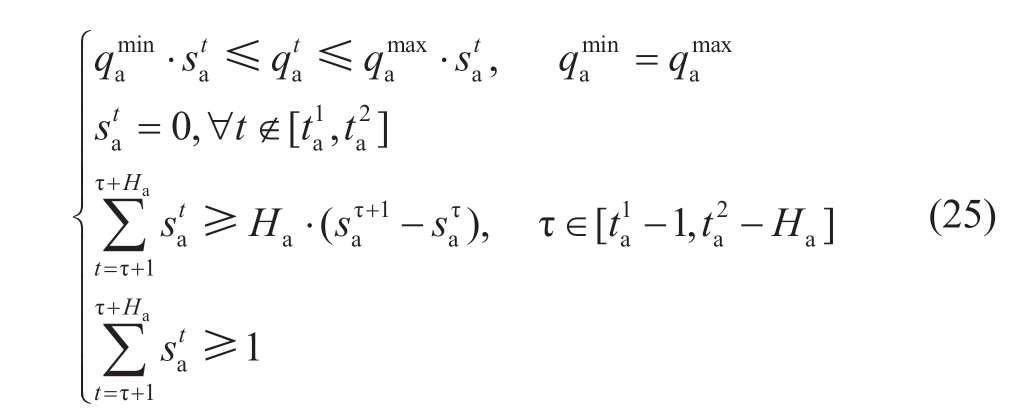
where indicates the operation time interval of the load participating in the demand response,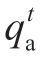indicates the actual load power during the period t;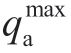and 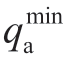 indicate the upper and lower limits of the electric load power,respectively,Ha indicates the period of continuous operation of the load,and  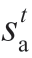is a 0-1 state variable.

2.3 Processing of constraint functions

Some of the constraints given above have no nonlinear term and may be expressed linearly;therefore,the compact form of the constraints may be expressed as a matrix [18]:

where x and y are the binary and continuous optimization variables,respectively,expressed by the following formula:

where σ corresponds to the coefficient matrix of the startup and shutdown costs of conventional generators;c corresponds to the coefficient matrix of costs;D,E,M,N,and Lu correspond to the coefficient matrices of the variables in the constraint conditions;d,s,h,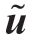are column respectively.

Among the constraints in compact form,the first row represents the inequality constraints,including the constraints of piecewise linearization of conventional generators,the constraints of the upper and lower limits of the translatable load,and the transmission constraints of the line.The second line includes the constraints of the power balance of supply and accommodation,including the translatable load.The third line is the mixed constraint,mainly the upper and lower limits of the conventional generators and the limit of the ramp rating speed.The fourth line represents the predicted output power of the winddriven generators in each period.

The above models may be considered mixed-integer linear programming problems,which may be solved using the general method for deterministic optimization problems.However,the result of the solution is highly dependent on the predicted value of the wind power.However,in an actual power system,many random factors often disturb wind power prediction and may not achieve satisfactory accuracy.The obtained results may not accurately reflect the randomness of wind power.To consider the deterministic optimization model and randomness of wind power,considering the maximum fluctuation range of wind power in each time period,a set U of the uncertain output power of wind-driven generators [19-22] is constructed:

where 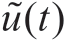represents the predicted value of the output power of wind-driven generators in each time period,Δu max (t)represents the maximum allowable prediction error of the output power of the wind-driven generator in each time period,and u(t)represents the uncertain value of the output power of the wind-driven generator in each time period,which fluctuates in the strip formed by the predicted value and the predicted error value and forms an uncertain set.

As shown in (1),the problem in the first stage is a minimization problem.At the first iteration,the output power of the wind-driven generator in this stage is preset as the predicted value ,and the optimization variables are the starting and stopping state variable x of the generators and the continuous variable y representing the output power of the generators.The optimization variables in the second stage are y and u,which represent the uncertain output power of the wind-driven generator.The optimization in the second stage involves determining the most economical operation cost of the uncertain variable u in a harsh scenario based on the startup and shutdown statuses of the generators in the first stage.The variables y and u are optimized in opposite directions,and the maximum-minimum iterative solution is implemented.After several alternative solutions,the global optimization scheme with the most economical results is obtained when the uncertain variable u changes in the direction of the worst scenario in the uncertainty set U:the best generator startup and shutdown and unit commitment schemes.

3 The solving method

The two-stage robust optimization problem was solved using the C&CG algorithm.The basic principle of the algorithm is to decompose the original problem into main and sub-problems,which are solved alternately.The main problem and sub-problem participate in each iteration,in which there are two output sets in the form of a column vector:xi and ui.xi is the initial input value of the subproblem in the ith iteration and ui is the initial input value of the main problem in the i+1 iteration.In the same iteration,according to the characteristics of the algorithm,the solution of the main problem must be the upper bound of the solution of the original problem,and the solution of the subproblem must be the lower bound of the original problem.Theoretically,the unit startup and shutdown combination xi+1 in the i+1 time is better than xi alone for coping with severe wind power scenarios.As the number of iterations increases,the upper bound of the solution of the main problem (i.e.,the original problem)gradually decreases or remains unchanged,and the lower bound of the original problem gradually increases or remains unchanged.After many iterations,if it converges,it is the optimal solution to the original problem.

The second stage is a max-min problem.The variables y and u were optimized in the opposite direction.Considering the dual problem of the minimum problem,the direction of dual variable optimization is opposite to that of the variable y so that the max-min problem may be changed into a maxmax problem.The second stage of the original problem is described as follows:

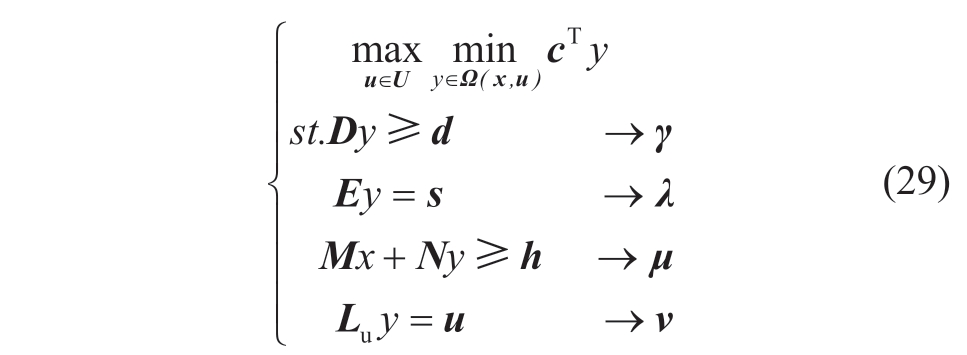
where variable γ, λ,μ and v is respectively the dual variable corresponding to each constraint in the second minimization stage;In the second stage,u is the optimization variable of the outer layer problem when the inner layer problem is solved;d,s and h is constant column vector.

In the second stage,the inner layer problem may be combined with the outer layer maximum problem after being dual to obtain the following dual problems:

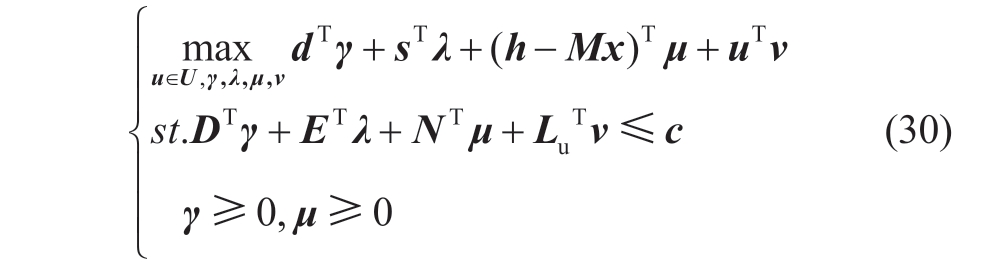
According to the dual theory,the dual variables γ and λ representing inequality constraints are more significant than zero,and the dual variables μ and v representing equality constraints are free variables.The optimal solution u* of the dual problem is the pole of the uncertainty set U of the output power of wind-driven generators.In other words,when Eq.(29)takes the maximum value,the value of the uncertainty variable u should be the lower bound of the fluctuation in the predicted value of the wind-driven generators,which increases the cost of grid operation.Therefore,(28)can be rewritten as:

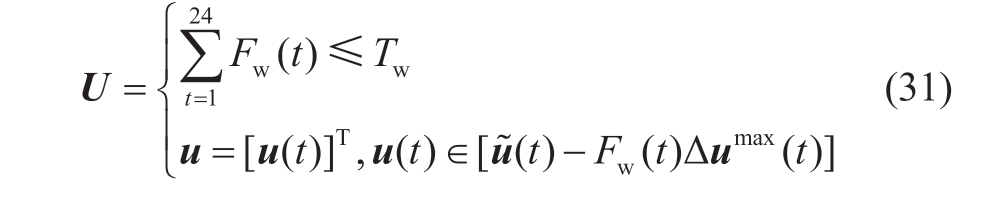
where F=[ Fw (1),Fw (2),...,Fw (24)] is a binary variable and Fw (t)is 1,which means that the output power of the wind-driven generator fluctuates to the lower bound of the uncertainties set at the t time period.Tw represents the total number of maximum periods of fluctuation in the output power of the wind-driven generator.By setting the value of the parameter,it may be used to describe the uncertainties of wind power and may indirectly adjust the conservatism of the optimization scheme.When Tw is set to 0,the uncertainties of wind power are not considered,and the scheme is not robust;the larger the value of Tw,the worse the scenario of the output power of the wind-driven generator,the more conservative the scheme,and the better the robustness of the system.

After rewriting Equation (28),the multiplication term uTv of the two continuous variables in Equation (30)can be rewritten as the product FTv of the binary and continuous variables.According to the theory of product linearization,if auxiliary variables are introduced,the following formula can be obtained:

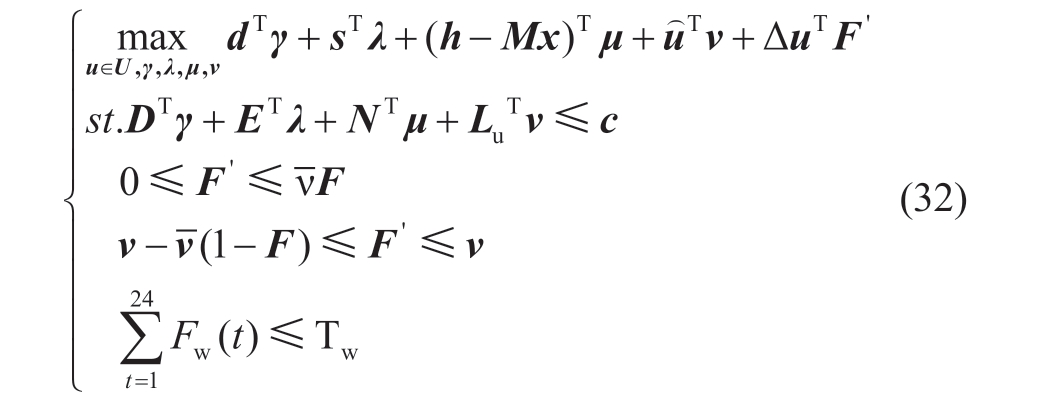
where Δu= [Δu max (t)]T,F'=[ Fw ' (t)]T,the auxiliary variable F' and variable F and v are coupled by the third and fourth line constraints of the above formula and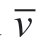is a sufficiently large constant,which is the upper bound of the dual variable.After inspection,the value of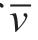was set to 5000.

After linearization,the max-min problem in the second stage is finally transformed into a mixed-integer linear programming problem,as in Equation (32).Combined with the main problem in the first stage,the specific solution process is as follows:

(1)The total number Tw of maximum periods of fluctuation of the output power of a given wind-driven generator and the predicted value 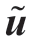of the output power of the wind-driven generator.

(2)Set the upper and lower bound parameters U=+∞,L=-∞ of the original problem,iteration number k,and convergence judgment value ε.

(3)The uncertain parameter u of the first iteration of the main problem is set as the predicted value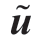of the power output of wind-driven generators.In the k-1 iteration,the solution uk-1 of the sub-problem is transferred to the uncertain parameter u of the main problem in the kth iteration.This main problem was resolved.The solution xk obtained from the main problem is transferred to the subproblem for further optimization,and the solution uk of the subproblem is obtained by repeating the above process,where the main problem and the subproblem may update their input and output alternately.

(4)The objective function value 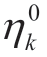of the main problem at the kth iteration is transferred to the lower bound L.In the same way,the objective function value 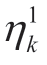of the main problem in the kth iteration represented is transferred to the lower bound U.When the difference between the upper and lower bounds of the original problem is less than the convergence judgment value U L-≤ε,the algorithm converges,and the solution is obtained.Any upper or lower bounds value can be used as an optimal solution to the original problem.The following equation was obtained:

whererepresent the solutions obtained after optimizing the main problem and subproblem in the kth iteration,respectively.

4 Study case

In order to verify the effectiveness of the two-stage robust optimization method,an improved IEEE-30 system is used in this paper.Node 6 is not a power or load node,and the loads at nodes 28 and 18 are used for the demand response.Nodes 1,2,5,8,11,and 13 are power nodes;the remaining are load nodes,as shown in Fig.2.

It is assumed that the minimum output power of the wind-driven generator is 150.8 MW,the maximum output may reach 650 MW,and the generator exhibits obvious antipeak characteristics.Four coal-fired generators were used as conventional generators,one of which was a fast-startand-stop generator for providing reservation services.Thenuclear-driven generator adopts the “12-3-3-6” operation mode,as shown in Fig.3.

Table 1 The parameters of coal-fired generator

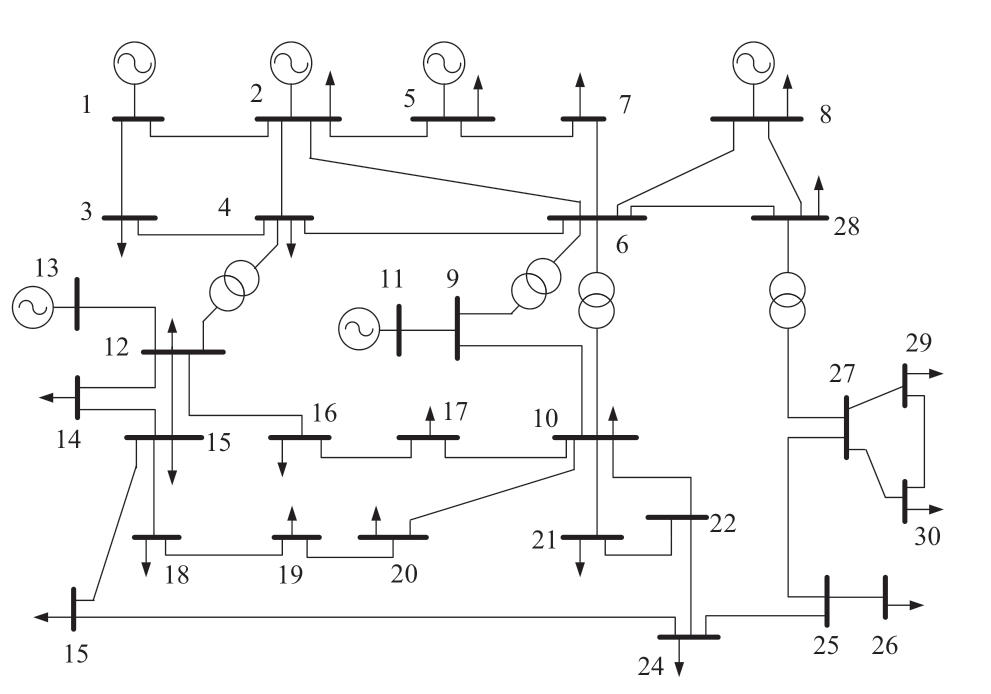
Fig.2 A modified IEEE-30 System

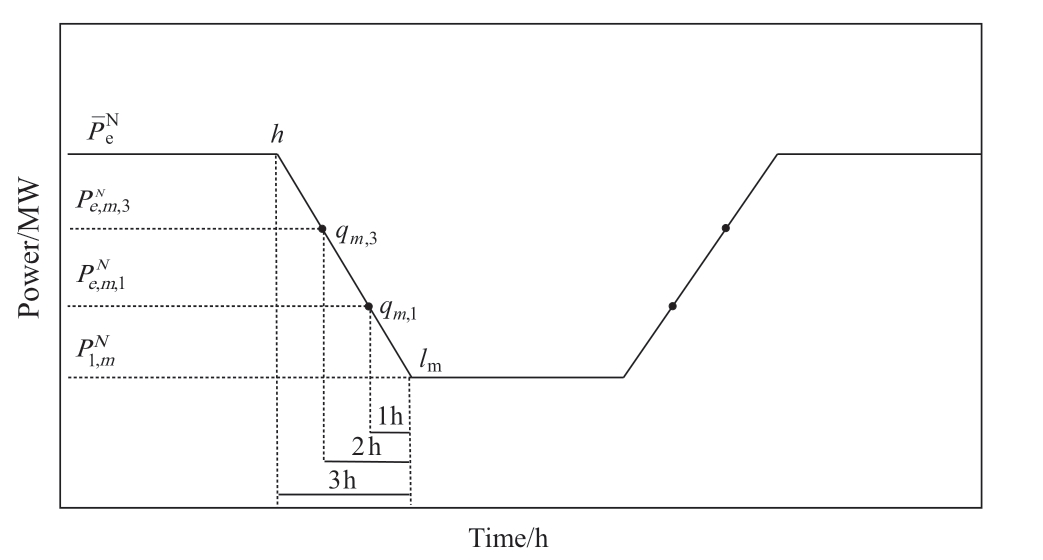
Fig.3 “12-3-3-6” operating mode of nuclear-driven generator

The upper power limit of the nuclear-driven generator was set to 492 MW,and the power at the low-power stage was 420 MW.In this example,owing to the operational characteristics of nuclear-driven generators and the uncontrollability of the output power of wind-driven generators,conventional generators are fully responsible for the peak shaving of the system.The parameters of the coalfired generator are listed in Table 1.

In this study,the unit commitments of a coal-fired,nuclear,and wind-driven generator are adopted and connected to the power nodes in the system in different orders.Different injection orders of power nodes affect the interaction of the power supply,transmission network,and demand response load,affecting the cost of wind power accommodation.

Because of the large number of power nodes involved,a certain amount of time is required for the algorithm to solve the problem.It is inappropriate to use exhaustive methods to verify the node-injection sequence of each generator connected to the grid.Therefore,after a quantitative analysis of the characteristics of the IEEE-30 system,three representative schemes for the node injection sequence of the generators connected to the grid were selected,as listed in Table 2.

Table 2 Node injection sequence of the generator connected to the grid

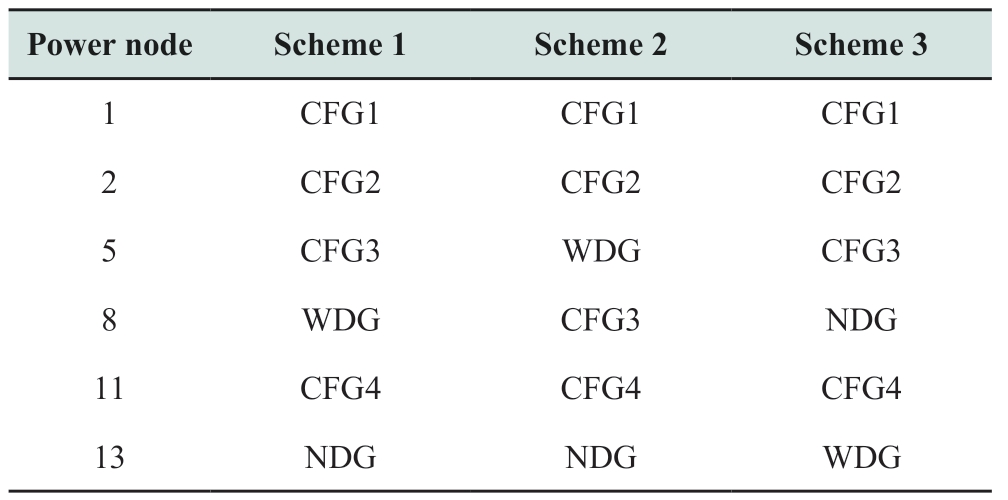
CFG:coal-fired generator;NDG:Nuclear-driven generator;WDG:Wind-driven generator.

In Scheme 2,wind power occupies the position of node 5,which means that if the grid wants to accommodate wind power as much as possible,it must partially reduce the output power of the coal-fired generators or shut down some coal-fired generators to participate in the regulation control of peak power.In schemes 1 and 3,the transmission capacity limited the wind power accommodation.The capacity of the transmission line connected by Nodes 8 and 13 was the same,and Node 13 was closer to the load.Schemes 1 and 3 realize wind power accommodation as safely as possible without reducing the rotating reserve capacity.

The optimization calculation Tw was set to six,and the predicted fluctuation deviation of the output power of the wind-driven generators was set to 0.15.A foursection linearization method was used to linearize the power generation cost curve of coal-fired generators.The C&CG algorithm is used to solve the proposed optimization problem.The optimization results are listed in Table 3.

Table 3 Optimization Results

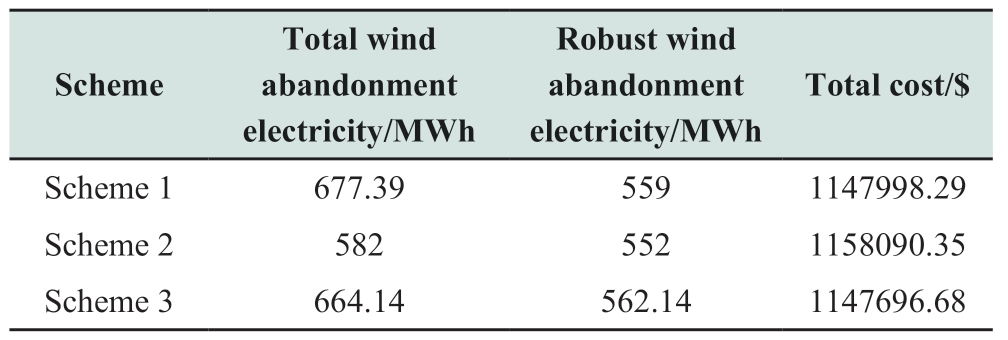
During 10:00-15:00,the difference between the load power and output power of the wind-driven generators is the largest,and the system has the largest demand for a rotating reserve.In an actual power system,the reserves include load reserve,emergency reserve,and maintenance reserve,but only the load reserve factor of hp=0.05 is considered in this study.It may be seen from the optimization results that the abandoned wind power in scheme 2 is 582 MWh,but the cost is the highest among the three schemes.Although the No.5 power generation node,where a wind power station is connected,has the lowest amount of curtailed wind owing to the limitation of transmission capacity,the coal-fired generator 3 is subject to the transmission capacity limit at node 8,resulting in a decline in the rotating reserve.In addition,when the reverse peak-shaving period occurred,it was necessary to purchase the capacity of the rotating reserve from conventional generators to meet the system’s demand for load reserve.

In Scheme 3,the amount of abandoned wind owing to the limitation of transmission capacity or the oversupply of wind power in a specific period is 102.44 MWh,whereas the corresponding amount of abandoned wind in Scheme 1 is 118.39 MWh.

The peak-shaving capacity of conventional generators is reduced to accommodate wind power in Scheme 2,which often leads to an insufficient rotating reserve of the system.Therefore,the robust algorithm causes the output power of the generators to fluctuate to the lower limit of the output range during periods of insufficient reserves.When the reserve factor increases,the disadvantages of the scheme become increasingly evident,operating costs increase,and the impact on the system increases.Schemes 1 and 3 focus more on the security of the reserve capacity of the system.Compared with Scheme 1,Scheme 3 has a lower abandoned wind power volume owing to the transmission capacity limitation and a higher abandoned wind power volume owing to the robust strategy,but the cost is the lowest.

Node 13 was close to the load node.Compared to a nuclear-driven generator with inflexible operation,connecting the wind-driven generator to Node 13 is more conducive to accommodating wind power.In the most conservative case,the three options are as follows:

Fig.4 Scheduling result

The first optimization stage aims to determine the startup and shutdown status of traditional generators to minimize operating costs.The second stage of the optimization goal is the lowest operating cost of the system under the worst-case output power of wind-driven generators,as shown in Fig.4.

Fig.4(a)shows the possible abandoned wind volume formed under the maximum allowable output power of the wind-driven generators.From Fig.4(a),it can be seen that the abandoned wind volume and operating costs are not strictly positively correlated.Compared to selecting six time periods with the highest output power for the abandoned wind volume,the abandoned wind time period selected after robust decision-making not only causes a shortage of electric power supply and increases reserve costs but also causes coal-fired generators to operate under harsh working conditions,increasing carbon emissions and unit energy consumption costs.

The convergence results are shown in Fig.4(b).After the second iteration,the upper and lower bounds of the original problem converged quickly.This is because,in this example,only the state variables for the start and stop of the coal-fired generators are small in computational complexity,making it easy to converge during the iteration process.The predicted fluctuation deviation of wind power is set to 0.15.At the same time,the capacity configuration of conventional generators is relatively large,so the numerical value of wind power fluctuations is insufficient to affect the start and stop of most conventional generators.There was no significant difference in the start and stop statuses of the main and subproblems.

Fig.4(c)shows the scheduling results obtained using the proposed robust optimization model for demand response management with source-grid-load collaboration to consume wind power.From Fig.4(c),it can be seen that during period 5,the abandoned wind volume was 59.1 MWh,and the coal-fired generators operated at a low output power.During Period 18,the abandoned wind volume was 53.6 MWh,and the coal-fired generators operated at a high output power.During period 18,the operation plan for abandoning wind resulted in a higher energy consumption per unit of power supply.After robust optimization of the decision to abandon wind,coal consumption increased by 130.59 tons,and operating costs increased by $75396.9.After optimization,the system is robust,and the wind power output fluctuates over six time periods that maximize the cost,providing a robust scheduling solution for power grid decision-makers to address the impact on grid stability.

The results of the participation of the translatable load in demand response are shown in Fig.4(d).The continuous working period of the translatable load was set to 5 h with a power of 5 MW from 2:00-21:00.During the period from 4:00-7:00,there was a high incidence of wind power in the low valley of electricity consumption.To prevent conventional generators from shutting down,the translatable load from 17:00-22:00 was transferred to the period–4:00-7:00 to fill the valley.During the peak electricity consumption and low wind power generation periods of 11:00 to 15:00,the convertible load can be transferred to the low electricity consumption period to reduce the load.

5 Conclusions

Given the uncertainties and inverse peak-shaving characteristics of the output power of wind-driven generators,this study adopts a two-stage robust optimization method to solve the problem through the cooperation of the source-network-load tripartite participation.Satisfactory convergence accuracy and speed were achieved.The optimization results are as follows:

1)The power system must allocate a specific reserve capacity for wind power.Therefore,it may not consume wind power indefinitely.Proper wind abandonment is more conducive to the stable operation of the power system.For a power node with a general accommodation capacity,the participation degree in the peak-shaving task is low,and it is suitable for injection by wind-driven generators with unregulatable capacity.Even if the nodes with the same transmission capacity are close to the load point,they are more capable of accommodating wind power.

2)Based on the robust idea of minimization–maximization,the original problem is divided into two stages to solve the optimization problem,which ensures that any subset of the uncertain set of wind power will not significantly deteriorate the system reliability or economy.The output power of the generator may operate in the most economical state,even in the worst-case scenario.

3)Considering the comfort and compensation cost of the demand-response load,the grid restricts the use of the demand-response load to alleviate the inverse peak regulation characteristics of wind power.

Acknowledgements

This work was supported by the Special Research Project on Power Planning of the Guangdong Power Grid Co.,Ltd.

Declaration of Competing Interest

The authors have no conflicts of interest to declare.

References

[1] Katinas V,Marčiukaitis M,Gecevičius G,et al.(2017)Statistical analysis of wind characteristics based on Weibull methods for estimation of power generation in Lithuania.Renewable energy,113:190-201

[2] Lin X M,Zhang Y J,Xiao Y,et al.(2019)A two-stage optimal dispatching model for energy internet in power-to-gas parks considering the start-up and shutdown of equipment.Guangdong Electric Power,32(10):62-70

[3] Wang B,Liu C,Zhang J,et al.(2015)uncertainties Estimation of Wind Power Prediction Based on Monte-Carlo Method.High Voltage Technology,41(10):3385-3391

[4] Yang H,Yan Y J,Wang Y (2020)Applicability of Beta Distribution in Wind Power Forecasting Error Model.Electric Measurement and Instrumentation,57(11):37-41+48

[5] Li Z W,Zhao S Q,Liu J S (2019)Combined optimal dispatch of wind-light-water-gas-fire-storage based on opportunityconstrained goal programming.Electric Power Automation Equipment,39(08):214-223

[6] Cui Y,Zhou H J,Zhong W Z,et al.(2020)Low-carbon dispatching of power systems including wind power considering uncertainties on both sides of the source and load.Electric Power Automation Equipment,40(11):85-93

[7] Li Z W,Zhao S Q,Liu J S (2019)Combined optimal dispatch of wind-light-water-gas-fire-storage based on opportunityconstrained goal programming.Electric Power Automation Equipment,39(08):214-223

[8] Du G,Zhao D M,Liu X (2023)A Review of Optimal Dispatch Considering Wind Power Uncertainty.Proceedings of the Chinese Society for Electrical Engineering,43(07):2608-2627

[9] Zhang S,Wang Z H,Zhang S C,et al.(2023)Optimal scheduling of cascaded water-solar-storage-storage joint based on datadriven distributed robust optimization.Engineering Science and Technology,55(02):128-140

[10] Xiao C Y,Wang N B,Ding K (2010)Research on wind power regulation methods in Jiuquan,Gansu.Proceedings of the CSEE,30(10):1-7

[11] Shao Y G (2019)Research on Wind Power-Nuclear Power Coordinated Optimal Dispatch Considering Nuclear Power Peak Shaving.Wuhan University

[12] Shao Y G,Zhao J,Liu D C,et al.(2019)Wind power-nuclear-power coordinated optimal dispatch considering peak shaving of nuclear-power.Chinese Journal of Electrical Engineering,39(04):1018-1029

[13] Hu D G,Pan Z J,Xu H L,et al.(2017)Estimation of peak shaving space of natural gas units under the condition of largescale renewable energy grid connection.Power System Protection and Control,45(03):87-93

[14] Feng Y,Liu C,Huang X C (2021)Optimal dispatching of microgrid with shiftable load based on dynamic time-ofuse electricity price.Journal of North China Electric Power University (Natural Science Edition),48(02):30-39

[15] Liu W Y,Wen J,Xie C,et al.(2015)Multi-objective optimization method for power system source-load collaboration considering wind power accommodation.Proceedings of the CSEE,35(05):1079-1088

[16] Chen M,Fan X W,Zhang W H,et al.(2022)A two-stage sourcenetwork-load-storage interactive optimization operation strategy to promote distributed photovoltaic accommodation.Power Grid Technology,46(10):3786 -3799

[17] Xu Q S,Deng C H,Zhao W X,et al.(2014)Multi-scenario Robust dispatching Method for Power Systems Including Wind Power.Power Grid Technology,38(03):653-661

[18] Liu Y X,Guo L,Wang C S (2018)Two-stage Robust Optimal Economic dispatching Method for Microgrid.Chinese Journal of Electrical Engineering,38(14):4013-4022+4307

[19] Fu Y,Xing X Y,Li Z K,et al.(2022)Multi-stage Robust Optimization Planning for Microgrid Group Based on Master-Slave Game.Electric Power Automation Equipment,42(04):1-8

[20] Chen Z X,Zhang X M,Wang X F,et al.(2021)Distribution Robust Optimal Configuration Method for Distributed Photovoltaic Power Stations Connected to Distribution Network.Power System Protection and Control,49(13):30-42

[21] Shi J K,Bao Ya,Chen Z,et al.(2021)A Robust Optimal Configuration Method for Charging Station Energy Storage Considering Charging Load uncertainties.Automation of Electric Power Systems,45(20):49-58

[22] Li X S,Wang M (2023)Robust Optimal dispatching and VCG Mechanism Bidding Strategy for Multiple Microgrids Considering Source-load uncertainties.Power Grid Technology,47(02):1-15

Scan for more details

Received:29 May 2023/

Revised:14 July 2023/

Accepted:21 August 2023/ Published:25 December 2023

Jiekang Wu

wujiekang@163.com

Xiangfeng Zhou

zxf12@csg.cn

Chunyuan Cai

caicyy@csg.cn

YongJian Li

lyjee@csg.cn

Yaoguo Zhan

15626457674@163.com

Yehua Sun

15625130396@163.com

2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Xiangfeng Zhou is affiliated with the Zhongshan Power Supply Bureau of Guangdong Power Grid Co.,Ltd.His research topics include power system operation and control.

Chunyuan Cai is affiliated with the Zhongshan Power Supply Bureau of Guangdong Power Grid Co.,Ltd.His research topics include power system operation and control.

Yongjian Li is affiliated with the Zhongshan Power Supply Bureau of Guangdong Power Grid Co.,Ltd.His research topics include power system operation and control.

Jiekang Wu was born in China,on Dec.9,1965.He graduated from Zhejiang University.His employment experience included being an engineer in the Power Supply Bureau,an engineer at the Electrical Engineering Design Institute,a professor at Zhejiang University,Guangxi University,Guangdong University of Technology,and an engineer in large enterprises.His special interests include power systems using renewable energy.Wu Jiekang has received honorary degrees from higher learning institutions,including Zhejiang University,South China University of Technology,and Guangxi University.Wu Jiekang is the lead corresponding author.

Yaoguo Zhan is the second corresponding author and is affiliated with the Guangdong University of Technology,China.His research topics include power system operation and control.

Yehua Sun is affiliated with Guangdong University of Technology,China.His research topics include power system operation and control.

(Editor Yanbo Wang)