0 Introduction

An energy system is a complex system that manages the relationships between energy generation and conversion,as well as between transmission and each of distribution,storage,and consumption to satisfy the terminal energy demand under the constraints of technical capacity and energy consumption [1].Modeling and optimizing the energy system is conducive to improving the security,economy,and equipment asset utilization of such systems and is thus critical for enhancing the efficiency of comprehensive energy utilization and the structure of energy supply [2,3].Based on the different time ranges of different models,the optimization of energy system models can be categorized into long- and short-term optimizations.Unlike short-term energy system model optimization,which focuses on energy scheduling,long-term energy system model optimization focuses on the optimal allocation of production capacity for energy technology and the optimal transformation approach for future energy.Therefore,such optimizations can provide solutions for various energy and environmental policies involving public interest problems [4].

Conventional long-term energy system model optimization typically considers only a single objective related to system investments,such as the total system cost,and optimizes the production capacity of energy technology under the constraints of resource limitation and supplydemand balance,thus resulting in the optimal technology production capacity ratio and approach [5].However,the optimization of energy system models is complex as it involves not only economic goals,but also multidimensional goals such as those related to the environment,society,and energy security.Therefore,multi-objective optimization must be performed for energy system models.Compared with the environmental and social objectives related to the optimization of energy system models,such as carbon dioxide emissions and employment opportunities,energy security objectives are more likely to be overlooked by researchers.However,owing to the significant effects of complex and volatile international environments on the global energy system,the latter must maintain an energy supply and demand balance and price stability.Energy security goals must be considered in the optimization of long-term energy system models,particularly in terms of energy supply security.

The simultaneous inclusion of these different dimensional objectives in the optimization may result in conflicting objectives,such as maximizing power generation and agricultural and household water use in hydroelectric power systems,which renders it difficult to obtain optimal solutions.The rationality and accuracy of the optimization results can be improved by selecting the appropriate multiobjective optimization methods.Some researchers have categorized multi-objective optimization methods into prior,posterior,and interactive methods based on the preferential expression of decision makers [6].This classification method can reflect the timing and participation degree of decision makers in the optimization of energy models,thus providing an important basis for selecting better optimization methods.

Although the objectives and methods of optimization for energy system models are crucial,current studies primarily focus on summarizing models and algorithms for optimizing energy system models [7,8].Meanwhile,comprehensive reviews regarding objectives and methods,particularly those pertaining to multi-objective optimization,for long-term energy system models are scarce.This paper summarizes the optimization objectives and methods for the multi-objective optimization of long-term energy system models.This article organized is as follows: First,the multi-objective optimization for long-term energy system models investigated in this study is defined,and the relevant methods are briefly elaborated.Second,the optimization objectives of the long-term energy system models,which are classified into economic,environmental,social,and energy security aspects,are introduced.Third,the classification and description of multi-objective optimization methods applied to energy system models are presented.Finally,the important objectives and methods of multi-optimization for long-term energy system models are summarized,and the focus for future multi-objective optimization is proposed.

1 Overview of long-term energy system model optimization and multi-objective optimization methods

1.1 Optimization of long-term energy system models

The optimization of energy system models providesa future development scenario of energy systems via optimization.Therefore,the time scale selected for energy system models significantly affects the results of the scenario considered.The optimization of energy system models can be categorized into short- and longterm optimizations,depending on the timescale of the models.Short-term energy model optimization is generally measured in hours and focuses on optimizing the operation of the energy system (typically for one year); examples include HOMER and URBS.Long-term energy model optimization is generally measured in years and focuses on the optimal allocation of energy technologies (typically for decades) [5]; examples include TIMES and MARKAL.The latter contributes more significantly to energy system planning and macro energy policy analysis.Through longterm energy model optimization,the effects of different energy technologies and policies on the future development of energy systems can be evaluated,thus providing policymakers with a scientific decision-making basis.The feasibility and accuracy of this analysis method depend on the time scales and optimization targets selected; therefore,selecting long-term energy systems at the national level (or at least the city level) as optimization targets is meaningful and valuable.

Owing to the increasing interest in energy transformation and security,the objective of optimizing energy system models has expanded from a single objective of system operation or investment to multiple objectives pertaining to economy,society,environment,and energy security.Between short- and long-term energy models,the manner by which the four abovementioned aspects is characterized differ slightly,as shown in Table 1.In general,short-term energy models focus on the current effects of operations on the objectives,with greater emphasis on the efficiency of system operations and competitiveness in the energy market.By contrast,the characterization of objectives in long-term energy systems considers the effect of time,with greater emphasis on achieving a sustainable,efficient,and low-carbon energy system over the next few decades.

Table 1 Similarities and differences in characterization between long-term and energy system model optimization objectives

A typical multi-objective optimization for long-term energy system models is shown in Fig.1.The primary aim of this optimization is to minimize system costs and environmental pollution under the constraints of environment,resource,energy supply and demand balance,production capacity,and changes in energy system stocks.This optimization comprehensively considers resource exploitation,transportation,storage,and utilization to satisfy the final energy requirements.Additionally,it forms the technological investment or energy transformation schemes for energy systems for the next few decades [9].Optimizing long-term energy system models is conducive to improving the energy supply structure,thus reducing energy costs and carbon emissions as well as realizing the coordinated development of economic and environmental benefits [5,10].

Fig.1 Schematic diagram of multi-objective optimization for long-term energy system models

This study focuses on multi-objective optimization for long-term energy system models (with spatial boundaries at the city level),with emphasis on the objectives and multiobjective optimization methods.

1.2 Multi-objective optimization methods

The energy system optimization problem is complex and diverse.In energy system planning,decision makers must consider multiple objectives,such as economic efficiency and environmental sustainability.Different objectives typically present conflicts and tradeoffs,thus complicating the optimization problem.Unlike multiobjective optimization methods,conventional singleobjective optimization methods cannot fully address these multi-objective problems.In fact,multi-objective optimization methods can consider multiple objectives by generating a series of solutions and using evaluation metrics to assess the solutions comprehensively [11].This approach can provide decision makers with a more comprehensive range of selections and assist them in identifying a suitable balance point.Multi-objective optimization is expressed mathematically as shown in equation (1).

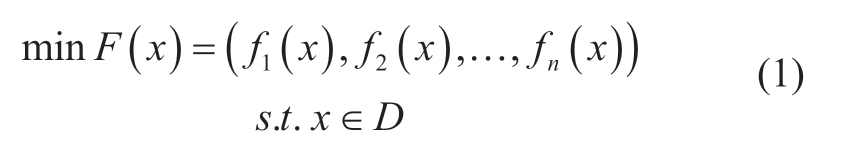
where n (n ≥ 2) is the number of optimization objective functions,xf=(x1,x2,…,xn) is the decision variable vector,D is the feasible solution space,and F(x) is the optimization objective comprising different optimization functions f(x).

Throughout the multi-objective optimization process,the involvement and subjective preferences of decision makers are required.Decision makers are not only key decision makers for solving the problem,but also the ultimate evaluators of the results.Participation in the decision-making process and expression of opinions are crucial to the feasibility and acceptability of the final outcome.Therefore,multi-objective optimization methods incorporate the subjective preferences of decision makers into the optimization process to ensure the reliability and accuracy of the optimal solution.Depending on the timing of the preference information provided by decision makers,multi-objective optimization methods can be categorized into three types: prior,posterior,and interactive methods.In prior methods,decision makers must provide preference information for different objectives before optimization and transform the multi-objective problem into a singleobjective problem.In posterior methods,decision makers must select the optimal solution from the generated effective solutions (all or sufficient).In interactive methods,which combine the advantages of a priori and a posteriori methods,decision makers dynamically express their preferences for each selection,as described in Section 3.

In practice,multi-objective optimization methods can be applied to both short- and long-term energy system models without significant differences in terms of the usage method.However,the emphasis of these methods may vary depending on the time horizon of the energy system being optimized.In short-term energy systems,the selection of strategies and operational decisions exerts an immediate effect on the deployment of energy systems.Decision makers in this context prioritize the accuracy and comprehensiveness of calculations as well as the ability of optimization methods to respond promptly to market changes,thus enabling real-time decision support.Conversely,long-term energy systems require decision makers to prioritize the complexity and operational efficiency of the optimized model.As long-term energy systems span a larger timeframe,the models used are more complex and computationally more demanding than those used for shortterm systems.Hence,the multi-objective optimization methods should be selected based on the specific demands of decision makers while considering the complexity and longterm planning requirements of the energy system,instead of merely based on the time scale of the model.

In summary,this article focuses on the multi-objective optimization of long-term energy system models (with spatial boundaries at the city level and beyond),with particular emphasis on the objectives and methods of multiobjective optimization.The aim is to provide rational decision-making support for the sustainable development of long-term energy systems.

2 Multi-dimensional objectives

Owing to the progress of investigations into energy systems,researchers have gradually realized that the optimization of energy system models should account for not only economically related objectives,but also various practical factors.These factors,e.g.,social acceptance,affect the successful deployment of the energy system.Additionally,they affect the properties of the energy system,such as the system reliability.The optimization goals of the energy system have diversified gradually.Based on different research fields,we categorize the objectives of multi-objective optimization into economic,environmental,social,and energy security aspects,as shown in Fig.2.

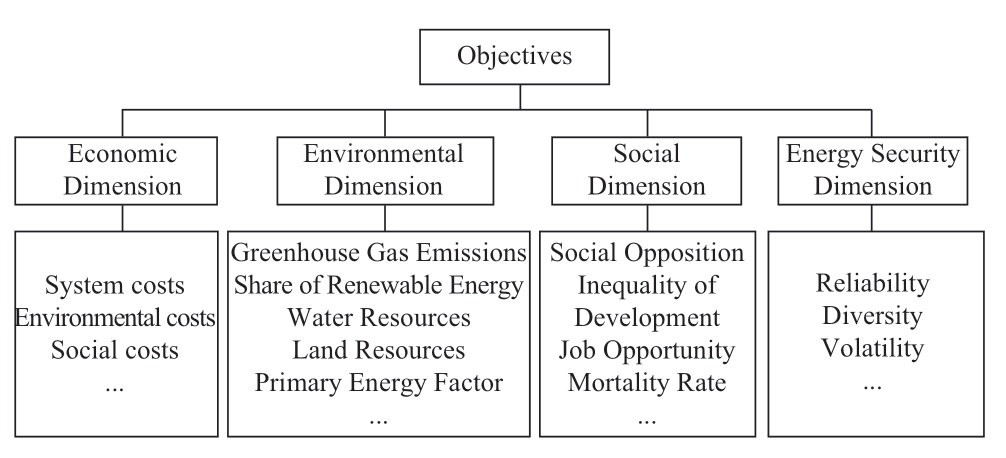
Fig.2 Multi-dimensional objectives of multi-objective optimization for long-term energy system models

2.1 Economic aspect

In the optimization of long-term energy system models,decision makers typically prioritize the economics of the energy system during its deployment.Economic objectives are the most considered optimization objectives and can be regarded as the most basic optimization objectives,as shown in Table 2.The most important objective function is the energy system cost (minimization) objective because the other objectives are considered only when the system costs are acceptable.

Table 2 Economic objectives of multi-objective optimization for energy system models

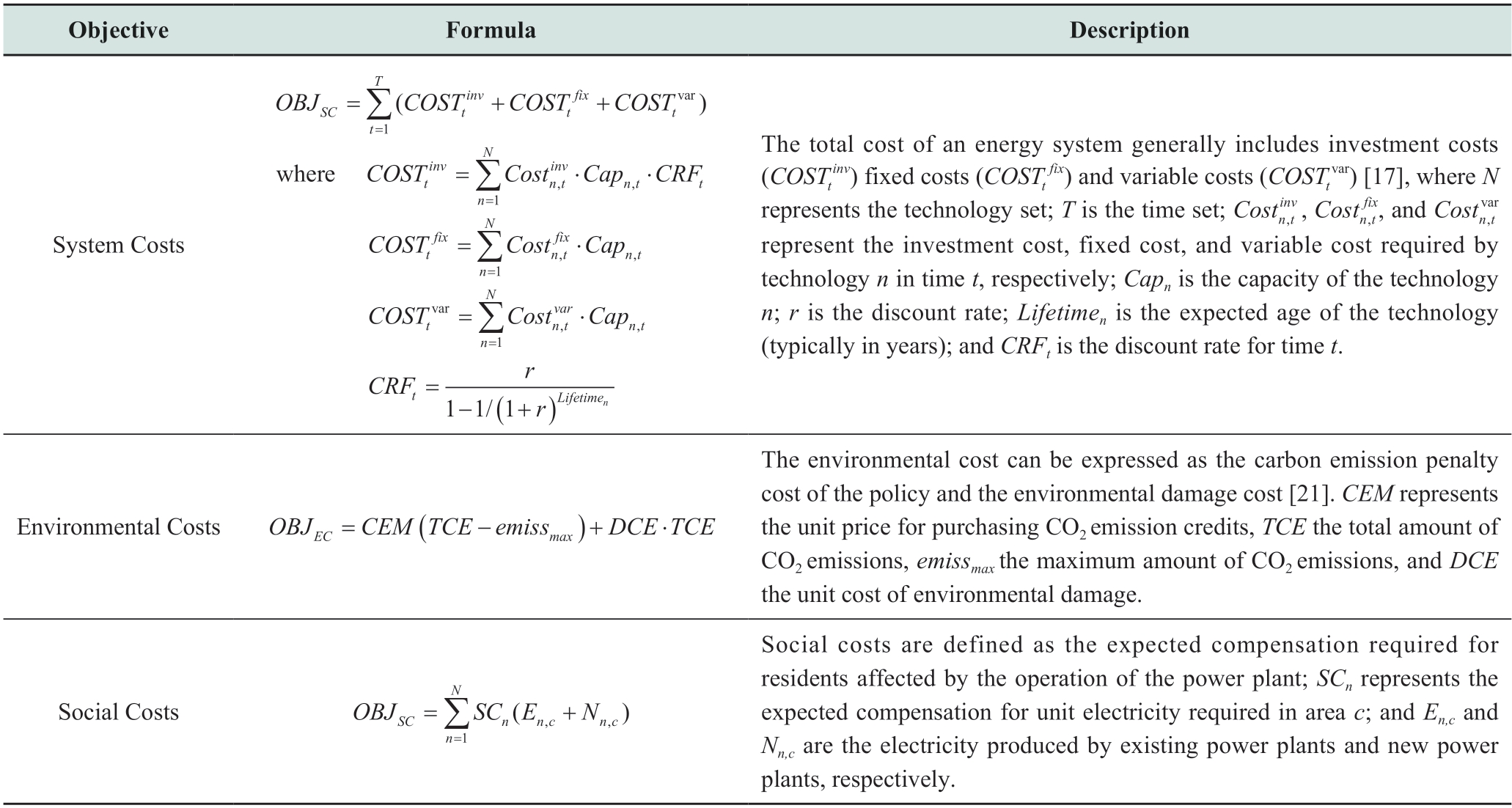
Table 3 Environmental objectives of the multi-objective optimization for long-term energy system models

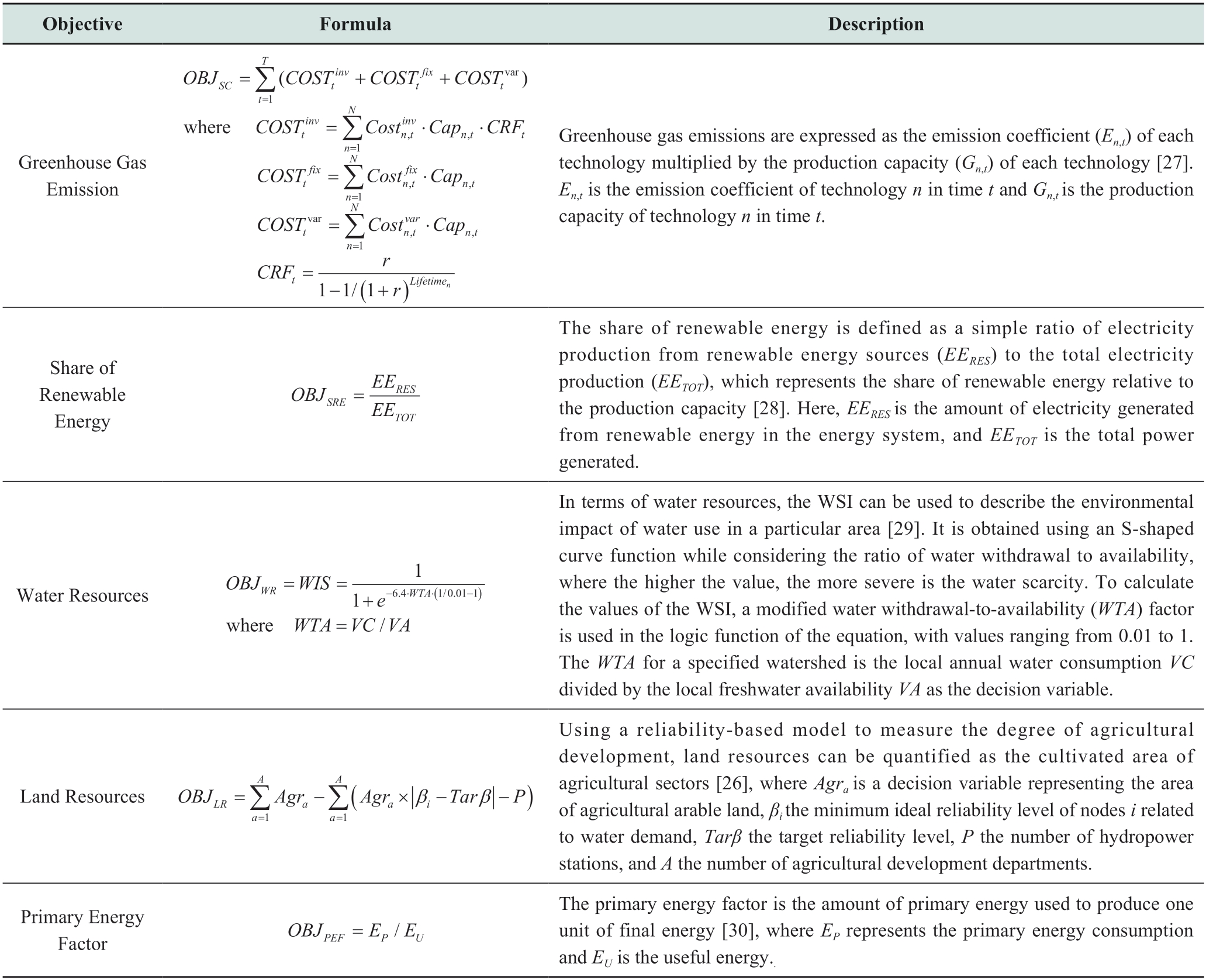
System Costs. Currently,the system costs considered in the models generally include investment,fixed,and variable costs [12].Investment cost refers to the capital cost of purchasing resource production facilities and related infrastructure,such as cables,power plants,generators,and other facilities for power generation,transmission,and distribution,in terms of the grid model construction.Fixed costs refer to fixed annual maintenance and replacement costs [13].The variable cost is the cost that varies with changes in technical capacity,such as fuel cost,variable operation and maintenance costs,and transportation and storage costs of CO2 [14].Notably,the variable cost is negative when it manifests as a systemic benefit.For example,Si et al.considered hydropower production to be one of the objectives when investigating the relationship among water,energy,and food in the upper reaches of the Yellow River Basin [15].In addition,some researchers combined variable and fixed costs into O&M costs [16-20].

Environmental Costs. Environmental costs typically refer to the cost of the carbon emission penalty or environmental damage.In most cases,it is regarded as a variable cost.However,the introduction of a carbon tax and the implementation of a carbon trading market are considered separate economic goals for energy systems.Environmental costs are typically used as an assumption pertaining to policies,i.e.,carbon-related policies are assumed to emerge in the future.For example,Noorollahi et al.incorporated environmental costs into their economic objectives to optimize an energy system model for a generation expansion plan that included renewable energy;additionally,they assumed that companies are required to purchase a certain amount of carbon credits annually and pay emission penalties if they exceed them [21].

Social Costs. The expansion of the technical production capacity of the energy system may adversely affect the lives of residents,such as the partial occupation of land resources and the use of water resources.Therefore,economic compensation must be provided to the residents.However,few studies have considered these occurrences or incorporated them into economic goals.Ratanakuakangwan et al.considered this aspect and proposed social costs,which were defined as the expected compensation required by residents affected by the operation of a power plant [22].

Different methods have been used to calculate the costs.The cost can be represented by the net present value cost,system cost per unit timescale,and unit energy production cost [13].The net present value cost is based on the total cost of the system,which considers inflation and interest rates; as such,all costs in the life cycle are converted into the initial moment cost of the system.For example,Zidan et al.used the net present value cost to calculate the total cost of a renewable energy generation system [12].The system cost of a unit timescale is the system cost in a unit time span,typically one year.Abdoos and Ghazvini selected the minimization of the annual system cost as one of multiple objectives for the optimization of a hybrid energy system model [23].The unit energy production cost is the system cost required to produce one unit of available energy and is rarely used as a costing method for long-term energy systems.Prebeg et al.minimized the unit power generation cost as an optimization goal [24].The net present value cost is a typical energy system optimization objective.Researchers typically have perfect foresight throughout the entire planning scope and optimize systems that have been used for decades; in other words,they typically optimize the entire system cycle instead of optimizing every operation period (such as one year).

2.2 Environmental aspect

Owing to the significant degradation of industrial development and environment,the effect of energy systems on the environment is gradually being emphasized,particularly the greenhouse effect caused by significant amounts of carbon dioxide emissions.An increasing number of countries have incorporated environmental protection strategies into their laws.Considering that the deployment of energy systems can significantly affect the environment,environmental objectives are increasingly being incorporated into energy system model optimization.Researchers typically consider both the economic and environmental aspects of goals,such as carbon dioxide emissions and system costs.Regarding environmental objectives,previous studies typically considered only carbon dioxide emissions,whereas only a few studies delved into other environmental factors,such as the limitations of water[25] and land resources [26],as shown in Table 2.

Greenhouse Gas Emissions.Owing to the increasing number of prominent environmental problems,greenhouse gas emissions that cause global warming have received increasing attention from researchers worldwide.However,most researchers consider only the minimization of CO2 emissions as an optimization objective.For example,Purwanto et al.used the coefficient of CO2 emissions to calculate the CO2 emissions of a system when evaluating the economic,environmental,and adequacy of local energy[27].Only a few studies have recognized the importance of other pollutant emissions and converted them into carbon emissions.For example,Ren et al.considered PM 2.5,SO2,and other pollutants in the emission reduction target of a mixed multi-criteria decision support model used in the steel industry to analyze the environmental impact [31].

Share of Renewable Energy. Renewable energy includes non-fossil energy sources,such as hydropower,photovoltaics,wind,geothermal,and bioenergy,which can be regenerated and minimally affect the environment.Therefore,promoting a high proportion of renewable energy sources and minimizing the use of fossil fuels to reduce carbon emissions are indispensable in future energy system planning.Noussan et al.expressed it as the share of renewable energy in the production capacity and incorporated it into the optimization system.Based on their findings,the share of renewable energy contributes positively to the primary energy factor and carbon dioxide emission coefficient [28].

Water Resources.Hydropower is one of the most mature power-generation technologies that utilize renewable resources.However,the electricity sector involves a significant number of water users,and the use of hydropower involves the utilization of fresh water for agriculture and households,which may result in water shortages when it is used for agricultural and domestic purposes,particularly in arid and semiarid regions.To balance water resources between water use for energy systems and social purposes,the use of freshwater in the energy system must be minimized during the optimization of energy systems.Moreover,the measurement of water resources should be discussed in the future.Si et al.used the shortage index proposed by the US Army Corps of Engineers [32] to evaluate the degree of water shortage in a system [15].Zhang et al.[29] used a water stress index(WSI) to describe the impact of water use in a specific area [29].

Land Resources. The development of the energy industry requires land resources.An increase in the number of power plants implies a partial occupation of the land resources,which depletes the cultivated area.By contrast,in arid and semi-arid areas,hydropower requires some of the water used for upstream farming,thus increasing the difficulty of land cultivation.Therefore,land resources must be incorporated into the optimization system when optimizing an energy system.In this regard,Al Shidhani et al.set the land area required to build power plants in a model as an objective function to maintain land use at minimum levels [33].Hatamkhani et al.used a reliabilitybased model to quantify agricultural development as the arable land area in the agricultural sector [26].

Primary Energy Factor (PEF).The PEF represents the amount of primary energy used per unit of final energy produced and is widely used in energy planning,policymaking,and energy system simulation [30].It correlates the primary energy with the final energy,thus reflecting the environmental impacts of different primary energy sources.Noussan et al.used the PEF to measure the environmental impact of Italian power plants [28].

2.3 Social aspect

Social effects must be considered when optimizing energy systems and incorporated into multi-objective optimization.Energy system planning significantly affects society may result in irreversible consequences; therefore,decision-makers must consider its effect on society.However,if the implementation of the system does not satisfy the expectations of the public,certain obstacles will be encountered during the implementation process,thereby affecting the visibility of the entire energy system.Few studies have included social factors in the multi-objective optimization of energy systems.The specific social objectives are listed in Table 4.

Table 4 Social objectives of multi-objective optimization for long-term energy system models

Social Opposition.Low social acceptance can hinder the deployment of energy systems; therefore,social effects must be considered when optimizing energy systems.Social acceptability can be regarded as a goal in the social aspect.However,Al Shidhani et al.reported that quantifying social acceptance is challenging and that translating it into social disapproval is easier.They expressed the degree of social opposition by assessing the progression of energy systems or technologies (opposition levels 1-5) [33].The ratings present certain limitations as they are based on the subjective judgment of energy experts and do not fully represent the collective opposition degree of society.In addition,the level of social opposition tends to evolve over time,and the social opposition levels of different countries can vary significantly.

Inequality of Development.The progress ofenergy transition differs from one region to another,and policymakers must consider uneven development when optimizing an energy system.Trotter et al.described this inequality as the maximum absolute discrepancy in electrification between urban and rural areas and the maximum discrepancy of the total electrification rate between any two regions [34].However,the descriptions do not fully represent the energy transition process of the regions.Therefore,researchers have attempted to measure this optimization objective more accurately.

Job Opportunity.The deployment of energy systems will result in the replacement of industries,i.e.,the loss of old jobs and the creation of new jobs.Therefore,employment is key to a smooth energy transition.Parkinson et al.defined social goals as employment opportunities and used the total job years of full-time equivalent (FTE)employment to quantify employment opportunities [16].

Mortality Rate. The potential death factors and probability in energy technology are not identical; for example,during the transportation of hydrogen,explosions can occur and cause casualties,whereas air pollution from coal-fired power plants can result in diseases such as asthma,cancer,and heart disease.The mortality rate estimates the potential mortality risk to humans caused by various technology combinations in various periods,and selecting energy system solutions with lower mortality rates is conducive to the deployment of energy systems.Al Shidhani et al.used it as a social indicator when measuring the economic,environmental,and social indicators of energy systems to select an optimal solution [33].

2.4 Energy security aspect

Because of the significant impact of the current complex and changing international relations with respect to global energy and mining systems,the instability of energy prices and supply has gradually been emphasized to achieve energy security and,in recent years,has been considered in the multi-objective optimization of energy systems.The energy security objectives are listed in Table 5.

Table 5 Energy security objectives of multi-objective optimization for long-term energy system models

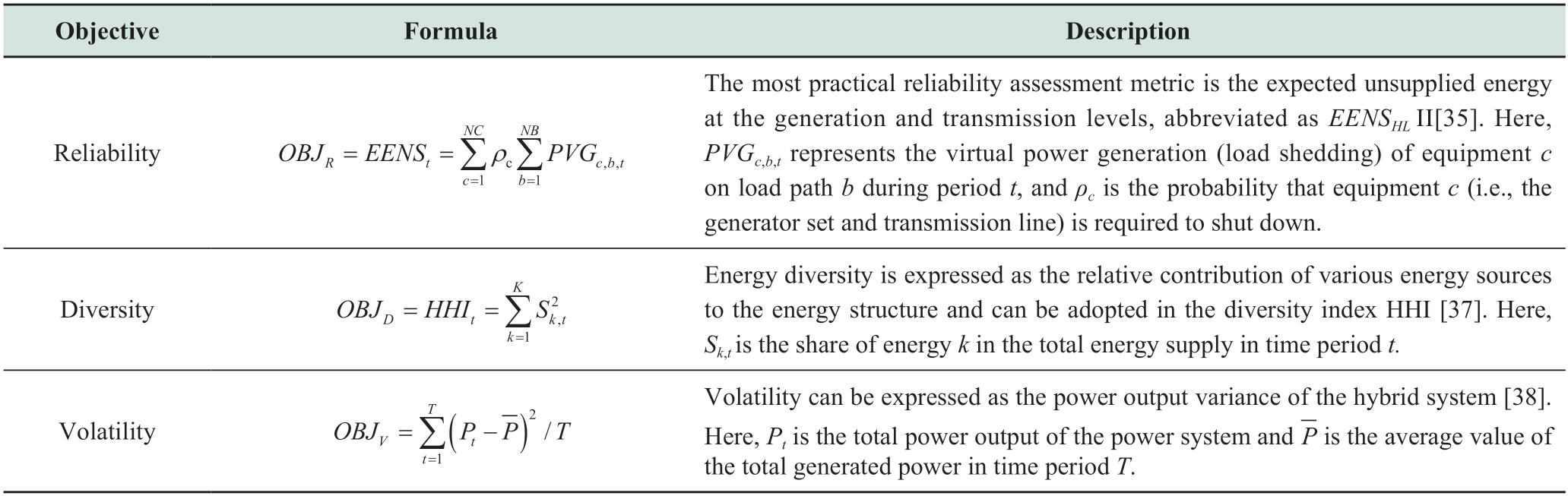
Reliability. During the planning of energy systems,the reliability assessment of the energy system is crucial.However,few studies have incorporated this into the multi-objective optimization of long-term energy systems.Javadi et al.discussed different reliability indicators when investigating Iran’s national power grid,which integrated renewable energy sources,and demonstrated that the most practical reliability assessment indicator was the expected energy not supplied (EENS) at the generation and transmission levels,denoted as EENSHL-Ⅱ [35].Aghaei et represented the reliability of a power system based on its adequacy [36].

Diversity.The instability of international relations results in fluctuations in energy prices,and extreme weather can affect energy supply.Diversification is not only beneficial to energy systems for addressing external changes and impacts,but can also prevent excessive dependence on a single energy source [39].Jing et al.defined energy diversity as the relative contribution of various energy sources to the energy structure;they expressed it as a diversity indicator represented by the Herfindahl-Hirschman index (HHI) [37].This index,which is developed by Herfindahl and Hirschman,is a widely used and relatively reliable index in economics,market power assessments,and power market diversity [24].An HHI with a lower value signifies greater diversity.Notably,several diversity indicators exist.To investigate the effects of different energy sources on energy security,Chuang et al.proposed various diversity indicators that can be used as energy security goals for future energy systems [40].

Volatility.To ensure that the power output from an energy system enters the grid smoothly,one should minimize fluctuations in the output power.Volatility is typically portrayed in short-term energy models but rarely inlong-term energy systems.To investigate long-term multiobjective optimization for a hydraulic photovoltaic power generation system model,Li and Qiu described volatility as the variance of the power output of a hybrid system [38].In the future,long-term energy systems can be optimized based on the goals of short-term energy models.

In previous studies,minimizing the system cost was considered the main goal,and other goals were specified based on the specific system model requirements.Table 6 summarizes the objectives pertaining to the multi-objective optimization of the long-term energy system.Most researchers specify two-dimensional goals for optimization and focus on the economic and environmental aspects.Although social and energy security goals are important,few studies have incorporated them into optimization,and none have considered both social and energy security objectives.Hence,the inadequacies above should be considered in future studies.

Table 6 Primary studies pertaining to multi-objective optimization for long-term energy system models

3 Multi-objective optimization methods

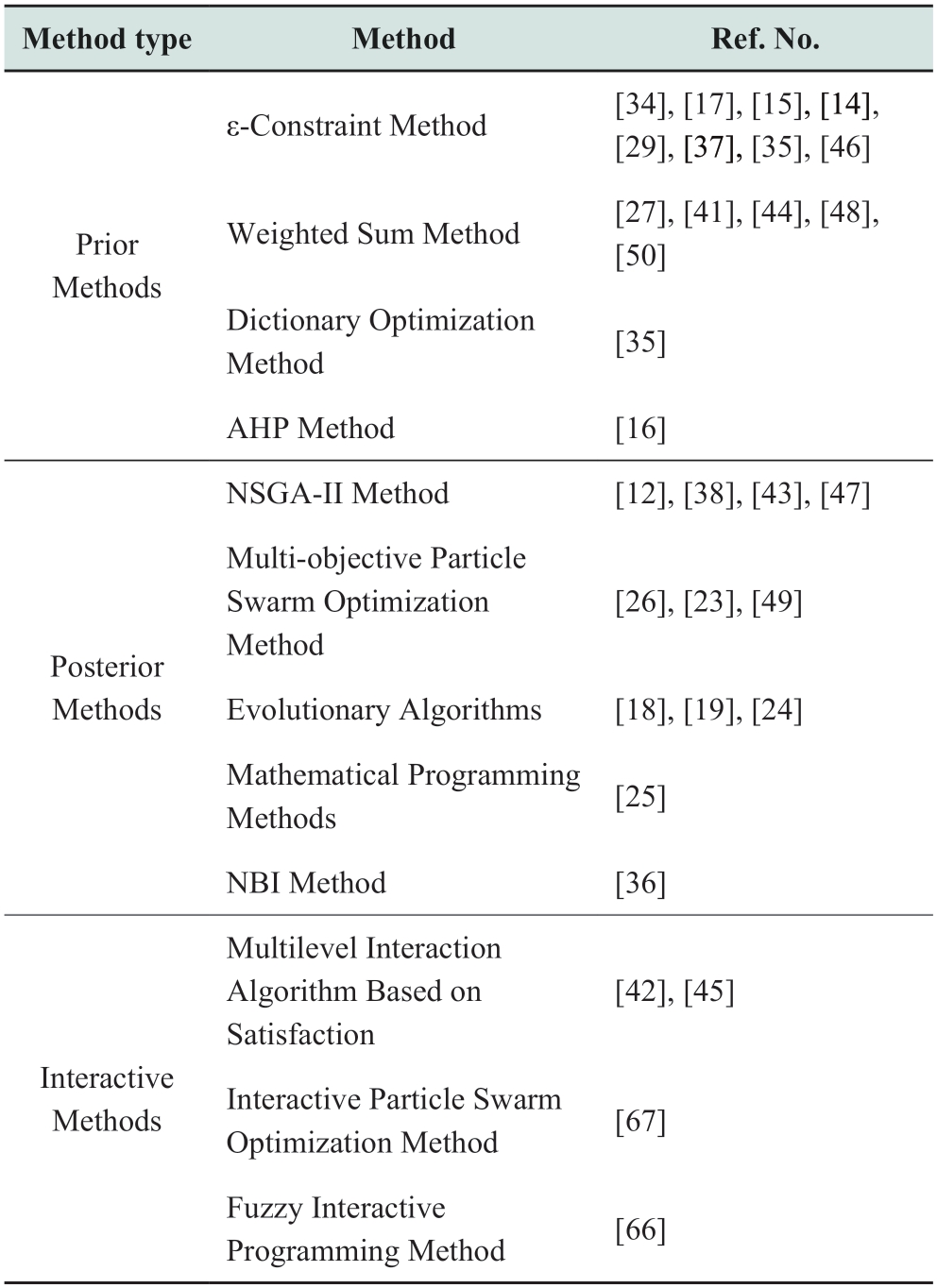
Multi-objective optimization methods significantly affect the optimization results and efficiency of long-term energy system models.To address multi-objective problems,the objectives are typically converted directly into a single objective and classical optimization algorithms are used to obtain the optimal solution.When applying this method,the importance degree of each objective (i.e.,the weight) must be determined by the decision makers.Based on the time order in which decision makers determine weights,multiobjective optimization methods can be categorized into prior methods (before searching for a solution),posterior methods (after searching),and interactive methods (during searching).Fig.3 summarizes multi-objective optimization methods applied to long-term energy system models.

Fig.3 Classification of multi-objective optimization methods

3.1 Prior methods

In previous methods,the decision maker first prioritizes objective functions and then converts multiple objectives into a single objective.Typical prior methods include the weighted sum,ε-constraint,and analytic hierarchy process(AHP) methods.

Weighted Sum Method. For n optimization objectives fi(x),I=(1,2,…,n),the weighted sum method can be used to convert multiple objectives into a single objective.Subsequently,the single-objective optimization algorithm can be used to solve the problem,which is expressed as shown in equation (2).

Here,wi ≥ 0,i=(1,2,…,n) is the set of weighting coefficients,and  Although this method is adopted widely because of its simplicity and efficiency,it presents some shortcomings.This method requires one to ensure the correctness of the objective function weights;additionally,it may not be able to solve nonconvex problems [51].

This method is widely used to solve multi-objective optimization problems.For example,Zhang et al.used the weighted sum method to solve the dual-objective optimization problem of water shortage risk minimization and CO2 emission minimization [29].Di Somma et al.proposed a stochastic integer programming model that converts the minimization of total energy costs and carbon dioxide emissions into a single objective using the weighted sum method; subsequently,they used the branch-andcut method to solve the issue investigated [52].Alabi et al.proposed a zero-carbon multi-energy system modeling strategy that combines the effects of energy storage aging and comprehensive demand response; additionally,they used the weighted sum method to simulate a realistic and highly flexible zero-carbon multi-energy system [53].

ε-Constraint Method.In this method,one of the objective functions is considered as the optimization objective,and the other objective functions are converted into constraints.Equation (3) is a general expression for the ε-constrained method.

where εi is the estimated upper bound of the objective function value,the objective fm(x) is optimized,and the remaining m-1 objective functions are transformed into constraints.The difficulty of the ε-constraint method is in estimating the upper limit of the objective function value,and the rationality of the value is typically determined by the experience of the decision maker.If the upper bound is extremely small,then the algorithm may fail to obtain a feasible solution; if the upper bound is extremely large,then other objectives,such as constraints,may incur a significant loss [11].Nonetheless,this method can solve both convex and nonconvex optimization problems [54] and does not require any weights for the objective function,thereby reducing the additional operations required by different weight combinations [55].

The ε-constraint method has been widely used in longterm energy systems.For example,Si et al.established a water-energy-food relationship model in the upper and middle reaches of the Yellow River Basin and used LINGO’s multi-start solver and the ε-constraint method to perform multi-objective optimization; consequently,they obtained the trade-offs among water,energy,and food [15].Sharafi et al.applied the ε-constraint method and particle swarm optimization simulation-based methods to solve multiobjective optimization problems [56].Nojavan et al.modeled the optimal and environmental performance problems of a hybrid power system,used the ε-constraint method to solve a multi-objective model,and then employed a fuzzy-satisfying technique to select the optimal solution [57].

AHP Method.This method first decomposes the target into multiple indicators and combines them into different hierarchical structures to form a system based on the interrelated effects and affiliation relationships between the indicators,thereby forming a hierarchical tree in which all nodes and child nodes (i.e.,targets and indicators)show different weights depending on their importance.Subsequently,based on this hierarchical tree,the final weights of each alternative scheme relative to the total target are calculated.The optimal solution has the highest final weight [58].The evaluation of the indicator weight can be objective or subjective.If real data are used,then the evaluation is objective; if no data is available or the available data cannot express the preferences of decision makers,then the corresponding priority can be obtained by subjectively comparing pairs to express the preferences of decision makers [59].

When weighing problems using several evaluation and sub-evaluation criteria,researcher prefers the AHP method.This method is typically combined with other multi-objective optimization methods to obtain a more accurate solution.For example,to analyze the long-term development of Iran’s power industry from the perspectives of economy,environment,society,and sustainability,Atabaki et al.,used the AHP method to allocate expertbased weights to the objective function and solved multiobjective optimization by applying a weighted method based on fuzzy membership functions [16].For the established multi-objective optimization of a multi-energy flow coupling system,Zong proposed and utilized an AHPimproved entropy weight method to weigh the considered targets and convert them into a single-objective optimization problem [60].In addition,Yue et al.proposed an energywater-food nexus optimization method that integrated the AHP and other methods for the sustainable management of agricultural recycling systems [61].

3.2 Posterior methods

In posterior methods,a set of potential non-dominated solutions must be generated first; subsequently,the decision maker selects from these solutions.Typical posterior methods include mathematical programming and multiobjective evolutionary algorithms.

Mathematical Programming Methods.A typical used mathematical programming method is the normal boundary intersection (NBI).

The advantage of the NBI method is that its performance is not affected by the scale of the objective function,and that it can generate uniformly distributed points on the Pareto surface [36].The first step in the method is to generate the income matrix,as shown in equation (4),where the value of the objective function i is expressed as fi(x).First,we determine the optimal values of all objective functions,obtain the optimal solution  corresponding to fi(x),and calculate the values of the other objective functions (i=1,2,…,n) based on .Therefore,row i in the income statement is  Similarly,the other rows of the earnings matrix can be calculated to compensate for the earnings statement.

The optimal solution obtained by optimizing objective function fi separately.The maximum and minimum values of each column in the payoff matrix express the range of variation of the objective function fi(x),which are known as the utopia and nadir points,respectively [62].If the objective function of the problem are of different sizes or feature different physical concepts,then the objectives must first be normalized to obtain a Pareto solution exhibiting a Pareto front [62,63].

Compared with the weighted sum method,this method has been used on a wider scale to solve nonconvex and high-dimensional multi-objective problems.For example,to investigate a multi-objective model of a short-term hydrothermal scheduling problem,Simab et al.used the NBI method to transform a nonconvex optimization problem into a convex optimization problem [62].NBI methods are constantly evolving.For example,to solve a multi-objective problem and obtain a Pareto surface,Zhu et al.proposed an improved NBI method [63] and Aghaei et al.implemented the corrected normal boundary intersection(CNBI) method [36].Compared with the classical weighted sum and ordinary NBI methods,the CNBI method can determine the minimum cost of resource addition more simply,effectively,and accurately.

Multi-objective Evolutionary Algorithms (MOEAs).MOEAs are random search methods that imitate the survival process of the fittest in natural ecosystems.These algorithms possess strong adaptability and self-organization [11] and are typically classified into three categories: aggregation-,domination-,and index-based algorithms.

The aggregation-based algorithm decomposes the multi-objective problem into multiple single-objective subproblems and solves them simultaneously.The typically used aggregation-based MOEAs are multi-objective evolutionary algorithms based on decomposition (MOEA/D).For example,Huang et al.focused on the reuse of retired electric vehicle batteries (REVB) in renewable energy systems and proposed a PV-hydrogen-REVB hybrid energy system.To calculate its objective functions,the non-dominated sorting genetic algorithm (NSGA-II)and MOEA/D were applied to generate a Pareto set for residential usage,and their performances were compared[64].

Dominance-based algorithms are the most typical type of MOEA reported in the literature,and the most typical among them is NSGA-II.Li and Qiu proposed a longterm multi-objective optimization for a hydro-photovoltaic power system model; they considered the smoothness of the power output process and the total amount of annual power generation of the system simultaneously,and used an improved version of the NSGA-II for optimization [38].Noorollahi et al.used the NSGA-II to optimize a multiobjective problem[21].

Meanwhile,in indicator-based algorithms,indicator functions are used to measure the population quality in MOEAs.Keshavarzzadeh and Ahmadi used multiple methods,such as NSGA-II,generalized differential evaluation,an indicator-based evolutionary algorithm,a speed-constrained multi-objective,and strength Pareto evolutionary algorithms,to optimize an established multi-objective model and compared the results of these algorithms [65].

3.3 Interactive methods

In interactive methods,the decision maker must express a preference for each objective at each optimization to obtain the Pareto optimal solution of interest.Compared with prior and posterior methods,interactive methods are used less frequently in long-term energy system models owing to their complexity.Typical interactive methods include interactive fuzzy programming,interactive particle swarm and simplex methods,satisfaction-based interactive-solving algorithms,and interactive tradeoff algorithms.Zarrinpoor et al.established various modeling frameworks to design a biofuel supply chain and used the fuzzy interactive programming method to solve multi-objective models [66].Chen et al.developed a multilevel programming model for a shale gas supply chain system from the perspective of the lifecycle and proposed an improved multilevel interactive solution algorithm based on a satisfactory degree to improve computational efficiency [42].Feng et al.developed a multi-objective bi-level programming model by considering the mutual interactions between government and power projects and solved the model via interactive particle swarm optimization and a simplex method [67].

As shown in Table 7,in the long-term energy model,interaction methods are used less frequently,whereas prior and posterior methods are used more frequently.Among them,prior methods are widely applied because of their simplicity and efficiency; however,one may not be able to obtain all Pareto solutions using this method,and the decision maker cannot determine whether the criterion weights are reliable [6].Posterior methods require an exhaustive method to invoke the energy system model and generate a Pareto solution set.Therefore,they are inefficient for solving complex models such as energy technology systems.Meanwhile,interactive methods allow decision makers to participate in the entire model optimization process,and the model results are more consistent with the actual requirements of the decision makers [25,31].Interactive methods only calculate the scheme preferred by the decision maker,thus significantly reducing theamount of calculations.Furthermore,they allow decision makers to further analyze the conflict between goals by solving the preferences for a better adjustment.This shall be investigated in future studies.

Table 7 Optimization methods used in primary studies of multi-objective optimization for long-term energy system models

4 Conclusion and discussion

Herein,studies related to long-term energy systems were systematically reviewed and analyzed from the perspective of optimization objectives and methods to determine the optimization objectives and methods that should be focused on in the modeling of long-term energy systems.This enables decision makers to select the appropriate optimization objectives and optimization methods based on the focus of optimization problems and the model type.The main conclusions are as follows:

Owing to the increasing demand for energy system modeling,the optimization objectives have become more diverse.Most previous studies only considered two optimization objectives and primarily focused on economic and environmental objectives,whereas few studies considered other optimization objectives,particularly social and energy security objectives.However,social and energy security objectives must be considered when optimizing energy systems.Furthermore,energy system planning affects society significantly; thus,the energy system must be optimized to reduce its adverse effect and ensure the smooth progress of energy transition.However,owing to the acceleration of the energy transformation process,energy systems have become more sensitive to economic,environmental,and social activities.Energy security can guarantee the smooth operation of an energy system in cases involving major disturbances.Therefore,the anti-risk abilities of energy systems must be measured.Maximizing the energy security of the energy system or minimizing the social impact to minimize the system cost shall be investigated in the future.

To obtain the optimal solution accurately and rapidly through multi-objective optimization,various methods can be used,which can be classified into prior,posterior,and interactive methods.Among them,prior methods are the most widely used because of the simplicity and efficiency of the algorithm,followed by posterior methods.The least used methods are interactive methods.However,compared with a priori and posterior methods,interactive methods can map the preference of the decision maker to the goal of model optimization; consequently,the model results are more consistent with the actual requirements of the decision maker.Owing to the diversity of research objectives,multi-objective optimization using interactive methods is invaluable and should be further investigated in the future.In addition,researchers should adopt various multi-objective optimization methods to compare their differences in terms of performance and computational efficiency such that the best optimization method can be selected to ensure the accuracy and efficiency of the model optimization results.

This study systematically analyzed the multi-objective optimization of energy system models from the perspectives of optimization objectives and optimization methods.The optimization of target differences can be further improved,as the classification of multi-objective optimization objectives and the proposed optimization methods are affected by spatial scale and do not involve the analysis of the distribution of energy systems in different geographical areas.

Acknowledgements

This research was financially supported by the National Natural Science Foundation of China (No.72371102).

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] Fan H,Wang CY,Liu L,et al.(2022) Review of uncertainty modeling for optimal operation of integrated energy system [J9].Frontiers in Energy Research,9: 641337

[2] Hong BW,Zhang WT,Zhou Y,et al.(2018) Energy-Internetoriented microgrid energy management system architecture and its application in China.Applied Energy 228: 2153-2164

[3] Clegg S,Mancarella P (2015) Integrated electrical and gas network flexibility assessment in low-carbon multi-energy systems [J].IEEE Transactions on Sustainable Energy 7(2): 718-731

[4] Lund H,Arler F,Ostergaard PA,et al.(2017) Simulation versus optimisation: Theoretical positions in energy system modelling.Energies 10(7): 840

[5] Ringkjob HK,Haugan PM,Solbrekke IM (2018) A review of modelling tools for energy and electricity systems with large shares of variable renewables.Renewable & Sustainable Energy Reviews 96: 440-459

[6] Nagy M,Mansour Y,Abdelmohsen S,et al.(2020) Multiobjective optimization methods as a decision making strategy.International Journal of Engineering Research and Technology 9(3): 516-522

[7] Bouaouda A,Sayouti Y (2022) Hybrid meta-heuristic algorithms for optimal sizing of hybrid renewable energy system: A review of the state-of-the-art.Archives of Computational Methods in Engineering 29(6): 4049-4083

[8] Naz MN,Mushtaq MI,Naeem M,et al.(2017) Multicriteria decision making for resource management in renewable energy assisted microgrids.Renewable & Sustainable Energy Reviews 71: 323-341

[9] Zhou YB,Yang F,Yu XX,et al.(2022) Realization pathways and key problems of carbon neutrality in China’s energy and power system.Electric Power 55(05): 1-11 (in Chinese)

[10] Zhao J,Chen L,Wang YN,et al.(2021) A review of system modeling,assessment and operational optimization for integrated energy systems.Science China-Information Sciences 64(9):191201

[11] Cui YF,Geng ZQ,Zhu QX,et al.(2017) Review: Multi-objective optimization methods and application in energy saving.Energy 125: 681-704

[12] Zidan A,Shaaban MF,El-Saadany EF (2013) Long-term multiobjective distribution network planning by DG allocation and feeders’ reconfiguration.Electric Power Systems Research 105:95-104

[13] Khezri R,Mahmoudi A (2020) Review on the state-of-the-art multi-objective optimisation of hybrid standalone/grid-connected energy systems.IET Generation Transmission & Distribution 14(20): 4285-4300

[14] Louis JN,Allard S,Kotrotsou F,et al.(2020) A multi-objective approach to the prospective development of the European power system by 2050.Energy 191: 116539

[15] Si Y,Li X,Yin DQ,et al.(2019) Revealing the water-energyfood nexus in the Upper Yellow River Basin through multiobjective optimization for reservoir system.Science of the Total Environment 682: 1-18

[16] Atabaki MS,Aryanpur V (2018) Multi-objective optimization for sustainable development of the power sector: An economic,environmental,and social analysis of Iran.Energy 161: 493-507

[17] Murray P,Orehounig K,Grosspietsch D,et al.(2018) A comparison of storage systems in neighbourhood decentralized energy system applications from 2015 to 2050.Applied Energy 231: 1285-1306

[18] Fischer R,Elfgren E,Toffolo A (2020) Towards optimal sustainable energy systems in Nordic municipalities.Energies 13(2): 290

[19] Viesi D,Crema L,Mahbub MS,et al.(2020) Integrated and dynamic energy modelling of a regional system: A cost-optimized approach in the deep decarbonisation of the Province of Trento(Italy).Energy 209: 118378

[20] Ma WW,Zhang YC,Fan JQ,et al.(2022) An innovative datadriven energy planning framework for developing regions based on multi-objective optimization and multi-index comprehensive evaluation.Journal of Renewable and Sustainable Energy 14(2):026303

[21] Noorollahi E,Fadai D,Ghodsipour SH,et al.(2017) Developing a new optimization framework for power generation expansion planning with the inclusion of renewable energy-A case study of Iran.Journal of Renewable and Sustainable Energy 9(1): 015901

[22] Ratanakuakangwan S,Morita H (2022) Multi-aspect efficiency measurement of multi-objective energy planning model dealing with uncertainties.Applied Energy 313: 118883

[23] Abdoos M,Ghazvini M (2018) Multi-objective particle swarm optimization of component size and long-term operation of hybrid energy systems under multiple uncertainties.Journal of Renewable and Sustainable Energy 10(1): 015902

[24] Prebeg P,Gasparovic G,Krajacic G,et al.(2016) Long-term energy planning of Croatian power system using multi-objective optimization with focus on renewable energy and integration of electric vehicles.Applied Energy 184: 1493-1507

[25] Parkinson SC,Makowski M,Krey V,et al.(2018) A multicriteria model analysis framework for assessing integrated waterenergy system transformation pathways.Applied Energy 210:477-486

[26] Hatamkhani A,Moridi A (2019) Multi-objective optimization of hydropower and agricultural development at river basin scale.Water Resources Management 33(13): 4431-4450

[27] Purwanto WW,Pratama YW,Nugroho YS,et al.(2015)Multi-objective optimization model for sustainable Indonesian electricity system: Analysis of economic,environment,and adequacy of energy sources.Renewable Energy 81: 308-318

[28] Noussan M,Roberto R,Nastasi B (2018) Performance indicators of electricity generation at country level—The case of Italy.Energies 11(3): 650

[29] Zhang YY,Wang JQ,Zhang LM,et al.(2020) Optimization of China’s electric power sector targeting water stress and carbon emissions.Applied Energy 271: 115221

[30] Bilardo M,Galata S,Fabrizio E (2022) The role of Primary Energy Factors (PEF) for electricity in the evaluation and comparison of building energy performance: An investigation on European nZEBs according to EN 17423: 2020.Sustainable Cities and Society 87: 104189

[31] Ren HT,Zhou WJ,Makowski M,et al.(2023) A multicriteria decision support model for adopting energy efficiency technologies in the iron and steel industry.Annals of Operations Research 325(2): 1111-1132

[32] Cooley RL,Harsh J,Lewis DC (1972) Hydrologic Engineering Methods for Water Resources Development,v 10

[33] Al Shidhani T,Ioannou A,Falcone G (2020) Multi-objective optimisation for power system planning integrating sustainability indicators.Energies 13(9): 2199

[34] Trotter PA,Cooper NJ,Wilson PR (2019) A multi-criteria,longterm energy planning optimisation model with integrated on-grid and off-grid electrification - The case of Uganda.Applied Energy 243: 288-312

[35] Javadi MS,Nezhad AE (2019) Multi-objective,multi-year dynamic generation and transmission expansion planningrenewable energy sources integration for Iran’s National Power Grid.International Transactions on Electrical Energy Systems 29(4): e2810

[36] Aghaei J,Akbari MA,Roosta A,et al.(2013) Multiobjective generation expansion planning considering power system adequacy.Electric Power Systems Research 102: 8-19

[37] Jing R,Lin YF,Khanna N,et al.(2021) Balancing the Energy Trilemma in energy system planning of coastal cities.Applied Energy 283: 116222

[38] Li FF,Qiu J (2016) Multi-objective optimization for integrated hydro-photovoltaic power system.Applied Energy 167: 377-384

[39] Chuang MC,Ma Hw (2013) Energy security and improvements in the function of diversity indices—Taiwan energy supply structure case study.Renewable and Sustainable Energy Reviews 24: 9-20

[40] Chuang MC,Ma HW (2013) Energy security integrated and improvements in the function of diversity indices-Taiwan energy supply structure case study.Renewable & Sustainable hydrophotovoltaic Energy Reviews 24: 9-20

[41] Groissböck M,Pickl MJ (2016) An analysis of the power market in Saudi Arabia: Retrospective cost and environmental optimization.Applied Energy 165: 548-558

[42] Chen YZ,He L,Guan YL,et al.(2017) Life cycle assessment of greenhouse gas emissions and water-energy optimization for shale gas supply chain planning based on multi-level approach:Case study in Barnett,Marcellus,Fayetteville,and Haynesville shales.Energy Conversion and Management 134: 382-398

[43] Prina MG,Lionetti M,Manzolini G,et al.(2019) Transition pathways optimization methodology through EnergyPLAN software for long-term energy planning.Applied Energy 235:356-368

[44] Gbadamosi SL,Nwulu NI (2020) A multi-period composite generation and transmission expansion planning model incorporating renewable energy sources and demand response.Sustainable Energy Technologies and Assessments 39: 100726

[45] Toloo M,Taghizadeh-Yazdi M,Mohammadi-Balani A (2022)Multi-objective centralization-decentralization trade-off analysis for multi-source renewable electricity generation expansion planning: A case study of Iran.Computers & Industrial Engineering 164: 107870

[46] Vergara-Zambrano J,Kracht W,Díaz-Alvarado FA (2022)Integration of renewable energy into the copper mining industry:A multi-objective approach.Journal of Cleaner Production 372:133419

[47] Uen TS,Chang FJ,Zhou YL,et al.(2018) Exploring synergistic benefits of Water-Food-Energy Nexus through multi-objective reservoir optimization schemes.Science of the Total Environment 633: 341-351

[48] Pratama YW,Purwanto WW,Tezuka T,et al.(2017) Multiobjective optimization of a multiregional electricity system in an archipelagic state: The role of renewable energy in energy system sustainability.Renewable & Sustainable Energy Reviews 77:423-439

[49] Yuan M,Thellufsen JZ,Sorknaes P,et al.(2021) District heating in 100% renewable energy systems: Combining industrial excess heat and heat pumps.Energy Conversion and Management 244:114527

[50] Tulus V,Abokersh MH,Cabeza LF,et al.(2019) Economic and environmental potential for solar assisted central heating plants in the EU residential sector: Contribution to the 2030 climate and energy EU agenda.Applied Energy 236: 318-339

[51] Miettinen K,Ruiz F,Wierzbicki AP (2006) Introduction to multiobjective optimization: Interactive approaches.In: Miettinen K,Ruiz F,Wierzbicki AP (eds) Dagstuhl Seminar on Practical approaches to multi-objective optimization.Schloss Dagstuhl Germany,v 5252,p 27

[52] Di Somma M,Graditi G,Heydarian-Forushani E,et al.(2018)Stochastic optimal scheduling of distributed energy resources with renewables considering economic and environmental aspects.Renewable Energy 116: 272-287

[53] Alabi TM,Lu L,Yang ZY (2021) A novel multi-objective stochastic risk co-optimization model of a zero-carbon multienergy system (ZCMES) incorporating energy storage aging model and integrated demand response.Energy 226: 120258

[54] Miettinen K,Ruiz F,Wierzbicki AP (2008) Introduction to Multiobjective Optimization: Interactive Approaches In: Branke J,Deb K,Miettinen K,Słowiński R (eds) Multiobjective optimization.Springer Berlin Heidelberg

[55] Mavrotas G (2007) Generation of efficient solutions in Multiobjective Mathematical Programming problems using GAMS.Effective implementation of the ε-constraint method.Applied Mathematics and Computation 213: 455-466

[56] Sharafi M,Elmekkawy TY (2014) Multi-objective optimal design of hybrid renewable energy systems using PSO-simulation based approach.Renewable Energy 68: 67-79

[57] Nojavan S,Majidi M,Najafi-Ghalelou A,et al.(2017) A costemission model for fuel cell/PV/battery hybrid energy system in the presence of demand response program: ε-constraint method and fuzzy satisfying approach.Energy Conversion and Management 138: 383-392

[58] Kablan MM (2004) Decision support for energy conservation promotion: an analytic hierarchy process approach.Energy Policy 32(10): 1151-1158

[59] Chatzimouraddis AI,Pilavachi PA (2009) Technological,economic and sustainability evaluation of power plants using the Analytic Hierarchy Process.Energy Policy 37(3): 778-787

[60] Zong XJ,Yuan Y,Wu H (2022) Multi-objective optimization of multi-energy flow coupling system with carbon emission target oriented.Frontiers in Energy Research 10: 877700

[61] Yue Q,Guo P,Wu H,et al.(2022) Towards sustainable circular agriculture: An integrated optimization framework for croplivestock-biogas-crop recycling system management under uncertainty.Agricultural Systems 196: 103347

[62] Simab M,Javadi MS,Nezhad AE (2018) Multi-objective programming of pumped-hydro-thermal scheduling problem using normal boundary intersection and VIKOR.Energy 143:854-866

[63] Zhu ZA,Wang X,Jiang CW,et al.(2021) Multi-objective optimal operation of pumped-hydro-solar hybrid system considering effective load carrying capability using improved NBI method.International Journal of Electrical Power & Energy Systems 129: 106802

[64] Huang ZY,Xie ZL,Zhang CZ,et al.(2019) Modeling and multi-objective optimization of a stand-alone PV-hydrogenretired EV battery hybrid energy system.Energy Conversion and Management 181: 80-92

[65] Keshavarzzadeh AH,Ahmadi P (2019) Multi-objective technoeconomic optimization of a solar based integrated energy system using various optimization methods.Energy Conversion and Management 196: 196-210

[66] Zarrinpoor N,Khani A (2021) Designing a sustainable biofuel supply chain by considering carbon policies: a case study in Iran.Energy Sustainability and Society 11(1): 1-22

[67] Feng Q,Wu ZB,Zhang W (2020) Carbon emissions market adjustment in the electricity supply sector: A government perspective.Journal of Cleaner Production 275: 123132

Received: 6 June 2023/ Accepted: 3 September 2023/ Published: 25 October 2023

✉Hongtao Ren

ren@ecust.edu.cn

Wenxin Chen

y30211357@mail.ecust.edu.cn

Wenji Zhou

zhouwenji@ruc.edu.cn

2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Wenxin Chen is working towards master’s degree at East China University of Science and Technology,Shanghai.Her research interests include energy technology system modeling,multi-objective optimization.

Hongtao Ren received the Doctor’s degree at Japan Advanced Institute of Science and Technology,Japan,2007.He is working in East China University of Science and Technology,Shanghai.His research interests include energy technology system modeling,energy system multi-criteria analysis.

Wenji Zhou received the Doctor’s degree at Tsinghua University,Beijing,2011.He is working in Renmin University of China,Beijing.His research interests include energy system integration modeling,energy economy.

(Editor Dawei Wang)