0 Introduction

Energy systems are affected by several uncertainty factors during long-term planning. Uncertainty arises from the limitation of human knowledge on concerning issues[1]. Uncertainties can be divided into model parameters and structure uncertainties [2, 3]. Model parameter uncertainty arises from a lack of experience related to the model parameters, which is the primary focus of this study. Examples of such uncertainties include uncertain carbon prices [4], energy demand [5] and renewable energy generation [6], which cannot be ignored in the long-term modeling of energy systems. Many studies have divided parameter uncertainty into randomness and fuzziness [7]. In random uncertainty, there is no necessary correspondence between the result and the given scenario or the characteristics of the given scenario are incomplete. Therefore, it is also known as objective uncertainty. Fuzzy uncertainty is also called subjective uncertainty, which refers to the uncertainty of classification caused by the unclear concept of the object itself or an unclear measurement scale. For specific problems, a comprehensive trade-off should be made according to the research objectives, modeling difficulties, etc. Due to the different knowledge and information about uncertain factors available to different researchers, thesame uncertain factor may be modeled as random or fuzzy uncertainty in different studies. For instance, for fuel price, some studies use probability density function to describe it [8], while others use membership function to model it [9]. Reasonable longterm planning for an energy system adds complexity by considering additional uncertainties. The main methods for addressing uncertainty include the probabilistic method [10],possibilistic method [11], hybrid probabilistic-possibilistic method [12], information gap decision theory [13], robust optimization [14], interval analysis [15], style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">To address the problems mentioned above, this study systematically organizes the uncertainty factors and modeling methods of a long-term energy system optimization model. One of the goals of this study is to discuss the attributes, advantages, and limitations of the quantitative methods of important uncertain factors in the long-term energy system optimization model. This discussion will help decision-makers choose appropriate modeling methods according to the nature of the target problems and sources of uncertainty. Consequently, the risks posed by uncertain factors in the decision-making process can be reduced.

The remainder of this paper is organized as follows.Section 1 introduces the typical structure of a long-term energy system optimization model. Section 2 discusses the uncertain parameters in the long-term energy system optimization model and divides these uncertainties into three categories: policy, economic, and technical factors.Section 3 summarizes various uncertainty modeling methods and their applications in long-term energy system optimization. Section 4 presents the conclusion and future research directions for uncertainty analysis in long-term energy system modeling.

1 Long-term energy system optimization model

1.1 Energy system model

It is important to choose an appropriate energy system model to analyze existing national and multiregional energy systems and predict potential future development scenarios.Energy planning models can be divided into short-term and long-term energy models based on the time scale of energy planning. The short-term energy model can describe the hourly operation of an energy system in a more detailed manner; however, it cannot reflect the medium- and longterm optimal allocation of energy technologies. Long-term energy models generally use years as the optimization unit,and the planning period is usually of several decades. It is widely used in energy policy analysis. The modeling method used can be classified as bottom-up, top-down, or hybrid.The bottom-up model analyzes the comprehensive effects of changes in the technical energy parameters and their impact on the economy through optimization and simulation. The top-down model quantifies the impact of macroeconomic development on various areas through macroeconomics,economic equilibrium, and other methods. But it considers fewer technical details, and mainly emphasizes the relationship between energy production and consumption.

A hybrid model is created by combining the advantages of the bottom-up and top-down models; however, it is often more complicated.

The long-term energy model constructed using the bottom-up modeling method can elucidate the underlying mechanisms driving resource consumption and greenhouse gas emissions. It analyzes different technologies for changes in resource consumption, greenhouse gas emissions,and energy system costs. Furthermore, the model aids in planning the allocation of energy technology capacity based on its output. It has become the mainstream tool for studying the optimization of energy technology systems under environmental objectives, and the representative models are MESSAGEix and TIMES/MARKAL [17-20].

In recent years, a growing number of researchers have been extending the scope of energy system models. Owing to the low-carbon transition realized by energy systems,renewable energy technologies have been expanded on a large scale. These new energy technologies often rely on more critical metals than traditional energy technologies.The relationship between energy technology and critical metals has attracted the attention of researchers, leading to the development of a research paradigm focusing on the energy–metal relationship. The material flow analysis method is used to predict the demand for critical metals in the low-carbon transition of energy systems. However, the demand for critical metals, as projected through material flow analysis, often changes significantly, corresponding to the demand for specific energy technology. This can lead to an inaccurate estimation of the demand for key metals in the low-carbon transition of energy systems. Therefore,some studies have added critical metals to long-term energy system optimization models. For example, Grandell et al. [21] studied the demand for critical metals to support the global energy transition by 2050 based on the TIMES energy model. The results showed that the demand for metals such as platinum, tellurium, and cobalt would exceed their reserves, restricting the low-carbon transition of the energy system. In their study, Wang et al. [22] integrated the global change assessment model (GCAM v5.2),dynamic material flow analysis, and life-cycle sustainability assessment methods. This integrated framework was used to evaluate the implications of price fluctuations in critical metal materials (Li, Co, Ni, and Mn) on transportation electrification and carbon emissions in China.

This study discusses a bottom-up long-term energy system optimization model, focusing on the uncertainty analysis of uncertain parameters within the scope of model planning.

1.2 Structure of the long-term energy system optimization model

The typical structure of a long-term energy system optimization model constructed using a bottom-up modeling method is shown in Fig. 1. It comprises objective functions and constraints. Based on accurate and sufficient data (such as resource, technical and economic, and highfrequency market data), the model plans the energy technology capacity, activity level, and investment on a staged timescale according to the objective function and constraints. Optimization of the model can improve the energy supply structure and reduce the cost of energy use and carbon emissions, thus achieving synergy between economic and environmental benefit [23].

The objective function of a long-term energy system optimization model usually aims to minimize the total system cost. Amid growing global concerns about climate change, energy transition, and energy security,the operational optimization of energy systems has evolved a singular objective of total cost consideration to a multiobjective approach that encompasses various indicators. These indicators include system economy,environmental protection, energy efficiency, and flexibility.For instance, optimization goals now include overall emission minimization [24], overall energy efficiency level maximization [25], and energy structure optimization [26].Minimization of system cost is an indispensable optimization goal in system planning (as shown in equation (1)).

where TCt is the total cost converted to year t, ICt is the total annualized initial investment cost of the equipment converted to year t, OMt is the total operation and maintenance cost of the equipment, and ECt is the emission cost.

Fig. 1 Schematic diagram of the long-term energy system optimization model structure

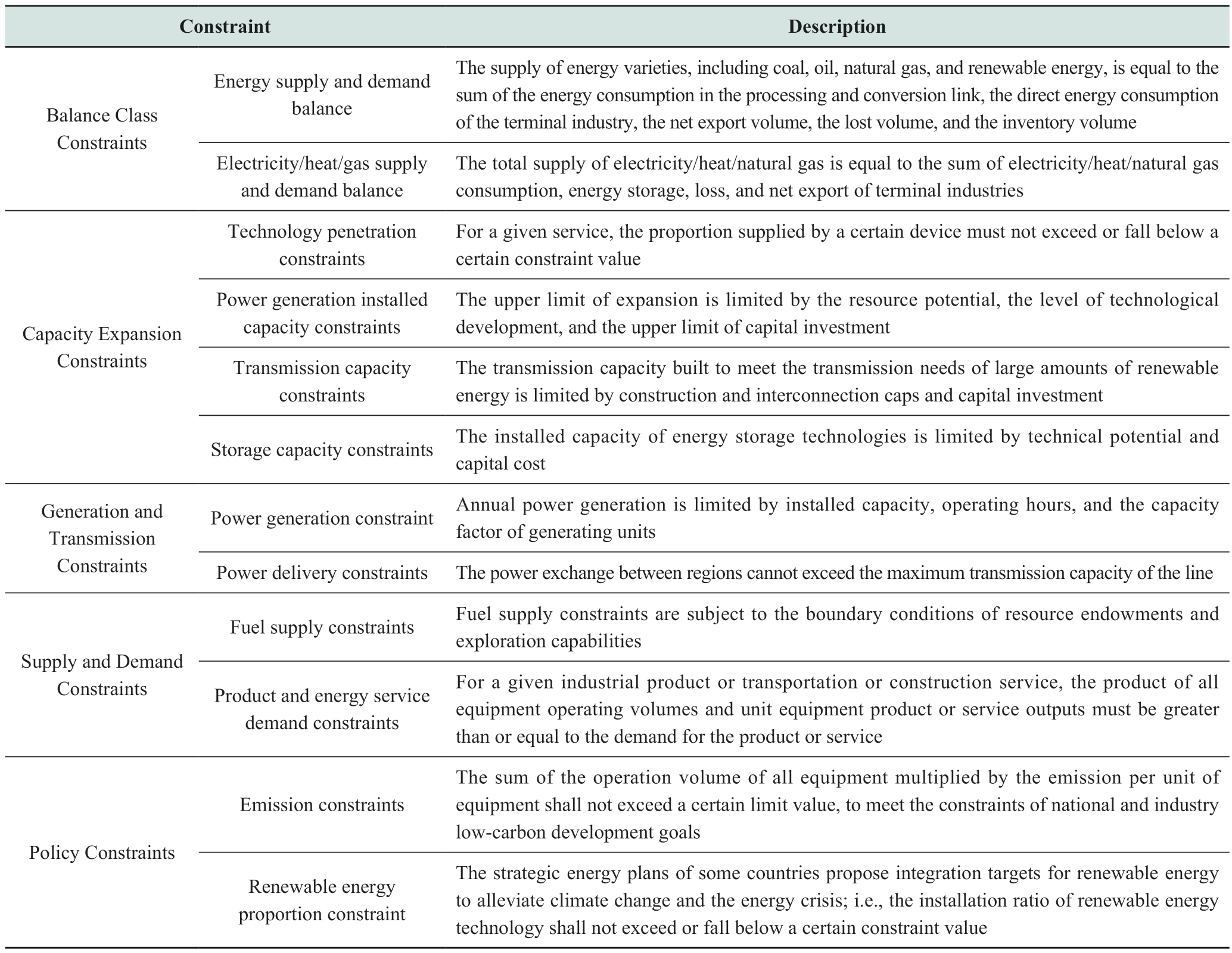
In addition, the energy system must satisfy the constraints of the economy, environment, and society in long-term planning. These constraints include system balance [27], capacity expansion [28], resource potential[29], and policy [30] constraints (the constraints of the longterm energy system optimization model are not limited to those listed in Table (1). The standardized formula for these constraints is given in (2).

where A is the parameter, x is the decision variable, and B is the boundary.

However, the parameters A in the energy model are usually provided exogenously, and the selection of input data will have a considerable impact on the modeling results and the decision-making of the entire energy system. In particular, in long-term planning, some parameters will change, resulting in significant uncertainty. Therefore, it is necessary to study how the parameters in the long-term energy system optimization model evolve and to effectively model these uncertainties to make technical path decisions for the energy transition.

2 Uncertainty in long-term energy system optimization modeling

Optimization of the energy system model requires a large number of parameters. Researchers have determined the key technical and economic parameters used in the energy system planning model regarding the generation,transmission network, energy storage, and demand sides[23]. With an increase in the share of renewable energy,new uncertainties have arisen in various long-term decisionmaking processes, such as introducing new technologies,implementing relevant policies, and planning optimal paths for future energy systems. Owing to many uncertainties in the optimization of energy system models, researchers have realized the necessity of considering uncertainties in energy system optimization models. The uncertain parameters in the bottom-up long-term energy system optimization model can be divided into three categories: policy, economic, and technical factors.

Table 1 Long-term planning constraints

2.1 Policy factors

Policy uncertainty refers to the uncertainty of making changes to existing policies or implementing new policies in the future. The policy input parameters include carbon price,subsidies, carbon emission reduction, and resource supply security. Considering the uncertainty factors in policies will help enhance policy flexibility.

2.1.1 Carbon price

The carbon price refers to the trading price of greenhouse gas emission rights established under a clean development mechanism. Reasonable carbon price signals can guide the optimal allocation of carbon emission reduction resources, thereby reducing the cost of emission reduction for society as a whole and guiding capital flows. According to previous studies, market mechanisms(such as carbon quotas), temperature, and heterogeneous environments (such as global financial crises) result in carbon price fluctuations [31]. Carbon and energy prices also affect each other, increasing uncertainty in market operation mechanisms [32]. Governments are increasingly using carbon pricing as an environmental protection policy to curb greenhouse gas emissions [33]. Although the current carbon price shows an upward trend, carbon prices in different carbon trading markets vary significantly and are uncertain.The EU carbon trading market is the most mature in the world, whereas China’s carbon trading market is immature and has a weak carbon price foundation [34]. Therefore, it may be more appropriate to refer to the EU carbon trading price. Currently, most energy system studies that considers carbon prices are based on simulations or direct reference to EU carbon trading prices. For example, Ren et al. Reference[35] compared and analyzed the total water consumption and carbon emissions of electrolytic aluminum based on different carbon price scenarios. On the other hand, Ding et al. Reference [36] conducted a scenario analysis based on the predicted EU carbon trading price and investigated the impact of rising carbon prices on the technology mix of China’s liquid fuel industry. Their results showed that rising carbon prices can significantly reduce carbon dioxide emissions. However, carbon trading alone cannot achieve a peak in carbon emissions by 2030, and the wide application of various clean energy technologies in the energy system is also required.

2.1.2 Subsidies

Subsidies are also important fiscal measures. Financial subsidies for renewable energy power generation must be adjusted according to decomposed phased targets. In the context of carbon peaking and carbon neutrality, the transition from traditional to clean energy has become a national consensus in China. Given the high costs of power generation through variable renewable energy, China has adopted subsidy policies to support the development of wind power, photovoltaics, and other industries. Subsidy policies have been adjusted to a certain extent through the rapid development of new energy technologies. By 2030, when wind and photovoltaic subsidies cease, the new installed capacity of renewable energy will be reduced. Assuming constant subsidies may result in an overestimation of the electricity share of variable renewable energy after 2030[23]. Therefore, the uncertainty of the subsidy policy must be considered in the modeling. Lecuyer and Quirion [37]developed an analytical and numerical model for the EU electricity market. The predictions of future renewable energy subsidies made by this model were proven to be reasonable according to CO2 emission reduction. Yu et al.[38] explored several scenarios with different utilization levels of renewable energy and different subsidy policies in their study on energy system modeling.

2.1.3 Carbon emission reduction

Governments control carbon emissions by setting carbon prices and carbon emission caps. Estimating carbon emissions usually require information such as corporate pollutant emissions and total emissions, which are asymmetric between the government and enterprises. Once actual emissions exceed the emission cap, the corresponding economic penalty may increase the uncertainty of emission reduction. The actual carbon emissions and emission reduction targets of an energy system change dynamically over time and space. These changes result in uncertainty and complexity in the carbon emission reduction process of the energy system [39]. In addition, the identification and solution of energy planning problems are closely related to the experience and knowledge reserves of decisionmakers. However, the limitations of human reasoning cause many uncertainties in planning [40]. In addition, when constructing an energy system emission reduction planning model, it is generally necessary to simplify the actual energy system and set the corresponding assumptions and boundary conditions. This results in a difference between the theoretical and real values, which also leads to uncertainty[41]. Estimating carbon emissions requires measuring the gains and losses caused by potential risks and uncertainties.The estimation results are generally based on assumptions regarding the probability distribution and scenario. For example, Zhen et al. [42] established a dual-interval-stage fuzzy credibility-constrained planning model. Moreover,they compared and analyzed the energy technology planning of future regional energy systems by considering low- and high-carbon emission scenarios.

2.1.4 Resource supply security

Owing to the significant uncertainty in the duration and development trends of the energy crisis caused by geopolitical conflicts, many countries are facing great risks in the security of their energy resource supplies. For example, with the spread of the conflict between Russia and Ukraine, the flow of global energy sources such as oil and natural gas has changed, impacting the global energy supply system [43]. In addition, the future demand for critical metal mineral resources will increase significantly with the promotion of the low-carbon transition of the energy system. The global supply pattern of metal resources is extremely unbalanced, and most metal resources are nonrenewable, which intensifies geopolitical conflicts driven by strategic metal resources. It is predicted that the geopolitical focus of resources will shift in the future from oil and gas to critical metals such as copper, lithium, and nickel [44]. Some researchers have investigated the potential conflicts between the supply and demand of rare earth metal resources in ten regions worldwide by 2050. Moreover, they have found that the existing global supply structure of rare earth metal resources, as well as increasing geopolitical and environmental restrictions, may inhibit the rapid expansion of wind power generation [45].

2.2 Economic factors

Economic uncertainty refers to the uncertainty in the values of economic parameters that must be incorporated into the energy system optimization model. The economic input parameters include the energy price and energy demand.

2.2.1 Energy price

The energy price is a key parameter of the longterm energy system optimization model, and the energy price input in the deterministic model is usually the value corresponding to the current price when the system is designed [46]. However, energy prices fluctuate owing to factors such as geopolitics, energy markets, and trade policies within a long-term planning period [47]. For example, the sources of uncertainty in future oil prices may include factors such as oil supply, demand, and economic development [36]. The future trend of energy prices is unpredictable; therefore, energy prices are regarded as an uncertain factor. Some studies have noted that geometric Brownian motion can be used to describe this by analyzing the change patterns of electricity prices [48]. Even for parameters with sufficient historical data (such as oil prices), statistical laws may not necessarily apply to future scenarios [7]. Stochastic and robust optimization models are two widely discussed approaches for dealing with uncertain oil prices.

2.2.2 Energy demand

Energy demand includes primary energy (such as crude oil and natural gas) and secondary energy (such as electricity and petroleum products). In long-term planning,energy demand is affected by various uncertain parameters,such as national economic development level, population size, energy price, technology level, resource supply,climate conditions, behavior, and government energy policy orientation [30, 49]. The sudden slowdown in energy demand growth owing to the sudden global COVID-19 epidemic is a vivid example [50]. Electrical energy is an important component of a country’s overall energy strategy,and its demand is particularly sensitive to economic and demographic changes. There are two common methods for forecasting electricity demand: calculating the average annual electricity demand in the previous few years as a hypothetical electricity demand [51] and predicting power demand based on factors such as GDP, population,fuel prices, and energy efficiency [52]. However, these two methods are only suitable for short- and mediumterm forecasting. In the long run, uncertainties related to electricity consumption behavior and energy efficiency policies will continue to affect future electricity demand and pose greater challenges to forecasting. Therefore, long-term forecasting of energy demand must focus on these factors.The main method for forecasting long-term energy demand is a scenario-based method. Its uncertainty can be expressed by considering multiple possible time trajectories and their corresponding probabilities.

2.3 Technical factors

Technical uncertainty is the uncertainty of the input technical parameters required by the energy system optimization model. The technology input parameters include technology cost, energy conversion efficiency, and renewable energy resources.

2.3.1 Technology cost

Investment cost refers to the capital cost that manufacturers invest in the production of resources, whereas operation and maintenance costs involve consumption and maintenance costs related to resources or technologies.Owing to factors such as technological progress, changes in market supply and demand structure, and policy influences,the investment, operation, and maintenance costs of each technology in the future may differ from the costs assumed in the design stage. This is considered a type of uncertainty[53]. For example, with the advancement of technology,the cost of energy storage will decrease significantly;therefore, the investment, operation, and maintenance costs related to energy storage technology should consider the impact of learning effects on long-term planning [23].Costs are influenced by trends in future technology prices,and forecasts of future energy technology prices often use learning curves. The learning curve shows how, for a given technology, the investment cost per unit capacity decreases as cumulative capacity increases. The learning curve has a representative parameter called the learning rate. Many researchers have attempted to set the learning rate to a specific value and predict the future prices of renewableenergy technologies based on this learning curve. However,the learning rate estimated based on historical data may vary due to different geographical scopes, data collection methods, and characteristics of technologies at different stages of the life cycle [54]. Rubin et al. [55] summarized several studies that estimated learning rates for various renewable energy technologies. They demonstrated large differences in learning rates across regions and over time.Based on the different learning rates, the predicted prices of renewable energy technologies differ. Therefore, estimating the learning rate as a specific value for predicting future technology prices may bring the risk of investment decisionmaking mistakes.

2.3.2 Energy conversion efficiency

Energy conversion efficiency refers to the ratio of the number of various energy products produced after energy is processed to the number of various energy inputs processed and converted within a certain period. It reflects the comprehensive energy utilization capacity of a country or region. Improvements in the energy conversion efficiency can reduce the intensity of energy consumption and enhance the ability to achieve sustainable energy development. These improvements aid in controlling carbon emissions, which is of great significance for economic growth and environmental protection. It is generally believed that progress in energy technology can improve the energy conversion efficiency of individual energy products or services. However, for overall energy economic efficiency, progress in energy technology may not always promote a reduction in energy consumption. In addition,the development speeds of various advanced technologies involved in the energy system are uncertain, which further increases the uncertainty of energy conversion efficiency [7].Energy conversion efficiency is closely related to energy prices, environmental regulations, pollution control, and other factors [56].

2.3.3 Renewable energy resources

With the introduction of a high proportion of renewable energy, the uncertainty of the renewable energy supply has been highlighted. Traditional generator sets can provide electricity stably because of their solid technical characteristics, such as capacity factor and generation efficiency [23]. However, renewable energy generation(such as wind power generation and photovoltaic power generation) is easily affected by weather factors. The climate system is subjected to multidimensional and multiscale changes, and the interaction between the climate and energy systems is complex. Therefore, quantifying the impact of weather on the output of renewable energy and planning the energy system reasonably is challenging. In long-term planning, accurate weather information (such as temperature and cloudiness) is difficult to obtain, making it more challenging to predict future renewable-energy power generation. In recent years, significant progress has been made in understanding the influence of weather on the longterm planning of energy systems. For example, Perera et al.[57] developed a stochastic robust optimization method to quantify the impact of extreme weather on energy systems.The results showed that the penetration rate of renewable energy in most cities could exceed 30% if the impact of climate change were appropriately quantified. Feron et al.[58] used a global climate model to evaluate how temperature and cloudiness caused by climate change affect photovoltaic power output. They found that by the middle of this century,the photovoltaic power output in the Arabian Peninsula may deteriorate, while that in southern Europe may improve. Fu et al. [59] proposed a key technology for applying advanced artificial intelligence to renewable energy power generation planning under uncertain weather conditions.

3 Uncertainty modeling methods and applications

Various uncertainty modeling techniques have been developed to solve long-term energy system planning problems under uncertain conditions. The main difference between the uncertainty modeling methods is the uncertainty of the input parameters. For example, probabilistic methods use probability density functions to describe uncertain parameters, whereas possibilistic methods use membership functions to model uncertain parameters.However, they both aim at quantifying the effects of the input parameters on the model output. Existing methods for long-term planning of energy systems that consider uncertain factors cover a wide range. Figure 2 shows the various uncertainty modeling methods for long-term energy system optimization, and Tables 2–5 summarize the specific applications of the uncertainty processing methods.

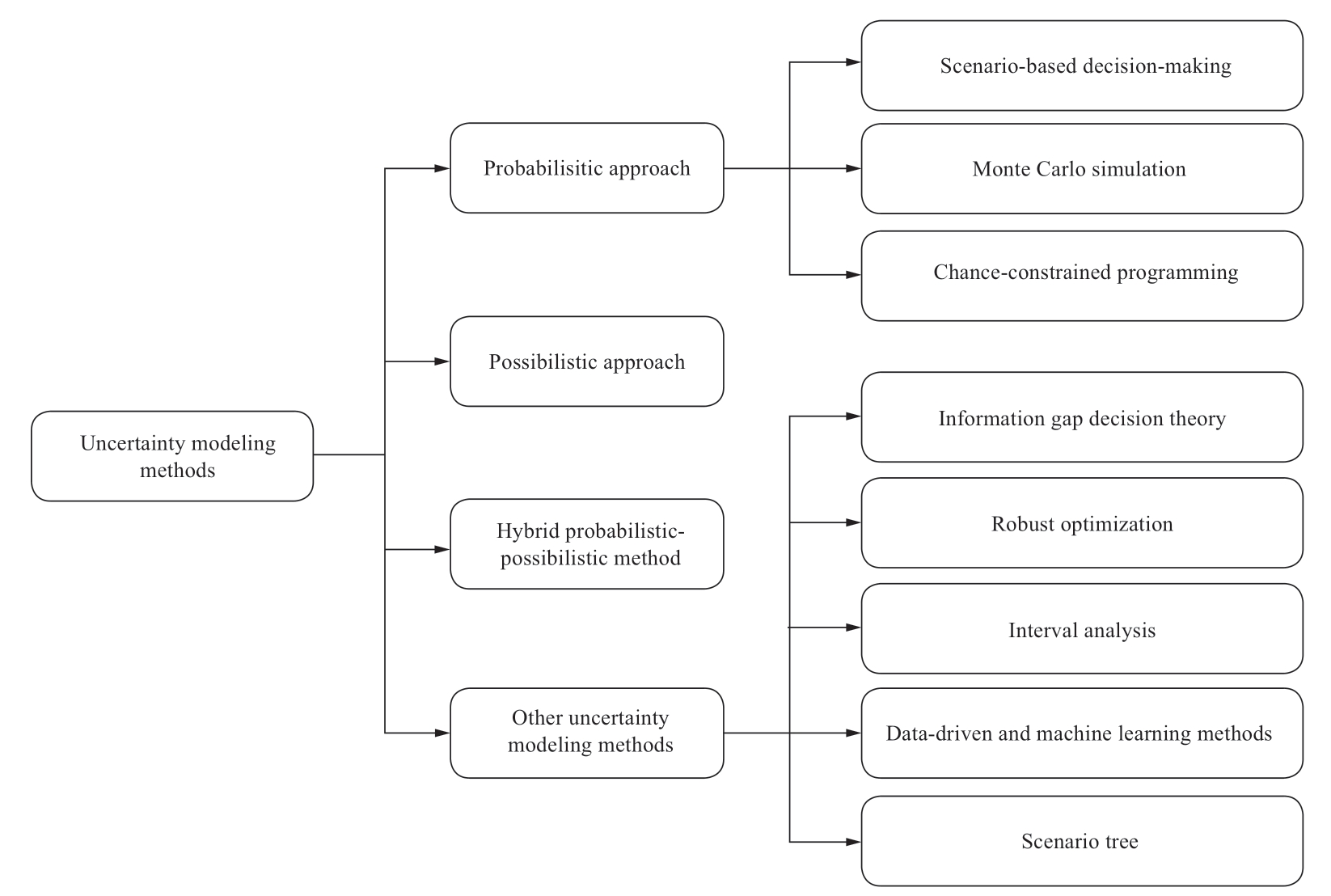
Fig. 2 Uncertainty modeling methods

3.1 Probabilistic approach

The probabilistic approach is the most used method to address the uncertainty of an energy system. This method assumes that the input variable of the model is a random variable with a known probability density function, and the goal is to obtain the probability density function of the output variable [60]. Probabilistic methods applied to long-term energy system planning include scenario-based decision-making, Monte Carlo simulations, and chanceconstrained programming.

3.1.1 Scenario-based decision-making

Scenario-based methods can simplify stochastic problems into multiple deterministic problems, which are mostly used to predict energy demand and policy uncertainty. As early as 1998, Kanudia and Shukla [61] set up economic growth scenarios and carbon tax scenarios based on the MARKAL model, considering the uncertainty of energy demand and carbon emission reduction. They analyzed India’s future energy supply, carbon emissions,and power generation technology capacity. Broad et al.[62] applied the long-term UK TIMES model framework to analyze UK residential heating systems and investigated residential heating schemes under different carbon budget scenarios. Riepin et al. Reference [63] constructed scenarios for European electricity and natural gas markets.Furthermore, they analyzed and compared the influences of uncertain input parameters, such as natural gas and electricity demand and fuel and carbon dioxide prices, on the quality of solutions to energy system scheduling and investment optimization problems. However, scenario-based methods have difficulty dealing with multidimensional uncertainties and are not suitable for large-scale systems.Moreover, different assumptions regarding future trends in different studies often produce very different and confusing results [64].

3.1.2 Monte Carlo simulations

A Monte Carlo simulation is relatively intuitive, easy to perform, and has gradually become a widely used method for modeling uncertainty in long-term energy systems.Santos et al. Reference [65] used a power system with a high contribution of renewable energy as an example.They incorporated the uncertainty of renewable energy into long-term planning through a combination of Monte Carlo simulations and a deterministic optimization model.Mavromatidis et al. [64] reported that uncertain energy demand parameters obey a discrete uniform distribution.Moreover, they used a Monte Carlo simulation to quantify the impact of this uncertainty on energy system planning.Their results showed that the optimal allocation of the energy system generated by this method deviates from the results obtained by the deterministic model, confirming the risk of suboptimal decision-making in the deterministic design process. Ioannou et al. Reference [8] proposed a multistage stochastic optimization method. This method uses a normal probability density distribution to represent the uncertain fuel price and quantifies it using a Monte Carlo simulation to plan the best power generation mix in the medium and long term. Zhang and Chen [66] combined Monte Carlo analysis with the bottom-up China-TIMES model to generate 3000 cases with different technological development paths and carbon peak times. They analyzed the uncertainty of technological development and accumulated carbon budget, as well as the unique impact of peak emission time on technology selection and energy transition costs. However, as the degrees of freedom of the solution space increase, the number of simulations required by the Monte Carlo method also increases, resulting in a greater computational workload.

3.1.3 Chance-constrained programming

Chance-constrained programming, as a stochastic optimization method, has also been applied to the uncertainty modeling of energy systems. Odetayo et al.Reference [69] proposed a probabilistic programming approach based on a chance-constrained programming method for planning electricity and natural gas distributionsystems with uncertain electricity demands. Min et al.Reference [70] considered the uncertainties associated with renewable energy technologies in their study. They designed a new stochastic optimization model that converted chance constraints into an equivalent linear model for the longterm capacity expansion planning of power systems,encompassing large-scale renewable energy technologies.Their study provided valuable insights for energy planning practitioners in Korea. In addition, methods such as sampling average estimation and scene approximation can be used to transform and solve stochastic optimization problems with chance constraints.

Table 2 Main literature on probabilistic approach for uncertainty

3.2 Possibilistic approach

When historical data are missing or imprecise, the probability density functions of the parameters may not be defined and must be expressed in a different way, i.e.,by using possibilistic theory. In the possibilistic approach,the input parameters of the model are described by a fuzzy membership function, and the possibility distribution is used to model its uncertainty [60]. The α-cut method is used to determine the membership function of the output variable, and then a defuzzification strategy is applied to obtain a clear output value. For example, Cunico et al. Reference [9] considered the uncertainty of fossil resource prices, the trend of demand growth, and changes in the availability of fossil reserves. They proposed a fuzzy model for investment planning in Argentina’s energy sector. Based on the possibilistic theory, Gan et al.Reference [71] used improved triangular fuzzy numbers to simulate the variable management cost and proposed a comprehensive optimization model for investment portfolios. This model can be used as an effective decisionmaking tool for decision-makers in the sustainable development of hydropower projects. Zarrinpoor and Khani [72] used the fuzzy interactive programming method to address uncertainties such as market demand and supply chain cost.

Table 3 Main literature on probabilistic approach for uncertainties.

3.3 Hybrid probabilistic–possibilistic method

In the real world, when probabilistic and fuzzy variables exist together, the difficulty of uncertainty assessment increases, and hybrid probabilistic possibilistic methods arise. This method is widely used to quantify the multiple uncertainties in energy systems. To address the uncertainty of carbon emission reduction, Li et al.Reference [40] developed a comprehensive optimization model that considered the uncertainty of carbon emission reduction through emission trading and clean development mechanisms. This model is based on two-stage stochastic programming and interval fuzzy programming technology.Moreover, this model was applied to a case study of planning carbon emission reduction in power systems. Zhou et al. Reference [73] developed a fractional comprehensive planning method with fuzzy chance constraints to solve the problem of sustainable management planning of power systems in a complex and uncertain environment. This method can effectively solve a dual-objective problem with fuzzy and stochastic uncertain parameters. Moreover, it can help decision-makers make appropriate decisions under different input scenarios.

3.4 Other uncertainty modeling methods

In addition to the three main methods for addressing uncertainty mentioned above, other methods are required for uncertain parameters that cannot be represented by probability or fuzziness. This section briefly introduces information gap decision theory, robust optimization,interval analysis, style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">3.4.1 Information gap decision theory

The information gap decision theory is a common approach for dealing with severe uncertainties in power systems. Moreover, this theory is used in situations where the uncertainty cannot be modeled with probability densityfunctions or membership functions because of a lack of sufficient historical information. It measures the deviation of the error and not the probability of an outcome. To address the uncertain problem of “what would happen if the realized uncertain parameters differ from our estimates,” decision-makers can use two different strategies: riskaverse and risk-seeking strategies. The information gap decision theory can address uncertain energy market prices and energy consumption in energy systems [74]. Yadegari et al. Reference [75] proposed a comprehensive model for the long-term planning of various cogeneration units in an integrated heat and power network. The model applied the risk aversion strategy of information gap decision theory,considering uncertain power loads and market prices. Their results showed that the risk avoidance strategy improves the robustness of the integrated heat and power network to uncertainties.

Table 4 Main literature on dealing with uncertainty using hybrid probabilistic–possibilistic methods.

3.4.2 Robust optimization

Robust optimization provides a new approach for solving optimization problems subject to uncertainty,especially in the absence of full information on the nature of uncertainty. In robust optimization, uncertainty sets are used to describe the uncertainty of the input parameters, and are often described using boxes, polyhedra, ellipsoids, and cardinalities. The selection of an uncertain set is essential in dealing with uncertainty problems in robust optimization.Currently, robust optimization is mostly used to address uncertain energy demands and prices in energy systems.For example, Chen et al. Reference [76] proposed a robust interval stochastic optimization method that was applied to a regional power system planning case considering a carbon dioxide trading scheme. Moreover, they improved the security of the energy supply with a lower level of system failure risk and reduced the total carbon dioxide emissions under an effective trading scheme. Tsao and Thanh [77]considered the uncertainty of demand, intermittency of renewable energy, and cost parameters in their study. They adopted a multiobjective fuzzy robust programming method to solve the problem of sustainable and reliable power system design in Vietnam in an uncertain environment. The results showed that this method required less calculation time than the scenario-based stochastic programming method. Ding et al. [36] established a robust model based on an ellipsoid uncertainty set to quantify uncertain oil prices.Moreover, they analyzed the capacity allocation of four different liquid fuel production technologies considering future oil price uncertainty in China.

3.4.3 Interval analysis

In interval analysis, it is assumed that uncertain parameters are obtained from known intervals; that is, the upper and lower bounds of each uncertain input parameter value are defined. This approach is similar to probability modeling using a uniform probability density function[60]. However, because of extreme weather conditions and other unexpected events, the upper and lower bounds of the interval may change. Luo et al. Reference [78] proposed an interval stochastic dynamic programming model for evaluating the stability of engineering structures with random and interval variables. This method directly utilizes the original information of uncertain system parameters and has significant flexibility, thereby improving the effectiveness of structural safety assessments. Li et al.Reference [79] quantified power demand as a double interval and proposed a dual-interval mixed integer linear programming model that integrates interval programming,dual interval programming, and integer programming.Moreover, this model can address both discrete interval uncertainty and double uncertainty without distribution information but with rough upper and lower bound estimation. Compared to traditional methods, the interval decision variables solved by this model have stronger robustness and greater decision flexibility.

3.4.4 style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">With the development of uncertainty modeling techniques, style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">3.4.5 Scenario tree

Scenario-tree methods are widely used in decisionmaking models under uncertain conditions. A scenario treefor uncertain input parameters can be constructed according to qualitative or quantitative methods. The main criterion for distinguishing between qualitative and quantitative methods is whether to use a mathematical model based on historical data to determine the probability and value of a scenario. Representative methods for scenario tree generation include quasi-Monte Carlo sampling, optimal quantization, and moment-matching methods [87]. Among these, the moment-matching method is the most suitable for generating scenario trees based on multistage stochastic programming energy system models. This method has two advantages: it can generate a scenario tree with multiple variables, and it can be applied to many scenario reduction methods. Several studies have used scenario trees based on qualitative or quantitative methods to model various parameters. For example, Mirkhani and Saboohi [47]developed the MESSAGE energy system model into a multistage stochastic programming problem and described uncertain fuel prices using geometric Brownian motion.An approximate probability scenario tree for fuel prices was generated using the Cox–Ross method [88], and the influence of fuel price fluctuations on the future capacity expansion of renewable energy technology was analyzed.Kim et al. Reference [85] considered learning rate changes and uncertainties in their study. Moreover, they used the moment-matching method to generate a scenario tree of photovoltaic module prices. Seljom et al. Reference [86]considered uncertain variable renewable power generation in the TIMES model and adopted different scenario generation methods to generate scenario trees for photovoltaic and wind power generation. The quality of the corresponding model values was compared and evaluated through stability testing. Lei et al. Reference [89] proposed a multistage scenario tree generation method based on a conditional generation countermeasure network, random forest, and Markov chain to solve the problems of incomplete load data, low accuracy of single-load forecasting, and weak regularity of energy price fluctuations.

Table 5 Main literature on using different methods to address uncertainty

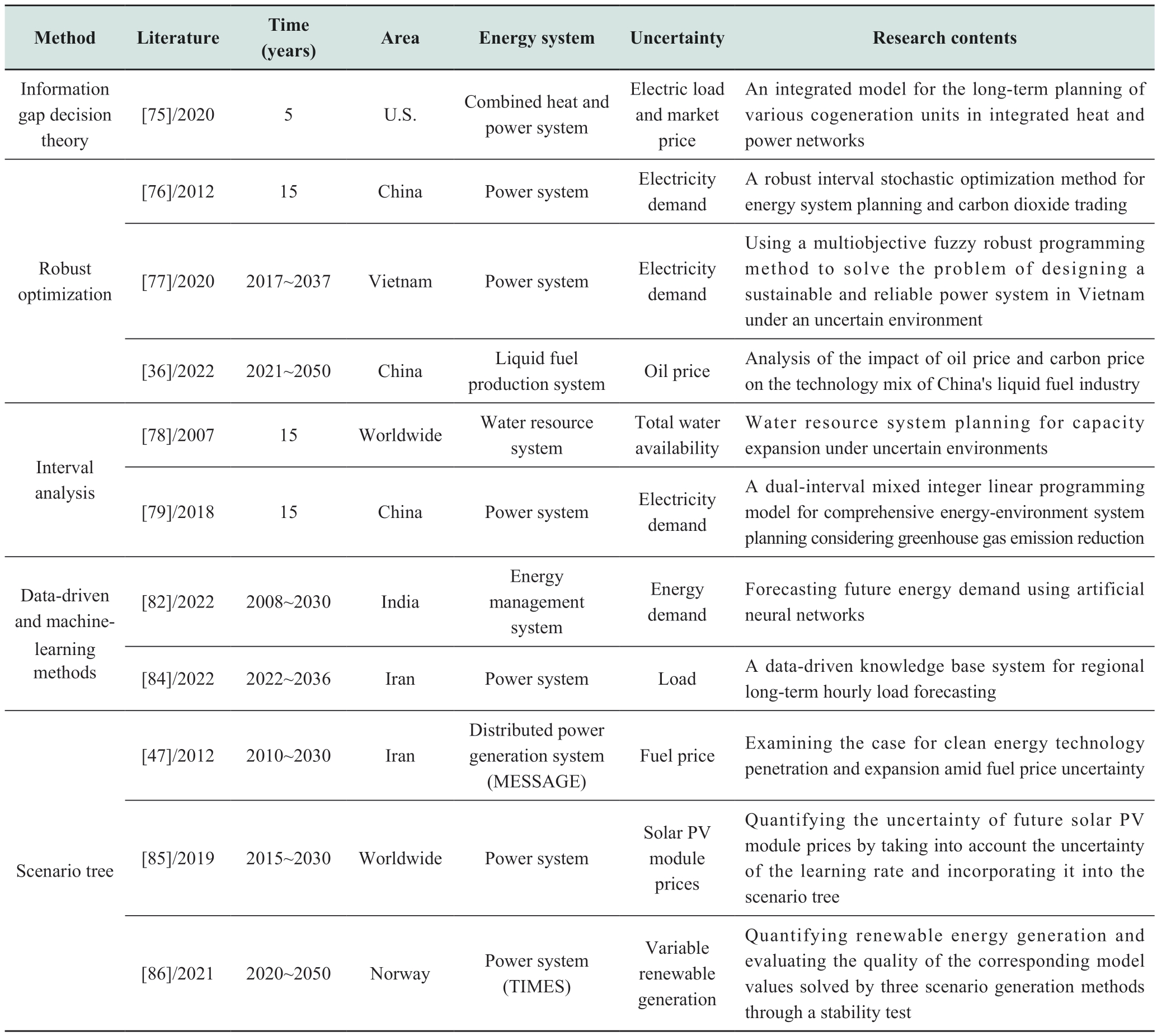
Table 6 Comparing different uncertainty modeling methods

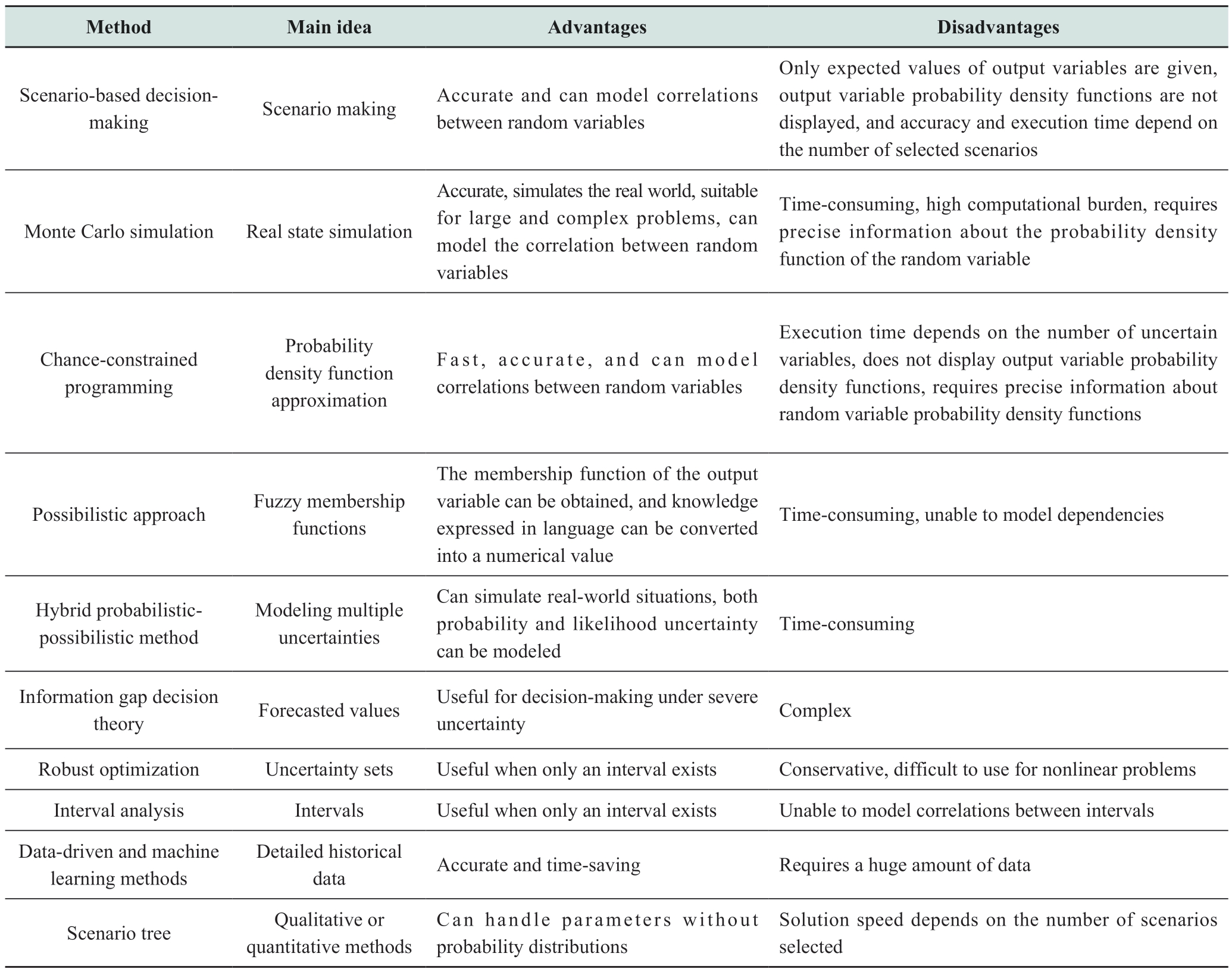
3.5 Comparison of uncertainty modeling methods

There are many uncertainty modeling methods, and an appropriate method for representing uncertainty should be selected according to the nature of the problem considered,the type of random variables, the information available, and the availability of historical data. Therefore, each uncertainty modeling approach can be evaluated by considering its properties, strengths, and limitations. Table 6 summarizes the characteristics, advantages, and disadvantages of various methods for addressing uncertainty. It can be seen that there is no single best method for dealing with uncertainty in long-term energy systems, and each method is suitable for some specific situations.

4 Conclusion and prospects

This paper reviews the common uncertainties and uncertainty modeling methods for long-term energy system planning. First, long-term energy system optimization models are introduced. Second, uncertainty is divided into three categories: policy uncertainty, economic uncertainty,and technological uncertainty. Third, the main uncertainty modeling methods are described and compared. The focus of this paper is to identify the important uncertain factors in the long-term energy system optimization model and summarize the attributes, advantages, and limitations of the uncertainty modeling method. This review will help decision-makers choose the appropriate modeling method according to the nature of the target problem and the source of uncertainty,thus enhancing the robustness of their decision-making and mitigating the risks brought about by uncertain factors.Notably, the proposed modeling methods are not independent of each other, and a combination of different methods can be used for a more comprehensive analysis. An overview of the uncertainty analysis of future long-term energy system optimization modeling is provided below.

In terms of long-term energy system models, the low-carbon transition of an energy system imposes higher requirements on the system modeling. The lowcarbon transition of the global energy system requires a substantial increase in the consumption of critical metals while reducing fossil fuel consumption, leading to a gradual shift in the energy system from relying on fossil fuels to relying on critical metals. This requires traditional energy system modeling to expand from fossil energybased energy utilization and conversion processes to critical metals, thereby providing a more accurate energy technology prediction method for energy system transitions.Although the long-term energy system optimization model has achieved fruitful results, some studies have added critical metals to their energy system optimization models.However, critical metal constraints have not been quantified as constraints or considered in the bottom-up long-term energy system optimization model. These constraints can be considered in future research.

Uncertainty factors are widely found in various links,such as energy production, transmission, conversion, and consumption. Although some achievements have been made in the uncertainty modeling of energy systems, most of these uncertainty quantification methods focus on a few uncertain parameters, such as the exogenous uncertain carbon price, energy price, and demand. Therefore, in addition to the uncertainty factors mentioned in this study,future research on uncertainty modeling needs to consider a wider range of uncertainty factors, such as model structure,political and social factors, and the endogenous uncertainty of technological change. Moreover, the correlation and interaction in the analysis of uncertainty factors should also be considered. With the expansion of clean energy technologies that rely heavily on critical metals, it is necessary to consider the influence of the uncertainties related to critical metals on the optimization results of energy systems. However,few studies have addressed the uncertainties associated with critical metals in energy system models.

In terms of uncertainty modeling methods, there are many uncertain factors in an energy system, and there have been many studies on modeling various uncertainties using different methods for dealing with uncertainties. However,a single uncertainty modeling approach is often insufficient for accurately handling the effects of multiple uncertainties.Therefore, to increase economic benefits, different model combinations should be considered for a comprehensive analysis. With the development of uncertainty modeling technology, precise uncertainty modeling methods based on a combination of system mechanisms and style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">Acknowledgements

This work was supported by Global Energy Interconnection Group Co., Ltd.: Assessment of China’s carbon neutrality implementation path and simulation research on policy tool combination (SGGEIG00JYJS2200059).

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] Roldán C, Mínguez R, García-Bertrand R, et al. (2019) Robust transmission network expansion planning under correlated uncertainty. IEEE Transactions on Power Systems, 34(3): 2071-2082

[2] Edenhofer O, Lessmann K, Kemfert C, et al. (2006) Induced technological change: Exploring its implications for the economics of atmospheric stabilization: Synthesis report from the Innovation Modeling Comparison Project. Energy Journal: 57-107

[3] Fais B, Keppo I, Zeyringer M, et al. (2016) Impact of technology uncertainty on future low-carbon pathways in the UK. Energy Strategy Reviews, 13-14: 154-168

[4] Vithayasrichareon P, Riesz J, MacGill I F (2015) Using renewables to hedge against future electricity industry uncertainties—An Australian case study. Energy Policy, 76: 43-56

[5] Cheng S, Gu C H, Yang X H, et al. (2022) Network pricing for multienergy systems under long-term load growth uncertainty.IEEE Transactions on Smart Grid, 13(4): 2715-2729

[6] Tian K P, Sun W Q, Han D, et al. (2020) Coordinated planning with predetermined renewable energy generation targets using extended two-stage robust optimization. IEEE Access, 8: 2395-2407

[7] Shu Y B, Xue Y S, Cai B, et al. (2018) A review of energy transition analysis part two uncertainties and approaches.Automation of Electric Power Systems, 42(10): 1-12 (in Chinese)

[8] Ioannou A, Fuzuli G, Brennan F, et al. (2019) Multi-stage stochastic optimization framework for power generation system planning integrating hybrid uncertainty modelling. Energy Economics, 80: 760-776

[9] Cunico M L, Flores J R, Vecchietti A (2017) Investment in the energy sector: An optimization model that contemplates several uncertain parameters. Energy, 138: 831-845

[10] Eshraghi H, de Queiroz A R, DeCarolis J F (2018) US energyrelated greenhouse gas emissions in the absence of federal climate policy. Environmental Science & Technology, 52(17): 9595-9604

[11] Li W, Bao Z, Huang G H, et al. (2018) An Inexact Credibility Chance-Constrained Integer Programming for Greenhouse Gas Mitigation Management in Regional Electric Power System under Uncertainty. Journal of Environmental Informatics, 31(2):111-122

[12] Dong Q Y, Sun Q Y, Huang Y J, et al. (2019) Hybrid possibilistic-probabilistic energy flow assessment for multienergy carrier systems. IEEE Access, 7: 176115-176126

[13] Eslahi M, Vahidi B, Siano P (2022) A flexible risk-averse strategy considering uncertainties of demand and multiple wind farms in electrical grids. IEEE Transactions on Industrial Informatics, 18(4): 2255-2263

[14] Moret S, Babonneau F, Bierlaire M, et al. (2020) Decision support for strategic energy planning: A robust optimization framework. European Journal of Operational Research, 280(2):539-554

[15] Yang D, Jiang C, Cai G, et al. (2020) Interval method based optimal planning of multi-energy microgrid with uncertain renewable generation and demand. Applied Energy, 277: 115491

[16] Shen F, Zhao L, Wang M, et al. (2022) name="ref17" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[17] Klemm C, Vennemann P (2021) Modeling and optimization of multi-energy systems in mixed-use districts: A review of existing methods and approaches. Renewable and Sustainable Energy Reviews, 135: 110206

[18] Lopion P, Markewitz P, Robinius M, et al. (2018) A review of current challenges and trends in energy systems modeling.Renewable and Sustainable Energy Reviews, 96: 156-166

[19] Scheller F, Bruckner T (2019) Energy system optimization at the municipal level: An analysis of modeling approaches and challenges. Renewable and Sustainable Energy Reviews, 105:444-461

[20] Ringkjøb H K, Haugan P M, Solbrekke I M (2018) A review of modelling tools for energy and electricity systems with large shares of variable renewables. Renewable and Sustainable Energy Reviews, 96: 440-459

[21] Grandell L, Lehtilä A, Kivinen M, et al. (2016) Role of critical metals in the future markets of clean energy technologies.Renewable Energy, 95: 53-62

[22] Wang H T, Feng K S, Wang P, et al. (2023) China’s electric vehicle and climate ambitions jeopardized by surging critical material prices. Nature Communications, 14: 1246

[23] Deng X, Lv T (2020) Power system planning with increasing variable renewable energy: A review of optimization models.Journal of Cleaner Production, 246

[24] Parkinson S C, Makowski M, Krey V, et al. (2018) A multicriteria model analysis framework for assessing integrated waterenergy system transformation pathways. Applied Energy, 210:477-486

[25] Wang Q W, Wang Y L, Ma Y Z, et al. (2020) Planning optimization of integrated energy system considering economy and integrated energy efficiency. IOP Conference Series: Earth and Environmental Science, 546(2): 022035

[26] Naveed M, Naz (2017) Multicriteria decision making for resource management in renewable energy assisted microgrids. Renewable and Sustainable Energy Reviews, 71: 323-341

[27] Yang N, Qin T, Wu L, et al. (2022) A multi-agent game based joint planning approach for electricity-gas integrated energy systems considering wind power uncertainty. Electric Power Systems Research, 204: 107673

[28] Ding Z Y, Wen X, Tan Q F, et al. (2021) A forecast-driven decision-making model for long-term operation of a hydro-windphotovoltaic hybrid system. Applied Energy, 291: 116820

[29] Cheng R, Xu Z, Liu P, et al. (2015) A multi-region optimization planning model for China’s power sector. Applied Energy, 137:413-426

[30] Hui J, Cai W, Wang C, et al. (2017) Analyzing the penetration barriers of clean generation technologies in China’s power sector using a multi-region optimization model. Applied Energy, 185:1809-1820

[31] Feng Z H, Zou L L, Wei Y M (2011) Carbon price volatility:Evidence from EU ETS. Applied Energy, 88(3): 590-598

[32] Fan H, Wang C Y, Liu L, et al. (2022) Review of uncertainty modeling for optimal operation of integrated energy system.Frontiers in Energy Research, 9: 641337

[33] Ren H T, Zhou W J, Makowski M, et al. (2021) Incorporation of life cycle emissions and carbon price uncertainty into the supply chain network management of PVC production. Annals of Operations Research, 300(2): 601-620

[34] Fan J H, Todorova N (2017) Dynamics of China’s carbon prices in the pilot trading phase. Applied Energy, 208: 1452-1467

[35] Ren H T, Guo Y, Zhou W J, et al. (2020) Multi-objective optimization of green aluminum supply chain network design under resource constraints. Systems Engineering – Theory &Practice, 40(08): 2090-2103 (in Chinese)

[36] Ding B, Makowski M, Nahorski Z, et al. (2022) Optimizing the technology pathway of China’s liquid fuel production considering uncertain oil prices: A robust programming model. Energy Economics, 115: 106371

[37] Lecuyer O, Quirion P (2019) Interaction between CO2 emissions trading and renewable energy subsidies under uncertainty: Feedin tariffs as a safety net against over-allocation. Climate Policy,19(8): 1002-1018

[38] Yu L, Li Y P, Huang G H (2019) Planning municipal-scale mixed energy system for stimulating renewable energy under multiple uncertainties - The City of Qingdao in Shandong Province, China.Energy, 166: 1120-1133

[39] Zhou Y B, Yang F, Yu X X, et al. (2022) Realization pathways and key problems of carbon neutrality in China’s energy and power system. Electric Power, 55(05): 1-11 (in Chinese)

[40] Li Y P, Huang G H, Li M W (2014) An integrated optimization modeling approach for planning emission trading and cleanenergy development under uncertainty. Renewable Energy, 62:31-46

[41] Schaeffer R, Szklo A S, De Lucena A F P, et al. (2012) Energy sector vulnerability to climate change: A review. Energy, 38(1):1-12

[42] Zhen J L, Zhang Y, Liu X R, et al. (2023) Optimization modeling for regional energy system management coupled with energywater nexus and carbon emission reduction: A case study.Environmental Engineering Science, 40(3): 114-126

[43] Iea (2022) World Energy Outlook. https://www.iea.org/reports/world-energy-outlook-2022. Accessed 17 May 2023

[44] Zhang L, Chen Z, Yang C, et al. (2022) Global supply risk assessment of the metals used in clean energy technologies.Journal of Cleaner Production, 331: 129602

[45] Li J, Peng K, Wang P, et al. (2020) Critical rare-earth elements mismatch global wind-power ambitions. One Earth, 3(1): 116-125

[46] Omu A, Choudhary R, Boies A (2013) Distributed energy resource system optimisation using mixed integer linear programming. Energy Policy, 61: 249-266

[47] Mirkhani S, Saboohi Y (2012) Stochastic modeling of the energy supply system with uncertain fuel price – A case of emerging technologies for distributed power generation. Applied Energy,93: 668-674

[48] Madlener R, Glensk B, Gläsel L (2019) Optimal timing of onshore wind repowering in Germany under policy regime changes: A real options analysis. Energies, 12(24): 4703

[49] Li Z M, Wu L, Xu Y, et al. (2022) Stochastic-weighted robust optimization based bilayer operation of a multi-energy building microgrid considering practical thermal loads and battery degradation. IEEE Transactions on Sustainable Energy, 13(2):668-682

[50] Norouzi N, Zarazua de Rubens G, Choupanpiesheh S, et al.(2020) When pandemics impact economies and climate change:Exploring the impacts of COVID-19 on oil and electricity demand in China. Energy Research & Social Science, 68: 101654

[51] Tafarte P, Das S, Eichhorn M, et al. (2014) Small adaptations,big impacts: Options for an optimized mix of variable renewable energy sources. Energy, 72: 80-92

[52] De Boer H S, Van Vuuren D (2017) Representation of variable renewable energy sources in TIMER, an aggregated energy system simulation model. Energy Economics, 64: 600-611

[53] Burhenne S, Tsvetkova O, Jacob D, et al. (2013) Uncertainty quantification for combined building performance and costbenefit analyses. Building and Environment, 62: 143-154

[54] De La Tour A, Glachant M, Meniere Y (2013) Predicting the costs of photovoltaic solar modules in 2020 using experience curve models. Energy, 62: 341-348

[55] Rubin E S, Azevedo I M L, Jaramillo P, et al. (2015) A review of learning rates for electricity supply technologies. Energy Policy,86: 198-218

[56] D’agostino D, Parker D, Epifani I, et al. (2022) How will future climate impact the design and performance of nearly zero energy buildings (NZEBs)? Energy, 240: 122479

[57] Perera A T D, Nik V M, Chen D L, et al. (2020) Quantifying the impacts of climate change and extreme climate events on energy systems. Nature Energy, 5(2): 150-159

[58] Feron S, Cordero R R, Damiani A, et al. (2021) Climate change extremes and photovoltaic power output. Nature Sustainability,4(3): 270-276

[59] Fu X Q, Wu X P, Zhang C Y, et al. (2022) Planning of distributed renewable energy systems under uncertainty based on statistical machine learning. Protection and Control of Modern Power Systems, 7(1): 1-27

[60] Morteza, Aien (2016) A comprehensive review on uncertainty modeling techniques in power system studies. Renewable and Sustainable Energy Reviews, 57: 1077-1089

[61] Kanudia A, Shukla P R (1998) Modelling of uncertainties and price elastic demands in energy-environment planning for India.Omega, 26(3): 409-423

[62] Broad O, Hawker G, Dodds P E (2020) Decarbonising the UK residential sector: The dependence of national abatement on flexible and local views of the future. Energy Policy, 140: 111321

[63] Riepin I, Mobius T, Musgens F (2021) Modelling uncertainty in coupled electricity and gas systems-Is it worth the effort? Applied Energy, 285: 116363

[64] Mavromatidis G, Orehounig K, Carmeliet J (2018) Uncertainty and global sensitivity analysis for the optimal design of distributed energy systems. Applied Energy, 214: 219-238

[65] Santos M J, Ferreira P, Araújo M (2016) A methodology to incorporate risk and uncertainty in electricity power planning.Energy, 115: 1400-1411

[66] Zhang S, Chen W Y (2022) Assessing the energy transition in China towards carbon neutrality with a probabilistic framework.Nature Communications, 13: 87

[67] Carvajal P E, Li F G N, Soria R, et al. (2019) Large hydropower,decarbonisation and climate change uncertainty: Modelling power sector pathways for Ecuador. Energy Strategy Reviews,23: 86-99

[68] Xu Z, Fang C, Ma T (2020) Analysis of China’s olefin industry using a system optimization model considering technological learning and energy consumption reduction. Energy, 191: 116462

[69] Odetayo B, Maccormack J, Rosehart W D, et al. (2017) A chance constrained programming approach to integrated planning of distributed power generation and natural gas network. Electric Power Systems Research, 151: 197-207

[70] Min D, Ryu J-H, Choi D G (2018) A long-term capacity expansion planning model for an electric power system integrating large-size renewable energy technologies. Computers& Operations Research, 96: 244-255

[71] Gan L, Jiang P, Chen X, et al. (2019) Sustainable Optimization for China’s Hydropower Project Investment Portfolio Using Multiobjective Decision Analysis. Mathematical Problems in Engineering, 2019: 6745320

[72] Zarrinpoor N, Khani A (2022) A biofuel supply chain design considering sustainability, uncertainty, and international suppliers and markets. Biomass Conversion and Biorefinery, 1-27

[73] Zhou C Y, Huang G H, Chen J P (2019) A type-2 fuzzy chanceconstrained fractional integrated modeling method for energy system management of uncertainties and risks. Energies, 12(13): 2472

[74] Majidi M, Mohammadi-Ivatloo B, Soroudi A (2019) Application of information gap decision theory in practical energy problems:A comprehensive review. Applied Energy, 249: 157-165

[75] Yadegari S, Abdi H, Nikkhah S (2020) Risk-averse multiobjective optimal combined heat and power planning considering voltage security constraints. Energy, 212

[76] Chen C, Li Y P, Huang G H, et al. (2012) A robust optimization method for planning regional-scale electric power systems and managing carbon dioxide. International Journal of Electrical Power & Energy Systems, 40(1): 70-84.

[77] Tsao Y-C, Thanh V-V (2020) A multi-objective fuzzy robust optimization approach for designing sustainable and reliable power systems under uncertainty. Applied Soft Computing, 92:106317

[78] Luo B, Maqsood I, Huang G H (2007) Planning water resources systems with interval stochastic dynamic programming. Water Resources Management, 21(6): 997-1014

[79] Gongchen, Li (2018) Planning of integrated energy-environment systems under dual interval uncertainties. International Journal of Electrical Power & Energy Systems, 100: 287-298

[80] Jain R K, Qin J J, Rajagopal R (2017) name="ref81" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[81] Ning C, You F (2019) Optimization under uncertainty in the era of big data and deep learning: When machine learning meets mathematical programming. Computers & Chemical Engineering,125: 434-448

[82] Baranitharan B, Sivapragasam C, Rajesh K (2022) Long term monthly prediction of energy requirements from a probabilistic perspective - A case study in southern States of India. Sustainable Energy Technologies and Assessments, 53: 102707

[83] Yang Y, Guo H G, Jin Y, et al. (2021) An ensemble prediction system based on artificial neural networks and deep learning methods for deterministic and probabilistic carbon price forecasting. Frontiers in Environmental Science, 9: 740093

[84] Kalhori M R N, Emami I T, Fallahi F, et al. (2022) A datadriven knowledge-based system with reasoning under uncertain evidence for regional long-term hourly load forecasting. Applied Energy, 314: 118975

[85] Kim H, Cheon H, Ahn Y H, et al. (2019) Uncertainty quantification and scenario generation of future solar photovoltaic price for use in energy system models. Energy, 168: 370-379

[86] Seljom P, Kvalbein L, Hellemo L, et al. (2021) Stochastic modelling of variable renewables in long-term energy models:Dataset, scenario generation & quality of results. Energy, 236:121415

[87] Loehndorf N (2016) An empirical analysis of scenario generation methods for stochastic optimization. European Journal of Operational Research, 255(1): 121-132

[88] Cox J C, Ross S A, Rubinstein M (1979) Option pricing: A simplified approach. Journal of Financial Economics, 7(3): 229-263

[89] Lei Y, Wang D, Jia H, et al. (2021) Multi-stage stochastic planning of regional integrated energy system based on scenario tree path optimization under long-term multiple uncertainties.Applied Energy, 300: 117224

Received: 3 April 2023/ Accepted: 10 July 2023/ Published: 25 August 2023

Hongtao Ren

ren@ecust.edu.cn

Siyu Feng

y30211363@mail.ecust.edu.cn

Wenji Zhou

zhouwenji@ruc.edu.cn

2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization. Production and hosting by Elsevier B.V. on behalf of KeAi Communications Co., Ltd. This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/ ).

Biographies

Siyu Feng is working towards master’s degree at East China University of Science and Technology, Shanghai. Her research interests included energy technology system modeling,uncertainty analysis.

Hongtao Ren received the Doctor’s degree at Japan Advanced Institute of Science and Technology, Japan, 2007. He is working in East China University of Science and Technology, Shanghai. His research interests included energy technology system modeling,energy system multiple-criteria analysis.

Wenji Zhou received the Doctor’s degree at Tsinghua University, Beijing, 2011. He is working in Renmin University of China,Beijing. His research interests included energy modeling, energy economics.

(Editor Dawei Wang)