0 Introduction

In the last century, the electricity network was designed and developed around the synchronous generators where their main fuel source, coal, was also mined.Unfortunately,the new clean energy resources, such as wind and solar, are often abundant in the remote regions, which are distant from population centers and lack power infrastructure [1, 2].This geographical feature determines that the most economic option of integrating renewable generators is to connect to the dead-end nodes, which yet creates shortfalls in system strength and potentially deteriorates system stability [3-5].These newly emerged challenges necessitate rigorous analysis on the adverse impacts from modern types of asynchronous generators on the existing power system.

Previously, classic power system stability theory has primarily focused on relatively slow electromechanical transients that are dominated by synchronous generators[6].With unprecedentedly significant connection of asynchronous generating units, e.g.voltage source converters (VSCs), their inherent characteristics of highfrequency switching and wide control bandwidth attract research interests in fast electromagnetic dynamics.Also,numerous unstable incidents with respect to renewable based generating plants were reported covering oscillation frequencies from tens to thousands of Hertz [7-10].Therefore, in 2020, IEEE published a task force report revisiting definitions and classifications of power system stability, mainly adding converter-driven stability and resonance stability to the original stability categories by considering new dynamic phenomena induced by power electronic interfaced technologies [11].

The state-of-the-art methods of evaluating power system small-signal stability can be summarized as of two types: by state-space model in time domain [12-14] and by impedance model in frequency domain [15-17].To investigate stability of the VSC integrated power system, impedance-based approach derives frequency characteristics of the VSC and the remaining system from the interfacing terminal.As asymmetrical dynamics that result in cross couplings between positive and negative sequence are noted in VSC control system [18], multi-input multi-output (MIMO)matrix has to be utilized to represent VSC impedance at its terminal, and Generalized Nyquist Criterion (GNC)needs to be adopted, which however is hard to distinguish the participation from VSC or grid impedance to the instability mode [19].Foregoing efforts have been also made to simplify MIMO impedance model into two sets of equivalent single-input single-output (SISO) frequency domain transfer functions, where the classical stability criterion can be applied to intuitively identify the correlation between controller parameters and the stability margin [20-22].Overall, the principal advantage of impedance-based analysis is that it enables black-box modelling of VSCs via frequency scan tool, which facilitates interaction analysis by different manufacturers.Nevertheless, this methodology provides limited insight on participation of state variables and the damping level of oscillatory modes.To overcome the shortcomings of impedance-based approach, eigenvalue analysis based on standard state-space modelling is often employed [6], although wide control bandwidth of VSC determines the state-space model is of high orders, which thus brings heavy computation burdens [23].

Replacing grid-following inverters with grid synchronous scheme of phase-locked loop (PLL) that may induce sideband oscillations in weak grid, grid-forming inverters that emulate swing equation of synchronous generators have gained popularity [24], with established analytical and experimental results demonstrating that gridforming inverters are superior to grid-following inverters in ultra-weak grid [25, 26].

In contrast, previous experiments in [27] and numerical analysis in [28] show that grid-forming inverters gradually exhibit worse stability in stiff grid.This is logically reasonable as in the extreme circumstance that voltagecontrolled grid-forming inverters cannot manipulate voltage at the infinite bus [28].However, the critical point and stability margin for grid-forming inverters have not been clearly defined.Additionally, most of the converter-driven power system stability analyses are based on single machine infinite bus (SMIB) scenario, where the system is equivalent to a voltage source with impedances behind.To authors'knowledge, there is still a lack of research that thoroughly models the system dynamics and rigorously identifies root sources of converter-driven stability issues via analytics.

To address the aforementioned concerns, this paper presents a modular technique to assemble the state-space model for a system fed with multiple inverters.Downstream eigenvalue analysis is conducted exploring the small-signal stability boundary for grid-following and grid-forming inverters.The main contributions are highlighted of two folds:

1) The state-space model for a generic power system with state-of-the-art inverters is developed covering fullorder dynamics of the corresponding control systems, yet with reduced computation efforts and increased scalability.

2) Small-signal driven stability margin is derived revealing risks for the connections of not only gridfollowing inverters, but also grid-forming inverters.Also,the root cause for potential converter-driven oscillations is clearly identified.

The remainder of this paper is structured as follows.Section 1 elaborates on the process to establish the overall state-space model.Section 2 presents analytical tools for system stability assessment.Section 3 validates theoretical analysis via numerical and simulation results.Section 4 draws the conclusion.

1 State-space modelling for multi-inverter system

1.1 Notations and preliminaries

The power electricity network is considered as a connected undirected graph G ( Γ,E ) , where Γ comprises of the electrical buses in the system, and E ⊆Γ×Γ refers to the line connection between two buses.Suppose the system has m buses, out of which there are g IBGs that are correspondingly connecting to g(g≤m) buses denoting the bus set as Γg, and l transmission lines.In this work, we model the transmission lines as π section and all loads as shunt resistance-reactance elements.The bus admittance matrix of the system is thus obtained as Y b = G - jB∈Cm× m,where C is the set of complex numbers.Furthermore, a single-line diagram for the IB generating plant is presented in Fig.1, where constant dc voltage, dc/ac inverters, L-type filters are modelled as per generic electrical layout, and measured signals to be fed to control systems are displayed.

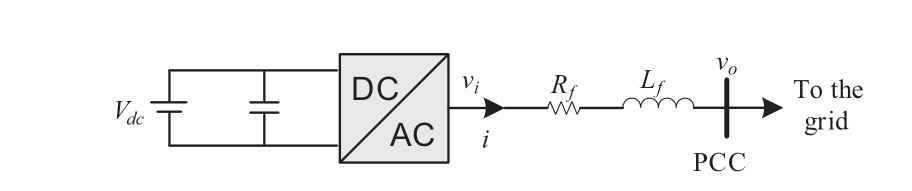
Fig.1 Single-line diagram for the inverter-based generating plant

The comprehensive state-space model for a power system interconnecting with multiple inverter-based DGs is constructed based on CCM.Taking the full advantage of the power system structure, CCM combines simplicity and modularity considering matrix algebra and sparsity.Compared to the traditional methodology, it is more computationally-efficient and scalable for the large system with inverters of complicated dynamic characteristics.The basic principle of CCM [29] is briefly summarized in the following context as a preliminary.

Assume the overall dynamic system can be partitioned into k individual subsystems, and the state-space model for the i-th subsystem provided in (1) is formulated by linearizing its set of nonlinear differential equations:

where xi, ai and bi represent state variables, input variables and output variables of the i-th subsystem, and Fi, Hi, Ji,Ki are state matrices for the corresponding substate-space model.Therefore, a composite model including all the dynamics in the system is organized as:

where u and y are inputs and outputs for the entire system.

Considering (2) and (3), the state-space model for an aggregated system can be standardized as:

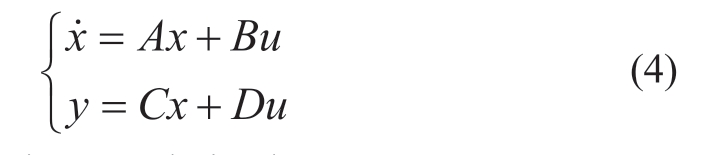
where the state matrices are derived as:

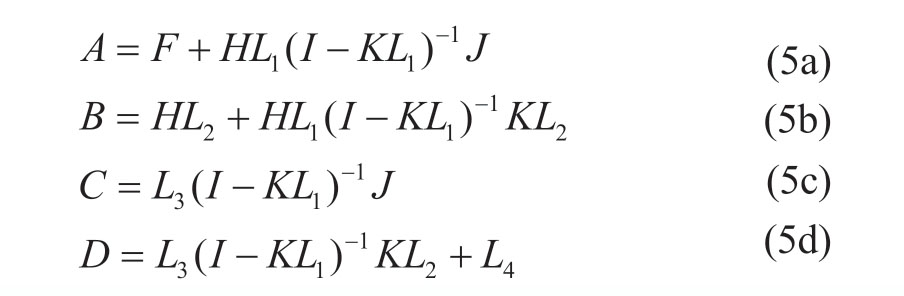
As illustrated in Fig.2, the application of CCM to build state-space model for a power system with inverters controlled by different prototypes, i.e., grid-following and grid-forming, is of two levels: 1) Primary level: Inverter control scheme is explicitly modelled; 2) Secondary level:each IBG is connected to the overall system as a component,and interconnection relationships are developed via the intrinsic characteristics of power system.

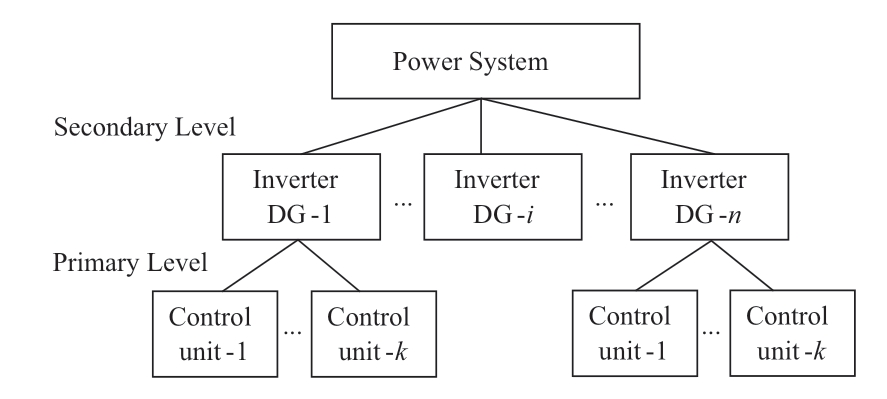
Fig.2 Illustration of two-level CCM

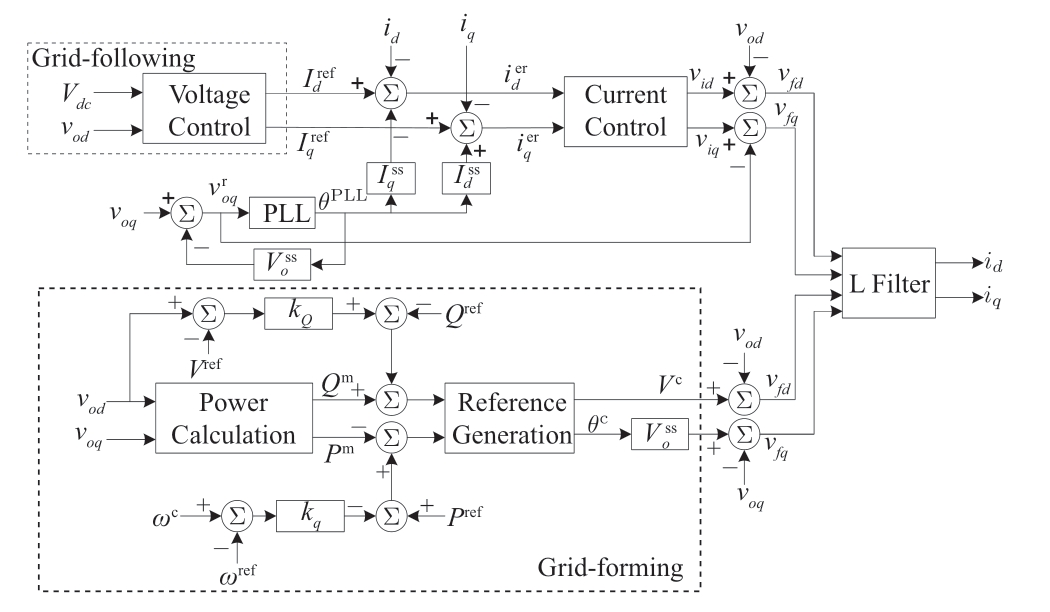
Fig.3 Linearized control schematic for grid-following and grid-forming technology

1.2 State-space model of grid-following inverters

Fig.3 depicts the control schematic for gridfollowing technology, implemented by dc and ac voltage control (VC), current control (CC) and PLL, with L filter(LF) dynamics also being interacted.Hence, we firstly build the substate-space model for each of the control components, such that:

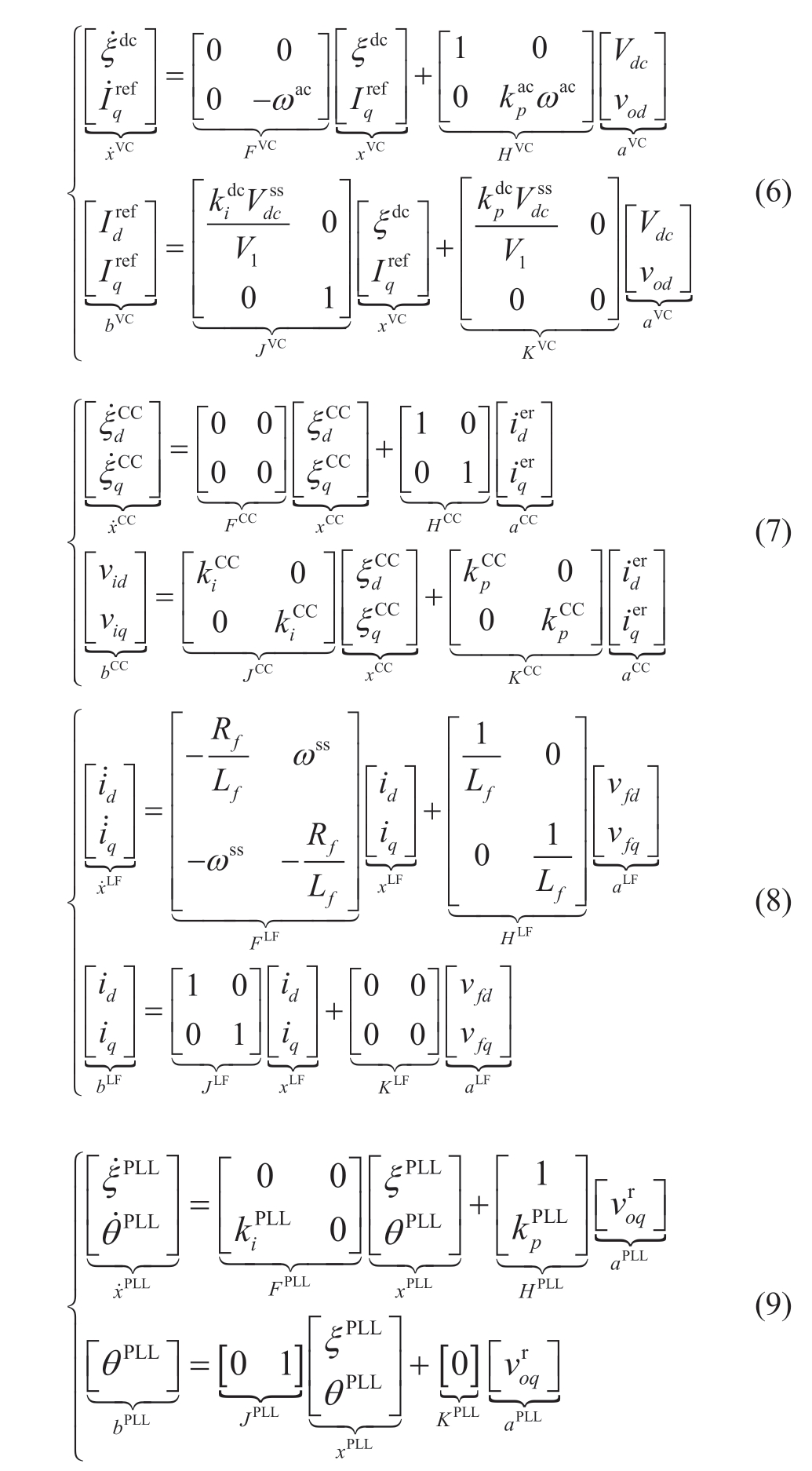
where the variables and deviation process are specified in Appendix A.

where θss represents steady-state phase of PCC voltage synchronized by PLL.Substituting the small-signal

Considering (6)-(9) and (13), the comprehensive state-space model for grid-following inverters can be obtained as:

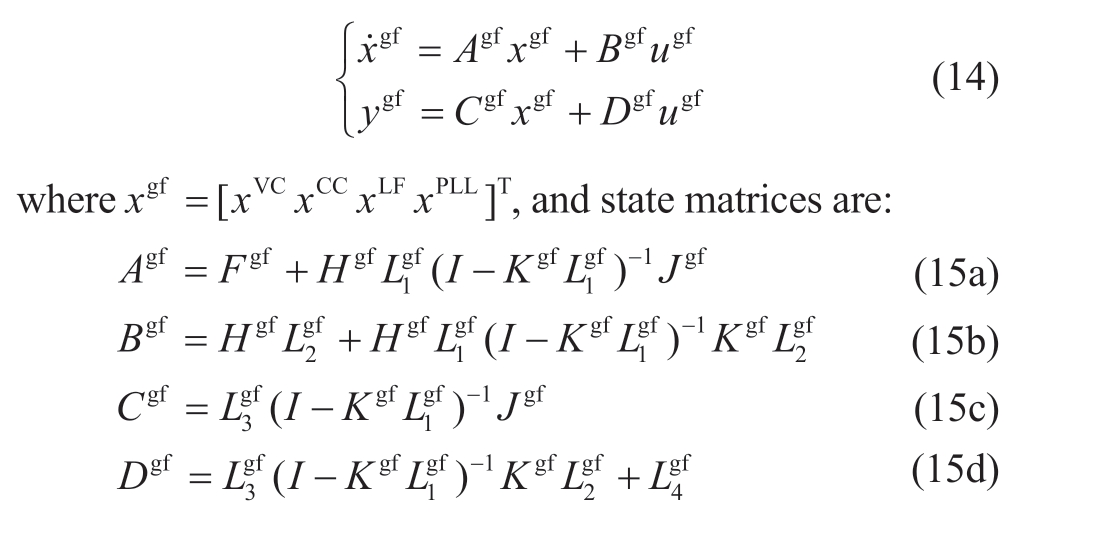
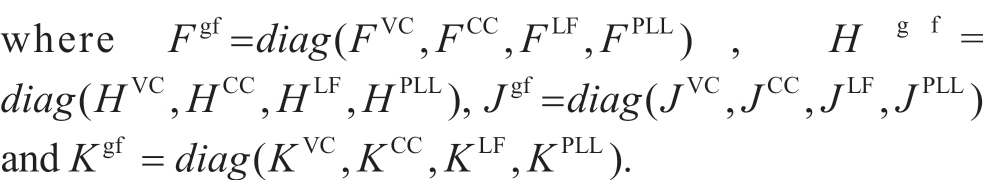
1.3 State-space model of grid-forming inverters

The fundamental principle for grid-forming inverter control is to mimic characteristics of synchronous generators that are regulated with inherently generated voltage references, rather than under current controlled mode as grid-following inverters.Accordingly, the control block for grid-forming inverter is depicted in Fig.3, from which the control loops for voltage reference generation will be analyzed as a combined dynamic subsystem, so that the substate-space model is:

The process of deriving the state-space model as in(16) is explicitly described in Appendix B.Additionally,grid-forming inverters share the same dynamic model of L-type filters interfacing to the grid with grid-following inverters.As a result, (8) will be utilized as a component for a substate-space model for grid-forming inverters as well.

In terms of the control schematic and the coupling due to Park Transformation, the linear relationship between (8)and (16) can be established as:

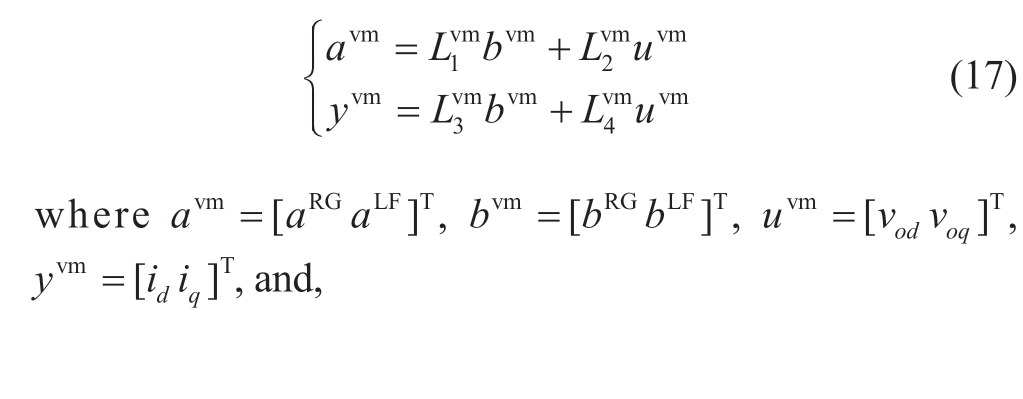
Lastly, the overall state-space model for grid-forming inverters can be formulated as:

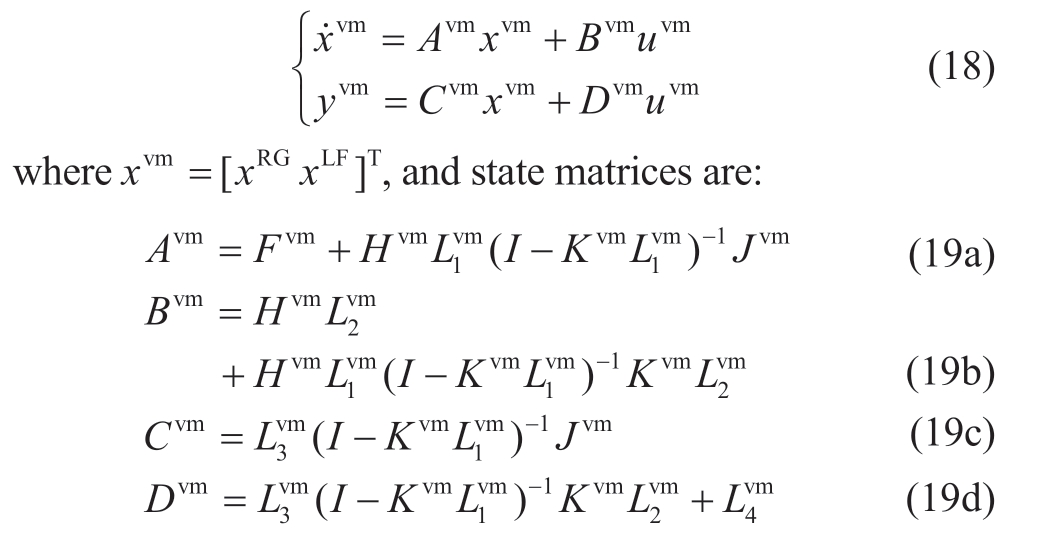
where Fvm=diag(FRGFLF), Hvm=diag(HRGHLF), Jvm=diag(JRG JLF), and Kvm=diag(KRG KLF).

1.4 State-space model of interconnected system

Denote  and as shunt resistance, inductance and capacitance at each node, and as branch resistance and inductance of each transmission line.The differential equations of a network can be obtained based on nodal voltage dynamics, nodal current dynamics and branch current dynamics, such that,

where ⊗ is the Kronecker product and the abovementioned matrices are defined as:

Define the m×l directed line connectivity matrix Γb by

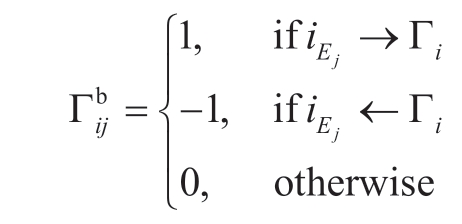
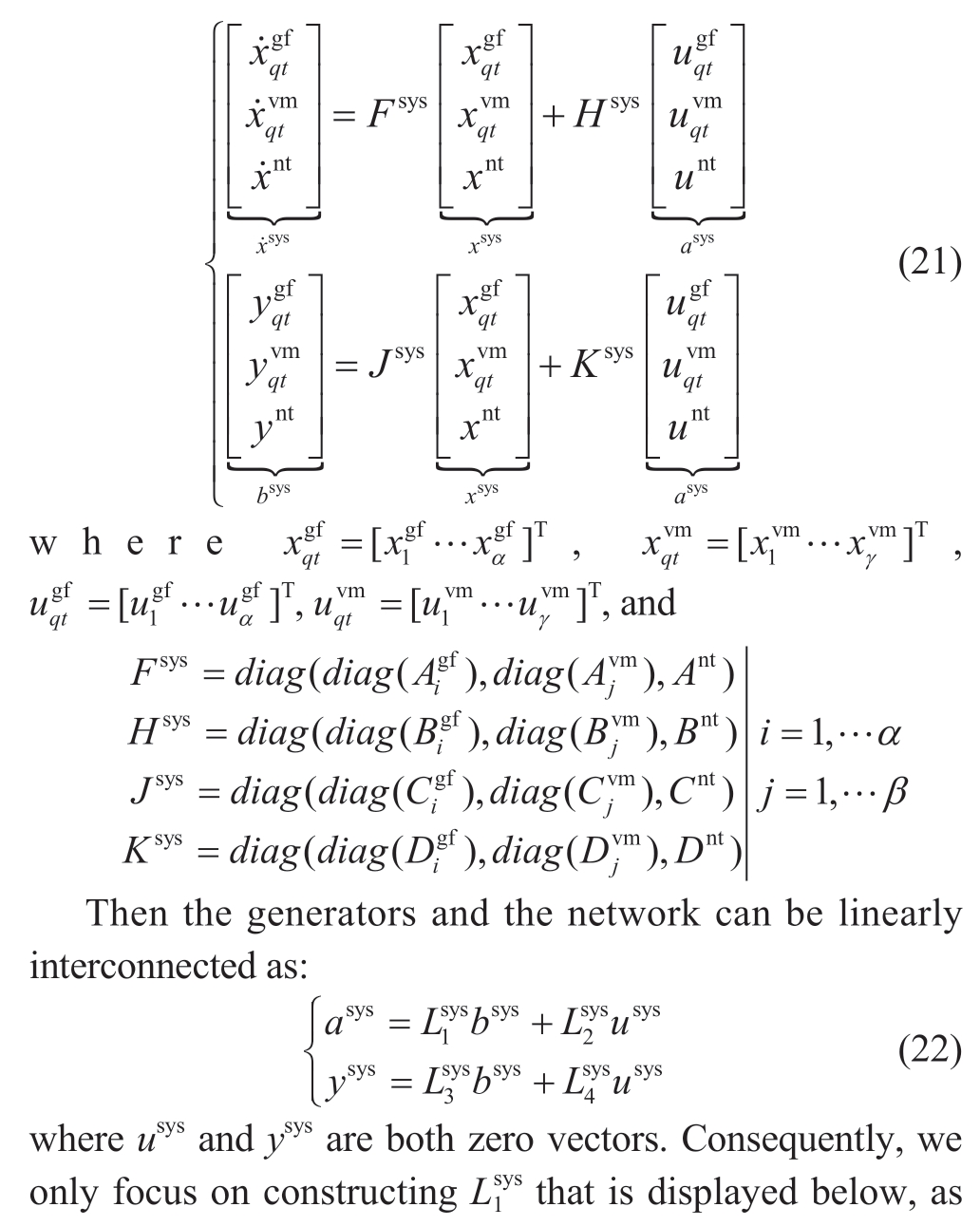
Suppose there are α grid-following generators and β grid-forming generators.Therefore, considering (14), (18)and (20), the composite system model including dynamics for all components can be expressed as:

where ϒpos is defined as a g×m matrix indicating the generator location in the network:

Hence, the state-space model for the overall system can be obtained as:

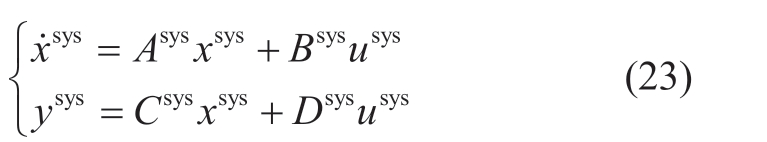
where state matrices are:

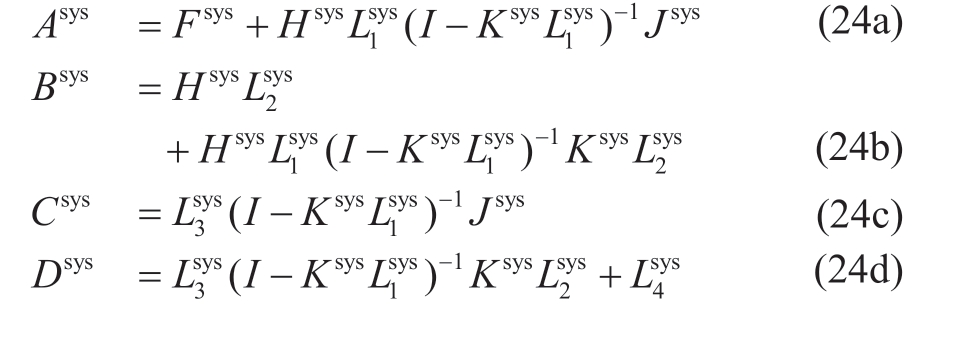
2 Small-signal analysis of multi-inverter system

In this section, small-signal stability of the multi-inverter system is analyzed, justified, and interpreted.Moreover,mathematic modelling and analysis reveals that the CCMbased state-space modelling is equivalent to designoriented impedance-based methodology, but with increased flexibility and transparency.The underlying principle of impacts of different inverter control schemes on system stability is also investigated.

The eigenvalues λ of the state matrix Asys as in (24a) are derived and utilized to evaluate the small-signal stability of the overall system, i.e.:

where the identity matrix I is as the same size of Asys.

Oscillatory mechanism of the interconnected network is further investigated with the participation factors relating system strength and interactions to the oscillatory modes.Define that the relative participation of the i-th state variable to the j-th mode, so that,

3 Case study

The IEEE 39-bus system is utilized in the case studies to test the efficiency of the proposed analytical theory, where details about the transmission network are derived from [32,33].Modifications with respect to the generators are made to the original system, where Table 1 gives details about the location of the generators (indicating by the bus number)that is replaced by grid-following or grid-forming inverters.Controller parameters are provided in Table 2 and Table 3 for grid-following and grid-forming inverters, respectively.

Table 1 Tested scenarios

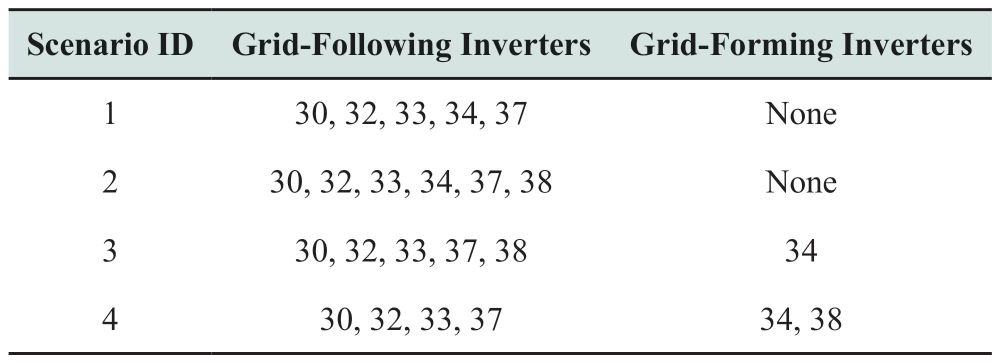
Table 2 Controller parameters of grid-following inverters

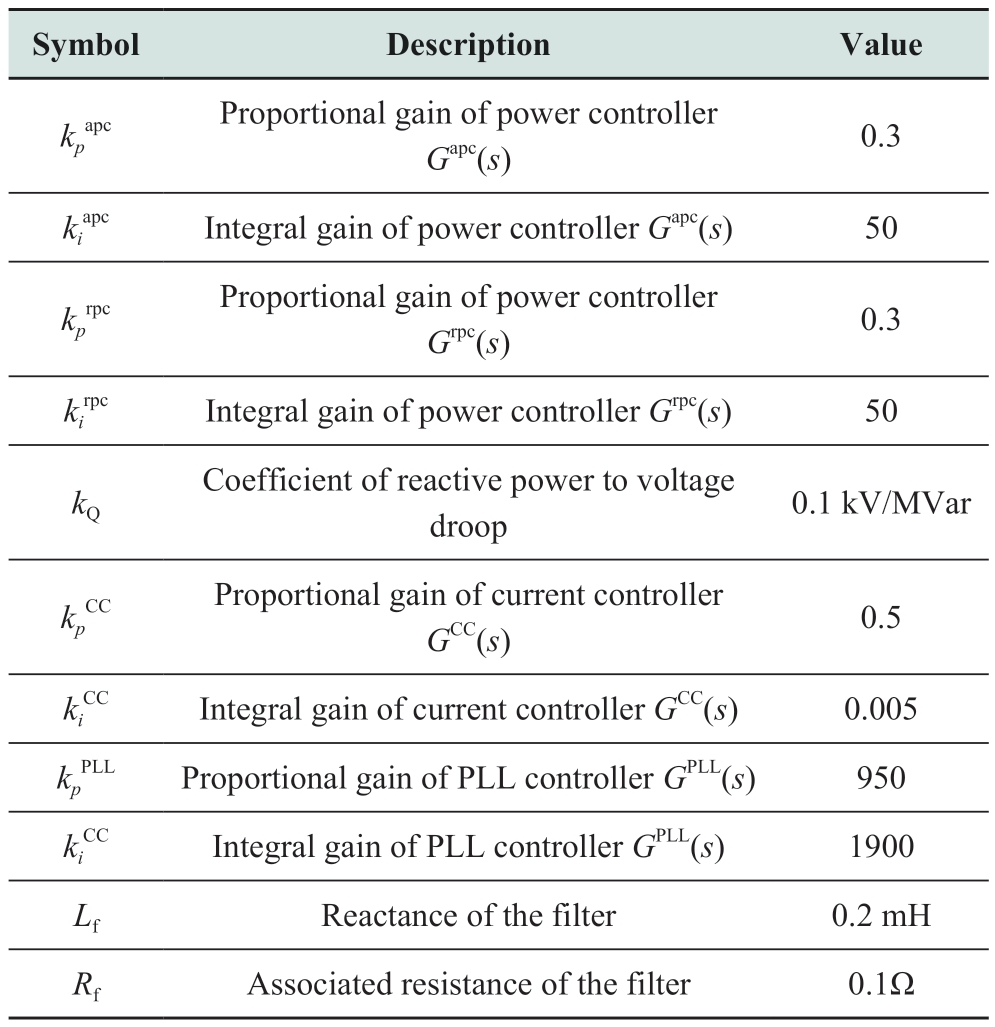
Table 3 Controller parameters of grid-forming inverters

continue

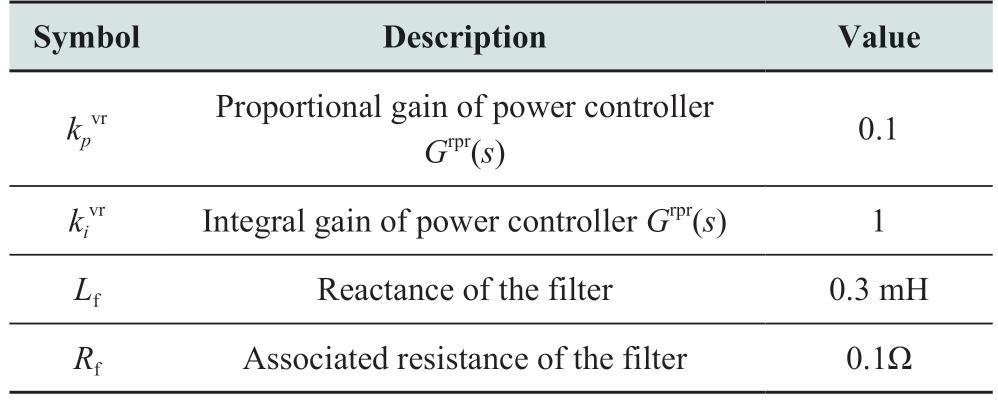
3.1 Numerical results

Given the controller parameters as specified in Table 2 and 3, the eigenvalues and participation factors are calculated based on (25) and (26).Numerical results are provided in Table 4, whereis the largest real part of the system eigenvalues representing the critical mode for the multi-inverter system, pmax is the maximum participation factor to the correspondingly critical mode, and the last column identifies the root source of the specific inverter contributing the most to the unstable mode.The analytical results in Table 4 show that: 1) Compared Scenario 2 to Scenario 1, adding grid-following IBG to the network reduces stability margin, which thus deteriorates smallsignal stability; 2) Compared Scenario 3 to Scenario 1,where a grid-following IBG is converted to a grid-forming IBG, stability margin with respect to low system strength condition is enhanced; 3) Compared Scenario 4 to Scenario 3, where a second grid-following IBG is modified to a gridforming IBG, stability issues regarding grid stiffness exist.

Table 4 Numerical results for tested scenarios

3.2 Simulation results

The IEEE 39-bus system, as well as detailed inverter models, have been developed in PSCAD/EMTDC.Studies are accordingly undertaken as per the scenarios listed in Table 1.Furthermore, capacitor switching tests are conducted to test the small-signal performances.Fig.4 depicts voltage performances and active power injection at the IBG buses.

In Scenario 1 and 2, the capacitor is switched in and out at 5s and 10s, respectively.After the small-signal disturbance, voltage and active power are well damped in Scenario 1.Nonetheless, 20Hz undamped oscillations are captured in Scenario 2.This observation is consistent with theoretical findings in Section 3 and numerical results in Table 4.

In Scenario 3 and 4, grid-forming IBGs are connecting to the system at 4s, followed by the small-signal test at 15 s and 20 s.Compared to the voltage performance in Scenario 2, 20 Hz oscillation does not exist in neither Scenario 3 nor 4.However, grid-forming inverter driven slow dynamic behaviour starts to appear.With only one grid-forming IBG in the network as of Scenario 3, the oscillation can be critically damped.Yet in scenario 4 where there is another grid-forming IBG integrated, the damping of the oscillation is worse, which is also consistent with corresponding analytical and numerical results.

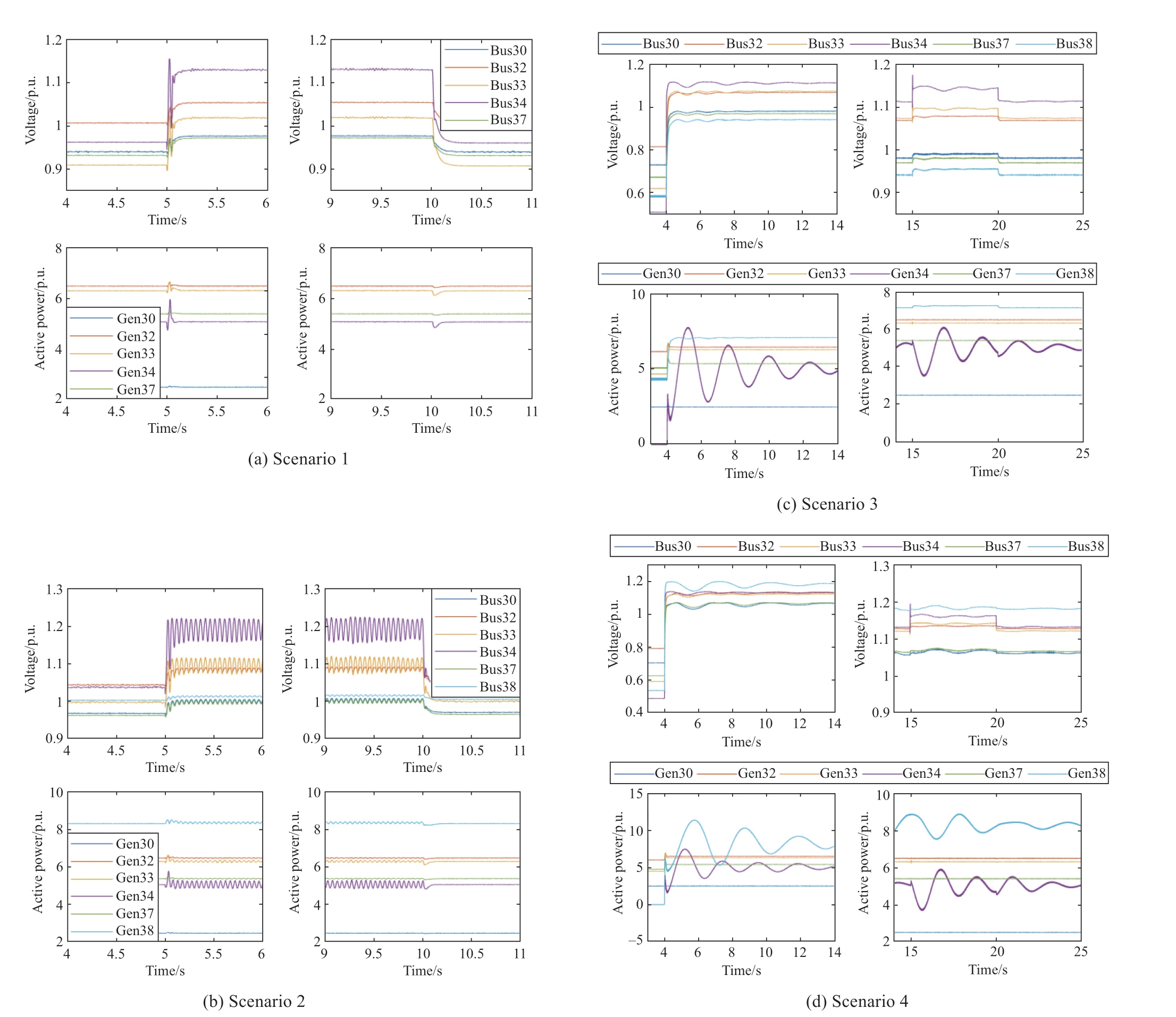
Fig.4 Voltage at the inverter buses and active power injection from the IBGs

4 Conclusion

The primary aim of this paper is to develop a generic state-space model for multi-inverter system, evaluate the small-signal stability of the inverters penetrated modern power system, and understand the root source of potential inverter-driven instability issues.Key points of this paper are summarized below:

1) Comprehensive state-space model for a power system with grid-following inverters and grid-forming inverters are developed in this paper, using efficient method of CCM that modularized control blocks and power system components.

2) Inverter-driven oscillations can be the consequence of grid-following inverter interacting with weak grid, and also grid-forming inverter interacting with stiff grid.

Appendix A

The current reference on direct axis of dq-frame is generated by dc voltage-square control scheme [34], which interprets as:

where 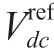 is the voltage reference at dc side, V1 is the ratedPCC voltage, and Gde(s) represents the PI controller in frequency domain written as:

Disturbing dc voltage by a small-signal perturbation, Idref in (27) becomes,

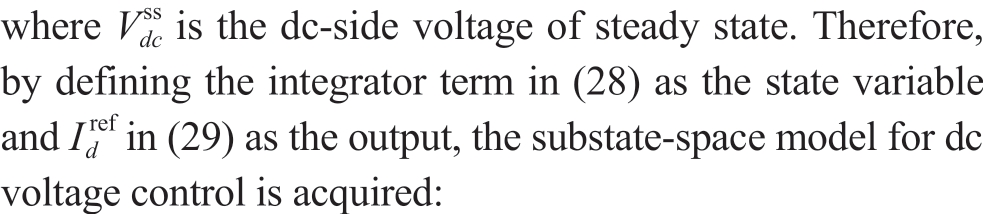
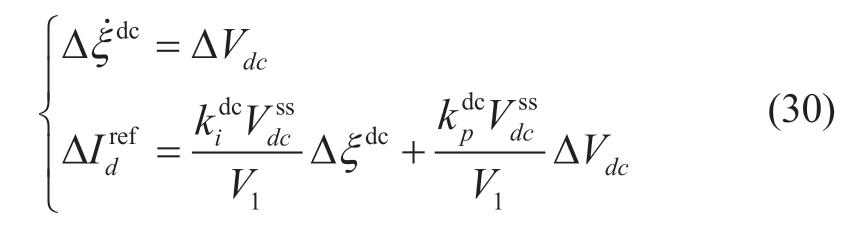
In addition, the current reference on quadrature axis of dq-frame is obtained through controlling ac voltage magnitude, given as:

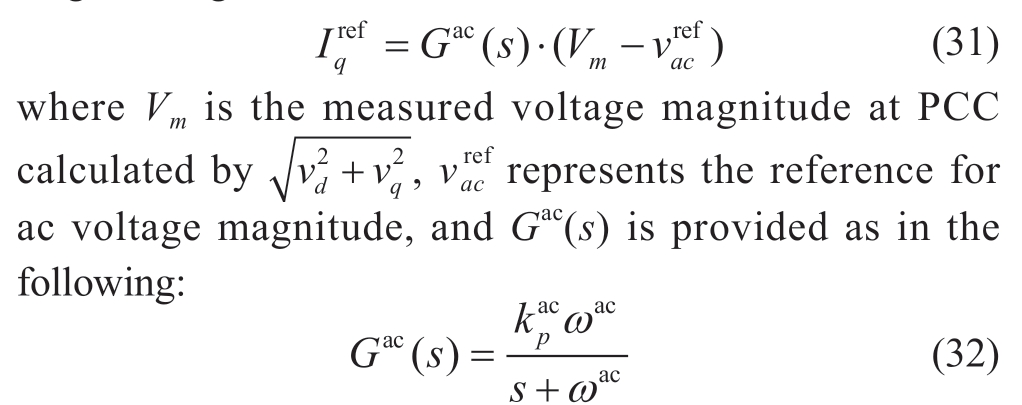
As a result, substate-space model for VC is integrated in(6) via combining (30) and (33), and disregarding the prefix“Δ”for simplicity.

Current controller in s-domain is expressed as:

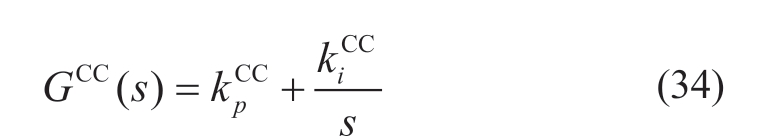
Also, define the integrator as the state variable  and, such that,

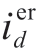where and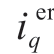 are current control errors between the references and the measured current.Neglecting the effects from control delay, the output of the current controllers is the voltage at inverter terminal, written as:

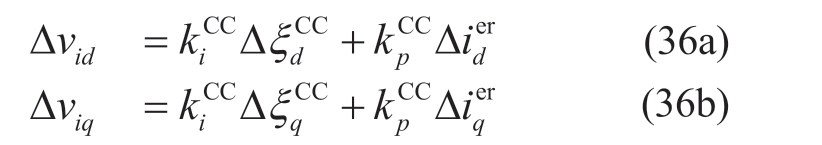
Organizing (35), (36a) and (36b) into the form of statespace model gives (7).

Current dynamics over the L-filter in dq-frame are formulated as:

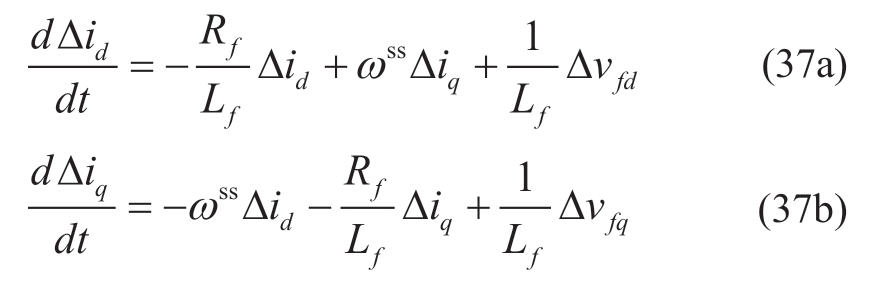
where vfd and vfq are the voltage cross the filter, Lf is the filter reactance, and Rf is the associated resistance.Taking the inverter current id and iq as the output, (8) is arranged from(37a) and (37b).

The phase synchronization is realized by the standard phase tracking scheme of synchronous reference frame PLL(SRF-PLL) as in [35], where there are three main control components: phase error detection (by dq-transformation in this methodology), loop filter (by PI controller on q-axis voltage) and voltage-controlled oscillator (VCO, by an integrator).The q-axis voltage controller is:

Define the integrators in the controller and VCO as the state variables ξPLL and θPLL, such that,

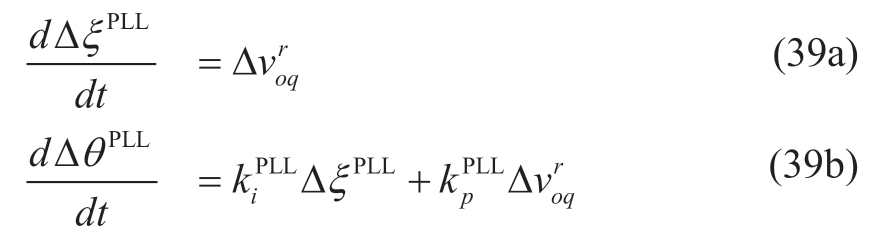
where Δvroq is derived in (11).Combining the fact that the output of PLL is the synchronized phase θPLL, the statespace model for SRF-PLL can be developed as in (9).

Appendix B

The voltage phase reference is generated based on the measured active power and the power deviation from frequency droop control.The transfer function for this loop is interpreted in frequency domain as:

where ωref is the nominal voltage frequency in radians, ωc is the generated reference for inverter frequency control, Pref is the reference active power, Pm is the measured active power injecting to the grid, and kP and J mimic the synchronous generators’characteristics of damping and inertia [36].Given small-signal disturbances on PCC voltage and current, and translating (40) into time-domain differential equations, we have,

Note that the output of this control loop should be the voltage phase, which yields the differential equation:

where θc is the voltage phase reference.

Furthermore, the voltage magnitude reference is generated by:

where Vref is the nominal voltage magnitude, kQ is the virtual damping factor for voltage control, K is the virtual inertia for reactive power control, and Qm is the measured inverter reactive power injected to the grid.Rearranging (43) into time-domain differential equation gives:

Provided (41), (42) and (44), the state-space model for the control system of voltage reference generation including phase and magnitude can be acquired in (16).

Acknowledgements

The work was supported partially by a MOE Tier 1 Thematic grant (23070749).

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] TransGrid (2020) New South Wales Transmission Annual Planning Report 2020.Tech Rep

[2] Nguyen H T, Yang G, Nielsen A H, et al.(2018) Combination of Synchronous Condenser and Synthetic Inertia for Frequency Stability Enhancement in Low Inertia Systems.IEEE Transactions on Sustainable Energy, 10(3):997-1005

[3] Song Y, Zheng Y, Liu T, et al.(2020) A New Formulation of Distribution Network Reconfiguration for Reducing the Voltage Volatility Induced by Distributed Generation.IEEE Transactions on Power System, 35(1):496-507

[4] Menck P J, Heitzig J, Kurths J, et al.(2014) How dead ends undermine power grid stability.Nat Commun 5:3969

[5] Song Y, Hill D J, Liu T (2019) Impact of DG Connection Topology on the Stability of Inverter-Based Microgrids.IEEE Transactions on Power System, 34(5):3970-3972

[6] Kundur P (1993) Power System Stability and Control.McGraw-Hill, Emeryville, CA

[7] Mollerstedt E, Bernhardsson B (2000) Out of control because of harmonics-an analysis of the harmonic response of an inverter locomotive.IEEE Control Systems, 20(4):70-81

[8] Xie X, Zhang X, Liu H, et al.(2017) Characteristic Analysis of Subsynchronous Resonance in Practical Wind Farms Connected to Series-Compensated Transmissions.IEEE Transactions on Energy Conversion, 32(3):1117-1126

[9] Adams J, Carter C, Huang S H (2012) ERCOT experience with Sub-synchronous Control Interaction and proposed remediation.Proceedings of the IEEE PES Transmission and Distribution Conference and Exposition, Orlando, FL, USA, 2012

[10] Li C (2018) Unstable Operation of Photovoltaic Inverter From Field Experiences.IEEE Transactions on Power Delivery,33(2):1013-1015

[11] Hatziargyriou N D, Milanovic J V, Rahmann C, et al.(2020)Stability Definitions and Characterization of Dynamic Behavior in Systems with High Penetration of Power Electronic Interfaced Technologies

[12] Wang Y, Wang X, Blaabjerg F, et al.(2017) Harmonic Instability Assessment Using State-Space Modeling and Participation Analysis in Inverter-Fed Power Systems.IEEE Transactions on Industrial Electronics, 64(1):806-816

[13] Leitner S, Yazdanian M, Mehrizi-Sani A, et al.(2018) Small-Signal Stability Analysis of an Inverter-Based Microgrid With Internal Model-Based Controllers.IEEE Transactions on Smart Grid, 9(5):5393-5402

[14] Pogaku N, Prodanovic M, Green T C (2007) Modeling,Analysis and Testing of Autonomous Operation of an Inverter-Based Microgrid.IEEE Transactions on Power Electronics,22(2):613-625

[15] Golestan S, Ebrahimzadeh E, Wen B, et al.(2021) dq-Frame Impedance Modeling of Three-Phase Grid-Tied Voltage Source Converters Equipped With Advanced PLLs.IEEE Transactions on Power Electronics, 36(3):3524-3539

[16] Rygg A, Molinas M, Zhang C, et al.(2016) A Modified Sequence-Domain Impedance Definition and Its Equivalence to the dq-Domain Impedance Definition for the Stability Analysis of AC Power Electronic Systems.IEEE Journal of Emerging &Selected Topics in Power Electronics, 4(4):1383-1396

[17] Shah S, Parsa L (2017) Impedance Modeling of Three-Phase Voltage Source Converters in DQ, Sequence, and Phasor Domains.IEEE Transactions on Energy Conversion, 32(3):1139-1150

[18] Bakhshizadeh M K, Wang X, Blaabjerg F, et al.(2016)Couplings in Phase Domain Impedance Modelling of Grid-Connected Converters.IEEE Transactions on Power Electronics,31(10):6792-6796

[19] Wang X, Blaabjerg F (2019) Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis.IEEE Transactions on Smart Grid, 10(3):2858-2870

[20] Yang D, Sun Y (2022) SISO Impedance-Based Stability Analysis for System-Level Small-Signal Stability Assessment of Large-Scale Power Electronics-Dominated Power Systems.IEEE Transactions on Sustainable Energy, 13(1):537-550

[21] Zhang C, Cai X, Rygg A, et al.(2018) Sequence Domain SISO Equivalent Models of a Grid-Tied Voltage Source Converter System for Small-Signal Stability Analysis.IEEE Transactions on Energy Conversion, 33(2):741-749

[22] Chou S-F, Wang X, Blaabjerg F (2020) Two-Port Network Modeling and Stability Analysis of Grid-Connected Current-Controlled VSCs.IEEE Transactions on Power Electronics,35(4):3519-3529

[23] Jian S (2009) Small-Signal Methods for AC Distributed Power Systems-A Review.IEEE Transactions on Power Electronics,24(11):2545-2554

[24] Wang X, Taul M G, Wu H, et al.(2020) Grid-Synchronization Stability of Converter-Based Resources An Overview

[25] Wu W, Zhou L, Chen Y, et al.(2019) Sequence-Impedance-Based Stability Comparison Between VSGs and Traditional Grid-Connected Inverters.IEEE Transactions on Power Electronics,34(1):46-52

[26] Pattabiraman D, Lasseter R H, Jahns T M Comparison of Grid-Following and Grid-Forming Control for a High Inverter Penetration Power System.Proceedings of the 2018 IEEE Power& Energy Society General Meeting (PESGM), Portland, OR,USA, 2018

[27] De Brabandere K, Bolsens B, Van den Keybus J, et al.(2007)A Voltage and Frequency Droop Control Method for Parallel Inverters.IEEE Transactions on Power Electronics, 22(4): 1107-1115

[28] Denis G, Prevost T, Panciatici P, et al.(2016) Improving robustness against grid stiffness, with internal control of an AC voltage-controlled VSC.Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA,USA, 2016

[29] Gaba G, Lefebver S, Mukhedkar D Comparative analysis and study of the dynamic stability of AC/DC systems.IEEE Transactions on Power Systems, 3(3):978-985

[30] Harnefors L Modeling of Three-Phase Dynamic Systems Using Complex Transfer Functions and Transfer Matrices.IEEE Transactions on Industrial Electronics, 54(4):2239-2248

[31] Wang X, Harnefors L, Blaabjerg F Unified Impedance Model of Grid-Connected Voltage-Source Converters.IEEE Transactions on Power Electronics, 33(2):1775-1787

[32] Athay T, Podmore R, Virmani S (1979) A Practical Method for the Direct Analysis of Transient Stability.IEEE Transactions on Power Apparatus and Systems, PAS-98(2):573-584

[33] Pai M (1989) Energy Function Analysis for Power System Stability.1st edn.Springer, Netherlands

[34] Ottersten R (2003) On control of back-to-back converters and sensorless induction machine drives.Chalmers University of Technology

[35] Chung S K (2000) A phase tracking system for three phase utility interface inverters.IEEE Transactions on Power Electronics,15(3):431-438

[36] Liu J, Miura Y, Ise T Comparison of Dynamic Characteristics Between Virtual Synchronous Generator and Droop Control in Inverter-Based Distributed Generators.IEEE Transactions on Power Electronics, 31(5):3600-3611

Received: 10 December 2022/ Accepted: 15 February 2023/ Published:25 June 2023

Yaran Li

yaran.li@unswalumni.com

Long Fu

long.fu@unswalumni.com

Qiang Li

35830342@qq.com

Wei Wang

wangwei@sgepri.sgcc.com.cn

Yubin Jia

yubinjia@seu.edu.cn

Zhao Yang Dong

zydong@ieee.org

2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co., Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/ ).

Biographies

Yaran Li received the Ph.D.degree in electrical engineering from the University of New South Wales, Sydney, Australia, in 2021, the B.E.degree in electrical engineering from Southeast University, Nanjing, China, in 2017.She also held industrial positions with Transgrid, Australia as a network planning engineer from 2018 to 2021.Since 2022, she has been working with State Grid Jiangsu Electric Power Research Institute, where she is currently a post-doctoral research fellow.Her research interests include microgrid control, renewable energy systems, and power system stability analysis.

Long Fu received the B.E.(Hon.) and Ph.D.degrees both in electrical engineering from The University of Sydney, Sydney, Australia, in 2016 and The University of New South Wales,Sydney, Australia, in 2021, respectively.He is currently a post-doctoral research fellow at NARI Group Corporation (State Grid Electric Power Research Institute), Nanjing, China.His research interests include microgrid planning and operation,distribution network reliability and resilience, optimization theory and its application in power systems.

Qiang Li received the B.Eng., M.Eng.and Ph.D.degrees in power systems and automation from Hohai University, Nanjing, China, in 2003,2006 and 2011, respectively.He is currently a Professorate Senior Engineer with the State Grid Jiangsu Electric Power Co., Ltd.Research Institute.His research interests include flexible transmission of the offshore wind power.

Wei Wang received Ph.D.degree in electrical engineering from The Harbin Institute of Technology.He is currently the Vice President of NARI Research Institute and Head of the State Key Laboratory of Smart Grid Protection and Operation Control in State Grid Corporation of China, and has presided over more than 20 major scientific and technological projects of national, provincial and state grid companies.His research interests include power electronic converters, virtual synchronous machines, grid-connected operation and control technology of renewable energy generation.

Yubin Jia received the B.S.and M.S.degree in automation, North China Electric Power University, Beijing, China, in 2012 and 2015, received the Ph.D.degree in School of Automation, Southeast University, Nanjing,China, in 2020.He is currently a Postdoctoral fellow at Southeast University.His research interests include wind model predictive control,power system, machine learning and renewable energy system.

Z h a o Y a n g D o n g i s w i t h N a n y a n g Technological University, Singapore.His previous roles include SHARP professor and Director of UNSW Digital Grid Futures Institute at the University of New South Wales,Director of ARC Research Hub for Integrated Energy Storage Solutions, Ausgrid Chair Professor and Director of the Ausgrid Centre for Intelligent Electricity Networks providing R&D support for the Smart Grid, Smart City national demonstration project of Australia.His research interests include power system planning and stability,smart grid and smart cities, renewable energy systems, and electricity market.

(Editor Tongming Liu)