0 Introduction
The demand response strategy of flexible load mainly includes electricity price and incentive guiding strategies[1, 2].A reasonable electricity price strategy can enable customers to actively respond to the power price signal,which can significantly improve the efficiency of electricity consumption, reliability, and economy of power system[3].Among the price guidance mechanisms, the time-ofuse (TOU) strategy has broadened applications in electrical power system [4-7].A reasonable TOU can effectively guide customer to shave peak load [8], effectively improve load smoothness [9], and improve the reliability of power system [10].
The premise of obtaining the optimal TOU of peak, flat and valley (PFV) is based on a period partitioning of load curve, and many relevant period partitioning algorithms have been studied [11, 12].Reference [11] proposed an equal step iterative technique for period partitioning, which can avoid the uncertainty of the traditional algorithms.Reference [12] developed a moving boundary method(MBM), which can effectively improve the partitioning efficiency and reduce the algorithm complexity.However,the above studies consider the distance between load points as the evaluation standard, which cannot fully reflect the period partitioning.So, the inter-class and intra-class distances of periods should be fully considered, that is,the Dunn Validity Index (DVI) [13] is incorporated as an objective function in this study, which can fully reflect the results of period partitioning, and the added constraint factor can effectively improve the partitioning efficiency.
Currently, the peak load with a seasonal characteristic is increasing annually [14].For example, the increase of air conditioning load in summer leads to the further increase of peak load.Under the TOU policy, the optimal effect cannot be achieved only through the independent response of customers.Considering the direct load control strategy to manage the high consumption load can also effectively reduce peak load and the peak-valley difference (PVD)of load curve.Reference [15] studies the air conditioning load aggregation under different TOU prices.Reference[16] mainly developed the equation model and sliding mode controller for real-time load management of constant temperature air conditioning, which controls the aggregate air conditioning load by adjusting the setting value of air conditioning.The direct load control on the curtailable flexible load can reduce the peak load and PVD of load curve; however, if TOU is further modified on this basis,the interaction between the two can achieve a better effect.
This study proposes an optimal flexible load guidance mechanism based on the direct load control and TOU price strategy.First, a period partitioning model with constraint factor is proposed for improving the efficiency, and the DVI is adopted as the objective function, which can comprehensively and effectively reflect the results of period partitioning.Second, the control strategies of curtailable and transferable flexible loads based on TOU are established.For the curtailable flexible load, the equivalent thermal parameter model is used to model the air conditioning,where the air conditioning load is directly controlled.For the transferable flexible load, an optimization model is proposed.Finally, the particle swarm optimization (PSO)algorithm is used to solve the problem.
The main contributions of this study are as follows:
(1) This study proposes a period partitioning method with constraint factor, and it adopts DVI as the objective function, which can achieve high accuracy and effectively improve the period partitioning efficiency.
(2) This study adopts the equivalent thermal parameter model to establish the curtailable flexible load model.On this basis, the peak load and PVD of the curtailable flexible load curve (FLC) can be effectively reduced through further modifying of TOU.
(3) This study establishes an optimization model of TOU with transferable flexible load and solves it by PSO algorithm.At the same time, the peak load shaving and valley load filling effect with different proportions of transferable flexible load is discussed.Appropriately increasing the proportion of transferable flexible load benefits further peak shaving and valley filling.
The rest of the paper is organized as follows: Section 1 introduces the PFV period partitioning optimization model with constraint factors.Section 2 investigates the flexible load modelling based on TOU, including the curtailable flexible load and the transferable flexible load.Section 3 proposes the solution method of flexible load control strategy and peak-valley electricity price model based on the PSO algorithm.Section 4 concludes the paper with an analysis of the case study.
1 PFV period partitioning model with constraint factors
The period partitioning on typical day is the premise to obtain the optimal TOU prices.Considering the shortcomings of the existing period partitioning methods,a period partitioning algorithm with constraint factors is proposed, and DVI is adopted as the objective function to establish the model.
1.1 Period partitioning model


where K represents the number of clusters; m and n denote classes m and n, respectively; xi and xj represent elements within a class.According to the definition of DVI, the ratio of the shortest distance (inter-class) between any two cluster elements to the maximum distance (intra-class) between elements in any cluster determines the DVI value.The increase in DVI value means the decrease in intra-class distance, increase in inter-class distance, and improvement in clustering effect.
1.2 The period partitioning algorithm based on an improved MBM
This study proposes an improved MBM to optimize the period partitioning, and constraint factors are added to constrain the PFV periods.The proposed improved MBM is described, and the corresponding flow chart is shown in Fig.1.

Step8: Output optimal period partitioning and the corresponding values of MV1 and MV2.
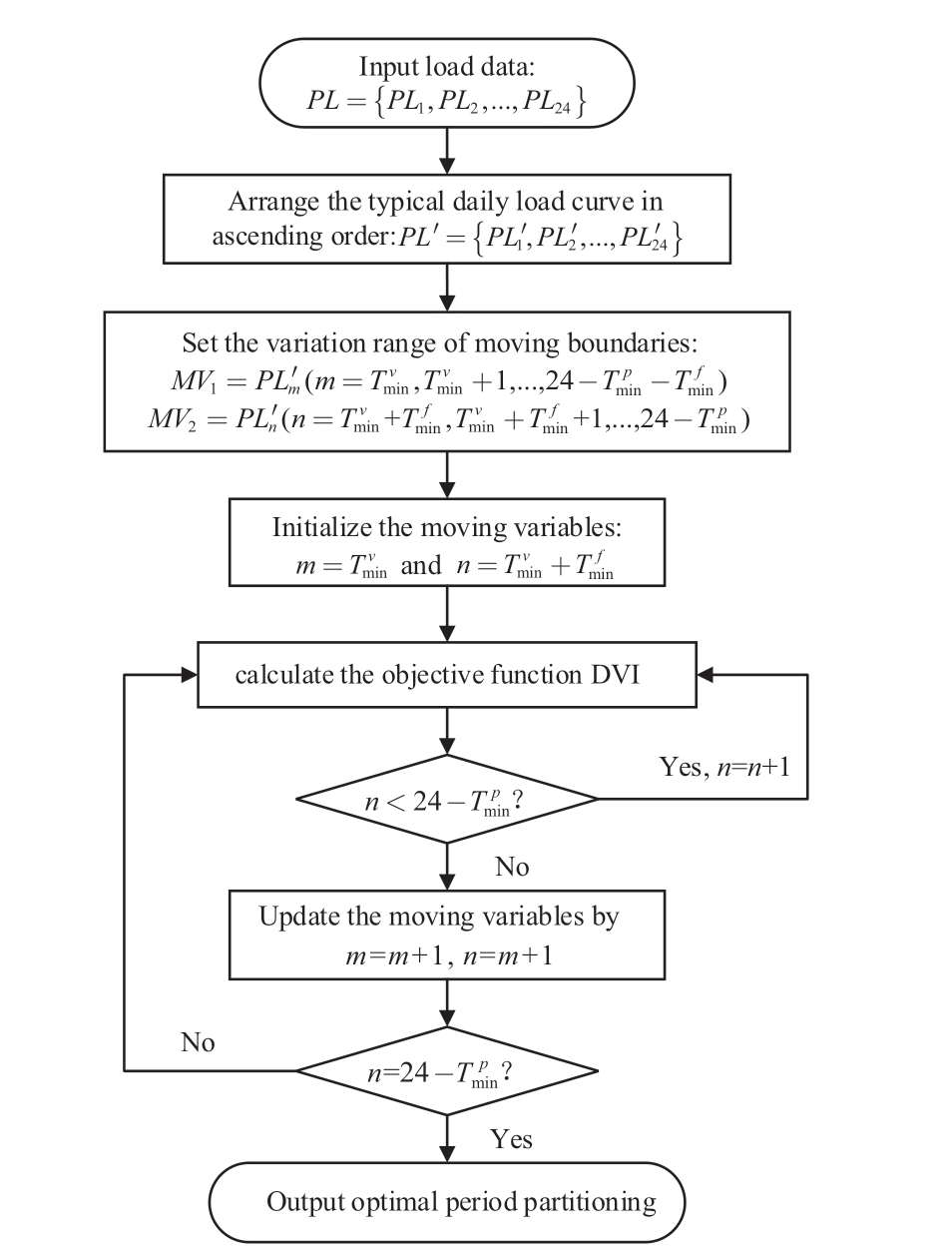
Fig.1 Flow chart of PFV period partitioning

2 Flexible load modeling based on TOU
The flexible load mainly refers to the curtailable [17]and transferable flexible loads [18].According to the characteristics of both flexible loads, models of them based on TOU, respectively, are established.
The curtailable load refers to the load that can directly be curtailed or interrupted in a short time and this action does not impact customers significantly.The air conditioning is one of curtailable loads.The operation power of air conditioning with the change of temperature can be expressed by heat pump load equivalent thermal parameters model [19]:

The actual working characteristics of the air conditioning involves the air conditioning refrigeration starts when the indoor temperature reaches the upper limit and turns off when the indoor temperature reaches the lower limit,therefore, the indoor temperature reaches the dynamic cycle under the action of the air conditioning.Setting the operation cycle of the air conditioner as ξ, and the opening and closing times as ξonand ξoff, respectively, and substituting the indoor temperature limit values Tin,max and Tin,min into the equivalent thermal parameter model:
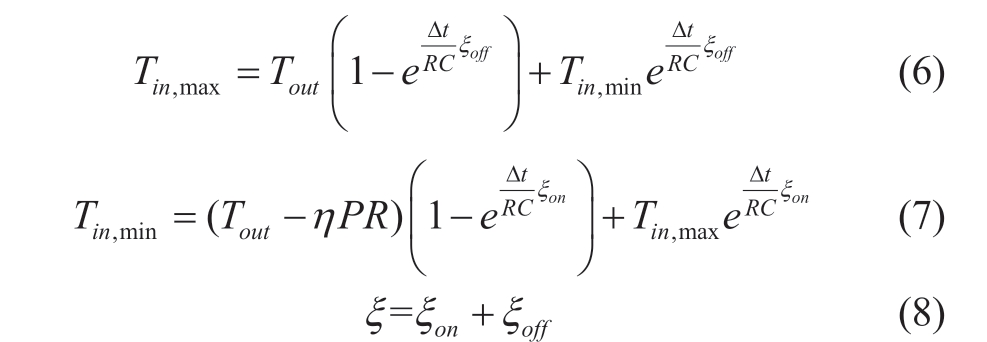
where η is the air conditioning energy efficiency ratio; P is the rated power of air conditioner.
According to the Equations (6)-(8), when the outdoor temperature is constant, the on and off times of the air conditioner are:
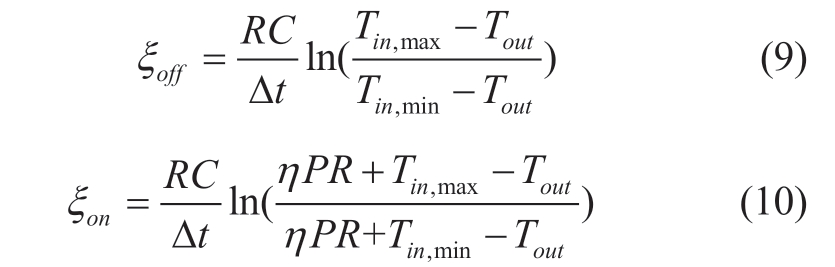
By linearizing the equivalent thermal parameter model of air conditioning, it can be obtained that the curtailment of conditioning load Pair ,c urtailment in Δt is:
where Pto tal( Δ t) is the total power of air conditioning in Δt.
The direct load control is adopted to curtail the air conditioning load, and the air conditioning load after curtailing is adjusted by the electricity price demand response strategy (i.e., TOU).Under the TOU strategy [20],the air conditioning load is further modified, and it can be expressed by :

where Pp 0,total , Pf 0,total , and Pv 0,total are the curtailable load powers in PFV periods before the implementation of TOU.Pp ,total , Pf ,total , and Pv ,total are the curtailable load powers in PFV periods after the implementation of TOU; p0 represents the initial electricity price before TOU; pp, pf and pv represent the electricity prices in PFV periods.E is the electricity price elasticity matrix [11], as shown below:

The transferable load refers to the flexible load with constant total operation power but variable operation time,such as electric vehicles or washing machines.By utilizing the characteristic of transferable flexible load that can be transferred from one to another period, the purpose of peak shaving and smoothening load curve can be achieved.
In this study, the electricity price elasticity matrix [21]-[23] describes the change of transferable flexible load:

where PTL ,peak , PTL ,flat , and PTL ,valley represent the powers of transferable flexible load before the implementation of TOU; PT′L ,peak , PT′L ,flat , and PT′L ,valley represent the power of transferable flexible load after the implementation of TOU.
The hourly transferable load after considering TOU can be expressed by:
where m = p , f ,v represents PFV periods.
3 Flexible load control strategy and optimization of TOU strategy
The difference of PFV electricity prices directly affect the transfer of load between different periods.This section details the adoption of the PSO algorithm to obtain the optimal electricity prices and provides the specific constraints and objective function.
3.1 The constraint conditions
(1) The electricity consumption of customer: the total electricity consumption of transferable load remains unchanged before and after TOU:
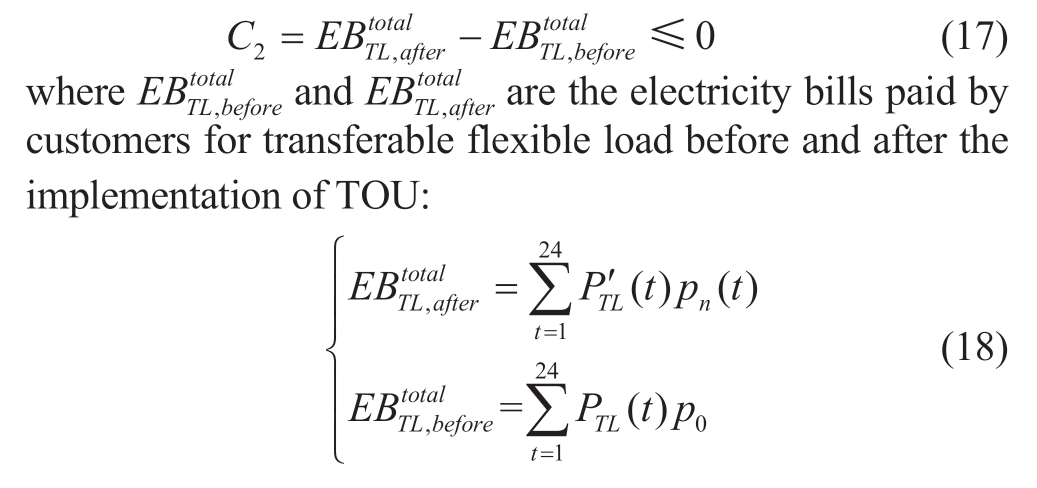
(2) The benefit of customer: for the transferable flexible load, the electricity charges of customers do not increase before and after TOU.The constraint can be expressed as:
(3) The power supplier’s benefit: TOU can reduce the investment cost of power supplier, and the total benefit after carrying out TOU should not be less than that before TOU:
where φ is a coefficient which can be found in reference [24].
(4) The temperature control load constraint: for temperature control load such as air conditioning, the indoor temperature has upper and lower limits:
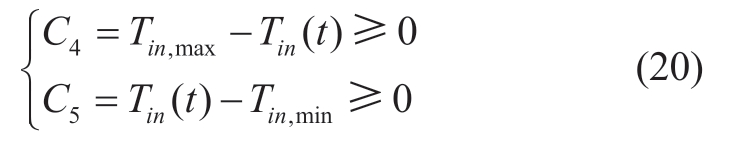
where Tin,max and Tin,min represent the upper and lower limits of indoor temperature, respectively.
(5) The curtailment amount constraint of the curtailable load: when the curtailable load can be curtailed, the curtailment amount of the curtailable load cannot exceed the total amount of the curtailable load:

(6) The electricity price constraint: the reasonable price should be limited for preventing peak and valley load inversion:

(7) The marginal price constraint: the electricity price in valley period shall not be lower than the marginal electricity price:
where pc is the marginal price.
3.2 Objective function
Designing a reasonable price demand response strategy for flexible load can effectively reduce PVD of load curve and smoothen the load curve.This study considers the objective functions for minimizing the peak load and PVD of the load curve.


In this study, a single objective problem is applied by transforming a multi-objective optimization problem, and it is:
where α and β are the weight coefficients of the objective function.H is the penalty function term [11].
3.3 Optimization algorithm
The PSO algorithm[25] can continuously iterate and calculate through particles, and the individual extreme values of particles and the global optimal solution of the entire particle swarm is updated in each iteration.The iteration does not stop until the optimal solution satisfying all constraints is found.
The flow chart of TOU optimization is shown in Fig.2.The solving steps of electricity price based on PSO optimization algorithm are as follows:

Fig.2 Flow chart of TOU optimization based on PSO algorithm.
Step 1: Initialize particle swarm parameters.Set the total number of particles to M, and set k=0.Randomly initialize the position and velocity of each particle:
where rmn is a random number between 0 and 1.

Step 7: Terminate the iteration when the maximum number of iterations is reached; Otherwise, k=k+1, go to step 3;
Step 8: Output the optimal PFV electricity prices.
4 Case study
In this study, the load curves in summer and winter are used to analyze the proposed method.The used load power in per-unit is listed in Table 1, and the load curves are drawn in Fig.3, and it includes the total load, curtailable load,transferable load and basis load for winter and summer.It can be seen from Fig.3 that there are two peaks at 11:00 and 20:00 for summer and at 8:00 and 19:00 for winter.The experiment is implemented on a PC with Windows 10 operating system, Intel Core i5-9400F 2.90GHz CPU and 8 GB RAM.
Table 1 Load data
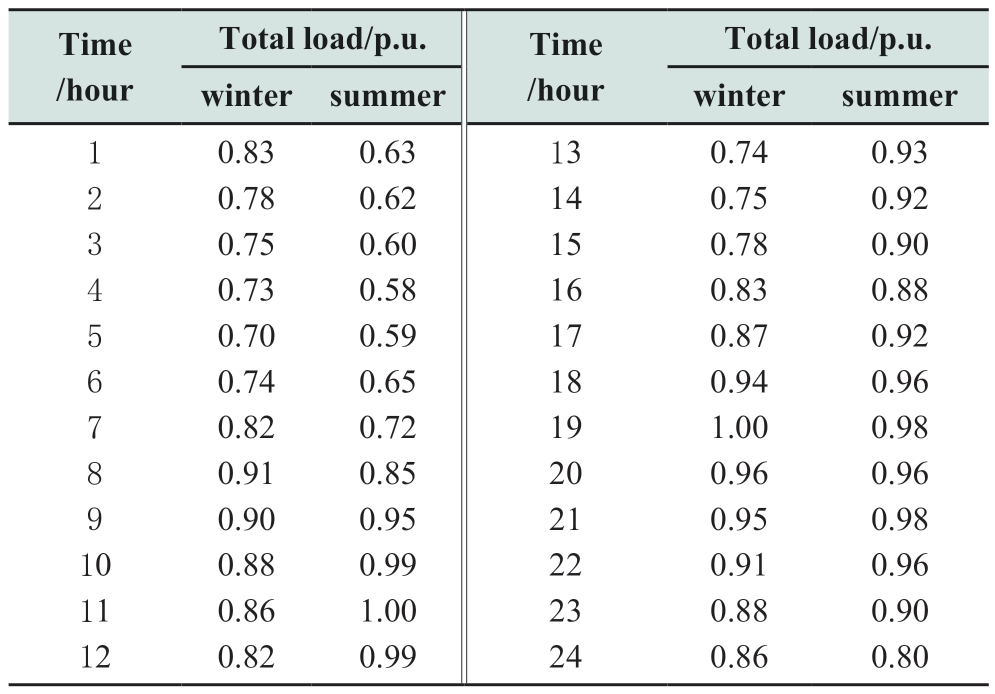

Fig.3 The typical daily customer load curves of a place in summer and winter


Fig.4 Peak load, valley load and PVD of the original load curves in summer and winter
4.1 Analysis for the curtailable load
Fig.5 shows the outdoor temperature and setting temperatures of the air conditioner in summer and winter.The CLCs in summer and winter before and after air conditioning control at different temperatures are shown in Fig.6 (a) and Fig.6 (b), respectively.It can be seen from Fig.6 (a) that when the setting temperature is higher than or equal to the outdoor temperature, the air conditioning load control will not be implemented, and the air conditioning load curve will not change.When the outdoor temperature is higher than the setting temperature, the air conditioning load is significantly reduced because of the direct control of the air conditioning load.Table 2 shows that the curtailable load at T2 is greater than that at T1, because the difference between T2 and the outdoor temperature is greater, so the power of the air conditioning load is greater than that at T1.As seen from Fig.6 (b), the PVD significantly reduces after air conditioning control.
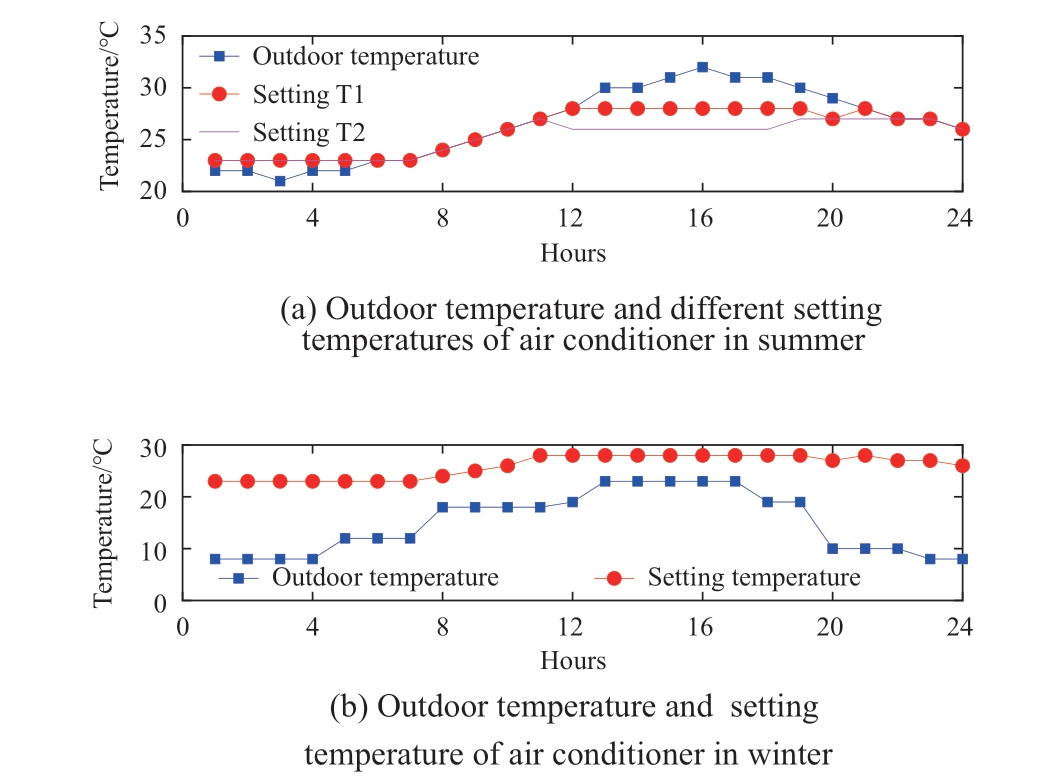
Fig.5 Outdoor temperatures and setting temperatures of air conditioner in summer and winter
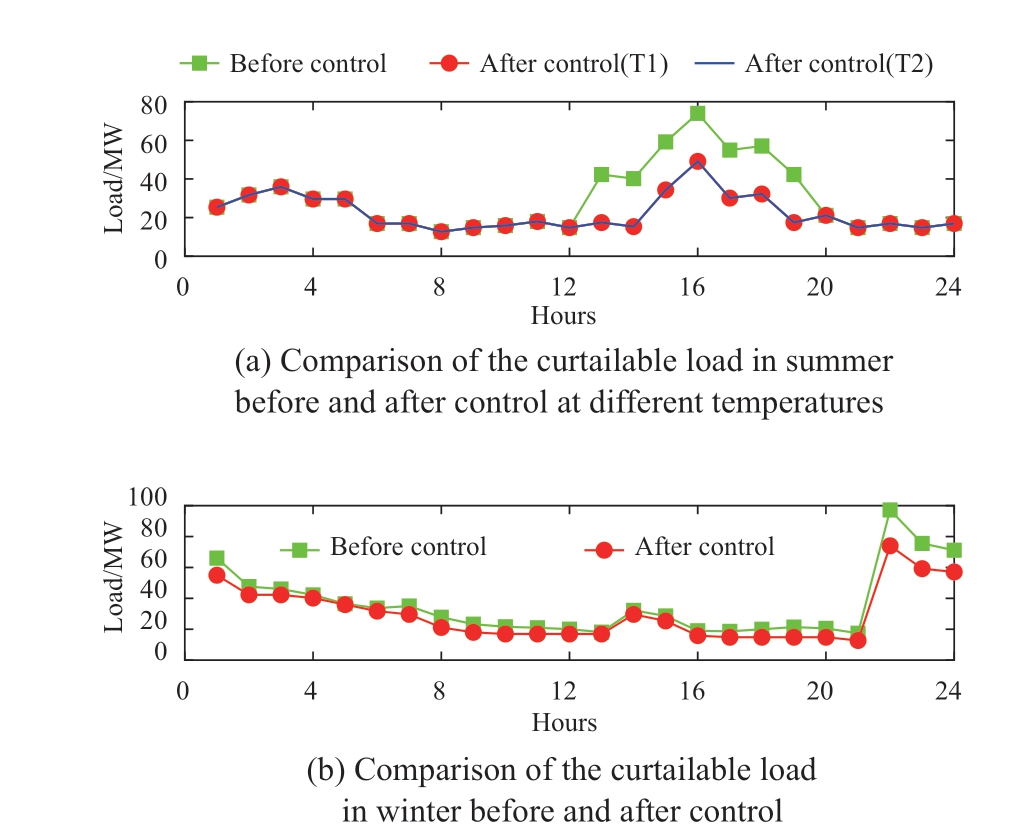
Fig.6 Comparison of the curtailable load before and after control
Fig.7 (a) shows the peak load, PVD, and valley load in summer at different setting temperatures before and after air conditioning load control.Before and after the control of curtailable load (i.e., air conditioning load), the peak load of curtailable load drops down to 49.10 MW from 74 MW(33.65%), and the PVD drops down to 36.42 MW from 61.31 MW (40.60%) at T1.The peak load of curtailable load drops down to 49.13 MW from 74 MW (33.61%),and the PVD drops down to 36.45 MW from 61.31 MW(40.55%) at T2.Fig.7 (b) shows the peak load, PVD, and valley load in winter before and after air conditioning load control.Before and after the control of curtailable load, the peak load of curtailable load decreased from 97.22 MW to 74 MW, a decrease of 23.88%, and the PVD decreased from 79.84 MW to 59.2 MW, a decrease by 25.85%.As the peak load of the curtailable load is mainly controlled, the valley load of the curtailable load does not change significantly.The load control of curtailable load can effectively reduce the peak load and PVD of curtailable load.

Fig.7 Comparison before and after control for peak load,PVD, and valley load of curtailable load
Table 2 Comparison of summer curtailable load after control at different temperatures

4.2 Analysis for period partitioning
When the curtailable load is curtailed, the period partitioning result of the typical FLC in summer based on improved MBM without and with considering period hours limitations are shown in Figs.8 (a) and 8 (b), respectively.As can be seen from Figs.8 (a) and 8 (b), if the period hour limitation is ignored, some period (e.g., peak) may have fewer hours, so the effect of peak shaving and valley filling can worsen.
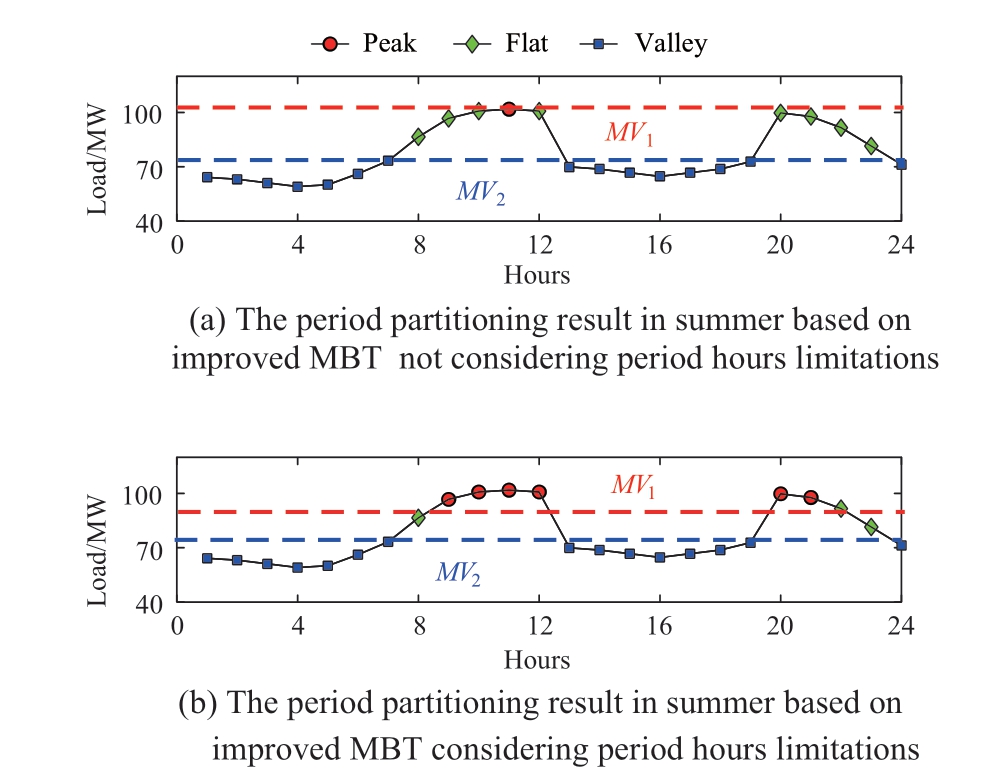
Fig.8 Comparison of the period partitioning results of the typical FLC in summer
The period partitioning result of the typical FLC in winter based on improved MBM considering period hours limitations is shown in Fig.9.In this study, the improved MBM is used to determine the PFV periods, and the DVI is adopted as the objective function.Different period partitioning methods are used to verify the efficiency of the proposed method.Comparisons of load curves in summer and winter under different period partitioning methods are shown in Table 3 and Table 4, respectively.As can be seen

Fig.9 The period partitioning result of the typical FLC in winter
from Table 3 and Table 4, DVI values of the three methods including the MBM, the “MBM + DVI”and the “improved MBM + DVI”are equal, but the method proposed in this study takes the least amount of time.
Table 3 Comparison of summer load curve under different period partitioning methods

Table 4 Comparison of winter load curve under different period partitioning methods

4.3 Transferable load analysis
The optimization results are shown in Table 5 and Table 6,respectively.Table 5 and 6 show that the initial electricity price is higher than that in the low period and lower than that in the peak period, while the electricity price in flat period changes slightly.
Table 5 PFV electricity prices of transferable FLC in summer at T1 based on PSO algorithm

Table 6 PFV electricity prices of transferable FLC in winter based on PSO algorithm

The TRLCs in summer and winter before and after TOU are shown in Fig.10.In Fig.10 (a), the transferable flexible load decreases in the peak period, increases in the valley period, and remains slightly changed in the flat period.In Fig.10 (b), as the curtailable load in winter has decreased whole day after the air conditioning control and the overall TRLC has decreased after being regarded as transferable load, the TOU also plays a role in reducing the PVD.The peak load, PVD, and valley load of transferable load in summer at different setting temperatures before and after TOU are shown in Fig.11 (a).The peak load, PVD, and valley load of transferable load in winter before and after TOU are shown in Fig.11 (b).TOU pricing strategy can effectively reduce the PVD and peak load of the TLC.
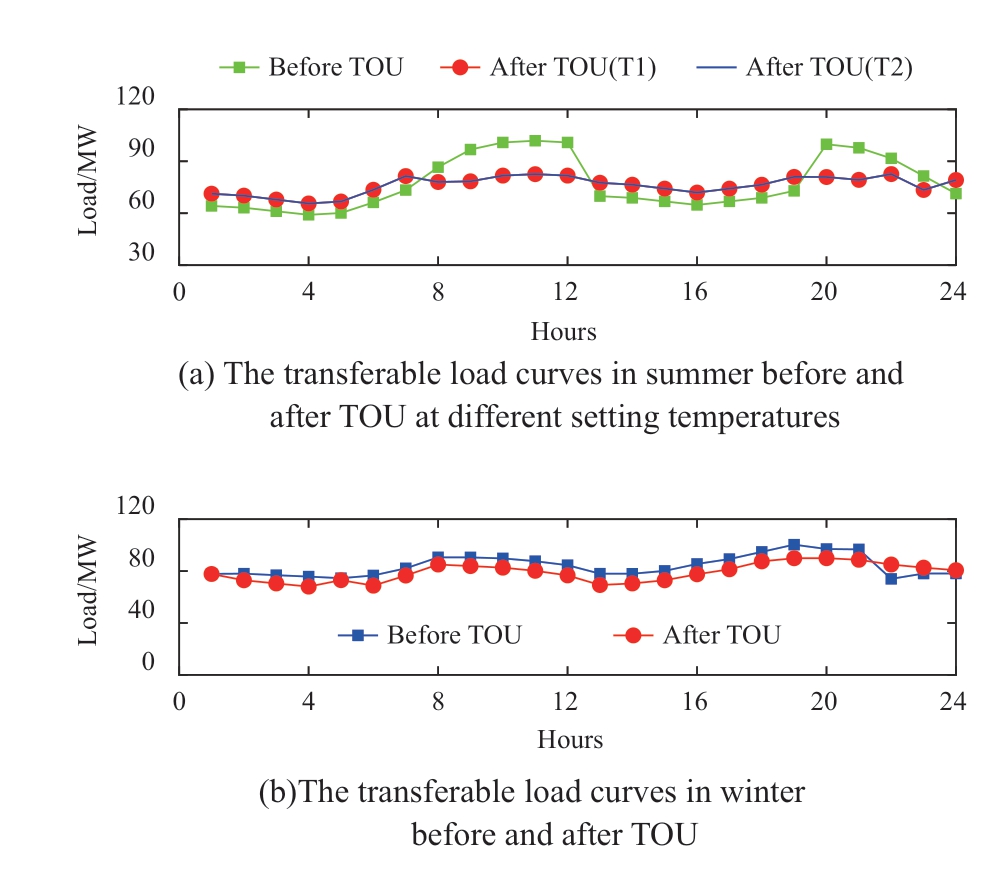
Fig 10 The TRLCs before and after TOU

Fig.11 Comparison of peak load, PVD, and valley load of transferable load before and after TOU
Fig.12 (a) shows the total FLC and the load curve in summer at different temperatures after TOU and load control.Fig.12 (b) shows the total FLC and the load curve in winter after TOU and load control.The load control strategy of curtailable load and TOU can effectively reduce the peak load.
To better reflect the impact of transferable flexible load,the proportion of transferable flexible load in summer is increased by 10% and reduced by 10%, respectively.Under the different proportions of transferable flexible load, the load transfer amount is shown in Fig.13.Due to the effect of TOU electricity price, the transferable flexible load in peak period is less than 0, which means that the load in peak period is reduced, while in flat period it is approximately equal to 0, indicating that the load in flat period is basically unchanged, and in valley period it is greater than 0,indicating that the load in valley period increases.That is,the load is transferred from peak period to valley period to achieve the purpose of peak shaving and valley filling.

Fig.12 Total FLC and load curve after TOU and load contro
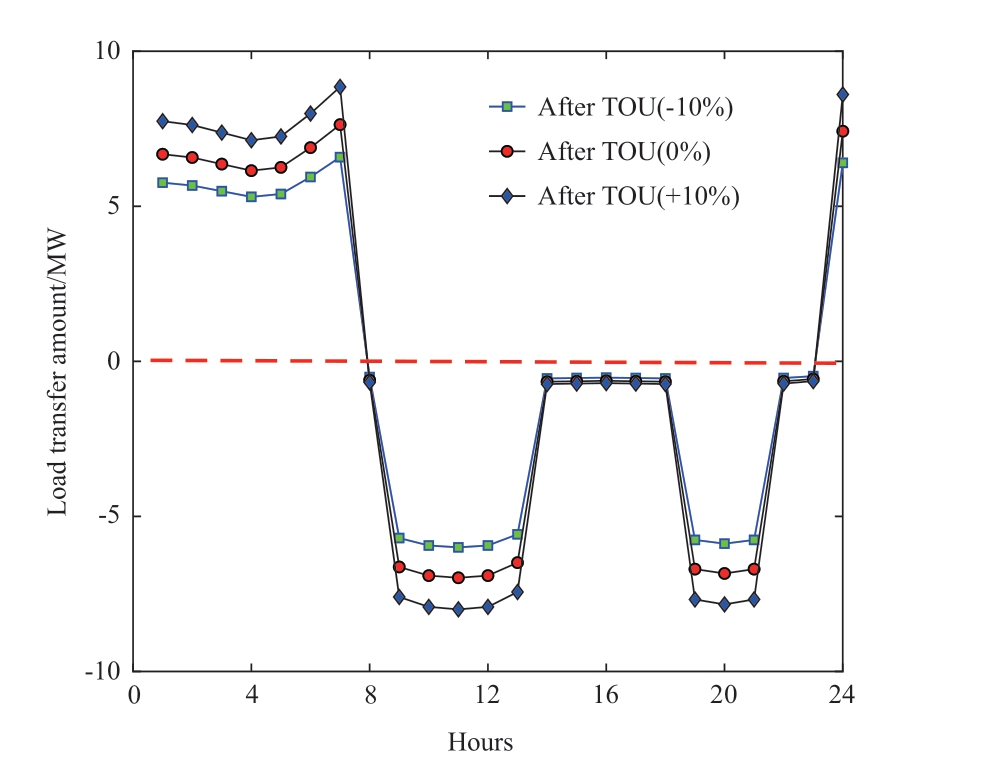
Fig.13 Load transfer amount under different proportions of transferable flexible load
Fig.14 shows the comparison of peak load, PVD,valley load of load curves in summer at temperature1 with different proportions of transferable load.With the increasing proportion of the transferable flexible load and the PVD gradually decreases.Therefore, the effect of peak shaving and valley filling will be better when the proportion of transferable load is increased.By properly increasing the proportion of transferable flexible load, not only the PVD can be effectively reduced, but also the peak-valley filling effect can be further improved.
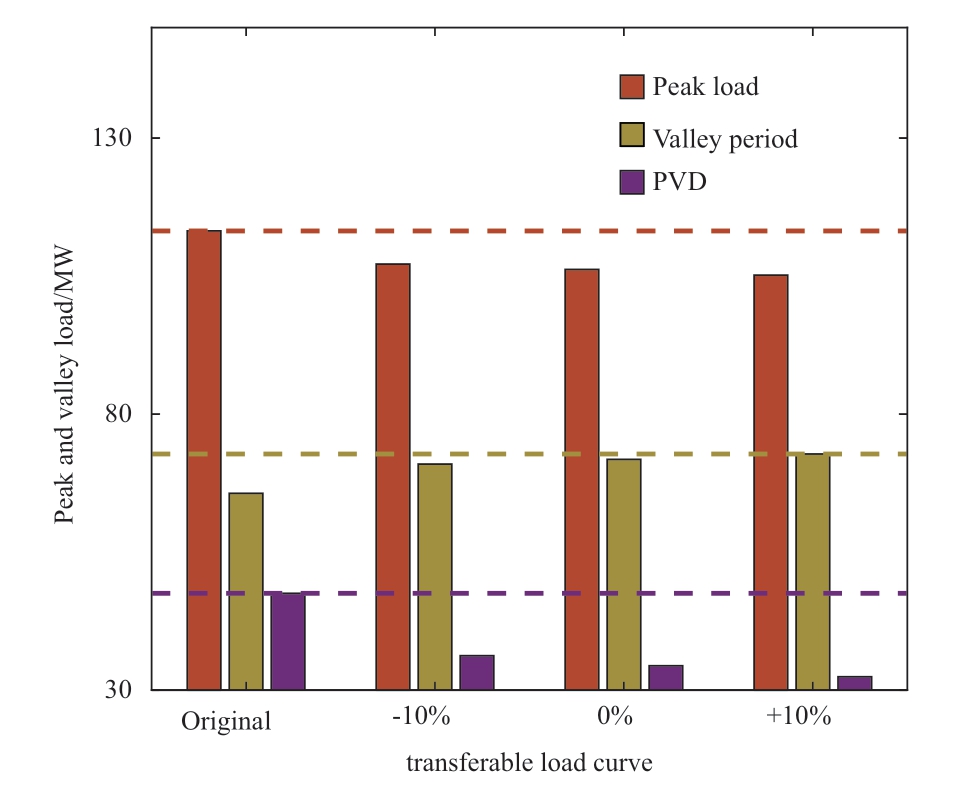
Fig.14 Comparison of peak load, PVD, and valley load of load curve in summer with different proportions of TRLC
5 Conclusion
This study proposes an optimal guidance mechanism of flexible load based on direct load control and TOU price strategy, and a period partitioning model with constraint factors is presented.First, this study proposes a period partitioning model, which can improve the partitioning accuracy, and a more reasonable DVI is adopted as the objective function.Second, the direct load control strategy is utilized for the curtailable load, and the optimal TOU model of transferable flexible load is established.The case study shows that the period partitioning model proposed in this study can effectively improve the efficiency of period partitioning while maintaining high accuracy.The TOU strategy can effectively reduce the peak load and PVD of transferable load.The load control strategy can directly control the curtailable load (e.g., air conditioning), and effectively reduce the peak load.After adopting the direct load control strategy and then adopting the TOU strategy,effect of the peak shaving and valley filling can be further improved.In addition, the TOU and curtailable load control strategy can work in combination to effectively improve the customer’s power curve.
However, in this study, the uncertainty of price elasticity for different types of flexible loads has not been deeply considered in the TOU optimization.In future study, this will be considered as a factor to incorporate into the TOU optimization, and its impact on TOU needs to be also further discussed.Moreover, the optimization algorithm used in this study has an improvement space in accuracy.Future study will consider using solvers to achieve higher accuracy.
Acknowledgements
This study was supported by open fund of state key laboratory of operation and control of renewable energy &storage systems(China electric power research institute)(No.NYB51202201709).
Declaration of Competing Interest
We declare that we have no conflicts of interest.
References
[1] Hu Y, Li Y Z, Chen L J (2019) Multi-objective optimization of time-of-use price for tertiary industry based on generalized seasonal multi-model structure.IEEE Access, 7: 89234-89244
[2] Asadinejad A, Rahimpour A, Tomsovic K, et al.(2018)Evaluation of residential customer elasticity for incentive based demand response programs.Electric Power Systems Research,158: 26-36
[3] Gunduz H, Jayaweera D (2018) Reliability assessment of a power system with cyber-physical interactive operation of photovoltaic systems.International Journal of Electrical Power & Energy Systems, 101: 371-384
[4] Zhou B, Yang R, Li C B, et al.(2018) Multiobjective model of time-of-use and stepwise power tariff for residential consumers in regulated power markets.IEEE Systems Journal, 12(3): 2676-2687
[5] Zeng B, Zhu X, Chen C, et al.(2019) Unified probabilistic energy flow analysis for electricity-gas coupled systems with integrated demand response.IET Generation, Transmission & Distribution,13(13): 2697-2710
[6] Assolami Y O, Morsi W G (2015) Impact of second-generation plug-in battery electric vehicles on the aging of distribution transformers considering TOU prices.IEEE Transactions on Sustainable Energy, 6(4): 1606-1614
[7] Chen S J, Alan Love H, Liu C C (2016) Optimal opt-in residential time-of-use contract based on principal-agent theory.IEEE Transactions on Power Systems, 31(6): 4415-4426
[8] Yang H, Li Y Z, Chen L J (2019) Multi-objective optimization of time-of-use price for tertiary industry based on generalized seasonal multi-model structure.IEEE Access, 7: 89234-89244
[9] Yang H J, Gao Y, Ma Y H, et al.(2022) Optimal modification of peak-valley period under multiple time-of-use schemes based on dynamic load point method considering reliability.IEEE Transactions on Power Systems, 37(5): 3889-3901
[10] Ming H, Xia B N, Lee K Y, et al.(2020) Prediction and assessment of demand response potential with coupon incentives in highly renewable power systems.Protection and Control of Modern Power Systems, 5: 1-14
[11] Yang H J, Wang L, Zhang Y Y, et al.(2019) Reliability evaluation of power system considering time of use electricity pricing.IEEE Transactions on Power Systems, 34(3): 1991-2002
[12] Yang H J, Wang L, Ma Y H (2019) Optimal time of use electricity pricing model and its application to electrical distribution system.IEEE Access, 7: 123558-123568
[13] Rathore P, Ghafoori Z, Bezdek J C, et al.(2019) Approximating Dunn’s cluster validity indices for partitions of big data.IEEE Transactions on Cybernetics, 49(5): 1629-1641
[14] Liu J, Wang H Y, Du Y P, et al.(2023) Multi-objective optimal peak load shaving strategy using coordinated scheduling of EVs and BESS with adoption of MORBHPSO.Journal of Energy Storage, 64: 107121
[15] Lu N, Chassin D P (2004) A state-queueing model of thermostatically controlled appliances.IEEE Transactions on Power Systems, 19(3): 1666-1673
[16] Bashash S, Fathy H K (2013) Modeling and control of aggregate air conditioning loads for robust renewable power management.IEEE Transactions on Control Systems Technology, 21(4): 1318-1327
[17] Aalami H A, Moghaddam M P, Yousefi G R (2010) Demand response modelling considering interruptible/curtailable loads and capacity market programs.Applied Energy, 87(1): 243-250
[18] Fang L, Niu Y G, Zu Q W, et al.(2018) Energy management strategy based on energy storage equalization technology and transferable load.International Transactions on Electrical Energy Systems, 28(9): 2599
[19] Lu N, Zhang Y (2013) Design considerations of a centralized load controller using thermostatically controlled appliances for continuous regulation reserves.IEEE Transactions on Smart Grid, 4(2): 914-921
[20] Sun J J, Zhang S Z, Zeng M D, et al.(2018) Multi-objective optimal control for flexible load in active distribution network considering time-of-use tariff.Transactions of China Electrotechnical Society, 33(2): 401-412
[21] Zhao C Y, Wang J H, Watson J P, et al.(2013) Multi-stage robust unit commitment considering wind and demand response uncertainties.IEEE Transactions on Power Systems, 28(3): 2708-2717
[22] Cao Y W, Wang L Y, Jiang S G, et al.(2020) Optimal operation of cold-heat-electricity multi-energy collaborative system based on price demand response.Global Energy Interconnection, 3(5):430-441
[23] Ferreira R D S, Barroso L A, Lino P R, et al.(2013) Time-of-use tariff design under uncertainty in price-elasticities of electricity demand: a stochastic optimization approach.IEEE Transactions on Smart Grid, 4(4): 2285-2295
[24] Jiang H L, Liu B Q, Wang Y W, et al.(2014) Multiobjective TOU pricing optimization based on NSGA2.Journal of Applied Mathematics, 2014(2): 1-8
[25] Yang H J, Xie K G, Tai H M, et al.(2016) Wind farm layout optimization and its application to power system reliability analysis.IEEE Transactions on Power Systems, 31(3): 2135-2143
[26] Zhao G S, Zhan T L, Xi H G (2016) Time-of-use price optimizing model and its solving method.Proceedings of the 2016 International Conference on Civil, Transportation and Environment, 892-896
Received: 3 November 2022/ Accepted: 25 April 2023/ Published: 25 June 2023
Siyang Liu
liusiyang@epri.sgcc.com.cn
Yuan Gao
hfutgy@126.com
Hejun Yang
cquyhj@126.com
Xinghua Xie
xiexinghua96@163.com
Yinghao Ma
yinghao_ma@126.com
2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co., Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/ ).
Biographies

Siyang Liu received the B.S.and M.S degrees from Xi’an Jiaotong University (Xi’an,China) and CentraleSupélec (Paris, France)in 2015 and 2018.She is working in State Key Laboratory of Operation and Control of Renewable Energy & Storage Systems, China Electric Power Research Institute (CEPRI).Her research interests include renewable energy planning & dispatching and electricity market operation.

Yuan Gao received the B.S.and M.S degrees in electrical engineering from Hefei University of Technology in 2019 and 2022, Hefei, China.His research interests include power system planning and reliability and demand response.

Hejun Yang received the Ph.D.degree in electrical engineering from Chongqing University, Chongqing, China, in 2014.He is currently an associate professor in school of electrical engineering and automation, Hefei University of Technology, Hefei, China.His main research interests include power system planning and reliability and demand response.

Xinghua Xie received the B.S.degree at North China Electric Power University, Hebei, China,in 2018.He is working towards the M.S.degree at Hefei University of Technology, HeFei, China.His research interests include planning and operation of microgrid and demand response.

Yinghao Ma received the Ph.D.degree in electrical engineering from Chongqing University, Chongqing, China.He is currently an Assistant Professor in school of electrical engineering and automation, Hefei University of Technology, Hefei, China.His research interests include power system planning and reliability.
(Editor Dawei Wang)
