0 Introduction

According to the statistical data of “Renewable Capacity Statistics 2022” released by the International Renewable Energy Agency,the power generation capacity of renewable energy increased by 257 GW in 2021.Moreover,the increase in solar photovoltaic (PV) capacity is 132.7 GW,which accounts for 51.6% of the total,indicating the strong development momentum of the PV industry [1,2].However,the randomness and intermittency of PV power have adverse effects when a large-scale PV power system is connected to the grid [3,4].An effective solution to resolve this is the accurate prediction PV power.This can assist the power dispatching department to formulate a reasonable power grid operation mode [5].

The prediction technology of PV power is based on the analysis and processing of historical datasets and numerical weather prediction,establishing the mapping relationship between characteristic input and power output [6].Presently,various PV power prediction methods have been devised.Three prediction categories are classified according to the length of the forecast period: ultrashort-term prediction(0–6 h),short-term prediction (6 h–1 week),and mediumterm and long-term predictions (1 week–1 year) [7,8].Ultra-short-term prediction can provide transient power information,and medium-term and long-term predictions are beneficial for the establishment and planning of new PV power stations.In contrast,short-term forecasting focuses on power scheduling,load tracking and forecasting,and other fields.Many studies have focused on short-term forecasting because it can stabilize the quality of the power grid and has relatively low requirements for the spatial–temporal resolution of meteorological data.

The most typical models used for short-term prediction are statistical methods,including regression model [9],autoregression model [10],Markov chain [11],support vector machine (SVM) [12–14],and artificial neural network (ANN) [15-18].Sobri et al.[19] discussed the prediction performance of regression algorithm,Markov chain,and various ANNs.They concluded that the ability of ANN to solve complex nonlinear prediction problems was outstanding.With continuous developments in deep learning,convolutional neural network (CNN),recurrent neural network (RNN),and long short-term memory(LSTM) neural network have produced favorable results in PV power prediction [20].Li et al.[21] established a PV power prediction model integrating wavelet packet decomposition and LSTM neural networks.Compared with the models established by RNN and multilayer perceptron,their model had better prediction capability.The LSTM neural network for time series data has been widely used in PV power prediction because of its selective memory function [22,23].Accordingly,the LSTM neural network is selected in this study to establish the prediction model.

However,the regularity of PV power generation can be ignored when the prediction model has a single composition.An effective approach is to build a hybrid model by combining two or more algorithms considering their various characteristics [24,25].Because the power curve considerably varies under different weather conditions,numerous studies on the integration of weather type classification algorithms into hybrid prediction models have been performed [26,27].Zhang et al.[28] used K-means algorithm to classify three weather types combined with improved backpropagation neural network to build a hybrid model.Chen et al.[29] grouped the three weather types according to irradiance and cloud cover and established a prediction model combined with the radial basis function.Gao et al.[30] divided official professional weather types into ideal and non-ideal weather states and established various prediction models.Compared with the single model,these hybrid models had better prediction performance.The K-means++ algorithm resolves the selection of initial clustering centers because K-means algorithm is sensitive to this problem and widely used in classification tasks.However,the clustering effect of K-means++ is not only related to its own algorithmic structure but also closely related to the input of eigenvectors.Currently,no study has been conducted to compare the clustering results corresponding to different feature vectors [4,31].To obtain the best weather type classification results,the calculation of the statistical characteristics of data series and the formation of different feature vectors for comparison with clustering results are proposed.

Then,the similar day approach is typically added as one of the steps to establish the hybrid model.Zhao et al.[32]built the OS–Elman model and employed the data of similar and adjacent days as input.Jiang et al.[33] used the fuzzy clustering algorithm and grey relational analysis (GRA) to select similar days based on temperature,humidity (H),and irradiance.They verified that the model based on similar days yielded satisfactory prediction results.They proved that using the data of similar days as model input can improve prediction accuracy.Currently,the methods for finding similar days include the GRA,cosine method,Euclidean distance method,and improved algorithms [34,35].The performance of different methods cannot be assessed because a basis for comparison has not been established.Accordingly,this study devises an evaluation indicator to determine the best method for finding similar days.

Based on the foregoing,this study focuses on the construction of a hybrid prediction model with superior performance.The hybrid model combines the improved K-means,GRA,cosine,and LSTM neural networks to predict PV power.The implementation of the hybrid model includes the following three steps.(1) The nine statistical indices of a power series are calculated to create different eigenvectors.To determine the best weather type classification,clustering results are compared.(2) The Euclidean distance among the cluster centers and the forecast day are calculated to determine its weather type.Under the same weather type,the linear combination method of GRA and cosine model is applied to find the best similar day of the forecast day.(3) The best similar day data samples and the meteorological factors of the forecast day are inputted into the LSTM neural network to obtain the prediction results.Then,to verify the superiority of the proposed HKSL (combines K-means++,optimal similar day approach,and long short-term memory (LSTM) network.)model,its prediction results are compared with those of the Elman (individual Elman neural networks),LSTM(individual LSTM neural networks),HSE (hybrid model combining similar day approach and Elman),HSL (hybrid model combining similar day approach and LSTM),and HKSE (hybrid model combining K-means++,similar day approach,and LSTM) models.

1 Analysis of influencing factors

1.1 Characteristics analysis

The characteristics of PV power generation are affected by several factors,which can be divided into deterministic and uncertain factors.

The deterministic factors are mainly related to fixed environmental and equipment conditions,such as the location of PV power station and characteristics of PV devices.The uncertain factors are caused by changes in the external environment,such as solar radiation intensity; H;ambient temperature (AT); air pressure (AP); wind speed(WS); wind direction (WD); weather type; and season type.For a designated power station,power fluctuations are mainly affected by uncertain factors.Therefore,correlation analysis is proposed to select strong correlation factors as the model input to enhance the prediction accuracy.

1.2 Correlation analysis

According to the foregoing,the correlations between uncertainty factors and PV power are analyzed.These uncertain factors mainly include global horizontal irradiance(GHI),direct normal irradiance (DNI),diffuse horizontal irradiance (DHI),AT,H,WS,WD,and AP.Then,the correlations are described quantitatively by Pearson’s correlation coefficient (R).This coefficient is calculated as follows:

whereNisthenumberof sampling points;Fi isthe valueof themeteorologicalfactor atthe ith point;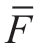isthe average value of all samples of meteorological factors; Pi is the value of PV power at the ith point; and 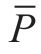is the average value of PV power of all samples.

The R value varies from −1 to 1.When the value of R is negative,the two factors are negatively correlated; when it is positive,the two factors are positively correlated [36].The value of R reflects the strength of correlation.The R values of various meteorological factors and PV power are listed in Table 1.

Table 1 R value between PV power and each meteorological factor

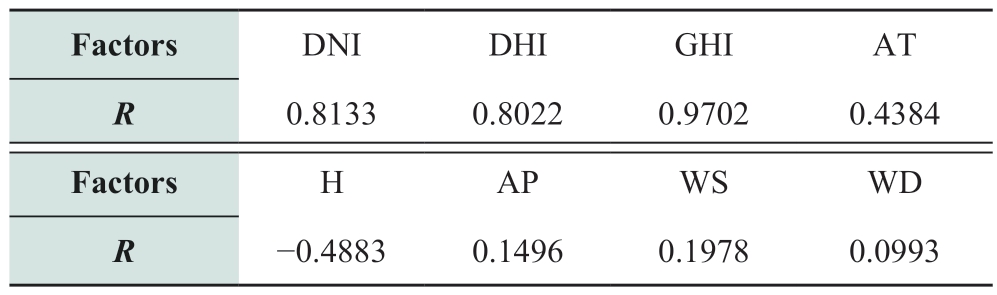
According to Table 1,GHI,DNI,and DHI have a strong positive correlation with PV power.The R value between AT and PV power is 0.4384,indicating that their correlation is moderate.The R value between H and PV power is−0.4883,indicating that a moderately negative correlation exists.The R values for WS,WD,and AP are between 0 and 0.2,indicating that the correlations between these three factors and PV power are considerably weak.Therefore,meteorological factors with large R values are considered as analysis and input factors.In this study,GHI,DNI,DHI,AT,and H are selected.

The fluctuation of PV power under various weather types also varies.The PV power curves of different weather types are compared in Fig.1.The weather type information is obtained from China Meteorological Administration.As shown in Fig.1,March 13 and April 29 are both sunny days.The total power on March 13 is low,whereas the overall trend of power generation on April 29 is stable.The PV power law of the two rainy days also considerably differ.In addition,although the weather type on April 9 and 29 differs,the power curves are more consistent.In summary,the official information on weather type does not effectively reflect the PV power law.Therefore,the K-means++ clustering algorithm is proposed to classify weather types with the same PV power law.

Fig.1 PV power curves under different weather types

2 Framework of hybrid prediction model

2.1 K-means++ clustering algorithm

The K-means++ algorithm is an improvement of the traditional K-means algorithm.It can effectively overcome the shortcoming that the convergence of K-means algorithm considerably depends on the initial status of the cluster center [28,37].Based on the K-means++ method,historical days with the same power law are divided into the same cluster using historical power data.In addition,the input of different feature vectors affects the clustering results.Accordingly,nine statistical indices of time series data are calculated and then different indices are combined to form feature vectors.The nine statistical indices are as follows.

(1) Maximum PV power(Pmax)

(2) Total PV power (Psum) is given by

where i represents the ith time point; N is 53 in this study;the time interval between 6:00 and 19:00 is 15 min; and Pi is the power value of each time point.

(3) Average PV power : this is expressed as

(4) Variance (σ 2): this is given as

(5) Standard deviation (σ): this is given by

(6) Coefficient of variation (cv): this is expressed as

(7) Skewness(Sk): this is defined as the measure of the asymmetry of the probability distribution of random variables.It is given by

(8) Kurtosis(Kur): this is used to measure the kurtosis of the probability distribution of random variables.It is expressed as

(9) Permutation entropy (PE): this describes the complexity of time series data; it is extremely sensitive to local changes.

The dimension of each index differs.If it is directly inputted into the clustering algorithm,the influence of indices with small values is negligible.Accordingly,this paper proposes the use of min–max normalization for each feature.Min–max normalization maps feature data between 0 and 1; it groups all features with the same weight,thus facilitating the comparison and aggregation of features.Moreover,compared with other types of normalization methods,such as Z-score,sigmoid,and decimal calibration,min–max normalization does not modify the original data distribution [38].The normalized equation is as follows:

where m represents the number of samples; Xmin and Xmax represent the minimum and maximum values of every index for all samples,respectively; and Xj represents the index value of the jth sample.

The different clustering results must be compared.In this study,silhouette (s) is used as the evaluation index of clustering results [39].The s(i) value of a single sample is calculated as follows:

where a(i) is the average distance between a sample and all other samples in the same cluster; b(i) is the average distance between a sample and all samples in the next nearest cluster; and m is the total number of cluster samples.

The value of S is defined as the average of all samples,s.According to (9),S ranges from −1 to 1.When the value of S is large,the clustering effect is excellent.In addition,the setting of the super parameter,K,affects the clustering results.Combined with the practical significance of weather type classification,the range of K is 3–6.The optimal K value is also determined according to S.Then,12 meteorological factors are used to calculate the center point of each weather type.The 12 meteorological factors are the maximum,minimum,and average values of H and AT,and the maximum and average values of GHI,DHI,and DNI.Based on these 12 meteorological factors,the weather type classification of a forecast day is determined using the Euclidean distance between the forecast day and center of each cluster.The Euclidean distance is as follows:

where j represents the jth factor of the sample; t is 12 in this study; x0 represents the meteorological factor vector of the forecast day; and xi is the factor feature vector of each weather type.

The process of determining the weather type of the forecast day based on the foregoing is summarized in Fig.2.

Fig.2 Determination process of weather type of forecast day

2.2 Methods for finding similar days

A frequently used method for multivariate statistical analysis is GRA.The core concept is to determine the degree of correlation according to the similarity of curve shapes between a reference sequence and multiple comparison sequences.Then,the cosine similarity method is applied to the cosine angle between two vectors.This method focuses on the similarity of change trends between two vectors.In contrast,the GRA algorithm focuses on the similarity of geometric curves.When the angle approximates 0°,the cosine value approaches 1,indicating that the two vectors are similar [35].

After determining the weather type of the forecast day,various methods are used to find the best day similar to the forecast day.To determine the best method,the scaled root mean square error (SRMSE) between similar and prediction days is proposed to evaluate different techniques.The SRMSE is as follows:

where N is the number of time points; N is 53; j represents one of the methods to find the similar day; and PA,i and PS,i are the actual power value and the power value during similar days at time point i,respectively.

2.3 LSTM neural network

The LSTM neural network,a special type of RNN,can selectively remember information and overcome the disadvantage of gradient disappearance [20].It was proposed by Schmidhuber and Hochreiter in 1997 [40].A group of cyclic memory block subnets forms the LSTM structure,and a self-connected memory cell and three multiplication control gates are combined into a memory block.The three multiplication control gates are the input,output,and forgetting gates designated as IT,OT,and FT,respectively.The framework schematic is shown in Fig.4.The combination of these functions enables LSTM to have a selective memory function as its feature [41].The input and output signals are calculated as follows:

Fig.3 Information transmission structure diagram of LSTM

Fig.4 Framework of proposed hybrid model

where it,ft,and ot are IT,FT,and OT,respectively; Wi,Wc, Wo,Wf,Ui,Uc,Uf,and Uo,represent the weight matrix;bi,bc,bf,and bo,represent the bias vector; and σ andtanh are sigmoid activation and hyperbolic tangent functions,respectively.

2.4 Hybrid forecasting model framework

This study establishes a hybrid short-term prediction model for PV power based on several algorithms.For this model,the division of weather types is realized by the improved K-means algorithm,and the cosine model and GRA are combined to determine the best similar day for the forecast day.The training and testing of the prediction model are based on the LSTM neural network.In addition,the combination of historical power data and meteorological factors is inputted into the model.With these data as input compared with using a single input,more accurate prediction results are derived.However,errors in weather forecast information are inevitable.Accordingly,instead of weather prediction data as input,historical meteorological data are inputted to avoid the introduction of systematic errors.The framework of the hybrid model is displayed in Fig.4.

3 Experiment and discussion

3.1 Dataset description

The datasets used in this study are those of a PV power plant in Shandong Province.Its installed capacity,10 MW,is the same as that reported in [30].Because the PV panels of the power plant are placed on a mountain,their installation angle is random.When the laying angles of PV panels differ,the incidence angle of sunlight has a negligible impact on the overall power generation in different seasons.The datasets include historical PV power data and multivariate meteorological factors collected for a period of 22 months (from January 2020 to November 2021).The data interval is 15 min,satisfying the requirements of the state grid for PV power prediction.

3.2 Evaluation indicator

The prediction accuracy of the hybrid model is evaluated based on four evaluation indices.Mean absolute error (MAE)and root mean square error (RMSE) are selected because they are widely used as evaluation indices.However,the RMSE value is closely related to the size of the dataset.For example,the RMSE of a dataset whose range is 0–1 is typically smaller than that of a dataset with the range 0–100.Accordingly,this paper proposes the use of normalized RMSE (NRMSE) [42].In addition,the installed capacity of each power plant has a certain impact on error level.The mean absolute deviation (MAD) in [30] is also selected to evaluate the model.As dimensionless indicators,the NRMSE and MAD can eliminate the data capacity,enabling the effective comparison of prediction models reported in other references.The indicator are defined as follows.

(1) The MAE is expressed by

where N represents the total quantity of time points; N is 53;Pf,i is the predictive value at time point i; and Pa,i is the true value at time point i.

(2) The RMSE is given by

(3) The NRMSE is

where Pmax and Pmin are the maximum and minimum of the actual power value of the selected forecast day,respectively.

(4) The MAD is as follows:

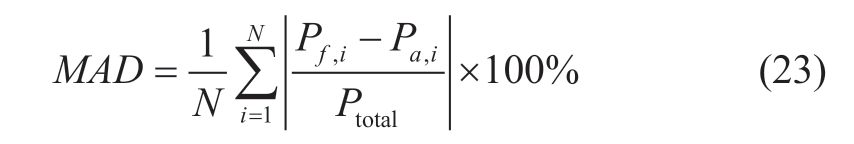
where Ptotal expresses the installed capacity of the PV power station,and Ptotal = 10 MW.

For different models,the concept of performance improvement percentage in [22] is used to compare their prediction performance.This paper selects the improvement percentages of RMSE (PRMSE) and MAD (PMAD),which can be expressed as follows.

(5) The PRMSE is given by

(6) The PMAD is as follows:

The establishment of a multiple evaluation system can considerably verify the superiority of the mixed model proposed in this paper.

3.3 Experimental results

3.3.1 Cluster analysis results

According to the process of dividing weather types using the K-means++ algorithm,the nine statistical indices of daily power are first calculated.Different indices are selected to form different feature vectors.The clustering results of different feature vectors using silhouette (S) as the evaluation indicator are summarized in Table 2.

Table 2 Clustering results of different feature vectors

Table 2 indicates that when the feature vector consisting of Pave,Pmax,Psum,and σ is inputted,the maximum S (K = 3)value is 0.4815,and the clustering result is optimal.The calculation equation of statistical indices shows that a certain relationship exists between Kur,cv, Sk,and σ.It indicates that satisfactory clustering results cannot be obtained when statistical indices of the input matrix are redundant.This is also consistent with the requirement of the K-means++algorithm for input data dimensions,specifically,the number of input dimensions is not proportional to the number of excellent clustering results.Accordingly,this study uses the combination of fundamental and discrete statistical indices or distributed statistical indices as the input vector to explore the optimal clustering results.The clustering of the fifth combination yields the best result,indicating that the use of the discrete statistical indices of the dataset yields favorable results.

In Table 2,I–IX represent Pave,Pmax,Psum,σ2,σ,cv,Sk,Kur,and PE,respectively.Among them,I–Ⅲ are the fundamental statistical indices; Ⅳ–Ⅵ are the discrete statistical indices; andⅦ–Ⅸ are the statistical indices of distribution.

According to the official list of weather types of the China Meteorological Administration,the number of various officially listed weather types in each cluster is counted.Then,the generalized weather type of each category is defined according to the statistical results summarized in Table 3.

Table 3 Number of official weather types included in each category

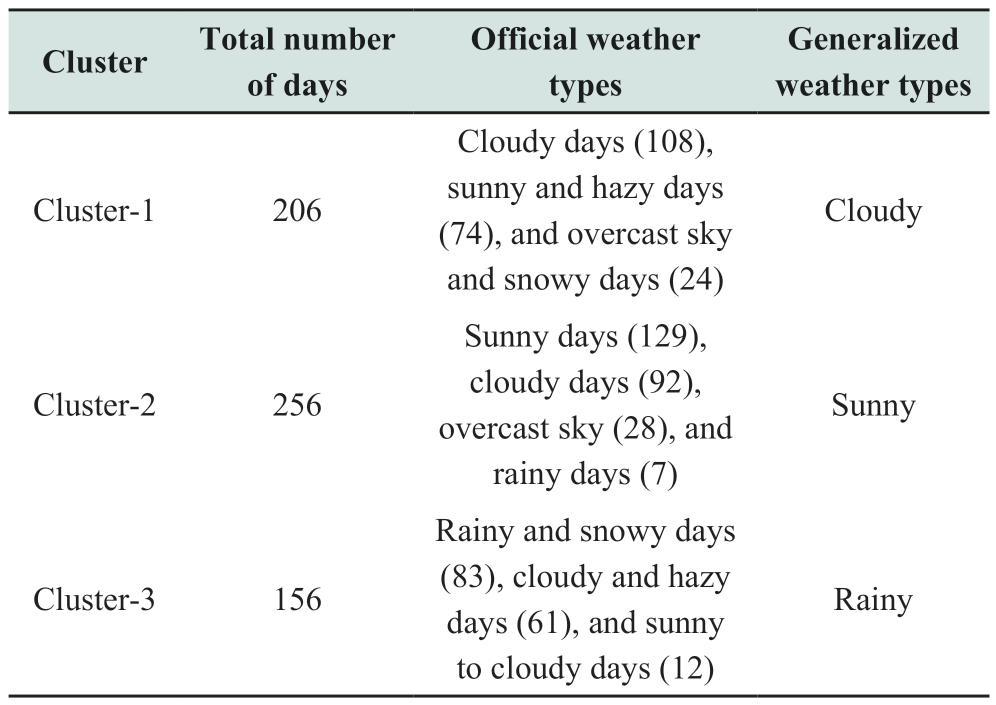
Table 3 indicates that each cluster includes diverse official weather types.According to the proportion of each weather type,the generalized weather types of the three clusters are defined as cloudy,sunny,and rainy.Although the official weather types in each cluster are not single,these types are divided into clusters because of the similarity of power generation laws.The foregoing observation is consistent with the analysis results of similar power generation curves,which are based on data collected on April 9 (cloudy) and 29 (sunny),as shown in Fig.1.

The three-dimensional power curves corresponding to 40 d of each weather type are shown in Fig.5.The power curves of sunny days show a relatively stable parabolic shape.For cloudy weather types,the power curves considerably fluctuate due to the influence of cloud random motion.For rainy days,the total power generation is extremely low due to the shielding of thick clouds.The PV generation law of each weather type is evident,verifying the superiority of the clustering results.

Fig.5 Power curves for three weather types

3.3.2 Determination of best similar day

The weather type of a forecast day is determined according to the Euclidean distance; the best similar day is found under the same weather type.This paper proposes the use of the SRMSE index to compare several commonly employed methods.For every weather type,a day is randomly selected as the target day.Then,different methods are used to find the best similar day,and the SRMSE value is calculated.The historical days in each cluster are traversed to find similar days and determine the average SRMSE of each cluster.The SRMSE results of different methods are summarized in Table 4.The linear combination of GRA and cosine method is the technique used in this study to find the similar day.Because the focus of GRA and cosine method on the similarity of feature vectors differs,the average power of two similar days obtained by the two methods is considered as the power value of the best similar day.

Table 4 SRMSE values of different methods for finding similar days

3.3.3 Prediction results

Based on the optimal similar day,the LSTM neural network is the last step in building the hybrid model.The LSTM neural network architecture is selected from Keras’deep learning software package.It is based on the Python 3.5 environment and uses the second-generation artificial intelligence learning system (TensorFlow) as backend.The normalization of data adopts the MinMaxScaler function in the Scikit-Learn module.

For evaluating the prediction of the model,5 d under different weather types are randomly selected as the forecast days for testing.The comparison between the actual and predicted value curves is shown in Fig.6.Evidently,the changing trends of the two curves fundamentally coincide.The actual power curves change smoothly on the 4th and 5th days (sunny),and the prediction curves virtually coincide with the actual power curves.For the 2nd and 3rd days (cloudy),the actual power curves considerably fluctuate.This is because the random movement of clouds affects the sunlight received by the PV panel.Consequently,the predicted power curve significantly fluctuates,and the prediction error of the power mutation point is considerable.The predicted value for the first day (rainy) fundamentally coincides with the actual value; however,the overall PV power is low.This leads to the conclusion that although the models slightly vary in performance under different weather types,they all perform well.

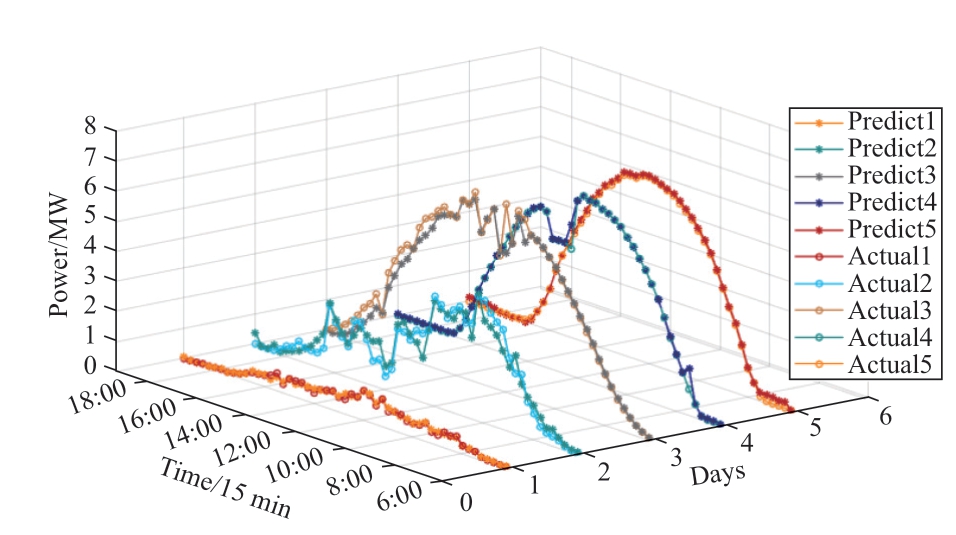
Fig.6 Predicted and actual output curves for five days

Next,the superiority of the prediction performance of the hybrid model must be verified through comparison with other models.The other five include the Elman,LSTM,HSE,HSL,and HKSE models.The performance indices of different models are shown in Fig.7,(a) and (b).The data are the average values of the prediction results of multiple forecast days.In Fig.7,the values of MAE,RMSE,NRMSE,and MAD of the HKSL model compared with those of the other five models are the lowest.This verifies the excellent prediction ability of the HKSL.In addition,the values of HSL and HKSL are considerably less than those of the other four models.This proves the effectiveness of the weather classification and LSTM in enhancing the accuracy of the prediction model.

Fig.7 Performance evaluation indices of different models

For a more intuitive comparison of the prediction performance of different models,1 d is randomly selected for analysis.The prediction results and absolute errors of the six models under different weather types (sunny,cloudy,and rainy) are shown in Figs.8–10,respectively.For sunny days,Fig.8(a) shows that the predicted value curve of the HKSL model is the most consistent with the true value curve.The predicted values of the Elman,LSTM,HSE,HSL,and HKSE models are less than the actual values from 10:00 to 14:00.In Fig.8(b),the error fluctuation range of the HKSL model is narrow,whereas the oscillation amplitude of the error curves of the other models is large.The black line in Fig.9(a) shows the actual power curve with a strong turning point considering the cloudy weather type.The predicted curve of the HKSL model compared with those of the other models is the most ideal.In particular,at the power mutation point,the predicted result of the HKSL model is more accurate.The range of errors shown in Fig.9(b) also highlights the advantages of the HKSL model.As shown in Fig.10(a),the overall PV power is low considering a rainy day.The predicted curves of the other models are clearly observed to fluctuate around the actual curve,whereas the prediction value of the HKSL model approaches the actual value.The improved forecast capability of the HKSL model is also observed in Fig.10(b).In conclusion,the predictions of the hybrid model are better than those of the other models under the three weather types.

Fig.8 Predicted results and errors of six models for sunny day

Fig.9 Predicted results and errors of six models for cloudy day

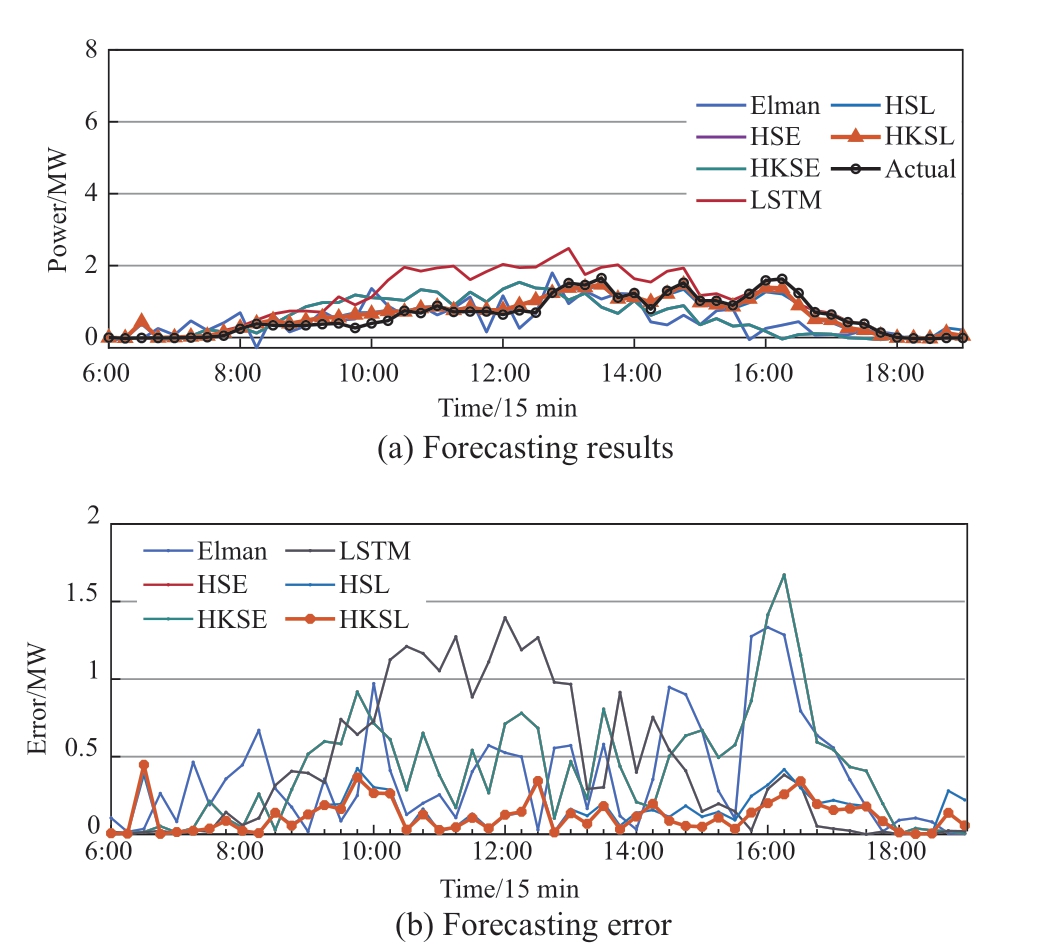
Fig.10 Predicted results and errors of six models for rainy day

In addition to the qualitative analysis based on the curves,quantitative measurements based on evaluation indicators must be implemented.Tables 5–8 summarize the MAE,RMSE,NRMSE,and MAD values,respectively,of the HKSL model and the other five models (Elman,LSTM,HSE,HLE,and HKSE) under three weather types.Then,the improvement percentage indices,PRMSE and PMAD,between two models are calculated.The results of the percentage increase are listed in Table 9.

Table 5 Comparison of daily MAE (MW) of different models

Table 6 Comparison of daily RMSE (MW) of different models

Table 7 Comparison of daily NRMSE (%) of different models

Table 8 Comparison of daily MAD (%) of different models

Table 9 PRMSE and PMAD

The average values of MAE and RMSE for the HKSL model in Tables 5 and 6 are 0.1642 and 0.2178 MW,respectively; these are lower than those of the other five models.Combined with the data in Table 10,the RMSE values of the HKSL model decrease by 66.73% and 70.51% compared with those of the individual Elman and LSTM models,respectively.This demonstrates the superior prediction ability of the hybrid prediction model.The improved RMSE of the proposed model compared with those of the HSE,HKSE,and HSL models proves the outstanding contribution of weather type classification and LSTM neural network to PV power prediction.

Then,the data in Tables 7 and 8 are used to reflect the relative level of prediction results.The minimum values of the average MAD and NRMSE of the HKSL model are 5.8073% and 1.6422%,respectively.The MAD value of the HKSL model compared with those of the other five models(i.e.,Elman,LSTM,HSE,HLE,and HKSE) improved by 65.12%,70.32%,66.30%,63.36%,and 8.96%,respectively;these results are consistent with the PRMSE values.The foregoing proves that the prediction performance of the HKSL model remains optimal based on the standard of relative indices.

Considering the sunny weather type,the NRMSE and MAD of the HKSL model,i.e.,2.5734% and 1.4429%,respectively,are extremely low.The prediction ability of the HKSL model for the rainy and cloudy days is compared with that of the model reported in [30] based on the same installed capacity.The mean MAD of the HKSL model is 1.7419%; this is a 48.57% improvement compared with the 3.3867% mean MAD reported in [30].This shows that the prediction performance of the proposed model is also excellent under cloudy and rainy weather types.

Based on the foregoing analysis,the prediction accuracy of the proposed hybrid model is found to be relatively reliable.With the increasing popularity of PV power generation,reliable prediction accuracy is crucial to the stable operation of power systems.Accordingly,the proposed hybrid model can benefit departments involved in managing power distribution in terms of specifying the scheduling plan to overcome the challenges resulting from the high penetration of PV power.

4 Conclusions

In this study,an innovative hybrid short-term prediction model for PV power is proposed.The model,named HKSL,is constructed by combining the K-means++,GRA,cosine,and LSTM neural networks.Historical power data and highly correlated meteorological factors are considered as the inputs of the HKSL model.First,the optimal result of dividing three weather types is obtained based on K-means++.Then,the SRMSE index is obtained to compare the different methods for finding the best similar day.The linear combination of GRA and cosine method is found to be the best technique for determining the foregoing.Then,the data of the best similar day are inputted into the LSTM neural network to generate predictions.The superiority of this HKSL model is proved through comparison with the other five models based on the datasets from a PV power station in Shandong Province,China.For the HKSL model,the average values of MAE,RMSE,NRMSE,and MAD are 0.1642 MW,0.2178 MW,5.8073%,and 1.6422%,respectively; they are all at a low level.The RMSE of the HKSL model compared with those of the Elman,LSTM,HSE,HSL,and HKSE models decreases by 66.73%,70.22%,65.59%,70.51%,and 18.40%,respectively; the relative evaluation index (MAD) improves by 65.12%,70.32%,66.30%,63.36%,8.96%,respectively.The excellent prediction performance of the HKSL model is proved through comparison of results.Accordingly,the proposed hybrid model for predicting short-term PV power is feasible.

Acknowledgements

This work was supported by the No.4 National Project in 2022 of the Ministry of Emergency Response(2022YJBG04) and the International Clean Energy Talent Program (201904100014).

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] E Kabir,P Kumar,S Kumar,et al.(2018) Solar energy: potential and future prospects.Renewable and Sustainable Energy Reviews,82:894-900

[2] IRENA (2022) Renewable capacity statistics.Renewable Capacity Highlights

[3] C Lupangu,R C Bansal (2017) A review of technical issues on the development of solar photovoltaic systems.Renewable and Sustainable Energy Reviews,73:950-965

[4] Lin P J,Peng Z N,Lai Y F,et al.(2018) Short-term power prediction for photovoltaic power plants using a hybrid improved K-means-GRA-Elman model based on multivariate meteorological factors and historical power datasets.Energy Conversion and Management,177:704-717

[5] J Li,Q Liu (2022) Forecasting of short-term photovoltaic power generation using combined interval type-2 Takagi-Sugeno-Kang fuzzy systems.International Journal of Electrical Power &Energy Systems,140:108002

[6] Zhang W S,Chen X,He K,et al.(2022) Semi-asynchronous personalized federated learning for short-term photovoltaic power forecasting.Digital Communications and Networks.https://doi.org/10.1016/j.dcan.2022.03.022

[7] H Long,Z Zhang,Y Su (2014) Analysis of daily solar power prediction with name="ref8" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[8] M Yang,M Zhao,D Huang,et al.(2022) A composite framework for photovoltaic day-ahead power prediction based on dual clustering of dynamic time warping distance and deep autoencoder.Renewable Energy,194:659-673

[9] M AlShafeey,C Csáki (2021) Evaluating neural network and linear regression photovoltaic power forecasting models based on different input methods.Energy Reports,7:7601-7614

[10] Rogier J K,Mohamudally N (2019) Forecasting photovoltaic power generation via an IoT network using nonlinear autoregressive neural network.Procedia Computer Science,151:643-650

[11] Miao S W,Ning G T,Gu Y Z,et al.(2018) Markov chain model for solar farm generation and its application to generation performance evaluation.Journal of Cleaner Production,186: 905-917

[12] Tesfaye Eseye A,Zhang J H,Zheng D H (2018) Short-term photovoltaic solar power forecasting using a hybrid Wavelet-PSO-SVM model based on SCADA and Meteorological information.Renewable Energy,118:357-367

[13] VanDeventer W,Jamei E,Thirunavukkarasu G S,et al.(2019)Short-term PV power forecasting using hybrid GASVM technique.Renewable Energy,140:367-379

[14] Y Zahraoui,I Alhamrouni,S Mekhilef,et al.(2022) Chapter one-Machine learning algorithms used for short-term PV solar irradiation and temperature forecasting at microgrid.Applications of AI and IOT in Renewable Energy,Amsterdam: Elsevier,1-17

[15] Liu L Y,Liu D R,Sun Q,et al.(2017) Wennersten,Forecasting power output of photovoltaic system using a BP network method.Energy Procedia,142:780-786

[16] Yang Z L,Mourshed M,Liu K L,et al.(2020) A novel competitive swarm optimized RBF neural network model for short-term solar power generation forecasting.Neurocomputing,397: 415-421

[17] Yadav A K,Sharma V,Malik H,et al.(2018) Daily array yield prediction of grid-interactive photovoltaic plant using relief attribute evaluator based Radial Basis Function neural network.Renewable and Sustainable Energy Reviews,81:2115-2127

[18] Ma X Y,Zhang X H (2022) A short-term prediction model to forecast power of photovoltaic based on MFA-Elman.Energy Reports,8:495-507

[19] Sobri S,Koohi-Kamali S,Rahim N A (2018) Solar photovoltaic generation forecasting methods: A review.Energy Conversion and Management,156: 459-497

[20] Agga A,Abbou A,Labbadi M,et al.(2022) CNN-LSTM: an efficient hybrid deep learning architecture for predicting shortterm photovoltaic power production.Electric Power Systems Research,208:107908

[21] Li P T,Zhou K L,Lu X H,et al.(2022) A hybrid deep learning model for short-term PV power forecasting.Applied Energy,259:114216

[22] Wang K J,Qi X X,Liu H D (2019) Photovoltaic power forecasting based LSTM-Convolutional Network.Energy,189:116225

[23] Ahmed R,Sreeram V,Togneri R,et al.(2022) Computationally expedient photovoltaic power forecasting: A LSTM ensemble method augmented with adaptive weighting and data segmentation technique.Energy Conversion and Management,258:115563

[24] Liu Z F,Luo S F,Tseng M L,et al.(2021) Short-term photovoltaic power prediction on modal reconstruction: A novel hybrid model approach.Sustainable Energy Technologies and Assessments,45:101048

[25] Zhang J L,Tan Z F,Wei Y M (2020) An adaptive hybrid model for day-ahead photovoltaic output power prediction.Journal of Cleaner Production,244:118858

[26] Wang F,Zhen Z,Liu C,et al.(2018) Time-section fusion pattern classification based day-ahead solar irradiance ensemble forecasting model using mutual iterative optimization.Energies,11(1): 184

[27] Wang F,Zhang Z Y,Liu C,et al.(2019) Generative adversarial networks and convolutional neural networks based weather classification model for day ahead short-term photovoltaic power forecasting.Energy Conversion and Management,181:443-462

[28] Zhang H P,Li D,Tian Z Y,et al.(2021) A short-term photovoltaic power output prediction for virtual plant peak regulation based on K-means clustering and improved BP neural network.In: Proceedings of 2021 11th International Conference on Power,Energy and Electrical Engineering (CPEEE).Shiga,Japan.IEEE,241-244

[29] Chen C S,Duan S X,Cai T,et al.(2011) Online 24-h solar power forecasting based on weather type classification using artificial neural network.Solar Energy,85(11):2856-2870

[30] Gao M M,Li J J,Hong F,et al.(2019) Day-ahead power forecasting in a large-scale photovoltaic plant based on weather classification using LSTM.Energy,187:115838

[31] Xu F,Tian Y,Wang Z,et al.(2018) One-day ahead forecast of PV output based on deep belief network and weather classification.In: Proceedings of the 2018 Chinese Automation Congress,Xi’an,China,30 November 2018,412-417

[32] Zhao J W,Yu H Y,Geng G C (2021) TransOS-ELM: A shortterm photovoltaic power forecasting method based on transferred knowledge from similar days.In: Proceedings of 2021 IEEE 5th Conference on Energy Internet and Energy System Integration(EI2).Taiyuan,China.IEEE,89-94

[33] Jiang Y M,Yang Y,Wu Q X,et al.(2019) Research on predicting the short-term output of photovoltaic (PV) based on extreme learning machine model and improved similar day.In: Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia).Chengdu,China.IEEE,3691-3695

[34] L Ge,W Lu,X Yuan,et al.(2018) Photovoltaic power prediction of power station based on improved similar days and ABC-SVM.Journal of Solar Energy,39:775-782.(in Chinese)

[35] T Chen,G Sun,Z Wei,et al.(2017) Photovoltaic power generation forecasting based on similar day and CAPSO-SNN.Electric Power Automation Equipment,37(3):66-71(in Chinese)

[36] Nguyen N Q,Bui L D,Van Doan B,et al.(2021) A new method for forecasting energy output of a large-scale solar power plant based on long short-term memory networks a case study in Vietnam.Electric Power Systems Research,199:107427

[37] Arthur D,Vassilvitskii S (2007) K-Means++: The Advantages of Careful Seeding.In: Proceedings of the Eighteenth Annual ACMSIAM Symposium on Discrete Algorithms,SODA 2007,New Orleans,Louisiana,USA,7-9 January

[38] H Yang,X Zhao,L Wang (2022) Overview of data normalization methods.Computer Engineering and Application,1-11.(in Chinese)

[39] Bae K Y,Jang H S,Sung D K (2017) Hourly solar irradiance prediction based on support vector machine and its error analysis.IEEE Transactions on Power Systems,March 2017,32(2):935-945

[40] S Hochreiter,J Schmidhuber (1997) Long short-term memory.Neural Computer,9(8): 1735-1780

[41] Zhou F T,Huang Z H,Zhang C H (2022) Carbon price forecasting based on CEEMDAN and LSTM.Applied Energy,311:118601

[42] Qu J Q,Qian Z,Pei Y (2021) Day-ahead hourly photovoltaic power forecasting using attention-based CNN-LSTM neural network embedded with multiple relevant and target variables prediction pattern.Energy,232:120996

Full-length article

Received: 23 October 2022/ Accepted: 3 January 2023/ Published: 25 April 2023

Yuetao Shi

shieddi@sdu.edu.cn

Ruxue Bai

2471280962@qq.com

Meng Yue

m15734079296@163.com

Xiaonan Du

2856417746@qq.com

2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Ruxue Bai received her bachelor’s degree from Harbin Business University,Harbin,in 2016.She is studying for a master’s degree at Shandong University,Shandong,China.At present,her research direction is photovoltaic power prediction model based on neural network.

Yuetao Shi received his bachelor’s degree from Shandong University of Technology,Shandong,China,in 1997,the master’s degree in engineering from Shandong University,Shandong,China,in 2000,and the Ph.D.degree from Xi’an Jiaotong University,Xian,China,in 2009.At present,he is a professor of Shandong University.His research interests include data mining and analysis in industrial processes and comprehensive energy load forecasting based on machine learning.

Meng Yue received his bachelor’s degree from Shenyang Architecure University,Shenyang,in 2018,the master’s degree at Shandong University,Shandong,China,in 2021.Now he is the office director of Harbin Shuangcheng District National Thermal Power Plant,mainly responsible for procurement and personnel management.

Xiaonan Du graduated from Shandong University of Science and Technology in 2017 with a bachelor's degree.She is studying for a master's degree at Shandong University,China.At present,her research direction is the performance analysis and energysaving optimization of the coupled compressed air energy storage system in thermal power plants.

(Editor Yanbo Wang)