0 Introduction

The increasing scarcity of fossil fuels,higher levels of acid rain,smog,and other extreme climate events can be efficiently addressed by wind power generation.However,as wind energy becomes more prevalent in the grid,its stability and security are affected by the volatility and unpredictability of wind energy.Transmission system operators mandate that wind farms connected to the grid adhere to grid-connection specifications [1] to deliver consistent electricity generation.

The power control center of a wind farm receives active power instructions from the transmission system operator and simultaneously sends the power instructions to each wind turbine [2].In practical applications,wind power plant control centers typically adopt wind speed-weighted power dispatching (WSWPD) algorithms.The WSWPD algorithm does not consider the running state of wind turbines.The wind turbine actuator runs frequently when the wind speed fluctuates,resulting in reducing the lifespan of the wind turbines.At present,there have been several studies on optimizing the wind farm active power dispatching(WFAPD) algorithm.In [3],the WFAPD algorithm was proposed for wind-speed prediction.A quasilinear control WFAPD algorithm was proposed in [4].However,the WFAPD calculation method in [3,4] often relies on windspeed prediction,and the mean square error (MSE) of the predicted wind speed is 0.8902 [5].

However,the wind speed prediction error is still large in reality,which may generate inaccurate commands at the wind turbine active power output.In [6],a distributed model predictive control algorithm for WFAPD was proposed.First,a piecewise affine model of a wind turbine was established,and then,a fast gradient method of dual decomposition was adopted to realize the distributed model predictive control (MPC) algorithm.In WFAPD [7],a particle swarm optimization (PSO) algorithm was used to reduce wind turbine loads.In [8],a WFAPD algorithm based on a (PSO) algorithm was proposed to minimize the power generation cost of wind farms under conditions.Literature [6-8] consider the state of wind turbines and saves the operating costs of wind farms.However,these optimization scheduling algorithms rely on accurate mathematical models of the wind turbines.It is challenging to generate precise mathematical models of wind turbines for practical applications because of the large blade size,production flaws,installation faults,aging components,and other factors.Simultaneously,MPC and multi-objective optimization algorithms exhibit the “curse of dimension” as the number of wind turbines increases.

The idea of style="font-style: italic;">I/O data obtained from a controlled system or knowledge gained from data processing,rather than using mathematical models [9].Some studies have used datadriven wind-generator condition monitoring [10,11],windfarm power maximization [12],and wind-generator faulttolerant control [13].Based on the style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">This paper proposes a WFAPD algorithm based on grey incidence (GI).From the start-stop operation data of the wind turbine,the weighting coefficients were evaluated using the GI method and B-spline function at different wind speeds.Thus,the power regulation capacity of the wind turbines was obtained,and the WFAPD was based on the power regulation capacity of the wind turbine.Finally,the GI-WFAPD was compared with WSWPD in MATLAB to validate the feasibility and effectiveness of the GI-WFAPD algorithm.

The remainder of this paper is organized as follows.The ability of wind turbines to regulate power is discussed in Section 1.In Section 2,GI and B-spline functions are used to evaluate the wind turbine power regulation capacity.In Section 3,based on the shortcomings of the WSWPD algorithm,the GI-WFAPD control method is proposed,and the structure diagram is drawn.Case studies that contrast the WSWPD algorithm are provided in Section 4,where the WFAPD is based on the wind turbine’s capacity for power regulation.Finally,the conclusions are summarized in Section 5.

1 The power regulation capacity of variable speed variable pitch wind turbine

The mathematical formula for a wind turbine with variable speed and variable pitch for harvesting wind energy is

where Pm represents the mechanical power of the wind turbine,ρ denotes the air density,R indicates the impeller radius,Cp is the power coefficient,which is a function of the pitch angle β and tip speed ratio λ,v denotes the wind speed,and ω symbolizes the wind turbine rotor speed.

The wind turbine operates in maximum power point tracking (MPPT) mode when the active power command exceeds the maximum power of the wind turbine.Unless otherwise specified,a wind turbine operates in power regulation mode.The active power of a wind turbine can be changed by varying the rotating speed or pitch angle using Eq.(1).Generally,wind turbines operate in the power regulation mode of WFAPD.

The power curtailment schematic of the wind turbines is shown in Fig.1 at 8 m/s,where β1=0,β1–β5 increase,Popt denotes the curve of the maximum power point,and Pmax denotes the maximum power of the wind turbine.Suppose that the wind turbine operates at point A when the active power command is Pset1.There are three power curtailment control strategies.The wind turbine only adjusts the pitch angle to operate at point B1 while maintaining the rotational speed at the maximum power point,which is variable pitch power curtailment control.The wind turbine only adjusts the rotor speed to operate at point B,whereas it does not adjust the pitch angle,which is variable-speed power curtailment control.The rotor speed and pitch angle are adjusted simultaneously to operate between points B and B1,which is variable speed combined with variable pitch power curtailment control.

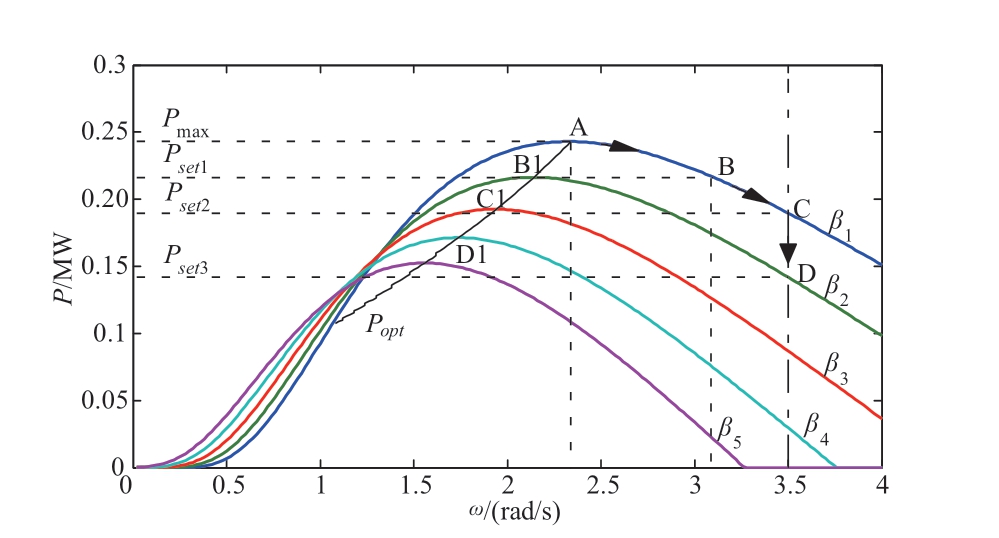
Fig.1 Curtailment power control schematic of variable speed and variable pitch wind turbine

The power regulation capacity can be determined from Fig.1 if the rotor speed and pitch angle of the wind turbines are known and the power coefficient Cp is predictable.Owing to the size of the blades and the lack of wind tunnel tests to test the aerodynamics of the blades worldwide,as well as other stochastic and uncertain factors,such as manufacturing errors,installation errors,material aging,humidity,dust accumulation,etc.,it is usually challenging to determine the Cp of wind turbines using a mathematical model [14].Therefore,a mathematical model cannot be used to determine the power regulation capacity of wind turbines,although it can be assessed using thorough assessment techniques.This is because the dynamics of the wind turbines are complex,imprecise,and uncertain.

The power regulation capacity of wind turbines is not only linearly connected to the cube of the wind speed but is also related to the rotor speed and pitch angle of a wind turbine,as shown in (1) and Fig.1.Regardless of the power limitation control mechanism used by wind turbines,when operating in the power regulation mode,there are two complementary scenarios: power regulation capacity increases and power regulation capacity drops.The pitch angle,ability to change the rising power,and capacity to modify the falling power all increase with the size of the gap between the rotor speed and the ideal rotor speed.This study makes the straightforward assumption that the power regulation capacity is linear.For simplicity,this study assumes that the absolute error between the wind turbine speed and the ideal speed and the cubic of the wind speed are directly proportional to the power regulation capacity.Consequently,(2) shows how well a wind turbine can regulate power.

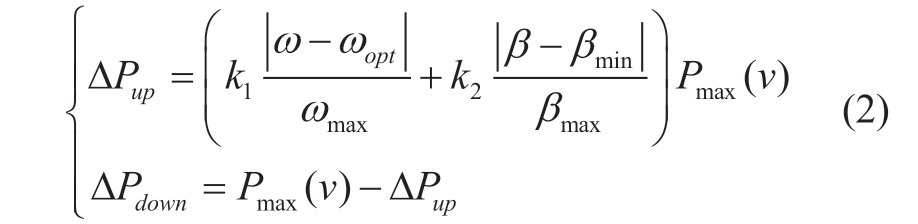
where ΔPup indicates the rising power regulation capacity,ΔPdown denotes the reduction power regulation capacity,ωopt corresponds to the optimal wind turbine speed,ωmax denotes the rated wind turbine speed,βmax denotes the maximum operation pitch angle,k1 and k2 are the weighting coefficients of the variable speed and variable pitch systems,respectively,and k1+k2=1.Pmax(v) represents the maximum power of the wind turbine and is a function of the cube of wind speed [15],which is expressed as

where PN denotes the wind turbine-rated power,and vN,vci,and vco denote the rated,cut-in,and cut-out wind speeds,respectively.

2 The wind turbine power regulation capacity evaluation based on the grey incidence

2.1 Grey incidence

From (2),it is imperative to obtain the weighting coefficients of a variable speed system and a variable pitch system to evaluate the power regulation capacity.If systems have partially known information and partially unknown information,they will be seen as grey [16],and the dynamics of wind turbines can be equivalent to a grey system.GI analysis is a multicriteria evaluation method.GI analysis can evaluate the relevance degree of each factor in the evaluated system and provide a quantitative measure for a system to develop a change in dynamics and is well suited for dynamic model course analysis [17].Let X0=(x0(1),x0(2),…,x0(n)) be the output sequence,and Xi=(xi(1),xi(2),…,xi(n)),where i = 1,2,3…,n,be the ith input sequence.The GI coefficient γ(x0,xi) of X0 and Xi is shown in (4),and the GI degree of the ith input sequence between the output sequence γ0i is shown in (5).

where ξ is the distinguishing coefficient,and generally ξ=0.5.

2.2 Evaluation of wind turbine power regulation capacity by grey incidence method

Owing to the complex dynamic characteristics of a wind turbine,the relative weight coefficient of the variable speed and variable pitch system changes under different wind speeds and power control strategies.The use of a mathematical model to calculate the weighting coefficient has the disadvantages of poor stability and low efficiency.However,subjective evaluation methods,such as fuzzy evaluation and Analytic Hierarchy Process (AHP),have the disadvantages of strong subjectivity and reliance on expert experience.Grey relational degree is an objective evaluation method that can overcome the shortcomings of subjectivity.The more important the input factor is to the system output,the greater the grey correlation degree.Therefore,the grey correlation method can be employed to evaluate the weight coefficient of variable-speed and variable-pitch systems in the output power control process of a wind turbine.The evaluation procedure for wind turbine power regulation capacity is as follows:

Step 1: Obtain the input and output sequences of a wind turbine at different wind speeds,and the output sequence is the output active power P0; the input sequences are the wind turbine speed ω0 and pitch angle β0.

Step 2: Normalize the input and output sequences of the wind turbine; the normalization of P0,ω0,and β0 is expressed in (6)–(8).

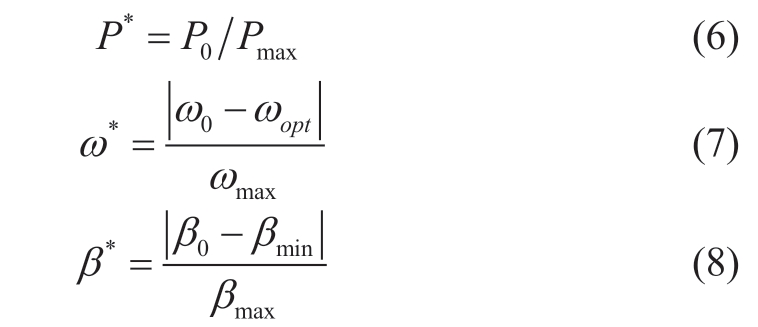
Step 3: Based on the calculation of the GI degree,calculate the GI degree of the variable speed system γω between P0 and ω0 and calculate the GI degree of the variable pitch system γβ between P0 and β0.

Step 4: Obtain the relative weighting coefficients k1 and k2 of the variable-speed and variable-pitch systems,respectively,as expressed in (9) and (10).

Step 5: Based on the rotor speed,pitch angle,and wind speed of the wind turbine,obtain the wind turbine adjustment capacities ΔPup and ΔPdown according to (2).

In practice,k1 and k2 are unequal at different wind speeds.To reduce the workload,we obtained k1 and k2 for partial wind speeds,and used the B-spline method to fit the full range of wind speeds.There are many papers on the B-spline method,so this paper does not introduce more.Simultaneously,to increase the reality of k1 and k2,the Monte Carlo method was used in this study to obtain the expectation.

3 The WFAPD based on grey incidence

The wind turbine power capacity is not only determined by the wind speed but is also affected by the pitch angle and rotor speed from (1).The WSWPD algorithm relies only on wind speed,and the power set of each wind turbine cannot be accurate.However,power regulation capacity is a multicriteria system evaluation.The evaluation of the power regulation capacity is more accurate based on the wind speed,pitch angle,and rotor speed than solely evaluating the wind speed.

In the third section,the ith wind turbine power regulation capacity ΔPi,up and ΔPi,down can be obtained from the operational data and can be the basis of power dispatching.Figure 2 shows the schematic of the GI-WFAPD.The wind farm active power dispatching center obtains the active power error ΔPfarm by comparing the active power command Pcmd and the active power of the wind farm point common coupling PPCC,as shown in (11).Simultaneously,the wind farm active power dispatching center receives the power regulation capacity ΔPi,up and ΔPi,down of the ith wind turbine.If ΔPfarm>0,all wind turbines in the wind farm have to increase their power,the active power set changes ΔPseti of the ith wind turbine,as shown in (12),and the active power set changes ΔPseti of the ith wind turbine,as shown in (13).The machine set process is tedious and can be roughly described by (14).

Fig.2 Schematic of GI-WFAPD

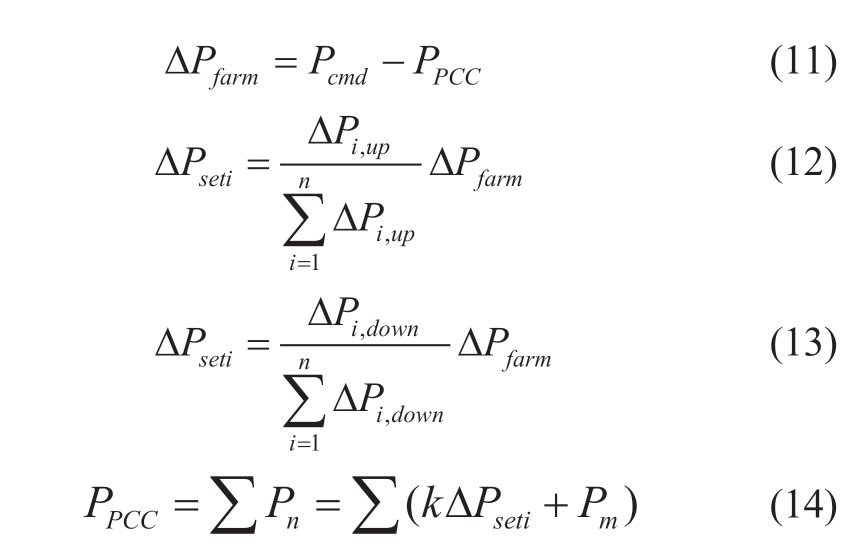
where k denotes the weight coefficient of each group of wind turbines obtained using the grey correlation method.

4 Case study

4.1 The wind turbine power regulation capacity evaluation based on GI

Suppose that the wind farm contains 10 wind turbines.The parameters of a wind turbine are listed in Table 1,and all wind turbines have good operating conditions.

Table 1 Wind turbine parameters

The power control strategy of wind turbines is the max-Ω control strategy,which maximizes the priority of the rotational speed of the wind turbine for its curtailment operation.The wind turbine power curtailment was simulated in MATLAB,and the curves of the wind turbine speed,pitch angle,and outpower are shown in Fig.4 at a wind speed of 8 m/s.The wind turbine speed,output power according to (15) and (1),and pitch angle are shown in Fig.3.

Fig.3 Schematic of GI-WFAPD

Fig.4 Curves of output power (a),rotating speed (b),and pitch angle (c) of wind turbine at 8 m/s

where Tm denotes the pneumatic torque of the wind turbine,φ indicates the torsion angle of the high-speed axis relative to the low-speed axis,Jr indicates the rotational inertia of the wind turbine,and Ks and Ds denote the stiffness and damping coefficients,respectively.

where ωref is the reference wind turbine speed,ω is the actual wind turbine speed,and θmax and θmin indicate the upper and lower limits of the pitch angle,respectively.

The power set is 0 at 20 s and maximum at 35 s.From the information theory,the entropy of the start-stop operation is the least,and the amount of information is greater.Therefore,this study selected sequences from 20 s to 35 s for GI evaluation.

From the GI evaluation in the 3rd section,the weighting coefficients of the variable speed and variable pitch systems are 0.576 and 0.424,respectively.

In addition,other weighing coefficients can be obtained by GI evaluation,and the weighting coefficients of the variable speed system are listed in Table 2.Using the B-spline method to fit the full range of wind speeds,the variable speed system weighting of a full range wind speed is depicted in Fig.5,where the variable speed weighting coefficient decreases as the wind speed increases.Moreover,the power regulation capacity is illustrated in Fig.6 at a wind speed of 8.5 m/s.

Fig.5 Weighting coefficient curve of the variable speed system based on the B-spline function fitting

Table 2 Variable speed system weighting value at different wind speeds

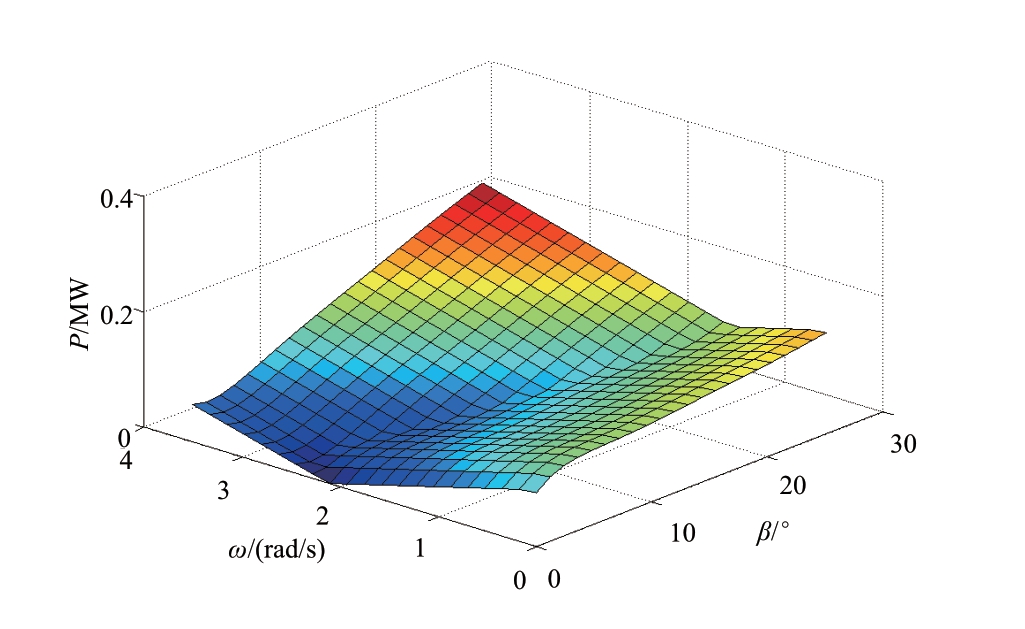
Fig.6 Power regulation capacity of the wind turbine at a wind speed of 8.5 m/s

4.2 WFAPD based on grey incidence

Suppose that the wind farm contains 10 wind turbines.To reflect the wind speed diversity of wind farms,the average wind speeds of wind turbines are uniformly distributed between 3 m/s and 13 m/s,and the wind speed profiles generated by the pulse generator for the 10 wind turbines are illustrated in Fig.7.The wind speed of the 10th wind turbine is the highest,the wind speed of other wind turbines decreases in turn,and the 1st wind turbine has the lowest wind speed.

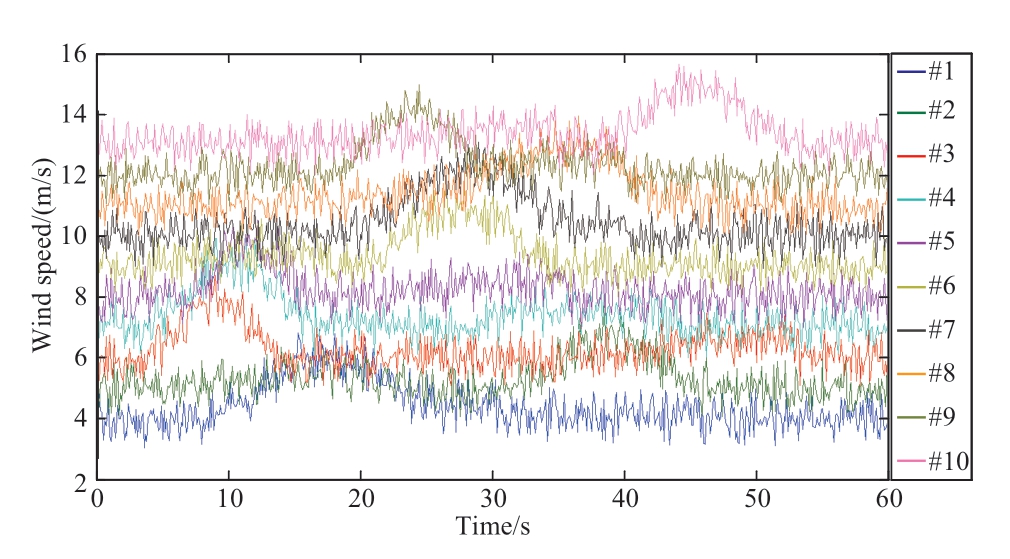
Fig.7 Wind speed of 10 wind turbines

The initial rotor speed and initial pitch angle of all the wind turbines are 1 rad/s and 0°,respectively.The output active power curves of the wind farms are depicted in Fig.8 when the active power command is 5 MW.From Fig.8,it can be observed that both the GI-WFAPD and WSWPD essentially meet the scheduling requirements; however,the GI-WFAPD algorithm results are better.The integrated absolute error (IAE) index of GI-WFAPD is 28,394,202,and the IAE of WSWPD is 30,375,949,which shows that the algorithm proposed in this paper has a better tracking effect.Moreover,the power smoothness definition of a wind farm is shown in (16) based on the study,where the power smoothness of GI-WFAPD is 24,022 and that of WSWPD is 40,488.This indicates that the GI-WFAPD algorithm can reduce the power fluctuation of grid-included wind farms.Additionally,it also exhibits better performance compared to the conventional active power allocation algorithm.

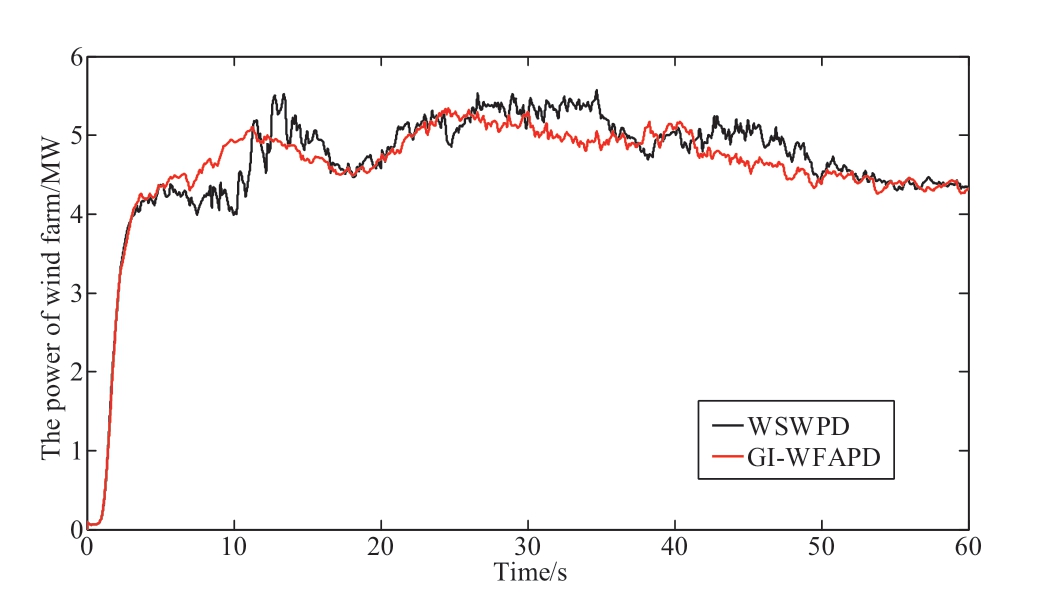
Fig.8 Wind farm active power curves of two dispatching algorithms

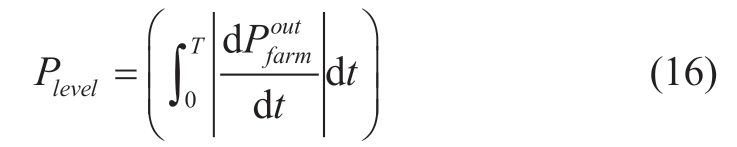
The rotor speed curves of the GI-WFAPD and WSWPD are shown in Fig.9 and Fig.10,and the rotational speed fluctuation of the GI-WFAPD algorithm is less than that of the WSWPD.The smoothness index of the rotational speed is defined in (17),where n indicates the number of wind turbines; the lower the smoothness index,the lower the shaft load.The rotational speed smoothness index of GI-WFAPD is 24,021,and the rotational speed smoothness index of WFWPD is 40,487.This shows that the GI-WFAPD algorithm can reduce the shaft fatigue of wind turbines and increase their lifespan [18].

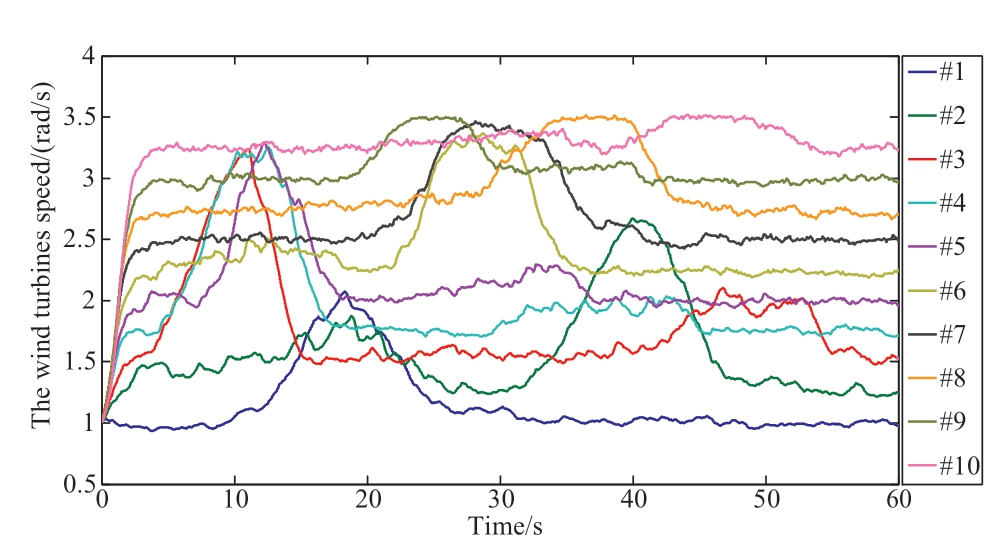
Fig.9 Rotor speed of the wind turbines using the WSWPD algorithm

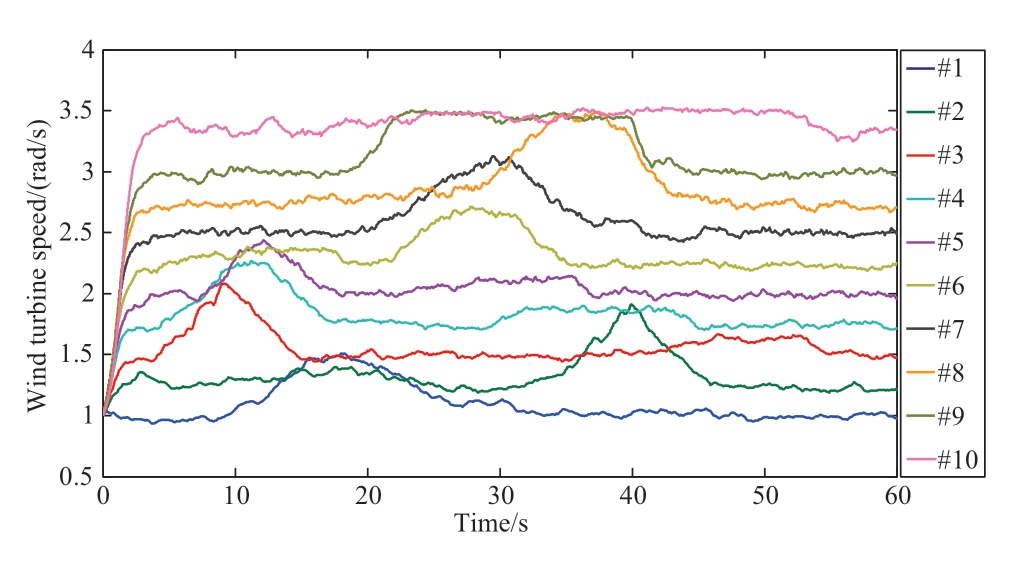
Fig.10 Rotor speed of the wind turbines using the GI-WFAPD algorithm

The pitch angle curves of the GI-WFAPD and WSWPD are shown in Fig.11 and Fig.12.The pitch travel is defined as (18),and the pitch travel of the GI-WFAPD and WSWPD are 339.85 and 311.86,respectively,and they are mostly equal.However,the pitch angle of the high wind speed wind turbine of the GI-WFAPD is less than that of the WSWPD,such as the 10th wind turbine.Therefore,the pitch angle balance index of the wind farm is defined as(19),k indicates the number of the highest wind speed wind turbines,the pitch angle balance index is large,and the total wind farm blade load is low.The pitch angle balance index of GI-WFAPD is 0.677,and the pitch angle balance index of WSWPD is 0.035.This shows that the high wind speed wind turbine blade load of GI-WFAPD is less than that of the WSWPD,which increases the lifespan of the blade.

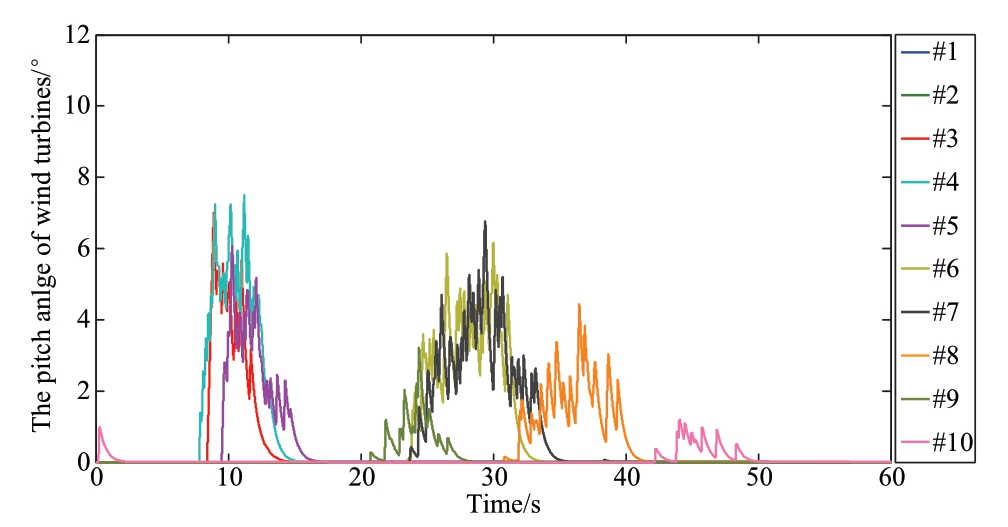
Fig.11 Pitch angle of the wind turbines using the WSWPD algorithm

Fig.12 Pitch angle of the wind turbines using the GI-WFAPD algorithm

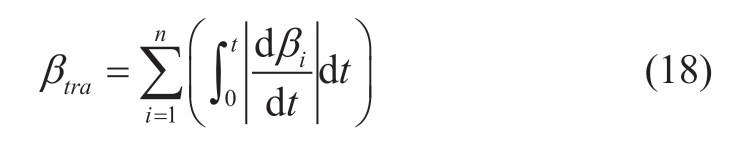
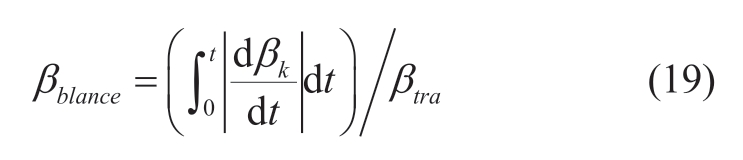
According to the active power command data history of the wind farm,suppose that the active power command range of the wind farm is 4–5 MW,and the initial rotor speed and initial pitch angle of the wind turbines do not change,as previously mentioned.The resulting IAE index,power smoothness,rotational speed smoothness,and pitch angle balance of the wind farms are shown in Fig.13,Fig 14,Fig.15,and Fig.16,respectively.The simulation results show that the power command tracking effect of the GI-WFAPD is better than that of the WSWPD,and the blade and shaft loads of the GI-WFAPD are less than those of the WSWPD.The GI-WFAPD algorithm can reduce the load on wind turbines,increase the stability of the grid,extend wind farm life,and reduce the maintenance costs associated with wind farms.

Fig.13 IAE index of the two dispatching algorithms

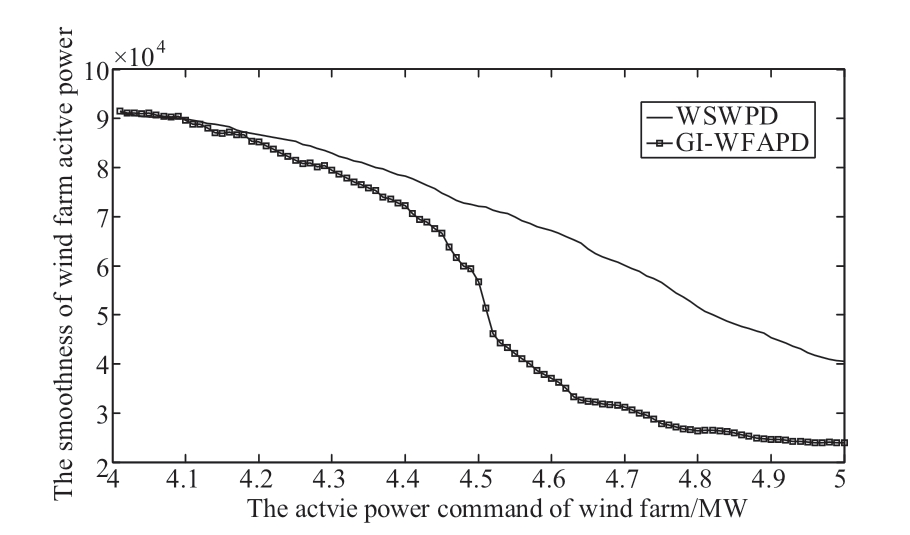
Fig.14 Power smoothness of the two dispatching algorithms

Fig.15 Rotor speed smoothness of the two dispatching algorithms

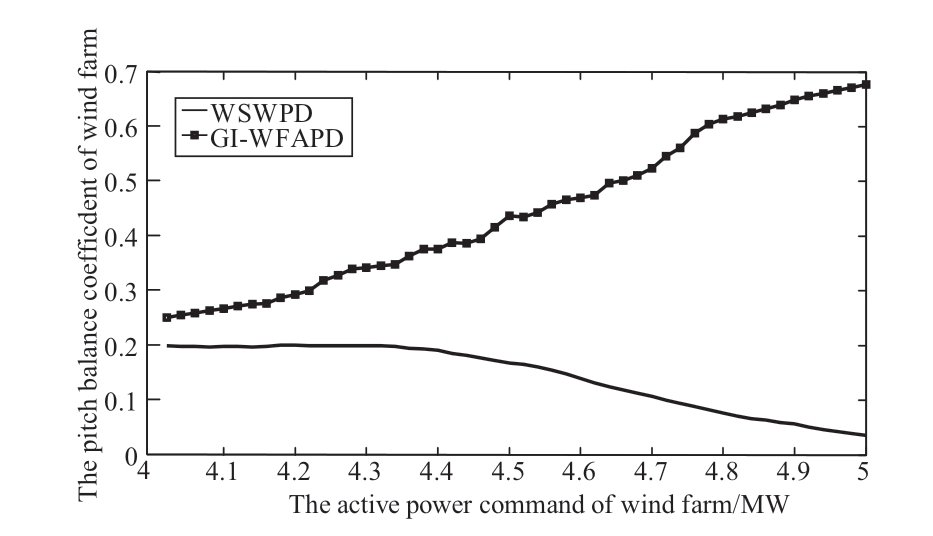
Fig.16 Pitch angle balance coefficient of the two dispatching algorithms

The findings when compared to WSWPD are satisfactory; however,it is also necessary to compare the results with the currently used new power allocation methods.In [19],a fuzzy C-mean clustering-based active power prioritizing allocation technique for wind farm layers was proposed.In [20] a id="generateCatalog_11" style="text-align: left; text-indent: 0em; font-size: 1.4em; color: rgb(195, 101, 0); font-weight: bold; margin: 0.7em 0em;">5 Conclusion

Some WFAPD algorithms are based on an accurate mathematical model of wind turbines.However,the reality of a wind turbine differs from that of a model.The wind turbine power regulation capacity was assessed using operating data to create a GI-WFAPD algorithm,which was proposed in this research.

This wind turbine power regulation capability is based on wind turbine data rather than on its model.The GI approach was used to assess the power regulation capacity of a wind turbine,and it successfully addresses the shortcomings of unreliable wind turbine models and the challenges associated with devising mathematical models.

The GI-WFAPD algorithm examines the power regulation capabilities in comparison with the WSWPD algorithm.In addition,the simulation results demonstrate a stronger tracking effect.Importantly,it can increase the lifespan of wind farms,reduce the costs associated with wind farms,and improve their efficiency.

Acknowledgements

This study was supported by the Special Scientific Research Project of the Shaanxi Provincial Education Department (22JK0414).

Declaration of competing interest

We declare that we have no conflict of interest.

References

[1] Liu Y,Cong Y,Yuan S,et al.(2021) Analysis and promotion of power quality and power control capability of wind farms.Proceedings of 2021 IEEE 4th International Conference on Automation,Electronics and Electrical Engineering (AUTEEE),pp 119-124

[2] Kazda J,Cutululis N A (2020) Model-optimized dispatch for closed-loop power control of waked wind farms.IEEE Transactions on Control Systems Technology,28(5): 2029-2036

[3] Xia X,Xie H,Zhao T,et al.(2020) Wind farm predictive coordination control strategy.Proceedings of 2020 IEEE 4th Conference on Energy Internet and Energy System Integration(EI2),pp 4004-4008

[4] Guo Z,Wu W (2022) name="ref5" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[5] Huang C,Yang H,Wang L,et al.(2020) name="ref6" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[6] Ye L,Zhang C,Tang Y,et al.(2020) Hierarchical model predictive control strategy based on dynamic active power dispatch for wind power cluster integration.Proceedings of 2020 IEEE Power & Energy Society General Meeting (PESGM),pp 1-1

[7] Xu R,Zhang G,Zhang K (2021) Coordinated control of wind farm power prediction based on PSO-MPC model.Proceedings of 2021 IEEE 2nd International Conference on Information Technology,Big Data and Artificial Intelligence (ICIBA),pp 1176-1180

[8] He D,Shen S,Wang H,et al.(2019) Wind farm combined forecasting method based on wavelet packet decompositionnew PSO-Elman neural network.Proceedings of 2019 IEEE 4th Advanced Information Technology,Electronic and Automation Control Conference (IAEAC),pp 534-537

[9] Dong H,Zhao X (2022) Wind-farm power tracking via previewbased robust reinforcement learning.IEEE Transactions on Industrial Informatics,18(3): 1706-1715

[10] Guo Z,Wu W (2022) name="ref11" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[11] Zhang S,Lu Z,Qiao Y (2021) Frequency regulation parameter identification of wind farm AGC system based on data driven technology.Proceedings of 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2),pp 3323-3328

[12] Caruntu C F (2019) Distributed predictive control for wind farms efficiency maximization: challenges and opportunities.Proceedings of 2019 6th International Conference on Control,Decision and Information Technologies (CoDIT),pp 452-457

[13] Yi Y,Bai X,Zhang J,et al.(2021) Second-order fast nonsingular terminal sliding mode fault tolerant control for windturbine system.Proceedings of 2021 International Conference on Control Science and Electric Power Systems (CSEPS),pp 29-34

[14] Pehlivan A S,Bahceci B,Erbatur K (2021) Performance analysis of a pitch angle controller for 2MW wind turbine under abrupt wind speed conditions.Proceedings of 2021 International Conference on Electrical,Computer and Energy Technologies(ICECET),pp 1-5

[15] Liu X,Zhao Q,Lu J (2020) Simulation method of semi-physical wind power generation based on combined wind speed and tip speed ratio.Proceedings of 2020 Chinese Automation Congress(CAC),pp 1805-1809

[16] Huang D,Li H,Cai G,et al.(2019) An efficient probabilistic approach based on area grey incidence decision making for optimal distributed generation planning.IEEE Access,7: 93175-93186

[17] Thodsaporn N,Kinnares V (2020) Wind turbine ssimulator equipped with real-time monitoring and user-friendly parameter setup controlled by C2000 microcontroller.Proceedings of 2020 17th International Conference on Electrical Engineering/Electronics,Computer,Telecommunications and Information Technology (ECTI-CON),pp 713-716

[18] Jellali A,Maatallah H,Ouni K (2022) Predicting remaining useful life of wind turbine bearing using linear regression.Proceedings of 2022 5th International Conference on Advanced Systems and Emergent Technologies (IC_ASET),pp 357-362

[19] Liu Y,Zhao Z,Wang X,et al.(2021) Active power distribution method for wind power cluster based on cluster analysis.Journal of Solar Energy,42(5): 430-436

[20] Liu J,Zhang B,Zhao C (2019) name="ref21" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[21] Lin Y,Zhang C,Tang Y,et al.(2018) Active power stratification predictive control approach for wind power cluster with multiple temporal and spatial scales coordination,Chinese Journal of Electrical Engineering,38(13): 3767-3780+4018

Full-length article

Received: 25 November 2022/ Accepted: 27 February 2023/ Published:25 April 2023

Chaobo Chen

chenchaobo@xatu.edu.cn

Binbin Zhang

624461918@qq.com

Mengxin Jia

215588836@qq.com

Kun Wang

wangk@xatu.edu.cn

Jichao Li

474501989@qq.com

2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Binbin Zhang received bachelor’s degree at Xi’an Technological University,Xi’an,Shaanxi,2008; received master degree at Xi’an Technological University,Xi’an,Shaanxi,2015; received phD degree at Xi’an University of Technology,Xi’an,Shaanxi,2021.He is currently working in Xi’an Technological University.His research interest covers intelligent control,wind turbine.

Mengxin Jia received bachelor’s degree at North China University of Science and Technology,Tangshan,Hebei,2017.She is pursuing a master degree at Xi’an Technological University,Xi’an,Shaanxi.Her research interests include wind turbines.

Chaobo Chen received bachelor degree at Xi’an Technological University,Xi’an,Shaanxi,2001; received master degree at Xi’an Technological University,Xi’an,Shaanxi,2009; received phD degree at Xi’an University of Technology,Xi’an,Shaanxi,2022.He is currently working in Xi’an Technological University.His research interest interests include intelligent control,fault diagnosis,and fault tolerant control.

Kun Wang received bachelor degree at Xi’an Technological University,Xi’an,Shaanxi,1998; received master degree at Xi’an Jiaotong University,Xi’an,Shaanxi,2005.She is working in Xi’an Technological University.Her research interests cover control theory and control engineering,pattern recognition,and intelligent systems.

Jichao Li received bachelor degree at Xi’an Technological University,Xi’an,Shaanxi,2013; received master degree at Xi’an Technological University,Xi’an,Shaanxi,2016.He is working in Xi’an Technological University.His research interests include intelligent control.

(Editor Yajun Zou)