0 Introduction

Considering the prominent issues of environmental pollution and the energy crisis,renewable energy has attracted more attention and developed rapidly,especially wind power (WP) and photovoltaics (PV).As the penetration rates of WP and PV increase,the integration of WP and PV presents many challenges to the operation of the grid.In particular,the peak-shaving problem is prominent [1-3].This is partly due to the increase in grid backup demand caused by the uncertain outputs of the WP and PV.Another reason is that the anti-peak characteristic of the WP output and the mismatch between the PV output and the peak load lead to an increase in the net load peakvalley difference of the grid.The increasing pressure of peak shaving not only reduces the economy of grid operation but also lowers the utilization ratio of power equipment,resulting in a significant waste of social resources[4-6].Therefore,it is practically significant to propose an appropriate method for relieving the peak-shaving pressure of a grid integrated with numerous WPs and PVs.

Energy storage technology with energy transfer characteristics has always been considered one of the most promising technologies for solving such problems [7-9].It can transfer the power in the peak period of the new energy output to the valley period,reducing the system peakvalley difference owing to the mismatch of the peak period between the power supply and requirement.In addition,energy storage can provide auxiliary services,such as capacity backup,making it an ideal peak-shaving resource[10].Currently,large-capacity energy storage technologies applicable to the grid for peak shaving mainly include pumped storage systems (PSS),electrochemical storage systems (ESS),and compressed air storage systems [11,12].

Research on peak shaving by adopting energy storage technology has been extensively explored and can be divided into the following two categories:

1) First,the energy storage methodology assisting conventional peak-shaving units.For instance,a regulation strategy for peak shaving of combined WP and energy storage systems was proposed in [13].The PSS is used to shift the WP output in time and space to smooth the net load curve and reduce the coal cost of the thermal power output.However,from a practical perspective,PSS have strict requirements regarding the geographical conditions.It is generally not suitable to build a pumped-storage power station in a place with rich WP resources.Ref.[14] proposed a double-level optimization model for the allocation of ESS,which was used to improve the operational efficiency of wind farms and the accommodation of WP.However,the impact of the ESS on the peak-shaving economy was not considered.There is a large capacity requirement for power and energy in WP peak-shaving scenarios,which means that the cost of the ESS cannot be underestimated.

2) The second is to coordinate the energy storage with other peak-shaving resources for optimal dispatching.For instance,in [15],the charging and discharging behaviors of electric vehicles were considered a means of peak shaving on the demand side and were coordinated with energy storage.Ref.[16] used a power-load storage system to reduce the peak-valley difference and large fluctuations of the microgrid tie-line power caused by the integration of large-scale renewable energy into the grid.The authors of[17] regarded flexible loads on the demand side and actual energy storage as generalized energy storage resources.A day-ahead and day-in two-stage rolling optimization model for peak shaving was proposed by combining generalized energy storage and thermal power units.However,in these studies,the transmission capacity of the transmission grid(TG) is not considered in the peak-shaving scenarios.The effective responses of various peak-shaving resources are related to the grid structure.In addition,the peak-shaving capacity of the power system is limited in the case of congested transmission or restricted power flow sections.

Based on the above analysis,this study proposes a combined hybrid energy storage system (HESS) and a TG model for peak shaving based on a time-series operation simulation (TSOS).The model applies the HESS to peak shaving and fully considers the operational variation characteristics of the grid.Under the given power system operation boundary conditions,it can simulate the peakshaving scenarios of a future high-proportion new energy system.The main innovations of this study are as follows:

1) The complementary advantages of different energy storage methods were considered.A new type of liquid compressed air energy storage (LCAES) has the advantages of high energy density,large capacity,and freedom from geographical constraints.However,it is relatively limited in flexibility [18,19].A HESS consisting of an LCAES,PSS,and ESS was proposed for peak shaving.A linear HESS operation model was established based on the powerefficiency (P-E) relationships of the energy storage.

2) By adding linearized power-flow constraints (LPFCs)of the TG,an operational simulation model for peak shaving considering the transmission capacity of the TG was established.

The remainder of this paper is organized as follows:Section 1 establishes the HESS operation model based on the linearized P-E characteristics.Section 2 describes TSOS-based HESS and TG combination models for peak shaving.Section 3 presents the case study,and Section 4 discusses the research conclusions.

1 Modeling of HESS

1.1 Linearization of HESS P-E characteristic

Different energy storages have unique charging and discharging P-E characteristics,which can be described by a P-E curve.However,the consideration P-E relations in optimization models usually implies the introduction of non-linear constraints.This leads to a mixed-integer non-linear programming problem,which belongs to the nondeterministic polynomial (NP) puzzle.Therefore,as shown in Fig.1,a linearization method is necessary to improve the validity and reliability of the model under the concordant operation strategy of the HESS.

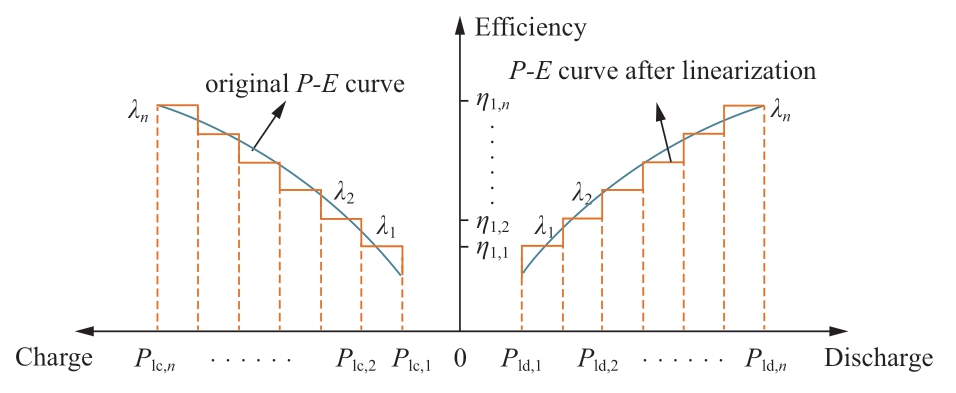
Fig.1 Piecewise linearization of P-E curve of LCAES

In Fig.1,the original non-linear curve reflects the P-E characteristics of LCAES.Its charging and discharging efficiencies increase when the output power approaches the rated range and are distinctly lower when the power is far from the rated power.Then,the discharging coordinate axis is divided into n-1 intervals by coordinating Pld,1,Pld,2,…,Pld,n and the corresponding efficiency of each interval endpoint is ηl,1,ηl,2,…,ηl,n.Breakpoints k = 1,2,…,n are associated with the continuous variable λk ∈[0,1].In addition,the integer auxiliary variables Z1,Z2,…,Zn are introduced to ensure that the number of adjacent nonzero variables of λk does not exceed two.The linearization process is illustrated in Fig.2.

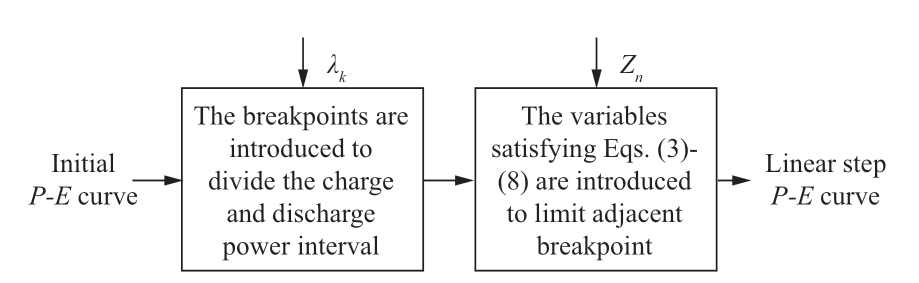
Fig.2 Linearization process of P-E curve

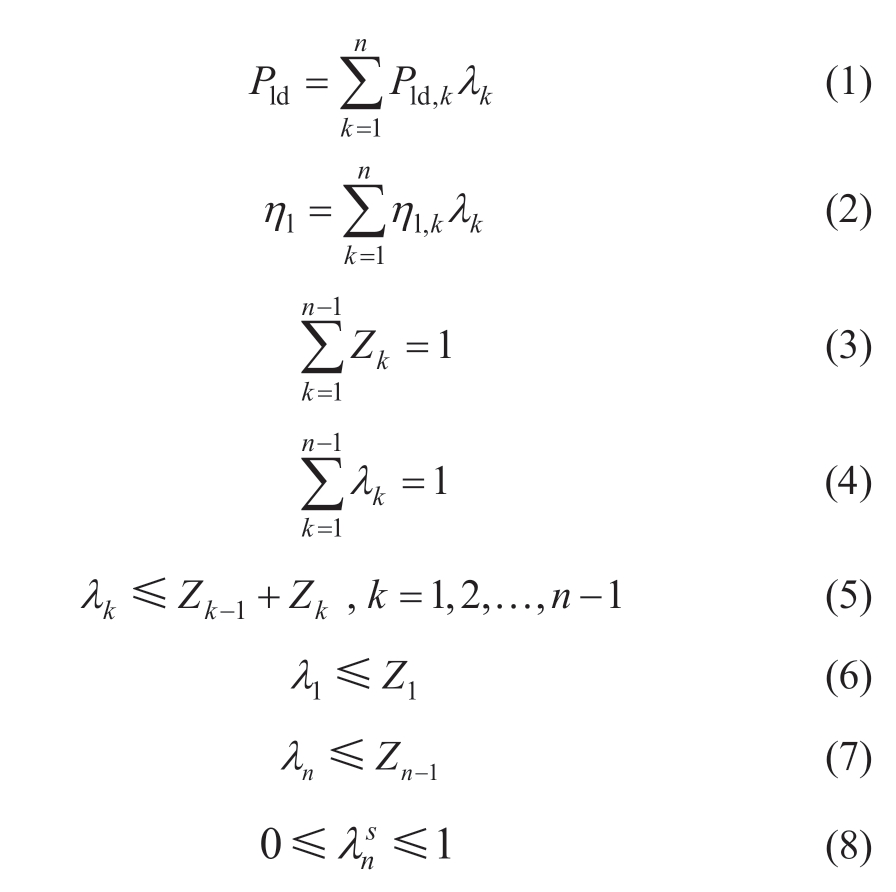
Equation (1) indicates that discharging power P1d can be expressed as the product of the different weight λk and the endpoint of the divided interval.Therefore,the efficiencyηl can be expressed as the product of the endpoint function value and weight λk.Equation (3) indicates that only one Zk can be considered as one,whereas the others are zero.Each function value is guaranteed to be represented by only two breakpoints.The adjacent λk cannot be zero,as guaranteed by Eqs.(4)-(8).

The charge efficiency of a general PSS is usually considered to be constant owing to the narrow charging power of a single pump,and its discharging P-E characteristics are similar to those of LCAES.In particular,ESS are considerably different.Its efficiency was relatively stable and close to a constant value.As shown in Fig.3 and Fig.4,the above linearization method was adopted for the P-E curves of PSS and ESS,respectively.

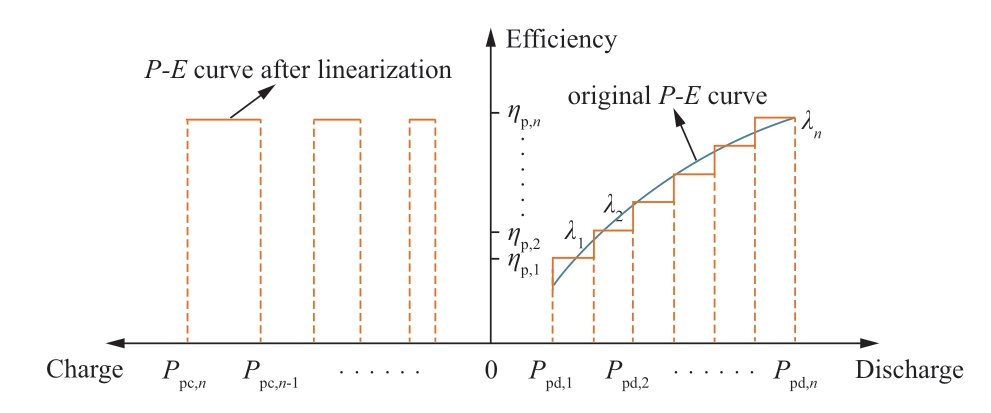
Fig.3 Piecewise linearization of P-E curve of PSS

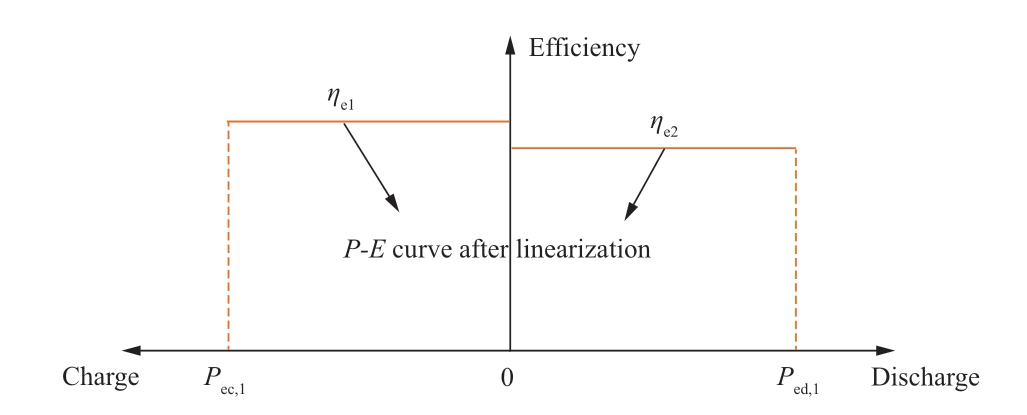
Fig.4 Piecewise linearization of P-E curve of ESS

1.2 Modeling of HESS operation

For the sake of economy and safety,energy storage must satisfy operational constraints.Therefore,based on the above linearized P-E relationship,this study establishes an operation model of the HESS.

1.2.1 Power and state constraints of HESS

Power constraints are required to ensure that the energy storage output is within the specified range,which can be modeled as follows:

(i) Power and state constraints of LCAES

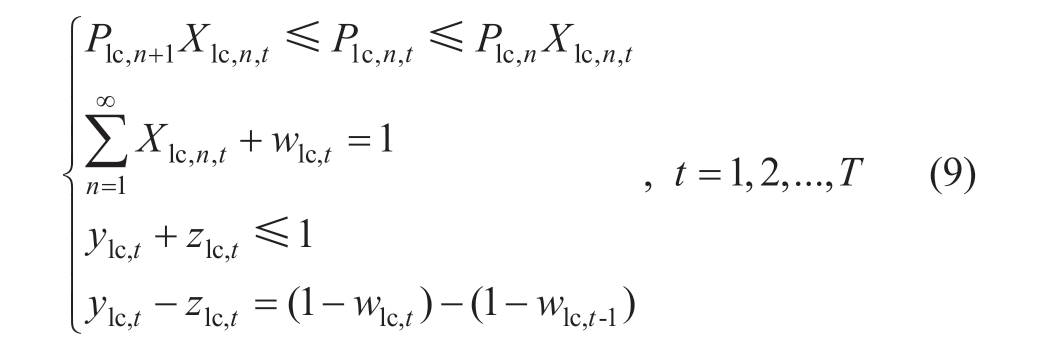
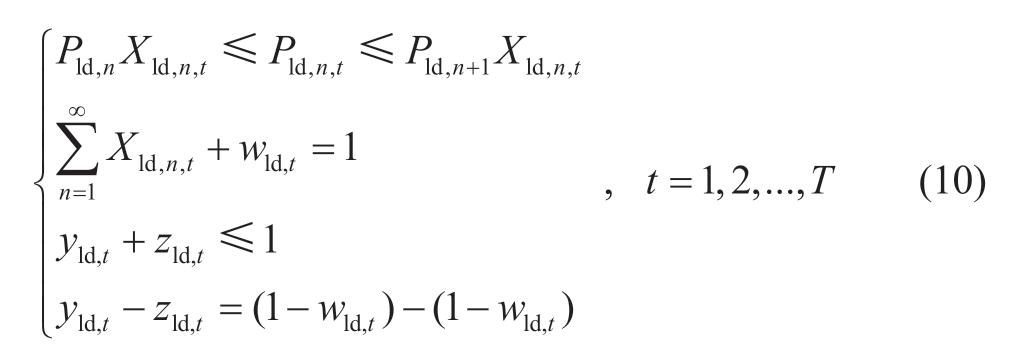
(ii) Power and state constraints of PSS

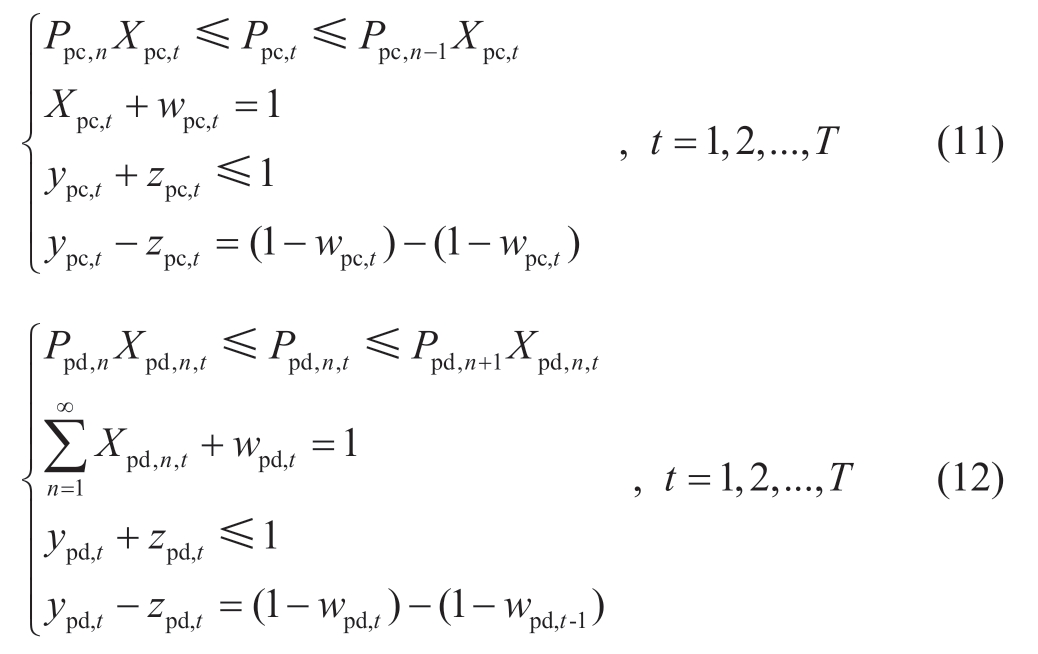
(iii) Power and state constraints of ESS

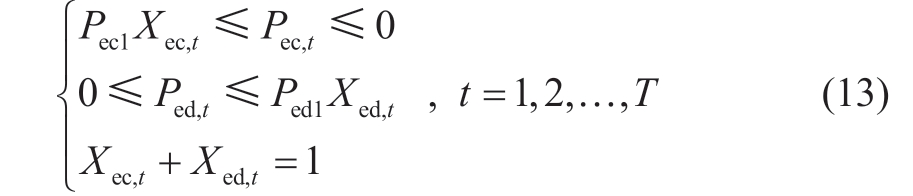
1.2.2 Electrical constraints

After linearization,the relationships among electricity,power,and energy storage efficiency can be described as follows:

(i) Electrical constraints of LCAES

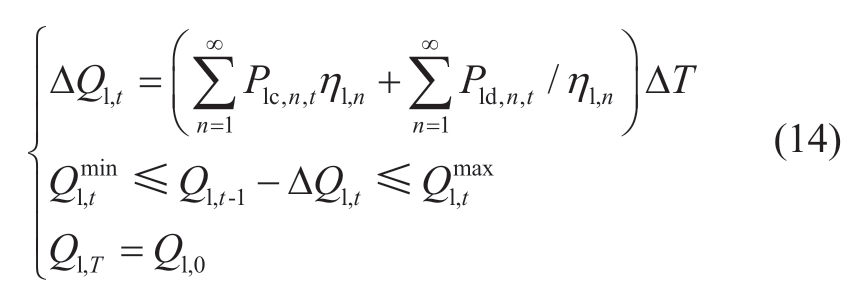
(ii) Electrical constraints of PSS

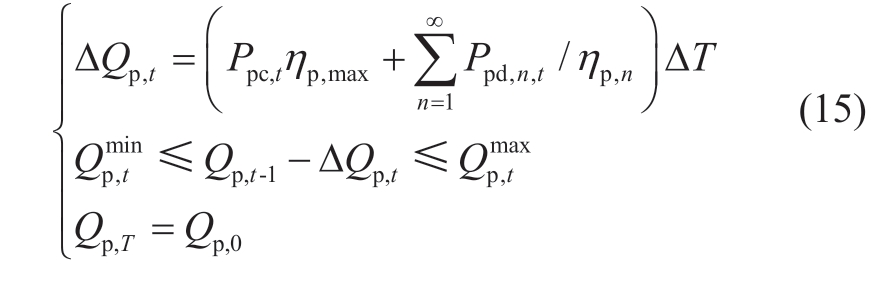
(iii) Electrical constraints of ESS

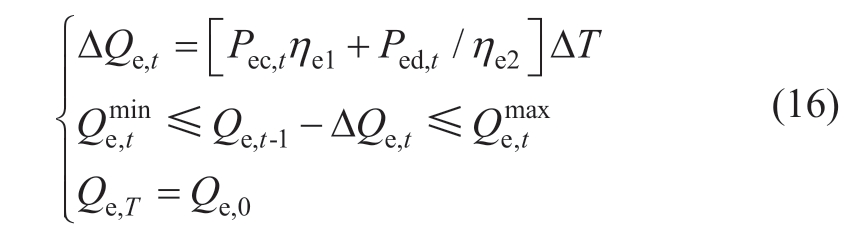
1.2.3 Minimum downtime constraints

Frequent start-ups and shutdowns cause damage to energy-storage devices.From an economic point of view,startup and shutdown also increase the operation cost.Therefore,it is necessary to limit the startup and shutdown times of energy storage.As the ESS in this study was used to respond to rapid load fluctuations throughout the day,the minimum downtime constraint of the ESS was not considered.

(i) Minimum downtime constraints of LCAES

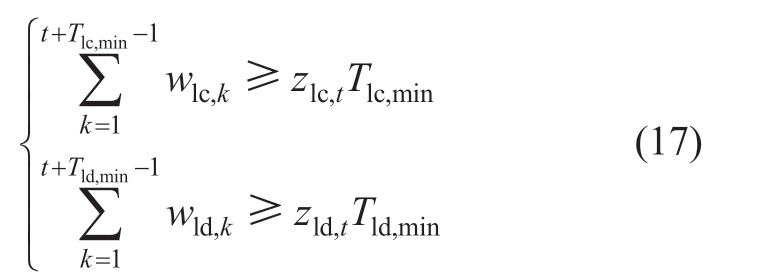
(ii) Minimum downtime constraints of PSS

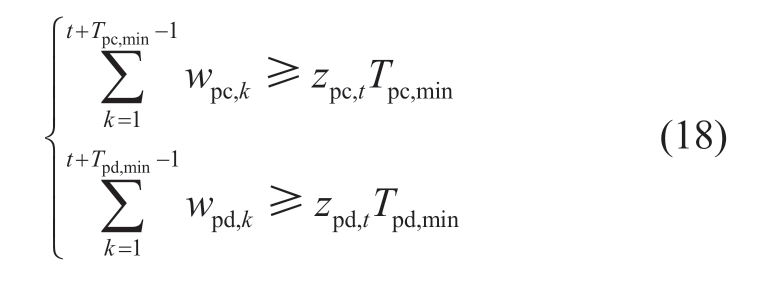
1.3 Energy management strategy of HESS for peak shaving

To provide the respective peak-shaving advantages of PSS,LCAES,and ESS in full play,this paper proposes an energy management strategy of HESS for peak shaving.The charge and discharge power thresholds of the LCAES and the PSS were set using this strategy.With the help of the large capacity of the two kinds of energy storage,the larger load in the “peak” and “valley” sections is reduced.Because the ESS has a small time range for shaving and filling,the lower charge and discharge threshold of the ESS is set to respond to smaller and fast-fluctuating loads.

A schematic of the peak shaving of the HESS is shown in Fig.5.In area 1,the load power did not reach the PSS charging threshold Ppc or PSS discharging threshold Ppd,so the load was completely supported by the ESS.In areas 2 and 3,the load power did not reach the LCAES charging threshold Plc or LCAES discharging threshold Pld.Larger loads were supported by the PSS.In areas 4 and 5,larger loads were applied by the LCAES and PSS to achieve peak shaving and valley filling.

Fig.5 Schematic diagram of peak shaving of HESS

2 TSOS-based HESS and TG combination model for peak shaving

2.1 TSOS model of HESS for peak shaving

2.1.1 Objectives function

Considering the requirements of China’s clean power transition,the objective of the model is to maximize the sum of the WP output minus the operating cost.Here,the cost is the electricity consumed and is not converted according to the time of use (TOU) price.If the TOU price is considered,the income and cost of the objective function can be converted accordingly.

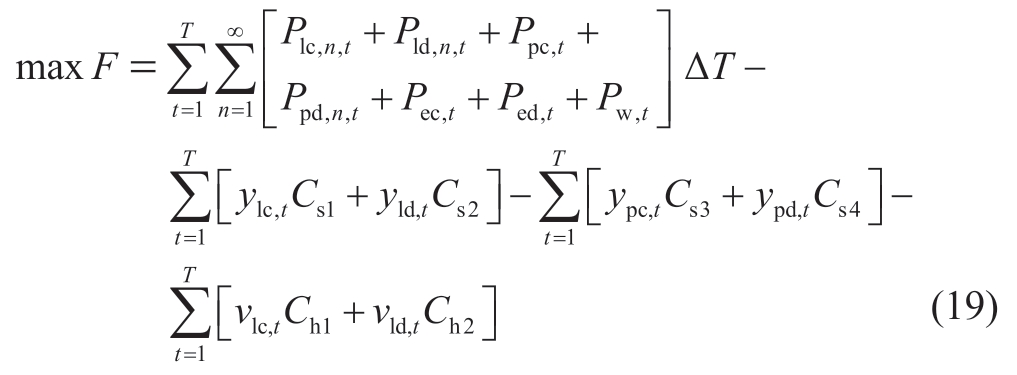
2.1.2 Constraint conditions

2.2 Proposed model considering LPFCs

2.3 Solution method and flow

The optimization software CPLEX was developed using MATLAB and Yalmip to solve the TSOS model at a time scale of 24 h.The solution flow is shown in Fig.6,and the main solution processes are as follows:

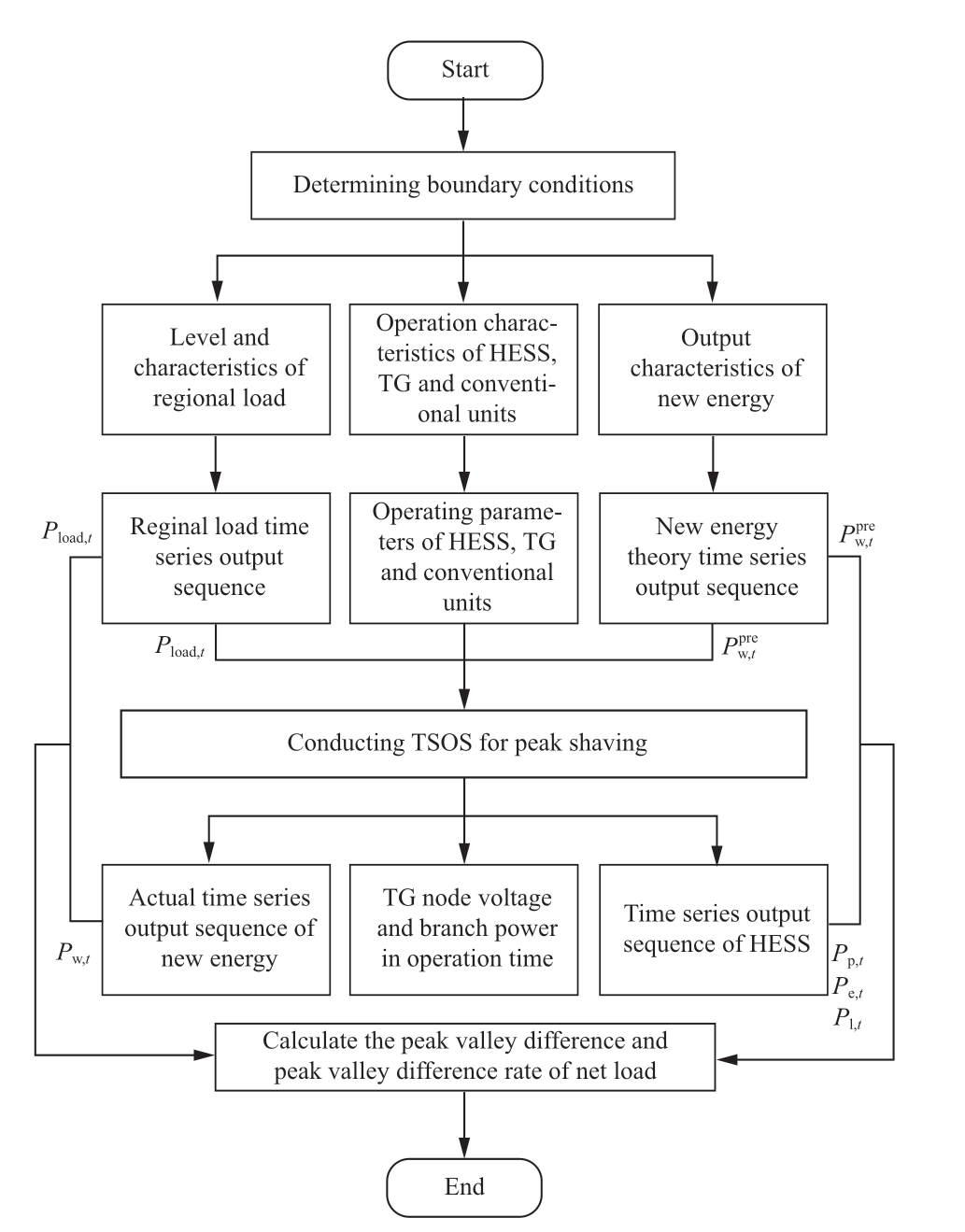
Fig.6 Flow chart of the TSOS model

1) According to the output characteristics of the new energy and regional loads,the load time-series output sequence Pload,t and the new energy theory time-series output sequence during the TSOS period are obtained.The operating characteristics of the TG,HESS,and conventional power sources are considered to obtain the operating parameters.These were used as the input boundary conditions for the TSOS.

2) Under the above boundary conditions,the TSOS for peak shaving was calculated based on the proposed model.Through optimization,the peak-shaving operation results of the grid during the TSOS period,such as the actual timeseries output sequence of new energy Pw,t and the time-series output sequence of HESS Pl,t,Pe,t,and Pp,t,are obtained.

3) According to the TSOS results of the new energy and HESS output,combined with the load output level and new energy theoretical output,the peak-shaving technical evaluation indicators,such as the peak-valley difference of the net load,the peak-valley difference rate of the net load,and new energy accommodation volume were calculated.

3 Case study

3.1 Case settings

This study used the modified IEEE39 bus system for analysis.As shown in Fig.7,a 400 MW wind farm was used to replace the No.2 thermal power unit.PSS,ESS,and LCAES were integrated into buses 14,19,and 24.The value of n in Eqs.(1) and (7) is taken as 4.The boundary conditions and scenes were set as follows:

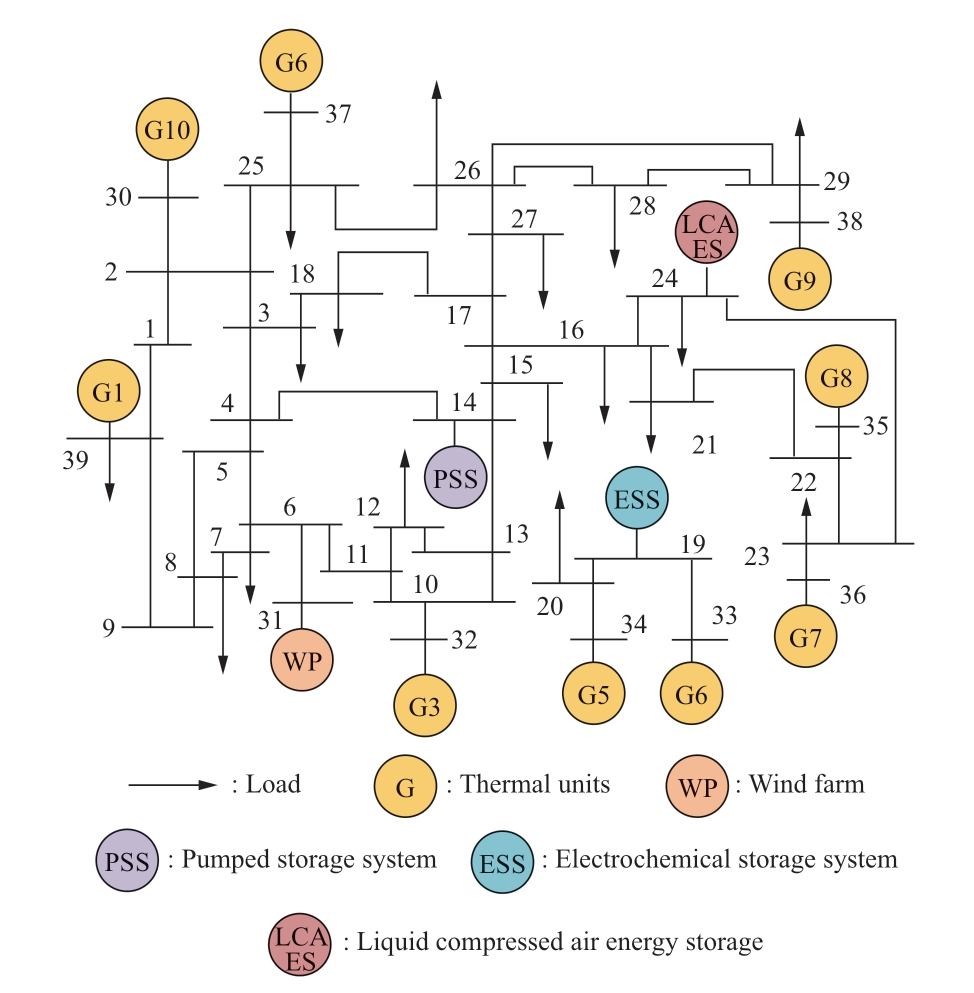
Fig.7 IEEE 39 bus system

(i) Load level and the output of WP

The TSOS was performed using time-series load data for 24 h,and the daily load utilization was approximately 18 h.The WP output data were obtained from the simulation results of a wind farm in China.The theoretical utilization time of WP was approximately 16 h.The data comprehensively considers probability division,spatiotemporal correlation,and circadian rhythm.

(ii) Boundary condition

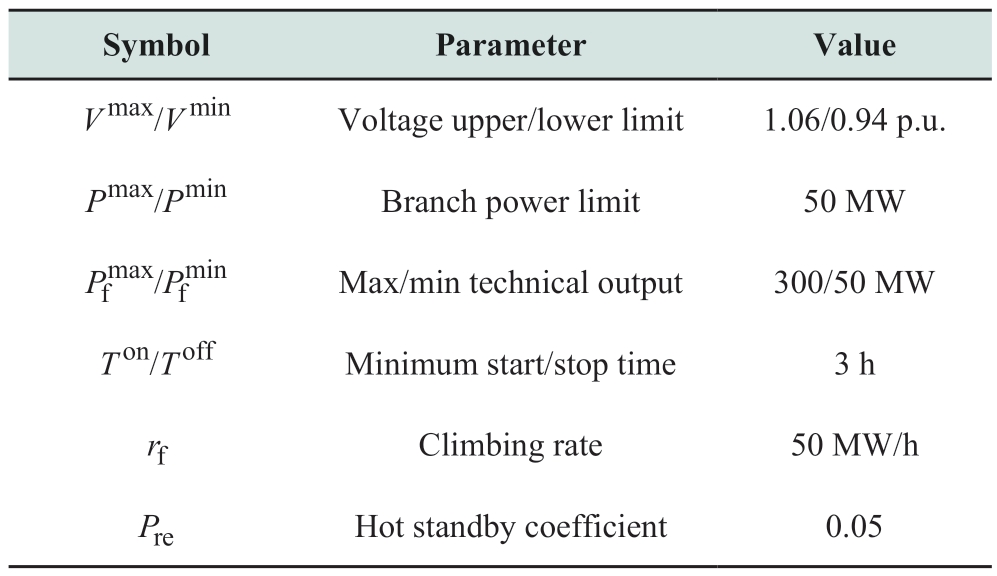
Setting the appropriate grid operation boundary conditions is an important prerequisite for accurate operational simulations.The boundary conditions of the conventional units,the HESS,and the TG were considered in the proposed model.The boundary conditions are listed in Tables 1 and 2.

Table 1 Boundary conditions of HESS

continue

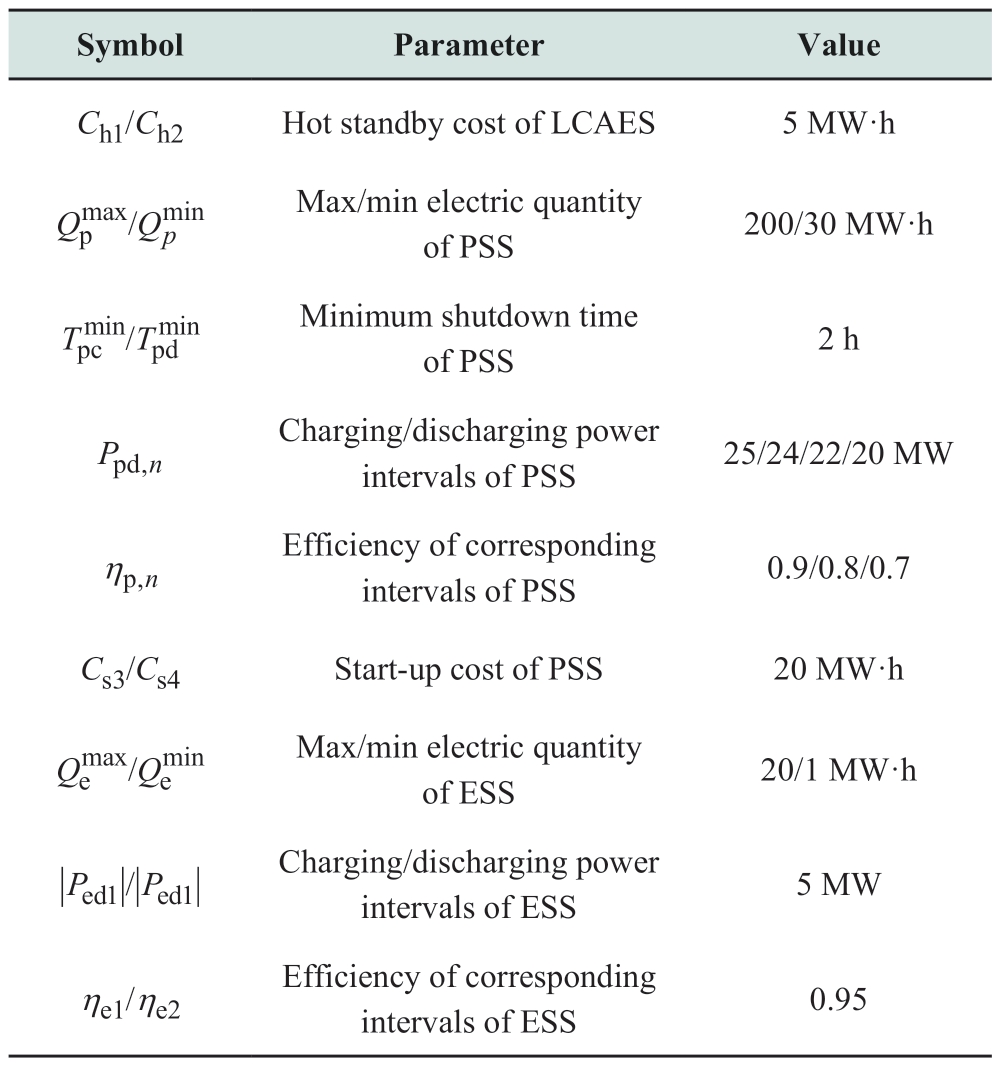
Table 2 Boundary conditions of conventional units and TG

(iii) Case scenarios

To verify the effectiveness and accuracy of the combined HESS and TG models for peak shaving,TSOS was performed for the scenarios listed in Table 3.Specific descriptions of the scenarios are as follows:

Table 3 Peak shaving operation simulation scenarios

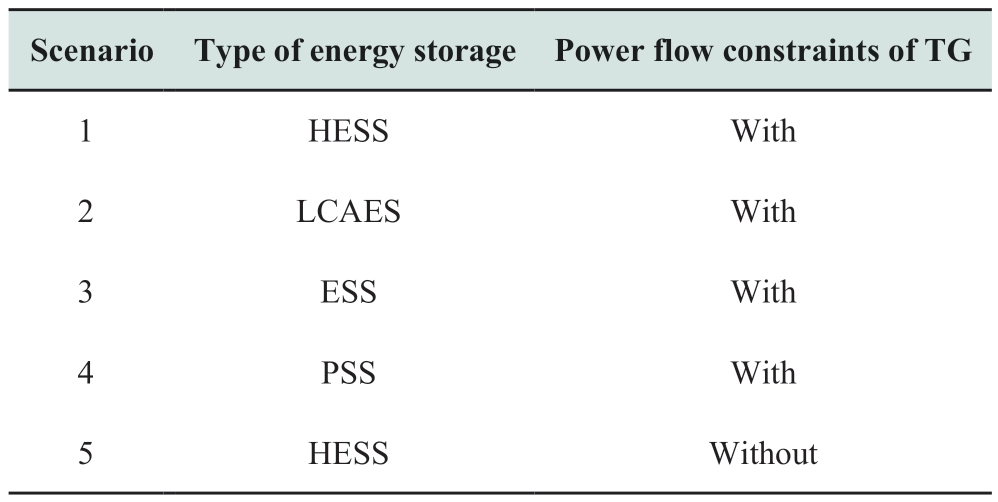
1) Scenario 1: Using the original model for peak shaving.

2) Scenarios 2–4: Based on the original model,the HESS is replaced successively by a single energy storage with equal capacity.

3) Scenario 5: The transmission capacity of TG is not considered.Others are consistent with the original model.

3.2 Analysis of operation simulation results

Figs.8 and 9 and Table 4 compare the peak-shaving effects of Scenarios 1–4.The net system loads before and after peak shaving under the four scenarios are shown in Fig.8.According to the net load curves,the maximum peak-valley difference in Scenarios 1–4 is 99.6 MW,125.3 MW,140.1 MW,and 110.2 MW,respectively,and the peak-valley difference for the entire day decreases most evidently in Scenario 1.This is also illustrated by the indices used to evaluate the degree of variation of the peak-valley difference shown in Fig.8.The maximum peak-valley difference variation (MPV),maximum peakvalley difference variation rate (MPVR),average peakvalley ratio variation (APRV),and average peak-valley ratio variation rate (APRVR) in Scenario 1 were 110 MW,49.1%,30.86%,and 37.75%,respectively.On average,they were 19% higher than the indicators in Scenarios 1–3 on average.Therefore,the decrease in the peak-valley difference in Scenario 1 is the most significant.Meanwhile,the WP accommodated in Scenario 1 is 5657 MW,and the WP accommodation rate is 91.6%,which is 11.2% higher than that of the other scenarios on average.In general,the peak -shaving effect in Scenario 1 was the best.This also means that the HESS has more advantages in terms of two important indicators for evaluating the capacity for peak shaving: the ability to reduce the peak-valley difference and accommodate new energy.

Table 4 WP accommodation in scenarios 1‒4

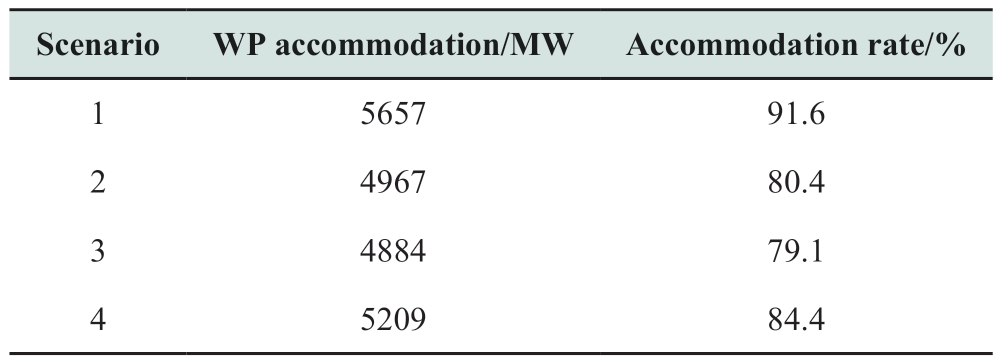
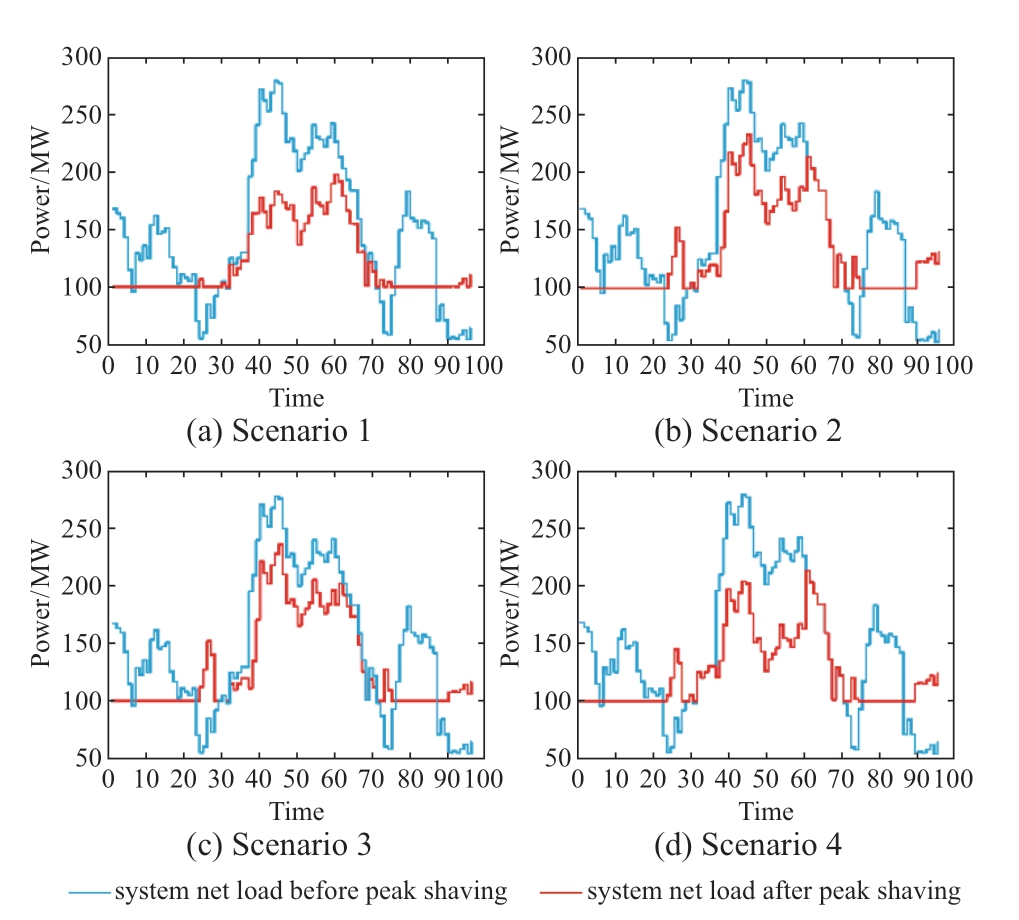
Fig.8 Net load curve of scenarios 1‒4

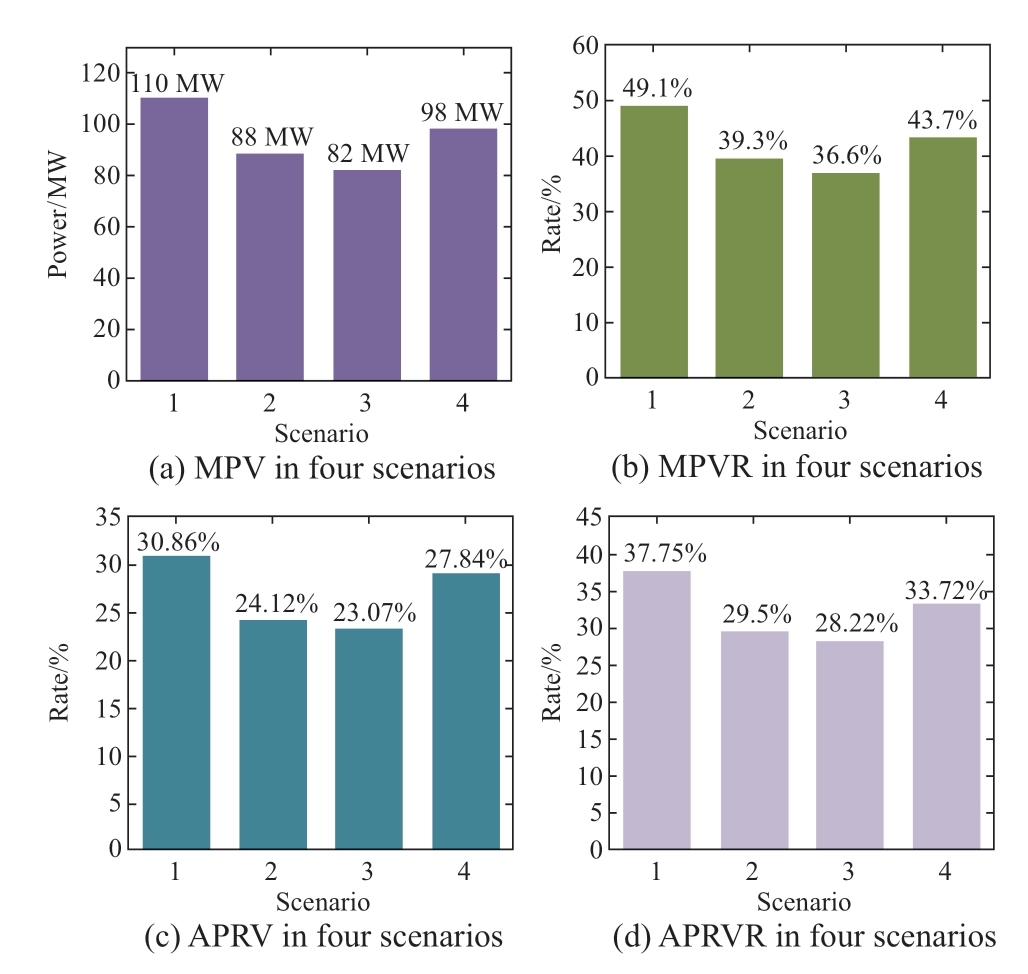
Fig.9 MPV,MPVR,APRV,APRVR for scenarios 1‒4

The output of the HESS curve,shown in Fig.10,accounts for its advantages.The LCAES and PSS can absorb the WP near the rated power during wind abandonment at time points 1–25 and 75–92,and discharge as close as possible to the rated power during the peak load period at time points 38–65.Small-amplitude loads were supported by the ESS throughout the day.Their behavior corresponds to the energy management strategy of the HESS.In addition,during the operation periods of the LCAES and PSS,such as near the three to six time points,the ESS can increase its charging power by discharging.The reasonable actions of the three types of energy storage verified the validity of the above HESS model for peak shaving.

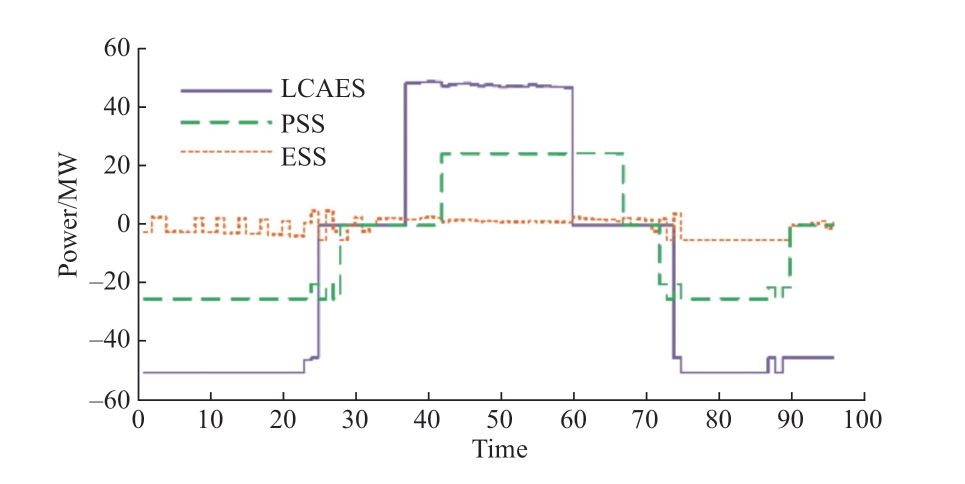
Fig.10 Output of HESS in 24 h

The peak-shaving effects between scenarios 1 and 5 are compared in Fig.11 and Table 5.The WP accommodated in Scenario 5 was 5915 MW,which was 258 MW higher than that in Scenario 1.The net load at each time point in Scenario 5 was 6.3 MW lower than that in Scenario 1 on average.This means that the obtained peak-shaving effect will be optimistic if the transmission capacity of the TG is not considered in the TSOS of the peak shaving.The addition of LPFCs to the simulation limited the system capacity for peak shaving to a certain extent.However,it is more consistent with actual production operations and schedules to consider them.This ensures that the grid can accommodate new energy to the greatest extent possible,without the voltage and power exceeding the limit during peak shaving.Thus,the operation simulation can more accurately reflect the system capacity for peak shaving,which is meaningful for evaluating the peak-shaving capacity of the system.

Table 5 WP accommodation in Scenario 1 and Scenario 5

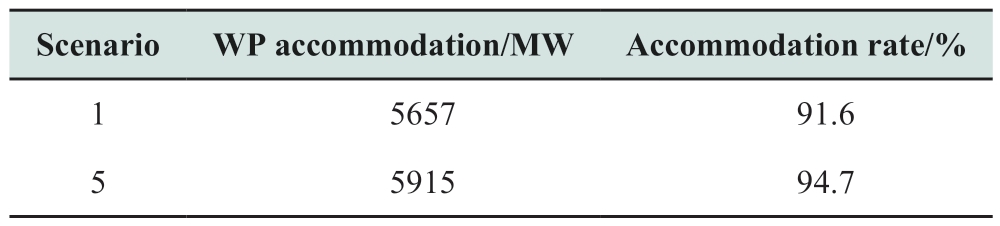
Fig.11 System net load after peak shaving in Scenario 1 and
Scenario 5

Figs.12(a) and (b) show the node voltage amplitudes in Scenarios 1 and 5 within 24 h.As shown in Fig.12(b),in the TSOS without LPFCs,the voltage amplitude of some nodes exceeds the limit at certain time sections.However,as shown in Fig.12(a),the voltage amplitude at each node at each time section was within the specified allowable range during the simulation with the LPFCs.

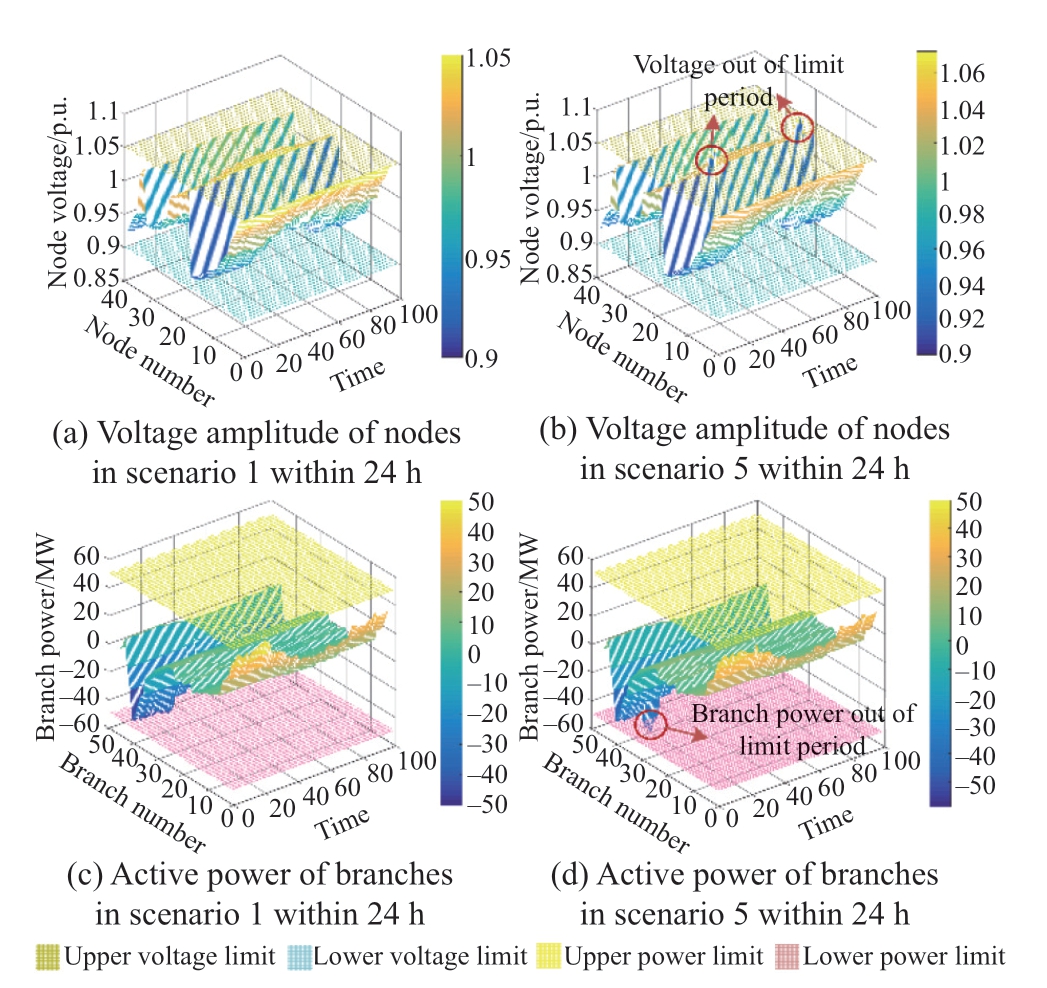
Fig.12 Node voltage and branch active power in scenario 1 and scenario 5

Figs.12(c) and (d) show the branch active powers in Scenarios 1 and 5 within 24 h.As shown in Fig.12(d),in the TSOS without LPFCs,the active power of some branches exceeded the limit in certain time sections.However,as shown in Fig.12(c),the active power at each branch in each time section was within the allowable range during the simulation with LPFCs.

3.3 Model comparisons

The solution of the new energy accommodation model based on the TSOS is a complex optimization problem with high dimensionality and multiple constraints.In this study,CPLEX was used to solve this problem by establishing a linear TSOS model.To verify the accuracy of the proposed model,the TSOS solution results are compared by applying the penalty function method based on particle swarm optimizer (PSO) [22] at different time precisions.The TSOS was performed using the two models under the same boundary conditions.Comparisons between the solution results and efficiency are presented in Table 6.The variable scales of the two models are compared in Table 7.

Table 6 Solution results and efficiency of the CPLEX and
PSO models

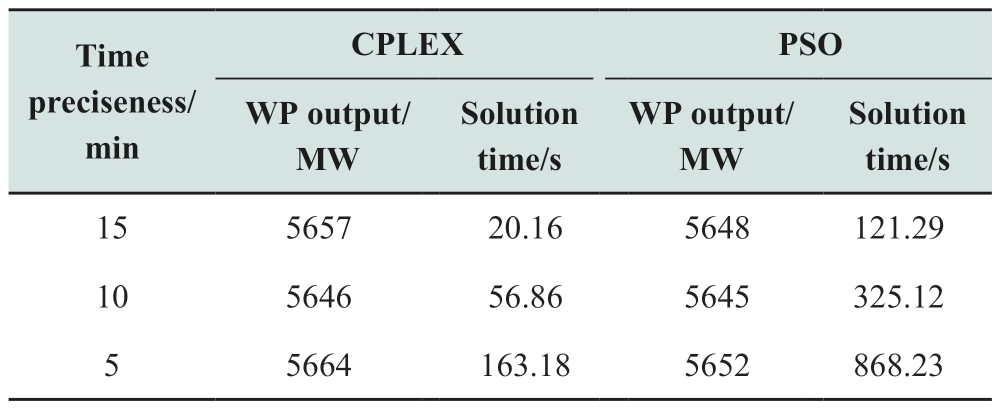
Table 7 Comparison results of different model scales

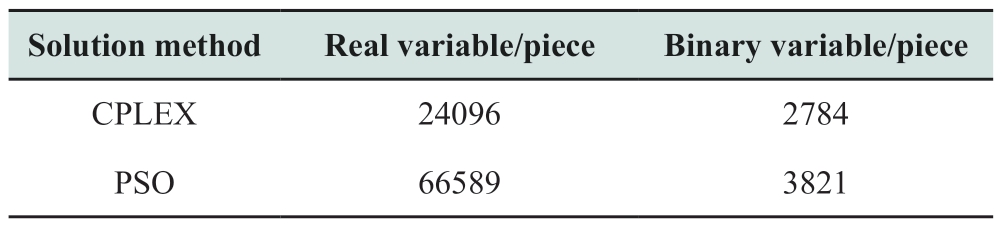
Table 6 shows that the maximum difference of WP output under different time preciseness is 18 MW.Compared with the results of PSO,the maximum difference between the two models is 9 MW for the same time preciseness.This is mainly because the power loss of TG is ignored in LPFCs.However,PSO takes more time to solve the non-linear constraints in the TSOS model.However,the linear model proposed in this study has greater advantages in solving speed.Variable scales in Table 7 explain the solving speed advantage of the model established in this study.Compared with the model solved by PSO,the variable numbers of the proposed model are lesser by 40000.Therefore,the proposed model provides a possibility for the TSOS solution acceleration while maintaining considerable feasibility.

3.4 Scalability analysis

To further illustrate the applicability of the proposed model in a more diversified renewable energy scenario,the modified IEEE-118 bus system was analyzed.The system included six wind farms,34 thermal power units,six LCAES power stations,five hydropower stations,and five ESS units.The parameters of each unit remained unchanged compared with those in Table 1–2.The predicted load values are presented in Fig.13.The installed capacity of the WP was 1800 MW,and its output accounted for approximately 46% of the total load.

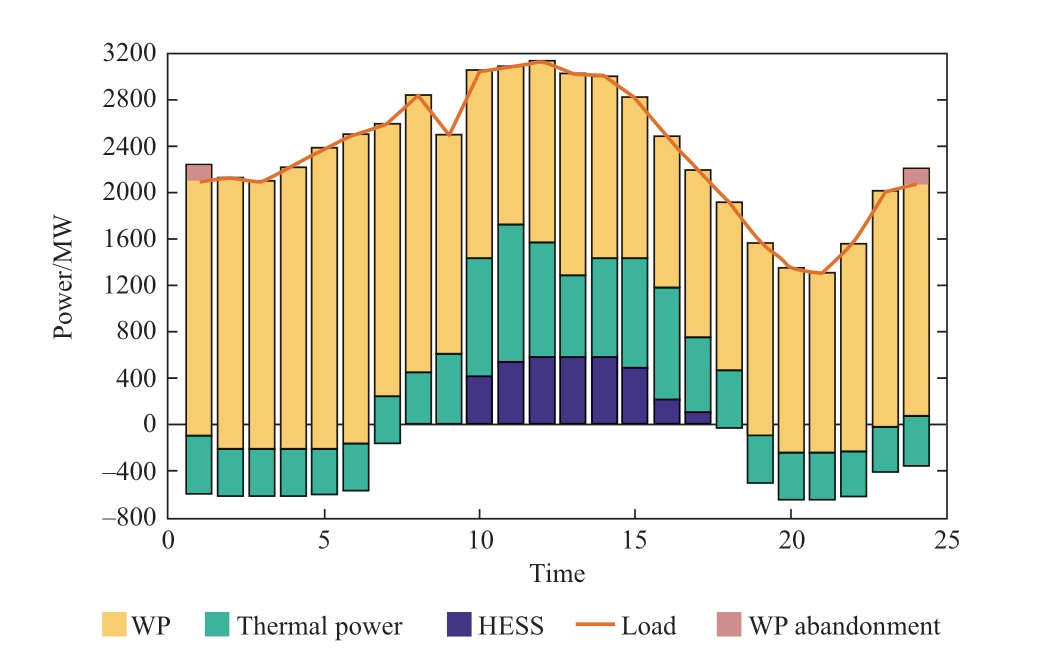
Fig.13 System power balance

The power balance of the system is shown in Fig.13.During the TSOS period,the power sources maintained a power balance with the load and the wind abandonment rate was 5.32%.The HESS accommodates 23018 MW of WP during the wind abandonment period at 0–25 and 75–96 time points,and releases 17852 MW of energy during the peak load period at 35–65 time points.The node voltage and branch power at each time point are shown in Fig.14,and are all within the allowable range.Therefore,the proposed model is scalable and effective for complex renewable energy integration scenarios.

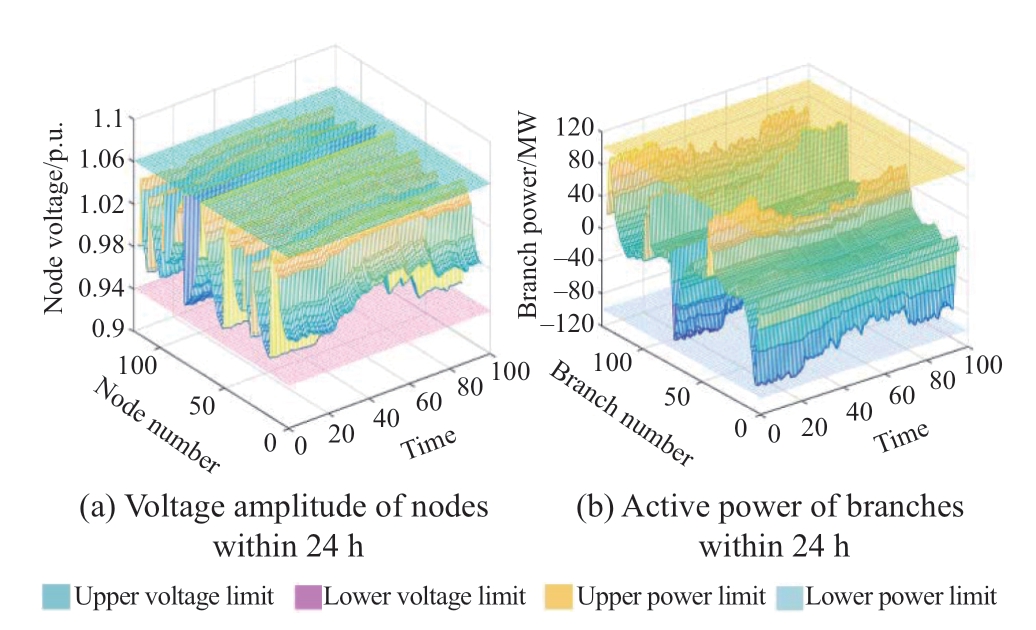
Fig.14 Voltage amplitude of nodes and active power of branches within 24 h

4 Conclusion

In this study,a TSOS-based HESS and TG combination model for peak shaving is proposed,considering the P-E relationships of energy storage and the transmission capacity of the TG.The proposed model is used to simulate the peakshaving scenario of a wind farm in China.The peak-valley differences of the net load,accommodated WP,and other simulation results under different peak-shaving strategies were analyzed.The conclusions are as follows:

1) The HESS exhibited a good peak-shaving effect.It transfers 4080 MW of WP from the low-peak period to the peak-load period.The maximum peak-valley difference of the regional net load was reduced by 50.4%,and the WP accommodation rate was increased by 20.6%.Compared to single energy storage,the new energy accommodation rate using the HESS for peak shaving increased by 10.4% on average,and the maximum peak-valley difference decreased by 9.2%.

2) The transmission capacity of the TG in the TSOS of peak-shaving is more consistent with the actual production operation and dispatching.This makes the production simulation more accurate for the assessment of the system capacity for peak shaving,which has a guiding significance for future power system planning.

3) The linear TSOS model established in this study has significant advantages in terms of solving efficiency and has practical value in complicated,high-proportion new energy integration scenarios.

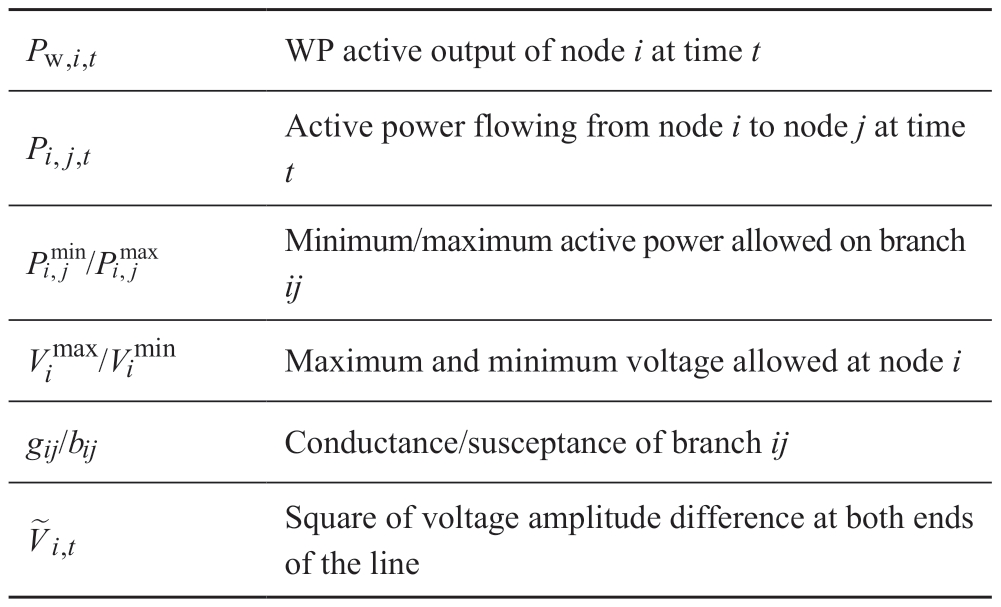
Nomenclature

continue

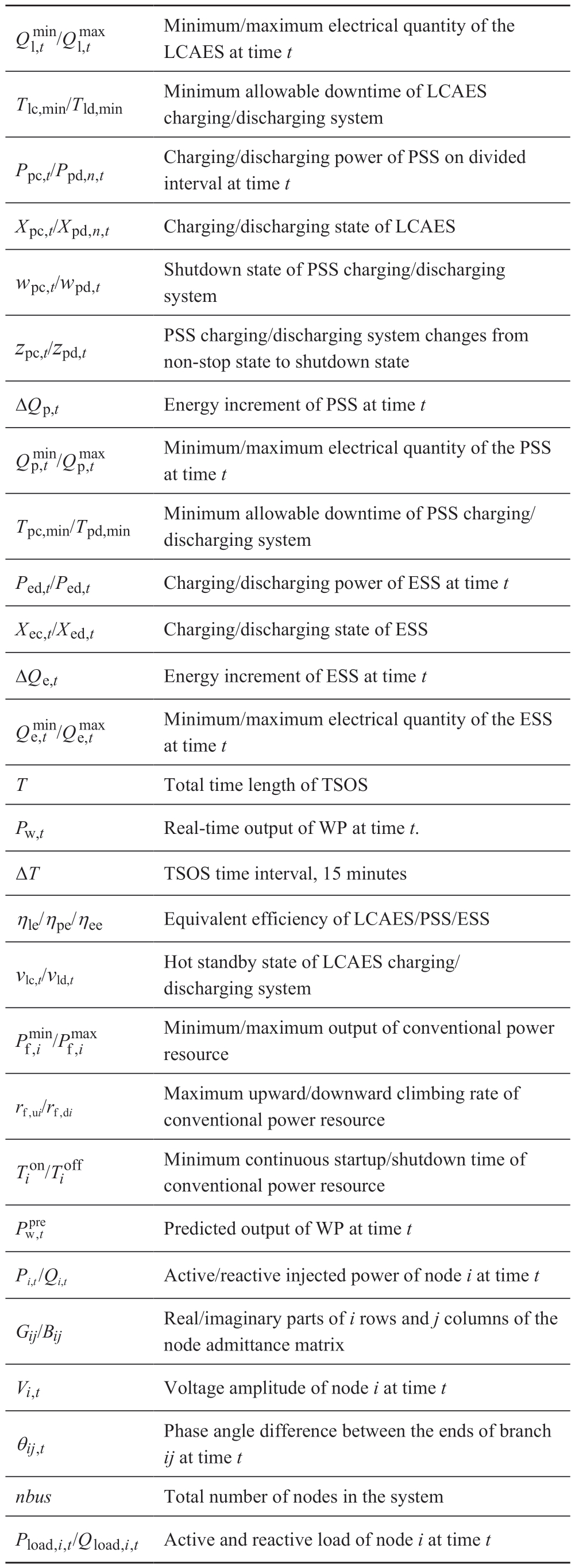
continue

Acknowledgements

This study was supported by the State Grid Science and Technology Project (No.52999821N004).

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] Zhang L,Ye T,Xin Y,et al.(2010) Problems and measures of power grid accommodating large scale wind power.Proceedings of the CEEE,30(25): 1-9

[2] Zhu L,Chen N,Han H,et al.(2011) Key problems and solutions of wind power accommodation.Automation of Electric Power Systems,35(22): 29-34

[3] Xu G,Chen H,Ma Z,et al.(2017) A review of planning methods for energy storage systems to relieve grid peaking pressure.Electric Power Automation Equipment,37(8): 3-11

[4] Shu Y,Zhang Z,Guo J,et al.(2017) Study on key factors and solution of renewable energy accommodation.Proceedings of the CEEE,37(1): 1-8

[5] Lu Z,Li H,Qiao Y,et al.(2017) Flexibility evaluation and supply/demand balance principle of power system with highpenetration renewable electricity.Proceedings of the CEEE,37(1): 9-20

[6] Zhuo Z,Zhang N,Xie X,et al.(2021) Key technologies and developing challenges of power system with high proportion of renewable energy.Automation of Electric Power Systems,45(9):171-191

[7] Yan G,Feng X,Li J,et al.(2012) Capacity allocation method of energy storage system for relaxing peak shaving bottleneck.Proceedings of the CEEE,32(28): 27-35+22

[8] Tong J,Hong Q,Lv H,et al.(2021) Overview of the development status and application prospects of power-side energy storage technology.Huadian Technology,43(7): 17-23

[9] Amrouche S O,Rekioua D,Rekioua T,et al.(2016) Overview of energy storage in renewable energy system.International Journal of Hydrogen Energy,41(45): 20914-20927

[10] Xu S,Li X,Hui D,et al.(2013) A survey of the development and demonstration application of large-scale energy storage.Power System and Clean Energy,29(8): 94-100

[11] Sheng S,Sun X (2014) An economic dispatching strategy of peak load shifting by wind farm and pumped storage plant.Power System Technology,38(9): 2484-2489

[12] Yan G,Xie G,Li J,et al.(2011) Energy storage system application in power system.Journal of Northeast Dianli University,31(3): 7-12

[13] Li J H,Wang S (2017) Optimal combined peak-shaving scheme using energy storage for auxiliary considering both technology and economy.Automation of Electric Power Systems,41(9): 44-50

[14] Xu G,Cheng H,Fang S,et al.(2016) An optimization model of battery energy storage system configuration to improve benefits of wind farms.Automation of Electric Power Systems,40(5): 62-70

[15] Wang X,Huang W,Tai N,et al.(2020) A tie-line power smoothing strategy for microgrid with heat and power system using source-load-storage coordination control.Transactions of China Electrotechnical Society,35(13): 2817-2829

[16] Cui Y,Zhou H,Zhong W,et al.(2021) Two-stage day-ahead and intra-day rolling optimization scheduling considering joint peak regulation of generalized energy storage and thermal power.Power System Technology,45(1): 10-19

[17] Luo X,Wang J,Dooner M,et al.(2014) Overview of current development in compressed air storage technology.Energy Procedia,62: 603-611

[18] Brett G,Barnett M,Sarkadi L,et al.(2014) The application of liquid air energy storage for large scale long duration solutions to grid balancing.EPJ Web of Conferences.EDP Sciences,79:03002

[19] Morgan R,Nelmes S,Gibson E,et al.(2015) Liquid air energy storage-analysis and first results from a pilot scale demonstration plant.Applied energy,137: 845-853

[20] Zhu J,Shi K,Li Q,et al.(2022) Time series production simulation considering power flow constraints of transmission network and evaluation of new energy consumption capacity.Power System Technology,46(5): 1947-1955

[21] Fan Z,Zhu J,Yuan Y,et al.(2019) Distributed generation planning model of active distribution network and linearization method based on improved DC power flow algorithm.Power System Technology,43(2): 504-513

[22] Peng X,Li H,Zhen G,et al.(2020) Research on renewable energy consumption evaluation method based on time series production simulation.Acta Energiae Solaris Sinica,41(11):26-30

Full-length article

Received: 8 October 2022/ Accepted: 20 February 2023/ Published: 25 April 2023

Qiu Meng

mq975611768@163.com

Mingkui Wei

wmk1666@163.com

Yiyu Wen

287618178@qq.com

Shunwei Zheng

zheng_shunwei@foxmail.com

Yuyang Luo

luoyuyang1015@foxmail.com

Kai Liao

liaokai_lk@hotmail.com

2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Mingkui Wei received the B.S.degree at North China Electric Power University,Beijing,China.He is currently working in State Grid Corporation of China.His research interests include power system planning and power system operation analysis.

Yiyu Wen received the master degree at Chongqing University,Chongqing,China.He is currently working in State Grid Corporation of China.His research interests include power system planning and power system operation analysis.

Qiu Meng is currently working towards the master degree in Southwest Jiaotong University,Chengdu,China.His research interests include renewable energy power system planning and operation.

Shunwei Zheng is currently working towards the Ph.D.degree in Southwest Jiaotong University,Chengdu,China.His current research interests include renewable energy integration,and power system operation optimization.

Yuyang Luo is currently working towards the master degree in Southwest Jiaotong University,Chengdu,China.His research interests include renewable energy power system planning and scheduling,and power system operation optimization.

Kai Liao received the Ph.D degree at Southwest Jiaotong University in 2016,Chengdu,China.He is currently an Associate Professor in the School of Electrical Engineering with Southwest Jiaotong University,Chengdu,China.His research interests include wind power system control,and power system stability.

(Editor Tongming Liu)