0 Introduction

Unexpected events,such as extreme weather conditions and natural disasters can lead to massive power outages and damage to power equipment.These threats adversely affect various social activities and economic development.For instance,an ice storm in Southern China in 2008 caused 14 million homes to lose power support for several days [1].In Japan,the Fukushima Earthquake in 2011 led to massive power service disruptions for 8.5 million customers [2].In 2021,the winter storm Uri hit the United States and caused outages across most parts of Texas,with more than 3.8 million electricity customers [3].With the occurrence of extreme events,power system resilience has received wide attention in academia and industry [4].

Resilience refers to the capability of a power system to withstand extreme events and quickly restore critical loads after a power outage [5].In extreme events,power devices are damaged,resulting in the service interruption of utility territories,becoming an island.In this case,local distributed energy resources (DERs),such as controllable distributed generators (DGs),wind turbines (WTs),solar photovoltaic arrays (PVs),and energy storage systems(ESS) can be utilized to restore the loads of the distribution networks.Distribution service restoration (DSR) is designed to guarantee a continuous and reliable electricity supply in outage areas by sequentially switching operations and orderly dispatching of multiple resource generation.As a result,the resilience of power systems is markedly enhanced.

In current DSR studies,a traditional tie switch (TS)-based network reconfiguration is adopted to improve the power flow distribution and enhance the restoration performance.However,the insufficient regulation ability of the TS limits further improvement in the critical load restoration level.Thus far,a soft open point (SOP) is used to replace the traditional TS [6].Compared to TS,SOP can perform reactive power compensation while continuously controlling active power flow,which greatly enhances the flexible regulation ability of distribution networks and provides new opportunities for the improvement of the load restoration performance [7,8].Previous studies have validated the benefits of SOP for optimal power flow operation [9],economic dispatch [10],and reactive voltage optimization [11].Studies on DSR utilizing SOP have recently been conducted on outages.The authors in[12] studied the positive effect of SOP on load restoration.In [13],a DSR strategy with multiterminal SOPs was developed.However,renewables were not considered in the aforementioned SOP-based DSR studies.The authors in [14]considered renewable uncertainties and proposed an SOPbased robust load restoration model to increase the level of load restoration.However,the restoration model formulated in [14] is a single-time period optimization problem that does not involve both the coupling and interdependence of control actions over a time sequence.Therefore,the SOPbased DSR over a time horizon still needs to be investigated further,in which both the renewable uncertainty and the multiperiod DSR problem solution are the two main challenges.

For the first challenge,the scenario-based stochastic optimization method is recognized as an effective tool for addressing the renewable uncertainty problem.Technically,the approach generates multiple typical scenarios based on the probability distribution characteristics of renewable energy and obtains the optimal scheme by minimizing the expected objective function in those scenarios.The scenariobased stochastic optimization method has been applied to many power system optimization applications,such as optimal power flow [15],reactive power optimization [16],and optimal scheduling [17].However,it has not been widely reported in the DSR and can be extended to uncertain service restoration in this study.Furthermore,the power outputs of the WT,PV,and loads are correlated owing to their geographical proximity.Sometimes,they exhibit a non-normal distribution.Such features pose challenges for the extraction of typical scenario sets.Fortunately,the Gaussian mixture model (GMM) is a linear combination of multiple normal distribution functions that can describe the probability distribution characteristics of random WT,PV,and loads.Compared with single probability distribution models,they can accurately reflect random fluctuations with irregular or multimodal distribution properties [18].Thus,GMM is suitable for establishing a scenario-based stochastic load restoration model.

For the second challenge,it is necessary to develop a computation-effective algorithm for solving a multiperiod DSR problem.From the perspective of mathematical properties,a DSR is essentially a mixed-integer nonlinear programming problem (MINLP) with nonlinear power-flow constraints and many integer variables [19].Second-order cone relaxation techniques and linearization methods are typically employed to simplify the computational burden.In this regard,mixed-integer second-order cone programming(MISOCP) and mixed-integer linear programming (MILP)models were formulated in [20] and [21],respectively,to improve the solution efficiency of service restoration.However,for a stochastic optimization-based multiperiod load restoration problem,the dramatically increased dimension of the problem space,including both load restoration and shedding status will cause significant difficulties in obtaining a feasible solution within an acceptable time.

Based on the above discussion,this paper proposes a multi-source coordinated load restoration strategy for a distribution network with an SOP over a time horizon,which considers the uncertainties of intermittent DGs and loads.The main contributions of this study are as follows:

1) It proposes a multi-source coordinated load restoration scheme for a distribution network with an SOP,in which the flexibility of the SOP and the uncertainty of the DGs and loads are considered.The proposed restoration strategy coordinates the scheduling of the DERs and operations of the SOP to increase the load restoration level while mitigating voltage deviations over a time horizon.Considering the uncertain DGs and loads,a scenario-based stochastic programming approach is adopted to enable renewable resources to participate well in the DSR,thereby enhancing system resilience.

2) A two-stage solution algorithm is proposed to solve the stochastic optimization-based load restoration problem with large-scale variables.Using convex relaxation and linearization methods,the original DSR problem was reformulated as a MISOCP model.To handle many integer variables,a computation-effective solution with a two-stage structure is developed,which allows us to solve a relaxed SOCP problem in the first stage to determine the operations of the ES,and a small-scale MILP problem is calculated in the second stage to determine the load status and outputs of the DGs and SOPs,step by step.The proposed algorithm reduces the computational burden while maintaining the accuracy of the solution.

The remainder of this paper is organized as follows:Section 1 describes the construction of typical scenario sets based on GMM.A stochastic restoration model with a two-stage solution algorithm is introduced in Section 2.Numerical simulation studies are described in Section 3.Section 4 concludes.

1 Restoration framework and scenario set extraction

In this section,a multi-source coordinated stochastic restoration framework is introduced.The GMM is then used to generate correlated renewable resources and load power output scenarios,which are then cut down to a few typical scenarios for establishing a stochastic restoration model.

1.1 Multiple sources restoration and analysis framework

We assumed that the main grid suffers severe device damage after an extreme event,resulting in widespread power outages,which often take hours or even days to fix.During such blackouts,the upstream grid cannot provide electric power support to distribution networks.Then,the local resources,including DGs,PV/WT,ESS,and SOPs,can only restore the critical loads in a distribution network.The proposed multisource coordinated restoration and analysis framework are illustrated in Fig.1.Local resources are utilized,including controllable and uncontrollable DG units,to restore the critical load as much as possible.To cope with uncertainties,a stochastic optimization method was adopted,enabling intermittent WT and PV to participate in the DSR.Furthermore,a flexible SOP was explored to improve the service restoration performance.The coordination of multiple resources over a time horizon can enhance the load-restoration level and simultaneously reduce voltage deviations.However,stochastic DSR is an MINLP problem with many integers.To solve this problem efficiently,convex relaxation and linearization methods were introduced to convert the original MINLP model into a MISOCP model.Thus,a two-stage solution algorithm is used to obtain a feasible solution within an acceptable time.

Fig.1 Service restoration and analysis framework

1.2 Scenario generation based on Gaussian mixture model

Utilizing WT/PV systems under inadequate local power after an extreme event can further enhance the resilience of the distribution network.Unfortunately,these resources are intermittent.Furthermore,the load is uncertain.Their uncertainties have two features and can be summarized as follows: 1) the power outputs of the WTs/PVs and the loads are greatly affected by weather conditions and have strong uncertainty and randomness,with complex probability distribution functions that cannot be accurately described.2) They are correlated because of their geographic proximity to a distribution network.Thus,for a more accurate model,it is necessary to guarantee the accuracy and correlation of the probability distribution functions.To address these problems,in this study,we employed a GMM to represent the joint distribution of sources and loads.As shown in Fig.2,the GMM is essentially a probability model that is linearly weighted by multiple Gaussian models.It is assumed that the actual power output of a renewable resource is determined by the forecasted value and superimposes the prediction error.Let the random vector X=[Xt,1,Xt,2,...,Xt,K]T denote the actual power output of the K-th renewable source and load in the period t.Then,the probability density function (fX(x)) of X can be given by a GMM as follows:

Fig.2 Probability distribution fitting based on GMM

where ωm represents the weight,M denotes the number of Gaussian components,and Nm(x | μ m ,σ m) represents the mth multivariate Gaussian component with the mean vector μm and covariance matrix σm.By adjusting the parameter set Σ= {ω m ,μ m,σ m|m =1,2,...,M },the GMM can characterize the joint probability distribution of different types of random variable vectors.These values are calculated using the EM algorithm.In this study,we adopted the function “fitgmdist”in MATLAB to obtain the parameter set Σ according to the sampling data.The correlated power output samples can then be obtained using the Monte Carlo method.

1.3 Obtaining typical scenarios using sample reduction

Theoretically,if the scenario set generated by the Monte Carlo method is large,the uncertainty of renewable sources can be accurately presented,thus obtaining a globally optimal solution.However,as the scale of the scenario set increased,the computational burden increased significantly,leading to no feasible solutions in a short time.To address this,scenario reduction techniques can be used to ensure that the extracted typical scenarios can well represent the original scenario set.Subsequently,the computational complexity can be simplified while maintaining an accurate solution.It has been extensively applied in optimal power system operations.The simultaneous backward reduction method was used in this study to reduce the initial correlated samples.In this process,a reduced scenario set and probability were obtained.The detailed scenario reduction method can be found in [22].

2 Stochastic restoration model with twostage solution

In this section,the formulation of the stochastic restoration problem,which sufficiently utilizes the coordination of the SOP and multiple DERs to restore the load of the distribution network is described in detail.Using convex relaxation and linearization methods,the original MINLP problem is converted into a MISOCP,which can be effectively solved using the proposed two-stage algorithm.

2.1 Objective function

During an outage,the main task of a distribution network is to restore the critical load as much as possible.In this process,voltage distribution is an important indicator for evaluating the reliability of the power supply.It can be properly addressed through multisource coordination and flexible regulations.Thus,maximizing load restoration and simultaneously minimizing voltage deviations are selected as the objective functions in this study,which are given by:

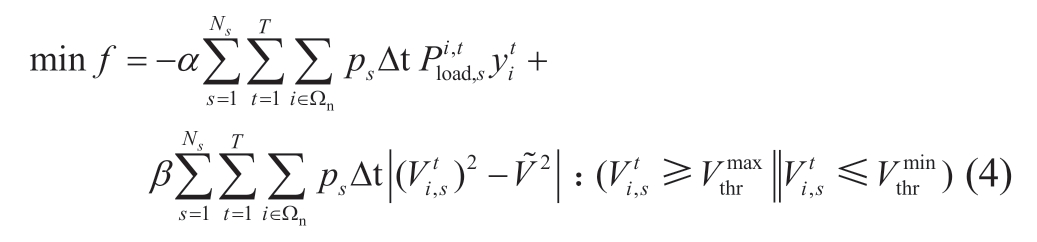
where Ns is the total number of scenarios; T is the outage duration; Ωn denotes the set of nodes; ps denotes the probability of scenario s;is the active power load at node i,scenario s,and period t;are binary variables: 1-load i at period t is restored,otherwise it is shed.Δt is the time interval;is the voltage of node i at scenario s at period t; α and β are the weight coefficients.The first term in (4) is the weighted restored load.The second term is the threshold function reflecting the extent of voltage deviations,and such expression is widely adopted in [9],[23],and [24].As shown in Fig.3,in interval 1,,set.In interval 2,the voltage magnitudeis within the desired range,set,the value of this term is 0.In interval 3,,set.Thus,when the voltage amplitude exceeds the desired range,the function of this term will contribute to reducing the extent of deviation from the desired range,thereby improving the voltage profile of the network.

Fig.3 Schematic diagram of the voltage deviation objective function

2.2 Constraints

1) Distribution network power flow constraints

The DistFlow power-flow model was adopted in this study to describe the power-flow constraint:

where,Ωb is a set of nodes; represent the active/reactive power flow of branch ij at period t at scenario s,respectively; rij and xij donate the resistance and reactance of branch ij,respectively;represents the branch current;represents the injected active power of node j at period t at scenario s,including the power output of DGs ,the power output of WT ,the power output of PV,the power output of SOP ,the power output of ESS j,and the load power of node j; denotes the injected reactive power of node j at period scenario ,such as the reactive power output of DGs ,the reactive power output of SOP ,and the load reactive power of bus j.Specifically,constraints (5) and (6) imply the active and reactive power balances,respectively.The active/reactive power injections at node j are expressed in (7) and (8),respectively.Constraint (9) denotes the DistFlow equations.The branch current constraint is given by (10).

2) Operation constraints of SOP

An SOP is a fully controllable power electronic device that is usually installed between feeders to replace the traditional TS in distribution networks.A typical schematic of an SOP installation is shown in Fig.4.This study uses back-to-back voltage source converters (B2B VSC) to analyze the steady-state model of an SOP.Compared to the traditional TS,the advantages of SOPs are summarized as follows: 1) they can regulate the active power flow continuously,which improves the power flow distribution;2) they can provide reactive power compensation to enhance the active power utilization efficiency of DGs.

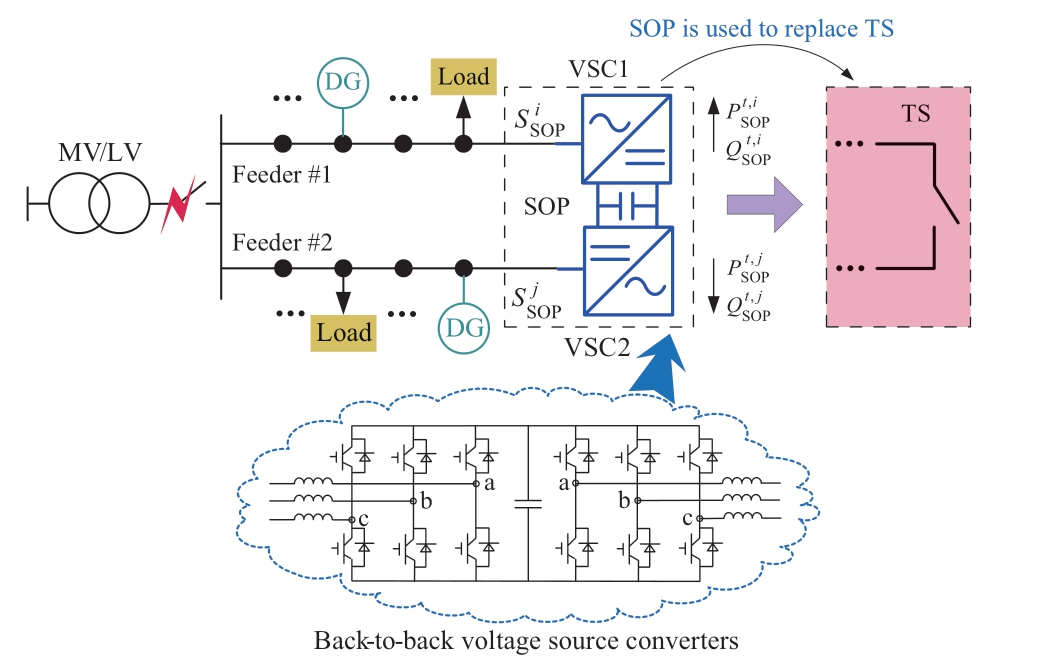
Fig.4 Installation schematic diagram and topological for an SOP

During an operation,the active and reactive power outputs of the two converters were controlled independently,and an active power balance constraint was applied.The B2B VSC was efficient,thereby ignoring power losses in this study.Reactive power flows must satisfy their security constraints owing to DC isolation.In addition,each converter was subjected to capacity constraints.Thus,the SOP optimization model is formulated as follows:

where,represent the minimum/maximum reactive power output of the SOP,respectively,and denotes the capacity of the SOP.

3) ESS operation and security constraints,

where,EtSOC represents the state of charge of the ESS at period t,and its lower and upper are given by ESOC,min and ESOC,max,respectively; Pstor,min and Pstor,max are the active power output limits of the ESS,and the minimum and maximum power outputs of the DGs are PDG,min and PDG,max;SDG denotes the capacity of the DGs; Vi,min and Vi,max are the lower and upper voltage limits,respectively.Constraints(14) – (16) represent the operational constraints of the ESS.The active power and capacity limits of the DGs are given by (17) and (18),respectively.The system voltage security constraint is expressed as (19).

Using constraints (4) – (19),the original stochastic load restoration model is formed,which essentially belongs to the category of an MINLP problem with nonlinear power flow constraints and many integer variables.Furthermore,both multiple periods and scenarios dramatically increase the problem space scale of the model,making it difficult to obtain a feasible solution within an acceptable time.Therefore,an accurate and efficient solution is urgently required.

2.3 Convex relaxation and linearization transformation

1) Convex relaxation

The aforementioned stochastic restoration model cannot be efficiently solved using the existing methods.Using convex relaxation and linearization methods,the original MINLP problem was transmitted into a MISOCP model to improve the feasibility of the model solution.

The quadratic terms of the current amplitude and voltage amplitude exist in constraints (5),(6),(9),and (19).Let and  denote,respectively.The linearized expressions are obtained as follows:

After substituting the variable,constraint (10) continues to be nonlinear because of the product term,which can be relaxed to the following second-order cone constraint.

2) Linearization

The feasible regions limited by the capacity constraints in(13) and (18) are mathematically represented as the interiors of the circles.Typically,they are linearized using a polygonal inner approximation approach [25],as illustrated in Fig.5.

Fig.5 Diagram of a polygonal inner-approximation approach

Thereupon,several linear equations are expressed as:

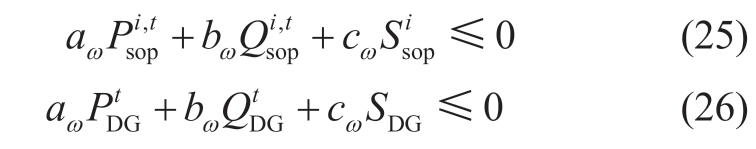
where,aω,bω,and cω are coefficients.

The nonlinear voltage deviation function in (4) is linearized by introducing an auxiliary variable,.

Some relevant constraints,that is,(28) – (30),should be supplemented to make this linearization equivalent [11].

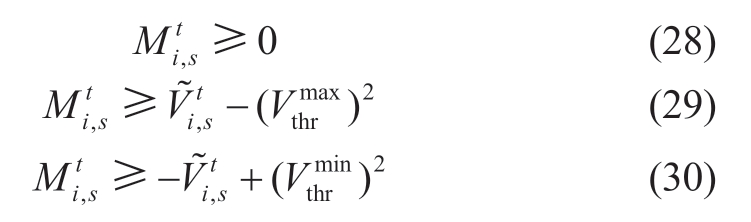
2.4 Two-stage solution algorithm

With convex relaxation and linearization,the original MINLP problem is converted into a MISOCP problem,F0,which is compactly expressed as:

where f is the objective function,that is,constraint (27); h and g are the inequality and equality constraints,including constraints (7),(8),(11),(12),(14) – (17),(20) – (26),and (28) – (30); y is the vector of the load restoration and shedding status,which is a binary variable; and c is the vector of the remaining continuous variables.It is worth noting that the problem expressed in (31) contains many integers,making it challenging to solve.To address this problem,a two-stage solution algorithm was proposed.

1) Stage 1: a relaxed SOCP deciding ESS scheduling

In stage 1,a relaxed SOCP problem for F0 was introduced to determine ESS scheduling.The modified SOCP model F1 can be compactly expressed as:

Notably,the load restoration or shedding status variable is relaxed,allowing any value to be taken in [0,1].The objective functions subject to the constraints in F1 are the same as those shown in F0.There are no binary variables in F1,which is a second-order cone programming (SOCP)model.In general,the SOCP is mathematically a convex programming problem,which can be solved accurately in an acceptable time using a commercial solvent.

2) Stage 2: small-scale MISOCP solution step by step

After determining the schedules of ESS,the operation constraints (14) – (16) are removed from DSR problem F0.Thus,the multiple-period restoration problem can be decomposed into a step-by-step single-period optimization problem .Compared with the original multi-period problem F0,it is a small-scale MISOCP problem,and greatly improves the solution feasibility of the restoration model.At the optimization time slot t,is compactly expressed as:

where the objective function of is (27); the inequality and equality constraints include constraints (7),(8),(11),(12),(17),(20) – (26),and (28) – (30); and T represents the outage period.Notably,the objective and constraints in involve only a single period,and the vector of load restoration and shedding status is the binary variable.By solving step by step,we can obtain the load status as well as the outputs of the DGs and SOPs during the outage period.

3) Implementation of the two-stage algorithm

Figure 6 shows the flowchart of the two-stage algorithm.The procedure is as follows:

Fig.6 Flowchart of the proposed two-stage algorithm

Step 1: Generate correlated scenarios for the WT,PV,and loads.Then,use the simultaneous backward reduction method to obtain typical scenarios.

Step 2: Formulate the original stochastic restoration model and use convex relaxation and linearization methods to transform it into a MISOCP problem F0.

Step 3: Relax the binary variable y to continue the variable between [0,1].On this basis,we formulate and solve the relaxed SOCP problem F1 to obtain ESS scheduling.

Step 4: Formulate the small-scale MISOCP problem and solve it step-by-step to determine the load status as well as the outputs of the DGs and SOPs.

4) Discussion of the feasibility of the two-stage algorithm

The application of the two-stage algorithm to power system optimization problems can be found in current studies.In [26],the feasible restoration paths are determined in stage 1,then the critical load restoration strategy is obtained in stage 2.In [27],a network reconfiguration strategy was developed using a two-stage structure: stage 1 is to maximize the loss reduction loop,and stage 2 is to perform switch options.Using the two-stage algorithm,the decision variables of a complex problem are sequentially determined in two stages.For the studied restoration problem,the advantage of using the two-stage approach is that it can obtain an approximate solution to the original single-stage restoration problem with significantly decreased computational complexity.

In our study,ESS scheduling is first optimized in stage 1,aiming to roughly determine the power flow distribution status of the restored network.Then,the load restoration or shedding status,as well as the outputs of the DGs and SOPs,are adjusted in Stage 2.Thus,the two-stage algorithm can obtain a feasible solution,as validated in [26] and [27].

3 Case Study

In this section,the feasibility of the proposed multiplesource-coordinated stochastic restoration strategy using the two-stage method is verified.The simulation was carried out in MATLAB R2018b with YALMIP,which was solved using the CPLEX 12.8 optimizer.The experiment was conducted on a win 10-based computer with an Intel(R) i7-8550U CPU @1.80 GHz with 8 GB RAM.

3.1 Modified IEEE 33-bus system

The modified IEEE 33-bus test system is illustrated in Fig.7,where the switch between buses 0 and 1 is open owing to a blackout.The relevant modifications are as follows: The ESS was connected to Bus 14.Two controllable DGs are placed at buses 10 and 26,in which DG1 is relaxed to maintain the power balance.Two renewable resources (PV and WT) were integrated into the distribution network at buses 16 and 30.Two SOPs are connected to the network between buses 8 and 21,and between buses 9 and 15.

Fig.7 Topology diagram of the modified IEEE 33-bus test system

The total load of the distribution network was 3.715+j2.3 MVA.The voltage reference was 12.66 kV.The allowable voltage range is [0.95 1.05] p.u.The desired voltage range was [0.98 1.02] p.u.The capacities of the two DGs were 1000 and 700 kVA,respectively.The active power capacity of the WT is 500 kW,and 400 kW for the PV.The allowable state of the ESS was 200–900 kWh.The maximum charging/discharging value for the ESS was 100 kW.The maximum reactive power of the SOP is 450 kVar.Its capacity was 600 kVA.For weight coefficients α =0.67 and β =0.33.In this study,the outage period was assumed to be 24 h.The day-ahead forecast curves for the WT,PV,and load power in the distribution networks are shown in Fig.8.

Fig.8 Power output prediction curves of WT,PV,and load

3.2 Results of scenario generation and reduction

Typically,if the actual historical data of the WT,PV,and loads are known,we can obtain the GMM using them.In this study,the correlated power output sample data of the WT,PV,and loads were generated by the Nataf transformation and the Latin Hypercube Sampling method [28].

As illustrated in Fig.9,the probability density functions(PDF) of the forecast errors of the WT,PV,and load do not satisfy the normal distribution characteristics,and they are correlated.The GMM with 10 Gaussian components can then be used to obtain the joint probability distribution.The results are shown in Fig.10.

Fig.9 PDF curves and correlation matrix of WT,PV,and load

Fig.10 Results of GMM: (a) PDF curve based on GMM of WT; (c) scenarios reduction results of WT; (b) PDF curve based on GMM of PV; (d) scenarios reduction of PV; (e) PDF curve based on GMM of loads; (f) scenarios reduction of loads

The marginal PDF of the WT,PV,and loads can be obtained from a GMM,in which sample scenarios can be generated,as depicted in Fig.10 (a),(c),and (e).It is evident that the PDF given in Fig.10 is the same as that in Fig.9.These results reveal that GMM can accurately present arbitrary joint probability distribution characteristics,which enhances the effectiveness of the PDF description for uncertain sources and loads.The reduced scenarios and their probabilities for WT,PV,and loads are shown in Fig.10 (b),(d),and (f).Based on the GMM,1000 Monte Carlo samplings were performed.By superimposing them to forecast the values of WT,PV,and loads,we can obtain a large number of correlated initial samples.Using the simultaneous backward reduction method,ten typical scenarios were reserved to provide a typical scenario set for establishing a stochastic restoration model.

3.3 Performance of stochastic restoration model

To verify the effectiveness of the stochastic restoration model,the following three schemes were compared.

Scheme 1: The controllable DGs and ESS are utilized to restore critical loads,in which the intermittent WT/PV are not taken into consideration;

Scheme 2: The restoration strategy is implemented with DGs,ESS,and the predicted value of WT,PV,and loads;

Scheme 3: The proposed multiple resources coordinated stochastic restoration strategy is conducted.

The load restoration results for the three schemes are illustrated in Fig.11.Compared with Scheme 1,the intermittent resources WT/PV are utilized in Schemes 2 and 3,which greatly improves the load recovery level.We can observe that the total restored load in Scheme 2 is 1.76% higher than that in Scheme 3.This is because the uncertainties of the intermittent resources WT/PV and loads were considered in Scheme 3.Thus,it can satisfy the stable operational demand for several typical scenarios with source and load fluctuations.It can be observed that the restoration strategy in Scheme 3 is conservative.Although there is a slightly higher load restoration level in scheme 2,it is difficult to accurately predict the operation scenario in real situations.This means that Scheme 2 has a higher probability of load shedding when implementing the restoration strategy.Therefore,the reliability of scheme 2 is poor.In summary,the proposed strategy can improve the load-recovery level while ensuring solution reliability.

Fig.11 Results of the load restoration level in three schemes

Fig.12 presents the optimized results.It is obvious that during the period from 1:00 to 10:00,the load level is low.In this situation,the majority of the loads are restored through the coordinated regulation of the DERs,and the ESS is charged.A high level of the load exists from 10:00 to 24:00,but the power production of local DERs is not enough to restore all loads.Load shedding is adopted,and the ESS is in the discharge mode for increasing the load restoration level.The voltage profiles with or without considering the voltage deviation function are expressed in Fig.13 (a) and(b),respectively.We can see that the voltage range in Fig.13(b) is from [0.98,1.0] p.u.,which is within the desired range,and this in Fig.13 (a) is from [0.971,1.0] p.u.The results illustrate that the proposed model can effectively adopt local DERs for load restoration and reduce voltage deviations.

Fig.12 Optimized results by the proposed operation scheme:(a) power output of ESS; (b) power of DGs and loads

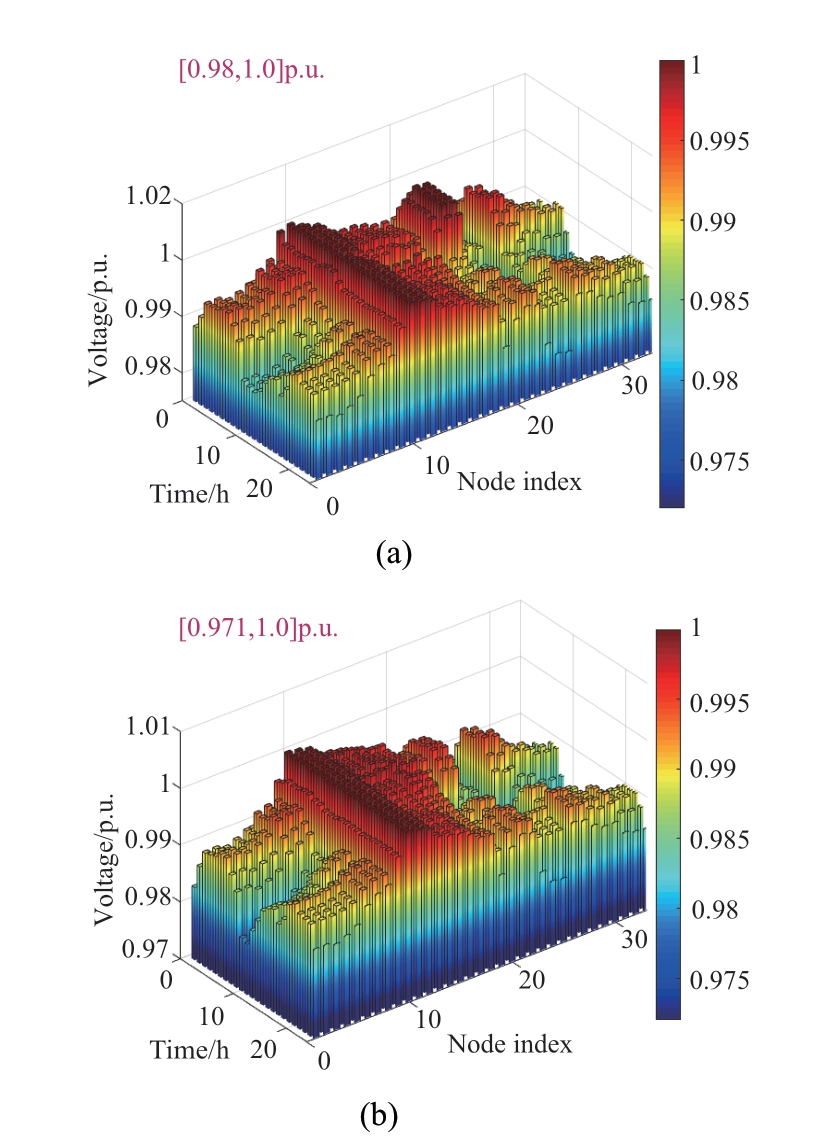
Fig.13 Voltage profiles: (a) reduced voltage deviation function is considered; (b) reduced voltage deviation function is not considered

3.4 Benefits of SOP and two-stage algorithm analysis

To demonstrate the benefits of SOP flexibility in DSR,we compared cases with and without SOPs,as shown in Fig.14 and Fig.15.

Fig.14 Optimized results of SOPs: (a) active power flow;(b) reactive power compensation

Fig.15 Results of load restoration without and with SOP

The power outputs of the two SOPs with ports i and j are shown in Fig.14.As shown in Fig.14,the active power flow can be flexibly regulated by the SOP,and it can provide reactive power compensation.Such benefits contribute to improving the network power flow distribution,thus,enhancing the active power utilization efficiency of DGs in an outage.As shown in Fig.15,the load restoration level with SOPs is markedly higher than that without SOPs,and the total load restoration level increases by 9.7%.These results illustrate that fully utilizing the flexible regulation ability of SOPs can increase load restoration performance.

The solution efficiencies of these two methods are listed in Table 1.It is evident that if a multiple-period stochastic restoration problem is solved directly,there is no feasible solution for more than 10000 s.We should note that by using the proposed two-stage solution method,we can obtain ESS scheduling in Stage 1 with 49.5 s.The load status as well as the outputs of the DGs and SOPs were determined to be 186.7 s in stage 2.The solution efficiency has been improved.The computational time for each step of Stage 2 is shown in Fig.16.It can be observed that each step can obtain solutions within an acceptable time.These results indicate that the proposed two-stage algorithm was feasible.

Table 1 Comparison of solution efficiency between two methods in an IEEE 33-bus system

Fig.16 Computational time of stage 2 in an IEEE 33-bus system

3.5 Effectiveness analysis in IEEE 123-bus system

In this section,we further observe the simulation results for a larger test system,that is,the IEEE 123-bus system,to verify the effectiveness of the proposed restoration model.For validation,the three-phase unbalanced IEEE 123-bus system was modified to a three-phase balanced system,and detailed parameter modifications can be found in [29].The other parameter settings are the same as those in Section 4.1.The modified test system topology is presented in Fig.17,and the results are as follows:

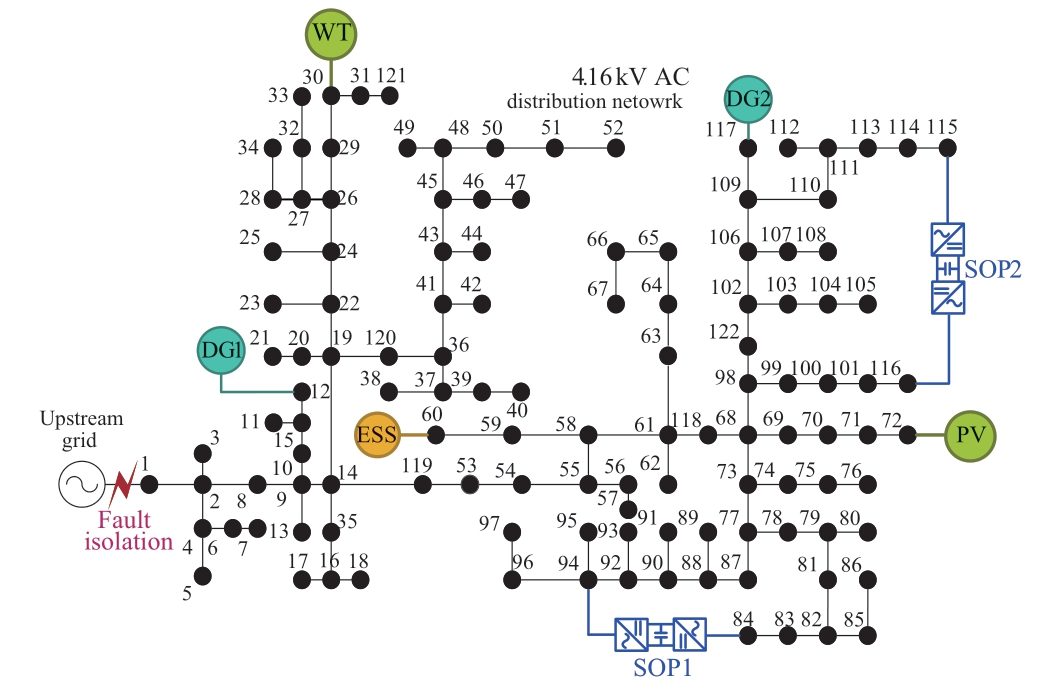
Fig.17 Topology diagram of the modified IEEE 123-bus test system

The optimized results for load restoration are shown in Fig.18.It can be observed that multiple sources are coordinated to restore 95.3% of the total load.The total restored load in Scheme 3 was 14.1% higher than that in Scheme 1.The load restoration performance in Scheme 2 was comparable to that in Scheme 3.However,the uncertainties of the WT,PV,and loads are fully considered in scheme 3,which can improve the load recovery level while ensuring solution reliability.Furthermore,the voltage range in Fig.18 (c) is [0.98,1.02] p.u.,which is within the desired range,and that in Fig.18 (d) is [0.98,1.028] p.u.Therefore,the proposed stochastic restoration strategy is effective for larger systems.

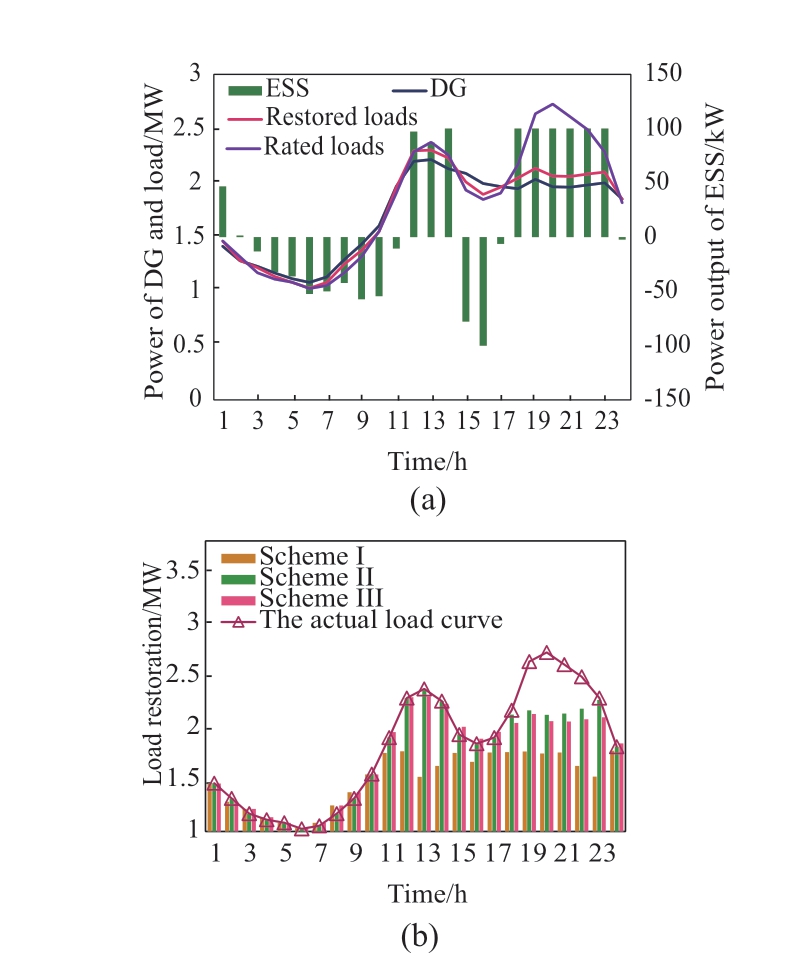
Fig.18 Comparison of optimized results in an IEEE 123-bus system: (a) restoration results; (b) results of the load restoration level in three schemes; (c) reduced voltage deviation function is considered; (d) reduced voltage deviation function is not considered

A comparison of the solution efficiency of the two methods in the IEEE 123-bus system is presented in Table 2.It can be seen that solving the solution directly is not feasible because of the long computation time (> 10000 s).Using the proposed two-stage algorithm,the ESS scheduling is determined in stage 1 by 78.7 s,and the load status and outputs of the DGs and SOPs are decided by 628.9 s to be 2.The computational time for each step of Stage 2 is shown in Fig.19.It can be seen that the optimized solutions can be obtained in each step with an acceptable time.The results validated the feasibility and effectiveness of the proposed two-stage algorithm on a larger system.

Table 2 Comparison of solution efficiency between two methods in IEEE 123-bus system

Fig.19 Computational time in IEEE 123-bus system at each step in the second stage

4 Conclusion

This study proposes a stochastic optimization-based DSR strategy for a distribution network with multi-source integration and SOP utilization.The first contribution is the formulation of a mixed-integer nonlinear programmingbased stochastic restoration model.The second contribution is to propose a solution algorithm with a two-stage structure by employing convex relaxation and linearization methods.A numerical simulation was conducted,and several key findings were obtained.1) The multi-source production and flexibility of the SOP can be utilized to enhance the system’s resilience while mitigating voltage deviations.2) The scenario-based stochastic optimization method ensures the reliability of the solutions while improving the load restoration level.3) The proposed two-stage algorithm can effectively solve the DSR problem over a multi-period horizon,and has a superior computational performance in obtaining the near-optimal solution,regardless of the scale of the system.

Acknowledgements

This work was supported by the State Grid Tianjin Electric Power Company Science and Technology Project(Grant No.KJ22-1-45).

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] Bie Z,Lin Y,Li G,et al.(2017) Battling the extreme: a study on the power system resilience.Proceedings of the IEEE,105(7):1253-1266

[2] Aki H (2017) Demand-side resiliency and electricity continuity:experiences and lessons learned in Japan.Proceedings of the IEEE,105(7): 1443-1455

[3] Bahrami A,Yan M,Shahidehpour M,et al.(2021) Mobile and portable de-icing devices for enhancing the distribution system resilience against ice storms.IEEE Electrification Magazine,9(3): 120-129

[4] Liu W,Chen Y,Ding F (2021) Distributed generator-based distribution system service restoration strategy and model-free control methods.Global Energy Interconnection,4(2): 126-135

[5] Wang J,Xie N,Wu W,et al.(2018) Resilience enhancement strategy using microgrids in distribution network.Global Energy Interconnection,1(5): 537-543

[6] Sarantakos I,Zografou-Barredo N M,Huo D,et al.(2021) A reliability-based method to quantify the capacity value of soft open points in distribution networks.IEEE Transactions on Power Systems,36(6): 5032-5043

[7] Bloemink J M,Green T C (2010) Increasing distributed generation penetration using soft normally-open points.Proceedings of IEEE PES General Meeting,Jul 2010,pp 1-8

[8] Yin H,Li Q,Liu Y,et al.(2020) Power flow calculation for a distribution system with multi-port PETs: an improved AC-DC decoupling iterative method.Global Energy Interconnection,3(4): 313-323

[9] Ji H,Wang C,Li P,et al.(2019) Robust operation of soft open points in active distribution networks with high penetration of photovoltaic integration.IEEE Transactions on Sustainable Energy,10(1): 280-289

[10] Sun F,Ma J,Yu M,et al.(2021) Optimized two-time scale robust dispatching method for the multi-terminal soft open point in unbalanced active distribution networks.IEEE Transactions on Sustainable Energy,12(1): 587-598

[11] Li P,Ji H,Wang C,et al.(2017) Coordinated control method of voltage and reactive power for active distribution networks based on soft open point.IEEE Transactions on Sustainable Energy,8(4): 1430-1442

[12] Ding T,Wang Z,Jia W,et al.(2020) Multiperiod distribution system restoration with routing repair crews,mobile electric vehicles,and soft-open-point networked microgrids.IEEE Transactions on Smart Grid,11(6): 4795-4808

[13] Li P,Ji J,Ji H,et al.(2020) Self-healing oriented supply restoration method based on the coordination of multiple SOPs in active distribution networks.Energy,195: 1-11

[14] Liu W,Fu M,Yang M,et al.(2020) A bi-level interval robust optimization model for service restoration in flexible distribution networks.IEEE Transactions on Power Systems,36(3): 1843-1855

[15] An Q,Wang J,Li G,et al.(2020) Role of optimal transmission switching in accommodating renewable energy in deep peak regulation-enabled power systems.Global Energy Interconnection,3(6): 577-584

[16] Ding T,Yang Q,Yang Y,et al.(2018) A name="ref17" style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">[17] Chen F,Huang K,Hou Y,et al.(2019) Long-term cross-border electricity trading model under the background of global energy interconnection.Global Energy Interconnection,2(2): 122-129

[18] Ke D,Chung C,Sun Y,et al.(2016) A novel probabilistic optimal power flow model with uncertain wind power generation described by customized Gaussian mixture model.IEEE Transactions on Sustainable Energy,7(1): 200-212

[19] Li Y,Xiao J,Chen C,et al.(2019) Service restoration model with mixed-integer second-order cone programming for distribution network with distributed generations.IEEE Transactions on Smart Grid,10(4): 4138-4150

[20] Sekhavatmanesh H,Rodrigues J,Moreira C,et al.(2020) Optimal load restoration in active distribution networks complying with starting transients of induction motors.IEEE Transactions on Smart Grid,11(5): 3957-3969

[21] Chen B,Ye Z,Chen C,et al.(2019) Toward a MILP modeling framework for distribution system restoration.IEEE Transactions on Power Systems,34(3): 1749-1760

[22] Dong L,Liu M,Chen N,et al.(2018) Coordinated optimal control of distributed energy based on stochastic model predictive control.Power System Technology,42(10): 3219-3226 (In Chinese)

[23] Mostafa N,Rachid C,Mario P (2014) Optimal allocation of dispersed energy storage systems in active distribution networks for energy balance and grid support.IEEE Transactions on Power Systems,29(5): 2300-2310

[24] Yang X,Xu C,He H (2021) Flexibility provisions in active distribution networks with uncertainties.IEEE Transactions on Sustainable Energy,12(1): 553-567

[25] Chen X,Wu W,Zhang B,et al.(2016) Robust restoration method for active distribution networks.IEEE Transactions on Power Systems,31(5): 4005-4015

[26] Wang Y,Xu Y,He J,et al.(2019) Coordinating multiple sources for service restoration to enhance resilience of distribution systems.IEEE Transactions on Smart Grid,10(5): 5781-5793

[27] Reddy V,Perumal N,Rajasekharareddy Y (2004) Loss reduction in distribution networks by network reconfiguration: a two stage solution approach.National Power&Energy Conference

[28] Li Y,Xiao J,Chen C,et al.(2019) Service restoration model with mixed-integer second-order cone programming for distribution network with distributed generations.IEEE Transactions on Smart Grid,10(4): 4138-4150

[29] Chen B,Chen C,Wang J,et al.(2018) Multi-time step service restoration for advanced distribution systems and microgrids.IEEE Transactions on Smart Grid,9(6): 6793-6805

Full-length article

Received: 15 August 2022/ Accepted: 6 November 2022/ Published: 25 April 2023

Tao Zhang

zhangtaotj@tju.edu.cn

Xianxu Huo

hulxianxu@163.com

Pan Zhang

pan.zhang@tj.sgcc.com.cn

Shiting Sun

1367643119@qq.com

Zhanyi Li

2116238211@qq.com

Lei Dong

hbdldl@126.com

2096-5117/© 2023 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Xianxu Huo received the Ph.D.degree in electrical engineering from Institute of Electrical Engineering,Chinese Academy of Sciences in 2014.From July 2014 to November 2016,he was a Post-doctoral Fellow at Tianjin University.He is currently a Senior Engineer of State Grid Tianjin Electric Power Research Institute.His research interests include renewable energy and distribution network,and integrated energy system.

Pan Zhang received the M.S.degree in electric engineering and automation from North China Electric Power University (NCEPU),Beijing,China,in 2008.He is currently working as a senior engineer in of State Grid Tianjin Electric Power Research Institute.His research interests include smart distribution network and smart substation technology.

Tao Zhang received the B.S.degree in electrical engineering from the Hefei University of Technology (HFUT),Hefei,China,in 2016,and the M.S.degree in electric engineering and automation from North China Electric Power University (NCEPU),Beijing,China,in 2019.(Corresponding author).His research interests include power system analysis,distribution network optimization,and service restoration.

Shiting Sun was in Liaoning,China,in 1999.She received the B.S.degree in electrical engineering from Liaoning University in 2021.She is currently pursuing the M.S.degree in electrical engineering at North China Electric Power University.Her research interests include integrated energy system restoration and optimized operation of the power system.

Zhanyi Li was in Hebei,China,in 1993.He received the master’s degree in electrical engineering from Yanshan University in 2020.Now he is an employee of Baodi Power Supply Branch of State Grid Tianjin Electric Power Company.His research interests mainly include new energy power generation technology and power conversion technology.

Lei Dong received the M.S.degrees in Electrical Engineering and Automation in 1996 from Tianjin University,Tianjin,China.Since 2001,she has been an Associate Professor in the Electrical Engineering Department with North China Electric Power University.Her research interests include power systems analysis and control,power system optimal dispatch and operation control,application of artificial intelligence in power system.

(Editor Yajun Zou)