0 Introduction

The dual pressures of energy crisis and environmental pollution urge people to reflect on the existing energy consumption mode and start to study the integrated utilization of electricity, gas, heat, and other forms of energy[1].The integrated energy system (IES) produces and uses multiple energy, such as electricity, gas, cold, and heat,which can realize the integrated dispatching control andcomplementary utilization of various energy sources [2].It also promotes better energy consumption and efficiency and boosts green-intensive social development [3].

With the continuous development of technologies such as the power to gas (P2G) and combined heat and power(CHP) generation, the coupling of the power grid, gas network, and heat network will soon be possible, which makes the coordinated optimization problem for IES have the characteristics of strong coupling, non-convexity, and nonlinearity.[4]realized the coordinated optimization of different energy entities in the electricity-gas regional IES by introducing consensus variables.In [5], a park CHP system has been constructed, which considered the chance constraint, but this study only considers the optimization dispatching of a single park and lacks research on multipark collaborative optimization.[6-7]have built an IES of electricity and gas with energy hubs (EH) as the decision center, realizing joint optimization dispatching of multiple regions, disregarding the influence of the heating system,the model is relatively simple.[8]developed a model for the IES in distributed parks with electricity, gas, cold, and heat, and have realized economic optimization dispatching of the system based on multiple scenarios.[9]proposed the new security constraints for integrated regional power and a natural gas network for a more realistic model.The complex coupling of multi-energy networks has been considered in most previous studies, and the internal structure of multienergy networks is usually linearized.However, there are differences between the model and the actual situations.In addition, a large amount of distributed energy is constantly connected to the IES, so the uncertainty problem in optimization cannot be ignored.Based on the CHP system, the randomness of wind, light, and load has been paid special attention to, and parts of the constraints were addressed as probabilities, making the CHP model more consistent with the actual situation [10].[11]considered the influence of the uncertainty of wind power, and proposed a distributed robust optimization-based dispatching model of electricity-gas-heat-hydrogen IES.However, the model results are extremely conservative and the uncertainty of loads was disregarded.[12]used a mixed-integer interval linear programming method to establish the IES optimization model, which considers the uncertainties of multi-energy coupled units, and the deep learning method deals with the uncertainty of wind and load.But it is difficult to ensure high efficiency based on the traditional solution method.In conclusion, the high-precision model for IES which takes multiple uncertainties into account and aligns with actual working conditions must be further studied.

However, the model structure of IES becomes more complex due to the participation of multiple energy.Centralized control has a large amount of data acquisition,high cost of communication, complex model and is difficult to solve.Therefore, distributed solutions have become a hotspot of current research.Architecture has been built for the IES with multiple EH.By comparing the centralized optimization results of the interior point method with the distributed optimization results based on the alternating direction method of multipliers (ADMM), we illustrate the feasibility of utilizing a distributed method to solve the optimization dispatching problem of IES [13].[14-15]established an IES model with multiple decisionmaking agents and used an ADMM algorithm to transform centralized optimization into distributed autonomous collaborative optimization.However, the alternative solution is slower than the parallel solution, and it cannot be applied online.ADMM algorithm has been utilized for distributed coordinated optimization of transmission,distribution, and natural gas system, but the model is non-convex due to the natural gas system, thus making ADMM algorithm difficult to converge [16].Distributed optimization algorithm based on generalized benders decomposition has realized the distributed coordinated optimization for the connected region of electricity and gas using limited interaction information.Compared with the centralized optimization method, the calculation speed is faster, and the adaptive ability is stronger than the ADMM method.However, the solver is highly dependent on the model and cannot deal with uncertainty, which must be resolved repeatedly, and the solving speed cannot meet the real-time requirements [17].Deep reinforcement learning is a model-free method independent of the knowledge of uncertain distribution.The algorithm has better self-adaptive learning and optimization decision-making abilities for nonconvex nonlinear problems [18-21].The method for multiagent deep reinforcement learning (MADRL) provides a new idea for multi-energy coordinated optimization based on a multi-agent system.[22]divided the power grid into three regions as three different agents, and the multi-agent reinforcement learning algorithm has been utilized to realize the coordinated operation of the multi-area power grid.In [23], the reinforcement learning technology based on Nash-Q learning has solved the decision-making problem of multi-agents with different benefit objectives.In [24],under the uncertainty of renewable energy and loads, we adopted fuzzy Q to realize the reliable energy management of microgrids.Previous studies constructed the multi-agent of the power system, but for the IES, the dimensions of observations will rise sharply with the increase of the state quantity, and the multi-agent algorithm will not converge.[25]constructed multi-park agents of electricity-gas IES,and adopted a style="font-size: 1em; text-align: justify; text-indent: 2em; line-height: 1.8em; margin: 0.5em 0em;">This study constructs a distributed model for IES based on multi-EH for the coordinated optimization problem of the electricity-gas-heat IES and proposes a distributed optimization solution method for IES based on multi-agent deep deterministic policy gradient (MADDPG) [26].By introducing the electrothermal dynamic distribution factor,the model can better realize multi-energy coordinated optimization and improve the economy of the system by considering the influence of energy market factors on system optimization.The centralized optimization problem for IES is transformed into a distributed optimization problem with multi-EH agents as the decision centers,which reduces the communication pressure of the system.The MADDPG method is adopted, and the uncertainties of the renewable energy and load are considered in the training process.The solving efficiency improves when the accuracy is ensured which benefits the online application.

The rest of the study is organized as follows.Section 1 introduces the distributed optimization model of an electricity-gas-heat IES based on a multi-agent system.Section 2 discusses the multi-agent deep deterministic policy gradient methods in detail and designs the multiagent deep reinforcement learning model for IES distributed optimization.The practice results are analyzed in Section 3.Section 4 concludes the study.

1 Distributed optimization model of an electricity-gas-heat integrated energy system based on multi-energy hubs

1.1 System modeling

EH can be defined as an input-output port model that describes the exchange and coupling relationship among energy, loads, and networks in a multi-energy system,which is flexible for modeling the multi-energy system[27].This study develops a distributed system of IES based on multiple EH, as shown in Fig.1, to carefully consider the internal constraints of the system.If the system were separated into EH regions, for instance, each EH region can represent distributed energy that is dispersed throughout various geographical locations.The EH area corresponding to each geographical location is connected to the external energy network, and the corresponding renewable energy can be accessed within its internal area.For example, an EH has high-quality wind resources due to geographical location,so it can develop corresponding wind power generation and supply the loads in its area, to reduce the pressure of the external network and increase flexibility.Meanwhile,the internal EH must meet the demands of electrical and heat load.Therefore, each EH area gathers and integrates corresponding coupling facilities, which mainly represent the energy conversion process.The coupling facilities can be designed according to the resources allocated in the actual area, to complementarily use the energy obtained from various energy networks and renewable energy, and meet the demands of various loads through energy conversion.

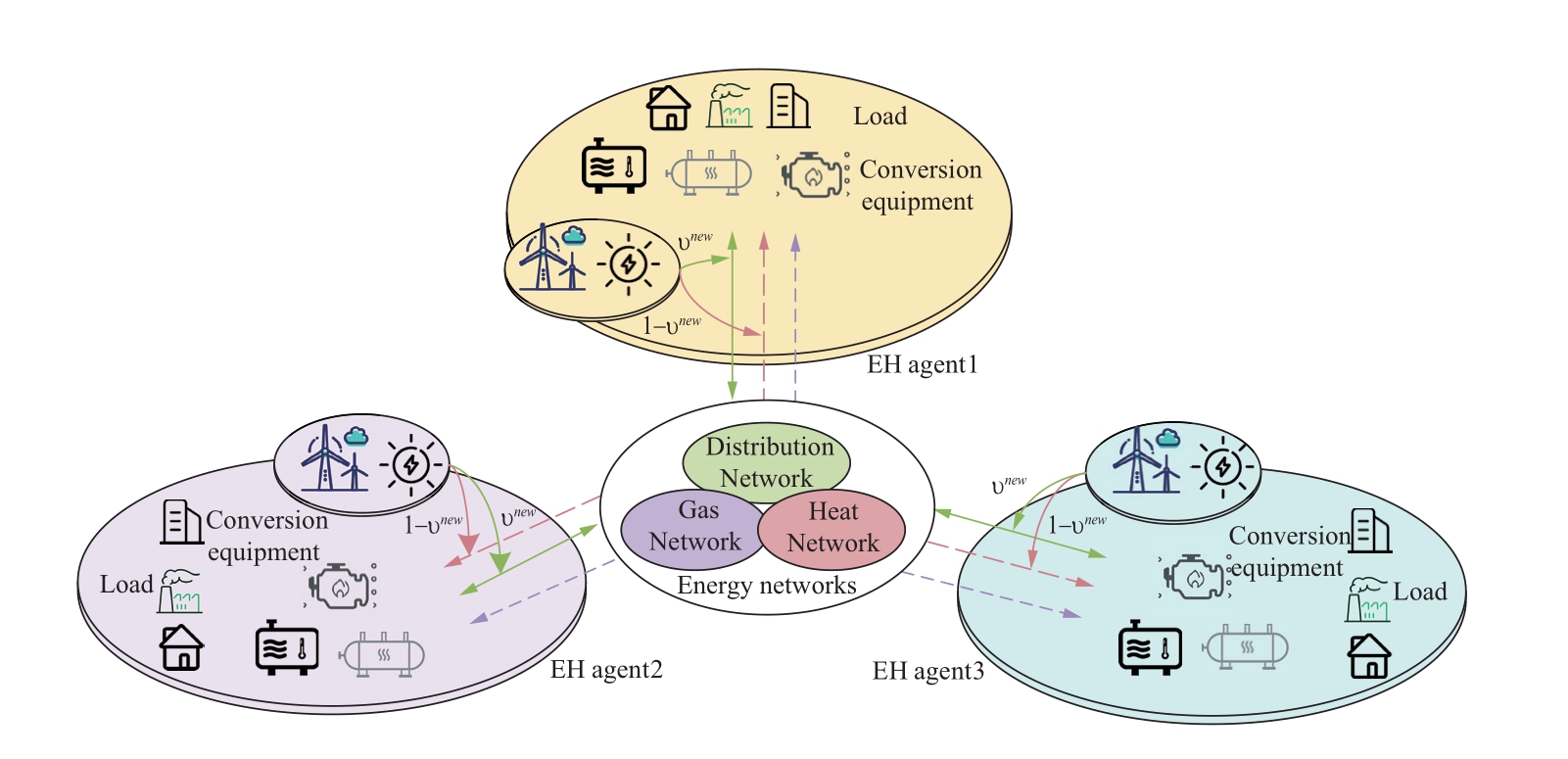
Fig.1 Schematic diagram of IES distributed structure based on multi-agents

The coupling facilities are located at a hub position that receives input and converts output in the EH area, which can comprehensively reflect all the operational states of the entire system.The facilities are highly flexible andcrucial for the system to operate.Therefore, the EH model represents the coupling facilities in this study.The model is built as follows:

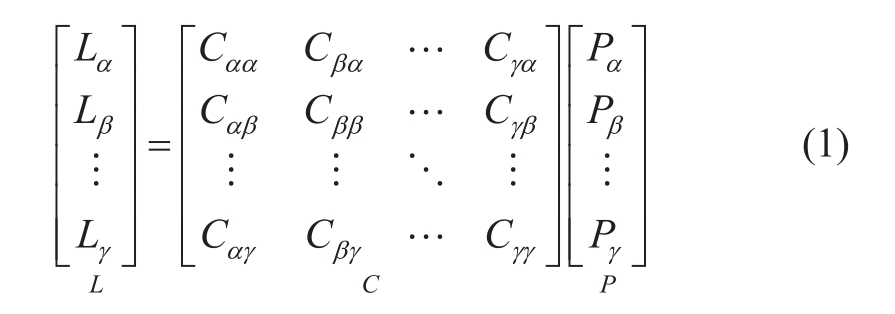
where α,β,…,γrepresent different types of energy.Land Pare the output and input power of EH.C is the conversion coupling matrix, which describes the mapping of EH from input power to output.

The internal conversion facilities of EH studied are mainly composed of the transformer, CHP, heat exchanger(HE), and electric boiler (EB).We assume that in steady-state conditions, energy loss in EH agents only occurs in conversion facilities [28].The specific model is built as follows:

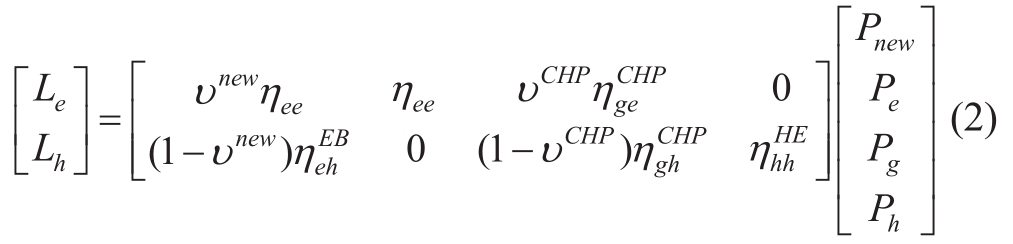
where subscripte,gandh are the input types of electricity,gas, and heat.Superscripts represent the conversion facilities.The coupling matrix mainly represents the distribution, transformation, or transmission of energy.υis the dynamic distribution factor, representing that all kinds of energy are allocated to different energy transmission or conversion facilities in a certain proportion.ηis the efficiency factor of the facilities, representing that the input energy is transformed through mechanical and chemical channels with a certain conversion efficiency [1].Le and Lh are the output electrical load and heat load from EH,respectively.Pnew represents photovoltaic or wind power.

Equation (2) represents the whole process from input to output of each EH area.Each EH area must purchase Pe, Ph and Pg from the three energy networks of electricity, heat,and gas, and then transmits or converts energy through the conversion facilities inside the area to meet the needs of Le and Lh at any time.Meanwhile, if there is renewable energy Pnew in the EH area, the corresponding energy purchase cost will be reduced, and the demands of Le and Lh can be met by Pnew.The electricity-heat distribution proportion depends on the dynamic distribution factorυnew.If Pnew is sufficient, there is no need to purchase power from the energy network.However, the surplus Pnew can be sold to the power grid for income.This study reflects the changes in real-time supply and demand by dynamic electricity prices.The system’s economics will be impacted by the combined uncertainties of renewable energy and the realtime fluctuation of electricity prices.Therefore, the EH area can independently select the electricity-heat distribution proportion by comprehensively considering multiple factors such as Pnew and dynamic electricity price at each time.

In conclusion, as shown in the system, each EH area can select the dynamic distribution factor and the amount of energy interacting with energy networks by collecting its regional load demands, electricity price, and renewable energy.Therefore, the IES model can be transformed into a distributed optimization model with multiple EH regions as the decision center.This reduces the pressure of system communication and avoids centralized optimization from collecting global information.Through the distributed cooperation of multiple EH regions, the multi-energy complementary optimization of electricity-gas-heat IES can be realized.

1.2 Objective function

The economy of regions where each EH agent is located is taken as the optimization objective.The cost of each EH agent is set as the cost of energy caused by the energy interaction between EH and energy networks.The objective function is expressed as follows:

where ce ,ch , and cgare cost coefficients of the energy interaction between EH and distribution network, heat network, and gas network, respectively.

1.3 Constraints

The equation constraints of the system mainly include energy networks and EH.EH constraints are shown in (2).Energy networks mainly include distribution, heat, and gas networks.

1.3.1 Constraints for distribution network

The distribution network uses the AC model.For the entire network, the power obtained from the distribution network is equal to the sum of the power consumed by the load and net loss of the system.The constraints are expressed as follows:

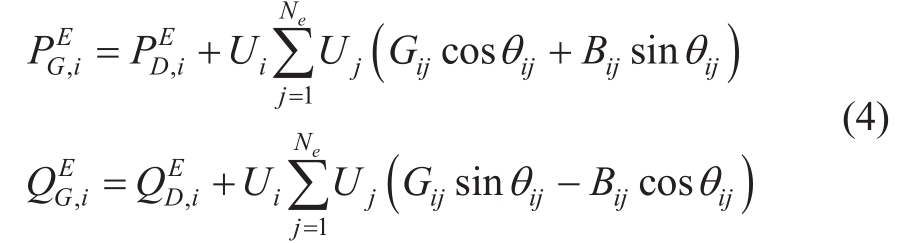
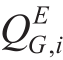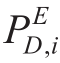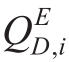where and are the active and reactive power obtained from the main network.and are the active and reactive power consumed by loads.Ne is the number of nodes of power distribution networks.U is voltage amplitude.G and B are conductance and susceptance,respectively.θij is the phase angle difference between node iand nodej.Superscripts E, H, and G are distribution, heat,and gas networks, respectively.

1.3.2 Constraints for heat network

Centralized heating is adopted in the heat network,which mainly includes heat sources, transmission pipes, and heat loads.

The heat power at a nodei is expressed as follows:

where Cp is the specific heat capacity of water.mq,i is water flow at a node i.Ts,i and To,i are the temperatures before and after nodeiis injected.

The temperature relationship between the beginning and end of the pipe is calculated as follows:

where Ti and Tj are the temperature at the beginning and end of the pipe respectively.Ta is the ambient temperature.Lij is the pipe length from nodeito nodej.λis the coefficient of heat conduction.

The relationship of mixing at nodes is calculated as follows:

where min,j is the flow from nodej into nodei,mout,k is the flow from nodeito nodek.Tin,j is the temperature when nodejflows into nodei.Tout,k is the temperature when node i flows to nodek.

In conclusion, the power balance equation of the heat network is expressed as follows:

where 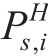is heat power for the heat source point.is the load power of heat.Nhis the number of nodes in the heat network.

1.3.3 Constraints for gas network

The gas network mainly includes gas sources, transmission networks, compressors, and gas loads.

The flow of the transmission network is calculated as follows:

where is the steady flow of the natural gas pipeline.πi and πj are the gas pressure of nodesiand j respectively.sij is a symbol vector, representing the flow direction of natural gas in the pipeline.Kij is the pipeline constant, calculated as follows:

whereµis the efficiency parameter of the natural gas pipeline.MC is the friction coefficient.ZK is the gas compression factor.G is the relative density of natural gas.LK is the pipeline constant.TK is the average temperature of natural gas in the pipeline.DK is the inner diameter of the pipeline.C0 is a constant coefficient.

The compressor model adopts the method proposed in[29], as in Fig.2 below:

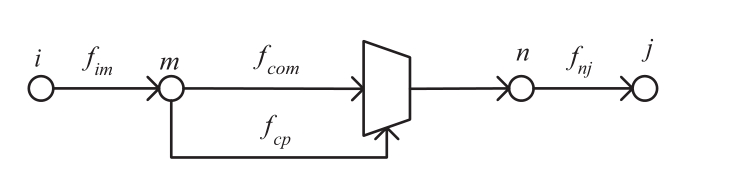
Fig.2 Schematic diagram of the compressor model

In Fig.2, fcom is the flow into the compressor.fcp is the flow consumed by the compressor.fim is the flow at the compressor’s inlet.fnj is the flow of the compressor’s outlet.The specific model is built as follows:

where kcpis the compression ratio of the compressor.qgas is the calorific value of natural gas.Tgas is the natural gas temperature, andais the variable coefficient.After calculation by the above method, the flow of the pipeline containing the compressor can be equivalent to a load of adjacent nodes fc,i.

The flow balance equation of the gas network is expressed as follows:

where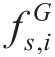is the gas supply at the gas source nodei,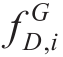is the gas consumed by gas loads at a nodei, andNgis the number of nodes in the gas network.

In addition to the equality constraints in the energy network model, the following inequality constraints must be satisfied to ensure the safety and stability of the system operation:where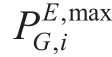 and are the maximum and minimum active power obtained from the main network, respectively,and and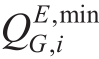are the maximum and minimum reactive power obtained from the main network,respectively. 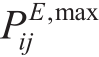andare the maximum and minim

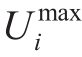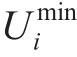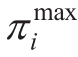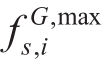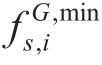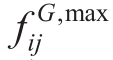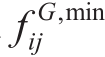um branch power of the distribution network, respectively.and are the maximum and minimum limits for the voltage of the node in the distribution network, respectively. andare the maximum and minimum air pressures of gas netwo rk nodes, respectively. andare the maximum and minimum limits for gas supply at the gas source nodes. andarethemaximumand minimum flow in the gas network pipeline, respectively.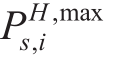and are the maximum and minimum heat capacity of the heat source nodes in the central heating network, respectively. andare the maximum and minimum limits of node temperature in the central heat network, respectively.υnewis the dynamic distribution factor.

In conclusion, equations (2) - (14) are the optimization model of an electricity-gas-heat IES based on multi-EH.The optimization problem presents the characteristics of strong coupling, non-convexity, and nonlinearity by introducing the dynamic distribution factor and considering the refined model of the energy network.Therefore, the traditional mathematical programming method is difficult to apply.The problem will then be solved using the multi-agent deep reinforcement learning algorithm.

2 The design of multi-agent deep reinforcement learning model for IES distributed Optimization dispatching

Each EH area in the system is considered a decisionmaking subject and is divided into agents (hereinafter referred to as EH agents).The IES optimization problem is transformed into a distributed optimization problem with EH agents as the decision centers.There are multiple EH agents in the system.If multiple single-agent algorithms are directly utilized, there is no interactive information among agents, and collaborative optimization cannot be completed.However, even if the information interface is established,for a single-agent algorithm, each EH agent interacts and affects the interaction of other EH agents as a part of the entire system.The environmental states are constantly changing, which will directly lead to the shaking and even collapse of training.Therefore, this study adopts the multiagent deep reinforcement learning method.

2.1 MADDPG algorithm

The MADDPG algorithm is an extension of the deep deterministic policy gradient algorithm (DDPG) in multiagent [30].Based on the actor-critic framework, each agent has an actor-network and a critic network.Different from DDPG, during training, each agent’s actor takes actions according to its state, and then the critic evaluates the actor’s actions.The actor updates its strategy according to feedback.Each critic obtains more accurate evaluation information by estimating the strategies of other agents.After training, each agent only needs to use an actor to take actions according to its state.Currently, there is no need to obtain information from other agents, and the decisions are completed by each agent independently.MADDPG obtains the optimal strategy through centralized training and only needs local information when applying it.Therefore, it is a mode of “centralized training and distributed execution”.A schematic diagram of the MADDPG algorithm is shown in Fig.3.

In Fig.3, the actor of agenti only needs to obtain its relevant state information si.ai is the action taken by agent i.ri is the reward earned.θi is the weight parameter of agenti.Suppose there areN agents, and the observation set x=(s1 , …,s N)is the state information of all agents.The actor constantly updates its parameter θito maximize the expected value of rewards, namely, to raise the assessed value of the critic.The rule for policy update of the actor is expressed as follows:

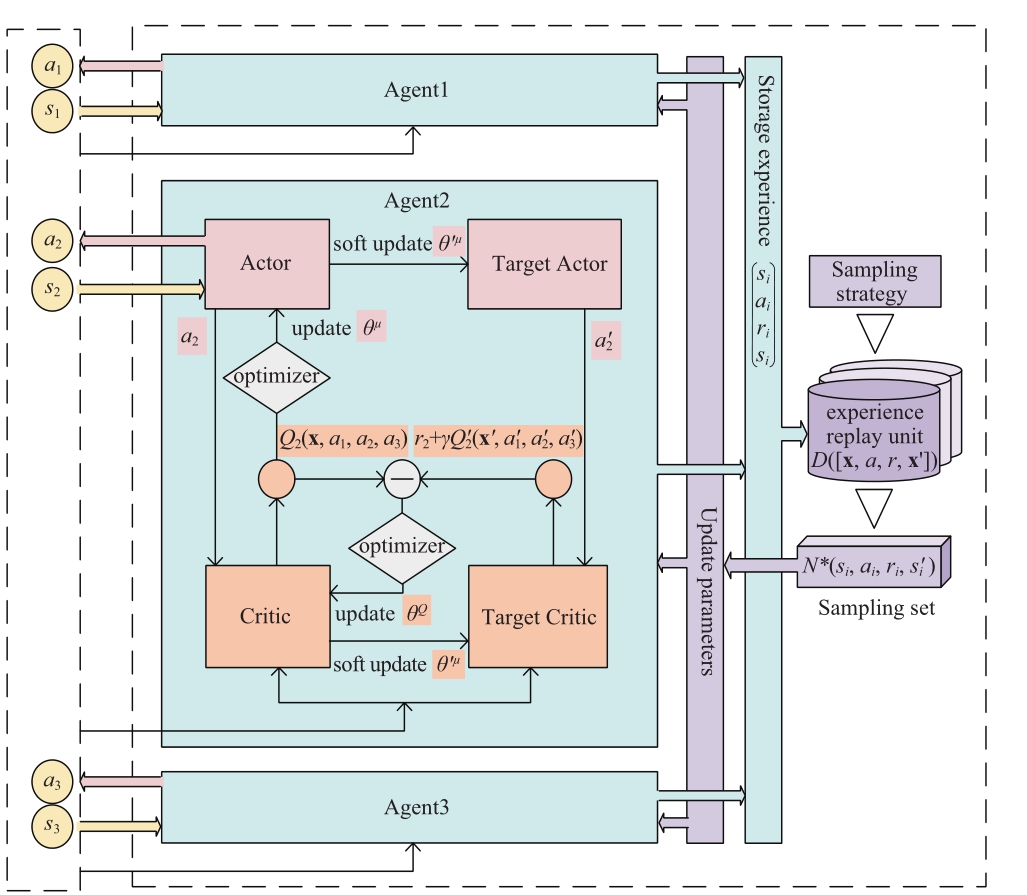
Fig.3 MADDPG algorithm diagram

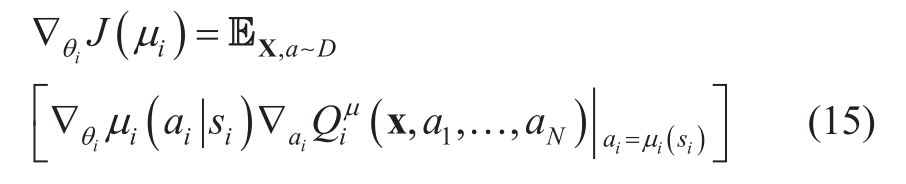
where 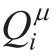 (x,a1 ,… ,a N)is a centralized state-action value function.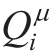is learned and updated by each agent independently, so each agent can have any form of thereward function.D = (x,x′,a1 , … ,a N ,r1 , … ,rN)is the experience replay unit which stores the experience of all agents, and a group is randomly selected for training at each training.Simultaneously, to solve the problem that an agent is difficult to converge when choosing an action in action distribution in the continuous space, MADDPG adopts the continuously determined strategy setµofNagents.

Critic mainly updates its parameters by minimizing the time difference error, and its loss function is expressed as follows:

such that

whereµ′is the policy settings of the target network.γ∈[0,1]is the discount factor.

Finally, the soft update mode is adopted by the target network to copy parameters from the valuation network periodically, shown as follows:

where θi′is the target network parameter of agenti.τis the soft update parameter, andτ≤1.

In a multi-agent environment, agents interact with the environment, simultaneously causing an unstable environment for each agent.MADDPG proposed a strategy integration method, in which the strategy µi of agentiis composed of K sub-strategies, and only one sub-strategy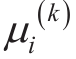is utilized in each training episode so that the overall reward of the strategy set is the highest in the whole training process.Therefore, the actor’s final policy is updated to:

2.2 State Space

The state space of the system mainly includes the output of renewable energy Pnew (including wind Pwr or photovoltaic power Psr ), electrical load Le, heat load Lh,electricity pricece, gas price cg, heat price ch, node voltage of power systemUE, node pressure of natural gas system πG , and node temperature of heat systemTHin each EH agent region, such that:

2.3 Action space

The action space variables correspond to the control variables of the studied system [31].In the system, each EH is considered as an agent.According to the EH model, as in(2), the action space variables include the powerPe , P h , Pg interacted between the agent and the energy networks and the dynamic distribution factorυnew , such that:

2.4 Environment design

Each agent’s actor takes actions according to the state at this moment, interacts with the environment, obtains rewards, and transfers to the state.Critic evaluates this action, and the agent is guided to take action at the next moment.For this process, take the IES model (4)-(14) as the environment.After each agent takes action at each moment, we conduct the power flow calculation for the IES.The relevant states of nodes in the distribution network,heat network, and gas network are fed back to calculate the reward function and transferred to the next moment, and cycling in this way.

2.5 Reward function

The algorithm’s reward function design is crucial and moderately impacts how well the algorithm converges.Therefore, the setting of the reward signal should be able to be transmitted to the target that the agent wants to accomplish, to guide the agent to improve the actions in the direction of maximizing the reward function.The opposite number of the objective function in the IES model represents an immediate reward for each agent.The optimization problem must meet the corresponding constraints.According to the constraints described in Section 1.2, if the corresponding variable does not meet the constraints, the penalty value rpush, together with the immediate reward, is set as the final reward function of the agent, such that:

In conclusion, each EH agent firstly takes actions according to the observations of the load information, the output of renewable energy, and the dynamic electricity price in its area, that is, determines the dynamic distribution factorυnew and the power required to interact with the energy networks, and transfers to the next states at random.The critic network evaluates the joint actions taken by all actors, calculates the reward function, and then guides the actors to take better actions.By continuously learning the feedback process, the cost reaches the maximum and the penalty goes to zero (i.e., the cost is optimal when the constraint conditions are met).This completes the loop process.

2.6 Algorithm process

The overall algorithm flow chart of a distributed optimization model for IES based on MADDPG is shownin Fig.4.The primary process of each agent is precisely the same when two agents are being optimized, for instance.In this figure, the blue line represents the synchronous process,and the red line represents the process of information interaction.The specific steps are as follows:

Fig.4 Solution flow chart of IES distributed optimization model based on MADDPG

Step 1: Each agent initializes parameters synchronously.Set the period T for optimization dispatching and the number of training rounds M of each agent.The initial values are all set to one.At the initial stage, the agent network parameters are set as θi randomly.

Step 2: Initialize the environment.Load the IES system model into the environment and set the interface file for the state and action in the MADDPG algorithm, so that the power flow can be calculated in real-time according to the state action and the corresponding environment states can be fed back.

Step 3: Each agent interacts with the environment.Each agent observes the states si of its area and takes actions ai by its actor-network.After taking action, the agent exchanges the actions with other agents.Then, the critic network of each agent interacts with the environment according to the joint action (a1 … a n)and calculates the reward ri based on the feedback of the states in response.The agent transfers the state to the next moment and observes the state of the next moment, and (x,a,r,x′)will be stored in experience replay unit D.

Step 4: Update network parameters.A set of(x( k ) ,a ( k ) , r ( k ) , x ′(k ))under the policykis randomly sampled from the experience replay unit D.The critic and actor parameters are updated according to (16) and (18), and the target network parameters are updated according to (17).

Step 5: Assess whether the current number of training rounds m reaches the set value M.if it reaches the set value,end the training, output, and save the results.If not, return to step 2 and start a new round of training.

3 A case study

This study uses a 6-node distribution network, a 6-node heat network, and a 5-node gas network.The three networks are coupled through the three regional EHs, forming the distributed optimization system of IES with three EH agents as shown in Fig.5.In the power system, electricity can be obtained by nodes 5 and 6 from the main network.Node 1 is the balance node.Nodes 2, 3, and 4 are nodes of electrical loads, and they are coupled with the gas network and heat network through EH as coupling nodes.In the gas network,the gas source node is set at node 4, and nodes 1, 2, and 3 are nodes of gas loads.In the heat network, the heat source node is set at node 1, and nodes 4, 5, and 6 are nodes of heat loads.This study has three EH agents in the system.EH1 is equipped with a wind power plant, and EH2 is equipped with a photovoltaic power station.EHs with wind power,photovoltaic, and no renewable energy are respectively corresponding to agents 1, 2, and 3.

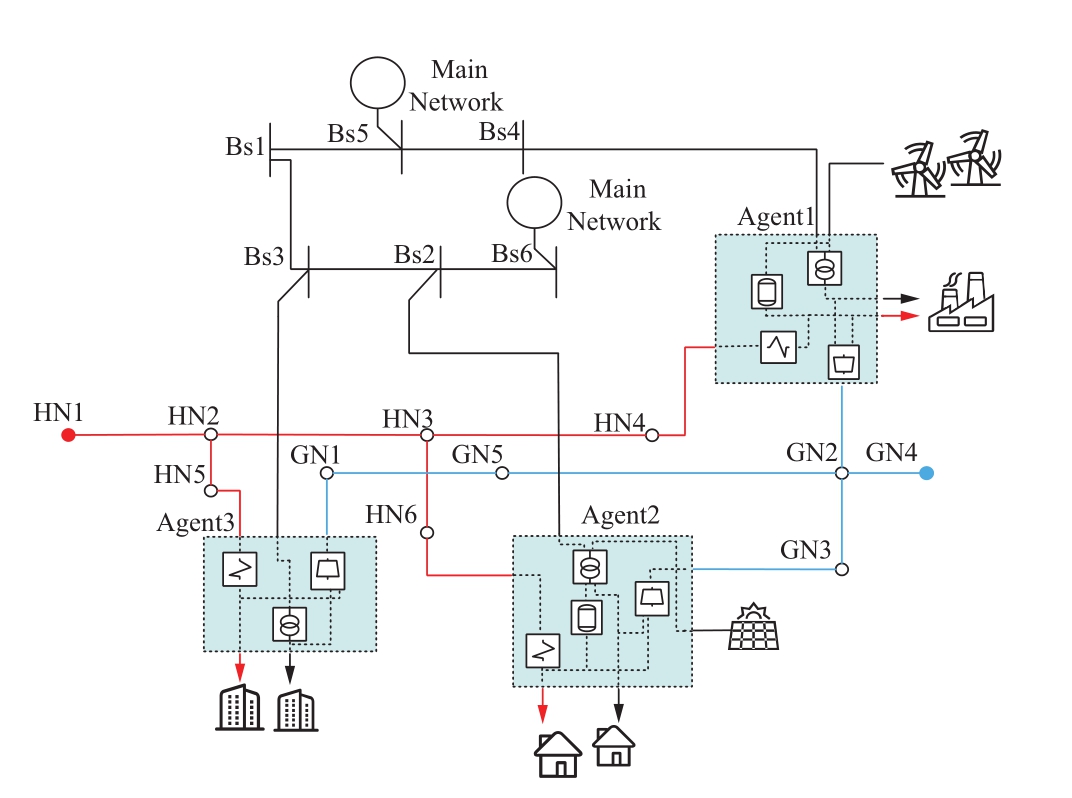
Fig.5 A case of distributed optimization system for IES with three EH agents

In this study, considering the dual uncertainties of renewable energy and loads, uncertainties are added to input data during model training.Alternatively, during MADDPG training, each EH agent must acquire observable state data within its area.When reading renewable energy data,unknown data is superimposed on the obtained data, namely the fluctuation range, as shown in Fig.6.

In Fig.6, Ew and Es represent the fluctuation range of wind power and photovoltaic power, which obey the normal distribution.Therefore, we ensured that regardless of how many rounds of training, the renewable energy data obtained each time are different, but they are both within the range.The size of the fluctuation range can be adjusted flexibly,and the loads are processed the same as renewable energy.

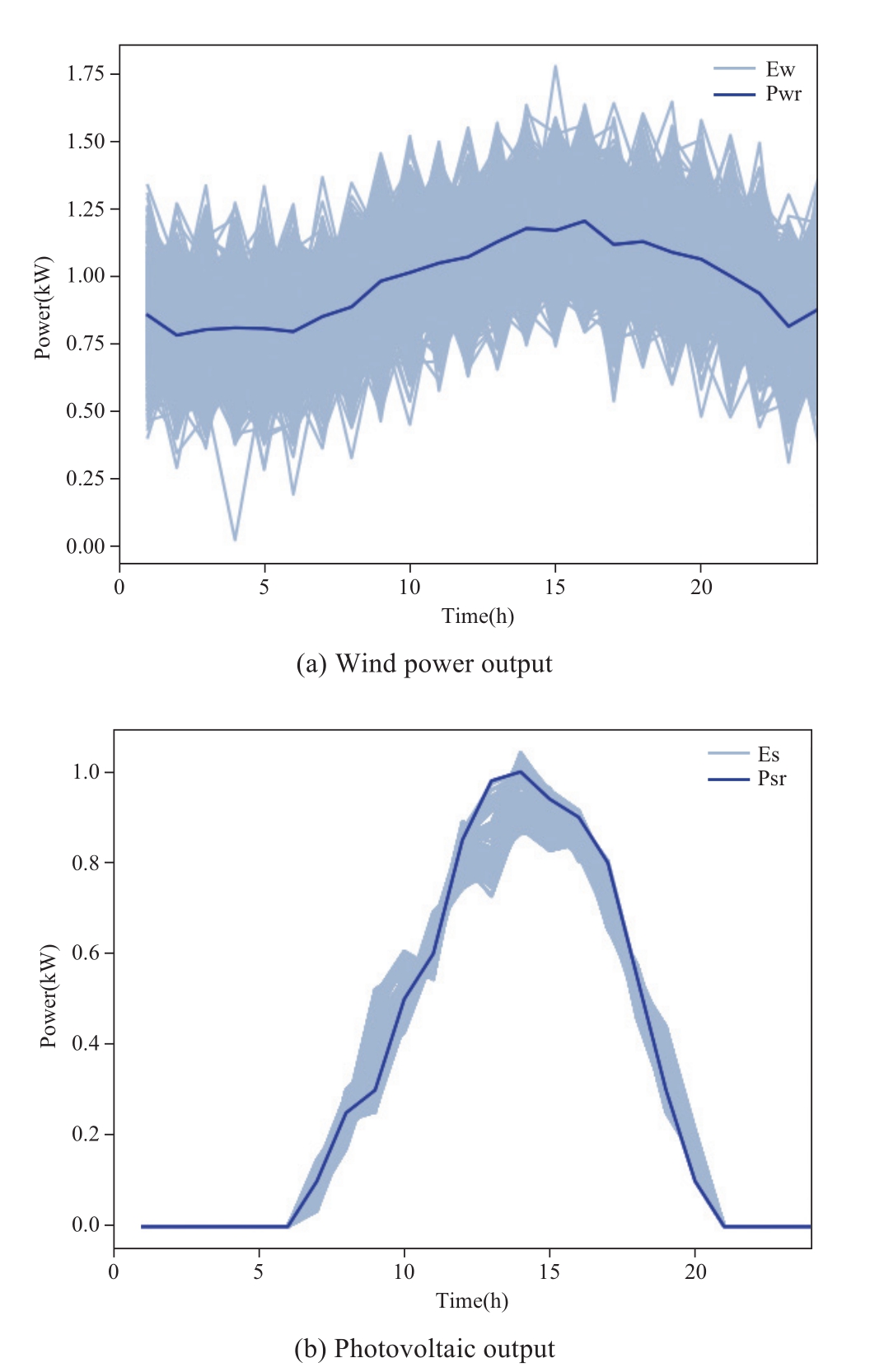
Fig.6 Outputs of wind power and PV

The optimization time takes 24 hours.The related parameters of the system, internal parameters of the agents,load data of each area, and the output data of renewable energy can be seen in the appendix.

3.1 Parameter Settings of MADDPG and Analysis of Training Results

3.1.1 Parameter settings

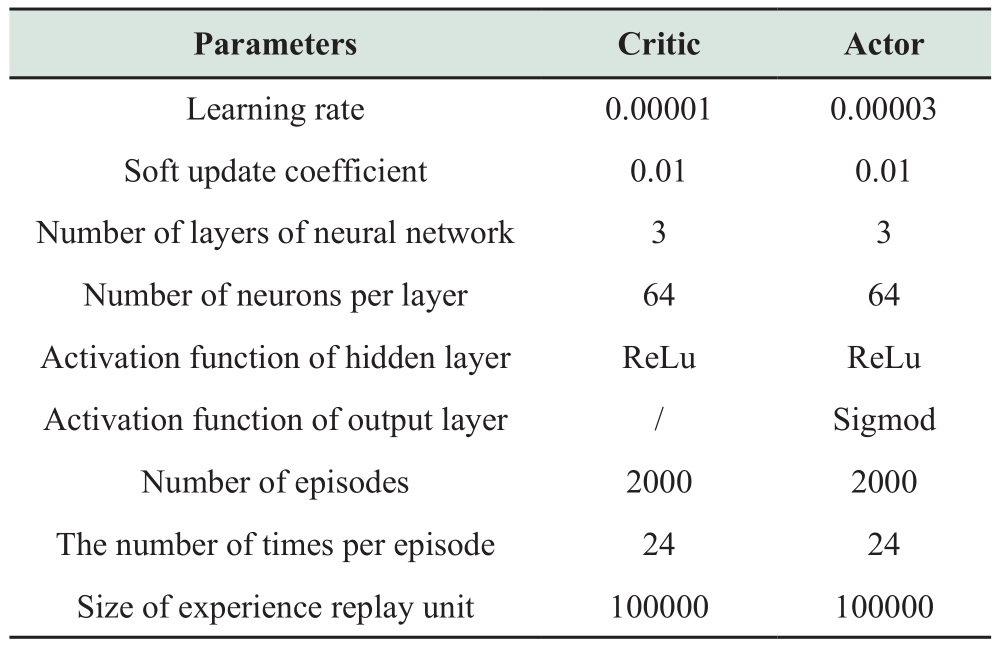
The MADDPG algorithm is written based on the Tensorflow framework.The actor and critic network parameters of the three agents are similar.Specific parameter settings in this model are shown in Table 1.

Table 1 Model-specific parameter settings

3.1.2 Analysis of training results

The training for the multi-agent reinforcement learning optimization model is conducted for the IES above.During training, the random method is used to explore the action space.The standard deviation of the action is taken as the random quantity.The random quantity is simultaneously applied when selecting the action, to ensure a larger exploration space and avoid falling into local optimization.There are 2000 rounds of training iterations, and the training results are shown in Fig.7 below.

In Fig.7, the agent begins in the exploration stage.With the increase of training episodes, the agent has converged at 750 episodes.Fig.8 shows the result of the penalty value of the agent.The penalty value of the agent becomes 0 around 700 episodes, and then the overall reward of the agent converges around 750 episodes.The agent gradually converges to the optimum after satisfying the constraints.In addition, due to the uncertainty of renewable energy and the different training samples each time, the reward value has a certain fluctuation after reaching convergence.

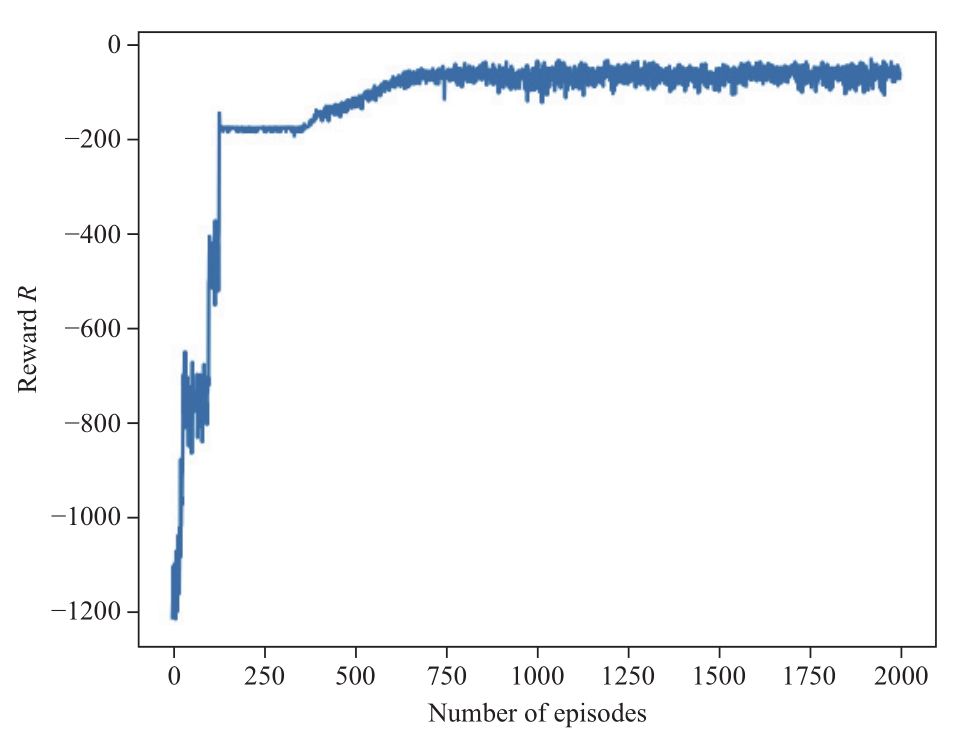
Fig.7 The overall reward value of the agent

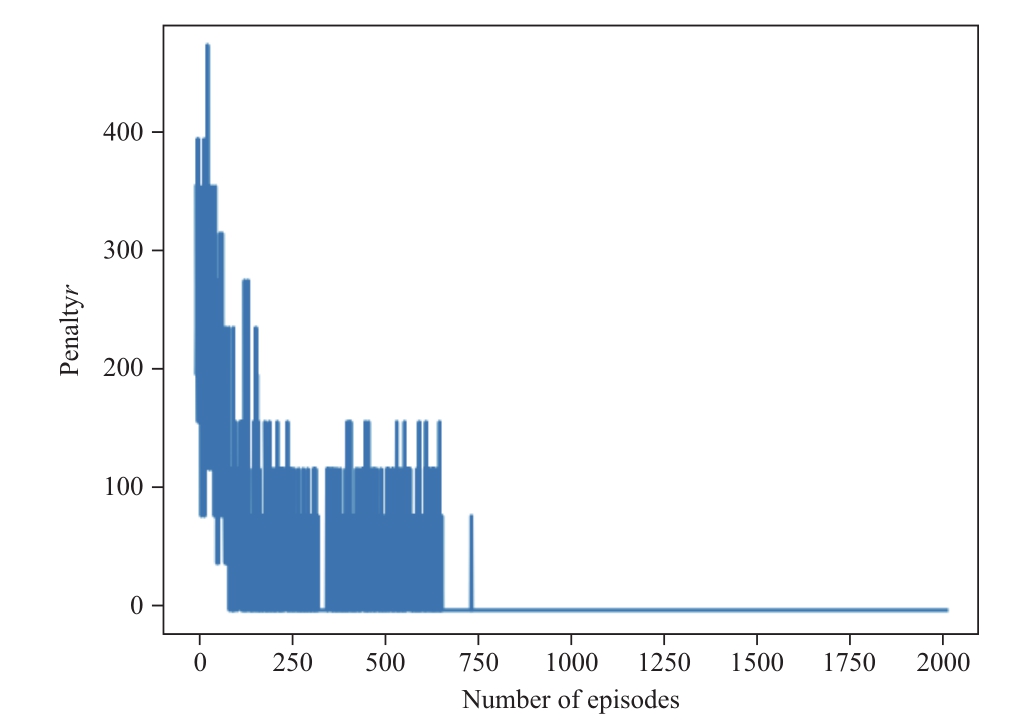
Fig.8 The overall penalty of the agent

3.2 Analysis of optimization dispatching results

To compare the impact of introducing dynamic distribution factors on system optimization, different scenarios are set as follows:

1) 1: the renewable energy in each agent area in the system can supply heat load through electricity to heat transfer, that is, the renewable energy in this area givespriority to meeting its regional load demand, and the excess power will be returned to the power grid.

2) Scenario 2: renewable energy in each agent area in the system can change the electricity-heat distribution proportion at any time according to the dynamic electricity price, that is, the dynamic distribution factor is introduced asυnew.

The optimization results of agent MADDPG are shown in Fig.9 (a) and 9 (b).Since there is no renewable energy set in agent 3’s area, agents 1 and 2 are taken as examples for analysis.From the comparison of optimization results of scenarios 1 and 2, the electricity-heat distribution proportion of renewable energy in the agent area in scenario 1 cannot change in real-time with the electricity price.After renewable energy meets the demands of the regional electric load, the excess electricity is supplied to the heat load through electricity conversion.If there is more excess electricity, it will be sent back to the power grid.In scenario 2, in the agent 1 area, from 4:00 to 9:00, the heat loads demand increases.Wind power is no longer fully supplied to the electrical loads.υnew decreases accordingly, and part of the heat loads will be supplied through the electric boiler.Currently, the electricity price is relatively low, and part of the electrical loads can obtain electricity from the power grid to meet the demands.From 10:00 to 19:00, the electricity price increases, andυnew increases accordingly.The wind power meets the demand of electricity load, and the surplus wind power is sent back to the grid for income.After 20:00, the electricity price drops andυnew is reduced accordingly.In agent 2’s area, the changing trend ofυnew is similar to that of agent 1.From 5:00 to 9:00, the demands of heat loads increase andυnew is small.From 10:00 to 19:00, the electricity price is the highest andυnew gradually increases.We obtain income by returning electric energy to the power grid.Table 2 shows the total cost of optimization dispatching in scenarios 1 and 2.The cost of scenario 2 is 20.6 % lower than that of scenario 1.In scenario 2, due to the consideration of the energy price factor, the agent adjusts the electricity-heat distribution proportion of renewable energy in real-time according to the change in supply and demand and reasonably distributes renewable energy.The economy of the system is improved while meeting load demands.

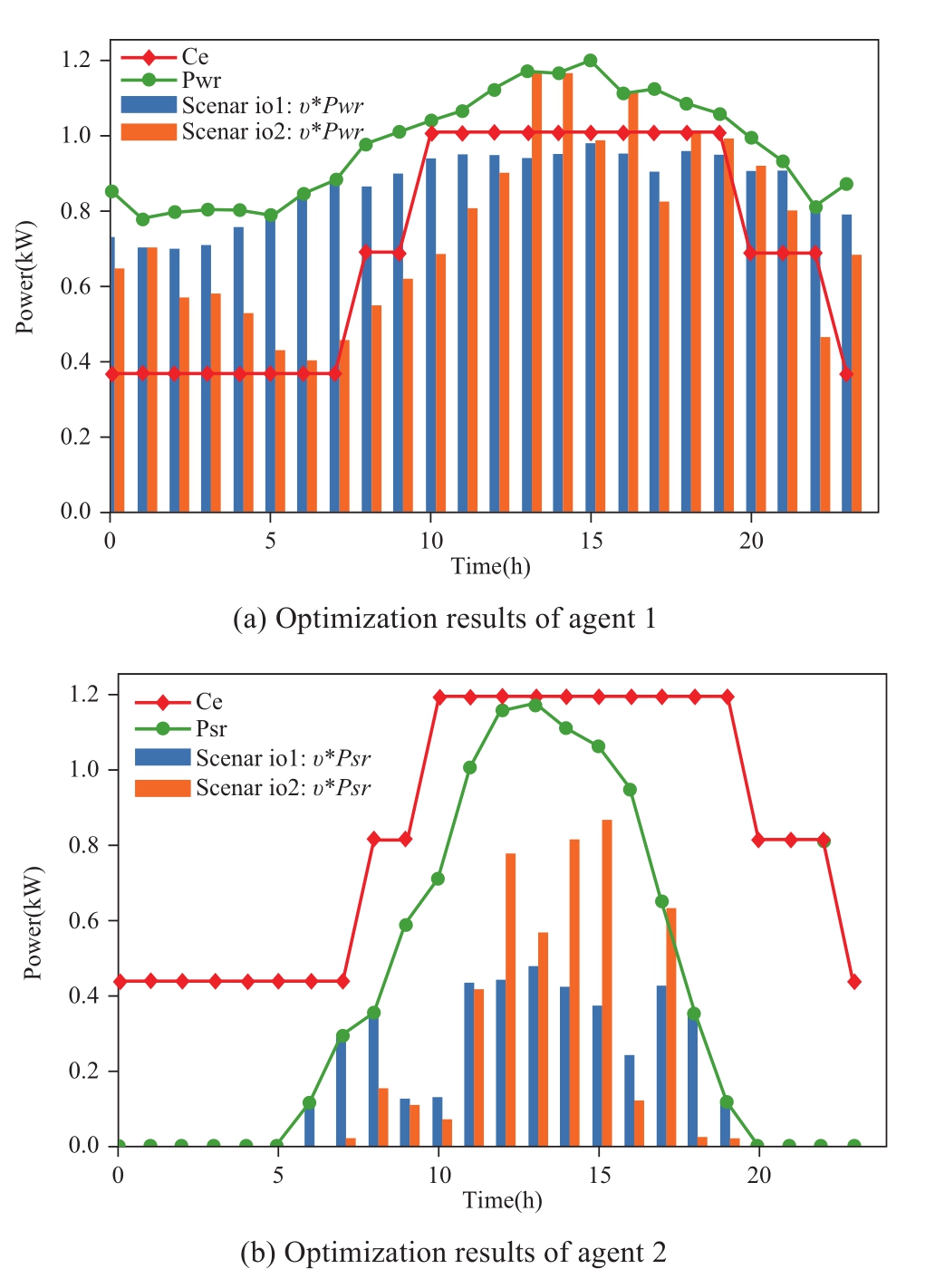
Fig.9 Optimization results of agent 1 and agent 2

Table 2 Cost comparison under different scenarios

To improve the model’s ability to deal with uncertainty and make the system able to deal with large fluctuations of renewable energy, various samples of renewable energy output data are used for MADDPG algorithm training.Taking Agent 1 as an example, typical wind power data for a certain day is selected during the test, and the optimization results are shown as follows:

In Fig.10, the policy of actions is the total power interacting with the energy networks.The trend of the policy curve (blue line) is consistent with that of the total load curve (orange line) minus the renewable energy curve (green line).For large fluctuations in renewable energy output,through the MADDPG algorithm, the trained model can generate a reasonable optimization policy in a short period of time without re-calculation like the traditional method.

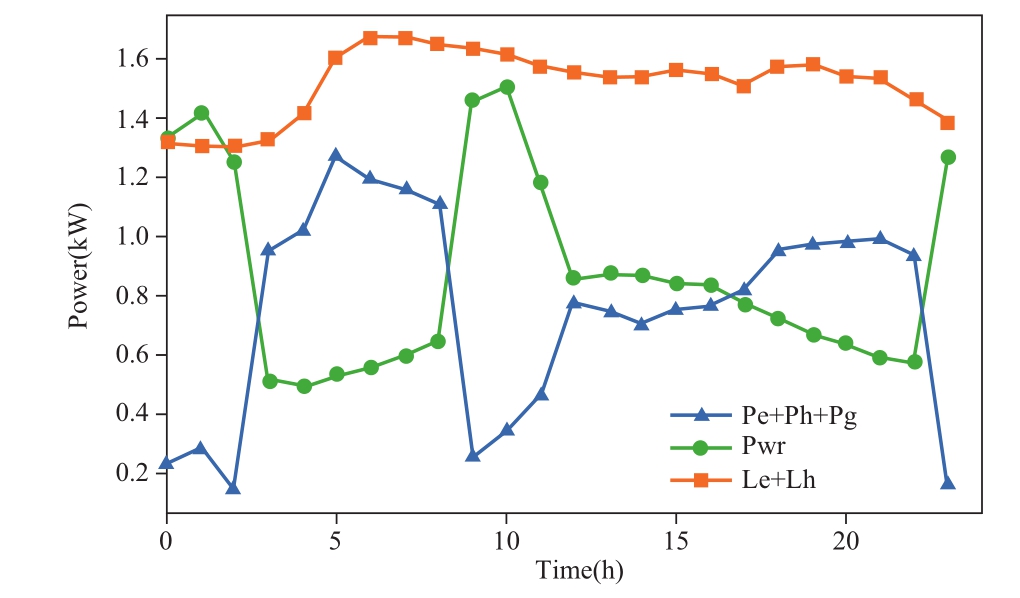
Fig.10 Optimization results of agent 1 in the extreme scenario

3.3 Comparative analysis

3.3.1 Comparison with the traditional centralized solution

To further compare the optimization performance of multi-agent deep reinforcement learning and traditional centralized solution methods, the proposed method is compared with the traditional mathematical programming method, which uses the solver IPOPT for unified solutions.Table 3 shows the comparison results.

Table 3 Comparison of different methods

Table 4 Comparison of different methods

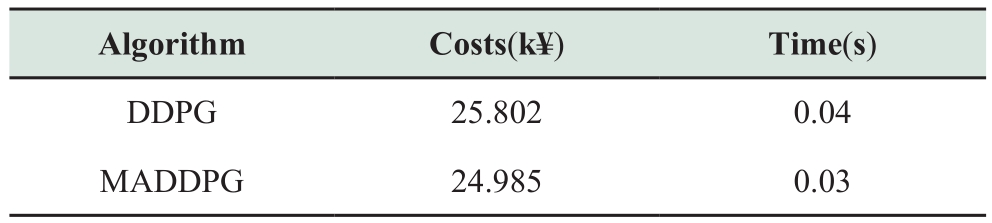
The IPOPT centralized solution and MADDPG distributed solution results, which are compared, show no variation in the overall power cost between the three agents and the energy network, demonstrating the viability and effectiveness of the proposed approach.

From the comparison results of solution time, it can be seen that there are many optimization variables for solving the IES model, which belongs to a high-dimensional nonlinear non-convex problem.It is difficult to solve with an IPOPT solver, so the solving time is long, and the load data need to be recalculated after changing.The MADDPG algorithm takes a long time to train, but after the model training, the optimization strategy can be given in the second level during the test, and there is no need to retrain the model.

3.3.2 Comparison with the deep reinforcement learning method

MADDPG is a deep reinforcement learning method in a multi-agent environment.To further compare with the single-agent deep reinforcement learning, the DDPG method is utilized to compare under the same uncertainty of renewable energy.The results are as follows:

From the comparison results, we conclude that both DDPG and MADDPG methods belong to intelligent algorithms with short execution times and can give nearly real-time decisions.However, the DDPG method takes all control variables as the agent’s actions, causing a sudden increase in the action dimension of the single agent.Fig.11 shows that DDPG training converges in 1100 rounds.Due to the slow convergence speed of the training procedurecompared to the MADDPG approach and the poor learning performance of the single-agent algorithm after convergence (Table 4), MADDPG is preferable in complex environmental issues.

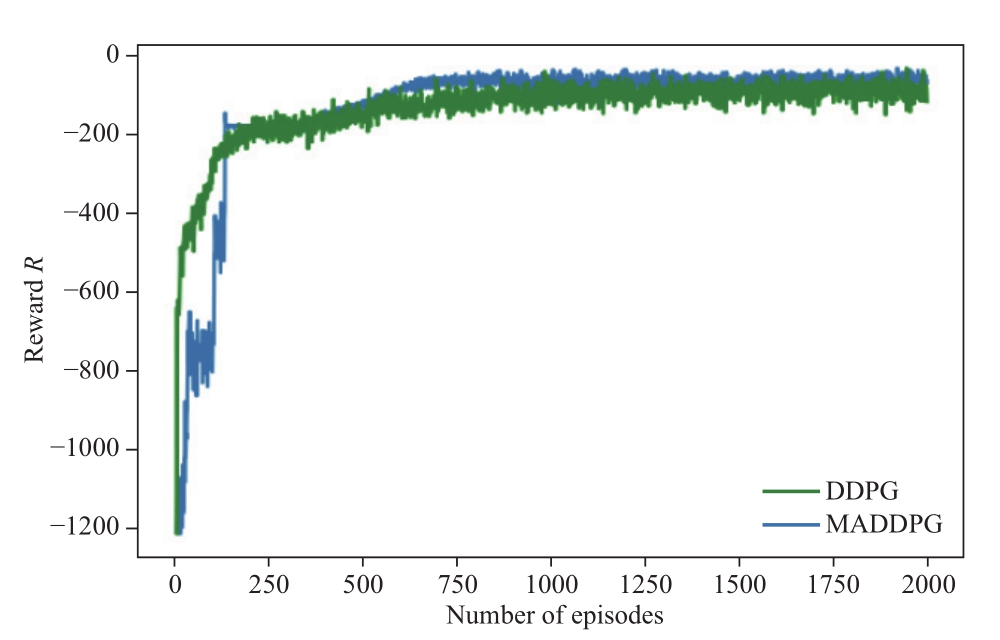
Fig.11 Comparison of training results between DDPG and MADDPG

3.3.3 Comparison under different working modes

In Section 3.2, each agent sets the same reward function,which takes the optimal overall economy of the system as the objective function.The agents are in a cooperative mode and conduct collaborative optimization as a whole.For the MADDPG algorithm adopted in this study, each agent has a centralized critic independently, so different agents can have any form of the reward function.To compare the effects of different working modes of agents on the system, scenario 3 is set based on scenario 2 as follows:

Each agenti sets a reward function separately, and the cost is expressed as:

For each agent, only the economy of its region is considered in the reward function and each agent changes from the cooperative mode to the competitive mode.The cost comparison results are shown in Table 5：

Table 5 Overall cost comparison under different working modes of agents

Table 5 shows the overall cost comparison results, which shows that in scenario 2, the agents are cooperative and primarily focus on the optimal overall economy.While in scenario 3, the agents are in the competitive mode, mainly considering their interests, which will increase the overall cost of the system.

Table A1 Internal parameters of the agents

Table A2 Parameters of heating pipeline

Table A3 Parameters of heating node

Table A4 Parameters of gas pipeline

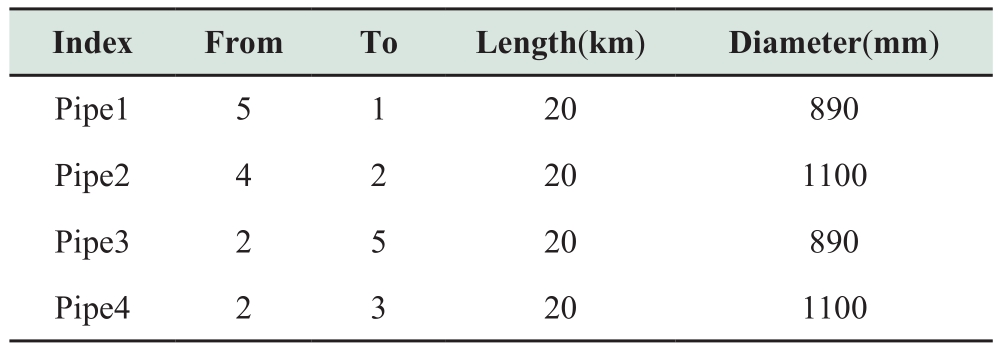
Table A5 Parameters of nodes in gas network

Table A6 Parameters of a distribution network branch

Table A7 Network parameters

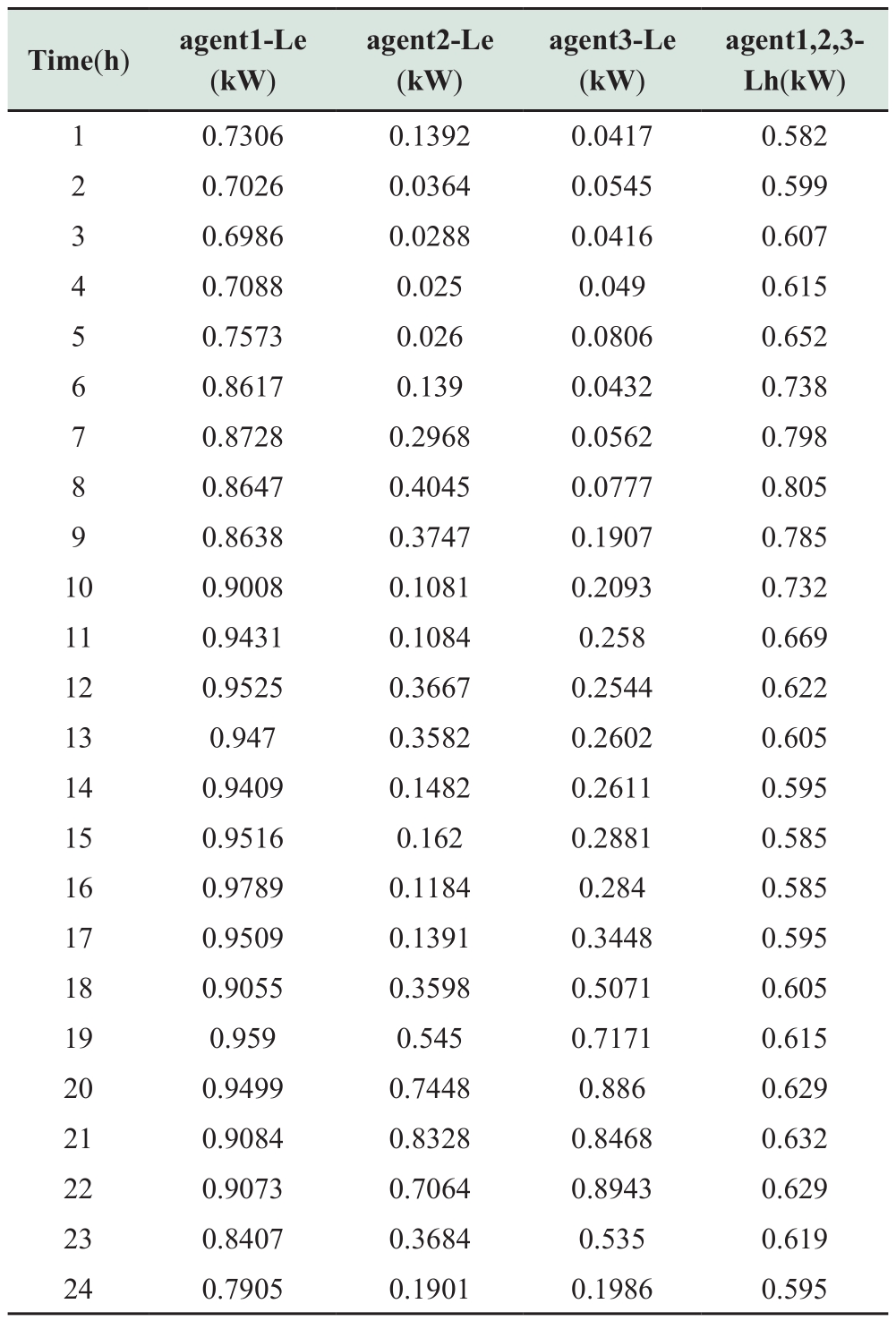
Table A8 Loads in different periods

4 Conclusion

For the optimization problem of IES with multi-EH,different EHs are divided into different agents in this study.Based on the MADDPG algorithm, a distributed optimization model with EH agents as the decision center is built to realize the distributed optimization of IES coupled with multi-EH.The conclusions are as follows:

1) The distributed optimization model with multi-EH as the decision center can overcome the problems of centralized optimization, such as the need to collect a large amount of information and complex modeling.The distributed solution method proposed can effectively improve the solution speed of the model when the results are almost similar to those of centralized optimization,which is conducive to the online application of the model.

2) The dynamic distribution factor is introduced into the model so that the randomness of renewable energy output can be self-adaptively learned to obtain the optimization dispatching results, which effectively improves the economy of the system considering the real-time supply and demand changes.

3) Leveraging MADDPG’s characteristics of“centralized training and distributed execution”, the coordinated optimization policy of IES is corresponding to the interaction mechanism between EH agents.The training process considers the dual uncertainties of renewable energy and load.The trained model can deal with uncertainty and realize nearly real-time decision-making.

Appendix A

Acknowledgements

This work was supported by The National Key R&D Program of China (2020YFB0905900): Research on artificial intelligence application of power internet of things.

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1]Y Wang, N Zhang, CQ Kang (2015) Review and prospect of optimal planning and operation of energy hub in energy internet.Proceedings of the CSEE, 35(22): 5669-5681

[2]ZG Guo, JY Lei, XY Ma, et al.(2019) Modeling and calculation methods for multi-energy flows in large-scale integrated energy system containing electricity, gas, and heat, Proceedings of the CSU-EPSA, 31(10): 96-102

[3]JW Lv, SX Zhang, HZ Chen, et al.(2021) Review on district-level integrated energy system planning considering interconnection and interaction.Proceedings of the CSEE,41(12): 4001-4021

[4]W Lin, XL Jin, R Ye (2021) A decentralized optimal scheduling method for integrated community energy system, Electric Power Construction, 42(11):44-53

[5]GL Wang, QS Zhao, DK Liang, et al.(2021) Economic dispatch of an energy hub in a business park considering chance constrained programming.Power System Protection and Control, 49(13):21-29

[6]X Yang, YW Yang, MX Zhang, et al.(2020) Coordinated dispatch of multi-energy network and energy hubs considering dynamic natural gas flow.Electric Power Automation Equipment,40(5):16-23

[7]YF Wen, XB Zhai, YQ Xiao (2019) Distributed coordinated optimal dispatch of mult-i regional electricity-gas integrated energy systems with energy hubs, Automation of Electric Power System, 43(9):22-30

[8]Q Sun, D Xie, QY Nie, et al.(2020) Research on economic optimization scheduling of park integrated energy system with electricity-heat-cool-gas load, Electric Power, 53(04):79-88

[9]Hemmati M, Abapour M, Mohammadi-Ivatloo B, et al.(2020) Optimal operation of integrated electrical and natural gas networks with a focus on distributed energy hub system.Sustainability, 12, 8320

[10]R Wang, W Gu, Z Wu, et al.(2011) Economic and operation of combined heat and power with renewable energy resources,Automation of Electric Power Systems, 35(08): 22-27

[11]XH Lu, KL Yang, SL Yang (2021) Optimal load dispatch of energy hub based on distributionally robust optimization approach in energy internet environment.Systems Engineering —Theory & Practice, 41(11):2850-2864

[12]CF Jiang, X Ai (2019) Integrated energy system operation optimization model considering uncertainty of multi-energycoupling units.Power System Technology, 43(08):2843-2854

[13]JQ Shi, H Hu, JH Zhang (2019) Distributed low-carbon economy scheduling for integrated energy system with multiple individual energy-hubs.Power System Technology, 43(1): 127-136

[14]HT Huang, JJ Zha, X Chen, et al.(2022) Research on distributed cooperative optimization of multi-agent integrated energy system based on ADMM algorithm.Electrical Measurement &Instrumentation:1-9

[15]HZ Yang, GH Dai, P Zhang (2022) Research on multi-agent collaborative optimization operation strategy for integrated energy system based on ADMM-RGS algorithm.Proceedings of the CSU-EPSA, 34(06):25-33

[16]P Lan, XD Shen, G Wu, et al.(2021) Distributed optimal scheduling for transmission-distribution-natural-gas system based on alternating direction method of multipliers, Automation of Electric Power Systems, 45(23): 21-30

[17]HY Zhang, XY Qiu, SR Zhou, et al.(2020) Distributed optimal dispatch based on chance constrained goal programming for multi-area integrated electricity-natural gas energy systems.Electric Power Construction, 41(07):82-91

[18]T Yang, LY Zhao, YC Liu, et al.(2021) Dynamic economic dispatch for intergrated energy system based on n deep reinforcement learning.Automation of Electric Power Systems,45(05):39-47

[19]K SUTTON R S, BARTO A G.(1998) Introduction to reinforcement learning.Cambridge, USA: MIT Press

[20]Ruelens F, Claessens B J, Vandael S, et al.(2017) Residential demand response of thermostatically controlled loads using batch reinforcement learning.IEEE Transactions on Smart Grid, 8(5):2149-2159

[21]J Qiao, XY Wang, C Zhang, et al.(2021) Optimal dispatch of integrated electricity-gas system with soft actor-critic deep reinforcement learning.Proceedings of the CSEE, 41(3): 819-833

[22]JY Zhang, TJ Pu, Y Li, et al.(2022) Research on optimal dispatch strategy of distributed generators based on multi-agent deep reinforcement learning, Power System Technology:1-10.doi:10.13335/j.1000-3673.pst.2021.1737

[23]HZ Li, L Wang, D Lin, et al.(2019) A nash game model of multiagent participation in renewable energy consumption and the solving method via transfer reinforcement learning.Proceedings of the CSEE, 39(14):4135-4149

[24]Kofinas P, Dounis A I, Vouros G A (2018) Fuzzy Q-Learning for multi-agent decentralized energy management in microgrids.Applied Energy, 219:53-67

[25]F Zhang, DH Wu, YP Chen, et al.(2022) Economic scheduling strategy for distributed park integrated energy system based on multi-agent deep reinforcement learning.Proceedings of the CSU-EPSA:1-12

[26]Lowe R , Wu Y, Tamar A, et al.(2017) Multi-agent actor-critic for mixed cooperative-competitive environments.NIPS.doi:10.48550/arXiv.1706.02275

[27]QY Sun, F Teng, HG Zhang,et al.(2015) Construction of dynamic coordinated optimization control system for energy internet.Proceedings of the CSEE, 35(14): 3667-3677

[28]Geidl M, Koeppel G, FavrePerrod P, et al.(2007) Energy Hubs for the future.IEEE Power and Energy Magazine, 5(1):24-30

[29]YR Wang, B Zeng, J Guo, et al.(2016) Multi-energy flow calculation method for integrated energy system containing electricity, heat and gas.Power System Technology, 40(10):2942-2951

[30]Lillicrap T P, Hunt J J, Pritzel A, et al.(2015) Continuous control with deep reinforcement learning, Computer Ence.doi: 10.1016/S1098-3015(10)67722-4

[31]L Dong, Y Liu, J Qiao, et al.(2021) Optimal dispatch of combined heat and power system based on multi-agent deep reinforcement learning, Power System Technology, 45(12): 4729-4738

Received: 1 July 2022/ Accepted: 31 August 2022/ Published: 25 December 2022

Jing Wei

614849253 @qq.com

Lei Dong

hbdldl@126.com

Hao Lin

linhao_work@126.com

Xinying Wang

wangxinying@epri.sgcc.com.cn

Biographies

Lei Dong received her master degree at Tianjin University, Tianjin, China.She is currently an associate Professor in the Electrical Engineering Department with North China Electric Power University, Beijing, China.Her research interests include power systems analysis and control, power system optimal dispatch and operation control, application of artificial intelligence in power system.

Jing Wei received master degree in the School of Electrical and Electronic Engineering, North China Electric Power University, Beijing,China, in 2022.Her research interests include application of artificial intelligence in power system.

Hao Lin is currently working towards the master degree in the School of Electrical and Electronic Engineering, North China Electric Power University, Beijing, China.His research interests include power system optimal dispatch and application of artificial intelligence in power system.

Xinying Wang received the PhD degree at Dalian University of Technology in 2015,Dalian, China.He is working in Artificial Intelligence Application Research Department of China Electric Power Research Institute(CEPRI).His research interests include artificial intelligence and its application in energy internet.

(Editor Yanbo Wang)