0 Introduction
Reducing the cost of energy utilization and ensuring the sustainable supply of energy in human society are common concerns worldwide [1].The integrated energy system(IES) changes the traditional modes of separate planning,design,and operation for different energy systems [2].The interaction and conversion of multi-energies are realized in the IES through reasonable planning and the operation optimization of multi-energy coupling systems including electricity,gas,and heat [3].Moreover,various types of energy,such as cold,heat,and power,in the IES can be flexibly supplied to users.The IES reduces environmental pollution and improves the efficiency and economy of energy utilization [4].The two key technologies to improve the comprehensive energy utilization efficiency of IESs are accurate prediction of uncertain source-load power [5]and suitable optimization dispatching method [6].
The source-load power prediction method can be divided into deterministic [7]and interval predictions [8].The former is a single-point prediction method capable of providing a specific value forthe future.A new hybrid method of the physical hybrid artificial neural network(ANN) was presented in [9]and the basic physical constraints of photovoltaic (PV) power plants were considered.The machine learning-based non-parametric model was used to develop flexible forecasting techniques.However,the challenges introduced by large-scale datasets to the model have not been resolved.Accordingly,a baseline method was studied in [10]and ANN was used to predict PV power within hours to improve prediction accuracy.A number of studies on load forecasting in IESs have been conducted.A deep long short-term memory(LSTM) network multi-load prediction method was used to forecast the cooling,heating,and power in the IES in[11].Deterministic prediction cannot provide prediction uncertainty and risk information,and its implementation in practice is extremely limited.In contrast,interval prediction provides the prediction error distribution (including uncertainty,risk,and other valuable information) of future time [12].Moreover,it is more suitable for dispatching modern power systems.In view of the foregoing,the uncertainty in source-load power interval prediction has become a research focus.For interval prediction,quantile regression and bootstrapping methods were proposed in [13]to realize the quantification of the uncertainty of PV power.The ability of wavelet transform and radial basis function neural network to generate the uncertainty in PV power prediction was investigated.An improved interval power prediction method using the Bayesian theory was designed in [14];however,its prediction accuracy was relatively low.A wavelet transform interval prediction model integrated with convolutional neural network (CNN) was developed in [15].The combination of bidirectional recurrent neural network (RNN) and LSTM was proposed in [16]to form bidirectional LSTM (BiLSTM).The BiLSTM offers the advantages of memory-saving and bidirectional processing and has played a significant role in time series forecasting.However,studies,such as the application of BiLSTM to interval prediction,are extremely rare.One research aim is to supplement existing study results and formulate a high-precision interval prediction model by integrating the bootstrap approach and beetle antenna search (BAS)optimization algorithm.
The optimal dispatching of IES is also a research focus in related studies of IESs [17-19].However,it is confronted with the problem of random changes in new energy power and various types of load power.Stochastic [20]and robust optimization [21]techniques are two typical approaches for solving optimization problems with uncertainties.Stochastic optimization describes the uncertainties through probability distribution,rendering the model more realistic.The fluctuation of new energy output was reduced in[22]by increasing the system reserve capacity.However,the probability distribution of the prediction error of the new energy output for determining the reserve capacity value is unknown to a certain extent.Analytical methods,such as stochastic programming and chance-constrained programming based on probability distribution,were adopted in [23]to deal with uncertain variables in IESs.However,frequent fluctuations in new energy power generation and many uncertainty variables cause difficulty in adequately obtaining an accurate probability distribution;consequently,the accuracy of the method is degraded.The scene reduction approach for finding a relatively accurate probability distribution function was used in [24].The approach reduces the amount of calculation involved in the stochastic optimization algorithm.However,it cannot possibly cover all operational scenarios in the system;certain risks remain involved.Robust optimization only requires the fluctuation range of uncertainty parameters[25].Different from stochastic and chance-constrained optimization techniques,robust optimization does not require a precise probability distribution;moreover,it significantly reduces the computational complexity.Fluctuations in wind and PV power were described in [26]using the uncertainty set approach.A two-stage robust optimization dispatching model was also built;however,its optimization result is relatively conservative.
To solve the foregoing problems in stochastic and robust optimizations,the use of model predictive control[27]is becoming increasingly popular.This is due to its advantages,such as flexible objective function design,convenient handling of constraints,and wide adaptability to diverse systems [28].Furthermore,an economic model predictive control (EMPC) can directly achieve the economic goal as an optimization function.Better global economic performance [29]is achieved by ensuring control performance and effectively dealing with multi-constraint and multi-variable practical problems.
To resolve the foregoing problems,a robust optimal dispatch method for IESs based on the REMPC and considering the source-load power interval prediction is proposed.First,an interval prediction method is proposed.The method is based on BiLSTM (optimized by BAS and bootstrap),which compensates for the inability of the LSTM to encode information from back to front.The bootstrap technique is also introduced into the interval prediction method to overcome the problems of time series heteroscedasticity,small sample size,and wide fluctuation range.To optimize the hyperparameters of the network,BAS is also employed.Then,a robust optimization dispatching scheme based on the REMPC for IESs is designed by considering the source-load interval prediction result and integrating robust optimization with the EMPC.The main contributions of the study are summarized considering two aspects.
1) The BiLSTM interval prediction model optimized by BAS is devised for the source-load power interval prediction of IESs and this model enhances the prediction accuracy.The developed prediction model provides a more accurate uncertainty interval and reduces the level of conservativeness of the REMPC.
2) A robust optimal dispatch approach based on the REMPC considering the source-load power interval prediction for IESs is presented.An accurate uncertainty interval can reduce the level of conservativeness of the REMPC.The proposed optimal dispatching scheme achieves a rational power distribution among various resources,lowers cost,and improves the economy of IESs in operation.
This paper is arranged according to the following structure.The composition and modeling of an IES are described in Section 1.The formulation of the interval prediction model is presented in Section 2.The constraint conditions and dispatching objective of the IES and its robust form are elaborated in Section 3.The optimal dispatching approach based on the REMPC is presented in Section 4 and the simulation analysis is discussed in Section 5.Section 6 summarizes the conclusions.
1 Structure composition and working principle of IES
The structure of the IES is shown in Fig.1.It comprises a PV power generation system;a combined cooling,heating,and power (CCHP) system;a gas boiler (GB);an electric conditioner (EC);a heat pump (HP);and energy storage equipment (such as cold storage (CS),heat storage(HS),and electrical storage (ES)).The CCHP system is composed of a gas turbine (GT),lithium bromide absorption refrigeration system,and waste heat boiler (WHB).

Fig.1 Device topology and energy flow of IES
The working principle of the IES,shown in Fig.1,is as follows.The GT provides the electricity to the customer and the high-temperature gas generated can be directly recovered by the high-temperature WHB or sent to the LiBr to satisfy the cooling and heating demands.If the GT cannot satisfy the power demand,it is supplemented by utility power.If the LiBr cannot satisfy the cooling demand,the refrigeration unit provides cooling to the customer.If the waste heat of the flue gas cannot supply adequate heat,the GB is used for heating.The energy storage equipment (i.e.,CS,HS,and ES) in the system can also provide cooling,heating,and power to customers.The controllable units of the system suppress the random fluctuations of PV power.When the load is low and PV power is at its peak,redundant PV power is converted into natural gas by the power-to-gas device.When the load is at its peak and PV power is low,the GT can be used to generate power for peak shaving.The PV power can be effectively accommodated by coordinating various devices in the system.
2 Source-load power interval prediction model considering uncertainty
2.1 BiLSTM network based on hyperparameter optimization
Compared with a traditional neural network,the BiLSTM network has memory ability,rendering the output more accurate.Its weights can be optimized to improve the prediction accuracy further.
A new technology for parameter optimization based on the foraging principle of beetles is BAS.This algorithm can automatically implement the optimization process and only one individual is involved;hence,the optimization speed is significantly improved.In this research,the hyperparameters of BiLSTM are optimized by the BAS algorithm,and the number of hidden layer neurons (two layers),batch size,and learning rate of BiLSTM are used as optimization objects.Consequently,the best combination of hyperparameters is found more rapidly,the complexity and uncertainty of manual tuning are reduced,and the model prediction accuracy is improved to a certain extent.
The optimization process is as follows.
Step 1: Initialize the beetle center of mass vector x.The step length,lstep,is 1;the ratio of the step length to the distance between the two whiskers is c = 3;and the number of iterations is q = 150.A g-dimensional direction vector of the right whisker of the beetle pointing to the left whisker is randomly generated and normalized;g is selected as 6.The initial position,x,and direction vector,rdir,of the beetle are

where rank is the randomly generated vector function.
Step 2: Calculate the coordinates of the left and right whiskers,xl and xr,of the beetle,respectively,as follows:

where d0 is the distance between the two whiskers of the beetle.
Step 3: The fitness function,f,is used to advance the search for beetle whiskers in the spatial region.It is obtained based on coordinates xl and xr:
where fleft and fright are the fitness functions of the left and right whiskers of the beetle,respectively.The next position of the center of mass of the beetle is
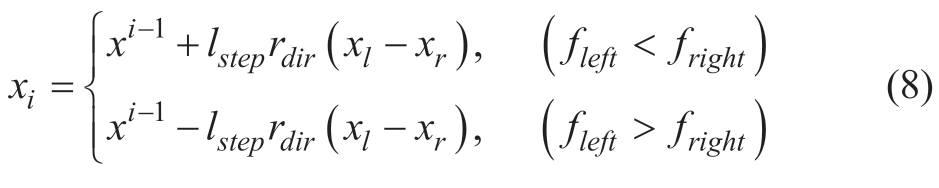
where (xi,xi-1) is the position of the center of mass of the beetle at the (i,i-1) th iteration.
Step 4: Determine whether the convergence condition is reached.If the loop reaches the maximum number of iterations or the desired fitness value is obtained,the iterative process is ended;otherwise,return to Step 1 and continue the iteration.
continue
Step 5: Construct a BiLSTM using the set of hyperparameters corresponding to the optimal solution,Xbest.
The BAS-BiLSTM flowchart is shown in Fig.2.
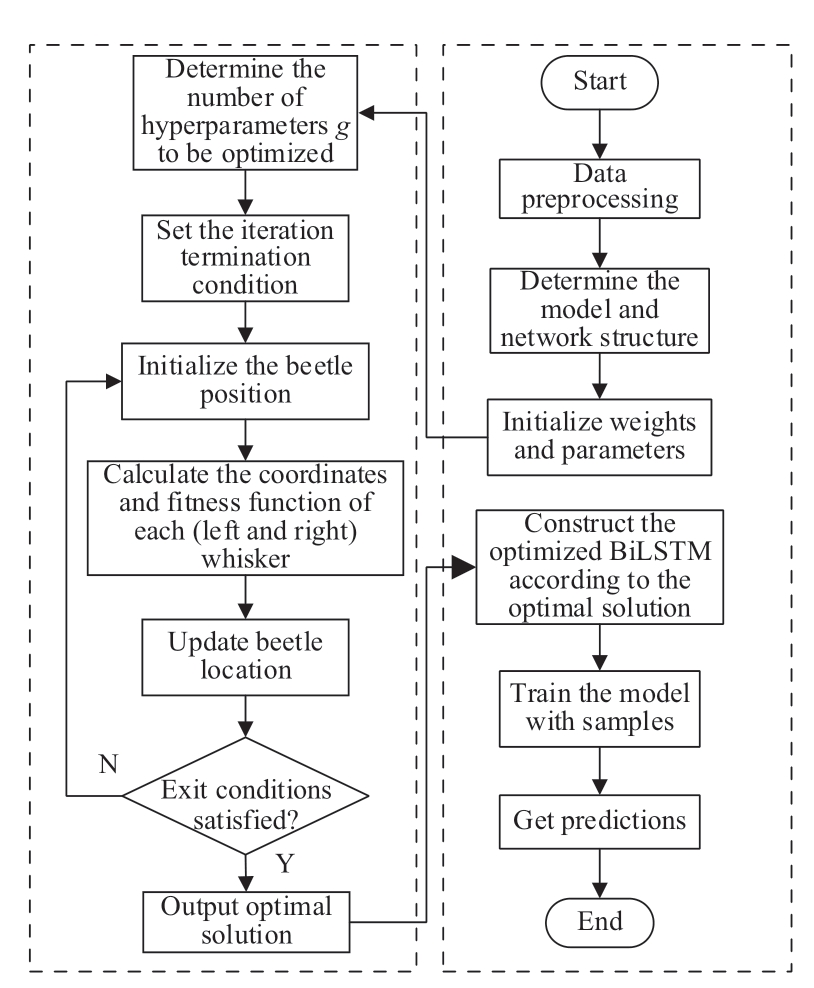
Fig.2 Flowchart of BAS-BiLSTM
2.2 Source-load power interval prediction model based on BAS-BiLSTM
With the excellent performance of BiLSTM in time series data modeling,an interval prediction model of BiLSTM optimized by BAS and combined with bootstrap is proposed and named BBAS-BiLSTM.This model reduces the area of the prediction interval while ensuring prediction accuracy.
The selected instance is PV power interval prediction.Its specific modeling process is as follows.
Step 1: Acquire historical PV power,irradiance,and temperature data to build a raw sample series.Normalize the training data for input to eliminate errors in magnitude and accelerate the training process.
Step 2: Apply the bootstrap method for resampling and establish N bootstrap samples to resolve the problem associated with the volatility characteristics of the power series.
Step 3: Input the training data of the original dataset into the network and develop the prediction model by training the network on the original training set using BASBiLSTM.Because of the error accumulation problem of consecutive multi-step predictions,the single-point prediction method is adopted in the research.The input data of the first (s) time sampling points are used to predict the next time sampling point to achieve rolling prediction and thus provide reliable PV power prediction information.
Step 4: Calculate the prediction value sequence;N predicted values are obtained for the next moment by BASBiLSTM in the previous step for each of the N samples.
Step 5: Estimate the prediction interval of PV power using the percentile interval estimation method.
3 Mathematical Formulation
In this section,the deterministic form for the IES device problem is first introduced.Then,the uncertainty parameters involved are modeled based on a robust form for the final formulation of the model.
3.1 Deterministic formulation
3.1.1 Device model
(1) For CCHP

where FgCCHP is the natural gas input rate of the CCHP unit;oCCHP is the start/stop state (1 indicating startup;0 indicating shutdown); is the electrical power output of the unit;ηCCHP is the power generation efficiency;LHV is the location calorific value of natural gas;πCCHP is the constant thermoelectric ratio;
is the electrical power output of the unit;ηCCHP is the power generation efficiency;LHV is the location calorific value of natural gas;πCCHP is the constant thermoelectric ratio; is the cooling power output of the unit;PhLR is the heating power output of the LiBr system;βLiBr is the heat-to-cold conversion efficiency of the LiBr system.
is the cooling power output of the unit;PhLR is the heating power output of the LiBr system;βLiBr is the heat-to-cold conversion efficiency of the LiBr system.
(2) For GB
where  is the consumption rate of natural gas in the GB;
is the consumption rate of natural gas in the GB; is the thermal power output;oGB is the start/stop state(1 indicates startup;0 indicates shutdown);and ηGB is the GB efficiency.
is the thermal power output;oGB is the start/stop state(1 indicates startup;0 indicates shutdown);and ηGB is the GB efficiency.
(3) For EC
where PEcC is the cooling power output;pEeC is the consumed electrical power;ηEC is the operating efficiency;and COPEC is the cooling coefficient.
(4) For HP
where PHhP is the thermal power output;PHeP is the electrical power input;and COPHP is the heating coefficient.
(5) For energy storage element
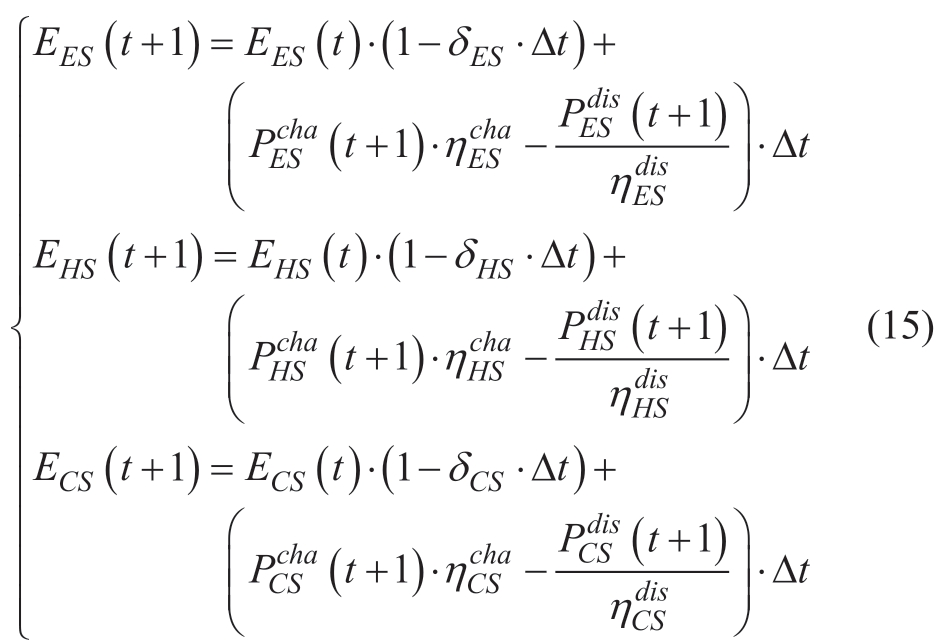
where ECS(t),EHS(t),and EES(t) are the stored energies of the cold,heat,and electrical energy storages over the t-period,respectively;ECS(t+1),EHS(t+1),and EES(t+1) are the stored electrical,heat,and cold energies in the next period,respectively;δ is the self-discharge efficiency of the energy storage;![]() are the storage charging efficiencies of electrical,heat,and cold energies,respectively;
are the storage charging efficiencies of electrical,heat,and cold energies,respectively;![]() are the storage discharging efficiencies of electrical,heat,and cold energies,respectively;
are the storage discharging efficiencies of electrical,heat,and cold energies,respectively;![]() are the storage charging powers of electrical,heat,and cold energies,respectively;
are the storage charging powers of electrical,heat,and cold energies,respectively;![]() are the storage discharging powers of electrical,heat,and cold energies,respectively;and Δt is the optimized operation time of the system.
are the storage discharging powers of electrical,heat,and cold energies,respectively;and Δt is the optimized operation time of the system.
During operation,the IES must satisfy certain equality and inequality constraints,such as power balance and various operating conditions.
(6) Power balance constraints
These constraints are mainly those of the power balances of cooling,heating,and power.The most important equilibrium to maintain first is electrical power balance.This means that the electrical power produced by the system must be equal to the customer demand.However,the cooling and heating powers may exceed the load demands.The loads are given by the following:
where PLe is the electrical load composed of the critical load(Pcri) and removable load (Pcur);Ppv is the PV power;PLc is the cooling load;and PLh is the heating load.All the loads are uncertainty variables.
(7) Device operation constraints
The operational constraints of devices in the IES include those of the CCHP units,GB,electric refrigeration system,HP,and energy storage equipment,as follows:
where![]()
![]() are the minimum and maximum power outputs of the CCHP unit,respectively;
are the minimum and maximum power outputs of the CCHP unit,respectively; and
and are the minimum turn-on and turn-off times of the CCHP unit,respectively;
are the minimum turn-on and turn-off times of the CCHP unit,respectively; t
t ( ) are the( ) and t turn-on and turn-off times until period t,respectively;
( ) are the( ) and t turn-on and turn-off times until period t,respectively;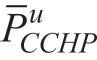 and
and are the maximum ramp-up and ramp-down rates of the CCHP unit,respectively;and
are the maximum ramp-up and ramp-down rates of the CCHP unit,respectively;and 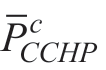 is the maximum cooling output of the CCHP unit.
is the maximum cooling output of the CCHP unit.
The key high-capacity devices supplying district heat loads to the IES by burning natural gas are GBs.Compared with traditional coal-fired boilers for heating,GBs considerably reduce pollutants and greenhouse gas emissions.In addition to the maximum and minimum output constraints in operating large-capacity GBs (e.g.,(20)),start-up and shutdown time constraints and ramp rate constraints,such as (21)-(24),exist.
The constraints in the operation of the storage of electrical energy,heat thermal energy,and cold energy include the state-of-charge constraint given by (25) and the stored energy constraints at the beginning and end expressed by (26),as follows:

where subscript S represents three types of energy storage devices: 0 indicates electrical energy storage;1 is heat energy storage;and 2 denotes cold energy storage.
The electric refrigeration system and HP must operate below their rated powers,as follows:

where  and
and 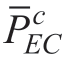 are the rated outputs of the HP and electric refrigeration system,respectively.(8) Load constraints
are the rated outputs of the HP and electric refrigeration system,respectively.(8) Load constraints
The electrical loads considered in the model are classified into two categories: critical and removable loads.The critical load is closely related to the fundamental activities in the daily life of users (e.g.,lighting).The electricity demand for such loads must be satisfied.The load cut does not necessarily have to run at the rated power.Moreover,working power has a certain adjustment range,such as that for air conditioners and ventilation equipment.The rate of the removable load,βcur,is expressed as
where 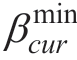 and
and  are the minimum and maximum ratios,respectively.The load cut can affect user comfort;hence,a penalty or compensation fee due to this cut must be considered when calculating costs.
are the minimum and maximum ratios,respectively.The load cut can affect user comfort;hence,a penalty or compensation fee due to this cut must be considered when calculating costs.
3.1.2 Objective function
Based on the relevant constraints that devices used in IESs are required to satisfy,the costs to be considered include the fuel cost of natural gas (consumed by the CCHP units and GBs),purchase cost of electricity from the grid(for the IES),maintenance cost of devices,turn-on and turnoff costs of large equipment (such as the CCHP units and GBs),and penalty for load cutting or compensation cost.An optimal operating scenario is achieved by considering the foregoing.The objective function of the robust optimization of the IES economic operation is
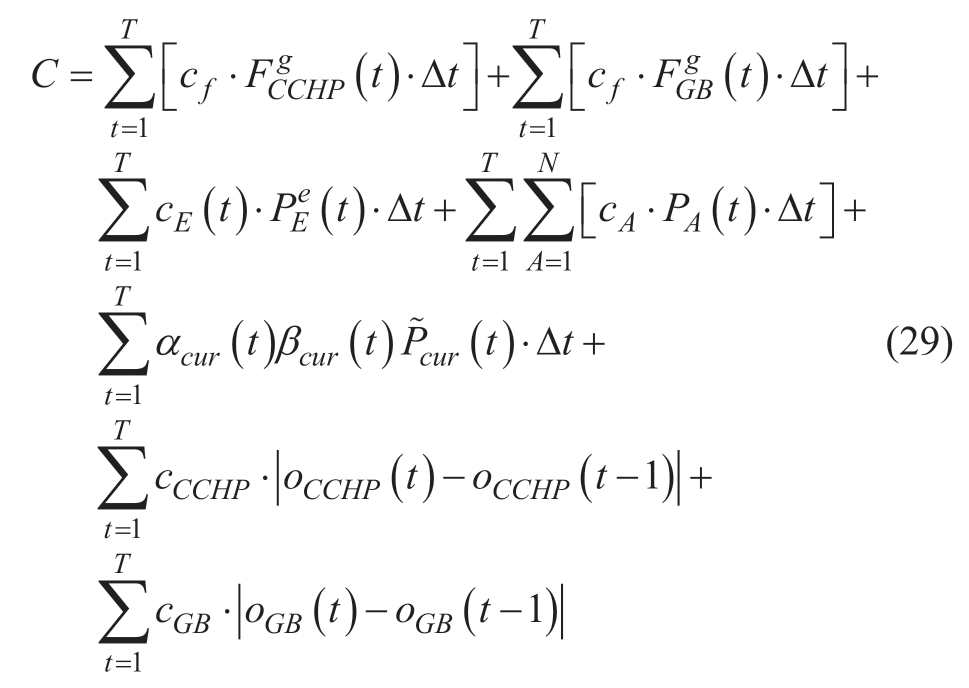
where cf is the price of natural gas;cE is the electricity purchase price from the grid;PEe is the power purchased from the grid;cA is the maintenance cost;N represents the total number of devices to be maintained in the IES(including CCHP units,GBs,ECs,HPs,and energy storage devices);PA is the output power of each device;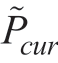 is the predicted power of the removable load;αcur is the penalty for cutting the load;and oCCHP and oGB are the turn-on and turnoff costs,respectively,for each CCHP unit and GB.
is the predicted power of the removable load;αcur is the penalty for cutting the load;and oCCHP and oGB are the turn-on and turnoff costs,respectively,for each CCHP unit and GB.
3.2 Incorporation of uncertainty form
Electrical (including critical and removable loads),heating,and cooling loads as well as PV power are all considered as variables.Their specific distributions can be obtained by the BAS-BiLSTM interval prediction model:
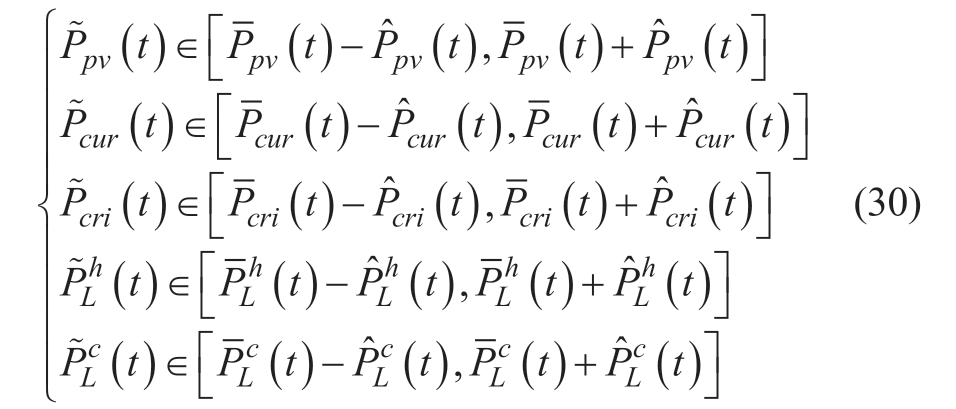
where![]() are the midpoints of the confidence interval of the predicted PV power,critical load,removable load,heating load,and cooling load power at time t,respectively;
are the midpoints of the confidence interval of the predicted PV power,critical load,removable load,heating load,and cooling load power at time t,respectively;![]()
![]() are the radii of the confidence interval of the PV power,critical load,removable load,heating load,and cooling load at time t,respectively,which can be obtained by the boundary value of the interval prediction.Because the power balance constraints and objective function contain random parameters,robust optimization is applied to transform their constraints and derive the corresponding robust form.
are the radii of the confidence interval of the PV power,critical load,removable load,heating load,and cooling load at time t,respectively,which can be obtained by the boundary value of the interval prediction.Because the power balance constraints and objective function contain random parameters,robust optimization is applied to transform their constraints and derive the corresponding robust form.
(1) Power balance constraints based on robust form
Because robust optimization modeling targets inequality constraints,the equality constraints are transformed into inequality constraints,as follows:
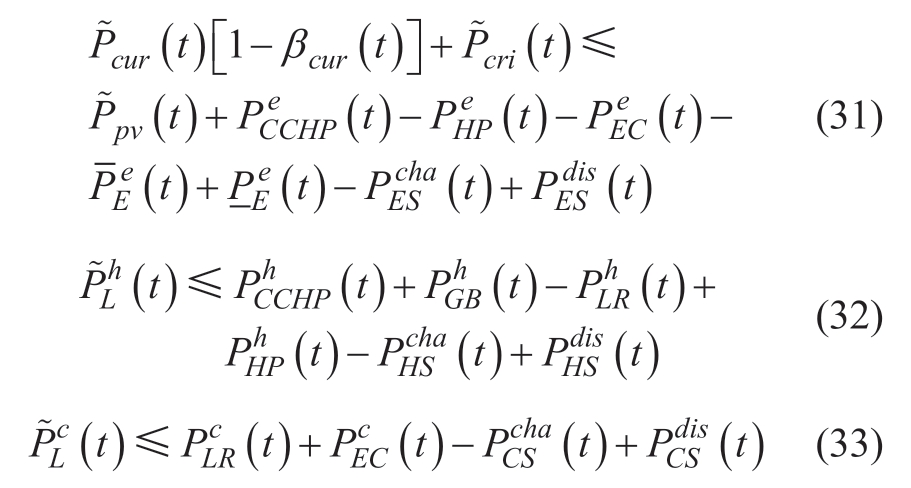
Because the IES aims to achieve the lowest economic cost,its optimization direction causes the constraint connotation of the foregoing equations to remain unchanged after the equal signs are removed.For the constraints mentioned above,random variables exist in the constant term and decision variable coefficient.Accordingly,they are rewritten in a robust form:
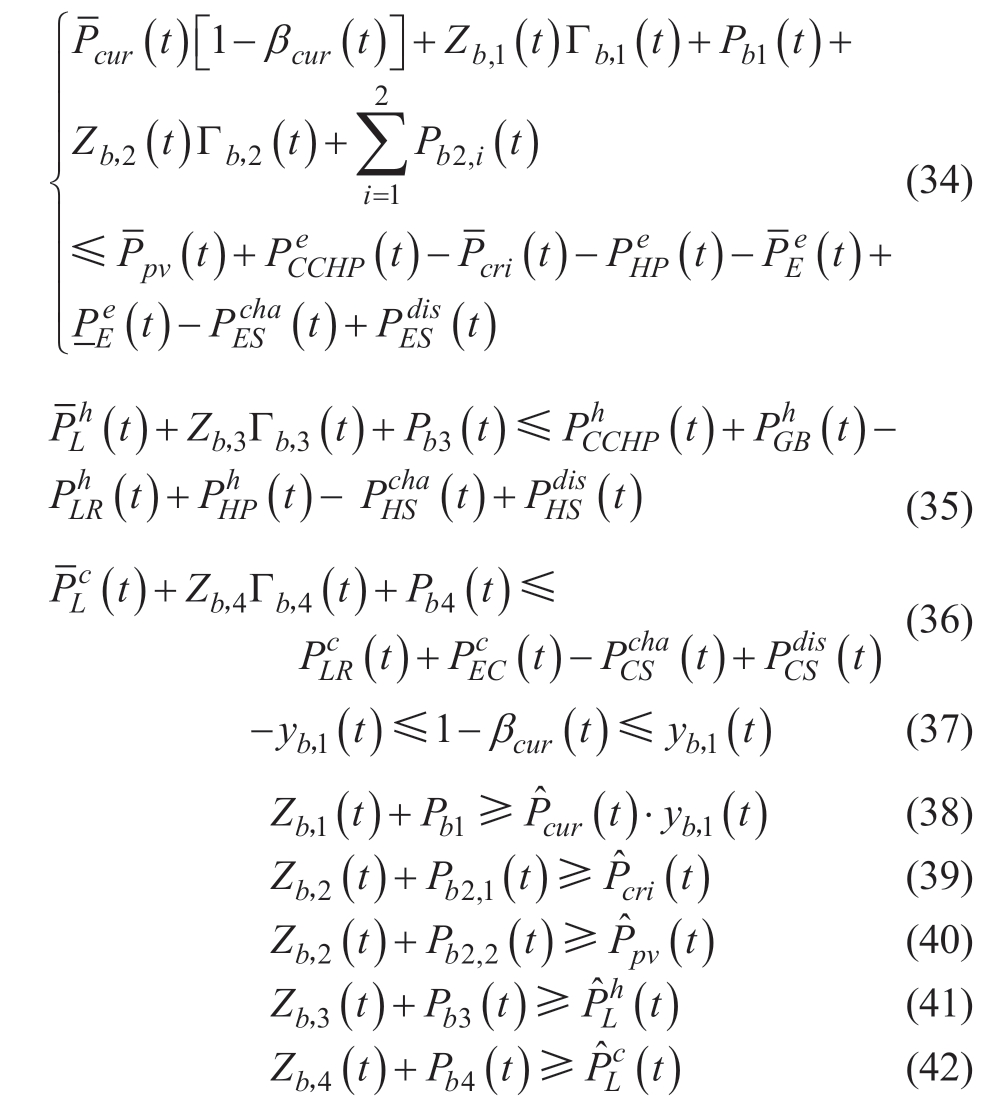
where Zb,i(t) and Pbi(t) are the ith auxiliary variables for decision-making;Γb,i(t) denotes the ith parameter to measure the degree of uncertainty;and Γb,2(t) ∈ [0,2].
(2) Objective function based on robust form
A number of random variables exist in the objective function given by (29);hence,an auxiliary variable,Zgoal(t),is introduced to represent the cost function.To be equivalent to the original model,a constraint must be introduced:
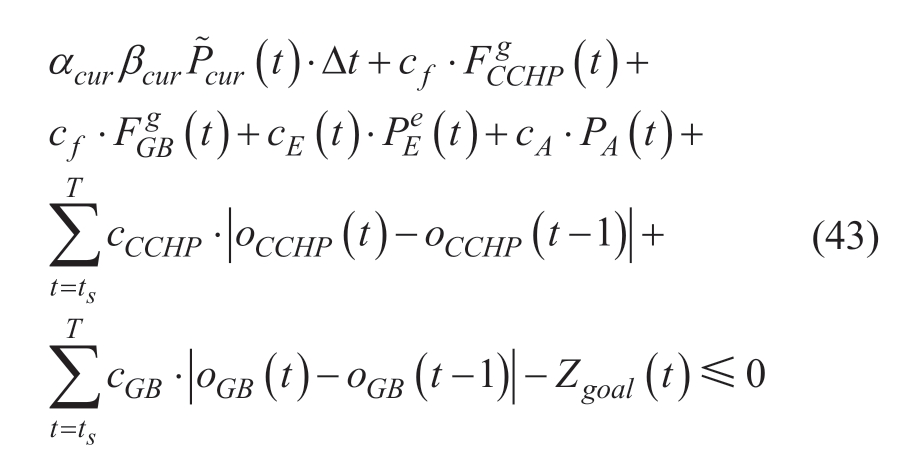
The robust form of the constraint given by (43) can be written in (44)-(47).
In summary,under the full consideration of uncertainty factors of the PV and cooling,heating,and electrical load powers in the IES,the optimal dispatching model based on robust optimization is given by (48).The expressions are
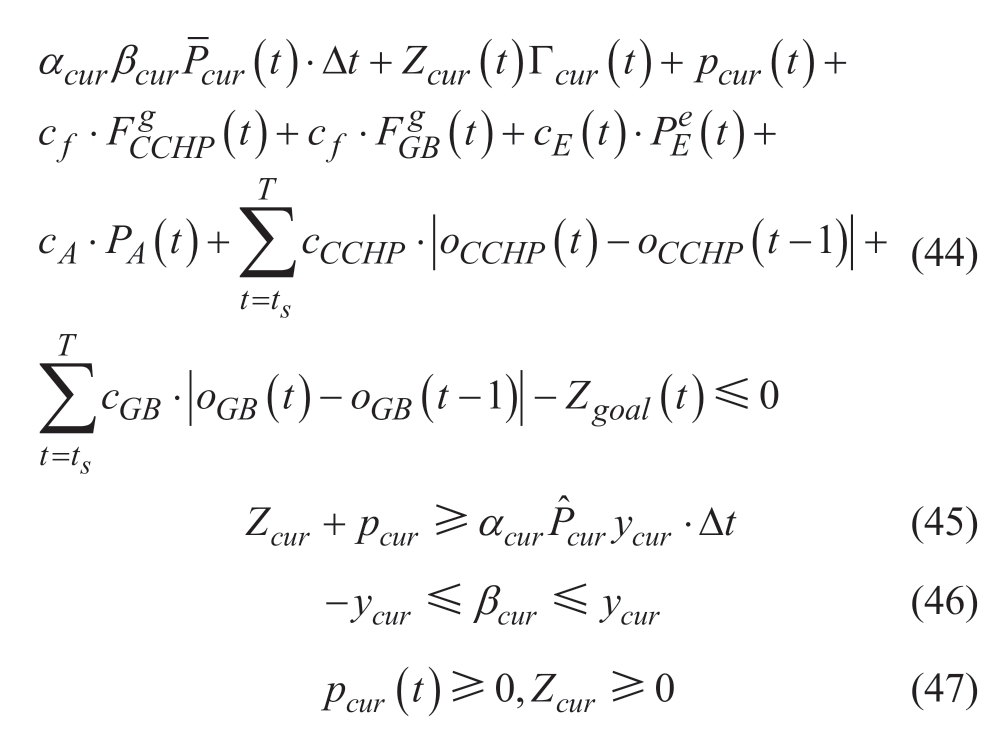
where Zcur(t), pcur(t),and ycur(t) are the auxiliary variables for decision-making at time t,and Γcur(t) is the parameter depicting the degree of uncertainty at time t.
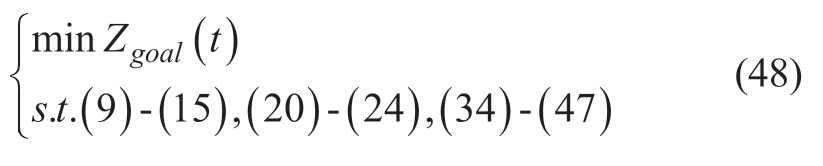
The parameters for measuring the degree of uncertainty in the model are normalized and written as Γ ∈ [0,1],which represents the degree of risk that the model can adapt to.If Γ = 1,the model is most conservative;if Γ = 0,it is a deterministic model.
4 Intraday dispatching optimization of IES based on REMPC
The uncertainties of PV and load powers in the IES increased the difficulty of controlling the balance between the power supply and demand within the IES and introduced risks to reliable operation.Accordingly,an optimal dispatching scheme based on REMPC and considering the source-load interval prediction is devised for the IES to deal with the uncertainties of new energy and load power;consequently,economy and robustness are improved.
The strategy is divided into two stages of rolling optimization and dynamic adjustment.The specific optimization strategy is as follows.In the rolling optimization process,the dispatch center of the regional IES forecasts the PV output and the electrical,heating,and cooling load data for the next 4 h.Then,the unit output plan for 4 h is formulated based on the forecast data and state information of the system;however,the system only executes the plan in the first hour.In the succeeding dispatch cycle,the scheduling window is shifted forward by a time interval,Δt.Based on the latest state of the system,the forecasting and optimization solution from t0+Δt to t0+nΔt is executed.With the foregoing repeated rolling,the scheduling plan for each first hour is executed each time until the scheduling plan for all periods in the scheduling cycle is completed.The proposed principle of REMPC is shown in Fig.3.
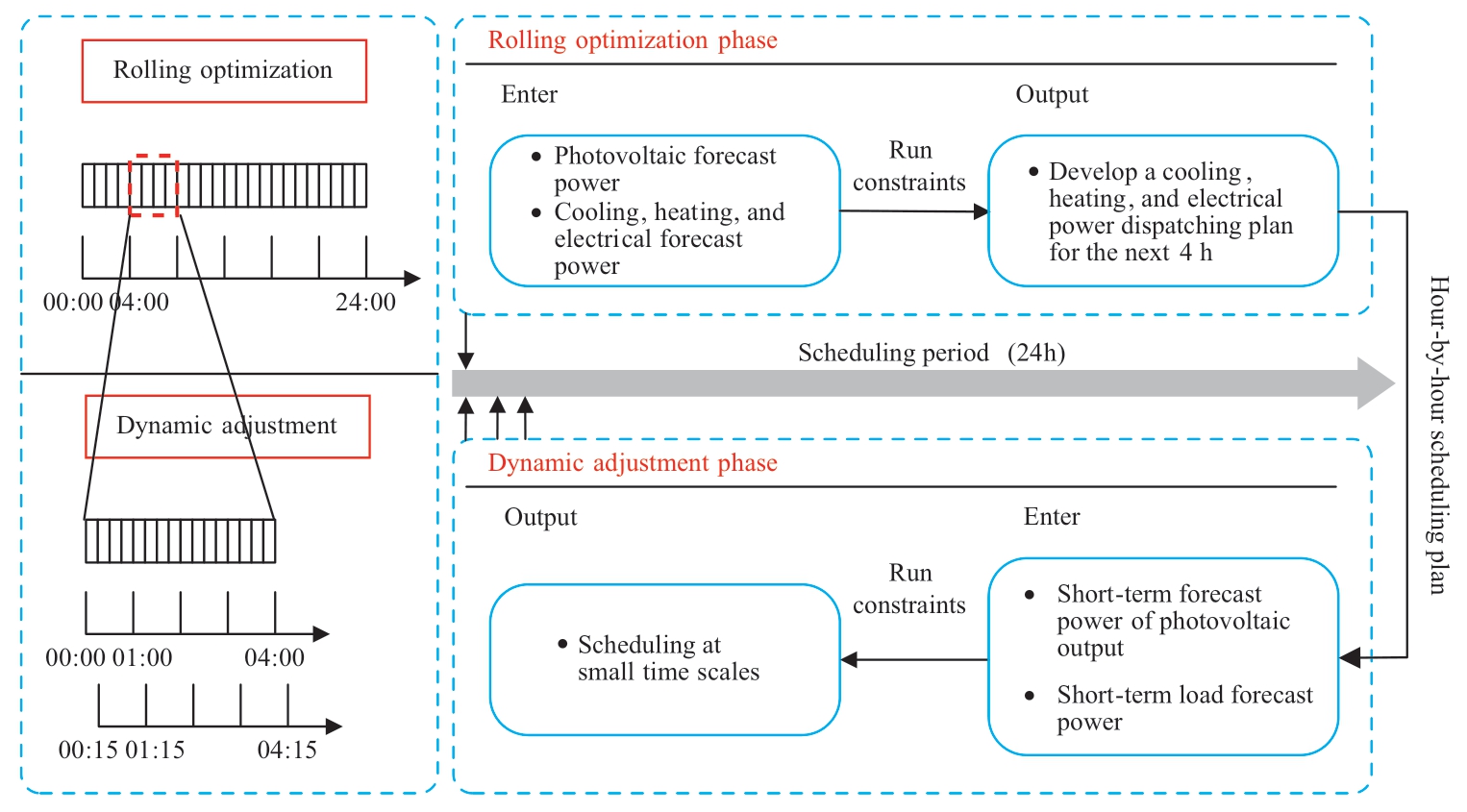
Fig.3 Two-stage dispatching optimization principle based on REMPC
The objective function of the rolling optimization stage has the lowest IES operating cost (including the costs of gas and electricity purchase,unit start/stop penalty maintenance,and removable load minimum penalty).The economic objective function of the rolling optimization stage is constructed according to (48).
In the operation,due to forecast errors and dynamic changes in the electrical,heating,and cooling loads,the scheduling plan developed in the rolling optimization stage deviates from the actual load demand;hence,dynamic adjustments on smaller time scales are required.For this purpose,the time interval,Δt,is split into M small time intervals,Δt′.For each time interval,Δt′,the system operation status is adjusted based on the rolling scheduling plan,real-time system status information,and real-time load and PV power to satisfy the real-time cooling,heating,and electricity demands.For the actual operation of the integrated regional energy system,each unit cannot be arbitrarily adjusted over short time intervals;consequently,it is frequently dispatched on an hourly basis.Therefore,when all M small time scale intervals are dispatched,the optimal dispatch plan obtained in the dynamic adjustment stage is returned to the rolling optimization layer as a reserve plan.For each time interval,Δt′,different power adjustment penalty coefficients are set for different equipment outputs.The optimization objective is to minimize the operating cost of compensating for the deviations from the target cost during the interval,as follows:

where αEe and αA are the adjustment penalty cost coefficients of the interactive power with the grid and the power of the energy storage equipment,respectively;Pcur,PEe,and PA are the adjustment values of the removable load,interactive power with the grid,and energy storage equipment power,respectively.
5 Case and analysis
5.1 Simulation system and parameters
The typical day data of the IES in summer are selected to conduct the simulations.The relevant parameters are summarized in Tables 1-3.
Table 1 Device parameters in IES
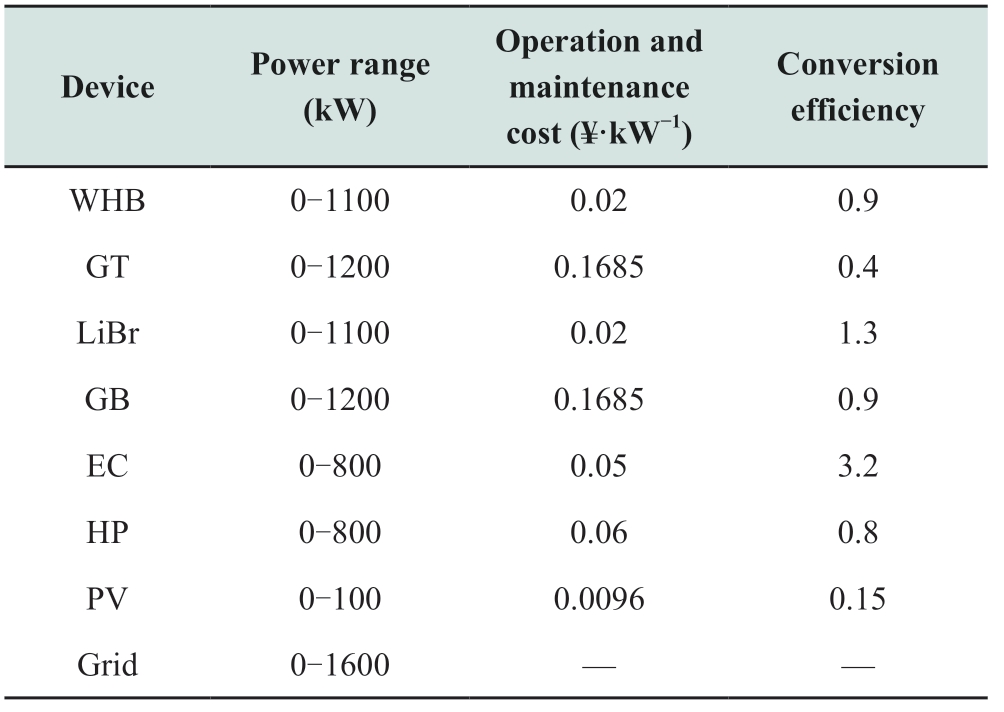
Table 2 Parameters related to energy storage equipment

Table 3 Time-of-use electricity price

5.2 Results and analysis of interval prediction model
5.2.1 Evaluation indices
The chosen evaluation indices of the interval prediction model are prediction interval coverage probability (PICP)and prediction interval normalized averaged width (PINAW)[30],as follows:

where Tt is the number of predicted samples;κ is a Boolean quantity (if the predicted value is included in the prediction interval,then κ = 1;otherwise κ = 0);R is the variation range of the predicted value used to normalize PINAW.
5.2.2 Prediction results and analysis
The presented BBAS-BiLSTM method is used to predict the PV and electrical,cooling,and heating load powers;the prediction results at the 90% confidence level are displayed in Fig.4,(a)-(d),respectively.
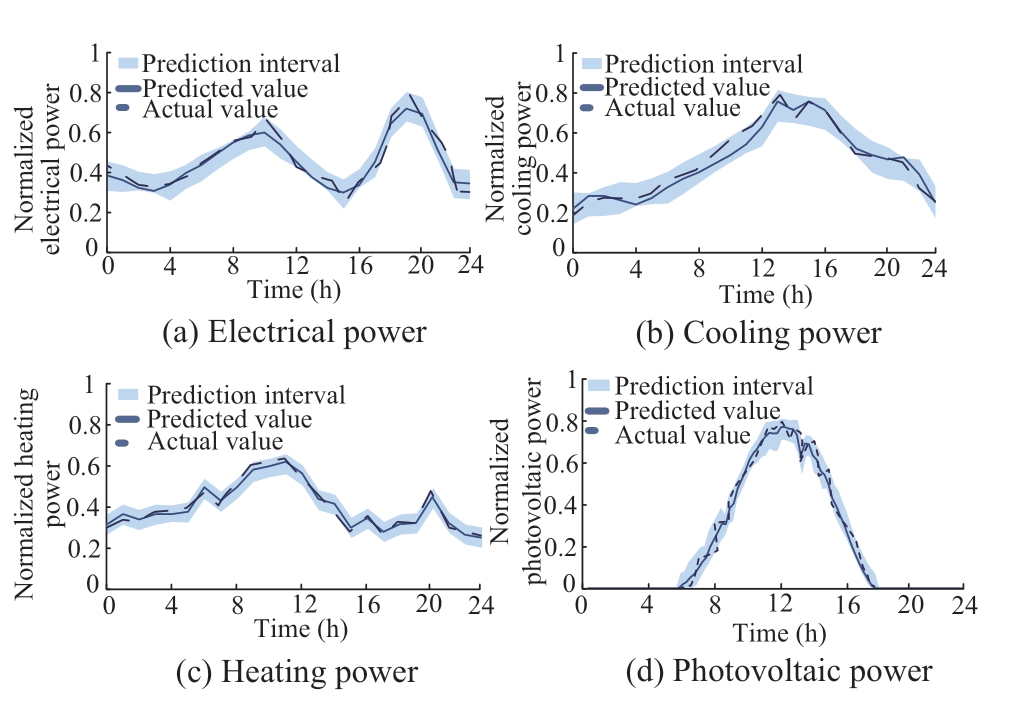
Fig.4 Typical daily load demands and PV output in summer
To evaluate the effectiveness better,the presented BBAS-BiLSTM method is compared with the BBASLSTM at the same 90% confidence level;the results of the algorithm comparison are shown in Fig.5.The figure indicates that the BBAS-BiLSTM method can cover the actual output power point to a greater extent and has a narrower bandwidth than that in BBAS-LSTM.
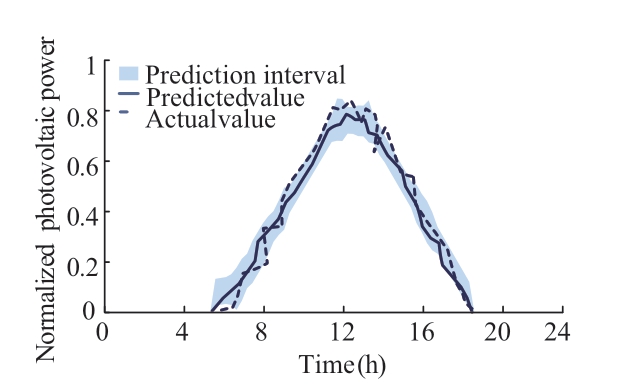
Fig.5 Prediction result of BBAS-LSTM
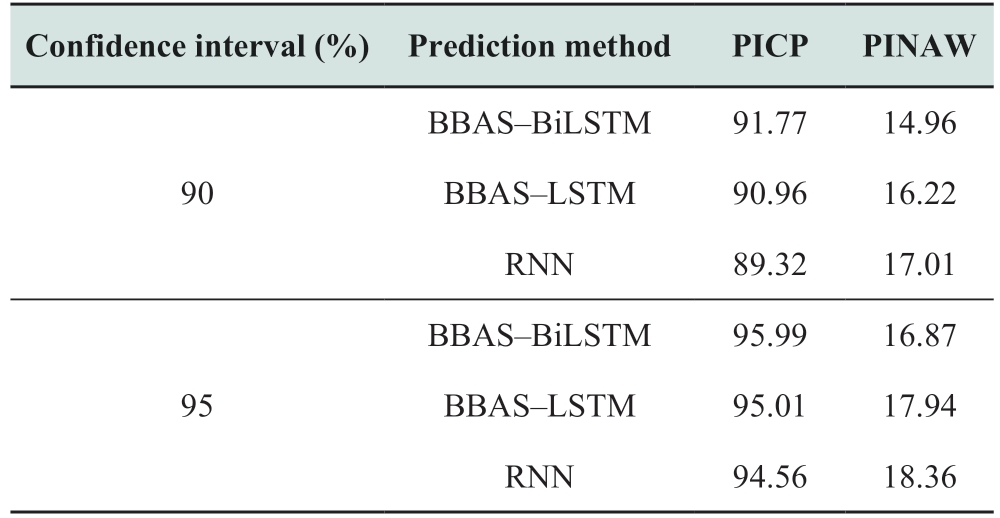
The comparison of the evaluation indices of the PV power prediction of BBAS-BiLSTM with those of the other methods at different confidence levels is summarized in Table 4.This indicates that the bandwidth increases with the confidence level;however,the effect of covering the actual power point improves.Under different confidence levels,the proposed BBAS-BiLSTM method has higher PICP and narrower PINAW values than those in other methods.
Table 4 Comparative results of various algorithms at different confidence levels (%)

5.3 Optimization dispatching results and analysis
5.3.1 Design of cases
To verify the economy and robustness of the designed REMPC model,the best scheduling IES cases for the three different scenarios summarized in Table 5 are selected for comparative analysis.In Case 1,the uncertainties of PV power and various loads are not considered and the deterministic scheme implements dispatching.In Cases 2 and 3,the optimal dispatching of the IES considers the uncertainties of PV power and various loads,and the BBAS-BiLSTM and BBAS-LSTM methods are adopted to predict the power range.In both cases,the REMPC strategy optimizes the dispatching process and the most economical optimal dispatching scheme for the IES is found.
Table 5 Scheme Settings

5.3.2 Results of optimal dispatching
(1) Operating cost
To demonstrate the economy of the REMPC model,parameter Γ is set to 0.15.
First,the operating costs in the three cases are analyzed;the results are summarized in Table 6.The table indicates that the operating cost in Case 1 is the lowest.The operating costs in Cases 2 and 3 are higher than that in Case 1 because they consider the source-load uncertainties.Case 1 does not consider the uncertainties on the supply and demand sides,leading to excessively high expectations for the total cost.The actual cost of the IES considering the sourceload uncertainties is higher than the expected value.These uncertainties introduce risks to the system;hence,the dispatching results conform with actual situations.
Table 6 Operating costs

In addition,in Cases 2 and 3,the operating cost of the IES increases with the confidence level.When the confidence level is high,the degree of uncertainty in the optimization model is also high.In this situation,more dispatching resources in the IES must be arranged to deal with uncertainties.Moreover,at the 90% confidence level,the interval coverage of BBAS-BiLSTM exceeds that of BBAS-LSTM;however,the operating cost of the IES is lower.This indicates that the BBAS-BiLSTM method includes more actual values while covering a small range,further demonstrating that its accuracy is acceptable for uncertainty interval prediction.
(2) Influence of robust parameter on model performance
To illustrate the effect of the robust parameter,Γ,on the performance of the REMPC model,its value was adjusted in Case 3.When Γ = 0,the robust model degenerates into a deterministic model in which the dispatching results correspond to optimal dispatching with the standard EMPC.
The effect of adjusting parameter Γ in the robust model on the operating costs at different confidence levels is shown in Fig.6.The figure indicates that when the confidence level is low,the optimization effect of REMPC is less than that of EMPC.When the confidence level is increased,the advantages of REMPC becomes evident.Overall,the system operating cost appears to decrease and then increase with the increase in Γ.This is because the robust model can avoid risks.Compensation costs or penalties due to user discomfort and additional dispatching costs are thereby reduced.Nevertheless,with the increase in the conservatism of the robust model,the system continues to generate excessive power although all loads have been satisfied,thus increasing the operating costs.Therefore,in practice,appropriate model parameters must be selected for different situations.
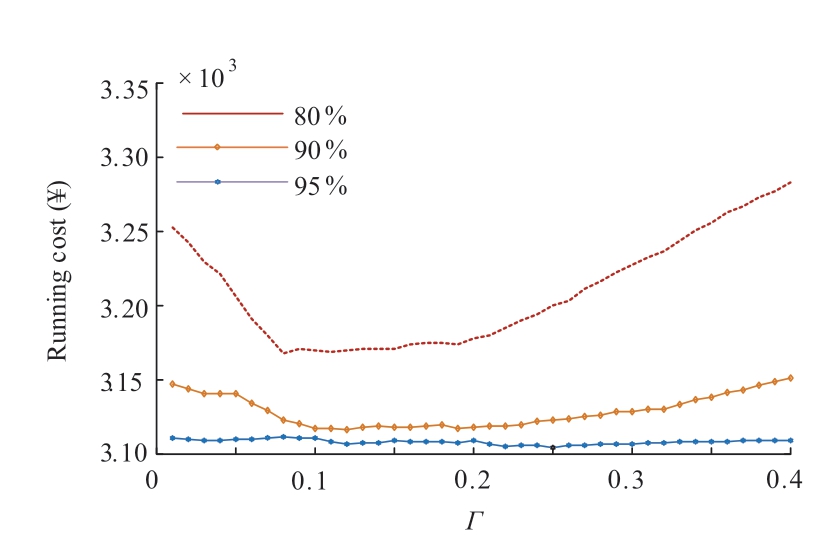
Fig.6 System operating costs under different robust parameters
5.3.3 Comparison of dispatching results
(1) Comparison of optimal dispatching results with/without source-load power interval prediction
To illustrate the effect of considering the source-load uncertainty of the REMPC model on system operations,a comparative simulation considering/ignoring source-load uncertainty is conducted.The REMPC strategy is applied to optimal scheduling and Γ = 0.15 is set with a 90%confidence interval.The simulation ignoring the sourceload uncertainty is based on the point prediction results of BiLSTM.For optimal scheduling,the REMPC degenerated into the EMPC is used.To solve the optimal scheduling model,the case study is modeled using the Yalmip optimization tool (under MATLAB R2015a compiled environment) and CPLEX commercial solver.
The results of the foregoing are shown in Figs.7 and 8.In Fig.7,the electrical,cooling,and heating loads of the system are coupled;they complement each other to complete the load supply throughout the dispatch period.
The results when the source-load prediction is considered are shown in Fig.7.From 23:00 to 07:00,the system prioritizes the use of low-valley electrical energy to supply electric load and power to the EC.This power supply supplements the partial shortage in the ES device.During this period,the heating load demand of the system is fundamentally satisfied by the GB.During the periods 07:00-11:00 and 17:00-22:00,the electricity consumption is at its peak.However,the electricity price is relatively high;hence,the GT supplies power and the removable load shedding and ES device are used for supplementary power supply to improve the economy.The GT provides a considerable amount of waste heat to the WHB,which directly converts this waste into usable heating energy to satisfy the heat load demand of the system.The off-peak periods of electricity price are 11:00-17:00 and 22:00-23:00;moreover,the electrical load demand is relatively low.During the aforementioned periods,the use of electricity is more economical than that in operating a GT.To prioritize the use of PV power,the electricity purchased from the power grid is used to satisfy the demand for electrical and cooling loads and to supplement the energies of ES and CS devices.Due to the limitation in power purchase,the GT supplements the power shortage.

Fig.7 Optimal dispatching results considering source-load uncertainty
The GT output is higher than the deterministic forecast when the source-load uncertainty is considered,as shown in Fig.8.The figure shows that due to the effect of the uncertainty on the source-load side of system operation,power generation is slightly high,thus reducing the risk of system undersupply.In contrast,the energy storage system effectively dissipates the oversupply and supplies power to the system in the subsequent dispatching process.The dependence on the grid is significantly reduced when the risk of system undersupply is low.The load removal is observed to be significantly less than that of the strategy with deterministic prediction,and the percentage of removal is relatively small.
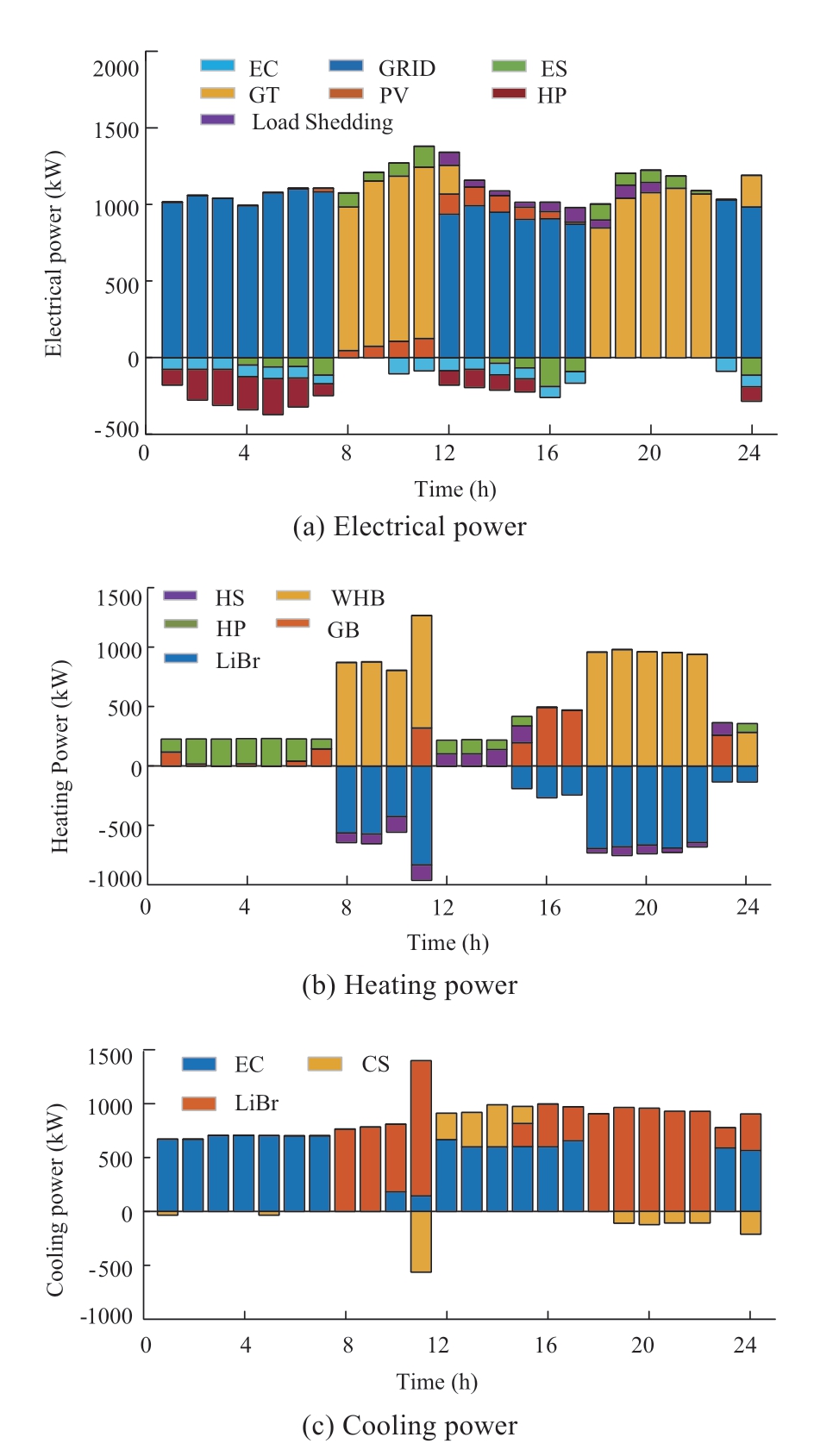
Fig.8 Optimal dispatching results without considering source-load uncertainty
The REMPC strategy has been proved capable of enhancing the ability of the system to cope with the risk caused by the prediction error as well as improving its reliability and safety.
(2) Comparison of proposed optimal dispatching method with robust optimization
The advantages of REMPC strategies in the optimal scheduling of the IES with a certain degree of uncertainty are investigated.Accordingly,the proposed method is compared with robust optimization strategy at a confidence interval of 90% in which parameter Γ is set to 0.15.The IES is optimally scheduled considering the uncertainty of the source-load using the REMPC and robust optimization strategies.The results of robust optimization are shown in Fig.9.
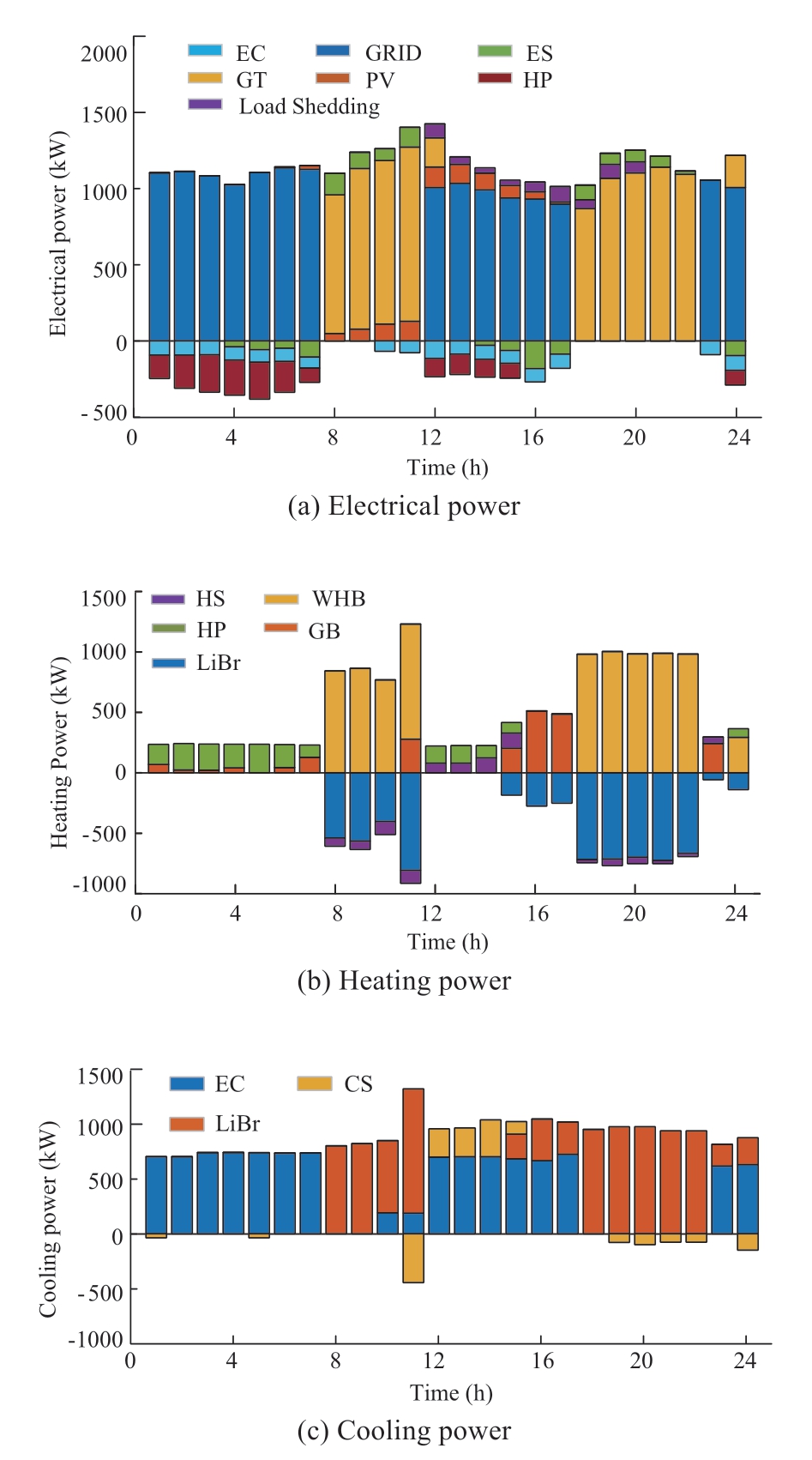
Fig.9 Dispatching results of robust optimization
Compared with the robust optimization strategy,the operation of the GT and LiBr unit are observed to be long,and that of the EC and HP is found to be short under the REMPC strategy.As shown in Figs.8 and 9,the REMPC optimization scheme has a high utilization rate of stored energy during the peak load period.Hence,the IES with the energy storage system must fully leverage the advantages of the storage system to facilitate the regulation in the daily energy supply.The IES can assume the role of the energy storage system for reducing peaks and filling valleys to improve the system’s economic efficiency.Robust optimization is slightly less economical than the REMPC strategy because its results are obtained when the system is under the worst case of uncertainty,and the IES must allocate more resources to cope with this unfavorable case.
In summary,the REMPC strategy is demonstrated to be effective for the optimal scheduling of the IES.Through rolling optimization,the power supply and working conditions of various energy supply devices are reasonably allocated over an extended time scale.Thus,the complementary operations of multi-energy systems in the IES are coordinated,further enhancing the economy of the system.Furthermore,the power supply and working conditions of the energy supply devices are rapidly adjusted over a short time scale in the dynamic adjustment phase based on the scheduling plan formulated in the rolling optimization phase.This improves the system’s ability to cope with the operating risks caused by the uncertainty source-load forecast errors.
6 Conclusions
An optimal dispatching method based on REMPC considering the source-load power interval prediction is proposed.Moreover,an optimal operation scheme for the IES is devised to respond to the uncertainties of the new energies and various types of loads in the IES.The results of the study are summarized as follows:
1) The formulated BiLSTM interval prediction model optimized by BAS and bootstrap exhibits higher prediction accuracy than the BBAS-LSTM method.The former can consider the uncertainty interval with a smaller coverage area than the latter at the same confidence level.Furthermore,the PICP improved by 0.81 and the PINAW decreased by 1.26.
2) The accurate prediction of the uncertainty interval reduces the level of conservativeness of REMPC results.Consequently,the operating cost is reduced by ¥405.77.Hence,an economical system operation is achieved for the dispatching scheme.
3) By fully considering the uncertainties of sourceload power in the IES,the proposed REMPC-based optimal dispatching scheme realizes reasonable power distribution.The operating cost slightly increases compared with that of the deterministic optimal dispatching scheme.However,the REMPC scheme improves the reliability and reinforces the ability of the system to deal with the risks introduced by prediction errors.
Acknowledgements
This work was supported by the National Key Research and Development Project of China (2018YFE0122200).
Declaration of Competing Interest
We declare that we have no conflict of interest.
References
[1]Li J,Wang D,Jia H,et al.(2021) Prospects of key technologies of integrated energy systems for rural electrification in China.Global Energy Interconnection,4(1): 3-17
[2]Hast A,Syri S,Lekavičius V,et al.(2018) District heating in cities as a part of low-carbon energy system.Energy,152: 627-639
[3]Shao C,Ding Y,Wang J,et al.(2017) Modeling and integration of flexible demand in heat and electricity integrated energy system.IEEE Transactions on Sustainable Energy,9(1): 361-370
[4]Lu X,Wang J,Liu G,et al.(2021) Station and network coordinated planning of integrated energy system considering integrated demand response.Global Energy Interconnection,4(1): 39-47
[5]Vegunta S,Watts C,Djokic S,et al.(2019) Review of GB electricity distribution system’s electricity security of supply,reliability and power quality in meeting UK industrial strategy requirements.IET Generation,Transmission and Distribution,13(16): 3513-3523
[6]Guo C,Wang H,Zhang Y,et al.(2019) Review of “sourcegridload” co-planning orienting to regional energy internet.Power System Technology,43(9):3071-3080
[7]Massaoudi M,Chihi I,Sidhom L,et al.(2021) An effective hybrid NARX-LSTM model for point and interval PV power forecasting.IEEE Access,9: 36571-36588
[8]Cartagena O,Parra S,Muñoz-Carpintero D,et al.(2021) Review on fuzzy and neural prediction interval modelling for nonlinear dynamical systems.IEEE Access,9: 23357-23384
[9]Almonacid F,Pérez-Higueras P J,Fernández E F,et al.(2014)A methodology based on dynamic artificial neural network for short-term forecasting of the power output of a PV generator.Energy Conversion and Management,85: 389-398
[10]Theocharides S,Alonso-Suarez R,Giacosa G,et al.(2019) Intrahour forecasting for a 50 MW photovoltaic system in uruguay:Baseline approach.In: 2019 IEEE 46th Photovoltaic Specialists Conference,Chicago,IL,USA,16-21 June 2019
[11]Liu E,Wang Y,Huang Y (2020) Short-term forecast of multiload of electrical heating and cooling in regional integrated energy system based on deep LSTM RNN.Paper presented at IEEE 4th Conference on Energy Internet and Energy System Integration (EI2),Wuhan,China,30 October-1 November 2020
[12]Wang S,Jia C (2015) Prediction intervals for short-term photovoltaic generation forecasts.In: 2015 Fifth International Conference on Instrumentation and Measurement,Computer,Communication and Control,Qinhuangdao,China,18-20 September 2015
[13]Wen Y,AlHakeem D,Mandal P,et al.(2019) Performance evaluation of probabilistic methods based on bootstrap and quantile regression to quantify PV power point forecast uncertainty.IEEE Transactions on Neural Networks and Learning Systems,31(4): 1134-1144
[14]Sun M,Feng C,Zhang J (2020) Probabilistic solar power forecasting based on weather scenario generation.Applied Energy,266: 114823
[15]Wang H,Yi H,Peng J,et al.(2017) Deterministic and probabilistic forecasting of photovoltaic power based on deep convolutional neural network.Energy Conversion and Management,153: 409-422
[16]Toubeau J,Bottieau J,Vallée F,et al.(2018) Deep learning-based multivariate probabilistic forecasting for short-term scheduling in power markets.IEEE Transactions on Power Systems,34(2):1203-1215
[17]Li J,Wang D,Jia H,et al.(2021) Prospects of key technologies of integrated energy systems for rural electrification in China.Global Energy Interconnection,4(1): 3-17
[18]Yuan G,Gao Y,Ye B (2021) Optimal dispatching strategy and real-time pricing for multi-regional integrated energy systems based on demand response.Renewable Energy,2021: 1424-1446
[19]Cao J,Meng K,Wang J,et al.(2014) Energy internet and energy router.Science China Information Sciences,44(6): 714-727
[20]Hu X,Zhou F,Zhao J,et al.(2021) Optimal operation of integrated energy system based on renewable energy scenarios.In: 2021 China Automation Congress,Beijing,China,22-24 October 2021
[21]Najafi A,Falaghi H,Contreras J,et al.(2016) Medium-term energy hub management subject to electricity price and wind uncertainty.Applied Energy,168: 418-433
[22]Wang C,Jiao B,Guo L,et al.(2016) Robust scheduling of building energy system under uncertainty.Applied Energy,167:366-376
[23]Kong A,Li C,Chen L,et al.(2020) ADMM-based distributed optimal dispatch of integrated energy system considering uncertainties of source and load.Paper presented at 2020 IEEE Sustainable Power and Energy Conference,Chengdu,China,23-25 November 2020
[24]Liu X,Xu W (2010) Economic load dispatch constrained by wind power availability: A here-and-now approach.IEEE Transactions on Sustainable Energy,1(1): 2-9
[25]Growe-Kuska N,Heitsch H,Romisch W (2003) Scenario reduction and scenario tree construction for power management problems.In: 2003 IEEE Bologna Power Tech Conference Proceedings,Bologna,Italy,23-26 June 2003
[26]Lu M,Li X,Li F (2020) Robust optimal scheduling of integrated energy systems based on hybrid energy storage and multiple time scales.In: 2020 IEEE Sustainable Power and Energy Conference,Chengdu,China,23-25 November 2020
[27]Yan M,Zhang N,Ai X,et al.(2018) Robust two-stage regionaldistrict scheduling of multi-carrier energy systems with a large penetration of wind power.IEEE Transactions on Sustainable Energy,10(3): 1227-1239
[28]Angeli D,Amrit R,Rawlings J (2011) On average performance and stability of economic model predictive control.IEEE Transactions on Automatic Control,57(7): 1615-1626
[29]Kou P,Liang D,Gao L (2017) Distributed EMPC of multiple microgrids for coordinated stochastic energy management.Applied Energy,185: 939-9524
[30]Jalali S M J,Khodayar M,Ahmadian S,et al.(2021) A new uncertainty-aware deep neuroevolution model for quantifying tidal prediction.Paper presented at 2021 IEEE Industry Applications Society Annual Meeting (IAS),Virtual conference,15 August 2021
Received: 27 June 2022/Accepted: 27 July 2022/Published: 25 October 2022
 Yang Yu
Yang Yu
ncepu-yy@163.com
Jiali Li
1255972327 @qq.com
Dongyang Chen
1334040096 @qq.com
2096-5117/© 2022 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Biographies

Yang Yu received bachelor’s degree at North China Electric Power University in 2005,Baoding;received master’s degree at Xi’an Jiaotong University in 2008,Xi’an;received PhD at North China Electric Power University in 2016,Beijing.Now,he is working as an associate professor in North China Electric Power University,Baoding.

Jiali Li received bachelor’s degree at North China Electric Power University Science and Technology College in 2019,Baoding.She is pursuing master’s degree at North China Electric Power University,Baoding.Her main research fields are power prediction and optimal dispatching for integrated energy system.

Dongyang Chen received the bachelor’s degree from North China University of Science and Technology,Tangshan,2020.He is currently pursuing master’s degree in North China Electric Power University,Baoding.His main research fields are electrical energy storage technology and renewable power generation technology.
(Editor Yanbo Wang)
