0 Introduction

Control operations undertaken by energy management systems (EMSs) or supervising control and data acquisition(SCADA) systems are based on the application of a steadystate model using telemetry.SCADA systems/EMSs typically provide instantaneous values of the frequency,active power,reactive power,voltage,and current using sporadic or cyclic principles.[1,2].

The steady-state analysis of a power system is a wellknown power flow problem,and its solution results in a power flow distribution (PFD) [3,4].The problem of steady-state analysis based on measurement data obtained from SCADA telemetry is known as state estimation(SE) [1,2].The aforementioned techniques form the framework of electrical power analysis and have been extensively investigated [1-4].The primary prerequisite for these problem solutions is the steady state in a grid,which satisfies all the electrical engineering laws at a given moment in time.In the classical SE problem,instantaneous measurements provide effective values of voltages,currents,and power at a discrete point in time.

On the contrary,electric energy (EE) billing measurements based on smart meters represent integral values typically recorded by automatic meter reading (AMR)or advanced metering infrastructure (AMI) systems.Despite the widespread use of interval EE measurements,the SE problem is typically solved using rough approximations based on the classical steady-state equations for instantaneous measurements,even if the measurement data are sourced from smart meters [5-10].This approach is widely adopted in distribution grids [11].However,the use of EE measurements for more accurate,reliable,and legitimate financial settlements is rather limited.Section 2 of this article reveals that owing to changes in the state and topology of a grid over time T,the use of SCADA telemetry,combined with classical laws of electrical engineering,leads to significant errors in the calculation of EE flows and losses.

In recent times,a practical data analysis based on electricity meters is conducted by compiling EE balances for various grid fragments,primarily as a simple summation of the inward and outward EE flows.However,precise computational mathematical models for calculating and analyzing EE flows and losses for all the grid elements are rather limited.Hence,this study aims to develop such a model.It is extremely necessary for the energy flow problem (EFP) to assess the accuracy and reliability of EE measurements.

For the EFP considered in this study,the primary measurements are not power measurements but EE flows in Watt (VAr)-hours,and the measurement data are not collected at a given moment but over a time period T between the start and finish of EE flow measurements.

Here,u denotes the voltage profile over time period T,and i denotes the current profile over time period T.Notably,such measurements are called interval measurements.However,the grid topology and state may fluctuate over time T,and considering these changes in the classical steady-state equations is often challenging.The primary scientific novelty of this study is that we developed a system of steady-state equations for the EFP,which is different from the classical one.Section 3 presents state equations for the EFP,which provide the distribution of EE flows and losses in a grid without resulting in methodological errors in the presence of topological and state changes over a time periodT.

The input data for the EFP comprise interval active(and optionally reactive) EE measurement data sourced from AMR/AMI systems.Such metering systems are often large-scale because EE meters are installed at all levels ranging from ultra-high voltage substations to low voltage distribution grids.In modern grids equipped with smart meters and AMR/AMI systems,the time interval T for monitoring EE flows can range from 2-60 min;this is because the EE costs may vary over time depending on the tariff policy and duration of the data collection period.At the low-voltage level,particularly if EE measurement data from conventional meters are collected manually by residentials,the data collection period can extend over a few months,and the costs may vary depending upon the tariff policy.

The EFP solution provides balanced EE flows and loss distribution at all the elements in an electrical grid;this solution is referred to as an energy flow distribution(EFD) [12].In this study,we extend a previously proposed EFP model [12]based on linear (Section 4) and nonlinear (Section 6) formulations.Section 4 describes the linear formulation of the EFP,supposing that the state equations are linear as EE losses for all grid elements are predetermined based on instantaneous measurements.Section 6 describes the nonlinear formulation of the EFP,describing the nonlinearity of state equations attributed to the need for determining losses.

The application of the SE theory to process interval EE measurement data opens up new avenues for AMR/AMI validation and detection of gross errors based on several predeveloped methods for conventional instantaneous SCADA measurements [13-17].Notably,the identification of gross and persistent systematic errors in EE measurements is crucial as EE measurement data are often used for financial settlements [18].Unlike EE measurements,the determined EE flows do not exhibit imbalances,and the conditions for EE balances are satisfied at all the nodes and branches in a circuit.The scope of the practical application of the EFP is primarily related to the validation of EE measurements.With sufficient redundancy in the EE measurements,the residuals of the EFP localize the distribution of nontechnical losses in the EE (Section 7)[19].A cyclic analysis of the EFD enables technical and metrological condition monitoring based on the AMR/AMI and the calculation and verification of technical EE losses(Section 8).Such an approach also provides fast bad data detection and a reduction in financial loss while eliminating the need for costly metrological tests.

This paper provides a unified framework for determining the EFD,including energy losses,in a grid over prolonged time intervals.The model can be adjusted depending on available data sources like the EMS or SCADA.Another contribution of this study includes a demonstration of practical advances presented by the proposed model,as well as bad data detection,detection of measurement errors,and nontechnical loss localization.

1 Problem of EFD Modelling

At the initial research stage,we believed that the mathematical model for the EFD could be easily obtained based on a transformation from the active (real) Wp and reactive Wq EE coordinates to the conventional P and Q power coordinates by dividing the EE by time T as follows:

Notably,the use of measurement data recorded by EE meters for SE has been described in several articles,but such descriptions are based on the classical equations of state [6-8].The laws of electrical engineering relate electrical and equivalent circuits only at a given moment when all parameters remain unchanged.However,changes may occur in the circuit topology and state over time T.The irrelevance of certain classical laws of electrical engineering for application in EFD modeling based on averaging over time (equation (2)) can be demonstrated based on a simple DC test circuit.Fig.1,a depicts a state that is completely stable during the first hour of monitoring.The numerical values of the EE flow over 1 hr (T=1) according to equation(2) are equal to the corresponding values of the power flow.The states during the second and third hours are depicted in Fig.1,b and Fig.1,c,respectively.Note that the lower branch is switched off during the third hour.The EE flows(in Wh) illustrated in Fig.1,d are obtained by summing the EE flows and losses over the first,second,and third hours.Note that the EE losses at the resistors (Fig.1,d) are equal to the sum of losses over 3 h (Fig.1,a,b,c).The state depicted in Fig.1,d represents the EE flow distribution for T=3 h.This EFD can be considered as a reference,as the EE parameters have no errors.In this example,all the EE flows are recorded using ideal meters without biases.

Fig.2 illustrates the power flows and losses obtained based on arithmetic division of the EE (Fig.1,d) by T = 3 h according to equation (2).Note that the left bus voltage is 100 V,as it was 100 V during the 3 h.Notably,the currents are obtained by dividing the power by voltage.For the power flows depicted in Fig.2,obtained based on equation (2),it is impossible to determine the currents and voltages that satisfy conventional formulations of electrical engineering laws.Thus,the possibility of applying the fundamental laws of electrical engineering to the analysis of power obtained from the energy according to equation (2) is analyzed.

Fig.1 EFD for a DC circuit: (a) first hour,(b) second hour,(c) third hour,(d) resulting EFD over three hours

Ohm’s law.According to Fig.2,for the upper branch,if determined from the left to right with a power of 200 W and a current of 2 A,the voltage drop is 2 V.Thus,the voltage at the right node is 98 V.However,if the right node power is considered to be 195.333 W,the current becomes 195.333 W/98 V=1.993 A.Typically,as the current in a branch is constant,the voltage drop across the upper branch calculated from the right to left is 1.993 V,instead of 2 V.Notably,an attempt to determine the EFD using Ohm’s law leads to contradictions.Our analysis reveals that if a branch current (power) changes over time,averaging it over time to calculate the voltage drops across different branch ends leads to varying results.

The second Kirchhoff’s law.Owing to the topological changes in a grid (disconnection of the lower branch for the third hour) with parallel branches of identical resistances,the voltage drop calculation leads to different results,which contradicts the second Kirchhoff’s law.Meanwhile,power flows,losses,and currents are not equal across parallel sections of the same resistors.

Joule-Lenz law.Power losses across the upper and lower branches differ from the values obtained as I2R.According to the formula,they must be equal to 4 W and 1 W;however,according to Fig.2,the load losses are 200-195.333=4.666 W and 100-98.333=1.666 W.This analysis demonstrates that even for a constant topology,if state changes arise during time T,the use of electrical engineering laws leads to discrepancies in the power values determined by dividing the EE byT.

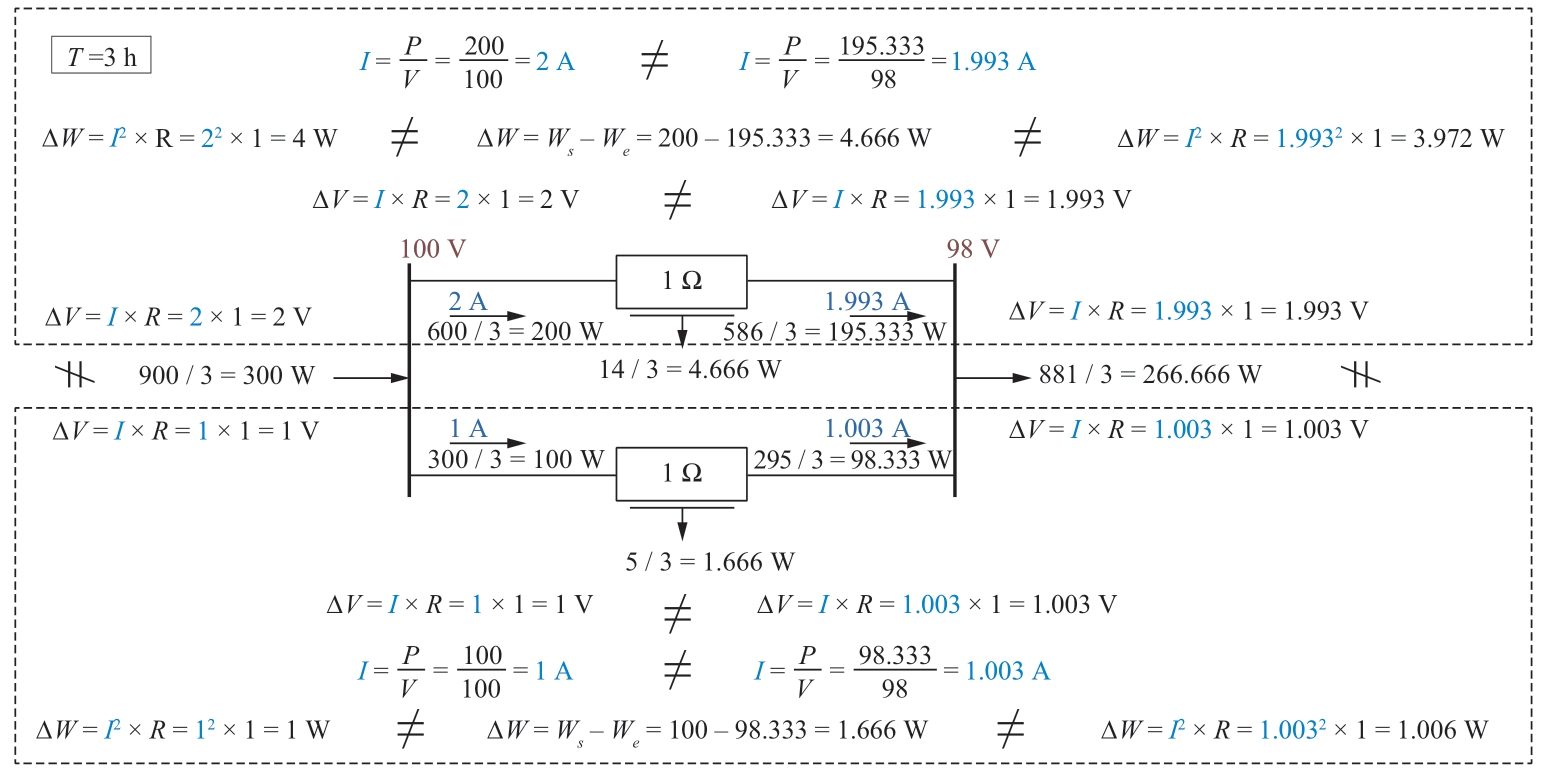
Fig.2 EFD averaging over T = 3 h using equation (2) and Fig.1,d

The primary circumstances complicating the use of conventional steady-state equations for EFD modeling are the variations in the grid topology during T.

As mentioned,considering topological changes in a grid within the framework of conventional steady-state equations is often challenging as such equations require constant parameters of the equivalent circuit.As reported in [8],classical power flow equations can lead to EE flow calculation errors ranging up to tens of percent for particular elements.Thus,conventional state equations can adequately describe the EFD only if the state and topology remain unchanged during time T.

Thus,the development of an alternate model is essential for an appropriate description of the EFD.

2 State Equations for the Energy Flow Problem

Notably,EE balances are valid at all the nodes and branches in a circuit for any topology and state changes over any interval of time.Therefore,the equations of EE balances for all the nodes and branches of a grid can be considered as the basis for the state equations of the EFP.Notably,the equations of EE balances do not have residuals owing to variations in the grid state and topology over time T,i.e.,they always remain relevant to the simulation.The equations of nodal EE balances for active (real) and reactive flows (Fig.1,d) can be described as follows:

where Wip,Wiq denote the injections of active and reactive EE at node i;W pij,W iqj denote active and reactive EE flows in the branch between nodes i and j;ωi denotes the set of nodes incident to node i;ΔWpi,ΔWqi denote shunt losses of the active and reactive EE at node i;and N denotes the number of nodes in the grid.The input and output flows are considered as positive and negative,respectively.The net electricity flow W is calculated by considering the signs according to the rules of arithmetic,that is,W =W +-W-,where W + denotes the positive direction,and W +denotes the negative direction.

The EE balances in branches are determined based on EE flows at the beginning of branch Wij,at its end Wji,and based on the load losses,as follows:

where M denotes the number of branches in a grid circuit.For the linear formulation,equations (3) and (4) constitute the state equation system of the EFP.The linear formulation implies that the losses given in equations (3) and (4) are not variables but numerically determined constants obtained from electricity meters or SCADA measurements (Section 5).These equations do not contain the parameters of the equivalent circuit;neither do they contain the voltage and current parameters.They ensure the aptness of EFD calculations with a variety of topologies and states without requiring any additional effort.A linear formulation of the EFP is presented in Section 4.

If no information source to determine EE losses is available,it is necessary to calculate the losses.Thus,the system of equations consisting of equations (3) and (4)must be supplemented with formulas for calculating the EE losses,which are nonlinear and contain the modules of nodal voltages and the parameters of the grid circuit (Section 5).In the nonlinear formulation of the EFP,the formulas for the measurements are nonlinear;therefore,the estimation problem is solved iteratively (Section 6).

The distribution of EE flows is determined by a single procedure over the entire time interval T,instead of sequentially evaluating a variety of electrical states based on telemetry and then integrating them to some average.

3 Linear Formulation of the Energy Flow Problem

A grid equivalent circuit and its parameters are generated in a manner similar to the conventional power flow problem and SE for the EFP.

The EFD represents EE flows that satisfy the system of state equations (3) and (4) using EE measurements.Notably,solving this problem based on state estimation approaches with the commonly used weighted least squares(WLS) function is often recommended.The number of active EE flows that are variables in the linear formulation of the EFP given in equations (3) and (4) is 2M + N.The same is true for the reactive EFD.The minimum number of measurements required for the determination of the EFD is equal to the number of variables minus the number of equations,that is,(2M + N)-(M + N) = M.The calculated state vector W ={W p ,Wq} contains active Wijp and reactive Wijq EE flows recorded at the beginning of the branches.

The dimension of the state vector W for the active and reactive EFP is 2M.Using equations (3) and (4),any measurement of the active EE can be represented as a linear combination of W.The measurements at the beginning of the branch 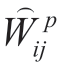,end of the branch 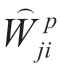,and nodal injectioncan be represented as follows:

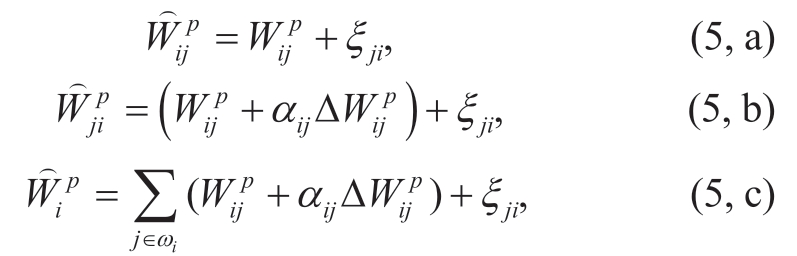
where ζ corresponds to the measurement error.αij assumes a values of 1 or-1 depending on the direction of the EE flow:positive if the flow ji is outgoing and negative if the flow ji is incoming.By analogy,the measurements of reactive EE are expressed only based on the reactive EE flows Wij q.In the matrix form,the measurements of active  and reactiveEE flows can be expressed as

Note that in the linear formulation of the EFP,no interrelation can be noted between the measurements of active and reactive EE flows;the off-diagonal blocks Hpq and Hqq are zero,while the diagonal blocks Hpq and Hqq are sparse.The nonzero elements of the diagonal blocks are equal to ± 1.Equation (5,d) for EE measurements in a compact form can be described as follows:

The number of equations in the system given in equation (6) is equal to the number of EE measurements,K.A necessary condition for solving the EFP is that the number of measurements is greater than the dimension of the state vector (K≥2M ),and the system of equations for measurements (equation (6)) is (over) determined.Further,additional measurements in a grid circuit are required if K＜2M .To match the measurements containing errors ξ,the most common approach in the SE theory is to use the WLS estimation and solve the system [3,4]as follows:

For the linear EFP,a single iteration is sufficient to obtain the solution (n = 0).As an initial approximation,we recommend the consideration of zero EE flows in branches W(0) =0;hence,

The weighted measurement coefficients in R-1 are inversely proportional to the dispersion values of measurement errors,which are generally unknown.However,metrological reports define maximum relative errors for EE measurements as reference [20]follows:

where δI,δU,and δW denote the percentage accuracy classes of the current transformer,voltage transformer,and EE meter,respectively;δL denotes a voltage drop in percentage across a cable between the meter and voltage transformer;and k denotes the index of the measurement in a set (a sequence) of measurements.The difference between the measured and calculated Wk EE flows determines the relative estimation residual of measurement,as follows:

Normally,however,if the number of EE measurements is less than the threshold,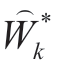should be corrected based on the minimum recommended load of a current transformer (typically 5%,[20]).The diagonal elements of the matrix R-1should be determined using the relative measurement errors δk% corresponding to EE measurements,as follows:

Thus,solving the system of linear equations given in equation (7) is equivalent to determining the minimum of the sum of squares of the relative measurement errors.This corresponds to a minimization of the function as follows:

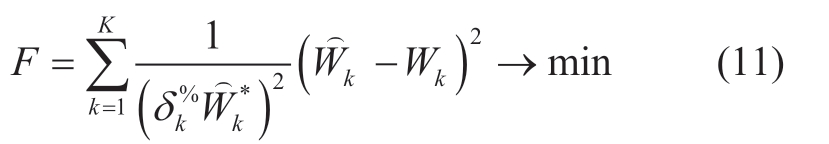
The EFP uses EE flows in the branches instead of the most popular state vector of nodal voltages for the SE.Hence,the EFP can be classified as a flow-branch model.The computational characteristics of this problem are close to the SE based on branch currents in polar [21,22]or rectangular [23-26]forms.

Generally,weighted measurement coefficients must be inversely proportional to the measurement error dispersions.However,these dispersions are often unknown.Hence,known(rated) electricity meter accuracy data (equation (8)) are used instead of the dispersions.The result of equation (11) may provide residuals as a difference between the measured and calculated values.If a residual is within the meter accuracy class,an error does not exceed the rated value,and the meter functions appropriately.In contrast,if a residual exceeds the accuracy class,it indicates bad data and nontechnical energy losses,as will be discussed in Sections 7-8.

4 Energy Loss Models

The electrical grid equivalent scheme for the EFP consists of traditional impedance series elements rij + jxij,their corresponding load losses ΔWi jp+ j ΔWijq,and shunt elements g i+ jbi with shunt losses 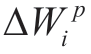+ j ΔWiq.The choice of a method for calculating EE losses depends on the availability of their accuracy measurements.

The resistance uncertainty is-24% to +8%,which is determined based on the temperature dependence.The reactance uncertainty is-10% to +8%,whereas the uncertainty in the shunt values is much greater [27-29].These uncertainties in the grid parameters enable the use of simplified methods for calculating losses because they cannot be calculated precisely.The EE loss per element is typically less than 1% of the transmitted EE,and a 20% loss calculation error results in an EE flow error of 0.2%.

The most precise method for calculating load losses involves integration of the square of the current over Nτ short time periodsτ for the entire period T.This can be described as follows:

Advanced smart meters can integrate I2 with a high time resolution,which is the most accurate approach to determine losses.As given in equation (12),the accuracy can be obtained using only two values: the average current and current dispersion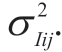 

The currents flowing in the upper branch in Fig.1 over 3 h are 1,2,and 3 A The corresponding currents flowing through the lower branch are 1,2,and 0 AThe load losses according to equations(12) and (13) are equal to the reference values depicted in Fig.1,d.For the upper and lower branches,these values are equal to 14 Wh and 5 Wh,respectively.For the lower branch,which was disconnected during the third hour,equations (12) and (13) produce an accurate result even under topological changes over the measurement interval.Further,no-load EE losses are determined based on the passport data of the equipment ΔPn.l .and ΔQn.l .of node i.The node disconnection time Ti discto be considered is as follows:

Notably,SCADA telemetry can increase information redundancy,improve the EFD calculation accuracy(particularly for analyzing the EE),and linearize the EFP.If the dependence of no-load losses on the voltage is considered,it is possible to determine the ground conductivity g i+ jbi for any of the i nodes based on ΔPn.l .and ΔQn.l ..Further,by analogy with equation (13),the use of the following expression is recommended:

where 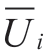denotes the mathematical expectation value,and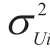denotes the dispersion of the voltage of node i during time T.and 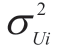can be determined using the statistical processing of the SCADA voltage data over time intervals of seconds.Equations (12)-(15) ensure the correctness of the loss calculations for any state and topological changes.Their application is effective under conditions wherein current and voltage data are stored in the archives of SCADA systems,and all losses ΔWi p,ΔWiq,ΔWijp,and ΔWijq can be calculated on their basis and subsequently used as the initial data for a linear EFP.

Notably,no special synchronization of the EMSs and SCADA systems is required for the considered application.From a marketing perspective,EFD calculations are reasonable over time intervals T with fixed market prices.In most countries,the price for an end customer changes once over a period of 1800 to 3600 s (from 30 to 60 min).According to the technical standards,the typical time accuracy of electricity meters and SCADA systems is less than 1 s.For example,according to the standards applicable to digital substations such as IEEE 1815 (NTP),which are relevant to meters,the time accuracy is 1 ms.The considered errors are negligible compared with T.The SCADA periodic sampling rate is typically a multiple of 1 s and is always greater than the EMS sampling rate.Hence,T includes T/t of the measurement data provided by SCADA systems with a time error not exceeding the above considered and coincident time marks (beginning of T and its end).This case is more complicated if SCADA sporadic sampling is used.In this case,data preprocessing must be performed to provide coincident time marks.

If SCADA measurement data are not available,it is necessary to use the calculated values to determine the losses.This approach presupposes a nonlinear formulation of the EFP and iterative refinement of losses.The primary expression for calculating load losses of the nonlinear EFP can be presented as follows:

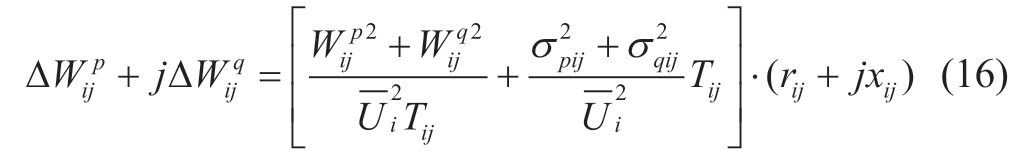
where Wijp and Wijq denote the calculated flows of active and reactive EE,respectively,and  and 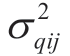denote the dispersions of active and reactive power flows (in Watts),respectively,determined from data obtained from the AMR/AMI archives.For the circuit depicted in Fig.1,the active flows in the upper branch for 3 h are 100,200,and 300 W(Wijp = 200 W,σ 2pij = 200/3).The corresponding flows in the lower branch are 100,200,and 0 W (Wijp = 100 W,σ 2pij =200/3).The load losses determined based on equation (15)for the upper and lower branches are 14 Wh and 5 Wh,respectively.The values correspond to the reference value in Fig.1,d.

If a branch does not have its corresponding SCADA measurement data and EE meter data,only the calculated flows of active and reactive EE can be used.In this case,no data for calculating variances are available,and a less accurate formula is used:

where kf denotes the shape factor of the load curve,calculated for the entire grid.The value of the shape factor for actual systems usually spans a range of 1.05-1.15 [30,31].An inaccuracy of 10%-15% can be considered acceptable because EE losses for a transformer or power line usually do not exceed 1% of the transmitted EE.

In the absence of voltage measurements,it is advisable to use equation (13) or the calculated voltages:

In this case,considering the disconnection time of the node or branch,Tidisc,Tijdisc,is essential.

Thus,various methods can be adopted for EE loss calculation for determining the EFD,depending on the data sources.

5 Nonlinear Formulation of the Energy Flow Problem

Using computational EE flows and voltages,instead of measurement data,in loss expressions given in equations(16)-(18) significantly changes the EFP as the problem now becomes nonlinear with respect to the EE flows and voltages.The primary group of measurements for linear and nonlinear problems is the same.These measurements constitute the measurements of active and reactive EE flows across nodes and branches.The equations for active EE flow measurements at a branch end contain nonlinear components owing to losses.

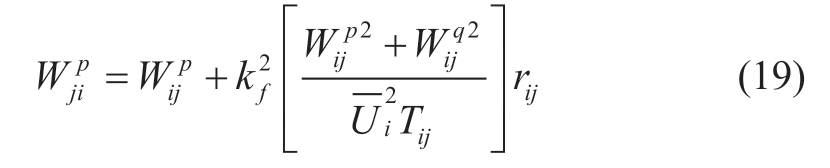
The residuals of equations for the measured active EE flows across nodes and branches can be represented as follows:

Similarly,the residuals for reactive measurements are as follows:

To linearize equations (20) and (21),it is necessary to calculate the derivatives of the active and reactive flows,as for the linear EFP.Moreover,the derivatives of the nodal voltage modules averaged over time T are required.The calculated vector of the variables,in addition to EE flows,should include the average nodal voltages X= { W p ,W q ,U}.To determine the average nodal voltage,processing SCADA measurement data over time T= τ·Nτ is recommended;this can be described as follows:

The residuals between the values obtained based on equation (22) and the calculated values of the average voltages can be represented as follows:

where NU denotes the number of nodes provided by the SCADA voltage measurements.The relative error corresponding to equation (23) is determined based on the accuracy classes of the voltage transformer δUi% and the voltage drop in the supply cable δΔUi%,as follows:

In the absence of SCADA measurement data,the average nodal voltages can be determined based on the calculated EE flows in the branches,as follows:

In equation (25),the power flows are replaced by EE flows based on equation (2).In Section 2,we stated that a methodical error arises if voltage drops are calculated based on EE flows.Calculating the voltage drops from different ends of a branch leads to different results.Therefore,the use of equation (23) allows residuals as for measurements.

The number of such equations equals the number of branches M in a grid circuit.Previous studies have revealed that the relative error corresponding to equation (26) is approximately 1.2 times higher than that for equation (24).

In the matrix form,the linearized system of equations containing equations (20),(21),(23),and (26) can be written as

In equation (28),the nonzero elements of the blocks dφ Wp/dWq and dφ Wq/dWp are occupied with the values of relative losses of EE.In actual circuits,these losses typically lie in a range of ± 0.05.In contrast to the linear formulation of the EFP,in the nonlinear formulation,the EE distribution of active and reactive EE flows is interrelated.This relationship is determined based on the mutual influence of active EE flows on reactive losses,and vice versa.Note that equation (23) for voltage measurements is represented in equation (28) using a unit diagonal matrix.The number of equations in equation (28) exceeds the number of variables.The matrix of the equation system presented in equation (28) is denoted by H in analogy with equation (5).The minimum value of the objective function in equation (11) is ensured by reducing the system of equations in equation (28) to the normal form and weighing it based on the relative errors-given in equation (10) using the matrix R-1 as follows:

The solution of equation (29) allows one to obtain the vector of corrections and an iterative solution for the nonlinear EFP to achieve the defined accuracy,as follows:

Hence,the minimization of the function in equation(11) can be achieved using equations (29) and (30).Notably,first-order iterative methods,such as the gradient descent,are sufficient for solving linear and nonlinear EFD equations (Sections 5 and 6,correspondingly) [2].The method of gradient descent is used for the calculations presented in Section 8 of this article.An iterative solution can be obtained in a single iteration because the objective function containing residuals is quadratic.Another approach involves the linearization of state equations for the EFD at each iteration (equation (29));for this,a second-order convergence iterative method,such as the Newton-Raphson method,may be used [2].

The nonlinearity in EE losses during state and topology changes is the primary reason for the nonapplicability of conventional electrical engineering laws while averaging states over time.The following loss error estimation approach can be obtained based on equation (16).The error corresponding to averaging includes a ratio of the EE losses in the EE flow that vary over T to the stable EE flow.

The error in loss values depending on a variation in the EE flow is depicted in Table 1.The total error in a state calculation depends on the share of losses in a grid.

Table 1 Possible error in EE losses owing to averaging

A major obstacle in the conventional formulation considering the second Kirchhoff’s law is the reverse power flow during T.The EFD may present two EE flows flowing into a branch from both sides and feeding EE losses,which is impossible for the conventional model.

6 Identification of Bad Data,Measurement Errors,and Nontechnical Loss Localization

If the grid circuit topology and parameters are appropriate and no errors exist in EE measurements,the calculated and measured EE flows should be equal.Large relative residuals in the EFP estimation denote errors or distortions in EE measurements [19,32],i.e.,EE bad data.The origins of the incorrect data may be different: typical negative bias of meters,an error in k measurements,absence of k measurement replaced by zero value,or unaccounted energy by meters.From a market perspective,no difference exists between the origins of bad data because all the losses are nontechnical losses leading to financial losses for a party with underestimated EE values and unfair gains for a party with overestimated EE values.

Typically,Joule (ohmic) losses in wires,transformer idle losses,leakage currents,and corona losses cause technical losses.These losses can be obtained with certain accuracies using equation (2) or can be calculated as discussed in Sections 5 and 6.Such types of losses are accounted for in the tariff policy and energy prices.By contrast,nontechnical losses can be attributed to electricity meter malfunctions and electricity thefts.Nontechnical losses are the losses most negatively affecting grid utilities,thereby leading to substantial financial losses [32].Although the EFD can highlight technical and nontechnical losses,the statement presented above is why we primarily concentrated on nontechnical losses.

Nontechnical active EE losses in a grid utility ΔW ntl are equal to the differences between the measured losses ΔW m and technical (calculated) losses ΔWc.The measured losses are defined as the sum of EE measurements ∑Wim at the boundaries of the energy utility,considering the directions of EE flows (μ is the set of boundary measurements).The technical losses are equal to the sum of the calculated EE flows ∑Wi c obtained from the EFP at the same bounds.Note that EE losses obtained based on the EFP for all grid elements are technical,i.e.,they denote calculated values.Thus,

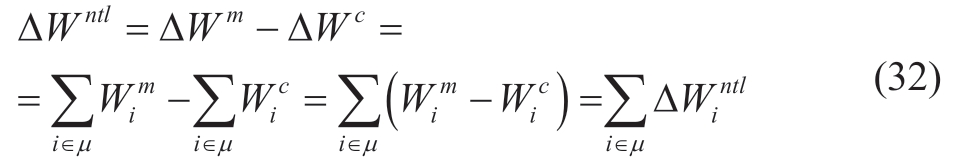
According to equation (32),the nontechnical EE losses of a utility are equal to the sum of the estimation residuals at all boundary points [19].Using the EFP to detect nontechnical losses of EE is an important research area.The high information redundancy of EE meters provides more precise nontechnical loss point localization [18,19].

7 Practical Applications of the Energy Flow Distribution

Further,a test application case of the EFP solution on a seven-node grid is considered (Fig.3).The resistances of all the branches are equal to 5 + j40 Ω.The variations in the state are modeled by EE measurements for 2000 h (Fig.3,c),which are obtained by summing state 1 (Fig.3,a) and state 2 (Fig.3,b) for 1000 h each.In state 2,one of the parallel lines 1-2 is switched off to create a topology change.EFD solution results using the proposed model are presented in Fig.1,d.The locations of all the available ideal meters for measuring active and reactive EE in Fig.3,c-e are indicated by circles.

To demonstrate the advantages of the EFD,conventional PFD analysis was performed on the same circuit using the averaging approach;additional details pertaining to this approach can be found in [6-8]and Sections 2-4,Section 6.Subsequently,energy flows and losses were calculated based on the PFD.The load power values were set as average values during the entire time period.Both EFDbased and PFD-based results are compared to the reference value obtained by means of integrated power,see formulas(1),(2).The results of the comparison are presented in Table 2.The reference values of energy flows are shown in Fig.1,c.

Table 2 Comparison of results between the EFD and PFD models

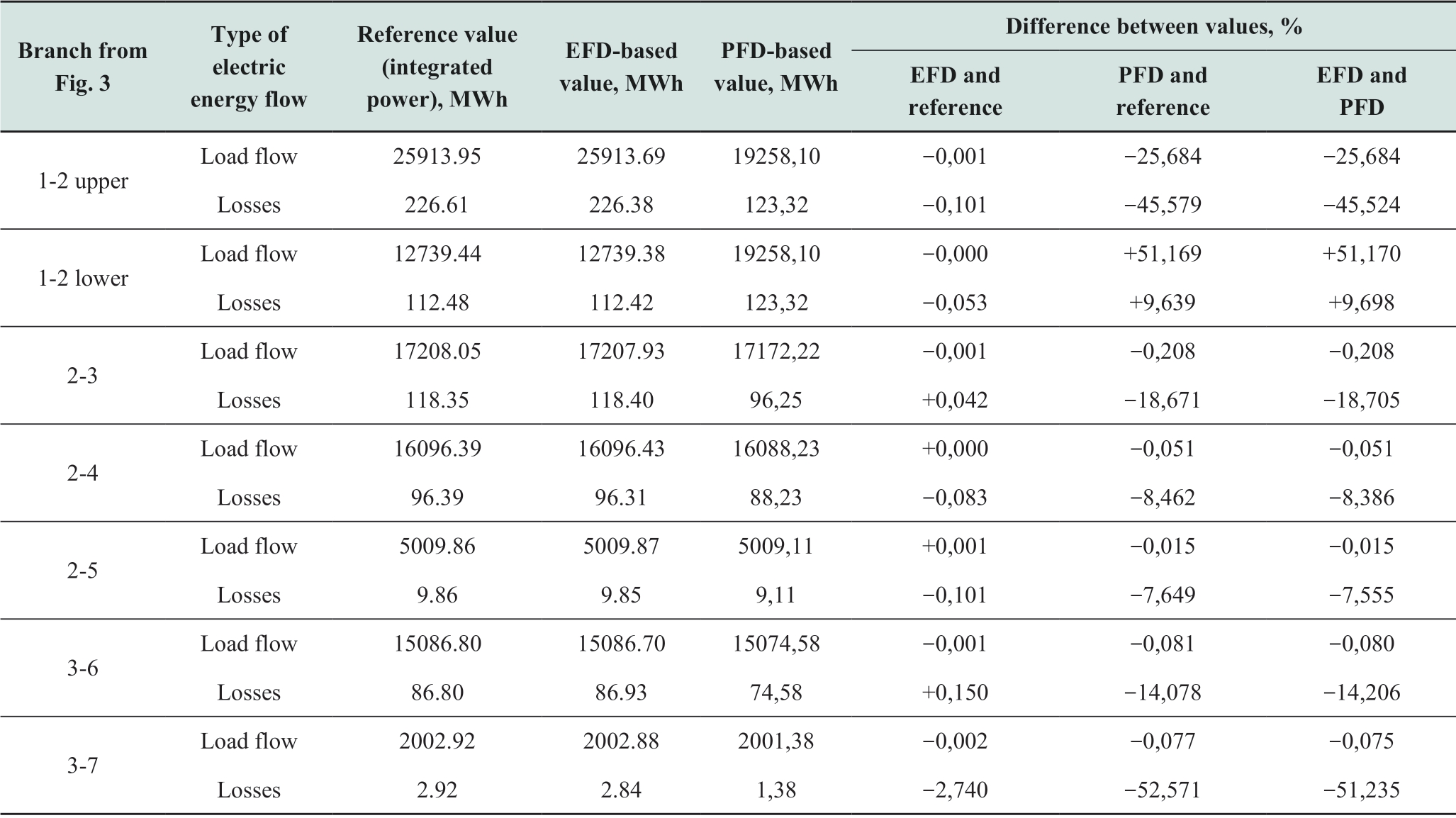
As it can be seen from the results of the test,the accuracy of EFD is very high and can be assessed at 0.005% for energy flows and 1% for electricity losses.As can be inferred from equation (17),the EFD results in a close resemblance between the calculated and measured EE flows.The maximum relative estimation residual is at branch 3-7 that was subjected to the load disconnection on its end at the second state.

The difference between EFD-based values and reference values is due to the assumptions regarding losses linearization and voltage dispersions (Section 6).The difference is estimation residuals spreading among grid components inversely proportional to measurement accuracy.The accuracy classes are set equal for all the meters in the case study,so the relative distribution of the residuals is homogenous.EFD accuracy is robust,especially considering that steady-state voltages rarely deviate more than ±10% from the rated voltage;the extent of the voltage non-linearity is relatively low.Energy output values can be fixed as constants to avoid their corrections during EFD calculation.However,it is inexpedient if non-technical losses detection is performed.

The table also indicates that a dramatic difference exists in the energy flow values calculated based on the EFD and PFD,particularly when some grid components are temporarily switched off (like 1-2 lower power line) or operate under no-load conditions (like 3-7 right transformer).The PFD cannot adequately represent the EFD for a long time interval.The example depicted in Fig.3,e illustrates the possibility of localizing nontechnical EE losses based on the EFD.Instead of the correct value of 5000 MWh,an incorrect measurement value of 4000 MWh is used in the calculation at node 5.Such an error can be considered a theft of 1000 MWh of EE at node 5;that is,this represents an example of nontechnical EE loss occurrence.The greatest difference between the measured(4000 MWh) and the calculated (4954 MWh) EE flow is observed for the incorrect measurement at node 5.

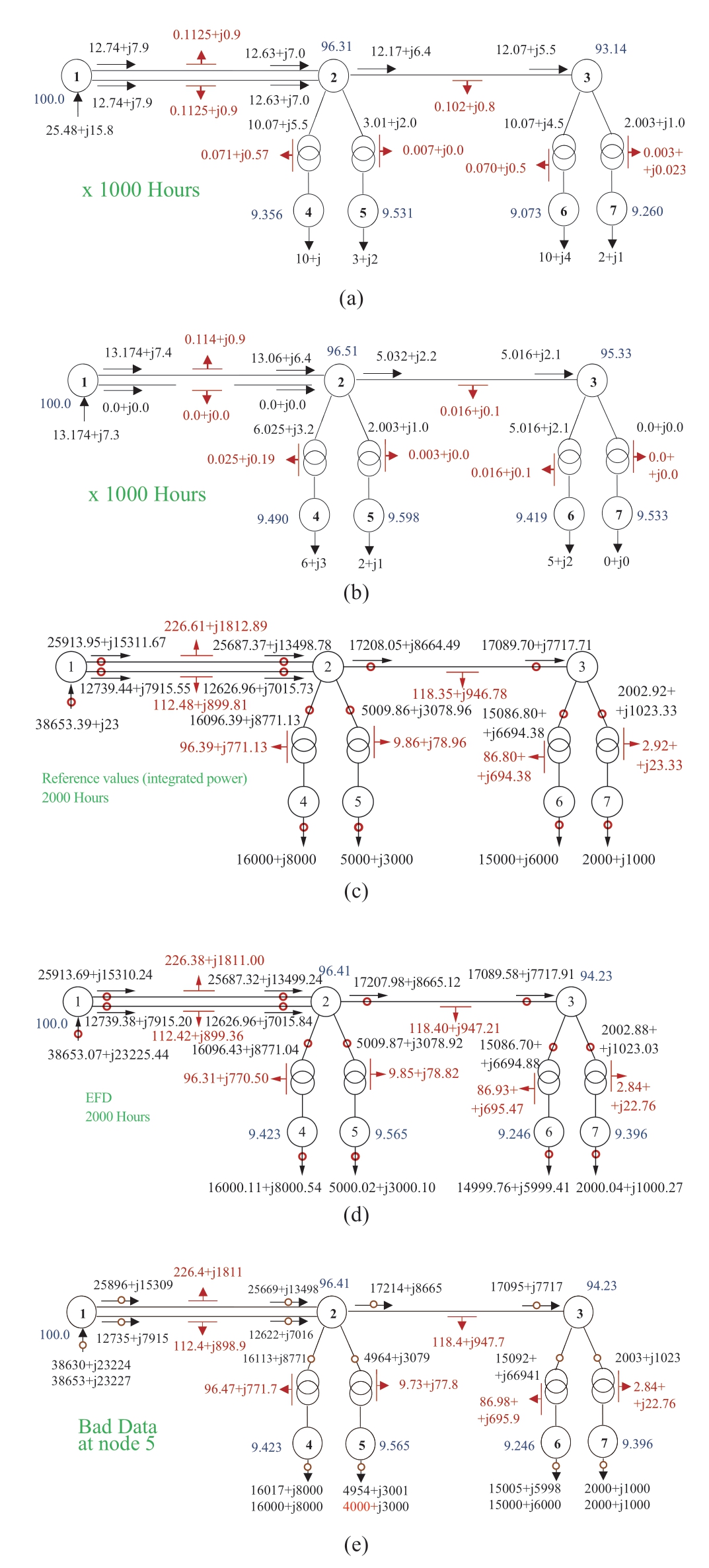
Fig.3 Distribution of (a) power flow and losses-state 1 (MW+ jMVAr),(b) power flow and losses-state 2 (MW + jMVAr)(the branch 1-2 is switched off),(c) electric energy flows and losses for 2000 h (MWh + jMVArh),(d) calculated energy flow distribution for 2000 h (MWh + jMVArh),(e) electric energy flow and losses for 2000 h (MWh + jMVArh);the consumption of node 5 is understated;its correction by means of energy flow distribution.

Owing to the information redundancy,the calculated EE flow corresponding to an incorrect measurement is approximately close to the true value of 5000 MWh(deviation of 1.03%).The sum of the EE calculated flows at the boundary measurements (located at nodes of the circuit)with regard to the directions and signs is 654 MWh.These represent technical losses of EE in the circuit.The sum of measurements of active EE at these points is 1653 MWh.These represent the measured losses of EE.The difference between the measured and calculated losses based on equation (31) constitutes the total nontechnical losses in the grid,1653-654 = 999 MWh.These total nontechnical losses are equal to the sum of the estimation residuals for the boundary EE measurements at nodes: ΔW1 ntl = 23 MWh,ΔW4ntl = 17 MWh,ΔW5ntl = 954 MWh,ΔW6ntl = 5 MWh,and = 0 MWh.Owing to the well-known blurring effect of errors [4],the introduced error of 1000 MWh is redistributed among the boundary nodes as estimation residuals.The EFP enables the classification of losses into technical and nontechnical losses and distributes the total nontechnical losses among meters,which is equivalent to localizing them.

The EFD calculations were conducted for 16 grid utilities in the Urals and Western Siberia regions of Russia from 2002-2016 [32].The calculation circuits included 300-1300 nodes at voltages of 10-500 kV.During the calculations,a switched-off state of the transmission lines and transformers for 220 and 500 kV was considered.

The results obtained indicate that nontechnical EE losses close to zero for utilities owning the primary share of EE meters and distributing EE at medium and high voltages of 6-110 kV.For the utilities powered by 0.4 kV grids,nontechnical losses exceeded the technical losses during certain intervals.High levels of nontechnical losses are typical of rural areas.

AMR/AMI archives enable the identification of bias(time-stable) errors in EE measurements by performing EFD calculations based on thousands of hours of EE measurements.Fig.4 depicts a plot of the distribution density of the relative estimated residual given in equation(9).As depicted in Fig.4,a,considering the dispersion,the mathematical expectation  of the relative estimation residual substantially exceeds the error threshold ±δi%given in equation (8).This is an example of a persistent negative bias,which corresponds to an underestimation of the actual EE consumption.This indicates a persistent underestimation of EE,which leads to nontechnical EE losses.Fig.4,b represents a positive case without biases.The residuals of the estimation given in equation (9) do not exceed the thresholds of the errors given in equation (8).

Fig.4 Estimation residual distribution density: (a)measurements with a strong negative bias;(b) measurements with Gaussian-distributed errors and small bias

The EFP can be used in advanced AMR/AMI systems for online monitoring of their serviceability.The output of the estimation residual beyond the limit ±δi%in equation (8)is a sign of the malfunctioning of one of the AMR/AMI components.

The calculation results for 10-110 kV grids containing 1240 thirty-minute AMR measurements for 2184 time intervals provide statistics of the distribution of relative estimation residuals given in equation (9) for all the measurements (Table 3).

The left row indicates the ranges of the relative estimation residuals corresponding to equation (9).The right row indicates the percentage of measurements in this range for all the 2184 calculations.The general statistics include more than 2.7 million measurements.

As can be observed from Table 3,for more than 2.5%of the EE measurements,the relative estimation residuals in equation (8) exceed the maximum value defined by the grid code error (equation (7)),corresponding to 1.0%.

Table 3 Distribution of measurements by error ranges

8 Conclusions

(1) A new approach for analyzing EE states in electrical grids based on state estimation approaches and joint processing of AMR/AMI and SCADA measurement data is developed.The problem is referred to as the EFP.The solution to this problem provides the calculated distribution of electricity flow and losses for all the circuit elements over a given time interval with no imbalances.

(2) Owing to the possible variations in grid topologies and states over a period T,using steady-state equations based on the classical laws of electrical engineering for the EFP may result in unavoidable imbalances.The state equations must be based on balanced active and reactive EE flows for all the nodes and branches in a grid.In this case,the equations are precise under any topological or state changes.

(3) If EE losses for all grid elements can be calculated based on measurements,the EFP is linear,and the computational vector includes only the EE flows in the branches.If the EE losses depend on the calculated flows,the EFP is nonlinear.In this case,the calculated vector should additionally contain the average values of the nodal voltages,and the problem must be solved iteratively.

(4) The EFP allows SCADA/EMS instantaneous measurements and AMR-AMI interval measurements to be used simultaneously to increase the measurement redundancy and to facilitate mutual verification.For the EFP,the equations for voltage drops across circuit elements and loop equations may be similar to the measurements;hence,they may have residuals.

(5) The EFP allows for the processing of measurement data from electricity meters used in financial settlements.To that end,the use of bad data detection methods developed for the SE of electricity measurements is very promising.Using this approach,it is possible to localize nontechnical electricity losses and identify bias measurement errors by analyzing the residuals of the EFD estimation in case of redundancy in electricity measurements.The EFP cyclic solution enables monitoring of the technical and metrological conditions of AMR/AMI systems.

This paper provides a unified framework of the EFP model,which can be used depending on the available initial data,in terms of the model complexity and linearity.The case study described herein indicates the application potential of the model in detecting and localizing all types of nontechnical losses and metering system malfunctions.

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1]Ahmad,M (2013) Power system state estimation.Artech House,Boston,USA

[2]Abur A,Exposito A G (2004) Power system state estimation:Theory and implementation,Marcel Dekker,New York,USA

[3]Grainger J,Stevenson W(1994) Power system analysis.McGraw-Hill,New York

[4]Berger AR (2009) Power Systems Analysis.Pearson Education,Delhi,India

[5]Baran M,McDermott T E (2009) Distribution system state estimation using AMI data.2009 IEEE/PES Power Systems Conference and Exposition,1-3

[6]Gao Y Q,Yu N P(2017) State estimation for unbalanced electric power distribution systems using AMI data.IEEE Power &Energy Society Innovative Smart Grid Technologies Conference.Washington,DC,USA.IEEE,1-5

[7]Abdel-Majeed A,Braun M(2012) Low voltage system state estimation using smart meters.47th International Universities Power Engineering Conference (UPEC).Uxbridge,UK.IEEE,1-6

[8]Pau M,Patti E,Barbierato L,et al.(2016) Low voltage system state estimation based on smart metering infrastructure.2016 IEEE International Workshop on Applied Measurements for Power Systems (AMPS).Aachen,Germany.IEEE,September 2016

[9]Golub I,Boloev E,Kuzkina Y (2019) Using smart meters for checking the topology and power flow calculation of a secondary distribution network.E3S Web of Conferences,139: 01059

[10]Kuzkina Y,Golub I (2018) Smart meters as a key component of modern measuring infrastructure providing observability and state estimation of low-voltage distribution networks.E3S Web of Conferences,69: 02012

[11]Primadianto A,Lu C N (2017) A review on distribution system state estimation.IEEE Transactions on Power Systems,32(5):3875-3883

[12]Pazderin A V,Kokin S E,Egorov A O,et al.(2009) Solution of energy flow problem using state estimation technique.35th Annual Conference of IEEE Industrial Electronics.Porto,Portugal.IEEE,1736-1741

[13]Handschin E,Schweppe F C,Kohlas J,et al.(1975) Bad data analysis for power system state estimation.IEEE Transactions on Power Apparatus and Systems,94(2): 329-337

[14]Mili L,Cutsem T V,Ribbens-Pavella M (1985) Bad data identification methods in power system state estimation-A comparative study.IEEE Transactions on Power Apparatus and Systems,PAS-104(11): 3037-3049

[15]D’Antona G,Perfetto L(2015) Bad data detection and identification in power system state estimation with network parameters uncertainty.2nd International Conference on Knowledge-Based Engineering and Innovation (KBEI).Tehran,Iran.IEEE,26-31

[16]Cramer M,Goergens P,Schnettler(2015) A Bad data detection and handling in distribution grid state estimation using artificial neural networks.IEEE Eindhoven PowerTech.Eindhoven,Netherlands.IEEE,1-6

[17]Pau M,Ponci F,Monti(2018) A Analysis of bad data detection capabilities through smart meter based state estimation.IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe.Palermo,Italy.IEEE,1-6

[18]Elena K,Andrew P,Alexandar S (2016) Testing equation method modification for demanding energy measurements verification.MATEC Web of Conferences,75: 01004

[19]Pazderin A V,Samoylenko V O (2013) Localization of nontechnical energy losses based on the energy flow problem solution.In: Proceedings of the 6th IASTED Asian Conference on Power and Energy Systems,Phuket,Thailand.IASTED,2013,pp.100-103

[20]RD 34.09.101-94 (1995),Typical instruction for EE metering in its generation,transmission and distribution (in Russian)

[21]Pau M,Pegoraro P A,Sulis S (2013) Efficient branch-currentbased distribution system state estimation including synchronized measurements.IEEE Transactions on Instrumentation and Measurement,62(9): 2419-2429

[22]Blaauwbroek N,Nguyen P,Gibescu M,et al.(2016) Branch Current state estimation of three phase distribution networks suitable for paralellization.IEEE PES Innovative Smart Grid Technologies Conference Europe.Ljubljana,Slovenia.IEEE,1-5

[23]Primadianto A,Lin W T,Lu C N (2016) Performance comparison of distribution system state estimation methods.2016 IEEE Innovative Smart Grid Technologies-Asia (ISGT-Asia),Melbourne,Australia,1121-1126

[24]Neto M S I,Asada E N(2016) State estimation for distribution systems using branch currents as state variables.12th IEEE International Conference on Industry Applications.Curitiba,PR,Brazil.IEEE,1-6

[25]Baran M E,Kelley A W (1995) A branch-current-based state estimation method for distribution systems.IEEE Transactions on Power Systems,10(1): 483-491

[26]Ugarte L F,Laburu F M,Fernes T R,et al.(2018) Assessing the branch current based state estimator under fault conditions.2018 IEEE PES Transmission &Distribution Conference and Exhibition-Latin America (T&D-LA).Lima,Peru.IEEE,1-5

[27]Kovalenko P Y,Berdin A S (2017) Defining the parameters of a power transmission line equivalent circuit on the basis of phasor measurements.Journal of Physics: Conference Series,870:012012

[28]Liao Y,Kezunovic M (2009) Online optimal transmission line parameter estimation for relaying applications.IEEE Transactions on Power Delivery,24(1): 96-102

[29]Bakhteev S,Pazderin A,Zajtsev V,et al.(2005) Generalized results of primary energetic examination of a number of electric grid enterprises at ‘Tyumen’energo’ opened joint stock company.Energetik,vol 7,pp 13-16

[30]Shvedov G V,Chorshanbiev S R,Shvetsova E V,et al.(2018)Impact of solar generation connected to 0.4 kV grid on the power losses and the shape factor of load curve.2018 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering.Moscow and St.Petersburg,Russia.IEEE,773-777

[31]Piao M,Ho Ryu K (2017) Local characterization-based load shape factor definition for electricity customer classification:local characterization-based load shape factor definition.IEEJ Transactions on Electrical and Electronic Engineering,vol 12,no 1,pp 110-116

[32]Lu C,Huang S,Lo Y (2013) Non-Technical Loss Detection using State Estimation and Analysis of Variance.IEEE Transactions on Power Systems,vol 28,no 3,pp 2959-2966

Received: 18 April 2022/Accepted: 10 June 2022/Published: 25 October 2022

Vladislav O.Samoylenko

vvsamoylenko@yandex.ru

Andrew V.Pazderin

a.v.pazderin@urfu.ru

Ilya D.Polyakov

polyakovid@ural.so-ups.ru

2096-5117/© 2022 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Andrew V.Pazderin is Sc.D.,professor,head of the Department of Automated electrical systems at Ural Federal University,Yekaterinburg,Russia since 2005.His research interests includes branch flow-based models,electric energy transmission and distribution.

Ilya D.Polyakov is a specialist at dispatch systems of System Operator of the United Power System since 2016.He defended Ph.D.at 2019.His research interests includes dispatch systems and state estimation.

Vladislav O.Samoylenko defended Ph.D.at 2017.Now he is associate professor at the Department of Automated electrical systems at Ural Federal University,Yekaterinburg,Russia.His research interests includes active distribution systems and distributed generation.

(Editor Dawei Wang)