0 Introduction

The security stability control system (SSCS) is used to maintain power balance and frequency/angular stability[1-4].It comprises communication channels and control stations.The former use the fiber-optic channels that are as long as hundreds or even thousands of kilometers;the latter includes multi-layer control stations.The bottom stations connect control resources,such as hydropower[5],pump storage,load shedding [6],energy storage,and converter stations of high-voltage DC (HVDC) [7],and maintain the power balance with pump curtailment,load reduction,and DC modulation.The SSCS can be activated by dynamic parameters or serious events;the low-frequency load shedding belongs to the former.The possible delay can be of several swings of the rotor angle during which the generator outage and blackout can occur.This deteriorates dynamic security of the power systems.Hence,soon after severe events,such as unipolar or bipolar block of ultra HVDC (UHVDC),the SSCS is expected to operate instantaneously against large power shortage and accelerate frequency recovery.The purpose of the SSCS involves providing event-activated protection with respect to large power shortage.Its configuration follows that of power systems,but the SSCS concerns only certain nodes in the main grid.The communication network is critical to the SSCS whereas power flow and stability analysis are required to design the operation rule.They are not essential for evaluating the performance and reliability of the SSCS.

Power system in China is characterized by unbalanced locations of energy source and consumption,necessitating interconnection of multi-regions through the high-voltage,large-capacity,and long-distance AC/DC transmission[8-10].With the tie lines,it is possible to share control resources of the SSCS with different systems;however,this increases the difficulty in designing and evaluating the SSCS.

The existing SSCS typically exhibits a tree structure[11,12],where the upper station controls one or more lower stations.If a station or its upstream channel fails,then all the downstream stations and channels are out of control.Standby stations can be added to the important stations to improve the reliability of the SSCS,which comes at the expense of high construction cost of stations,complex control,and large possibility of maloperation.The loop design of the SSCS can reduce the number of stations and increase the control paths for the control resources.Meanwhile,the loop design in the interconnected power systems realizes the sharing of the control resources.The loops are added to the tree SSCS as opposed to replacing the latter immediately.Given the small amount of data required for communication between stations of the SSCS and wide existence of fiber channels,it is not necessary to build new fiber channels in most cases;hence,the construction cost of fiber channels is not a concern.Meanwhile,the loop design can reduce the number of the stations,which can reduce the cost of the construction of the SSCS.The concept of loop design is proposed in [13].However,the research is not specific.

Loop design with respect to the SSCS is constrained by economic cost,control complexity,and reliability.The existing methods for reliability analysis include the state-space method [14-16],fault tree analysis [17,18],Monte Carlo sampling [19],and complex network [20-22].Furthermore,the reliability of the devices and SSCS are specified in [23]and [24],but the detailed topological model of the SSCS is not included.The control effect of the SSCS is decided not only by the availability of paths,but also by the controllable capacity of the control resources.For the loop design,it is difficult to identify the vulnerable components and estimate their impact on the reliability of the SSCS.

The SSCS maintains security and stable operation of grid based on the controllable capacity of the SSCS.When the controllable capacity of the SSCS is higher than the power shortage,the grid operates in a stable manner.The controllable capacity of the SSCS is uncertain due to the randomness of the controllable capacity of the EXs.As a feasible method,the evidence theory [25,26]divides the fluctuation variables into multiple focal elements,reduces the error of interval algorithm,and avoids calculating the probability distribution of the input data.Furthermore,there have been no studies that apply the evidence theory to the controllable capacity analysis of the SSCS.Based on the evidence theory,the randomness and controllability of EXcontrollable capacity and correlation of control paths of the EXs increase the difficulty of the uncertainty analysis of the controllable capacity of the SSCS.

In this study,bidirectional/loop channels are added to the tree-structure SSCS for the interconnected power systems.The reliability and sensitivity model of the SSCS are quantified considering the availability of the paths and controllable capacity mean of the EXs.Two new indices are proposed to quantify the reliability of loop-designed SSCS.Considering the randomness of the controllable capacity of the EXs,uncertainty analysis of controllable capacity,based on the evidence theory,is proposed to quantify the probability of the SSCS for balancing the active power deficiency of the grid.

The rest of the paper is organized as follows: The loop designed SSCS is presented in Section 1.The reliability and sensitivity models for the loop SSCS are presented in Section 2.The uncertainty analysis of controllable capacity of the SSCS is presented in Section 3.Numerical results are presented in Section 4.Finally,the conclusions of the study are presented in Section 5.

1 Loop design of the SSCS

There are many nodes in an actual power grid,and it is difficult to obtain the actual data of the configuration.Meanwhile,this study focuses on the calculation of the SSCS.An SSCS with tree structure is shown in Fig.1,where S and R denote the stations and resources respectively.The top station S1 connects two middle stationsS2 and S3 and controls six bottom stations and resources.With the outage of station or channel,some resource can be out of service.Hence,the tree structure should be improved.

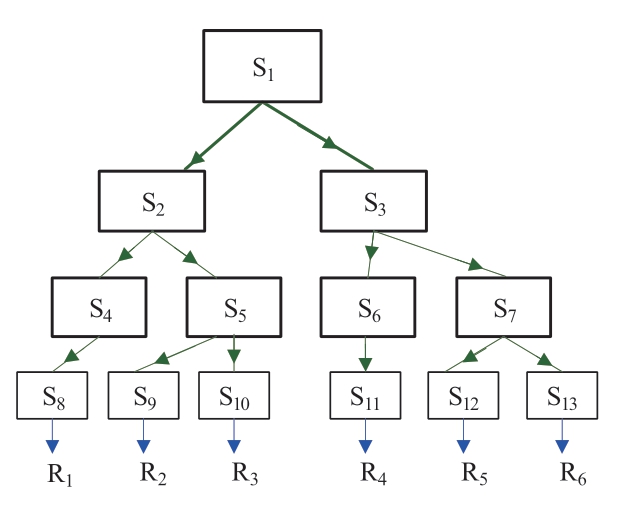
Fig.1 SSSCS with tree structure

A flat designed SSCS is shown in Fig.2.A horizontal channel is added between S6 and S7 for backup.A loop is designed for S2 to control the resources at S8-S10.With the flat design,there are more than one path for each bottom station,hence reliability of the SSCS is improved.

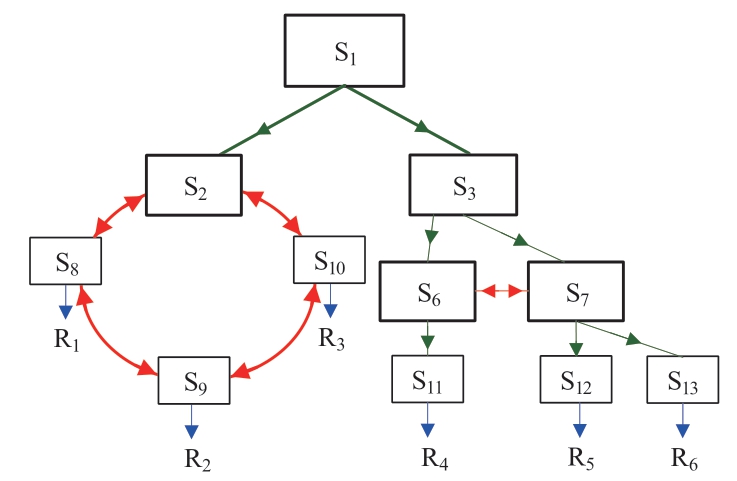
Fig.2 SSCS with partial flat design

The loop design may be further improved,as shown in Fig.3,where S8-S10 are controlled by S2 through the loop,and S11-S13 are controlled by S3.The station number is reduced,and the controllability of the SSCS is improved.

Fig.3 SSCS with loop design

To improve the security and stability operation of the power grid and utilization efficiency of the control resources,the structure of the interconnected power grid is established.Taking power grid of East China as an example,the power grid of Central China,Northwest China,and Southwest China adopt DC support to reduce the load curtailment [27],as shown in the Fig.4.Given the large number of nodes of the power grid in each region and lack of architectural information of the actual power grid,in this study,we use a simplified SSCS model derived from a regional system.

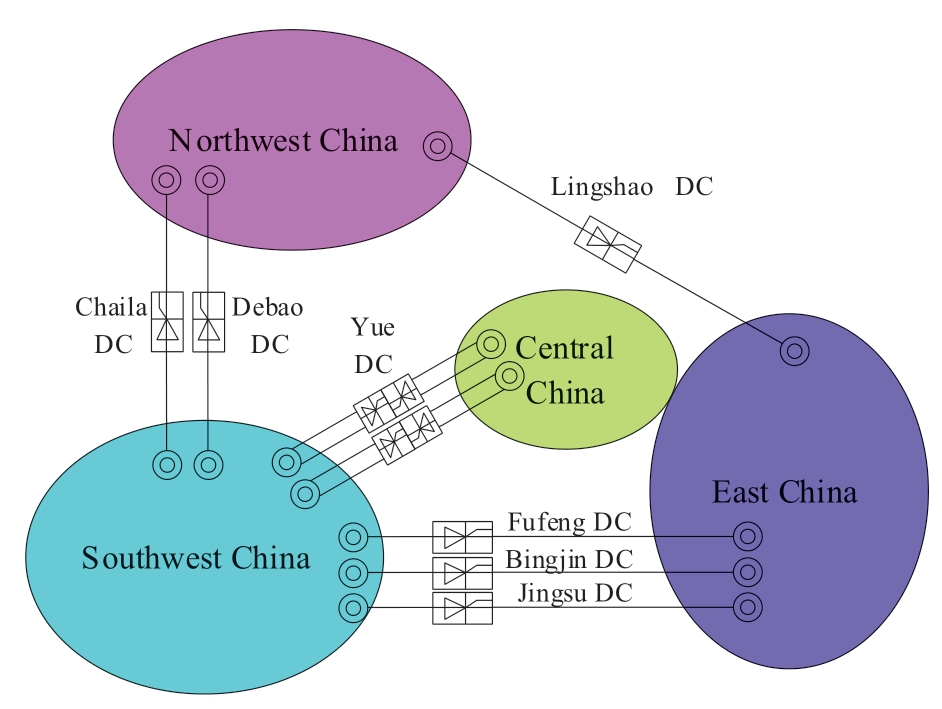
Fig.4 Interconnection of the power systems

For the interconnected power systems,the top stations of three SSCS are connected via a loop as shown in Fig.5.If the active power balance of one system is broken,then it can be supported by other systems.

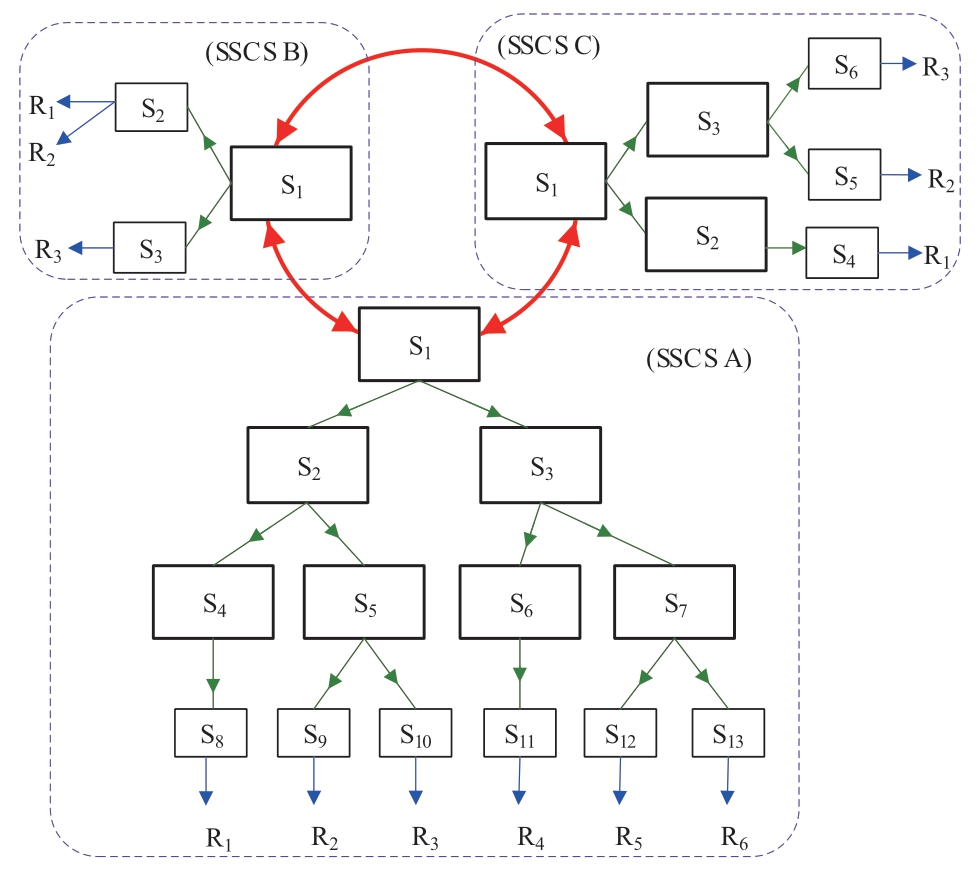
Fig.5 Loop SSCS for interconnected systems

With outage of the top station,the resources connected to it will be lost.Following the idea of standby,doublelayer loop structure among the top stations is applied in Fig.6,where B1 denotes the standby station.When S1 fails,B1 and the standby channel undertake the control task.

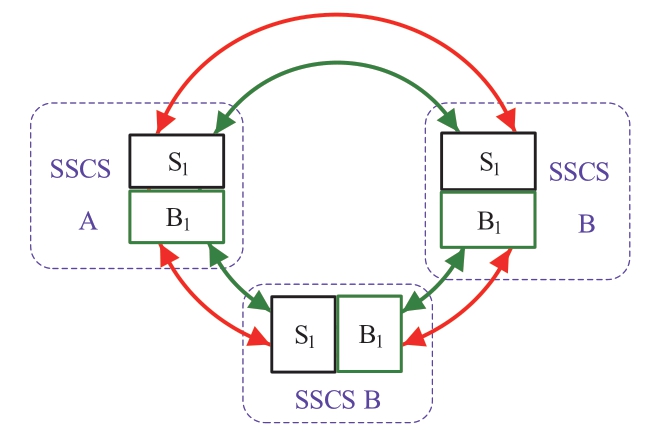
Fig.6 Loop SSCS of interconnected system with standby

In the loop design of the SSCS,the vulnerable stations obtained by the sensitivity analysis are set up as standby stations to improve the controllable capacity of the loop design of the SSCS,and the top stations are usually set up as backup.In the loop SSCS for interconnected systems,the top stations and channels between the top stations are all set as backups.

To implement the aforementioned loop design to the SSCS in actual power systems,more factors should be considered.

(1) When the power system fails due to,for example,blocking of HVDC,it results in the deficiency of the active power and frequency instability in the power grid.As the second line of defense,SSCS is activated immediately to balance the active power when the power failure occurs in the power grid.In this study,the ability of the SSCS to realize the balance of the active power and frequency stability of the power system is evaluated.Besides active power balance and frequency stability,var/voltage can also be controlled by the SSCS.However,the var control is local and not urgent for interconnected systems.Hence,the var/voltage is not examined in this paper.

(2) When changing the flat SSCS to the loop structure,the importance of the station,construction,and maintenance costs should be included.For example,some stations should remain near the central power stations,large generators,or load centers.

(3) Loop design adds control complexity.Hence,application of the loop design to the vulnerable components,which should be decided before loop implementation,is suggested.

2 Reliability and sensitivity models for loop SSCS

2.1 Control path search to SSCS

Identification of the control paths is the basis for reliability analysis of the SSCS.For the loop,as opposed to tree SSCS,it is difficult to find all control paths via inspection.Hence,the topology search is necessary.

By observing the SSCS as a graph,the station is the vertex,and channel is the edge.The adjacency matrix D=[dij]is used to describe the connectivity of the SSCS.If station i has a path to j,then dij = 1,otherwise dij=0.With the stations numbered,Fig.2 is redrawn in Fig.7.

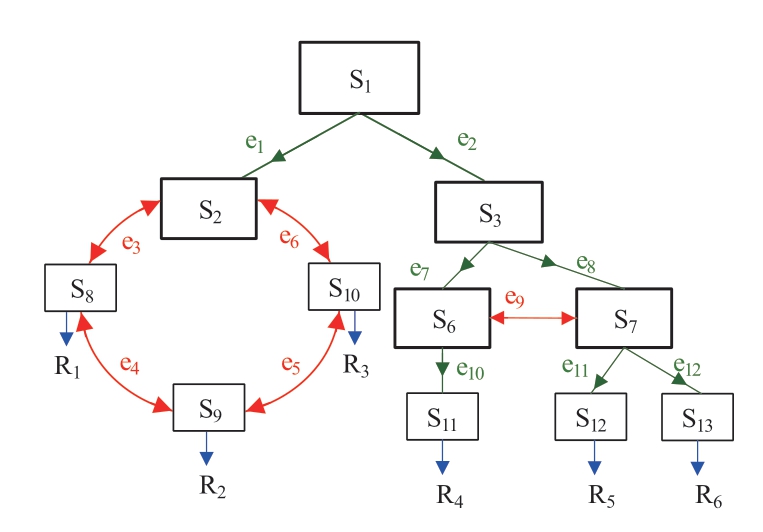
Fig.7 SSCS with stations renumbered

D is found in (1).For the tree SSCS,non-zero elements appear only in the upper triangle.However,for the loop SSCS,they also appear in the lower triangle.With the loop design,there are less stations;hence,the dimension of the adjacent matrix is reduced.All of the control paths of the SSCS are obtained based on D.

2.2 Reliability and sensitivity models to loop SSCS

The reliability of the SSCS can be quantified by its controllability with respect to possible outages and described by two aspects,i.e.,controllable probability and capacity.In this section,the controllable probability and capacity of the SSCS are newly defined to propose two reliability indices.Subsequently,an analytical sensitivity model is proposed to find the vulnerable components and improve the reliability of the loop SSCS.

2.2.1 Station controllability of loop SSCS

The components in the control path are in series.Hence,the path availability apath with n components is the product of the availability of the components,e.g.,ak for the kth component (2),which is similar for the tree and loop SSCS.However,the latter may have more control paths.

The elements associated with the path are stations and channels,and the fiber channel can face the mechanical,optical,and electrical risk,including lighting strike,and the channel availability can be expressed as follows:

where l denotes the length of the channel,and u0channel denotes the unit-length unavailability of the channel.

By combining (2) and (3),apath can be expressed as follows:

where and  denote the availability of  station and  channel,respectively.

The control paths for the same resource are in parallel,and the availability of jth resource is shown in (5),where mj denotes the total path number to jth control resource,and 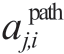denotes ith path availability of jth control resource.

Higher path availability and larger controllable capacity of the control resources yield higher reliability,i.e.,controllability of the SSCS.The controllability to the jth resource Cj is defined as a product of 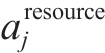 and its controllable capacity Pj of the bottom station as shown in (6).

Pj is related to the operation modes.For example,the HVDC with higher loading has a lower adjustable range;more pump units at pumping state yield higher power.

2.2.2 Reliability index of the loop SSCS

To facilitate the use of numerical quantification system reliability,the reliability index is defined.The reliability of the loop SSCS can be quantified by its controllability.It is the sum of all resources (7),where Nr denotes the total number of control resources.

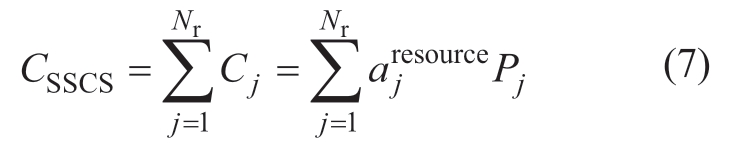
Flat design to the SSCS improves controllability and reduces the number of stations and levels.To describe the desirable effect,ratio αSSCS of CSSCS to the number of the station,i.e., Ns,is defined as follows:

The average associated path number with each station,i.e.,βSSCS,is defined in (9),where Mu denotes an odd number of the associated elements of uth path,and Np denotes the number of paths in the SSCS.

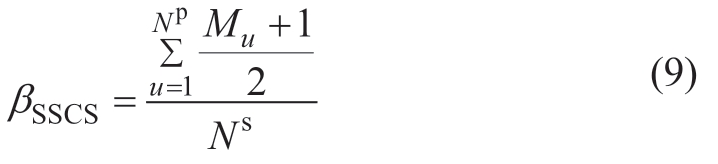
2.2.3 Analytical sensitivity model of loop SSCS

The partial flat structure and loop design of SSCS increase the number and complexity of control paths.Furthermore,it increases the difficulty of finding vulnerable components of the SSCS.Hence,the analytical algorithm for the identification of the vulnerable station of SSCS can be proposed.Additionally,the sensitivity of CSSCS to is calculated in (10).As the sensitivity increases,the impact of outage on SSCS increases.It can increase the maintenance or standby of the station or strengthen the flat design such as double layer loop structure as follows:

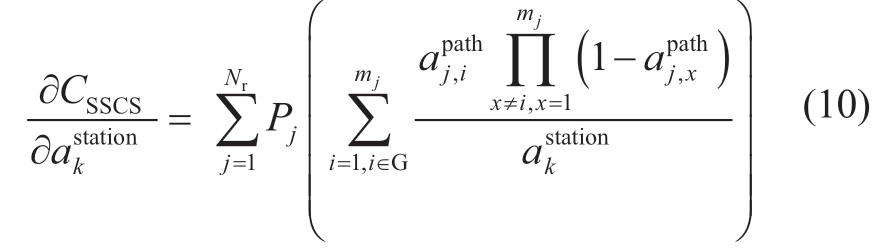
where G denotes a set of control paths containing the desired station,and x denotes the serial number of the control path.

3 Uncertainty analysis of controllable capacity of the SSCS based on evidence theory

The controllable capacity can be random based on the type of EXs.To quantify the controllable capacity of the SSCS in detail,the uncertainty analysis of the controllable capacity of the SSCS is conducted using evidence theory.

3.1 Applications of the evidence theory

Considering random controllable capacity of the Exs,it can be described using evidence theory.The identification frame Q is defined as 2Q,and event A is any subset of 2Q.Furthermore,m(A) is the function of the basic reliability allocation of A [28].A is defined as the focal element,and m is obtained as follows:

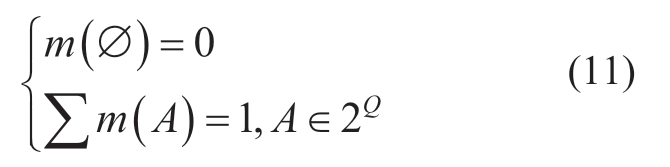
To evaluate the uncertainty of the A,Bel(A) and Pls(A)are defined to represent the minimum probability and maximum probability of A as follows:

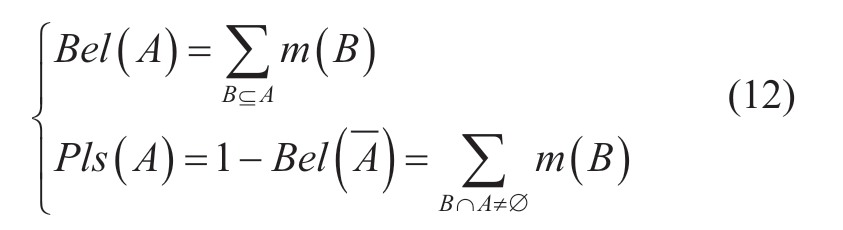
where Bel(A) and Pls(A) are defined as the belief function and likelihood function,respectively,and the probability interval of A is [Bel(A), Pls(A)].

For example,the basic probability assignment (BPA) of the controllable capacity of the new energy i is established as follows:

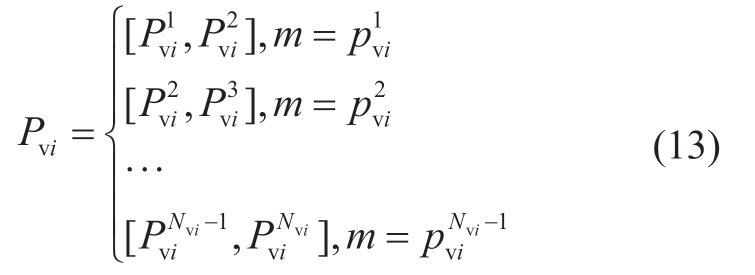
where  is divided into Nvi-1 intervals,and p denotes the probability of P in the current interval.The subscript vi denotes the ith station;

3.2 Uncertainty analysis of the controllable capacity of the SSCS

The controllable capacity of the SSCS is the sum of the controllable capacity of the EXs.Hence,model of the joint probability assignment (JPA) of the EXs is established.

3.2.1 JPA for controllable capacity of the EXs with dependence of the control paths

Based on the detailed topology of the SSCS,it is assumed that the middle station (MS) controls two EXs.There are two situations when EX is out of control:

(1) When MS is out of control,the JPA of the EXs is obtained in (14),and pss,i denotes the controllable probability of MSi.

(2) When SS is controlled,the JPA of the EXs is obtained in (15).Furthermore,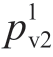 represents the probability that the controllable capacity of station 2 is in the range of

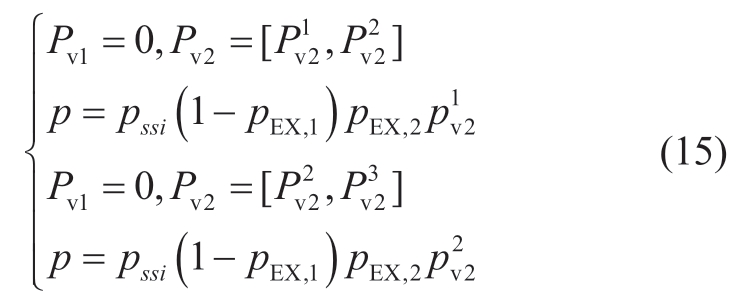
By combining (14) and (15),JPA includes the correlation of the control paths of the EXs obtained as follows:

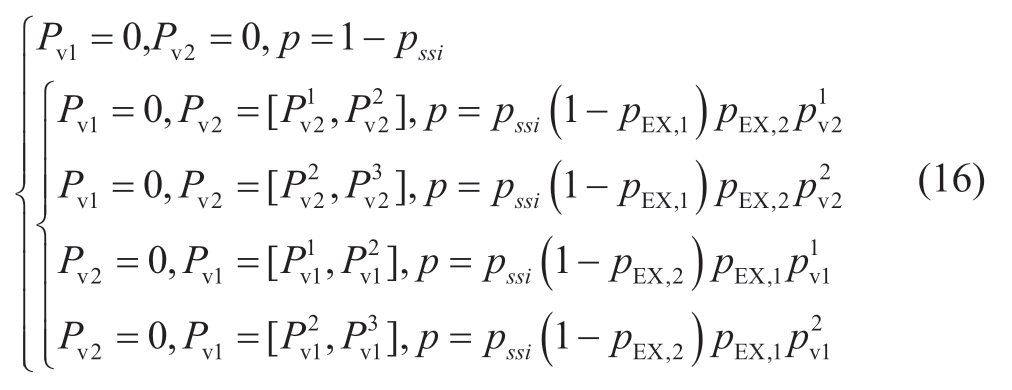
3.2.2 JPA for controllable capacity of the EXs with the independence of the control paths

When the control paths are independent of each other,the controllable capacity of the JPA of the EXs is directly established according to the BPA.

X = [x1,x2,…,xn]is assumed as an n-dimensional uncertain variable.Furthermore,f(x) is an uncertain dependent variable,as shown in (17),and Qi is obtained in (18).Furthermore,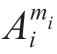 is 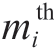 focal element of xi,and Ni denotes the total number of focal elements of xi.

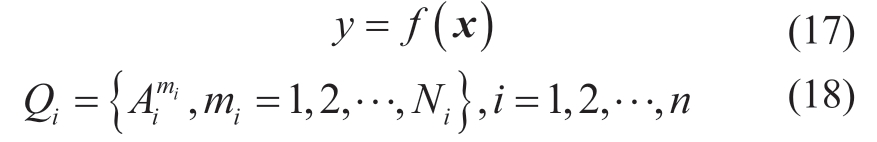
The JPA of x is obtained via a cartesian product,Qx is obtained in (19),and Aj is the focal element of the JPA. N is defined as the number of focal elements as follows:

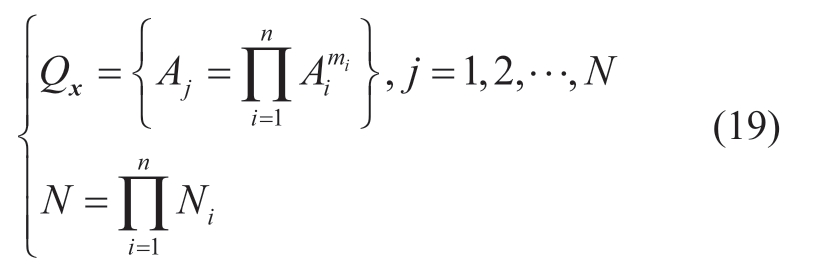
When there is correlation between variables,the cartesian product cannot be used to obtain the JPA directly.It is necessary to correct the JPA among related variables,which has a number of focal elements less than N.Furthermore,as the correlation becomes stronger,the number of focal elements decreases.

The number of EXs of the new energy and cutting load are assumed as x,whereas EXs of the pumping storage and DC are assumed as y.The JPA is established according to(19),where psi and puj are controllable probabilities of the stations,and  denotes the probability that the controllable capacity of pumping storage or cutting load station 1 is in the first interval.

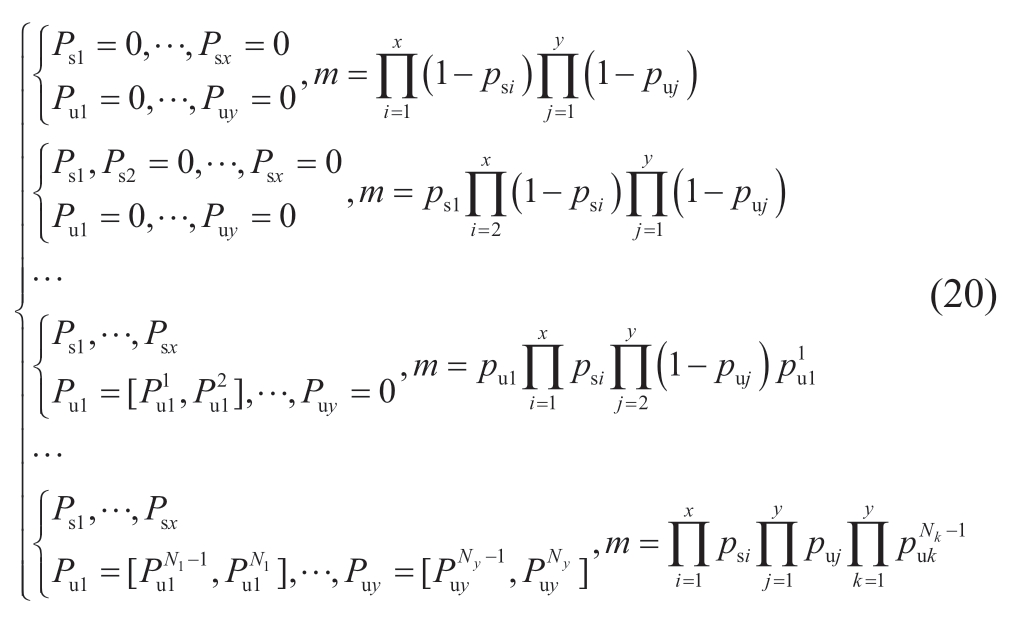
3.3 Analysis of controllable capacity and protection of the SSCS

PSSCS denotes the sum of current controllable capacities of all EXs. PSSCS is defined as the controllable capacity of the SSCS in (21).Furthermore, nW,nL,nC,and nD are defined as the number of EXs of new energy,load cutting,pumping storage,and DC,respectively.

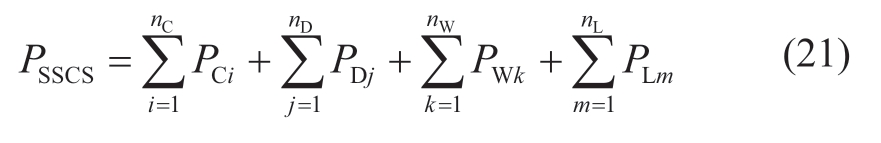
Belief cumulative probability distribution (BCPD) and likelihood cumulative probability distribution (LCPD) of the controllable capacity of the SSCS are obtained according to(12).The minimum and maximum probabilities,wherein the controllable capacity of SSCS is lower than Plost,can be obtained according to the BCPD and LCPD,which are defined as pBCPD(Plost) and pLCPD(Plost),respectively.Hence,the maximum and minimum probabilities that SSCS can balance Plost are obtained in (22) and (23).Furthermore,the flowchart of this study is shown in Fig.8.

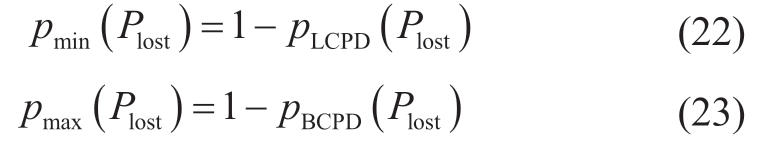
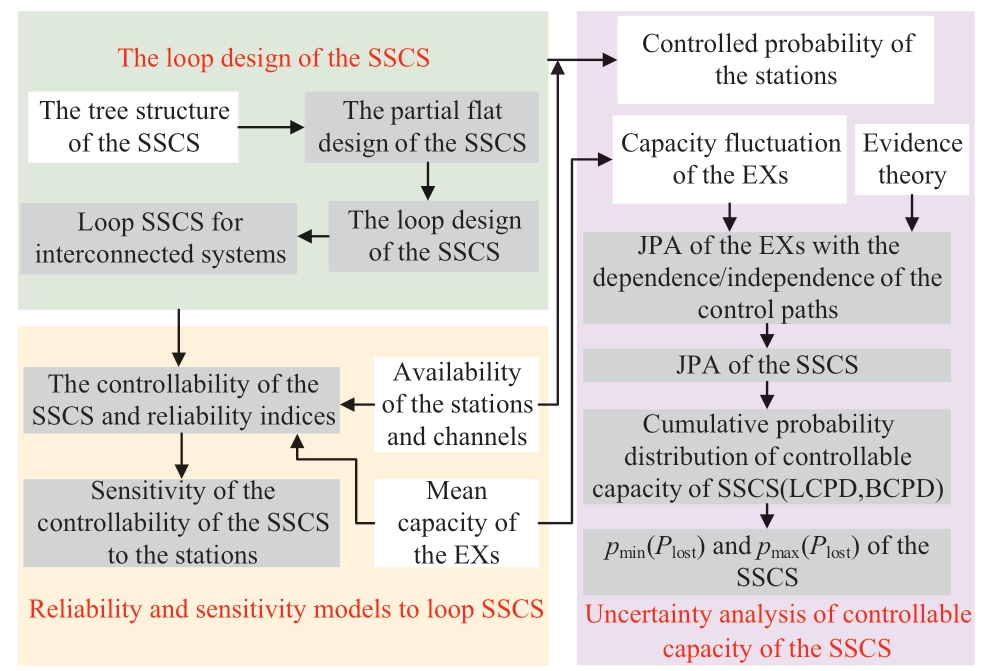
Fig.8 Flowchart of the proposed algorithm

4 Case studies

Station reliability parameters of SSCS are reported in[29],and channel reliability parameters are reported in [30].The mean capacity of control resources in SSCS A (power gird A of the SSCS) are listed in Table 1.

Table 1 Capacity of control resources in SSCS A

4.1 Reliability of SSCS with different structures

As the controllability increases,the reliability of the SSCS increases.Furthermore,Cj under tree structure,partial flat structure,and loop structure are shown in Fig.9.When compared with tree structure,the partial flat structure and loop structure can increase the controllability of the SSCS,and the controllability of SSCS in the loop structure is the best.Additionally,the number of stations and levels of SSCS in the loop structure are reduced.

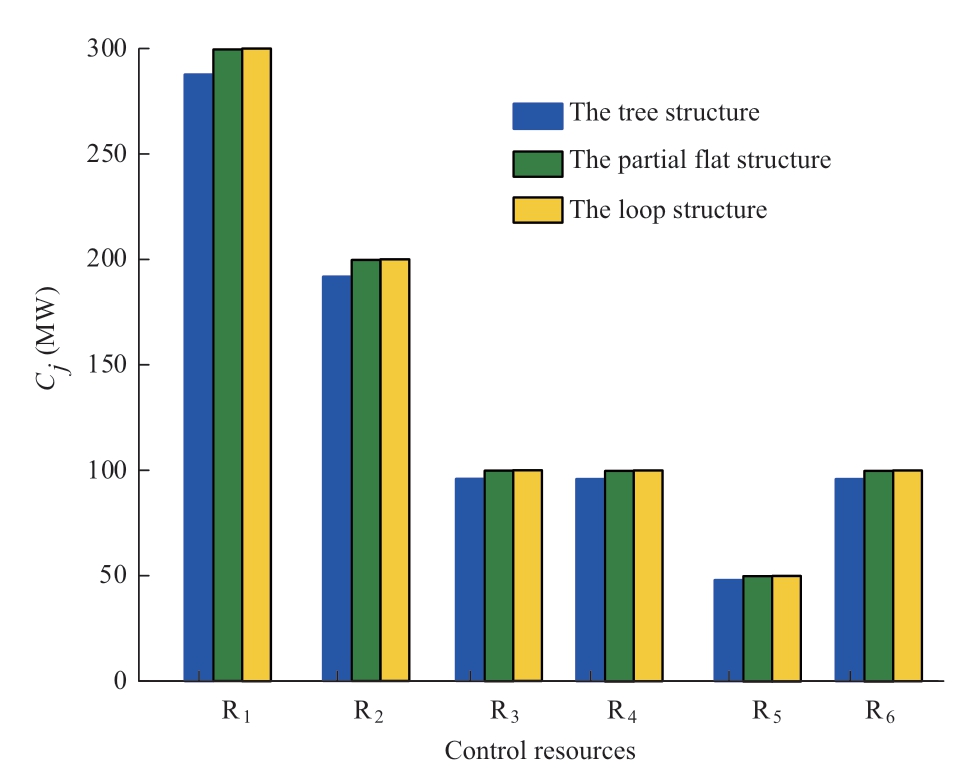
Fig.9 Cj in different structures

The loop structure is more important for regional SSCS interconnection.Moreover,the controllable capacities of SSCS B and C are listed in Table 2.Additionally,CSSCS of the SSCS A,B,and C in the structure of tree,loop interconnection,and double-layer loop interconnection are shown in the Fig.10.

Table 2 Capacity of control resources in SSCS B and C

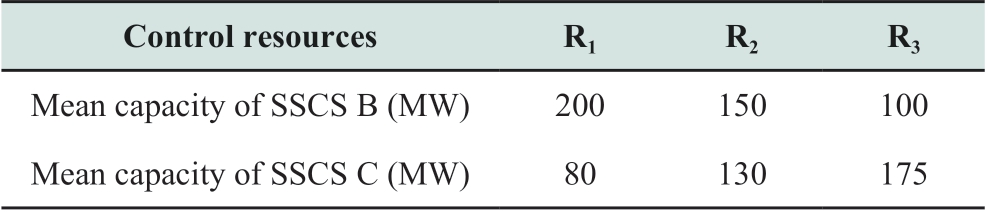
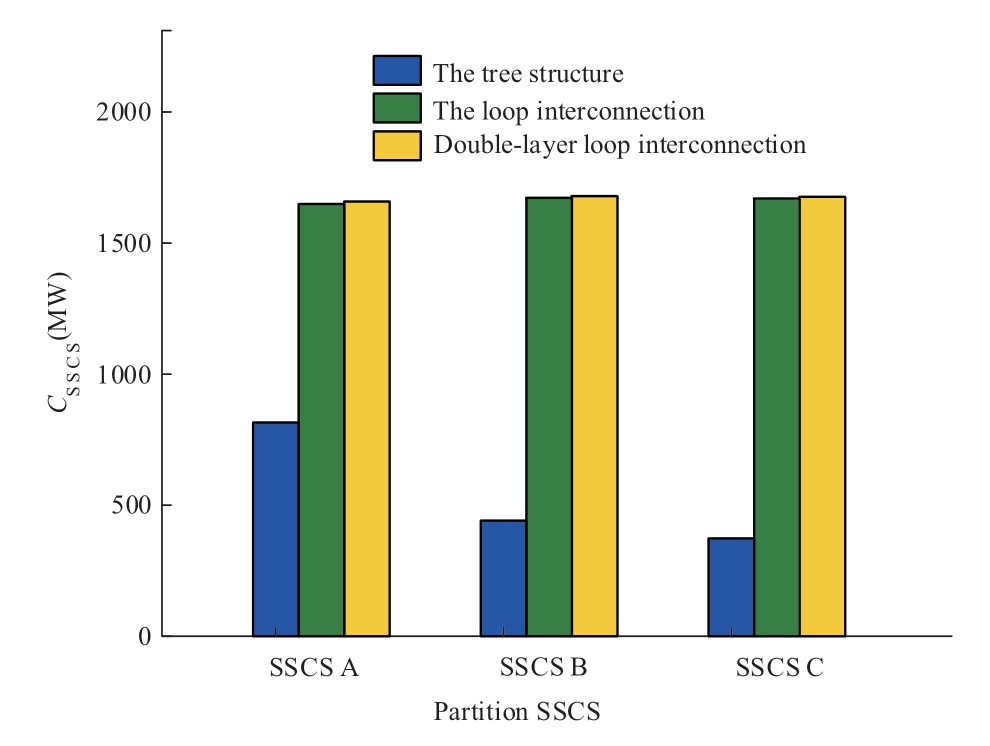
Fig.10 CSSCS in different structures

When compared with the tree structure of SSCS, CSSCS can be increased in the structure of interconnected SSCS.Furthermore,CSSCS of SSCS C exhibits the most evident improvement effect because its own controllability is small.Additionally,after interconnection of SSCS,the reinforcement controllability of SSCS of A and B is high.Compared with the loop interconnection,CSSCS under the double-layer loop interconnection is improved because the top stations and channels in each region can have standby station/channel,which increases the reliability of the regional interconnection structure.

4.2 Reliability indices calculation of the SSCS

For SSCS A,αSSCS and βSSCS of different structures are shown in Table 3.When Compared with the tree structure,αSSCS in the partial flat structure and loop structure increases,and αSSCS in the loop structure is the highest because the loop structure reduces the number and level of stations,increases the channels,and strengthens the controllability of SSCS.

Table 3 αSSCS and βSSCS of different structures

When compared with tree structure,partial flat structure and loop structure improve βSSCS.Furthermore,βSSCS in loop structure is approximately 6.5 times the βSSCS under tree structure and 4 times the βSSCS under partial flat structure.It indicates that SSCS exhibits the highest utilization rate of stations under the loop structure.

4.3 Sensitivity calculation of the SSCS

The sensitivity of SSCS to station availability is shown in Fig.11.In different structures,the sensitivity of CSSCS to each station exhibits the same trend,whereas the sensitivity of partial flat structure and loop structure are smaller than that of the tree structure.As the level of the station increases,the sensitivity of CSSCS of the station increases,i.e.,as the importance of the station increases,the top station exhibits the highest sensitivity in SSCS A.Among stations of the same level,as the controllable capacity of the station increases,the sensitivity of CSSCS to the station increases.Therefore,the top station exhibits the highest sensitivity in the SSCS A.Additionally,the flat structure can reduce the sensitivity of CSSCS to each station.

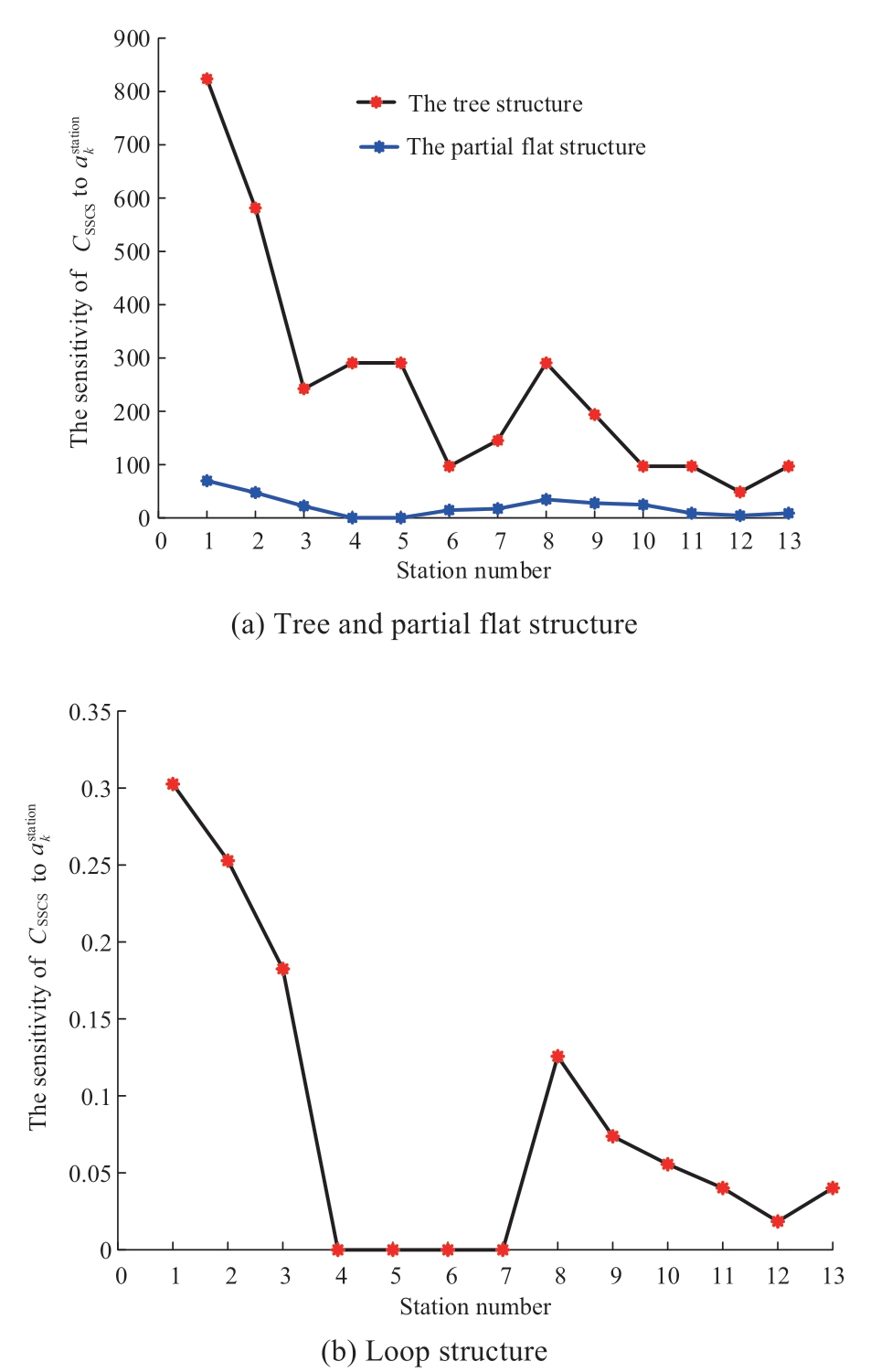
Fig.11 Sensitivity of CSSCS to akstation

S1 and S8 are set up as the standby stations based on the sensitivity analysis in the tree structure and loop design of the SSCS.After the standby stations are created,Cj in the tree structure and loop design are shown in Fig.12,andCj is improved by adding the vulnerable stations.When compared with the loop SSCS,Cj of the tree SSCS can be improved more evidently because the reliability of the tree structure is lower and an increase in vulnerable stations has a more evident effect on improving the reliability of SSCS.

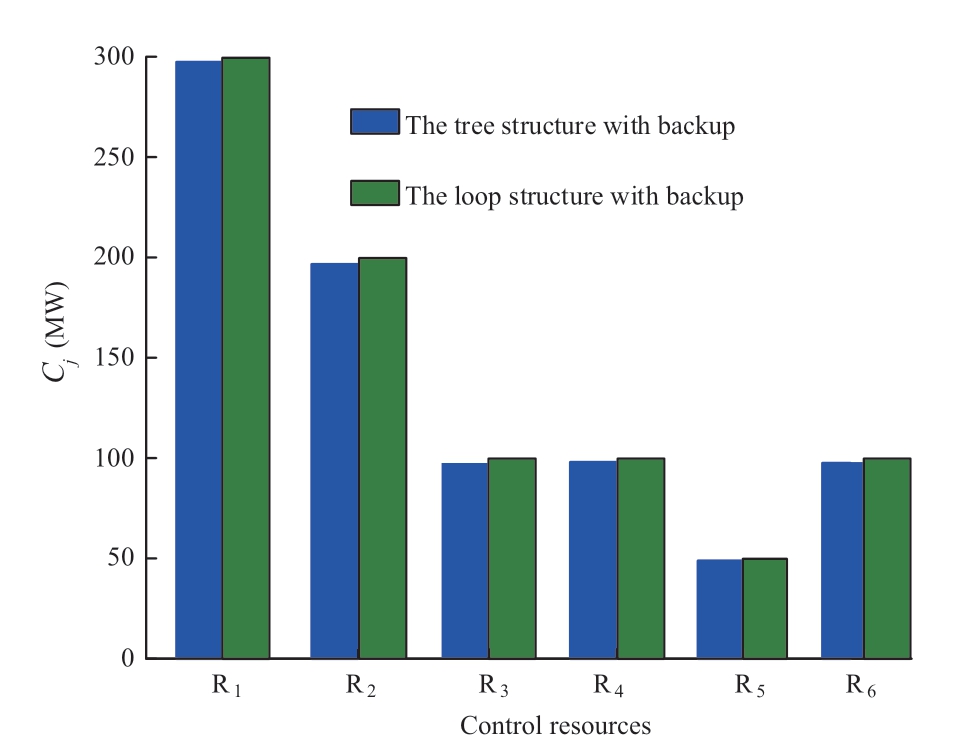
Fig.12 Cj in different structures with backup

To determine the vulnerable channels in the loop structure,the sensitivity of CSSCS to each channel is shown in Fig.13.The sensitivity of SSCS to channels 1,2,and 3 is higher because many connected control paths are present,and their failures affect control characteristics of R1-R6.Furthermore,the sensitivity of CSSCS to channels 9 and 10 is low because channels 9 and 10 mainly affect the control of R4-R6,and the controllable capacity of R4-R6 is relatively small.

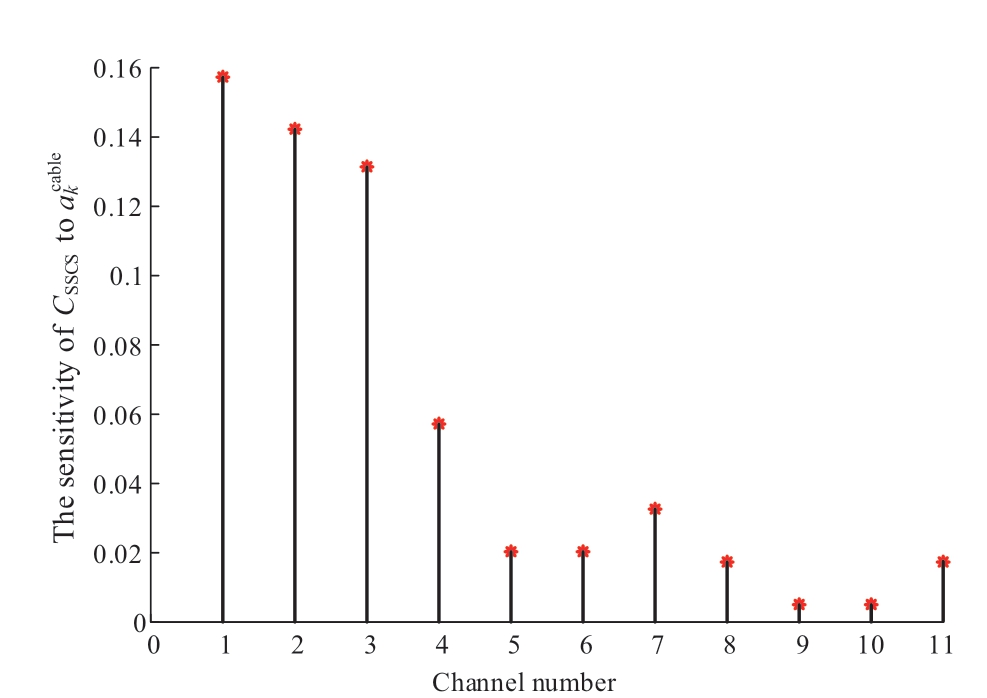
Fig.13 Sensitivity of CSSCS to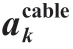 

4.4 Uncertainty analysis of the controllable capacity of the SSCS

The SSCS shown in Fig.3 is considered as an example;the BPA of R1 is constructed in Table 4.The fluctuation model of the controllable capacity of the SSCS is shown in Fig.14.The controllable capacity of the SSCS fluctuates in the range of 400-1200 MW.When the power shortage of the grid is less than 400 MW,SSCS is able to maintain the security and stable operation of the grid.When the power shortage is higher than 400 MW,the probability of SSCS maintaining the system operation is quantified by the controllable capacity fluctuation model of the SSCS.When the power shortage exceeds 1200 MW,the protection of the SSCS fails.When Plost is assumed as 800 MW,pmin and pmax are calculated as 0.5109 and 0.7923,respectively,according to BCPD and LCPD.The interval in which the SSCS balances the power deficiency of the grid is [0.5109,0.7923].

Table 4 BPA of R1

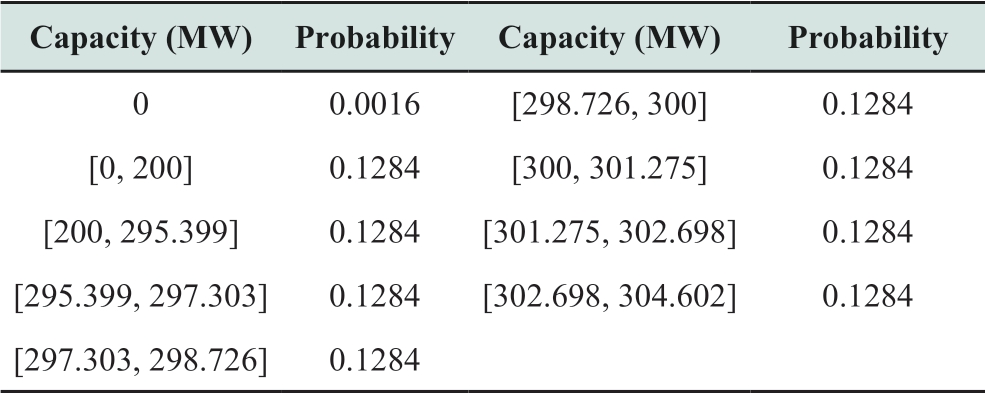
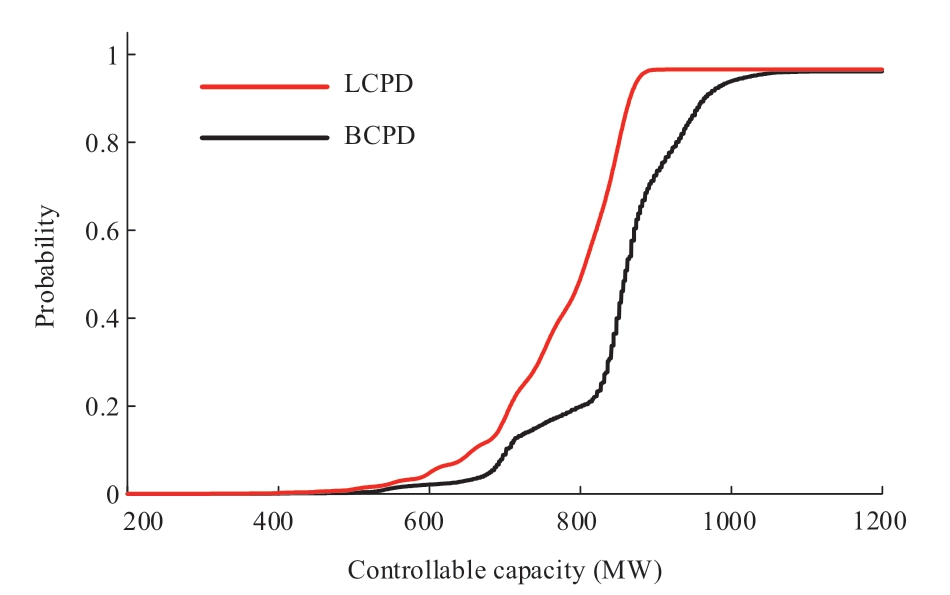
Fig.14 Controllable capacity of the SSCS

5 Conclusion

In this study,the flat structure and regional interconnection structure of SSCS are proposed.Furthermore,the reliability and evaluation indices of the loop SSCS are quantified,and the sensitivity model of loop structure of the SSCS is proposed to identify the vulnerable stations and channels.The uncertainty analysis of the controllable capacity based on the evidence theory is proposed to quantify the probability of the SSCS in balancing the active power deficiency of the grid with the fluctuation of the controllable capacity of EXs.

The conclusions of the study are as follows:

(1) The loop structure reduces the number of stations,increases the control path of SSCS,and improves the utilization of stations and channels.When compared with tree structure,partial flat structure and loop structure can increase the reliability of the SSCS,and the loop structure of the SSCS exhibits the best reliability.

(2) When compared with the flat design of SSCS in a certain region,regional interconnection of the SSCS exhibits a better effect on improving the reliability of SSCS.

(3) When more paths are associated with a station or channel and the controllable capacity of the path is higher,the station or channel becomes weaker.Hence,these vulnerable components should be given priority in the loop design of SSCS.

(4) The range of the controllable capacity of the SSCS is obtained based on the evidence theory,which is helpful in describing the capability of the SSCS with respect to the power shortage.When the power deficiency of the grid is less than the lower limit of the range,the active power of the grid is balanced by the SSCS.

The reliability and sensitivity are considered in the loop design of SSCS.However,the actual loop design of SSCS should also consider the control difficulty,fiber cost,and other factors,which need further examination.

Acknowledgements

This study was supported by Science and Technology Project of SGCC “Research on Flat Architecture and Implementation Technology of Security and Stability Control System in Ultra Large Power Grid”(52170221000U).

Declaration of Competing Interest

The authors declare that there is no conflict of interest.

References

[1]Dong X,Luo J,Cui X,et al.(2018) Whole control time and its constitution of security and stability control system.Automation of Electric Power Systems,42(5): 163-168

[2]Spanias C,Aristidou P,Michaelides M,et al.(2021) A passivitybased framework for stability analysis and control including power network dynamics.IEEE Systems Journal,15(4): 5000-5010

[3]Wang Q,Bo Z,Zhao Y,et al.(2019) Interconnected wide area protection and control for power grid security.CSEE Journal of Power and Energy Systems,5(2): 206-214

[4]Wang S,Xu T,Chen G,et al.(2019) Practicability assessment method of duty strategy for security and stability control system in power grid.Automation of Electric Power Systems,43(24):126-133

[5]Zhou Y,Liu F,Chang H,et al.(2020) Accurate control strategies of hydropower group for frequency emergency control.Automation of Electric Power Systems,44(11): 121-126

[6]Lu Q,Ren Z,Xu K,et al.(2016) Optimal generator tripping scheme based on implicit enumeration method.Automation of Electric Power Systems,40(5): 139-144

[7]He J,Chen K,Li M,et al.(2021) Active injection protection scheme for flexible HVDC grids based on amplitude of input impedance.Global Energy Interconnection,4(6): 532-542

[8]Li B,Qin X (2018) Discussion on the framework of smart and coordinated control system for security and stability of modern AC/DC hybrid power grid.Global Energy Interconnection,1(1):275-282

[9]Dong X,Singh C,Jia H,et al.(2019) Reliability analysis of security and stability control system with typical structure in power grids.IEEE Power and Energy Society General Meeting,Atlanta,GA,USA,1-5

[10]Yu W,Xue Y,Luo J,et al.(2016) An UHV grid security and stability defense system: considering the risk of power system communication.IEEE Transactions on Smart Grid,7(1): 491-500

[11]Shen F,Zhang W,Zhang H,et al.(2017) Design and practice of management system for safety and stability control devices adapted to interconnected mode of power grid dispatching and control.Automation of Electric Power Systems,41(23): 143-149

[12]Huang T,Deng L,Xue W,et al.(2015) Communication network structure and topology analysis of internet of things for power transmission and transformation equipment.High Voltage Engineering,41(12): 3922-3928

[13]Xin P,Yan P,Xiao Z,et al.(2013) Application of communication network technology in new generation smart substation.Electric Power Construction,34(7): 17-23

[14]Liu D,Tang S,Hu X,et al.(2018) The comparison and study of fundamental algorithms in power system simulation.Global Energy Interconnection,1(2): 137-143

[15]He R,Xie H,Deng J,et al.(2020) Reliability modeling and assessment of cyber space in cyber-physical power systems.IEEE Transactions on Smart Grid,11(5): 3763-3773

[16]Bai G,Liu T,Zhang Y,et al.(2021) An improved method for reliability evaluation of two-terminal multistate networks based on state space decomposition.IEEE Transactions on Reliability,70(3): 1084-1095

[17]Chen Y,Tian Z,Roberts C,et al.(2021) Reliability and life evaluation of a DC traction power supply system considering load characteristics.IEEE Transactions on Transportation Electrification,7(3): 958-968

[18]Gjorgiev B,Antenucci A,Volkanovski A,et al.(2020) An FTA method for the unavailability of supply in gas networks supported by physical models.IEEE Transactions on Reliability,69(2):740-753

[19]Zhu J,Qiu W,Sun N,et al.(2021) Reliability analysis of security and stability control architecture based on sequential Monte Carlo method.Automation of Electric Power Systems,45(15): 21-27

[20]Dai J,Huang K,Liu Y,et al.(2021) Global reconstruction of complex network topology via structured compressive sensing.IEEE Systems Journal,15(2): 1959-1969

[21]Zhu S,Zhou J,Chen G,et al.(2021) A new method for topology identification of complex dynamical networks.IEEE Transactions on Cybernetics,51(4): 2224-2231

[22]Vega C J,Suarez O J,Sanchez E N,et al.(2020) Trajectory tracking on uncertain complex networks via NN-based inverse optimal pinning control.IEEE Transactions on Neural Networks and Learning Systems,31(3): 854-864

[23]Zhao L,Wang M,Ni M,et al.(2016) Analysis of hardware system’s reliability of security and stability control device.Power System Protection and Control,44(13): 67-73

[24]Yan Y,Sun N,Zhang N,et al.(2021) Evaluation of unavailability risk of the security and stability control system of power systems based on optimization of the preventive maintenance period.Power System Protection and Control,49(17): 139-146

[25]Pan Y,Zhang L,Li Z,et al.(2020) Improved fuzzy bayesian network-based risk analysis with interval-valued fuzzy sets and D-S evidence theory.IEEE Transactions on Fuzzy Systems,28(9): 2063-2077

[26]Jiao Z,Gong H,Wang Y (2018) A D-S evidence theory-based relay protection system hidden failures detection method in smart grid.IEEE Transactions on Smart Grid,9(3): 2118-2126

[27]Li Z,Fang Y,Huang H,et al.(2020) Coordination control of cross-region DC frequency control and emergency power support in system protection.Automation of Electric Power Systems,44(22): 31-36

[28]Guo X,Gong R,Bao H (2019) Modeling of wind speed uncertainty based on evidence theory.Electric Power Automation Equipment,39(1): 78-83

[29]Yan Y,Sun N,Zhang N,et al.(2021) Evaluation of unavailability risk of the security and stability control system of power systems based on optimization of the preventive maintenance period.Power System Protection and Control,49(17): 139-146

[30]Zhao L,Wang M,Ni M,et al.(2016) Analysis of hardware system’s reliability of security and stability control device.Power System Protection and Control,44(13): 67-73

Received: 24 April 2022/Accepted: 28 July 2022/Published: 25 October 2022

Shenghu Li

shenghuli@hfut.edu.cn

Huimin Zhou

2020110380 @mail.hfut.edu.cn

Yunsong Yan

yanyunsong@sgepri.sgcc.com.cn

Wei Han

haiwei@ha.sgcc.com.cn

Jianfeng Ren

renjianfeng@sgepri.sgcc.com.cn

2096-5117/© 2022 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Shenghu Li received his B.Sc.,M.Sc.,and Ph.D.at Hefei University of Technology,Hefei,China,in 1995,2000,and 2003 respectively.He is a professor with Hefei University of Technology,Hefei,China,since 2008.His research interests include wind power system analysis and control,UHVDC/FACTS transmission,power system planning,and reliability.

Huimin Zhou received her B.Sc.at Anhui University,Hefei,China,in 2020.She is pursuing an M.Sc.at Hefei University of Technology,Hefei,China.Her research interests include reliability analysis of UHVDC and SSCS.

Yunsong Yan received his B.Sc.and M.Sc.at Nanjing University of Science and Technology,Nanjing,China,in 2003 and 2005,respectively.Currently,he is a senior engineer with NARI Group Corporation(State Grid Electric Power Research Institute),Nanjing,China.His research interests include power system stability control and analysis.

Wei Han is a senior engineer (professor level)with Electric Power Research Institute of State Grid Henan Electric Power Company,Zhengzhou,China.His research interests include power system relay protection and stability.

Jianfeng Ren received his B.Sc.from Nanjing University of Science and Technology,Nanjing,China,in 2003,and an M.Sc.from Nanjing Automation Research Institute,Nanjing,China,in 2006.Currently,he is a senior engineer with NARI Group Corporation(State Grid Electric Power Research Institute),Nanjing,China.His research interests include power system stability,control,and analysis.

(Editor Yajun Zou)