0 Introduction

Scheduling (forecasting) power system operations is a primary task in operational supervisory control.The scheduling results are used for organizing the repairs of power system equipment rationally,supplying the required volumes of energy resources to power plants,providing a reliable electricity supply to households and enterprises of other sectors of the economy,and adhering to the standards of permissible environmental impacts.For example,in Russia,scheduling is performed for short-term (a day),medium-term (a month,quarter,year),and long-term (up to 5 years) periods.The scheduling period is divided into time intervals (days,months,and quarters).

The introduction of large-scale market relations in the electric power industry,changes in the structure of market participants,and improvements in the rules of operational supervisory control have refined scheduling problem statements,changes in decision-making criteria,employed methods,and algorithms [1].New problem statements should consider the following.

-Medium-term electricity consumption has price elasticity [2,3].System operators should model the behavior of market prices more carefully and consider the possible responses of consumers to the changes.

-Most suppliers seek to maximize their profits [4].The minimum total cost of power generation in a power system is not the primary goal.

-Individual power plants are a part of generating companies (GenCos) that pursue corporate goals.Scheduling should not consider the individual interests of power plants but their behavior within the generating company.

-Individual suppliers can influence market prices.Electricity market exhibits imperfect competition [5].The scheduling problem should consider the oligopolistic nature of the wholesale market,in which a supplier must consider the possible behaviors of other suppliers while scheduling outputs.

-Most input data used in scheduling are random in nature [6].The statement of a medium-term scheduling problem should be consistent with the available information on the random data.

Constraints imposed in each time interval must be considered while estimating the medium-term scheduling period.It includes the possibility of changing the power generated in each or several intervals and constraints on the amount of electricity produced and consumption of energy resources.

Modeling the interests of suppliers (generating companies) in electricity markets involves game-theoretic models,including equilibrium models,which are widely used to study the strategic interactions between participants[7-9].The most widely used models include Cournot equilibrium and linear supply function equilibrium (LSFE)models.In our study,we used the LSFE approach to solve the scheduling problem.Suppliers’ actions vary from interval to interval.Several options are available for choosing the LSFE parameters for suppliers who affect the obtained equilibria [10].One price interval without demand uncertainty inevitably has several equilibrium states when all supply function parameters are varied.

Competition modeling consists of two levels.At the first level,suppliers maximize their profits.At the second level,prices are determined based on the maximization of public welfare [11].This is known as the Stackelberg problem.Such bi-level problems are inherently non-convex,and no algorithm can guarantee optimal solutions.Therefore,it is necessary to employ an approximate solution.One possible approach is to solve the problem iteratively using penalty parameters until equilibrium conditions are satisfied approximately.For example,in [11],the authors developed an LSFE-based model in which each strategic firm was assumed to manipulate the parameters of the supply functions.Our study also employed a two-level statement,which was formulated as a quadratic mathematical programming problem with equilibrium constraints (MPEC).We chose only one parameter to model the variation in the linear function of a company’s supply to the market.This allowed us to eliminate the non-convexity and multiplicity of the equilibria obtained [4,12].In this case,first-order optimality conditions (Karush-Kuhn-Tucker (KKT)conditions) were incorporated into the problem solved by each firm for maximum social welfare (or the market operator problem).This implied that the companies would consider how their actions affect nodal prices.

The present study aims to modify the statement of the problem of medium-term power system scheduling to be more consistent with the conditions of the Russian wholesale market.We model the market,as described above,by using a leader-follower model with several leaders.The presented approach factors in both the desire of electricity suppliers to maximize profits and the random nature of the data and the desire of electricity suppliers to maximize profits.We consider scheduling in several time intervals according to the crossinterval constraints and revised pricing of electricity at the generation and consumption nodes.The innovation lies in modeling the imperfectly competitive relations simultaneously for several intervals,given the multiplicity and duration of interactions.The presented medium-term model generates a result different from the results of the models that consider competition in separate unrelated intervals.We proposed methods for solving the optimization problem and illustrated the scheduling results through a simplified case study of a realworld power system.

In the first part of the article,we discuss and formulate a statement regarding the problem.In the second part,we focus on possible approaches for finding an equilibrium of supplier interests.One approach involves composing and solving a complementary system of equalities and inequalities.This system consists of the optimality conditions of two problems: maximizing the profits of each supplier and increasing the total effect for suppliers and consumers (maximizing public welfare).In the second approach,an iterative method is used to reach equilibrium.The third part of the study is devoted to evaluating the capabilities of the developed model mathematically.In addition,we studied the effects of cross-interval constraints and different types of market competitions (perfect and oligopolistic) on the calculation results.

1 A mathematical model for medium-term scheduling of power system operation

The electrical network and nodal prices must be represented accurately for scheduling the operating states.Usually,complete nonlinear models of load flow are used when the current normal operating states of the power system are considered in operational supervisory control.These models incorporate the active and reactive power balances at the network nodes.Such models consider the values of voltage magnitudes and phases,transformer transformation ratios,and generated and consumed reactive power.

In medium-term scheduling for the distant future,providing relatively accurate specifications of such data for complete models is difficult.The use of nonlinear load flow models for a large number of time intervals in complex power systems can be too time-consuming.

Hence,simplified load flow modeling can be used for scheduling future operating states.In simplified models,only active electricity dispatch is considered.It is assumed that the distribution of the reactive flows is known.In simplified models,electricity losses are most often represented as a percentage of the active electricity flow in the lines.In this study,we considered the simplified model of the steady states of the power system.

The proposed scheduling model captures the following properties of the modern wholesale electricity markets.

-Electricity suppliers (GenCos) are interested in maximizing their profits for the entire scheduling period.

-Scheduling the operating states helps in achieving an equilibrium of interests between suppliers and consumers.In the obtained operating state,GenCos and consumers do not seek to change the estimated values of ,

-Cross-interval constraints imposed on the parameters of the operating states in the several time intervals under consideration affect the levels of local market prices,increase the dimensionality of the optimization problem,and significantly increase the computational cost incurred in solving the problem.

-The process of scheduling involves determining the values of nodal electricity prices with which the change in electricity demand 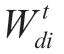in each time interval t can be modelled.Consumer demand in the medium term is mostly elastic [4,5].

-The random nature of electricity generated and consumed is considered,which depends on unforeseen changes in the conditions of the power system operation in the time intervals concerned.

The main problem of medium-term scheduling in a market environment is as follows: the profits Sf of the generating companies using TPPs must be maximized for the entire scheduling period.

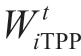where is the revenue of the company f from the sale of the electricity ≥0 at the prices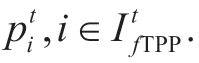 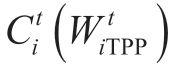is a function of the cost of electricity produced at the node i in the interval t, is the amount of electricity generated.In our model,only companies with thermal power plants were considered to earn maximum profits.Other suppliers of electricity generated from natural renewable resources,such as hydroelectric power plants,are price takers and do not pursue the goal of maximizing profits.

The maximum of function (1) is subject to powerflow parameter constraints,which provides the following equations.

Power balances at the nodes of the power system

Constraints on counter electricity flows in the same link.

Constraints on the amount of electricity generated at generating nodes.

Constraints on the amount of stored electric energy

Constraints on the electricity flow in the links

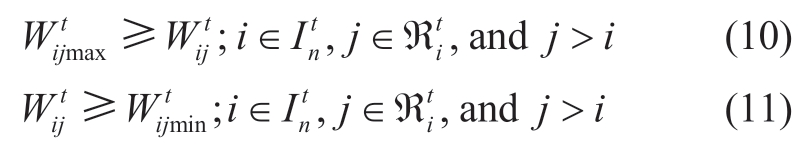
Constraints on the amount of electricity consumed at the nodes

Constraints (2)-(12) were considered for all intervals t= 1,…,T .

A difficulty in medium-term scheduling is the simultaneous consideration of several time intervals.The optimization problem involves cross-interval constraints relating the values of generated and consumed electricity,volumes of reserves,and consumption of energy resources at power plants.

In addition,reliable information regarding the powersystem operation conditions during upcoming time intervals is unavailable.In addition to unforeseen shortages of power plant equipment and power grids for operation,changes in the prices a consumer bids for electricity purchased from the market introduce uncertainty in operating conditions.In time intervals remote from the time of scheduling,the values of the consumed electricity  can be represented by random values It is difficult to predict the amounts of solar and wind energy,inflows,and quantities of water stored in HPP reservoirs for several months.Therefore,these values are often considered random.For example,the water inflows and volumes of stored water in a hydroelectric power plant are denoted by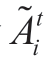and 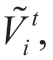respectively;i ∈ IHPP.

This study considers the following cross-interval constraints:Constraints on water consumption in HPPs in the interval t

Constraints on the amount of water stored in HPP reservoirs in the interval t

Constraints on water reserves in HPP reservoirs at the end of the interval t

Constraints on the amount of water consumed over M intervals

Constraints on the amount of electricity generated by a TPP,over M intervals

Constraints on the amount of electricity generated by a HPP,over M intervals

Constraints on the amount of electricity generated using natural renewable sources,,over M intervals

Constraints on the amount of stored electric energy,,over M intervals

Constraints (13)-(20) were added to constraints (2)-(12) in the problem statement.The system of equalities and inequalities (2)-(20) models the steady state of the power system.The variables of interest in the problem (1) subject to constraints (2)-(20) are the values of generated electric energy  stored electric energy demand for electricity electricity flows  in the links of the power system equivalent circuit,and the nodal pricesin all intervals t= 1,…,T.The values of the variables of interest were assumed to remain positive and unchanged during the time interval t.

Each node in the system has power plants owned by a single GenCo.Simultaneously,a single GenCo can include the capacities of several nodes.In addition,we assumed that there was no collusion between suppliers (GenCos) and did not consider the corporate behavior within industrial groups.

Notably,suppliers must rely on nodal prices when solving the profit maximization problem (1)-(20).In addition,the variables dual to the supply and demand balance constraints at node (2) in the problems (1)-(20) do not correspond to the marginal prices of electricity in the power system in question.These prices are determined by solving the auxiliary problem of maximizing the total effect(public welfare) on suppliers and consumers.

The auxiliary problem is a social welfare maximization problem solved by the market operator and its objective function is

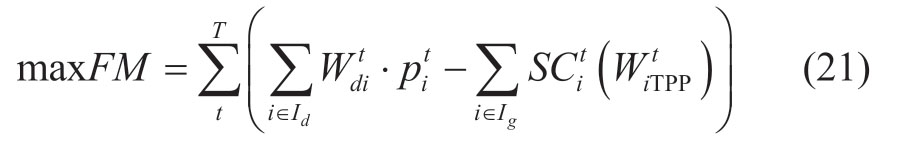
This is solved for all the time intervals under the constraints (2)-(20).One of the solutions to the auxiliary problem (21),(2)-(20) is the nodal price which coincides with the variables λit dual to the balance constraints (2). is the supply function submitted to the market operator by the supplier.In this case,it has a linear form and is based on the company’s cost functionThe auxiliary problems (21) and (2)-(20)are solved using the method applied for determining the equilibrium hourly prices at the nodes of power systems,which is used by the commercial operator of the Russian wholesale market [13].This is a bi-level problem that can be formulated using Stackelberg game theory.In this formulation,the upper level is described by the actions of the “leader” who has information regarding the behavior rules of the lower-level participants defined as the“follower.” In our problem,the “leaders” are the electricity suppliers who determine their behavior strategy based on the actions of the market operator.The scheduling problem has a stochastic nature because its solution considers random values for the inflows and amounts of stored water in HPP reservoirs,energy generated using renewable resources,and the demand for electricity.The statement considered assumes that all random variables have a finite number of possible realizations in the interval t.Problems (1),(21),and (2)-(20) were solved for each possible realization of the random variable considered.Subsequently,the expected value of the profits gained by each supplier was determined,based on which the decision on scheduling the operation for several time intervals ahead was made.

In summary,it should be noted that medium-term scheduling involves simultaneously solving the main problem (1),(2)-(20) and auxiliary problem (21),(2)-(20) with respect to the nodal prices pi t.In addition,it involves the determination of variables  andat the nodes with generation capacities,electricity consumption and electricity flows in the links in the intervals t ∈T.

2 Methods for solving the problem of medium-term scheduling in the wholesale electricity market environment

To solve the medium-term scheduling problem under the given stochastic information,we used an approach in which problems (1),(21),and (2)-(20) were stated in the form of complementary conditions,including KKT inequalities and equalities [14,15].Optimality conditions were established for each realization of the random variables considered.The values of the variables providing the maximum profits to the generating companies were searched in the set of solutions of this complementary problem [7,11,16,17].This technique is called mathematical programming with equilibrium constraints (MPEC) or equilibrium programming with equilibrium constraints (EPEC);the latter is a variant of the former.Similar statements for scheduling within a single period without dividing the period into intervals under stochastic demand for electricity and heat or stochastic generation from renewable sources were considered in[4,5,18,19].

The KKT conditions for auxiliary problems (21) and (2)-(20) are derived as shown.The conditions were formulated for all possible realizations of the random variables.The linear form of an inverse demand function,which includes the demand for stored electricity Wtis,in each time interval t and at each node i ∈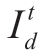is shown as follows.

Let the cost functions of electricity produced in a TPP for each supplier has a quadratic form.

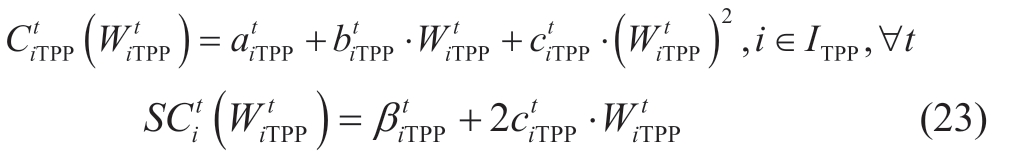
where  ;i ∈I TPP is the supply function variable,which is determined by the supplier while solving the main profit maximization problem (1).

The objective function (21) of the auxiliary problem,given in (22),is of the form

where the first term in parentheses is the demand at node i multiplied by the price (inverse demand).The objective function is concave with respect to the variables Thus,the problem has a unique solution [15]to the accuracy of the parameters of company’s supply functions 

Let ;i ∈ Int ,∀t be the variables dual to equality constraints (2).Let,∀t ∈T be the variables dual to the inequality constraints (3)-(20).The KKT optimality conditions [11]for auxiliary problems (21) and (2)-(20) are a mixed system of equalities and inequalities:

Solving the system (24)-(42) yields the nodal pricesat each node i ∈ Int in the time intervals t ∈ T for each possible realization of random variables and variable parameters of the supplier  These prices (in this case,linear functions of ) would be used by a supplier f to solve problem (1) to maximize their total profits for the entire planning period subject to (41).

To solve problem (1) subject to the constraints (24)-(42)the system (24)-(42) must be augmented with first-order conditions of function (1) for f ∈GK with respect to the variables 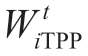and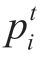at the nodes i ∈ ITPP in the intervals t∈T for each possible realization of random conditions.

However,this problem is difficult;firstly,the profit function of the generating company (1) is nonlinear.This function has a bilinear term: the revenue from the sale of electricity Secondly,the dimensionalities and computational costs of such problems is too high [4].

A possible approach for solving the problem of mediumterm scheduling is to find an equilibrium of supplier interests in an iterative manner [20,21].The iterative solution generates a system of KKT conditions for the main and auxiliary problems (1),(21),and (2)-(20).Further,at each iteration,one (but not all) supplier solves the problem of maximizing its own profits (1),treating the output of the other players as fixed.In the present case,this was an MPEC problem.Subsequently,the amount of electricity WfTPP of the f-th supplier was fixed.In the next iteration,given the known value of the electricity generated by other suppliers,another company maximizes its profits by solving the MPEC problem already formulated for this company.The procedure is repeated until all suppliers and consumers reach a state of equilibrium,wherein no one has any incentive to change the amount of electricity unilaterally.The number of iterations in a calculation cycle is equal to the number of suppliers.

Solving the scheduling problem using the iterative method with respect to stochastic conditions involves the following steps.Some possible realizations of all random variables are chosen for all intervals,t ∈T .The initial solution,which serves as the starting point for the algorithm,is determined from the solution of the auxiliary problem (21) and (2)-(20).Next,the joint problems (1),(21),and (2)-(20) are solved for all intervals t ∈T using the iterative method.The realization of the random variables obtained subsequently is then chosen.At the end of the iteration procedure,the expected value of each supplier’s profits is determined based on calculated for all possible realizations of the random variables.

Theoretically,the equilibrium state described above is not always unique [7,20].However,one can expect to find the equilibrium state for a wide range of specifications of real-world power systems using the described iterative approach [11].This is demonstrated below.

3 Numerical example to illustrate capabilities of the mathematical model

In this section,a power system that represents a simplified configuration of the equivalent circuit of a realworld power system is presented.There are 15 nodes in the circuit (nine nodes are electricity suppliers and 12 nodes consume electricity).The results of modeling the equilibrium state in the electric power market are presented.The random nature of amount of water reserves and inflows in reservoirs and their interrelation in time intervals within one scheduling period were considered.The results of the operating state scheduling obtained with respect to the maximum public welfare in the electricity market were compared with the results of the scheduling under imperfect competition.When imperfect competition was ignored,solving the extended auxiliary problem alone was sufficient to calculate the prices and amount of electricity.

Modeling imperfect competition involves calculating an equilibrium state in which each supplier seeks to maximize his or her profits.One can infer the possible market power of a supplier by comparing perfect and imperfect competition,that is,the ability of the supplier to gain additional profit by inflating prices relative to costs.To solve this problem,an iterative procedure was applied,in which the MPEC problem (1) (24)-(42) was solved sequentially for each supplier in all time intervals simultaneously.

3.1 Input information

Figure 1 shows the circuit of the power system considered in the case study.The scheduling period consisted ofthreetimeintervals: t1,t 2 ,and t3.Thermal and hydroelectricpowerplantswere the suppliersinthe system.

Fig.1 The circuit of the power system considered in the case study

Nodes 1,2,6,11,13,and 14 contain thermal power plants whose variable costs of electricity production follow the conditions shown below for all time intervals.

C1(W1TPP)=50W1TPP+0.2(W1TPP)2,

C2(W2TPP)=31W2TPP+0.2(W2TPP)2,

C6(W6TPP)=52.5W6TPP+0.25(W6TPP)2,

C11(W11TPP)=45W11TPP+0.16(W11TPP)2,

C13(W13TPP)=17W13TPP+0.5(W13TPP)2,

C14(W14TPP)=22.8W14TPP+0.5(W14TPP)2,

Suppliers’ cost functions were set based on the real costs of generating companies.

Nodes 8,9,and 10 represent the HPPs.The variable costs of HPPs were assumed to be zero.

Table A1 in the Appendix lists the limits of the amount of electricity set for all suppliers in the time intervals in question.

Table A2 in the Appendix lists the limits of electricity flows in some links and the percentage of electricity losses.In the remaining links,the losses as a percentage of amount of transmitted electricity are as follows: Δ 24=7.2%,Δ 34 =7%,Δ 56 =6.1%,Δ 67 =9.3%,Δ 78 =6%,Δ 69 =9.1%,Δ 610 =4%,Δ1 011 =9.2%,Δ1 112 =7.1%,Δ1 213 =7.2%,Δ 1215 =9.2%,and Δ 1415 =9.3%.

Table A3 in the Appendix lists the demand functions for the power system nodes.These differed depending on the time interval.Demand functions were set based on the assumption that consumers respond to price changes with an elasticity coefficient of approximately 0.15 [2].Representation of demand in terms of elasticity allows embedding consumers with self-generation into the model.In this case,their response to changes in the prices of the centralized grid will be correlated with the prices of their generation.

3.2 Modeling of cross-interval constraints

For medium-term scheduling,integral constraints that relate the parameters of the operating states at multiple time intervals play a significant role.If the power system under consideration contains HPPs,the integral constraints can be set for the total amount of water consumption 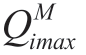for several time intervals M or for the entire planning period T ,i ∈I HPP.The water consumption amounts are related to the random volumes of water  accumulated at the beginning of each interval t and to the inflow 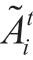 into the reservoir during interval t∈T.We chose the realization of the random variable  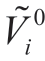at the beginning of the first period.

In addition to constraint (16),we considered constraints(17) and (18) on the total electricity generation at the nodes with HPPs (8,9,and 10) over intervals t1,t 2 ,and t 3.

For example,the cross-interval constraints (18) are shown as follows.

where i=8,9,10.

in (43) was determined by considering the head and permissible water consumption values in the HPP sites.

3.3 Results of modeling.Medium-term scheduling with respect to maximum public welfare and cross-interval constraints

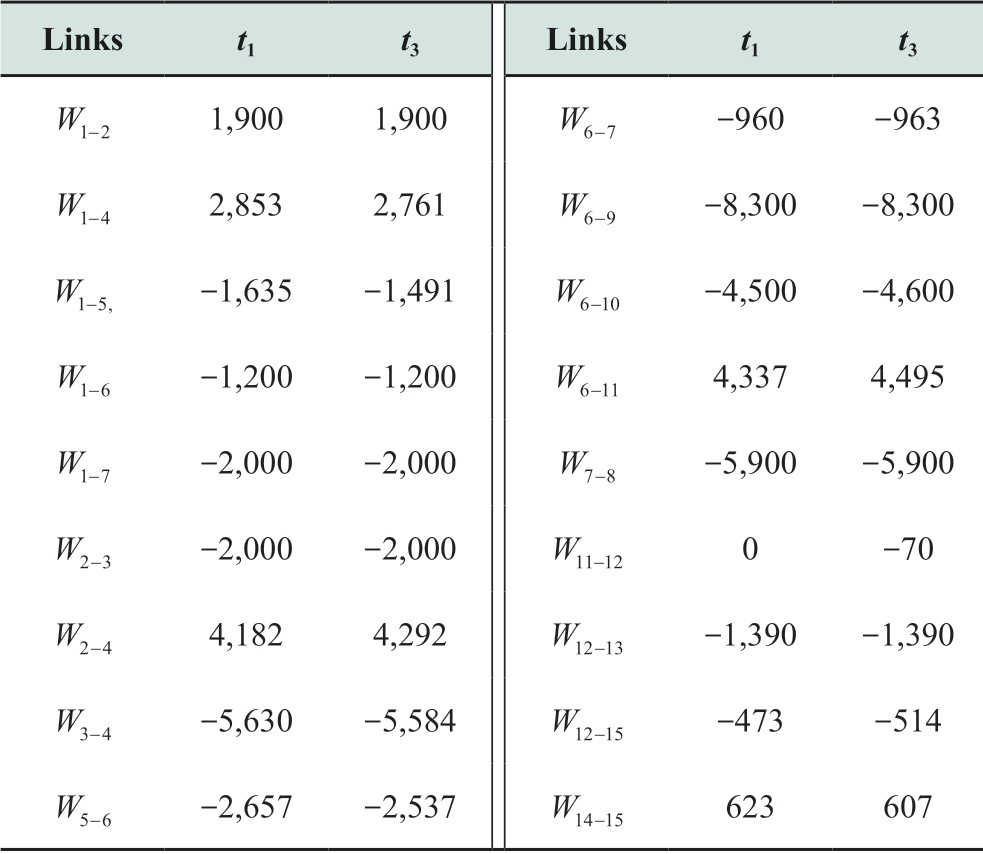
Tables 1 and 2 present the results of calculating the equilibrium of interests between electricity suppliers and consumers with respect to maximum public welfare (21)and constraints (2)-(20).The calculation was performed for a single realization of random variables representing water reserves and inflows in reservoirs and the demand for electricity  in intervals t1,t 2 ,and t 3.The data from Tables A1-A3 in the Appendix were used as the input information for the calculation.In Table 2,the flow in the forward direction along the link is indicated by a positive value and that in the reverse direction by a negative value.

Table 1 Values of the variables of interest at the nodes when scheduling is according to maximum public welfare

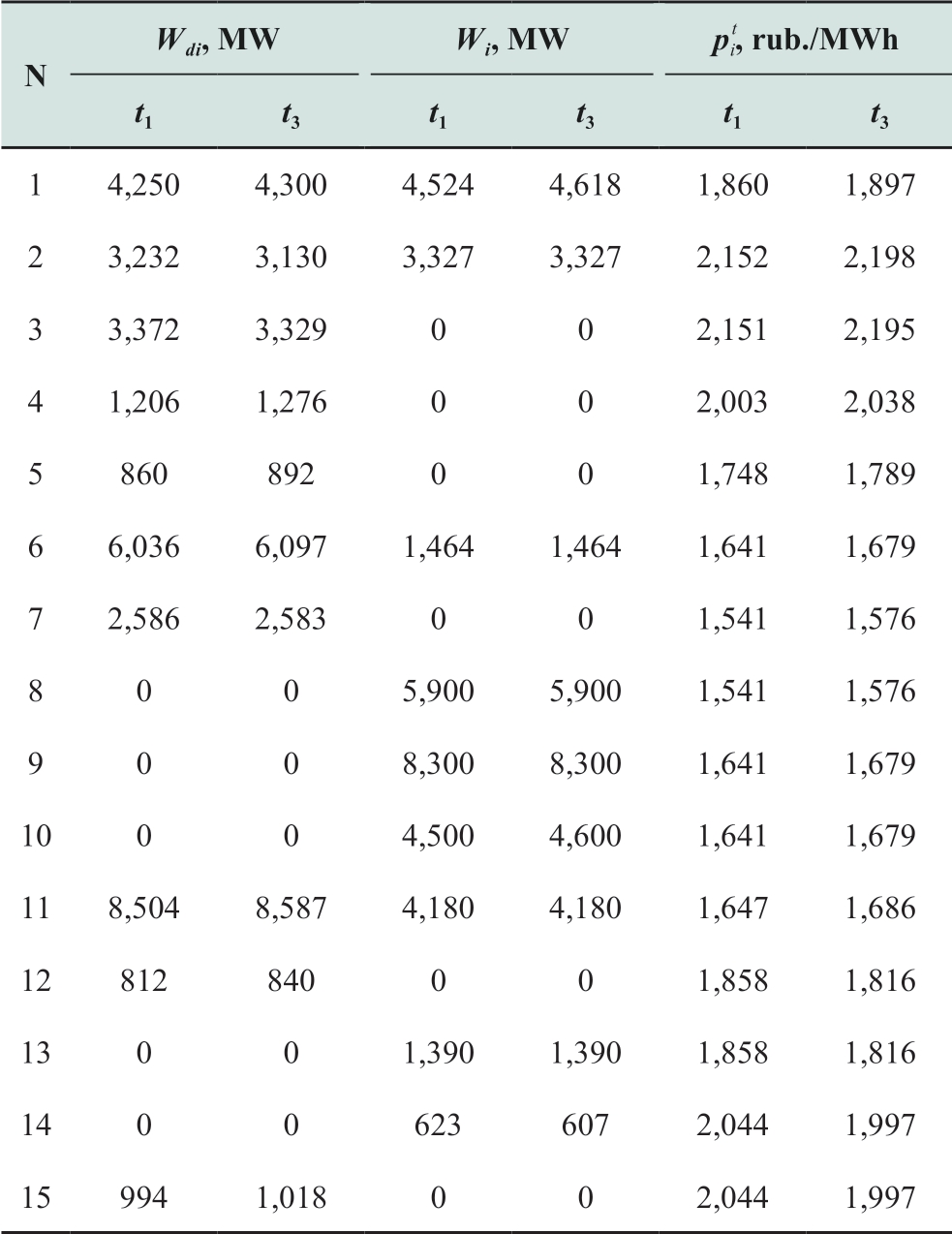
Table 2 Values of electricity flows between the nodes of the system when scheduling according to the criterion of maximum public welfare,MWh

3.4 Results of modeling.Medium-term scheduling in an imperfectly competitive market,where each supplier maximizes their profits with cross-interval constraints factored in

This paragraph presents the results of modeling compared to the maximum welfare modeling results discussed in the previous paragraph.Changes in electricity consumption and generation are shown in Figures 2 and 3.An iterative procedure is used for calculations.When considering several realizations of random variables for loads at consumer nodes,generated electricity amount,values of electricity flows and nodal prices,we determined expected values characterizing their average values under the considered possible states of random variables.

Figure 2 shows how much higher is the electricity consumption in the case of the welfare maximum criterion compared to that in the case of imperfect competition,where each generating company maximizes its profit.At the same time,in the case of imperfect competition,electricity generation goes down (Fig.3),while profits(Table 3) and prices (Fig.6) grow.Table 3 shows the values of generating companies’ profits for a single realization of random values of demand,water reserves and inflows to reservoirs.In addition,the expected values of profits in multiple simulations of random parameters are given.For comparison,we present the results of scheduling for two statements of the problem: when maximizing public welfare(problem (21),(2)-(20)) and when modeling imperfect competition (problem (1),(21),(2)-(20))

Table 3 Profits of generating companies,thousand rub.(WM-welfare maximization (16),(2)-(15),IC-Imperfect competition (1)-(16))

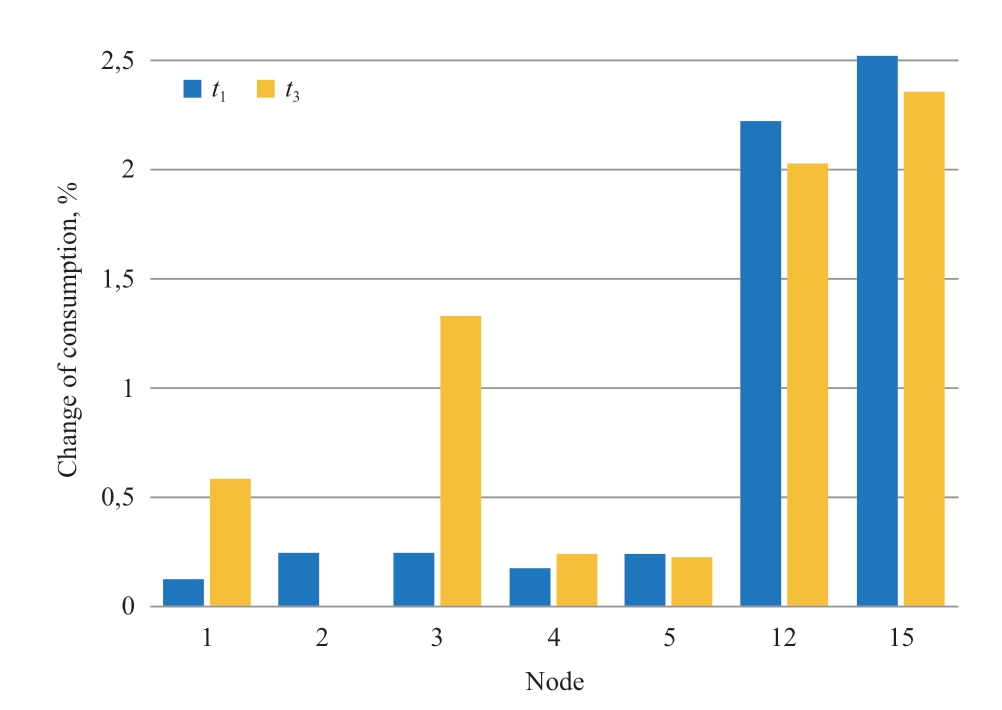
Fig.2 Change in the electricity consumption at several nodes in the case of social welfare maximization compared to the case of imperfect competition

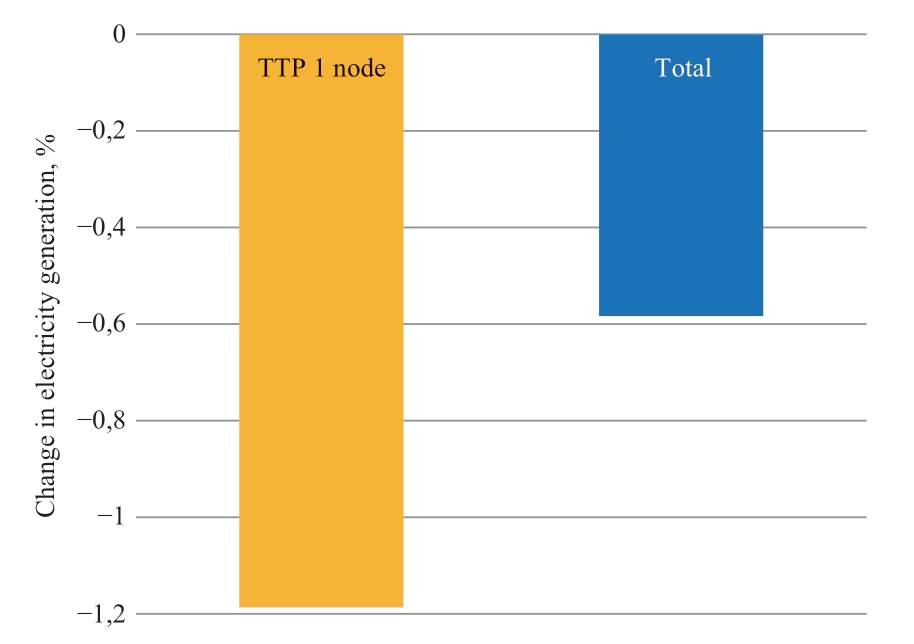
Fig.3 Change in electricity generation at TPPs at node 1 and in total for the system in the case of social welfare maximization compared to the case of imperfect competition

Figure 4 shows the alteration in profits of suppliers when the criterion of maximum social welfare changes to the criterion of profit maximization.Options with and without cross-interval constraints are presented.In our example,following these constraints,the supplier at node 6 with cheap generation reduces the output,thereby raising prices in the whole system and increasing the profits of other participants.

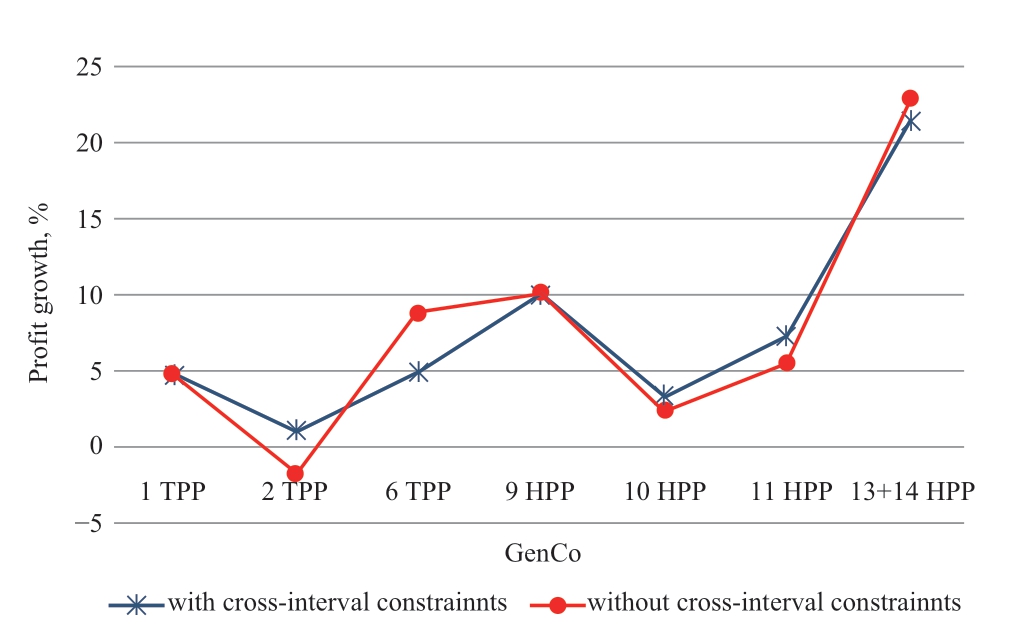
Fig.4 Increase in the profit of suppliers when switching to profit maximization with and without cross-interval constraints

Numerical modeling of different statements of the problem has shown that:

-The network constraints lead to different nodal prices(Fig.5).At the same time,in the case of social welfare maximization,the price at the consumption nodes is determined from the inverse demand function,and the price at the generation nodes is equal to the marginal cost.

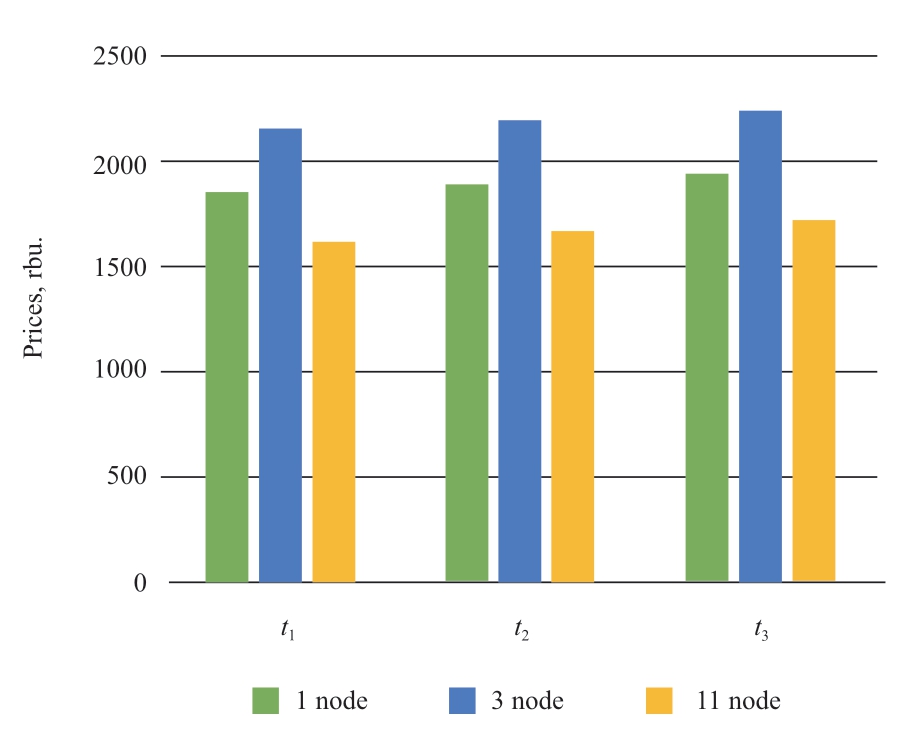
Fig.5 Prices at several nodes of the power system for the case of social welfare maximization

-Under imperfect competition,suppliers can raise nodal electricity prices (Fig.6) in contrast to the case of search for the maximum public welfare.This is because scheduling involves finding an equilibrium of suppliers’ interests.In the example considered,due to oligopolistic phenomena in the market,suppliers can raise prices up to 5% on average,and at some nodes-up to 13% (Fig.6).Accordingly,the suppliers’ profits,in this case,are higher than in the case of public welfare maximization (Table 3).In this example,suppliers’ profits increase on average from 1.5% to 3%.Consideration of various properties of competition is important in the medium-term scheduling of real-world power systems;

Table A1 Limits of electricity generated by suppliers

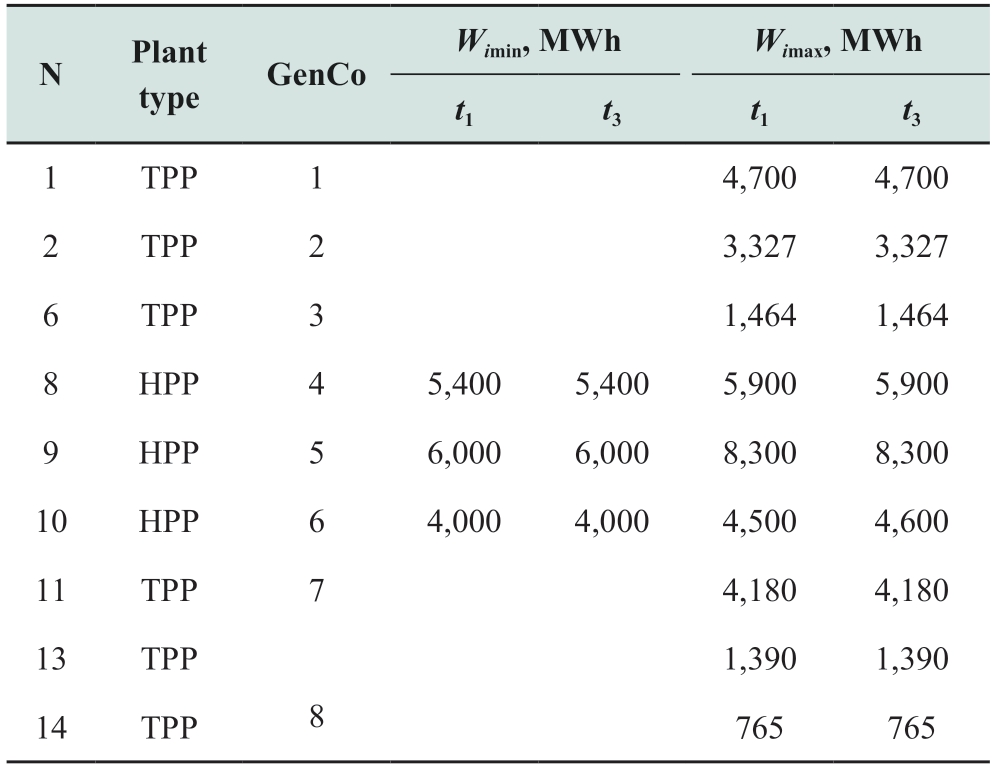
Table A2 Percentage of losses due to power flows and limit values of electricity flows in links,MWh

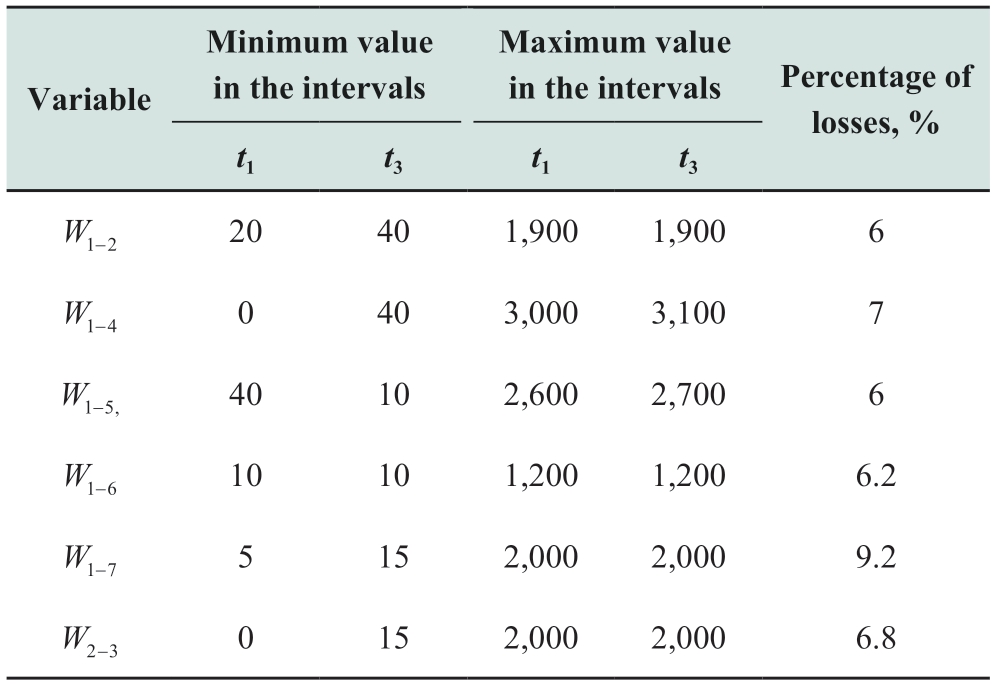
Table A3 Demand functions at the nodes in three time intervals,MWh

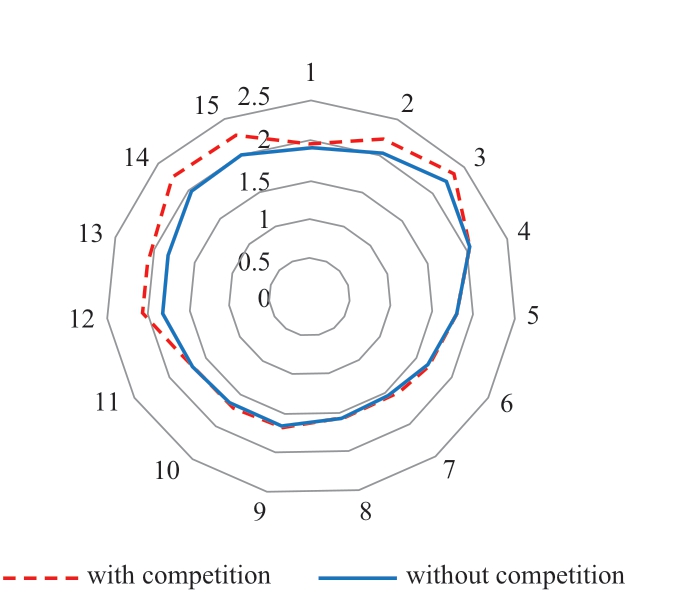
Fig.6 Nodal prices (thousand rub.) in the case of imperfect competition and in the case of social welfare maximization

-In the context of stochastic information,it is important to qualitatively model random variables.It is advisable to consider the expected values of the quantities of interest as scheduling results.This will improve the quality of power system scheduling.

4 Conclusion

This article presents a mathematical model for solving the problem of scheduling the medium-term power system operating states.The model considers the possibility of representing the scheduling period using several time intervals,the dependency of electricity consumption on the nodal price,and the representation of individual operation conditions of electricity suppliers using random values.

The proposed model is a bi-level game model of the“leader-follower” type.Notably,the presented statement has many leaders: the electricity suppliers (producers).The follower is a market operator.All of them know the rules by which the operator acts.There are several approaches to modeling interactions in the electricity market.In particular,they can be modeled using Cournot or perfect competition models [7].In our study,the Stackelberg option [22]was chosen because it describes the most plausible relationships between economic agents in the electricity market,including the actions of the electric power system operator.We considered two methods for solving the problem of mediumterm scheduling.One method was based on building and solving a joint system of optimality conditions for the primary and auxiliary problems.The other method,presented in the paper,involved finding the equilibrium state iteratively and was implemented in the example given in the article.An advantage of this method is that it can provide information about the possible actions of each supplier if the supplier is the only strategic player in the market.This is interesting in plans for asserting maximum state control over an industry.Such effects cannot be considered by solving the system jointly [11].

A distinctive feature of the presented example is the possibility of changing suppliers’ strategy from interval to interval under constraints that apply to the entire period.This has not been analyzed in other works considering MPEC problem statements [23],although it is important for the analysis of the behavior of suppliers and for the scheduling of electric power system operation.Additional consideration of multi-interval nature allows scheduling for a long term.This analysis is necessary both to assess current state of the system and to address expansion issues.A numerical study of the capabilities of the proposed mathematical model is illustrated using a case study of a simplified equivalent circuit of a real-world power system.We obtained and compared the scheduling results under maximum public welfare (the total financial gains of electricity suppliers and buyers) and imperfect competition market conditions (generating companies strive to maximize their profits).

The findings demonstrated the influence of representing some external conditions (demand for electricity,water reserves,and inflows to hydropower reservoirs) by random variables.When solving the scheduling problem in terms of stochastic information,using the expected values of the parameters of interest calculated from several possible realizations of random variables is recommended.

The study indicates that,under imperfect competition,generating companies can change their supply volumes and influence the price level in the market.In the example considered,owing to imperfect competition,suppliers could raise prices by 5% to 13%.Accordingly,the suppliers’profits in this case were higher than that in the case of public welfare maximization.

Nomenclature

The following notations are used in the text to describe the problem of medium-term scheduling of the power system operating states.

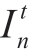is the set of numbers of nodes in the power system within the interval t.

t indicates the time interval considered.

T is the total number of time intervals considered in the scheduling period.

M is the number of time intervals with interrelated operating state parameters.

is the set of node numbers associated with the node i.

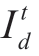is the set of node numbers with electricity consumption in the interval t.

ITPP,IHPP,and IR are the sets of node numbers with thermal power plans (TPPs),hydroelectric power plants (HPPs),and suppliers using renewable natural resources (R),respectively.

Is is the set of node numbers with electricity storage facilities.

IfTPP,IfHPP,IR are the set of numbers of nodes,where TPPs,HPPs,R are parts of the f-th GenCo.

pit is the price of electricity at node i in the time interval t.

 are the electricity generated from the TPP,HPP,and R at node i in the interval t,respectively.

Wist is the amount of electricity accumulated at node i in the interval t.

W fT PP ,W fH PP,WfR are the vectors of electricity generated by the f-th GenCo with numbers of nodes from I fT PP ,I fH PP,IR .

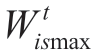andare minimum and maximum allowable values forrespectively.

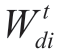is the demand for electricity at node i in the time interval t.

Wd is the vector of demand for electricity,

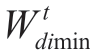 and  are minimum and maximum allowable values for 

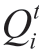is the water consumption at the ith hydropower plant site in interval t, i ∈I HPP.

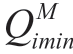 , are the maximum and minimum allowable amounts of water consumption,respectively,from the reservoir of the i-th HPP over M intervals,i ∈I HPP.

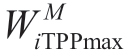are maximum and minimum allowable amounts ofrespectively.

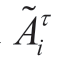andare the random amount of water reserve and water inflows in the reservoir of the i-th HPP at the beginning of interval τ,i ∈I HPP.

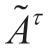 and are the vectors corresponding to 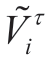and respectively(τ ∈T).

Wijt is power flow between nodes i and j in interval t;

 is the maximum allowable value for Wijt in interval t;

is the percentage of electricity loss due to the power flow Wijt in link i-j in interval t.

GK is a set of generating companies.

Appendix A

Acknowledgements

This work was conducted under the State Assignment Project (No.FWEU-754 2021-0001) of the Basic Research Program of the Russian Federation 2021-2030.

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1]Joskow PL (2008) Lessons learned from electricity market liberalization.The Energy Journal,29(Special Issue# 2)

[2]Nahata B,Izyumov A,Busygin V,et al.(2007) Application of ramsey model in transition economy: a Russian case study.Energy Economics,29(1): 105-125

[3]Shable G (2009) Demand is very elastic! IEEE Power &Energy 9(2): 14-20

[4]Day CJ,Hobbs BF,Pang JS (2002) Oligopolistic competition in power networks: a conjectured supply function approach.IEEE Transactions on Power Systems,17(3):597-607

[5]Cardell JB,Hitt CC,Hogan WW (1997) Market power and strategic interaction in electricity networks.Resource and Energy Economics,19(1-2): 109-137

[6]Sharma KC,Bhakar R,Tiwari HP (2014) Stochastic EPEC approach for wind power trading in competitive electricity market.Eighteenth National Power Systems Conference (NPSC),IEEE,December

[7]Ventosa M,Baıllo A,Ramos A,et al.(2005) Electricity market modeling trends.Energy Policy,33(7):897-913

[8]Newbery DM,Greve T (2017) The strategic robustness of oligopoly electricity market models.Energy Economics,68: 124-132

[9]Bompard E,Ma YC,Napoli R,et al.(2010) Comparative analysis of game theory models for assessing the performances of network constrained electricity markets.IET Generation,Transmission &Distribution,4(3): 386-399

[10]Baldick R,Grant R,Kahn E (2004) Theory and application of linear supply function equilibrium in electricity markets.Journal of Regulatory Economics,25(2): 143-167

[11]Hobbs BF,Metzler CB,Pang JS (200) Strategic gaming analysis for electric power systems: an MPEC approach.IEEE Transac.on Power Syst,15(2):638-645

[12]Holmberg P,Newbery D (2010) The supply function equilibrium and its policy implications for wholesale electricity auctions.Utilities Policy,18(4): 209-226

[13]NP Market Council (2011) The rules for competitive selection of price bids for the day ahead.Appendix No.7 to the Agreement on Wholesale Market Trading System Accession

[14]Zangwill WI (1969) Nonlinear programming: a unified approach.Englewood Cliffs,NJ: Prentice-Hall

[15]Luo ZQ,Pang JS,Ralph D (1996) Mathematical programs with equilibrium constraints.Cambridge: Cambridge University Press

[16]Jin S,Ryan SM (2013) A tri-level model of centralized transmission and decentralized generation expansion planning for an electricity market.IEEE Trans Pow Sys,29(1):132-141

[17]Guo L,Lin GH,Zhang D,et al.(2015) An MPEC reformulation of an EPEC model for electricity market.Operations Research Letters,43(3):262-267

[18]Couchman P,Kouvaritakis B,Cannon M,et al.(2005) Gaming strategy for electric power with random demand.IEEE Transact Pow Sys,20(3):1283-1292

[19]Mitridati L,Pinson P (2016) Optimal coupling of heat and electricity systems: a stochastic hierarchical approach.In Proceedings of IEEE International Conference on Probabilistic Methods Applied to Power Systems

[20]Bompard E,Lu W,Napoli R,et al.(2010) A supply function model for representing the strategic bidding of the producers in constrained electricity markets.Electric Power and Energy Systems,32:678-687

[21]Weber JD,Overbye TJ (1999) A two-level optimization problem for analysis of market bidding strategies.In Proceedings of IEEE PES Summer Meeting,2:682-687

[22]Luján Latorre M,Granville S (2003).The stackelberg equilibrium applied to AC power systems-a noninterior point algorithm.IEEE Transactions on Power Systems,18(2): 611-618

[23]Dimitriadis CN,Tsimopoulos EG,Georgiadis MC (2021)A review on the complementarity modelling in competitive electricity markets.Energies,14(21): 7133

Received: 9 March 2022/Accepted: 8 September 2022/Published: 25 October 2022

Palamarchuk S.

palam@isem.irk.ru,

Aizenberg N.zen@isem.irk.ru

2096-5117/© 2022 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Natalia Aizenberg received her diploma in Mathematics from Irkutsk State University in 1993.In 2000,she defended her doctoral thesis in mathematical economics at the Institute of Economics and Industrial Organization in Novosibirsk.In 2005,she was awarded the title of associate professor.Currently,she is a senior researcher at the Melentiev Energy Systems Institute SB RAS and a lecturer at the Institute of Economics at Far Eastern Federal University.Her research interests include mathematical modeling of wholesale and retail electricity markets,modeling of imperfect competition markets,game theory,contract theory,and spatial economics.She is the author of two books and more than 60 articles.

Sergey I.Palamarchuk graduated from Irkutsk State Polytechnic Institute,Irkutsk,Russia,in 1968.In 1997,he defended the postdoctoral thesis in electric power engineering at Melentiev Energy Systems Institute (ESI) of the Russian Academy of Sciences.At present,he is a chief researcher at ESI and part-time professor at Irkutsk State Technical University.His principal areas of research are the power industry restructuring,market design and organization.He is the author of more than 150 articles.

(Editor Yanbo Wang)