0 Introduction

With the shortage of nonrenewable resources and the accompanying environmental pollution,the development and utilization of renewable clean energy is becoming increasingly important.In particular,wave energy has attracted more and more attention owing to its high energy density,wide distribution,and inexhaustible characteristics[1].Wave power generation uses mechanical devices to capture the energy generated by the vertical and horizontal movements of sea waves and the difference in the pressure change of water in waves,and convert it into reciprocating mechanical energy,which is then transformed into the required electrical energy via an energy conversion system[2].The direct-drive system generally uses linear generators to directly convert the mechanical energy of waves into electrical energy,without other forms of energy conversion,and the core component of power generation is linear motors[3].Owing to their high density and high efficiency,linear permanent magnet motors are widely used in wave power generation.However,the price of a permanent magnet is expensive,and its magnetic performance is unstable in the harsh environment of humid and corrosive oceans,significantly reducing the reliability of the power generation system [4-5].To ensure a certain power generation efficiency,reduce costs,and improve the reliability of motors used for wave power generation,scholars have begun to study linear switched reluctance motors(LSRMs)without permanent magnets [6-9].This type of motor has a simple structure,low production cost,and no end effect.LSRMs are also widely used in propulsion systems such as elevators and vertical hoists owing to their high fault tolerance [10].The motor has only one side winding,small copper loss,and high energy utilization and power generation efficiency.It can adapt to such humid and harsh outdoor environments,and has good corrosion and moisture resistance [11].Therefore,these motors are often employed in railway track transportation and ocean wave power generation systems.

A variety of methods and strategies to improve power generation efficiency,such as winding placed on the stator side,short distance winding,and yokeless structure,have been proposed.The thrust was improved in the traditional form of the motor,and the effect is remarkable.Use of a cylindrical LSRM having a rotor without winding,light weight,small inertia,and good dynamic response enables reluctance torque operation,wide speed range,and flexible control [6-7].However,torque fluctuation occurs and the thrust and efficiency are low.As described in references[8-9],the whole-distance winding was used to replace the original short-distance winding,and the proposed structure was simple and reliable.The mutual inductance of the winding was used to generate thrust,which improved the thrust density of the motor to a certain extent.Nevertheless,the disadvantage is that the stator tooth width/pitch must be less than 0.5,thereby limiting some applications.To eliminate this limitation,the power density and output efficiency of the motor have been further improved.In reference [12-13],a yoke-free structure was proposed,and the ring magnetizer was used to replace the convex tooth.The motor structure is depicted in Fig.1.Although this yokeless motor has significantly improved power density and efficiency,it is still far inferior to the permanent magnet motor.

To achieve higher efficiency,the design of the LSRM proposed in the literature [14] was optimized in this study with the goal of maximizing energy density and output efficiency.Recently,scholars have proposed a variety of motor optimization analysis methods based on singleparameter sweeping,response surface methods,and genetic algorithms,among others [15].Several optimization approaches are compared regarding multi-parameter,multi-objective,global optimization capability,and time consumption herein.The comparison results are provided in Table 1.

Table 1 Comparison of common optimization methods

The LSRM considered in this study has a special structure of bilateral discrete magnetic conductive block stator.Various structural parameters were involved in the optimization analysis.Considering the interaction between parameters,using a certain optimization method alone has problems such as high computational cost and poor optimization ability.Although reference [19] efficiently reduced the amount of time for the multi-parameter and multi-objective optimization process and simplified the global optimization,the multi-objective weights selected in the sensitivity calculation layering were too subjective,which directly affected the final optimization results.Therefore,based on the sensitivity hierarchical optimization proposed in the reference [19],this study proposes an improved sensitivity hierarchical calculation method.The entropy method was adopted to objectively select the target weight,and the optimization process and algorithm were improved according to the actual situation to be suitable for the optimization of the LSRM.Considering energy density and output efficiency as the optimization design targets,different structural parameters were stratified based on the sensitivity analysis of the entropy method,and parameters of different levels were optimized based on simulated annealing(SA)algorithm,response surface optimization,and single-parameter scanning optimization analyses.Accordingly,the optimal structural size parameters of the motor could be determined.Finally,the electromagnetic performance of the motor under constant speed and variable speed state was analyzed using the finite element software combined with control current simulation,and the performance changes of the motor before and after optimization under different operating states were compared to verify that the optimized linear motor has higher efficiency and energy density.

1 Structure and parameters of motor

The structure of the LSRM is presented in Fig.1.The three-phase winding is placed on the external rotor,and the internal primary track comprises the magnetic block and the nonmagnetic structure alternately.

Fig.1 Diagram of motor structure

Without setting the primary yoke,the weight of the motor is considerably reduced and the utilization rate of ferromagnetic materials is improved.The problem of interphase insulation was not considered for the single-layer rotor winding.

The ratio of the number of poles of the stator and rotor of the traditional switched reluctance motor can generally be 6/4,8/6,12/8,etc.The three-phase 6/4 structure is the most common and widely used motor structure.Considering the simplicity of control operation,the 6/4 switched reluctance motor structure was selected in this study.The number of rotor slots is 6,and the corresponding primary part of the magnetizer is 4.When a phase is located in the nonmagnetic position,the path reluctance of the magnetic force line is the largest,and when the entire area of the magnetizer is aligned with that of the two teeth of a phase,the reluctance is the smallest.Based on the principle of minimum reluctance,the actuator can be driven from the position of maximum reluctance to that of minimum reluctance.

A photograph of the experimental wave-making pool is displayed in Fig.2.As the floating range of the LSRM is not suitable for deep waters,the movement stroke of the mover was 1 m.A smaller LSRM air gap ensures less flux leakage and better motor performance.However,the side tension of the LSRM increases with reduction of the air gap and processing difficulty,therefore,the final selection of the initial air gap was 0.6 mm.

Fig.2 Experimental wave-making pool

A tubular linear switch reluctance generator that has low cost and high power density is presented for marine wave energy conversion in reference [13].This structure eliminates the mover yoke,but improves the flux-carrying capacity and fault tolerance.However,the magnetic circuit is along the circumferential PHI coordinates,and the magnetic field lines are not closed upward on the cylindrical axis,which is difficult to process structurally.A novel double-sided LSRM with segmental stator is presented in reference [14] and compared with the well-known teethtype LSRM.Consequently,the proposed machine exhibited a higher propulsion force density,and the silicon steel sheet facilitates lamination processing.

The LSRM proposed in reference [14] was adopted as the generator for the wave power generation system in this work.The initial parameters and structure are presented in Fig.3 and Table 2.

Table 2 Motor structure parameters before optimization

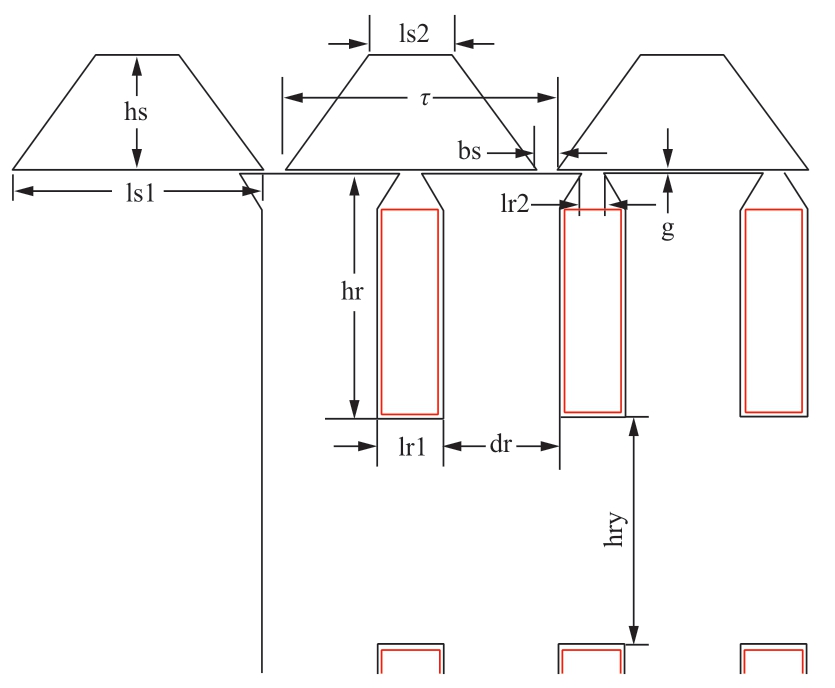
Fig.3 Motor structure parameters

2 Motor structure performance analysis

2.1 Analytical calculation of nonlinear magnetic saturation

The air gap flux density of the LSRM under load was solved using a nonlinear equivalent magnetic circuit.Under load,there is a local saturation phenomenon in the core,and the relationship between saturation and core permeability should be considered to calculate the magnetic pressure drop in the core.Fig.4 shows the nonlinear equivalent reluctance calculation model of the LSRM.

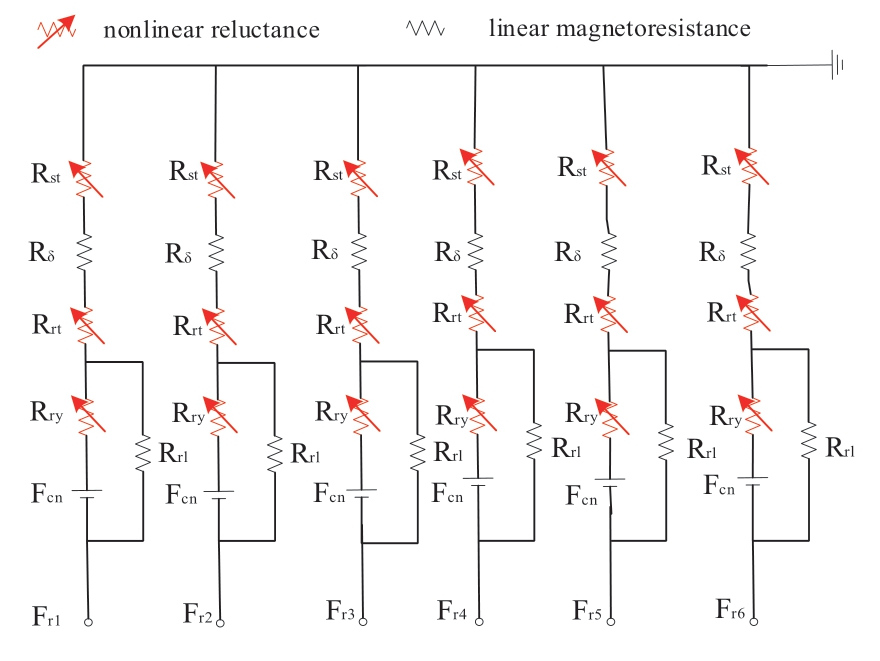
Fig.4 Nonlinear equivalent reluctance calculation model

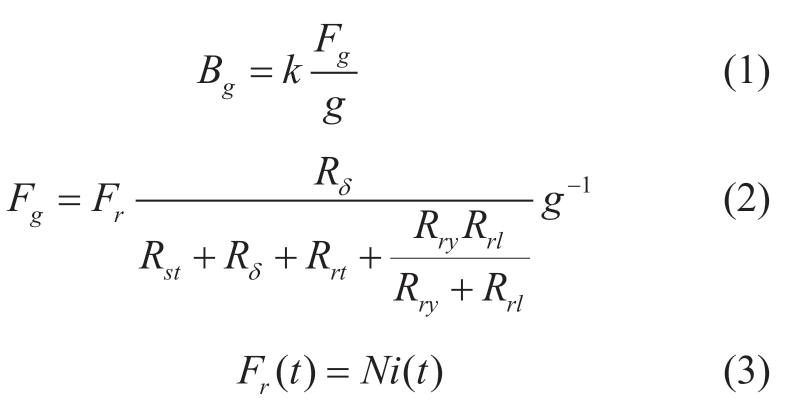
Here,k is the magnetic density calculation coefficient.The magnetomotive force generated by the rotor winding is the only magnetic source of the whole motor,which is equivalent to the magnetomotive force Fri in the middle of each slot; i represents different rotor windings 1–6.The connection between the slot and rotor yoke is equivalent to a fixed magnetic pressure source Fcn,which is connected in series with the corresponding rotor yoke reluctance Rry to form a magnetic branch.This is connected in parallel with the slot leakage reluctance Rrl,and then connected in series with the rotor tooth reluctance,air gap reluctance,and stator reluctance to form a complete motor magnetic circuit.

The parameter calculation formulae for the equivalent magnetic circuit model,at the time of alignment,are given by:

where μ0 and μr are the vacuum relative permeability and the permeability of the saturated ferromagnetic material,respectively; hry is the width of the rotor yoke; Rry is the rotor tooth reluctance; and ht1 is the wedge height.The slot leakage magnetoresistance Rrl is divided into two parts:the slot body leakage magnetoresistance and the slot mouth leakage magnetoresistance.According to the basic principal formula:

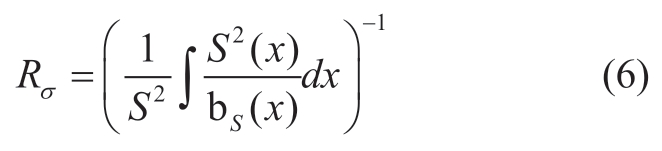
Derivation of total slot leakage magnetoresistance:

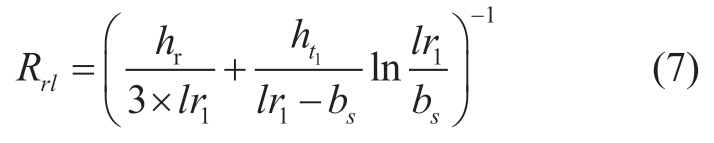
Air gap reluctance Rδ:

Stator reluctance:

A phase of the mover transfers from the nonaligned position with the magnetizer ring to the aligned position,and each reluctance changes according to the saturation current and the movement of the magnetizer block.For this part,the leakage flux of the adjacent two-phase winding turns to each other was ignored,as well as the local saturation effect of the magnetizer block and the edge of the slot tip.A simplified mathematical model for each part of the magnetoresistance was established as:

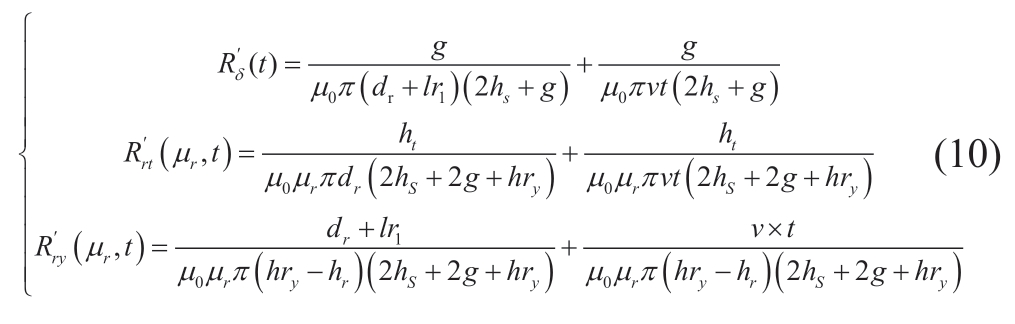
According to the simplified mathematical model and analytical calculation,g is observed to significantly influence the air gap reluctance,and has little influence on the reluctances of the stator and the rotor.bs is related to the slot leakage magnetoresistance,and increases with larger slot leakage magnetoresistance.The higher the values of lr1 and dr,the smaller the air gap reluctance,and the larger the rotor tooth reluctance.hr and hry are related to the saturated rotor part,and the larger the hr value,the larger the tooth and yoke magnetoresistance.hs and ls1 are only related to the stator part; the smaller hs,the greater the reluctance.In summary,the structural parameters including pole distance τ,slot width lr1,slot depth hr,magnetic permeability height hs,slot mouth bs,and air gap g are related to the saturated magnetic circuit characteristics of the motor,and considerably affect the output characteristics of the motor.

2.2 Analysis of influence of motor parameters on thrust density and efficiency

As shown in Fig.3,because g is linear to the air gap reluctance,a large air gap leads to larger air gap reluctance,which increases the excitation current of the rotor winding and the excitation loss.Consequently,the power factor of the motor is not high and will directly affect the output of the motor.Changes in permeability spacing bs significantly influence the magnetic flux leakage.According to the above nonlinear magnetic circuit analysis,the influence of various structural parameters on the reluctance at different positions is relatively complex.Combined with the coupling effect of non-sinusoidal input current and various parameters,optimization of the multi-parameter structure is difficult.Equations(11)and(12)provide geometric relations of the pole distance τ,magnetic distance bs,magnetic width ls1,slot width lr1,and rotor tooth width dr on the motor structure:

With constant magnetic permeability interval bs,the effect of varying τ on the target thrust and efficiency is consistent with ls1.When the pole distance is constant,the effect of groove width lr1 and tooth width dr is consistent.Therefore,assuming constant g and bs,the influence of multiple parameters including τ,hr,lr1,hry,hs and N on the performance of single-parameter motor was investigated in this study with the goal of achieving maximum thrust density and efficiency.

As the LSRM starts from the minimum reluctance to enter the current to the maximum reluctance position,followed by the power generated by the winding using freewheeling current,the thrust of the motor only occurs at half pole distance.To simplify the analysis,the influence of the leakage flux of the motor was ignored,and only the thrust generated by the main flux was considered here.Phase A was connected to 0–12 A current.The influence of single parameter variation performance under half pole distance is depicted in Fig.5:the pole distance τ changes from 36.163 mm to twice the initial pole distance; slot width lr1 and τ increase to 2.2 times the same multiple; lr1 increases 1.5 times under 1.4 times τ; hry and hr increased by 1.3 times their initial values; The magnetic height varied from the original value to 0.5 times higher.

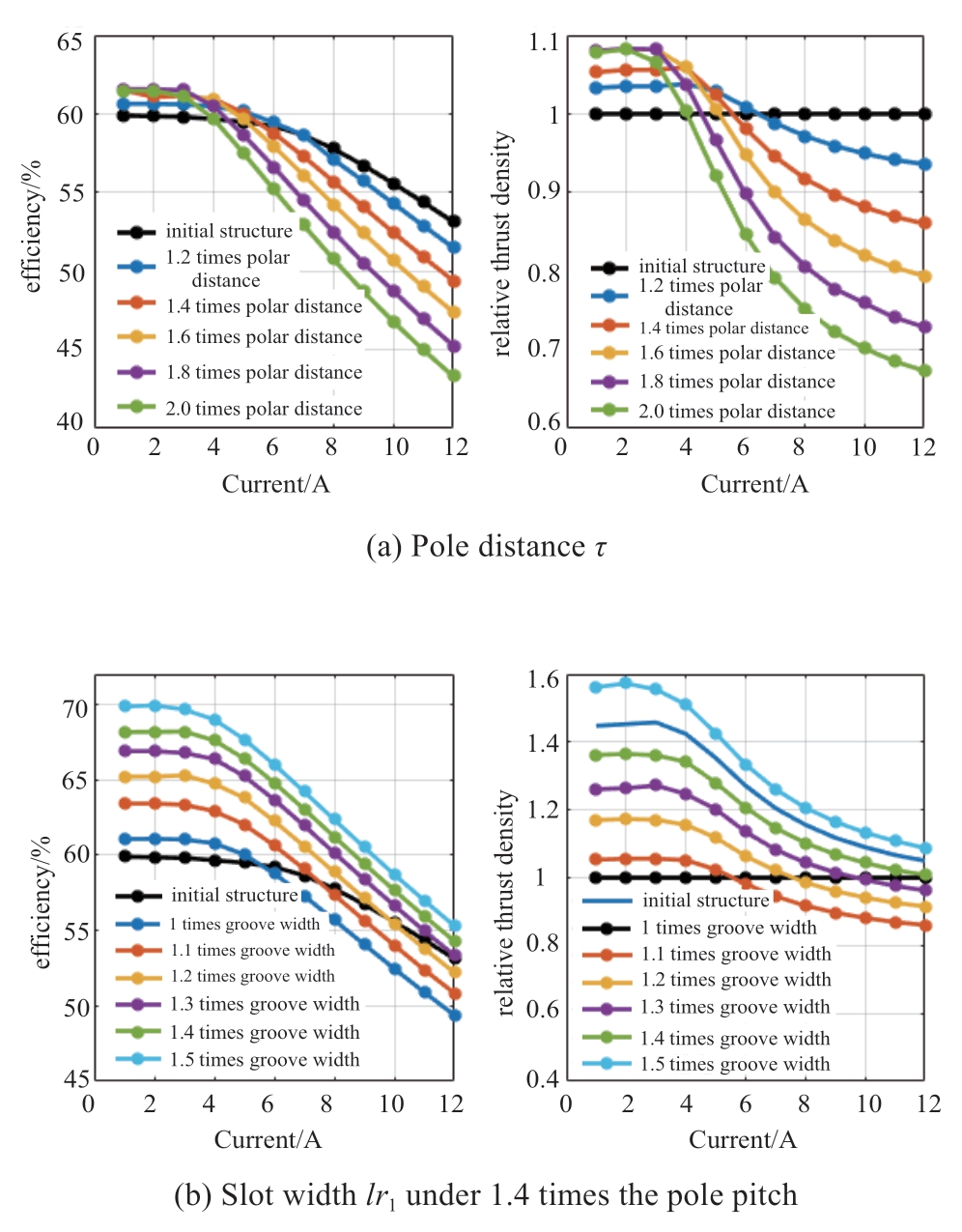
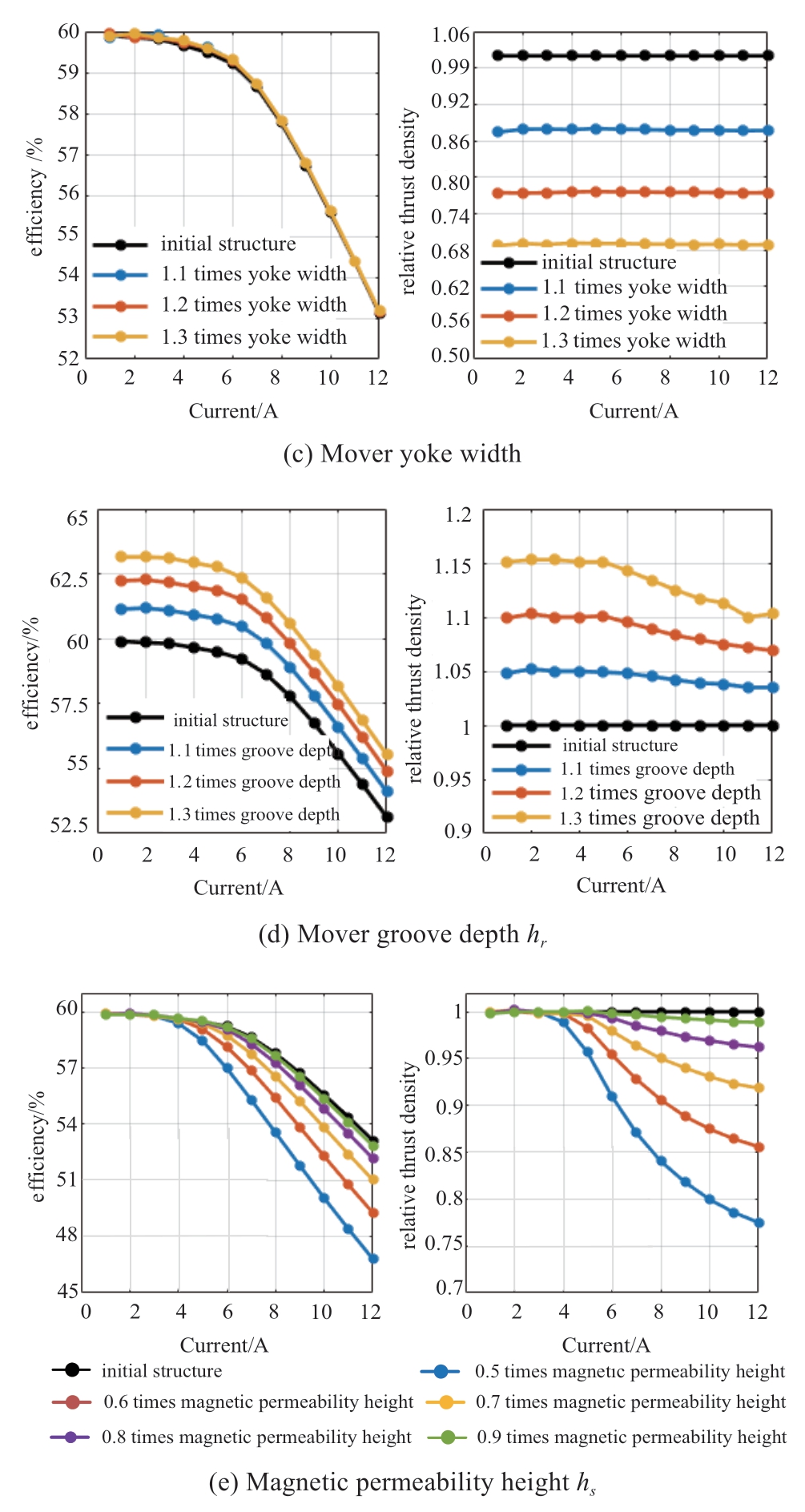
Fig.5 Performance analysis results of various parameters

Under the condition that the bare-line slot full rate is 42% and the copper wire resistance is constant,the winding turns N changes relative to motor parameters hr and lr1.It can be observed from Fig.5 that the larger the pole distance τ after the working current saturation,the smaller the thrust density and efficiency.Appropriate increase in lr1 is conducive to increasing motor thrust and improving motor efficiency; the smaller the magnetic height hs,the easier the magnetic block is to saturate,resulting in smaller efficiency and thrust density.hr and hry are basically in unsaturated state,and the larger the hr value,the better the motor performance.

The process of calculating the maximum allowable working current of the motor is as follows:

Tank full rate:

Conductor cross-sectional area:

Electric secret:

where Nt is the number of parallel roots,Ns is the number of conductors per slot(single layer=turns,double layer=2×turns),As is the slot area,d is the insulation diameter of the conductor strip,and di is the diameter of bare wire.Heat load=line load × electric density,for which the line load is given by:

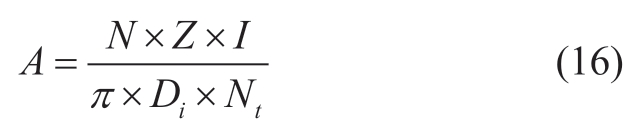
Under the condition of natural air cooling,the maximum thermal load of the motor could reach 4,000 A2/mm2cm,and the diameter of the motor remained basically unchanged.The amplitude of each working current of the motor under different parameters was not more than 8 A.

From comprehensive analysis,it can be concluded that within the maximum current range that the rotor winding can withstand,changing τ,lr1,and hr appropriately can improve the output efficiency of the motor and increase the thrust density of the motor.Consistent with 2.1 magnetic circuit analysis,the larger the pole distance τ,the larger the permeability area,the lower the magnetoresistance and the higher the efficiency.Increasing lr1 and hr appropriately will increase the magnetoresistance,but more windings can be placed,the magnetomotive force increases linearly and the thrust increases.Thus,hs and hry do not significantly improve motor performance,or even reduce the thrust density.

3 Multi-objective optimization of LSRM

3.1 Optimization process of LSRM

The primary purpose of multi-objective optimization is to determine the various design variables and related constraints of the motor.The LSRM has a special structure of bilateral discrete magnetic block stator,which has a large number of parameters to be optimized.To ensure improvement of the power generation efficiency of the system,multiple objectives such as motor efficiency and energy density were selected for optimization in this study.

Therefore,according to the influence of different design variables on the overall target,this study adopted design methods such as simulated annealing algorithm,response surface,and single-parameter scanning to conduct targeted optimization analysis.Figure 6 presents a flowchart of the optimal design of the bilateral LSRM.

Different structural parameters of the motor considered in this study have different effects on its various characteristics.In this work,the qualitative problem of pursuing high efficiency and energy density was transformed into quantitative analysis using multi-objective functions,defined as:

where ρ′N and η′N are the thrust density and efficiency under the initial structural parameters,respectively; fρ(xi)and fη(xi)are the response quantities of the motor energy density and efficiency when the motor design variablex takes a certain value,respectively.In the optimization objective function,the optimized initial value is placed on the numerator,and the denominator is the optimized response.The optimization requirement is to maximize the efficiency of wave power generation,that is,the pursuit of motor efficiency and energy density; the greater the better.Therefore,the minimum value of the total optimization objective was pursued according to the design requirements.λ1 and λ2 are the weight coefficients of different sub-goal weights,which represent the proportional weights of different indicators in the total optimization goal.

3.2 Entropy method to determine weights

At present,empirical values are often used or the weights of objective functions and sensitivity indicators are artificially selected according to applicable occasions.Different proportional weights selected subjectively have a greater impact on the optimization results.The entropy method is an objective weight determination method.Entropy is a measure of the degree of disorder in a system.It uses the characteristics of the amount of information expressed to objectively evaluate the utility of each index to multiple targets.The larger the entropy value,the higher the disorder of the parameters,the less information it contains,and the smaller the weight of the design variables.

Therefore,the entropy method was employed to determine the weight λ of the output efficiency and energy density in the sensitivity analysis calculation,and that γ of the multi-objective function when analyzing the magnetic permeability distance.

The two-attribute decision matrix for constructing efficiency and energy density is given by:

where a is the structural parameter sample that needs to be optimized and improved; W is the number of sample variables; η and ρE are the efficiency and energy density attributes of the structural parameters,respectively; xmn is the nth attribute value of the mth sample point.

Fig.6 Motor optimization flow chart

Under the nth attribute,the contribution degree Cmn of the mth sample am is the contribution degree of a certain structural parameter to each target attribute,expressed as:

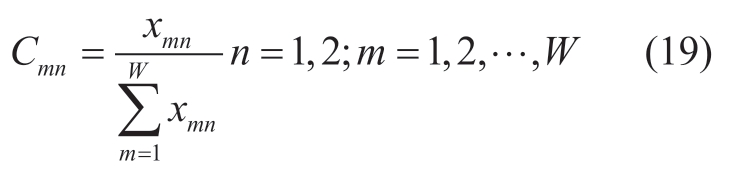
The total contribution of all structural parameters to each attribute,that is,the output entropy en of each target attribute,is written as:

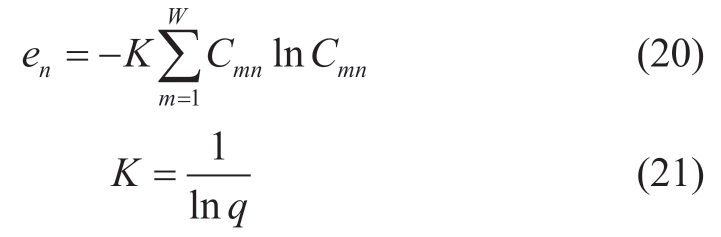
Here,K is a normal number and q is the number of attributes.The weight coefficient wn under each attribute is given by:

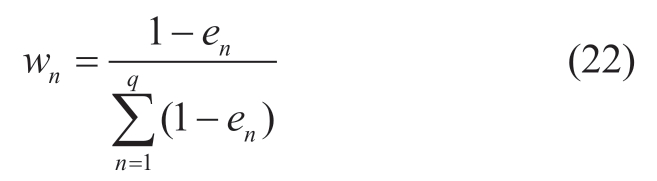
Through the analysis and calculation of the above entropy value,the sensitivity index function efficiency and energy density weight for hierarchical optimization were determined as 0.698 and 0.302,respectively.The overall objective function weights γ1,γ2,and γ3 are 0.69,0.189,and 0.121 for the single-parameter scanning optimization of the magnetic permeability spacing bs.

3.3 Parameter sensitivity analysis

In this work,finite element analysis of a single design variable was performed and the sensitivity value was calculated to identify the degree of its influence on the motor performance.Subsequently,different methods were used to optimize the structural parameters with different sensitivity values.The sensitivity index of the structure parameter xi to the target is as follows:

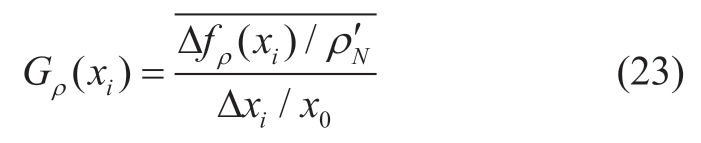
The total target optimization sensitivity S(xi)obtained by determining the weight based on the entropy method can be defined as:

Here,Δfρ(xi)is the difference between the optimized target under the fixed value and the target under the initial parameter when the design variable xi takes a certain value;Gρ(xi)and Gη(xi)are the sensitivity indicators of different structural parameters to the single target of energy density and efficiency,respectively.

The sensitivity analysis results for each structural parameter are presented in Table 3,and the corresponding histogram is displayed in Fig.7.

Table 3 Sensitivity analysis results for various structural parameters

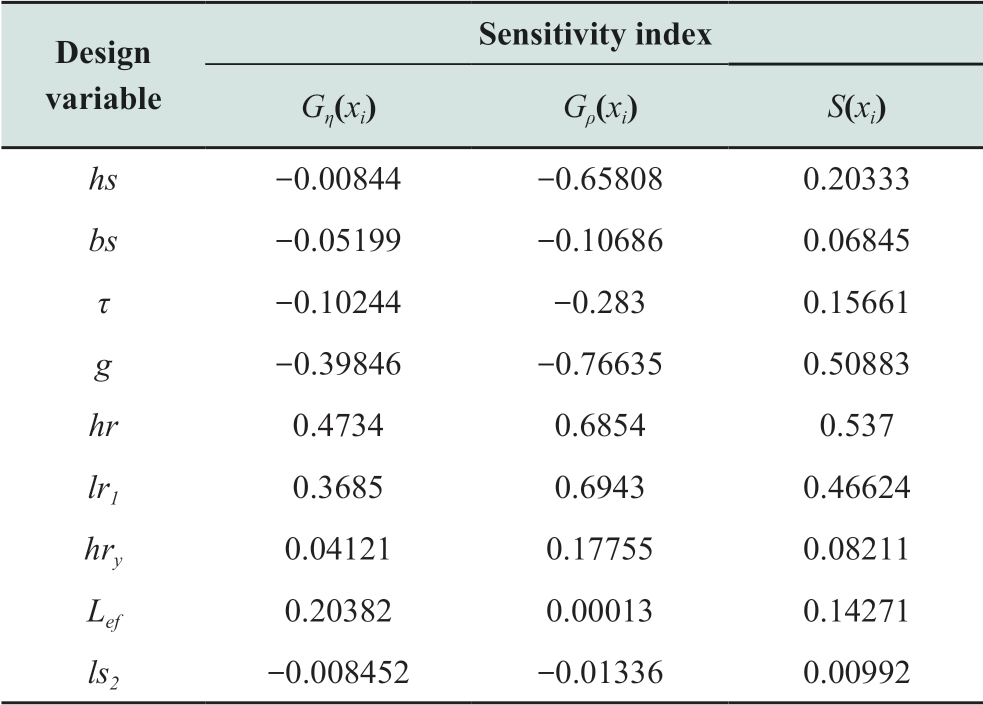
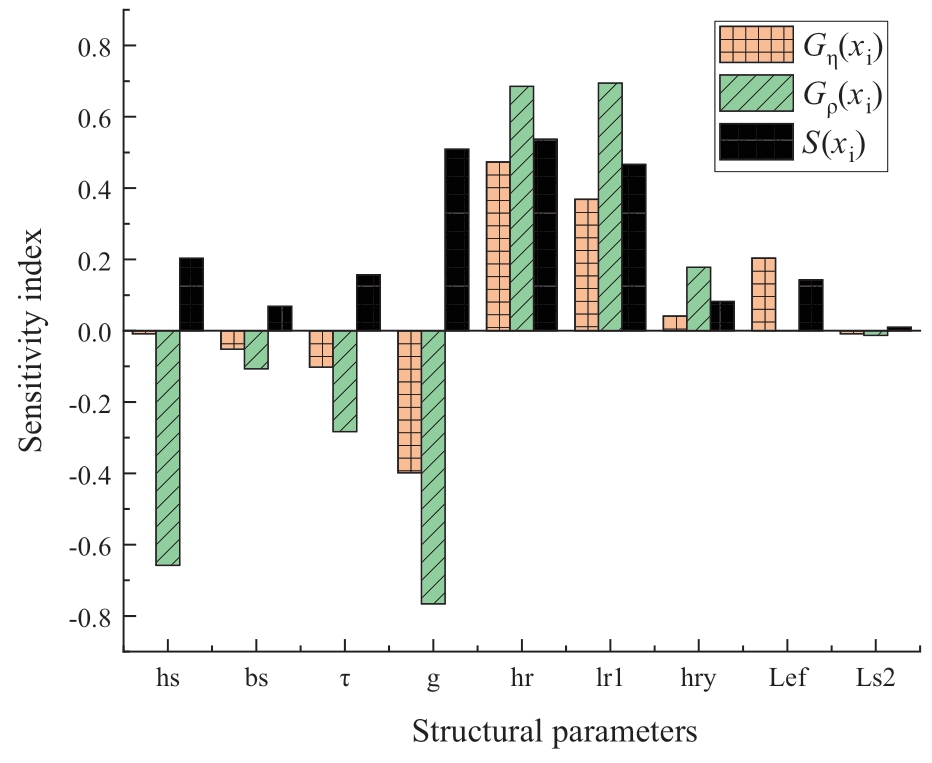
Fig.7 Sensitivity analysis results for structural parameters

As observed the above figure,different design variables have different influences on different optimization objectives.A positive sensitivity index implies that a structural parameter positively correlates with the target,while a negative value indicates negative correlation.

3.4 Hierarchical optimization

To improve the efficiency of the multi-design variable multi-objective optimization process,based on the above analysis and calculation of the sensitivity S(xi),the structural parameters with different sensitivities were divided into three levels:The design indexes g,hr,and lr1 of S(xi)>0.4 are higher sensitivity levels.The interaction between the parameters must be considered,and the SA algorithm was used for optimization.The structural parameters ofS(xi)>0.08 are of medium sensitivity,which are hs,hry,and Lef respectively.The two-dimensional parameter analysis was conducted via the response surface optimization method.The design variables ls2 and bs of S(xi)<0.08 are low sensitivity,and the single-parameter sweep method was used for optimization analysis.

In particular,τ has little effect on the efficiency and thrust density.Considering that it is closely related to hr and lr1 in the local structure and magnetic circuit,τ was also placed in the algorithm for optimization analysis simultaneously.

When the high-sensitivity parameters were optimized and analyzed based on the simulated annealing algorithm,the comprehensive optimization objective function F(x)was obtained through fitting of the second-order nonlinear regression model to its expression:

The quaternary quadratic function F(x) obtained by fitting the nonlinear regression method,and the target in the optimization process,is F(x) min.

In the process of motor optimization,it is also necessary to set constraints that meet the design requirements.Referring to the design experience of rotating reluctance motors,combined with the preliminary analysis of the magnetic circuit and performance of linear motors with finite element,the boundary constraints of structural parameters selected in this study are defined as:

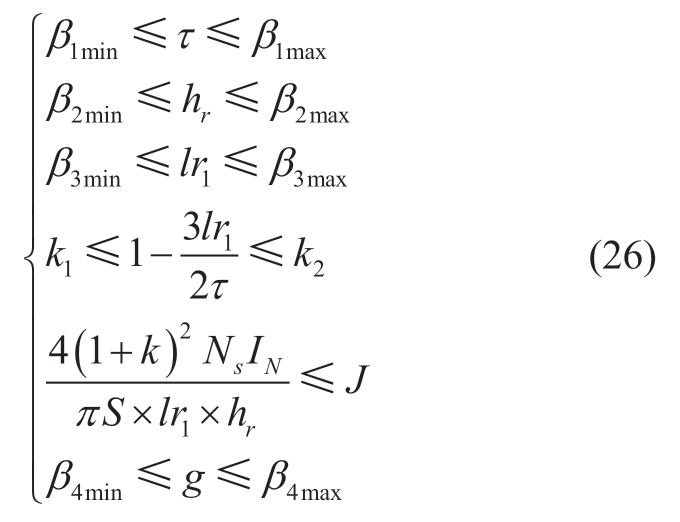
Here, β1,β2,β3,and β4 represent the reasonable value ranges of τ,hr,lr1,and g; k1 and k2 denote the tooth width/mover pole distance proportional coefficients selected according to the design experience; and J is the line current density.The copper loss is the main source of the loss of the linear reluctance motor,hence J remained basically constant.

The initial value F(x0)of the multi-objective function is used as the iterative starting point of the algorithm,and the evaluation standard is the difference between the two iterative solutions before and after ΔF(x)=F(xn)-F(x (n-1)):When ΔF(x)<0,take F(xn) as the current solution,otherwise let F(x (n-1)) be the current solution with the probability of e[-ΔF(x)/F(xn-1)] to avoid the model falling into a local minimum,and eventually tend to global optimum.

To ensure the global optimization ability of the SA algorithm,the number of iterations to terminate the algorithm was set to 2,500,and the known constraints were used as input conditions.In the optimization process,when the function value generated by successive iterations cannot become a new solution,the current solution is output as the optimal solution.As shown in Figure 8,from the iterative process based on the objective function of the SA,the final output optimal value is 0.715.

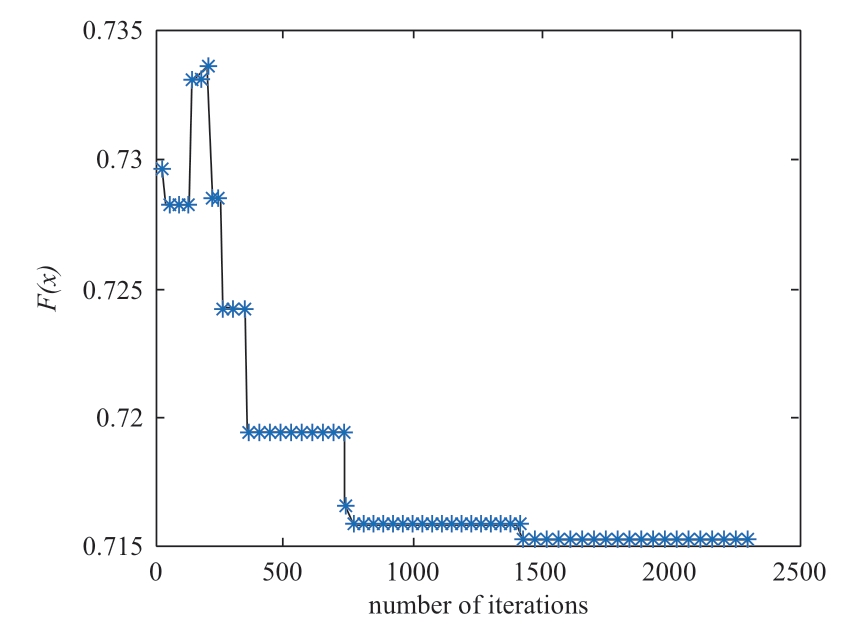
Fig.8 Iterative process of objective function based on simulated annealing algorithm

The response surface method was used to perform a two-dimensional optimization analysis on three moderately sensitive parameters,and the effects of different structural parameters on the efficiency and energy density were obtained,as shown in Figs.7 and 8.It can be seen from Fig.9 that the output efficiency of the motor first increases and then decreases slowly with the core stack length Lef.With the increase in the mover yoke width hry,the efficiency and thrust density increase slowly.Therefore,from the comprehensive analysis of the two,Lef =150 mm and hry=29 mm were selected.Figure 10 demonstrates that when the magnetic permeability width hs increases,the efficiency and density both increase first and then decrease.The final selection of hs =17 mm was considered.

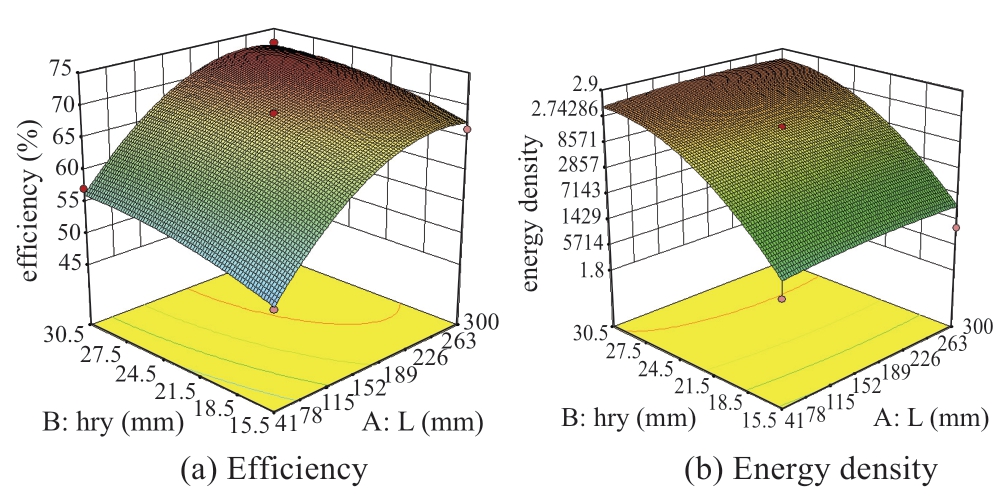
Fig.9 Response analysis results of optimization target under parameters hry and Lef

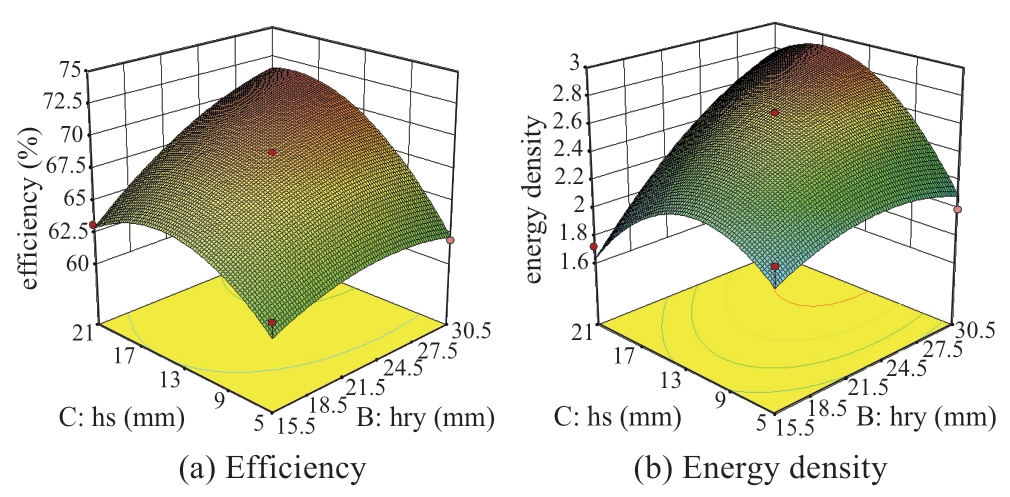
Fig.10 Response analysis results of optimization target under parameters hry and hs

For optimization of the low-sensitivity structural parameters ls2 and bs,the finite element single parameter scanning analysis method was used.The initial parameter values were 10.85 and 2.8 mm,respectively,with ranges of 0~42 and 1.6~3.4.The finite element analysis of ls2 was performed with the step size of 1 mm,and the analysis results for the efficiency,average energy density,and objective function f(x) were obtained as shown in Figure 11.With the increase inls2,the output efficiency gradually decreases,the energy density increases first and then decreases,and the total objective function f(x) takes the minimum value when ls2 =10 mm.

Fig.11 Analysis results of multi-objective changes with ls2

As the notch distance bs significantly affects the mutual inductance,when the adjacent two phases are turned on simultaneously,the negative thrust generated by the mutual inductance is the main reason for the sharp drop in the thrust.Therefore,in the parameter optimization analysis for bs,the optimization objective of thrust fluctuation should be considered.However,calculating the slope of mutual inductance at a certain moment is complicated.To simplify the analysis,the magnitude of the pulsation is equivalent to the difference of mutual inductance as:Mmax-Mmin.

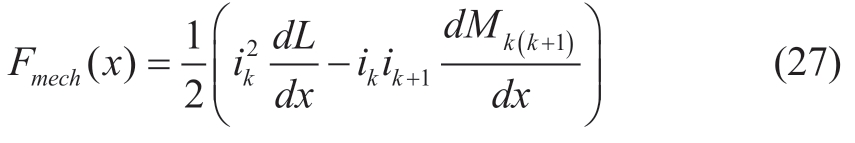
As shown in Figure 12a,the output efficiency,mutual inductance difference,and energy density are not all affected by varying bs.Owing to the conflict between the three optimization objectives,this study introduces an overall objective function Q(x):the optimization objective pursues the maximization of efficiency and density,and the minimum fluctuation.Based on the motor optimization requirements,the maximum value of the total objective function Q(x)maxshould be sought.The overall objective function weight γ was obtained objectively via the entropy method.It can be observed from Figure 12b that when bs =2.6 mm,the total objective function Q(x)achieves the maximum value.

Fig.12 Analysis results of multi-objective changes with bs

Through the analysis,design,and optimization of all the above structural parameters in different ways,the design variables and multi-objective changes before and after optimization could finally be obtained,as shown in Table 4.Accordingly,it can be seen that the output efficiency increased from 55.19% to 72.24% under the constant singlephase current input of the optimized motor based on the layered design,and the energy density under the effective unit volume increased from 1.603×10-5 to 2.958×10-5 J/mm3.

Table 4 Design variables and multi-objective changes before and after optimization

4 Electromagnetic performance analysis

Via finite element analysis,the electromagnetic performance of the motor with improved structural size was simulated and analyzed when it worked in the nonlinear region.Consequently,it was verified that the motor has higher efficiency and thrust density.As the motor works in the scenario of ocean wave power generation,the performance indicators of the motor were evaluated in a constant speed state,and a sinusoidal variable speed was considered to simulate the operation of a complete cycle of the motor in an offshore state simultaneously.

As shown in Fig.13,comparing the thrust of the motor and the loss of each part of the original structural parameters,due to the nonlinear operation region of the motor,the silicon steel sheet saturated and heated,and the iron loss increased instantaneously.The improved motor structure comprising silicon steel sheet is more likely to saturate,resulting in greater short-term iron loss; while the main copper loss of the motor was basically unchanged,the thrust increased from 190 to 580 N,the thrust density increased from 1.603×10-5 to 2.958×10-5 J/mm3,and the motor efficiency increased from 65.8% to 82.48%.

Fig.13 Motor performance comparison at constant speed of 0.5 m/s

As shown in Fig.14,the variable speed operating condition of LSRM at sea was simulated with a sine function.The greater the speed of the wave impacting the float,the greater the thrust on the mover connected to the float,and the winding induced current will increase.Combined with the control current,the stress situation of the motor in a complete running cycle was simulated:at 0~450 ms,the motor moves forward with variable speed and the output thrust changes proportionally with the speed;at 450~900 ms,the motor starts to run in reverse variable speed and the thrust reverse increases with the speed.

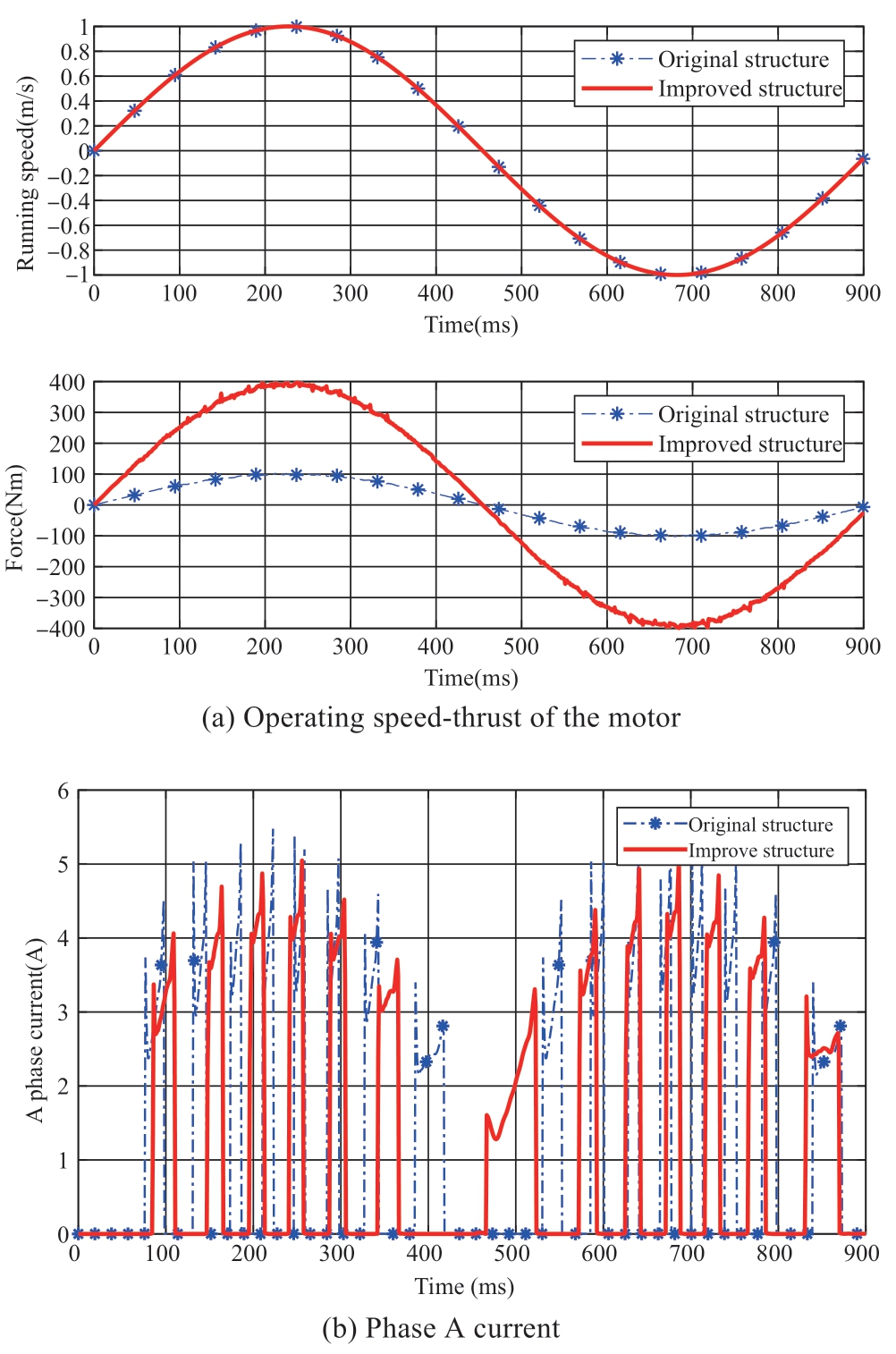
Fig.14 Motor performance comparison under sinusoidal speed

Under the variable speed condition,the motor thrust and running speed of the original structure are consistent with the improved ones; specifically,the output power remained unchanged,and the improved output efficiency was 72%,which is 3.5% higher than that of the original structure.Further,under the original scheme,the effective value of the current required for the same output torque of the motor is 1.91 A,while the improved current only needs 1.25 A,which is 34.55% smaller than the original structure.Comprehensive analysis of the motor running at constant speed and variable speed shows that the improved motor has better output performance in terms of efficiency and thrust.

The magnetic density of the improved motor working in the nonlinear region is depicted in Fig.15.The input current at the nonaligned position was small,the silicon steel sheet was basically unsaturated,and only partial saturation occurred in the narrower places such as the magnetic conductive tip and the tooth end.At the time of alignment,the current amplitude reached 7 A,the magnetic conductive block was partially saturated near the energized winding,and the magnetic density reached 2 T.In one operation cycle,although the motor had short-term local saturation and worked in a nonlinear region,the iron loss increased in a short time corresponding to Fig.13,however,the overall thrust of the motor increased,and the thrust density and output efficiency are improved.

Fig.15 Dense cloud images in different positions

5 Conclusion

Considering the complex optimization of various LSRM parameters,this study proposes an improved sensitivity hierarchical optimization method.The entropy method was employed to determine the sensitivity and weight coefficient corresponding to the multi-objective function,and the variables were accurately screened according to different applicable requirements,which ensures the global optimum of the optimization objective.First,according to the applicable occasion of the reluctance motor,the efficiency and energy density were determined as the optimization goals,and the parameter equations were deduced; parameters τ,Lef,ls2,hs,g,and bs are related to the optimization goals.Thereafter,based on the entropy value method,the relevant weight coefficients were determined,multi-objective functions and sensitivity indicators were established,and the parameters were stratified in combination with the special structure of the motor.According to the stratification of structural parameters,the SA algorithm,response surface method,and singleparameter scanning method were used to conduct multiobjective optimization analysis on parameters of different levels to determine the optimal structural size parameters for the motor.Finally,based on the two-dimensional finite element method,the electromagnetic properties such as thrust and efficiency of the reluctance motor were simulated under different operating conditions.The optimized motor energy density at constant speed increased from 1.603×10-5 to 2.958×10-5 J/mm3,the efficiency increased from 65.8%to 82.48%,and the efficiency at variable speed operation increased by 3.5%.Thus,the optimized linear motor has higher power generation efficiency and energy density.

As demonstrated,the proposed sensitivity hierarchical optimization method based on the entropy method improves the performance of the LSRM and is suitable for multiparameter and multi-objective motor optimization in other applications.The method can fully consider the interaction between multiple parameters,as well as realize the motor parameter values with excellent performance for multiple sub-targets while significantly reducing the time spent on optimization.Accordingly,the developed optimization approach has certain reference significance for the optimization of different types of motors with numerous parameters.

Acknowledgements

This work is supported by the National Natural Science Foundation of China(52077141),the Natural Science Foundation of Liaoning Province(2021-YQ-09)and the Liaoning Bai Qian Wan Talents Program,China.

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] You Y G,Li W,Liu W M,et al.(2010)Development status and perspective of marine energy conversion systems.Automation of Electric Power Systems,10(14):1-12

[2] Liu Y J,Jia R,Zhang J(2016)Research status and development prospects of wave energy power generation technology.Journal of Ocean Technology,35(5):100-104

[3] Xi X,Bai N Z,Kang Q,et al.(2014)A review of the development of wave power system and the research on directdrive wave power system.Transactions of China Electrotechnical Society,29(3):1-11

[4] Zhang H(2010)Optimization research on oscillating float structure of ocean wave power generation system.Dissertation,Tsinghua University

[5] Liu J(2015)Research on Permanent Magnet Linear Switched Reluctance Power Generation System.Dissertation,Shenzhen University

[6] M Blanco,G Navarro and M Lafoz(2009)Control of power electronics driving a switched reluctance linear generator in wave energy applications.In:Proceedings of the 2009 13th European Conference on Power Electronics and Applications,Barcelona,Spain,08-10 Sept 2009,9p

[7] Mueller,M.A.,Baker,N.J.,Brooking,et al.(2003).Low speed linear electrical generators for renewable energy applications.In:Proceedings of the conference on linear drives in industrial applications,Birmingham,UK,8-10 Sept 2003,4p

[8] Du J H,Liang D L,Xu L Y,et al.(2010)Modeling of a linear switched reluctance machine and drive for wave energy conversion using matrix and tensor approach.IEEE Transactions on Magnetics,46(6):1334-1337

[9] Liang D L,Sui H L,Du J H,et al.(2010)Modeling of wave power generation system for linear switched reluctance motor.Journal of Electrical Machines and Control,14(10):84-88

[10] Zheng H(2020)Principle Design and Optimization of Longstroke Large-thrust Linear Motor with Segmented Stator.Dissertation,Shandong University

[11] Hu Y N(2019)Research on cylindrical switched reluctance linear generator system for sea wave power generation.Science and Technology Guide,27(13):70

[12] Wang D H,Wang X H,Du X F(2017)Design and comparison of a high force density dual-side linear switched reluctance motor for long rail propulsion application with low cost.IEEE Transactions on Magnetics,53(6):1-4

[13] Wang D H,Shao C L,Wang X H,et al.(2016)Performance characteristics and preliminary analysis of low cost tubular linear switch reluctance generator for direct drive WEC.IEEE Transactions on Applied Superconductivity,26(7):1-5

[14] Wang D H,Shao C L,Wang X H(2016)Performance analysis and design optimization of an annular winding bilateral linear switch reluctance machine for low cost linear applications.IEEE Transactions on Applied Superconductivity,26(7):1-5

[15] Bao X H,Wu C J,Hu Y P,et al.(2018)A method for optimizing the performance of meter plug-in permanent magnet motor.Transactions of the China Electrotechnical Society,33(2):238-244

[16] Luo J,Kou B Q,Yang X B(2020)Optimization and design of double alternating pole transverse flux linear motor.Transactions of the China Electrotechnical Society,35(5):991-1000

[17] Chen Y Y,Zhu X Y,Quan L,et al.(2017)Optimal design and performance analysis of double salient permanent magnet double stator motor based on parameter sensitivity.Transactions of the China Electrotechnical Society,32(8):160-168

[18] Zhang B F,Cheng M,Wang S S,et al.(2020)Optimal design of flux-switched permanent magnet linear motors based on improved surrogate model optimization algorithm.Transactions of the China Electrotechnical Society,35(5):1013-1021

[19] Li X L,Li J Y,Yang G Y,et al.(2020)Multi-objective optimal design analysis of electrically excited double stator field modulation motor.Transactions of the China Electrotechnical Society,35(5):972-982

[20] Lee J J,Lee J,Kim K S(2018)Design of a WFSM for an electric vehicle based on a nonlinear magnetic equivalent circuit.IEEE Transactions on Applied Superconductivity,28(3):1-4

[21] Zhang L L(2022)An Efficient Modeling of Air Gap and Nonlinear Analysis of Magnetic Equivalent Circuit for Large Turbogenerators Under No-Load Condition.IEEE Transactions on Magnetics,58(2):1-8

[22] Zhang J,Yu H T,Chen Q,et al.(2014)Design and experimental analysis of AC linear generator with halbach PM arrays for direct-drive wave energy conversion.IEEE Transactions on Applied Superconductivity,24(3):1-4

[23] Pan J F,Cheung N C,Zou Y(2012)An improved force distribution function for linear switched reluctance motor on force ripple minimization with nonlinear inductance modeling.IEEE Transactions on Magnetics,48(11):3064-3067

[24] Lee K D,Lee J,Lee H W(2015)Inductance calculation of flux concentrating permanent magnet motor through nonlinear magnetic equivalent circuit.IEEE Transactions on Magnetics,51(11):1-4

Biographies

Zhao Xin received her master's degree in control theory and control Engineering from Shenyang University of Technology,Shenyang,China,in 2008.She joined the Shenyang University of Technology in 2008,where she is currently a researcher in electrical engineering.Her research interests include Special motor and its control system.

Dongqin Xiong received her master's degree from Shenyang University of Technology,Shenyang,China,in 2021.She is now working as an engineer in Jing-Jin Electric Technologies Co.,Ltd.Beijing,China.Her research interests include linear switched reluctance motor design.

Teng Yun received his doctor’s degree in electrical engineering from Shenyang University of Technology,Shenyang,China,in 2009.He joined the Shenyang University of Technology in 2010,where he is currently a professor in electrical engineering.He is a standing director as the IEEE PES DC Distribution Network Technical Subcommittee.His research interests include multi-energy system dispatching automation and smart grid control theory.

Zhe Chen received his B.Eng.and M.Sc.degrees from Northeast China Institute of Electric Power Engineering,Jilin City,China,and his Ph.D.degree from the University of Durham,Durham,U.K.He is a full professor with the Department of Energy Technology,Aalborg University,Aalborg,Denmark,where he is the leader of the Wind Power System Research program in the Department of Energy Technology.He is also the Danish Principle Investigator for Wind Energy of the Sino-Danish Centre for Education and Research.His research areas are power systems,power electronics and electric machines; and his main current research interests are wind energy and modern power systems.

Guangwei Liu received his B.Eng.,M.Sc.and Ph.D.degrees in electrical engineering from Shenyang University of Technology,Shenyang,China,in 2005,2008 and 2015 separately.He joined the Shenyang University of Technology in 2008,where he is currently a full professor in school of electrical engineering.His major research interests and activities are in the areas of permanent magnet electrical machines and its drive.

(Editor Dawei Wang)