0 Introduction

The generation maintenance scheduling mainly determines when to overhaul the generation unit,which aims to not only minimize the running cost of the power network and the generation system,but also ensure the reliability of the power system.As a significant factor in the production and operation of power systems,generation maintenance scheduling directly affects the risk of power shortage.If the power system is short for the reserve capacity of the generation side,unreasonable generation maintenance scheduling can result in a reduction in the frequency of the power system,and consequently,the power system will collapse,causing a large area outage.In addition,generation maintenance scheduling has an important impact on other electric power construction plans and the production of power systems,such as transmission maintenance scheduling and unit economic dispatch.

The 0–1 MIP problem—such as the generation maintenance scheduling problem and electric system planning problem — is essentially a largescale MIP problem with many decision variables and complex constraints that can hardly be used to solve.With the continuous increase in the power grid scale,the scale of decision variables and constraints in the model increases rapidly,which leads to nonlinear growth in the computational complexity of solving the MIP problem such as the generation maintenance scheduling problem.In addition,as the requirements of generation maintenance scheduling increase,increasingly complex constraints are added to the model,which will inevitably result in more time requirement to solve the model.It is difficult for the existing commercial solvers to meet the current needs of the generation maintenance scheduling problem.Thus,power systems urgently require a highly efficient optimal approach.

There are three categories of generation maintenance scheduling models under the traditional power system:the generation maintenance scheduling model with optimal economy [1–6],generation maintenance scheduling model with optimal reliability [7–14],and generation maintenance scheduling model with both reliability and economy [28–31].The aforementioned studies solve the maintenance planning problem using different algorithms:[1] uses a teaching–learning-based optimization(TLBO)as a prime optimization tool; [2] and [5] adapted Benders decomposition; [3]proposed a solution technique based on the penalty function mixed integer particle swarm optimization algorithm; and[4] employed ant colony optimization.For the generation maintenance model with optimal reliability as the objective function,the most common goal is to make the system reserve rate of each period as equal as possible.To operate the power network safely during the generation maintenance work,we attempt to minimize the sum of squares of all periods of the power system reserve [7–9],minimize the variance of all periods of the power system reserve(rate)[12],and maximize the minimum value of the power system reserve(rate)[13].[10] and [11] both used an evolutionary algorithm to tackle generator maintenance scheduling.In addition,minimizing some random safety indicators of the power system is also an effective method,including the loss of load expectation [14].A fast bounding technique accelerates the pruning node progress to improve the solution efficiency [15].

With the continuous increase in the scale of power systems,the scale of integer variables and constraints of the generation maintenance scheduling problem has increased rapidly.Meanwhile,a series of papers [16–17] have applied machine learning to solve combinatorial problems,which is a hotspot in the research of integer programming and combinatorial optimization.Compared to traditional algorithms,combinatorial optimization with machine learning has a series of advantages,such as faster solution speed and strong generalization ability.[18] proposed a new combination problem with learning; the solving speed of the proposed algorithm exceeded that of some professional solvers such as Google OR-tools and LKH3.[19] designed a graph pointer network(GPN)combined with a pointer network and graph neural network to solve largescale traveling salesman problem(TSPs).TSP with a time window constraint was tested,and its performance exceeded that of OR-tools and the ant colony algorithm.[20] proposes a supervised machine learning method to solve the integer programming problem in millimeter-wave communication resource scheduling.[21] attempted to learn to branch in the process of integer programming of resource allocation in wireless networks.[22] proposes a graph embedding method to solve the integer programming problem in wireless link resource scheduling and allocation.

The present paper has the following contributions:

(1)Considering various maintenance workflows and energy constraints of the power system,this paper proposes a generation maintenance scheduling model to maximize the reliability of the power system during generation maintenance.

(2)To solve the generation maintenance scheduling model problem efficiently,this paper presents a variable branching algorithm based on support vector machine(SVM)during the progress of branch-and-bound,which is based on the features of the proposed generation maintenance scheduling model.

The paper is structured as follows.Section 1 describes the objective and constraints of the generation-scheduling model.Section 2 proposes the variable-selection method based on SVM during the branch-and-bound process.Then,we use the IEEE 118-bus system to demonstrate the computational efficiency of the variable branching algorithm compared with the direct application of the commercial solver.Finally,Section 4 concludes the study.

1 Modeling of the generation maintenance scheduling problem

1.1 Objective

In general,maximizing the reliability index is the objective of the generation maintenance scheduling problem.The commonly used reliability index for generation maintenance scheduling is mainly divided into two categories:certainty and randomness.A certain reliability index includes maximizing the minimum reserve,equaling the reserve of every generation,equaling the reserve rate,etc.The random reliability index includes the expectation of the unserved energy and the rate of load rejection.Given that the optimization objective of a certain reliability index is clear and easy to realize,a reliability index,such as an equal reserve rate,is usually used for engineering applications.When the system reserve is sufficient,the variance of the reserve or the reserve rate in the entire period is minimized to reach an equal reserve or equal reserve rate,respectively.However,considering the nonlinear characteristics of the method,we propose the reliability index ζ as:

where T denotes the total annual maintenance schedule period.St is the system reserve in period t.Equation(1)ensures that the system reserve in adjacent periods is as close as possible,and we obtain an equal reserve in every period.

However,Eq.(1)is nonlinear,which is difficult to solve directly using a commercial solver.Therefore,we transform Eq.(1)into a linear form as follows:

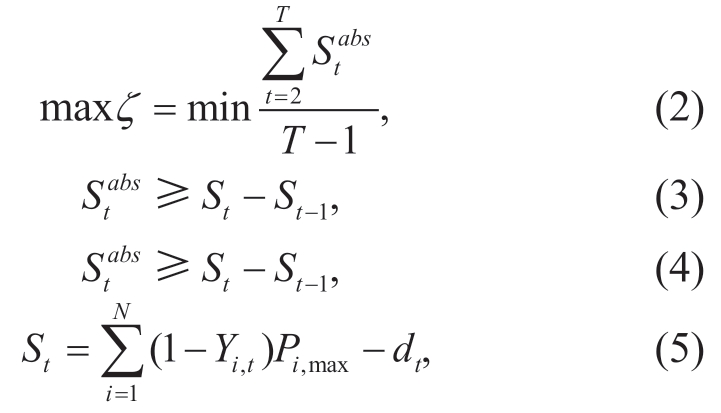
where Yi,t is the state of unit maintenance in period t,Pi,max is the maximum power of the generation,and dt is the total load in period t.

1.2 Constraints

(i)Integrality requirements:

The model introduces 0–1 decision variables for each maintenance generation unit per day.Xij,t is a maintenance status variable of the generation unit,and Xi,t=1 indicates that generation unit i is offline in outage window t.The integer constraint is expressed as follows:

where the quantity of the maintained generation units is Nm,and the maintenance window of generation units i is MTi.

(ii)Duration constraint of generation maintenance:

Given that every generation unit may need to be on maintenance more than once,the outage duration constraint of generation unit i is:

where MDi is the duration of unit maintenance.

(iii)Continuity constraint of generation maintenance schedule.

The maintenance of generation must be completed continuously.Then,the continuity constraint is

where

(iv)Mutual exclusion constraints for generation maintenance.

Given the personnel and material arrangement of power plants,they usually want generation units to be overhauled at different times.In addition,the operation of the power network control center also sets the generation unit maintenance at different times.

where Φel is the set of generation units overhauled mutually exclusively.

(v)Upper limit constraints of simultaneously maintained generation units.

The electrical power dispatch center usually limits the upper threshodsof the generation made offline for every maintenance window to coordinate the maintenance staff and tools.

where Φsm is the simultaneously maintained set of the generation units.Ns,t is the upper threshods of the simultaneous maintenance sets s in period t.

(vi)Sequential maintenance constraints.

If the generation unit g2 must undergo overhaul after generation unit g1,then the sequential maintenance constraint is:

where Φsq is the sequential maintenance set of the generation units.

(vii)Power system reserve constraints.

where dt denotes the total load of the power system.R is the power system reserve rate.

(viii)Power generation constraint of generation unit i:

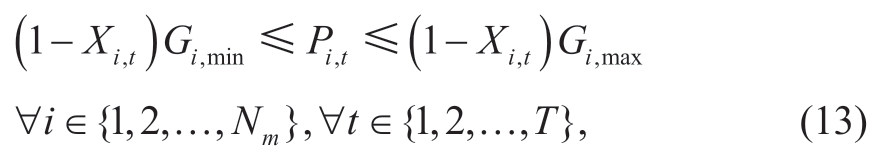
where Gi,min represents the minimum power of generation unit i and Gi,max is the maximum power generation.Pi,t is the power generation by the generation unit i.

If the generation is not requested to be on maintenance,then

(ix)Line transmission limit constraints.

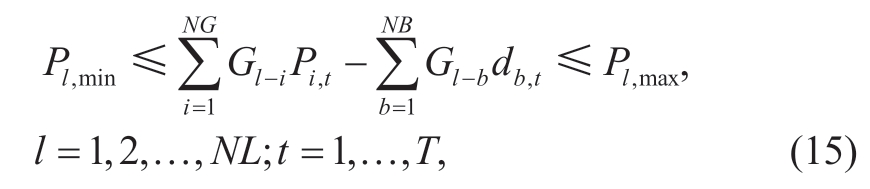
where NB is the number of buses in the power network,and NG is the number of generation units.Pl,min is the minimum limit of transmission line l and Pl,max is the maximum.Gl−i is the transfer distribution factor of generation unit ito transmission line l.Gl−b is the transfer distribution factor of bus i to transmission line l.db,t is the load of bus b in period t.

2 Solution of the generation maintenance scheduling model

The variable selection for branching during the branchand-bound process is the main component of commercial MIP solvers.During the branch-and-bound process,we first select one of the unassigned variables,and then add additional constraints to split its feasible region and expand the two child nodes in a search tree.In general,choosing suitable candidates to branch,often directly affects the number of nodes to solve an MIP model.In this study,we attempted to develop a variable selection strategy.

2.1 Problem definition

MIP is an optimization problem of the form:

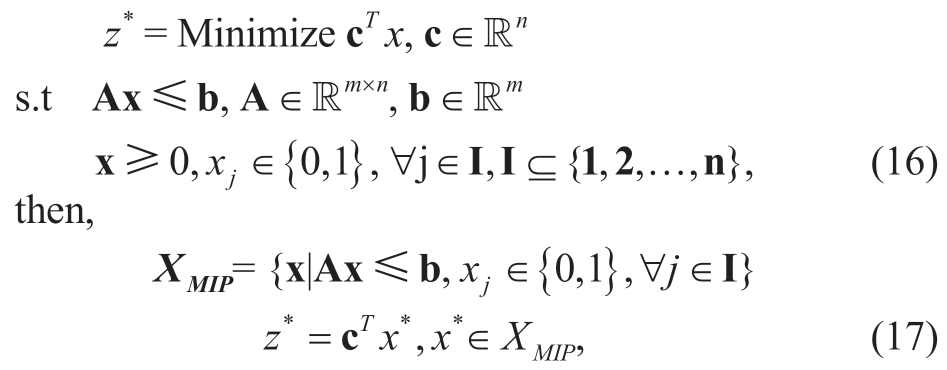
where x* is a feasible solution,z* is the objective,and XMIP is the solution set for problem(16).

Subsequently,the relaxation of the MIP is

2.2 Branch-and-bound and strong branching(SB)

The branch-and-bound algorithm for MIP iteratively divides each MIP problem into subproblems.During the progress of the branch-and-bound,are the new bounds for that variable in each of the two subproblems for the integer variable xj with an linear programming(LP)relaxation solution value x~j.In this study,we chose strong branching(SB)as the default branching strategy for measuring the quality of the branching on variable xj by computing the improvement in the dual bound.The SB strategy scores the total variables at a node,and then selects the variable with the highest score to branch.The score of SB strategy branching on variable xj is as follows:

where,is the LP value of node Nj,andare the LP values of the two child nodes,respectively.are the changes in the objective values while branching on xj downwards and upwards on xj.

2.3 Framework of learning to branch in MIP with SVM

This study attempted to develop a model that can rank candidate variables during the traditional branch-and-bound process of a commercial solver.The main framework for learning to branch was to observe and record the rankings induced by SB.The framework for a specific generation maintenance problem consists of the following three parts:

(1)SB:in the first θ nodes during branch-and-bound,the framework assigns labels to the candidate variables with the computed SB scores [23] and obtains the corresponding variable features.

(2)Model learning:the framework feeds the training data from the first θ nodes into a learning-to-rank algorithm based on SVM and obtains a vector of weights for the features.

(3)Learning-based branching:the framework scores the variables of the learned weight vector and branches on the node with the top-ranked score until the end of the branchand-bound process.

2.3.1 Labels and features of the data collection

For the variable selection strategy,we ran the branchand-bound algorithm with SB for the first θ nodes.The training data comprised the following parts:

(1)A set of branch-and-bound search tree nodes N={N1,N2,…,Nθ};

(2)A set of search candidate variables Ci for node Ni;

(3)Labelsfor candidate variables at each node Ni;

(4)A featureis the variable xj at node Ni with p features.

The labels and features of the collected data in the first θ nodes during SB are shown below.Firstly,the labelof node Nj in the candidate variables set Ci is as follows:

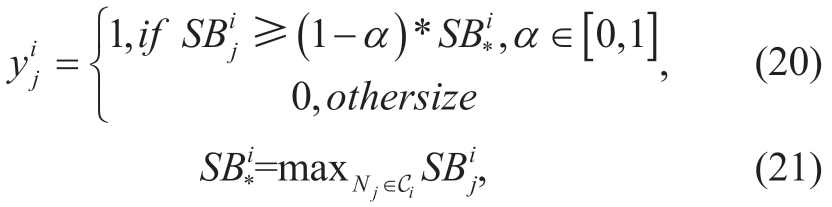
whereis the SB score for variable j in the set of candidate variables Ci of Ni.α ∈ [0,1] is the fraction of the maximum SB score that a variable should have in order to get a ‘1’ label.For instance,when α=0.2,variables whose SB scores are within 20% of the maximum score are assigned a label of ‘1’.is the label of the variable xj that is in the candidate variables set Ci of node Ni.

Second,the feature map Φ shows the computed state of the node of the variable.The features used in this study are listed in Table 1.

Table 1 Feature statistics of the dataset

The features of the objective function coefficient include three types of coefficient value:raw,positive,and negative.The features of constraint in the generation maintenance scheduling problem also include four types:the number of constraints,degrees of constraints,coefficients of constraints,and active or valid constraint coefficients.To explain the features of the constraint more clearly,four types of constraint features are shown below:(1)the number of constraints only includes the constraints that the decision variables participated in with a nonzero coefficient.The decision variables in the generation maintenance scheduling problem are the maintenance decision variables for each maintenance generation unit per day.(2)The degree of the constraint is the number of variables in the constraint.A variable may participate in multiple constraints,and statistics on the degrees of these constraints are used.To facilitate practical applications,the constraint degree is computed using the root linear programming subproblem.The four features of the constraint degree are the mean value,standard deviation,minimum value,and maximum value of the degree of each constraint.(3)The coefficients of constraints of the variables are positive and negative.The statistics of the coefficients include the number of positive coefficients,number of negative coefficients,mean value,standard deviation,and minimum and maximum values.(4)A valid constraint in a node linear programming problem is one that binds with equality at the optimum.The four features of the valid constraint include the dual cost of a constraint,sum of the coefficients of all the variables in a constraint,sum of the coefficients of only the candidate variables in a constraint,and sum of the coefficients other than the candidate variables.For every feature proposed above,we computed the sum value,mean value,standard deviation,minimized value,maximum value,and weighted number of active constraints in the candidate variable.

2.3.2 Learning and branching with a variable ranking function

Firstly,the learning problem can be described as follows:

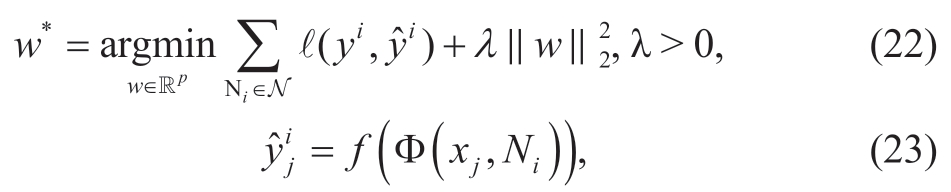
where ℓ(.)is the loss function of arranging the variables in order at node Ni based on Eq.(23).

The study learns a function f that minimizes the degree of pairwise ordering constraint violation to imitate SB rank variables:

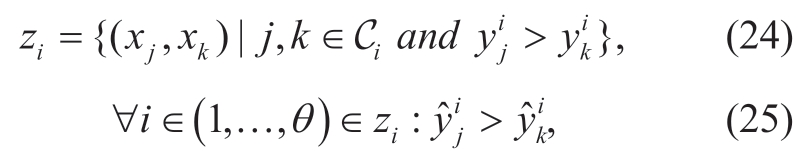
where zi is the set of pairs of node Ni; in this study,SVMrank[24–25] with a loss and weights of each term in the sum was used in Eq.(22)by 1/|Pi|.

Second,after selecting the variable θ nodes with the SB strategy during the branch-and-bound process,we learned the vector w from the collected data,and then transferred the variable selection strategy to the function f.

2.4 Algorithm procedure

(a)Construct a reliability index for the generation maintenance scheduling problem.

(b)Add the proposed constraints(6)–(15)and objective function(1).

(c)Set the upper error limit,σ.

(d)Run the SB strategy to select variables during the branch-and-bound process for the first number of nodes θ,and collect the features and labels of these nodes.

(e)Fit the branching strategy function with the SVM in the model-learning stage.

(f)Branch the variables with the learned branching strategy in the machine-learning stage.

(g)Terminate the process if the solution of the model is within the acceptable error range.

The solution process of the generation maintenance scheduling model is shown in Fig.1.

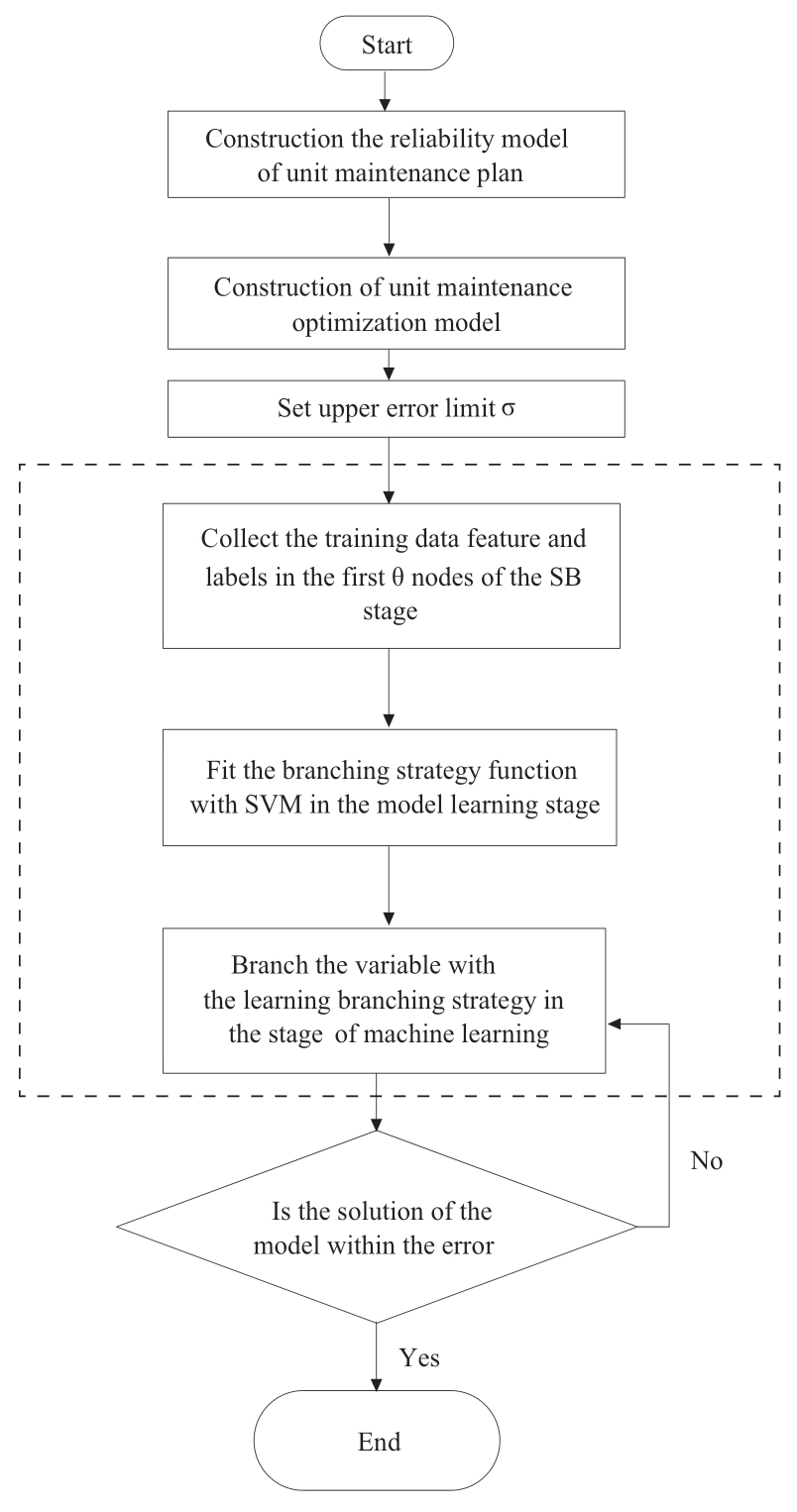
Fig.1 Flow of the algorithm

3 Experiment

This study demonstrates the rationality of the generationscheduling model to maximize the reliability of the power system and variable branching algorithm in the IEEE 118-bus system.We set 52 weeks for the generation-scheduling model per year.The Python API of CPLEX 12.6.1 was applied to maintenance problems.We used the callback function of the commercial solver to implement various strategies for variable selection during the branch-andbound process.

The lower limit of the reliability index ζ set by the dispatching center was assumed to be 0.0001.When the reliability index ζ of the power system is greater than the lower limit of ζ set by the dispatching center,the generation maintenance schedule satisfies the requirements of power system reliability.

To isolate the effects of the branching variables with the learned branching strategy,we set two policies for the solver:1.primal heuristics are disabled; and 2.only cuts at the root node are allowed.

3.1 Generation maintenance experiment data

The list of maintenance-related parameters of the generation units in the IEEE 118-bus system in Tables 2 and 3 are the set of generation units that must be shut down for service in different periods and the sequential maintenance set of generation units in Table 4.The annual load profile of the system is shown in Fig.2.In addition,the system reserve rate was set to 0.1 for the system load.Moreover,the upper number of generations overhauled in a period was set to 4.

Table 2 Generation maintenance schedule for 52 weeks

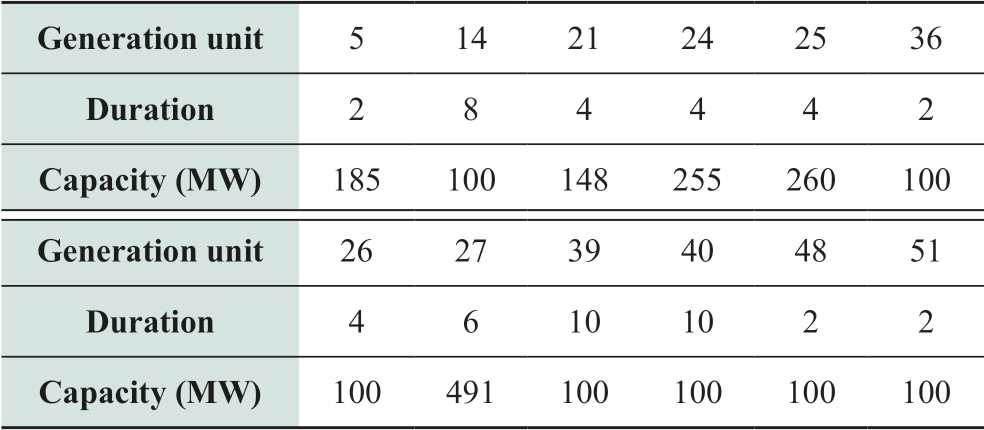
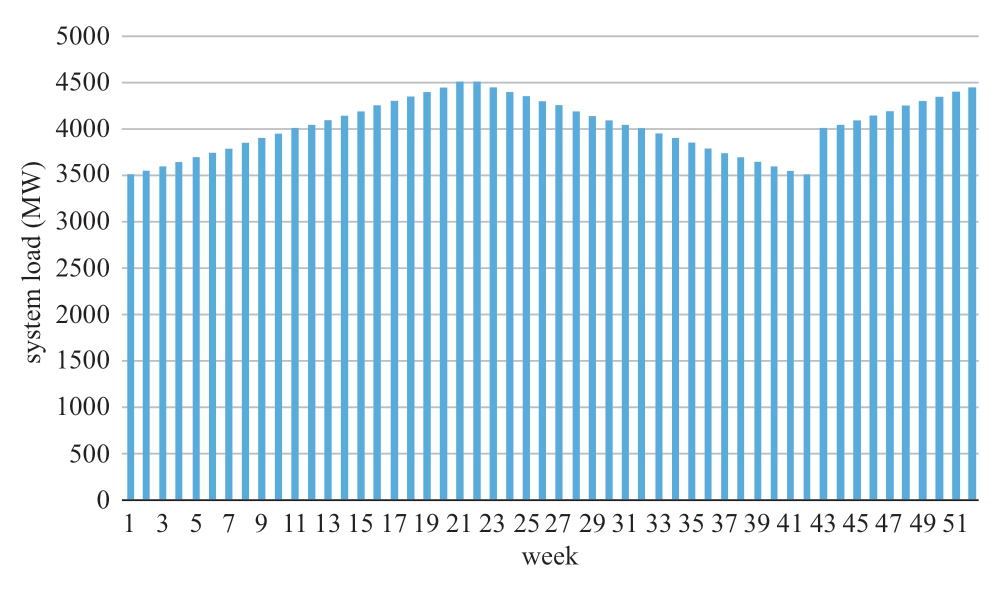
Fig.2 System annual load profile

Table 3 Mutual exclusion maintenance set of generation units

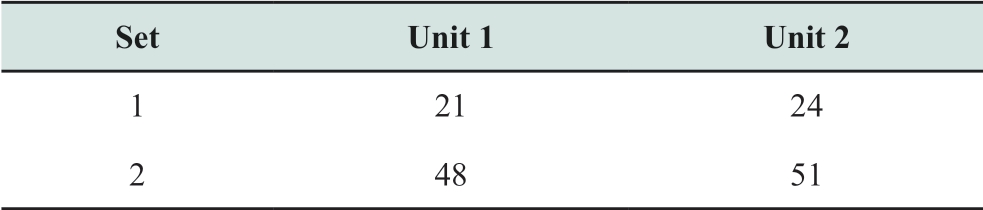
Table 4 Sequential maintenance set of generation units

3.2 Learning to branch with SVMrank

We experimented with SB strategies for the first 500 nodes and SVMrank strategies.We used α=0.2 and SVMrank strategies with C=0.1 [λ in Eq.(22)is a function of C]balance training error and margin.In the experiment,we chose the default variable selection rule CPLEX-D as the strategy that branches on the variable within a callback function.

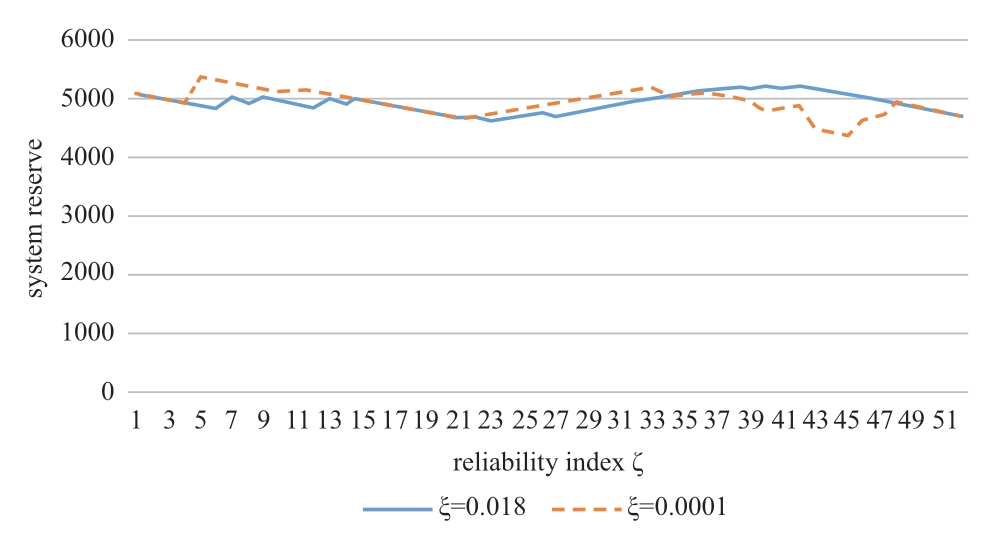
Fig.5 Comparison of the system with Gap=0.1%

3.3 Result analysis

According to the generation maintenance scheduling model based on safety and reliability,the dispatching center arranges the generation maintenance schedule,as shown in Fig.3.

Fig.3 Generation maintenance schedule for 52 weeks

In the experiment,the optimization objective function was 50.41,and the reliability index ζ was 0.18 when the gap was 50%.The reliability index ζ was greater than 0.0001;therefore,the proposed model satisfies the requirements of power system reliability.When the gap is between 1%and 0.1%,the reliability index ζ is sufficient to meet the requirements of the power system.

To show how the model proposed in this paper can improve the reliability of the power system,we set the reliability index ζ equal to the lower bound 0.0001 in the code,so as to compare the system reserve of the proposed model and the lower bound.Figure 4 shows that the system reserve of the proposed model(ζ=0.18)has smaller performance variability.In addition,the larger the reliability index ζ,the smaller is the volatility of the system reserve.More importantly,the proposed model(ζ=0.18)can clearly control the difference between the system reserves of adjacent periods in a small range,as shown in Fig.6.

Fig.6 Comparison of the absolute value of the system reserve difference

To illustrate the improvement in computation time achieved through the variable selection method based on SVM,Fig.4 shows the result of the difference in computational efficiency between the direct application of CPLEX for various values of the gap and the method proposed in this paper when solving the generation maintenance scheduling plan.The variable-selected method based on SVM improves the computational efficiency compared with the direct application of the commercial solver when there is a gap in the different values,as shown in Fig.4.Therefore,the variable selection method based on the SVM to solve the model is highly effective.

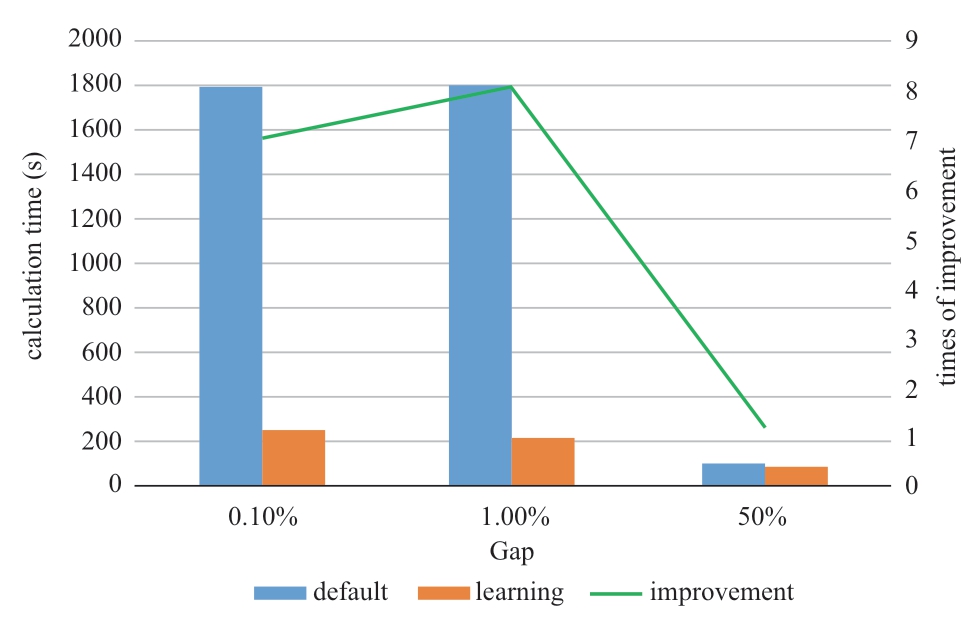
Fig.4 Comparison of the computation time

4 Conclusion

This paper proposes a generation maintenance scheduling model to improve the reliability of the power system during the shutdown and maintenance of generation units.Moreover,the model considers the network security and rationality constraints of the generation maintenance practice in the power system.In view of the computational complexity of the generation maintenance problem,a variable-selection method based on an SVM is presented to solve the problem.The experiment shows that the generation maintenance model can ensure the safety of the power system,and the branching algorithm based on the SVM during the branch-and-bound process can solve the model in a shorter time scale.

Acknowledgements

The authors thank the Key R&D Project of Zhejiang Province(No.2022C01056)and the National Natural Science Foundation of China(No.62127803).

Declaration of Competing Interest

We have no conflict of interest to declare.

References

[1] Abirami M S G,S Subramanian,et al.(2014)Source and transmission line maintenance outage scheduling in a power system using teaching learning based optimization algorithm.Applied Soft Computing,21(21):72-83

[2] Canto S P(2008)Application of Benders’ decomposition to power plant preventive maintenance scheduling.European Journal of Operation Research,184(2):759-777

[3] Ekpenyong U E,Zhang J,Xia X(2012)An improved robust model for generator maintenance scheduling.Electric Power Systems Research,92(92):29-36

[4] Fetanat A,Shafipour G(2011)Generation maintenance scheduling in power systems using ant colony optimization for continuous domains based 0-1 integer programming.Expert Systems with Applications,38(8):9729-9735

[5] Lusby R,Muller L F,Petersen B(2013)A solution approach based on Benders decomposition for the preventive maintenance scheduling problem of a stochastic large-scale energy system.Journal of Scheduling,16(6):606-628

[6] Mollahassanipour M,Abdollahi A,Rashidinejad M(2014)Application of a novel cost reduction index to preventive maintenance scheduling.International Journal of Electrical Power&Energy Systems,56(3):235-240

[7] Dahal K P,N Chakpitak(2007)Generator maintenance scheduling in power systems using metaheuristic-based hybrid approaches.Electric Power Systems Research,77(7):771-779

[8] Foong W K,Simpson A R,Maier H R,et al.(2007)Ant colony optimization for power plant maintenance scheduling optimization-a five-station hydropower system.Annals of Operations Research,159(1):433-450

[9] Mohanta D K,Sadhu P K,Chakrabarti R(2004)Fuzzy reliability evaluation of captive power plant maintenance scheduling incorporating uncertain forced outage rate and load representation.Electric Power Systems Research,72(1):73-84

[10] Reihani E,Sarikhani A,Davodi M(2012)Reliability based generator maintenance scheduling using hybrid evolutionary approach.International Journal of Electrical Power&Energy Systems,42(1):434-439

[11] Schlunz E B,Vuuren J H(2013)An investigation into the effectiveness of simulated annealing as a solution approach for the generator maintenance scheduling problem.International Journal of Electrical Power&Energy Systems,53:166-174

[12] Suresh K,Kumarappan N(2013)Hybrid improved binary particle swarm optimization approach for generation maintenance scheduling problem.Swarm and Evolutionary Computation,9:69-89

[13] Chen L,Toyoda J(1991)Optimal generating unit maintenance scheduling for multi-area system with network constraints.IEEE Transactions on Power Systems,6(3):1168-1174

[14] Volkanovski A,Mavko B(2008)Genetic algorithm optimization of the maintenance scheduling generating units in a power system.Reliability Engineering & System Safety,93(6):757-767

[15] Wang P,Wang Y,Xia Q(2012)Fast bounding technique for branch-and-cut algorithm based monthly SCUC.Proceedings of IEEE Power & Energy Society General Meeting,San Diego.

[16] Ybc B,Ala B,Apa B(2020)Machine learning for combinatorial optimization:A methodological tour d’horizon - ScienceDirect.European Journal of Operational Research

[17] Li KW,Zhang T,Wang R,et al.(2021)Research reviews of combinatorial optimization methods based on deep reinforcement learning [J].Acta Automatica Sinica,47(11):2521-2537

[18] Lu H,Zhang X W,Yang S(2020)A learning-based iterative method for solving vehicle routing problems.In:Proceedings of the 8th International Conference on Learning Representations.Addis Ababa,Ethiopia

[19] Ma Q,Ge S W,He D Y,et al.(2020)Combinatorial optimization by graph pointer networks and hierarchical reinforcement learning.In:Proceedings of the 1st International Workshop on Deep Learning on Graphs:Methodologies and Applications.New York,NY,USA:AAAI

[20] R Liu,M Lee,G Yu,et al.(2020)User association for millimeterwave networks:a machine learning approach.IEEE Transactions on Communications,68(7):4162-4174

[21] M Lee,G Yu,G Y Li(2020)Learning to branch:accelerating resource allocation in wireless networks.IEEE Transactions on Vehicular Technology,69(1):958-970

[22] M Lee,G Yu,G Y Li(2021)Graph Embedding-Based wireless link scheduling with few training samples.IEEE Transactions on Wireless Communications,20(4):2282-2294

[23] Achterberg T,Berthold T(2009)Hybrid branching.In CPAIOR.Springer.309-311

[24] Joachims T(2002)Optimizing search engines using clickthrough data.In KDD,133-142

[25] Joachims T(2006)Training linear SVMs in linear time.In KDD,217-226

Biographies

Jingcheng Mei is currently pursuing his Ph.D.degree at the College of Electrical Engineering,Zhejiang University,Hangzhou,China.His current research interests include maintenance optimization with power systems.

Jingbo Hu was admitted to a Master of Engineering program in Electronics and Communication Engineering from Zhejiang University in September 2018.Since 2014,he has been working in power supply companies in cities and counties,and he currently serves as the deputy general manager of the Huachuang branch.He specializes in the dispatching of control automation; the operation,maintenance,and overhaul of the distribution network; material planning management;science and technology management; energy big data analysis; and new energy operation.

Zhengdong Wan received his Bachelor’s degree from Huazhong University of Science and Technology,Wuhan in 2007,and Master’s degree from Harbin Institute of Technology,Harbin,in 2009.He is working at the Energy Development Research Institute,China Southern Power Grid,Guangzhou.His research interests include economic engineering and power grid engineering cost.

Donglian Qi is currently a professor at the Zhejiang University.Her current research focus is on cyber physical power systems(CPPSs).

(Editor Yanbo Wang)