0 Introduction

In the current energy landscape,the penetration rate of renewable energy has irreversibly increased because it is sustainable,clean,and has low operating costs [1].However,its intermittent and unpredictable characteristics limit its development [2].A battery energy storage system(BESS)can suppress the power fluctuation of renewable energy,which is an effective way to address this limitation[3-4].

In recent years,large scale renewable energy applications have required greater installed capacity and higher voltage levels.The traditional low-level structures of BESS cannot meet the demand for high power and voltage levels.The cascaded H-bridge converter has been effective in high-voltage applications because of its modularity,simple boosting voltage,and flexible controllability [5].Using this cascaded H-bridge converter topology,BESS can be deployed for large-capacity and high-voltage applications.

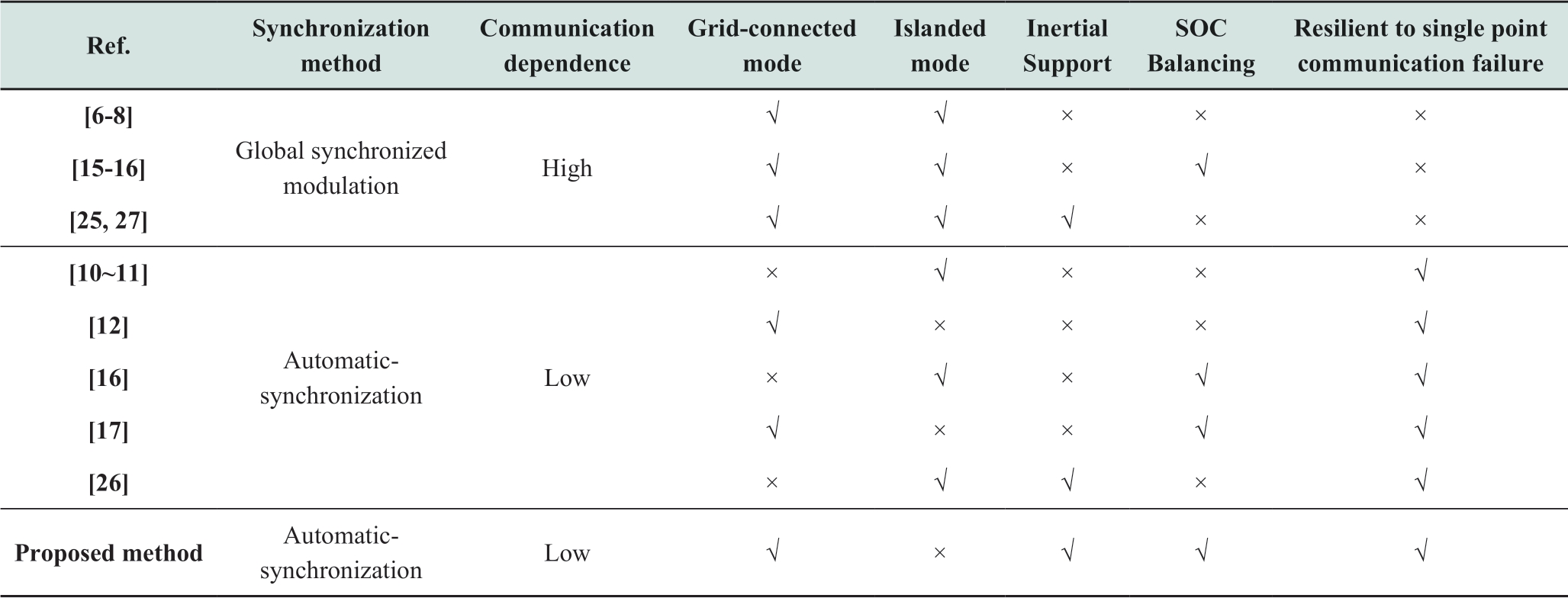
Traditional control strategies [6-8] rely on the central controller and high-bandwidth communication,in which all control commands are generated and transmitted by communication links.Although the central control has adequate control performance,the high computation load and communication vulnerability risks decrease the control reliability.Moreover,when the cascaded H-bridge-based BESS further expands into a larger scale,there will be regional differences between distributed generators(DGs).Moreover,the communication network of centralized control is complex and high-cost.These limitations restrict the development of centralized control.Decentralized methods are being studied by researchers to localize control and reduce the communication burden.He et al.[9]proposed the inverse power factor control,which enables synchronization and power-sharing.Sun et al.[10] analyzed the power transmission characteristics and proposed an f-P/Q control with wider application to resistor-capacitor(RC)loads.A fully decentralized control method has been proposed for grid-connected modes [11],which uses droop scheme control to realize the synchronization between modules.However,these decentralized methods have not taken the characteristics and function into account,such as offering inertia control for friendly grid connections and achieving SOC balance in each battery module.To achieve these,many researchers have been focusing on battery characteristics and their functions in grid or renewable systems.

Different initial SOC values and operation states lead to SOC unbalancing,which has adverse effects on battery life and operational safety [12-13].To address this issue,Maharjan et al.[14] proposed an SOC balancing method with zero-sequence voltage injection for a threephase cascaded H-bridge BESS.However,it relies on the central controller and cannot be applied to a singlephase cascaded H-bridge BESS.A hierarchical control[15],based on a central controller,has been proposed for frequency/voltage regulation and SOC balancing.To reduce computation load and communication burden,Shi et al.[16]proposed a decentralized method for SOC balance without communication in an islanded mode.However,with only local information,SOC balancing can be achieved with a low transient response,and the additional modification for SOC balancing can induce additional frequency deviation.In a grid-connected mode,this method is invalid for the fixed frequency limited by the grid.Xu et al.[17] proposed a distributed control for a cascaded H-bridge BESS in a grid-connected mode.This method can achieve accuracy in active and reactive power distribution and SOC balancing.However,frequency synchronization still relies on synchronized modulation and does not consider frequency inertial support capability.

On the other hand,as most renewable sources cannot support frequency inertia such as synchronous generators,the frequency stability problem will be exacerbated under the high penetration rate of renewable sources [18-19].For supporting grid frequency inertia,a virtual synchronous generator(VSG)control has been proposed [20],whereby the converter operates as a synchronous generator.To date,VSG control methods [21~24] with parallel converter systems,designed for low voltage levels,have been mainly studied.As for the cascaded H-bridge system,a grid-supporting strategy using the VSG algorithm for photovoltaics(PV)has been proposed[25],which is limited to low inertial support determined by the reserve active power.Li et al.[26] introduced a decentralized mutual damping control scheme of islanded cascaded-type VSGs to suppress power and frequency oscillation,which cannot be applied to grid-connected modes.As for pure BESS,a VSG control was designed by controlling the overall output performance as a VSG operation [27].Li et al.[28] proposed a stability enhancement VSG strategy for a cascaded-multilevel-converter-based energy storage system under weak grid conditions.However,these VSG control strategies for the cascaded H-bridge-based BESS depend on the central controller.As the scale of BESS increases,the central controller will no longer be feasible owing to the high computational load and communication vulnerability risk.

To address this limitation,this paper proposes a distributed VSG control for a cascaded H-bridge-based BESS in a grid-connected mode.The primary VSG control was conducted for frequency synchronization and frequency inertial support with only local information.In addition,the output power reference was modified with only local and neighboring SOC information to realize SOC balancing.Because the SOC varies gradually,the communication bandwidth for exchanging SOC information can be designed to be extremely low,which can reduce communication costs.As the primary VSG control was conducted without communication,communication failure and delay had little effect on the basic control of the BESS,which decreased the SOC balancing accuracy and convergence speed.Thus,compared with previous strategies for cascaded H-bridgebased BESS,the proposed method can simultaneously provide inertial support and accurate SOC balancing,as shown in Table 1.Moreover,the distributed control can improve the reliability over single-point communication failure.Finally,the stability of proposed control was verified using root locus analysis,and its feasibility was verified using a simulation test.

Table 1 Comparison with previous cascaded system strategies

The remainder of this paper is organized as follows:Section 1 presents the structure and the power transmission characteristics of the grid-connected mode.The proposed control design is discussed in Section 2.The stability analysis with root locus is addressed in Section 3.The simulation results are presented in Section 4 to verify the effectiveness of proposed control method.Finally,the conclusions are summarized in Section 5.

1 Configuration and mathematical model of BESS

Fig.1 shows the structure of the cascaded H-bridgebased BESS,which consists of n battery modules,and the output terminal of the interface converter is connected in series.The battery module and its interfacing converter can be equivalent to a voltage source unit.In Fig.1,the output voltage of the i-th unit is defined as Vi∠δi.and Vg∠δg represents the grid voltage.Zline and θline represent the impedance amplitude and angle of the line,respectively.According to circuit theory,the output voltage of the point of common coupling is derived as

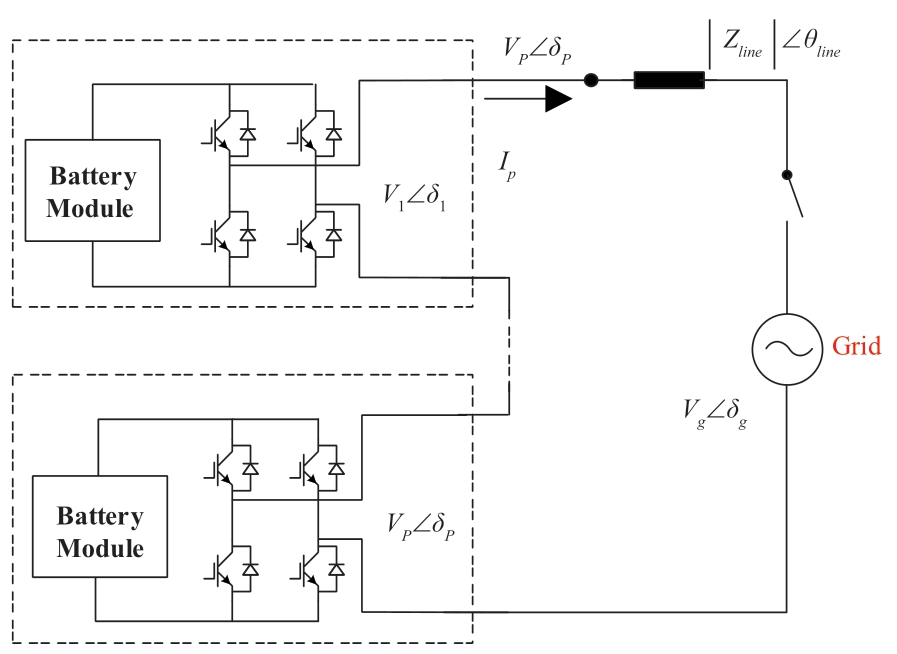
Fig.1 Structure of the cascaded H-bridge-based BESS

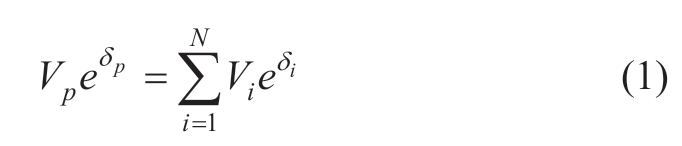
where Vp and δp are the voltage amplitude and angle of the power control center(PCC),respectively.

Because all units are connected in series,their output currents are the same,which can be derived as

where Ip and δp represent the common output current amplitude and angle of each unit,respectively.

Combining(1)and(2),the output active power and reactive power of i-th units in BESS can be derived as

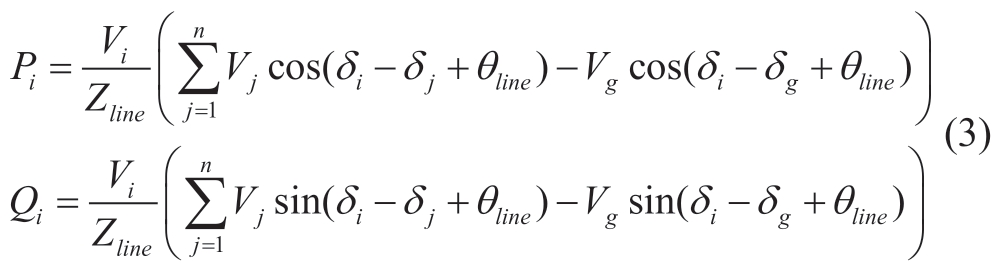
In this study,the basic Coulomb counting method was adopted to estimate the local SOC,given by

where SOCi0 is the initial SOC value of the i-th battery module,idc is the dc output current of the battery,and Ci denotes the nominal capacity of the i-th battery.

2 Control design of the proposed SOC-balancing control method

For a cascaded H-bridge-based BESS,the key control objectives are summarized as follows:

1.Frequency synchronization among all units and grid.

2.SOC balancing among all battery modules.

3.Initial support under varying grid frequencies.

This paper proposes a distributed VSG control to achieve the aforementioned goals.In this control scheme,frequency automatic-synchronization and inertial support capability can be achieved by simulating the behavior of the conventional synchronous generator.Moreover,a distributed SOC average algorithm was designed for realizing SOC balancing.

2.1 Estimation of the distributed SOC average

To achieve SOC balancing,a distributed SOC average estimation method,generated by local SOC information and averaged SOC information exchanged from neighbors,was designed.The expression of the i-th SOC average estimator is given as

where Ni represents the collection of neighboring nodes i,and aij represents the communication weight of node i receiving the data of node j.Generally,aij=1 if there is an edge connecting node i to node j,and aij=0,otherwise.

A low-bandwidth communication network is required to exchange information from neighboring units,which uses a ring communication structure,as shown in Fig.2.The communication links are bidirectional to connect with the neighboring nodes.Ni denotes the set of all neighbors of node i.

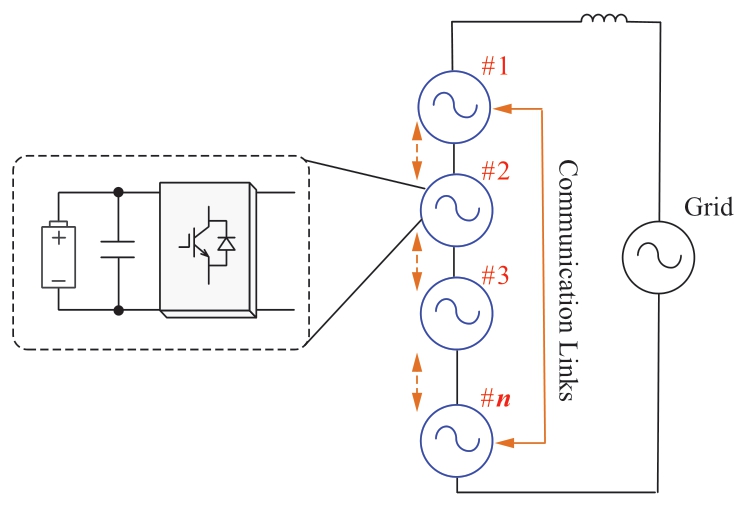
Fig.2 Communication topology of the cascaded H-bridge-based BESS

The dynamics of the SOC-balancing method can be rewritten in matrix form as

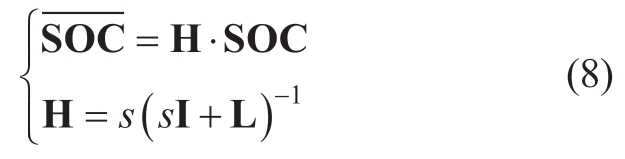
whereand SOC=I is the unit diagonal matrix,and H is the average SOC-estimator-transfer-function matrix.L is a Laplacian matrix carrying the information of the communication graph.According to Zhong et al.[29],if the Laplacian matrix L is balanced,the average SOC values converge,which means that all the elements of matrixconverge to the average SOC values of the BESS.Therefore,we have

2.2 Proposed VSG control scheme considering SOC balancing

As the change rate of the SOC is related to the output active power,increasing or decreasing the output active power of each battery module can alter the SOC change rate.Combining this characteristic and VSG control,the proposed control algorithm is given as

where Ji,Di,Pi,and SOCi are the inertia coefficient,damping coefficient,average output active power,and SOC value of the i-th battery module,respectively.denotes the average SOC of the BESS estimated by each average SOC estimator.k represents the SOC balancing coefficients,which are usually equal.

The overall control diagram is shown in Fig.3,which includes two-layer control.The primary layer control was designed based on the VSG control.It employs local active power information as a feedback signal to modify the output voltage frequency reference.Because of the coupling relationship between active power and frequency,the system can achieve synchronization autonomously[26].The second layer was designed for SOC balancing.First,a distributed SOC average estimation was devised to obtain an approximation of the global SOC average.Next,using the deviation of the local SOC and the estimated SOC average,the power reference of the primary VSG control was modified,aiming to balance the SOC.As the SOC varies slowly,the bandwidth of communication can be very low,which can decrease the communication dependency and cost.Moreover,each H-bridge converter was connected with an LC-filter to suppress additional harmonics,thereby ensuring an acceptable power quality.

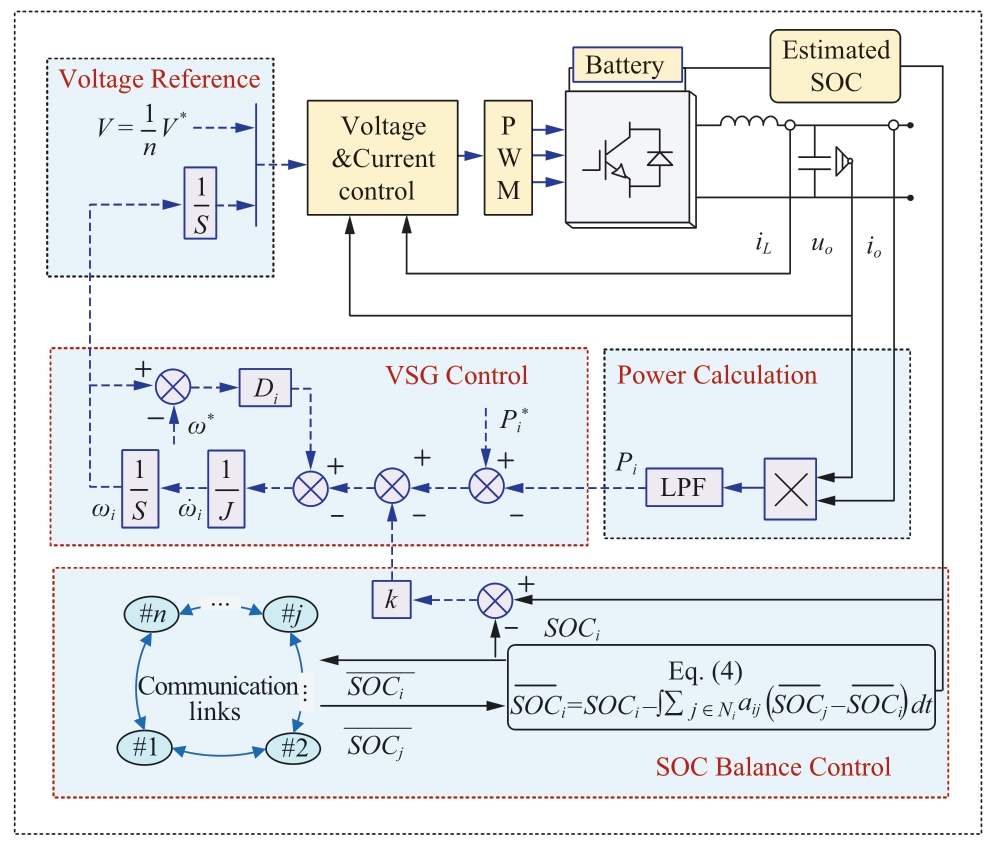
Fig.3 Proposed control scheme for the cascaded H-bridge-based BESS in grid-connected mode

2.3 Feasibility analysis of SOC balancing based on singularity theory

The frequency synchronization was achieved in steadystate,which is expressed as

As the SOC varies on a large time scale,according to the singularity theory,the SOC can be regarded as a constant when analyzing the steady-state of the primary VSG control[30].

Substituting(9)into(12),we can obtain

Eq.(14)shows that in discharging mode,when SOCi is larger than SOCave,Pi increases,and when SOCi is less than SOCave,Pi decreases.On the other hand,in charging mode,when SOCi is larger than SOCave,the charge power|Pi| decreases,and when SOCi is less than SOCave,the charge power |Pi| decreases.Therefore,there is a negative feedback to adjust the SOC.

Ignoring the power electronic loss,the SOC expression in Eq.(4)can be rewritten as

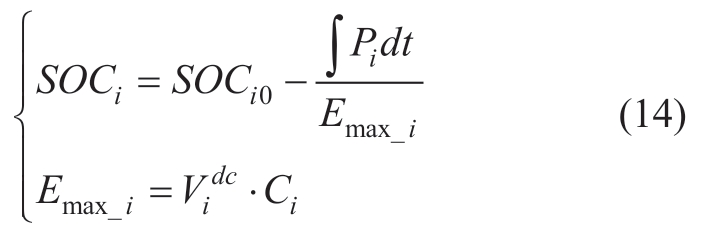
where Emax_i denotes the maximum energy of the i-th battery,and Vidc is the DC voltage of the battery.For simplicity,we assume Emax_i=Emax_j=Emax.

Substituting Eq,(14)into Eq.(13),we have

Because the SOC varies continuously,we defined Zij =SOCi -SOCj.Then,we can obtain

The solution of the differential equation is derived as

where

In the steady-state t=∞,we can determine that SOC balancing is eventually realized,as follows:

3 Stability analysis

To analyze the stability and dynamic response of the proposed control,root locus analysis was used to study the control parameters of the system,which considers the four VSGs connected in series as the research object [31].The parameters of the VSGs are shown in Table II.

The small-signal model of the output active power can be derived as

where the subscript s indicates steady-state.

By linearizing the first formula in Eq.(10),the matrixequation of the four VSGs grids can be obtained as

The small-signal model of the SOC average algorithm(7)and SOC estimation(14)are derived as

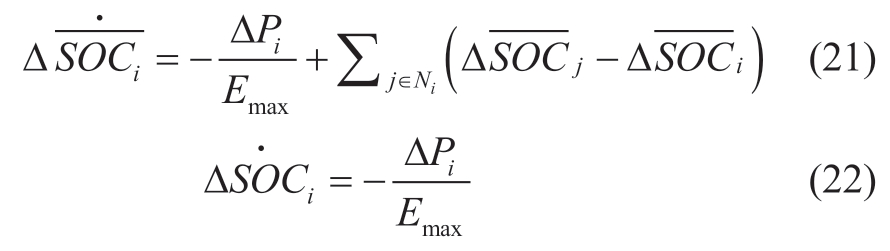
Combining Eqs.(19)~(22),the overall small-signal model is derived as

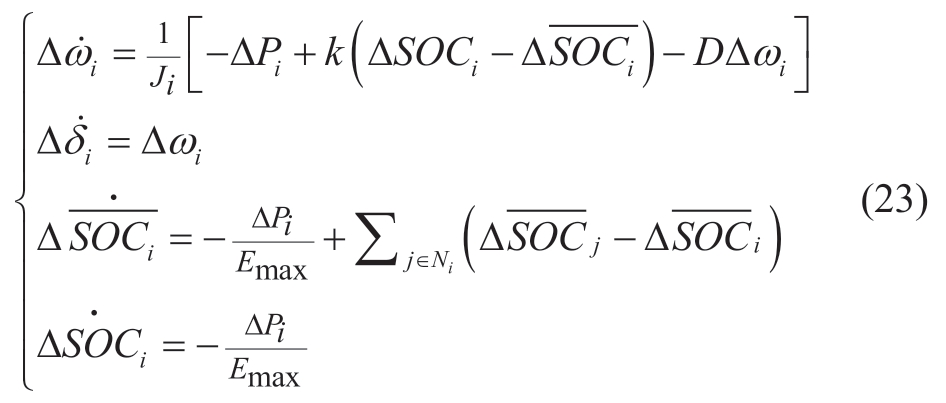
By rewriting Eq.(23)in matrix form,we have

where the state variable vector X and the system matrix A are shown in the Appendix.

To analyze the stability,the root locus of matrix A was determined [31].The effect of parameters J,D,and k on the stability of the system is discussed below.

Fig.4 shows the root locus of coefficient J,which varies from 450 to 550.As shown in Fig.4,all eigenvalues lie on the left half of the plane,which proves the stability of the system.When J increases,the dominant poles move away from the imaginary axis,implying a rapid convergence rate.Moreover,the conjugate poles move towards the real axis,resulting in a decrease in oscillations.Therefore,the larger the J,the better the dynamic performance of the system and the larger the region of stability.However,the size of J is related to energy.Selecting the right J depends on the specific situation; a larger J needs more support capacity.The physical condition must be considered when selecting J.

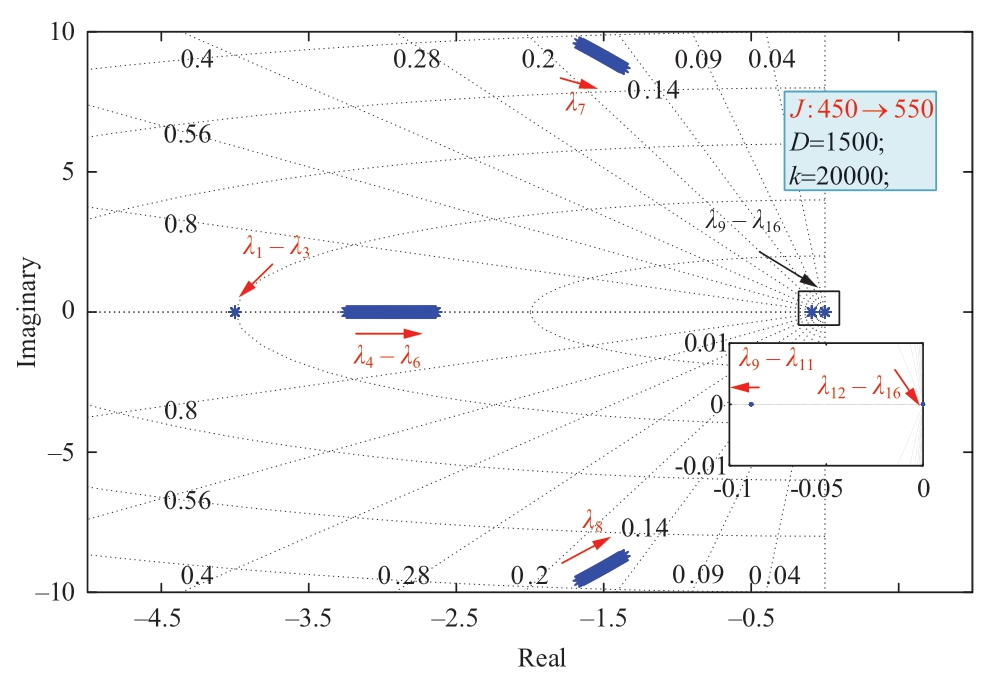
Fig.4 Root locus of J(increases from 450 to 550)

Fig.5 shows the root locus of coefficient D,which varies from 1200 to 1800.As shown in Fig.5,all eigenvalues lie on the left half of the plane,which proves the stability of the system.When D increases,the dominant poles move toward the imaginary axis,resulting in a slower convergence speed.Moreover,the conjugate poles move away from the real axis.Thus,the damping decreases,leading to an increase in oscillations.Therefore,a larger D has an adverse effect on the dynamic performance and stability.

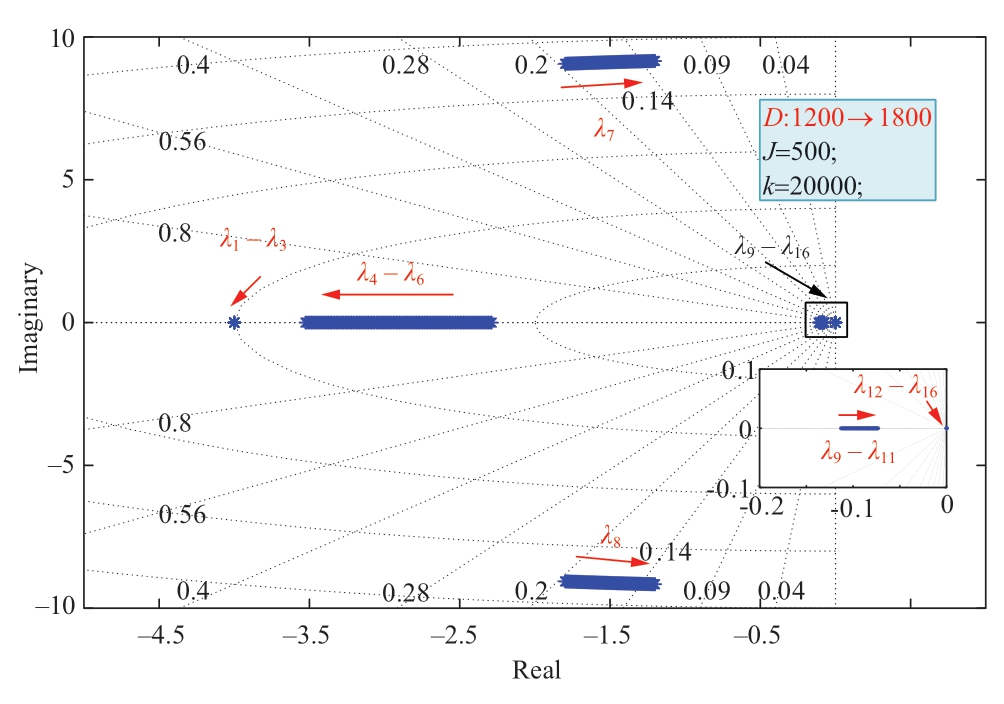
Fig.5 Root locus of D(increases from 1200 to 1800)

Fig.6 shows the root locus of coefficient k,which varies from 10000 to 20000.As shown in Fig.6,all eigenvalues lie on the left half of the plane,which proves the stability of the system.When k increases,the eigenvalues change slightly.Therefore,k has little effect on system stability.Eq.(17)shows that a larger k results in a faster convergence of SOC balancing.

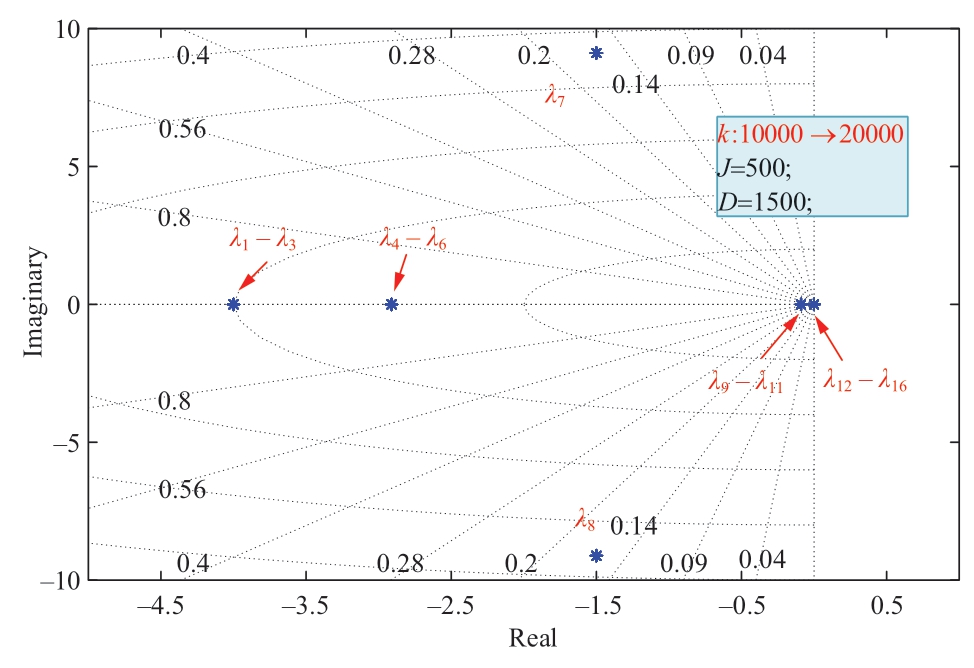
Fig.6 Root locus of k(increases from 10000 to 20000)

4 Simulation verification

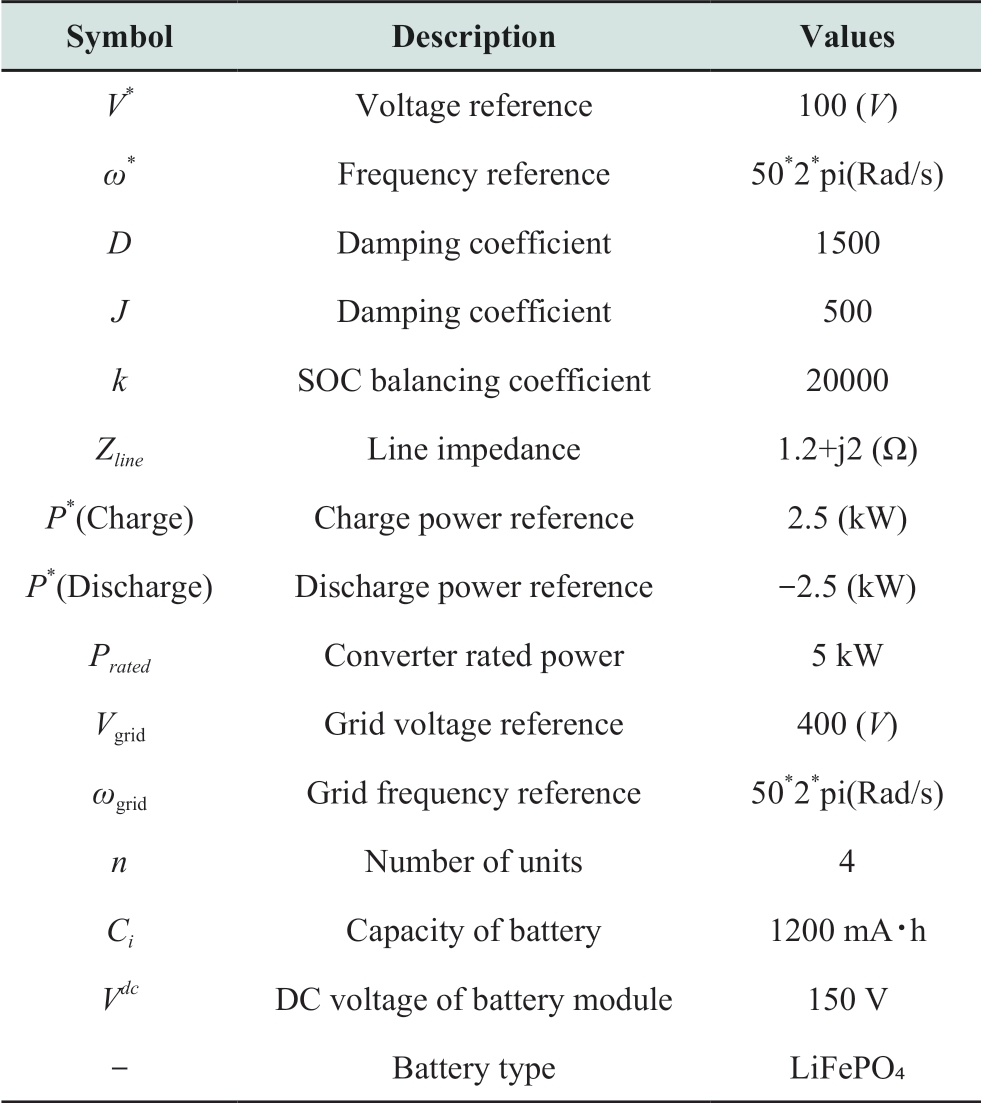
Simulation tests based on MATLAB/Simulink,which considered the four VSGs connected in series as the research objects,were performed to validate the effectiveness of the proposed method.The simulation parameters of the BESS are listed in Table 2.

Table 2 Control parameters of BESS

4.1 Simulation results in discharging mode

In this case,we considered different initial SOC values for each module.SOC10,SOC20,SOC30,and SOC40 were set as 87.5%,85%,82.5%,and 80%,respectively,for the discharging mode.The simulation results are shown in Fig.7.Clearly,SOC balancing and power-sharing are eventually realized,which proves the effectiveness of the proposed control in discharging mode.

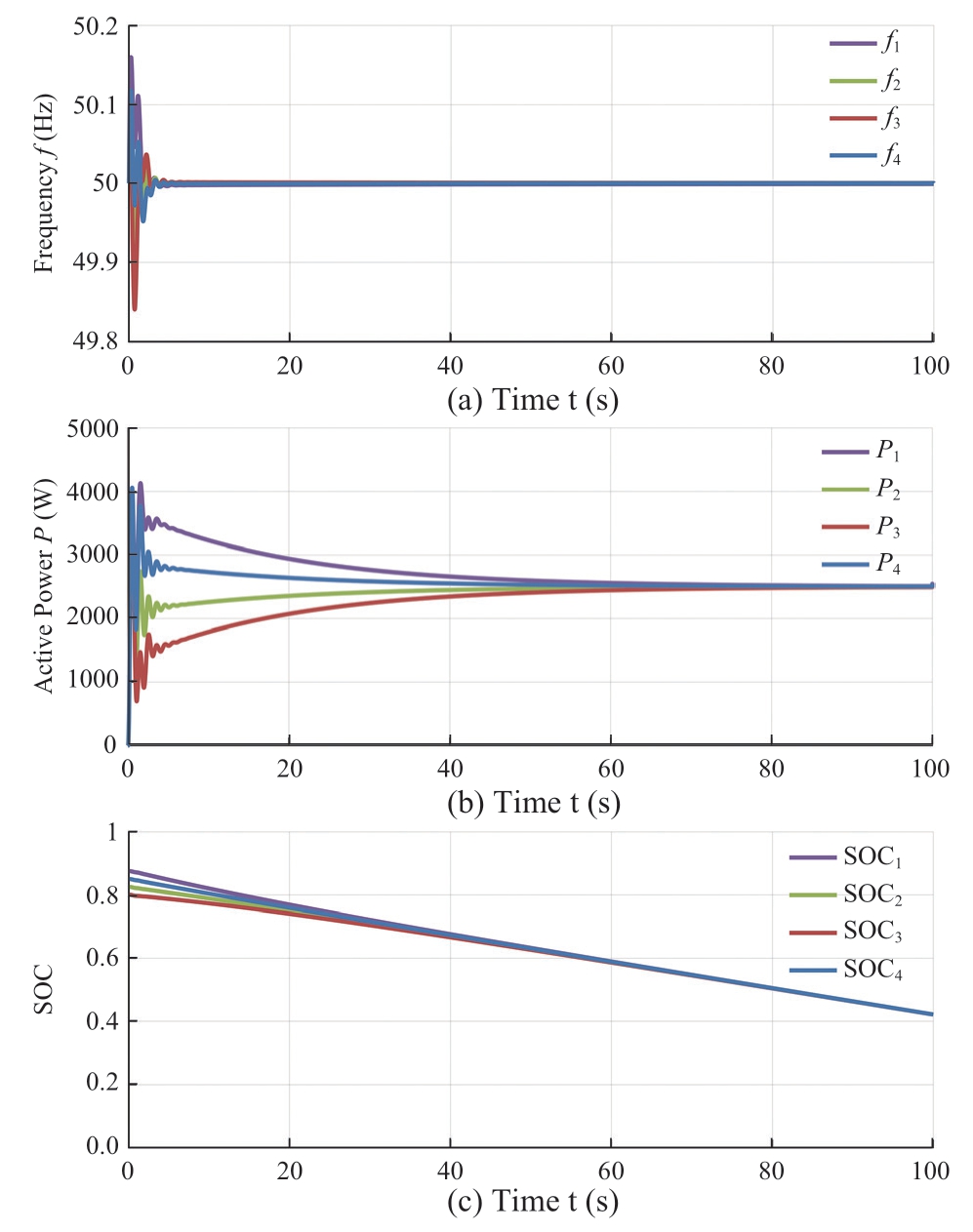
Fig.7 Simulation results in discharging mode

4.2 Simulation results in charging mode

In charging mode,SOC10,SOC20,SOC30,and SOC40 were set as 20%,22.5%,25%,and 27.5%,respectively.Fig.8 shows that the deviation ΔSoC and ΔP gradually decrease to zero as the system approaches steady-state.The results show that SOC balancing and power-sharing can be realized by the proposed method,which proves the feasibility of the proposed control.

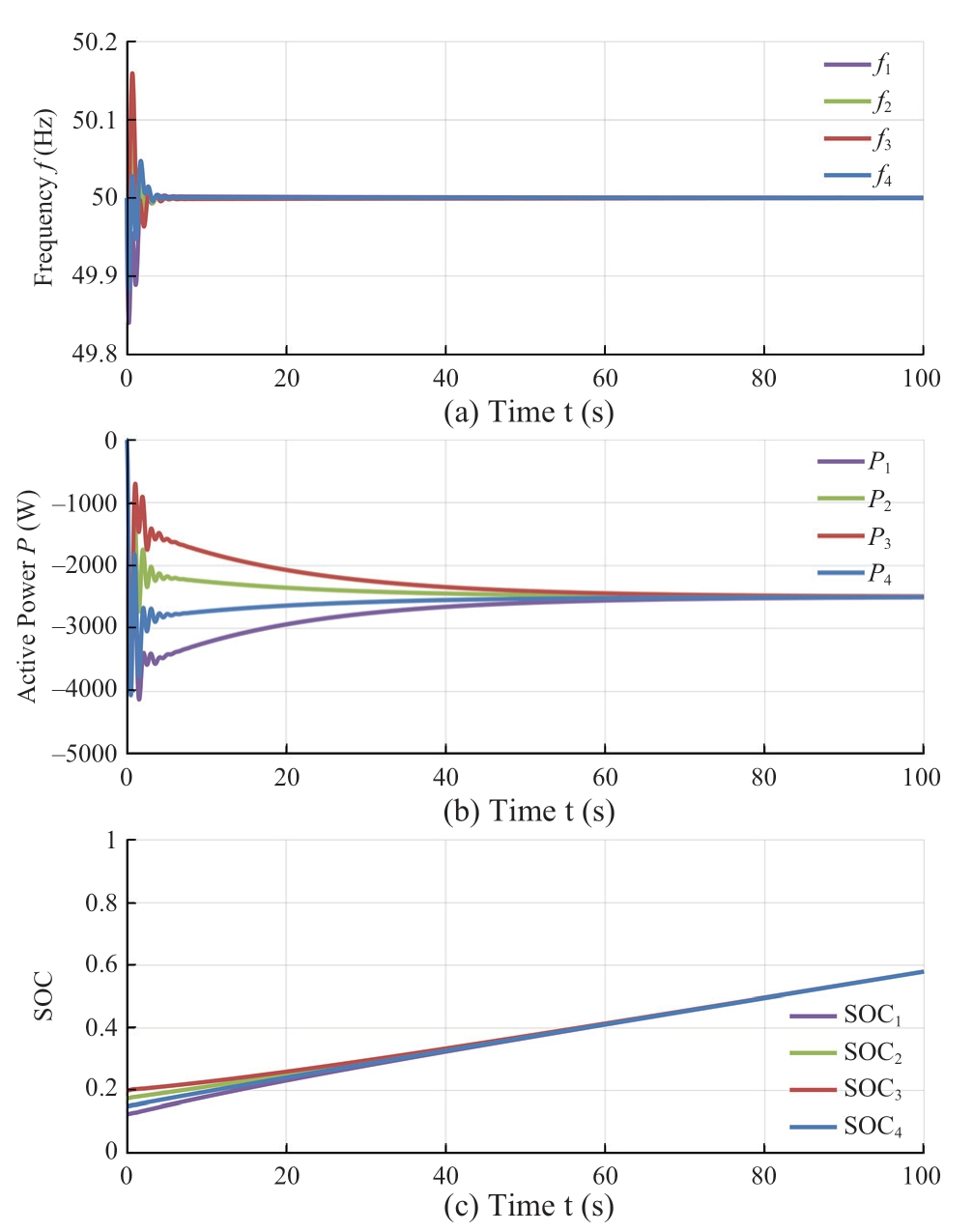
Fig.8 Simulation results in charging mode

4.3 Simulation results when transferring from charging mode to discharging mode

In this case,the operation mode is changing from charging to discharging.The initial values of SOC10,SOC20,SOC30,and SOC40 were set as 87.5%,85%,82.5%,and 80%,respectively.In the beginning,the system operates in a discharging mode.The mode changes to charging mode at t=100 s.Although the system has frequency and power fluctuations after the mode change,frequency synchronization,power-sharing,and SOC balancing are eventually achieved.Moreover,during the dynamic process,the rate of change of frequency(RoCoF)is within the allowable range,which is 1 Hz/s in China.Therefore,the proposed control method is effective during the discharge/charge mode change.

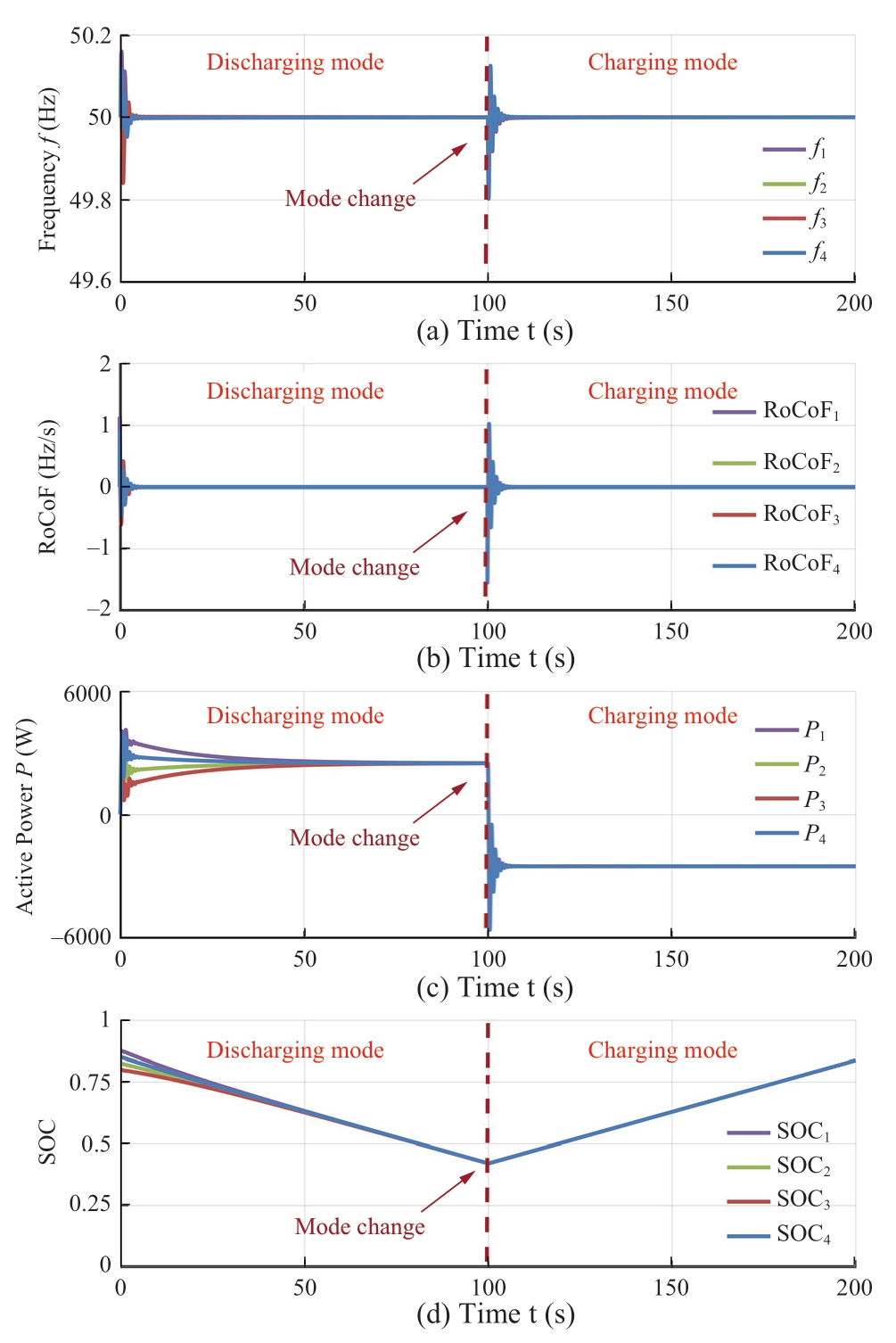
Fig.9 Simulation results when transferring from charging mode to discharging mode

4.4 Simulation results under grid-frequency drop

A simulation was carried out to verify the inertial support capability of the proposed control.The initial values of SOC10,SOC20,SOC30,and SOC40 were set as 87.5%,85%,82.5%,and 80%,respectively.At t=50 s,the grid frequency decreased to 49.8 Hz.Owing to the frequency drop,the active power of all battery modules was increased to slow the decline of the power-grid frequency.As shown in Fig.10(b),the RoCoF is within the allowable range,preventing the system from being disconnected from the grid.In addition,frequency synchronization,SOC balancing,and power-sharing are still ensured.All in all,the proposed control can work well even under a grid-frequency drop.

Fig.10 Simulation results under grid-frequency drop

5 Conclusion

A distributed VSG control method was proposed in this paper to realize SOC balancing and inertial support for a cascaded H-bridge-BESS in grid-connected mode.The primary control was carried out by VSG control,which can achieve frequency synchronization with only locally measured information.Thus,the reliability can be greatly improved in comparison with that of centralized synchronized methods.In addition,SOC-balancing control was achieved using the distributed average algorithm,which improved the reliability over single-point communication failure.Because the SOC value varies extremely slowly,the bandwidth of the communication link is limited,which can lower the communication dependency and cost.Furthermore,the feasibility of the SOC average estimation and the SOC balancing control were proved theoretically,and the stability was confirmed using root locus analysis.Finally,simulations were performed to verify the effectiveness of the proposed method in cases of different work modes,mode switching,and grid frequency drop.

Acknowledgements

This work was supported by National Natural Science Foundation of China under Grant U1909201,Distributed active learning theory and method for operational situation awareness of active distribution network.

Declaration of Competing Interest

We declare that we have no conflict of interest.

Appendix

where

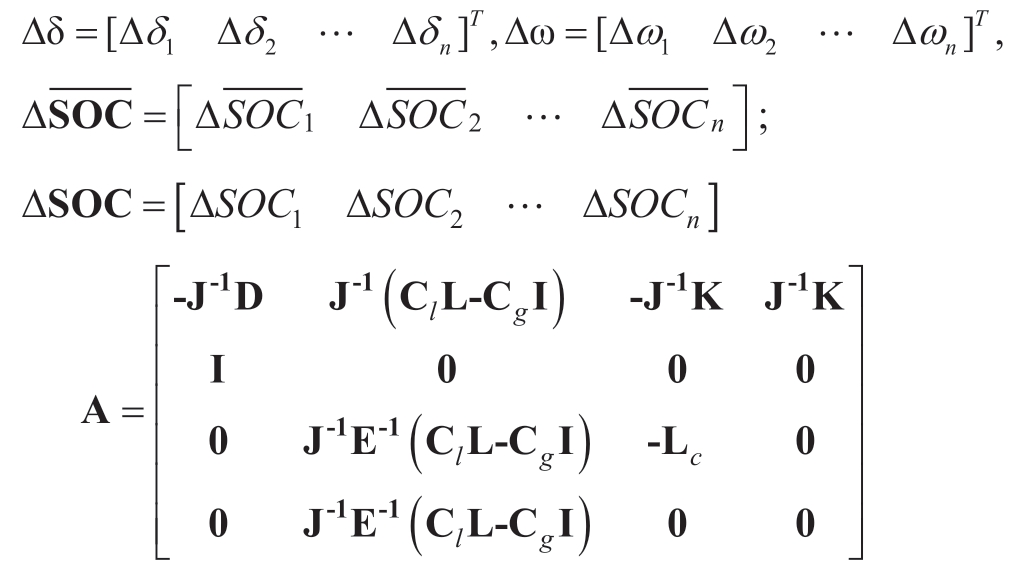
where D=diag[D1…Dn];J=diag[J1…Jn];

References

[1] A Ipakchi,F Albuyeh(2019)Grid of the future.IEEE Power and Energy Magazine,7(2):52-62

[2] O Edenhofer,R Pichs-Madruga,Y Sokona,et al.(2011)IPCC special report on renewable energy sources and climate change mitigation.Prepared By Working Group III of the Intergovernmental Panel on Climate Change,Cambridge University Press,Cambridge,UK.

[3] J M Carrasco,L G Franquelo,J T Bialasiewicz,et al.(2006)Power-electronic systems for the grid integration of renewable energy sources:a survey.IEEE Trans.Ind.Electron,53(4):1002-1016

[4] Q Tabart,I Vechiu,A Etxeberria,et al.(2018)Hybrid energy storage system microgrids integration for power quality improvement using four-leg three-level NPC inverter and secondorder sliding mode control.IEEE Transactions on Industrial Electronics,65(1):424-435

[5] A Lashab(2021)A cascaded h-bridge with integrated boosting circuit.IEEE Transactions on Power Electronics,36(1):18-22

[6] Zhao H,Yang Q,Zeng H(2017)Multi-loop virtual synchronous generator control of inverter-based DGs under microgrid dynamics.IET Gener Transm.Distrib,11(3):795-803

[7] M Hagiwara,H Akagi(2009)Control and experiment of pulsewidthmodulated modular multilevel converters.IEEE Trans.Power Electron 24(7):1737-1746

[8] L He,K Zhang,J Xiong,et al.(2015)A repetitive control scheme for harmonic suppression of circulating current in modular multilevel converters.IEEE Transactions on Power Electronics,30(1):471-481

[9] J He,Y Li,B Liang,et al.(2017)Inverse power factor droop control for decentralized power sharing in series-connected micro-converters based islanding microgrids.IEEE Trans.Industrial Electronics Early Access

[10] Y Sun,GZ Shi,X Li,et al.(2018)An f-P/Q droop control in cascaded-type microgrid.IEEE Transactions on Power Systems,33(1):1136-1138

[11] X Hou,Y Sun,H Han,et al.(2019)A fully decentralized control of grid-connected cascaded inverters.IEEE Transactions on Sustainable Energy,10(1):315-317

[12] W Huang,J A Qahouq(2015)Energy sharing control scheme for state-of-charge balancing of distributed battery energy storage system.IEEE Transactions on Industrial Electronics,62(5):2764-2776

[13] L Maharjan,S Inoue,H Akagi,et al.(2009)State-of-charge(SOC)-balancing control of a battery energy storage system based on a cascade PWM converter.IEEE Trans.Power Electron,24(6):1628-1636

[14] Maharjan L,Inoue S,Akagi H,et al.(2009)State-of-charge(SOC)-balancing control of a battery energy storage system based on a cascade PWM converter.IEEE Trans.Power Electron,24(6):1628-1636

[15] J He,X Liu,C Mu,et al.(2020)Hierarchical control of seriesconnected string converter-based islanded electrical power system.IEEE Transactions on Power Electronics,35(1):359-372

[16] G Shi,H Han,Y Sun,et al.(2021)A decentralized SOC balancing method for cascaded-type energy storage systems.IEEE Transactions on Industrial Electronics,68(3):2321-2333

[17] B Xu,H Tu,Y Du,et al.(2021)A distributed control architecture for cascaded h-bridge converter with integrated battery energy storage.IEEE Transactions on Industry Applications,57(1):845-856

[18] J Fang,H Li,Y Tang,et al.(2019)On the inertia of future moreelectronics power systems.IEEE Journal of Emerging and Selected Topics in Power Electronics,7(4):2130-2146

[19] J Chen,M Liu,F Milano,et al.(2020)Adaptive virtual synchronous generator considering converter and storage capacity limits.CSEE Journal of Power and Energy Systems

[20] Q Zhong,G Weiss(2011)Synchronverters:Inverters That Mimic Synchronous Generators.IEEE Trans.Ind.Electron.58(4):1259-1267

[21] Q C Zhong(2016)Virtual synchronous machines:a unified interface for grid integration.IEEE Power Electron.Mag.,3(4):18-27

[22] M Shi,X Chen,J Zhou,et al.(2021)Frequency restoration and oscillation damping of distributed vsgs in microgrid with low bandwidth communication.IEEE Trans.Smart Grid,12(2):1011-1021

[23] H Li,K Wang,Y Hu,et al.(2019)Impedance modeling and stability analysis of virtual synchronous control based on doublyfed wind generation systems.Proceedings of the CSEE,39(12):3434-3442

[24] Z Shuai,W Huang,Z Shen,et al.(2020)Active power oscillation and suppression techniques between two parallel synchronverters during load fluctuations.IEEE Trans.Power Electron,35(4):4127-4142

[25] X Zhang(2021)A grid-supporting strategy for cascaded h-bridge pv converter using vsg algorithm with modular active power reserve.IEEE Transactions on Industrial Electronics,68(1):186-197

[26] L Li,Y Sun,M Su,et al.(2022)Decentralized mutual damping control of cascaded-type vsgs for power and frequency oscillation suppression.IEEE Transactions on Industrial Electronics,69(10):10215-10226

[27] Y Shao,R Yang,X Li,et al.(2019)Battery energy storage system with energy spring based on VSG control strategy.2019 10th International Conference on Power Electronics and ECCE Asia(ICPE 2019 - ECCE Asia),1-5

[28] L Xin,G Z Chen(2020)Stability enhancement strategy of virtual synchronous generator for cascaded multilevel converter based energy storage system under weak grid conditions.IET Renewable Power Generation,14(5):695-704

[29] X H Ge,H Han,W J Xiong,et al.(2020)Locally-distributed and globally-decentralized control for hybrid series-parallel microgrids.International Journal of Electrical Power & Energy Systems,116(99):1-1

[30] A Narang-Siddarth,J Valasek(2014)Nonlinear time scale system in standard and nonstandard forms:analysis and control.Society for Industrial and Applied Mathematics

[31] Y Wang,X Wang,Z Chen,et al.(2018)Small-signal stability analysis of inverter-fed power systems using component connection method.IEEE Transactions on Smart Grid,9(5):5301-5310

Biographies

Yichi Cai is working towards B.Eng.degree at Zhejiang University,Hang Zhou,China.His research interests includes renewable energy.

Donglian Qi received the Ph.D.degree from the School of Electrical Engineering,Zhejiang University,China,in 2002.She is currently a Full Professor and a Ph.D.Advisor with Zhejiang University.Her current recent research interest covers intelligent information processing,chaos system,and nonlinear theory and application.

(Editor Yanbo Wang)