0 Introduction

The large-scale development and utilization of renewable energy sources has helped mitigate global energy and environmental protection problems and is,therefore,critical for improving the energy structure,addressing national economic issues,and order development.Notably,this is also an important strategic policy for achieving carbon peak and carbon neutrality [1-2].According to statistics,the installed capacity of the global wind power industry has exhibited a growing trend since 2016.The cumulative installed capacity of global wind power was 467 GW in 2016,which then increased to 702 GW by 2020,representing an average compound annual growth rate of up to 9.56%.By 2030,20% of the global electricity supply is expected to originate from wind power [3].Predictions also indicate that the capacity of wind power will reach 2.4 billion kW by 2050.Furthermore,renewable energy sources can be considered as alternative power sources,rather than supplementary ones,once the proportion of renewable energy generation reaches 60% [4].Moreover,rapid developments related to wind power have led to a significant increase in the size and number of wind farms;accordingly,the demand for incorporating wind power in power systems has also increased.

Over recent years,several wind power-related subsynchronous oscillations have been reported worldwide.For instance,in October 2009,a double-fed wind farm (with an installed capacity of approximately 1000 MW) located in Texas,USA,suffered from a cascading transmission line fault; this increased the series compensation degree from 50% to 75%,resulting in a large number of off-grid turbines as well as damage to the double-fed turbine crowbars [5-6].In December 2012,under the action of doubly fed induction generators (DFIGs) and cascade lines,approximately 100 sub-synchronous oscillations (SSOs) occurred in the Guyuan area of Hebei,China; this was accompanied by a rapid dispersion of the output current of the wind turbine during the initial stages of the oscillation phase,with an oscillation frequency of approximately 7.9 Hz.Furthermore,the wind turbine was tripped due to the protection mechanisms,resulting in a large-area off-grid with a current oscillation frequency of 6.2 Hz,which continued to decay.The system gradually converged after cutting off some of the wind turbines [7-8].In 2016,100 SSOs with a frequency of approximately 20 Hz occurred in the direct-drive wind farm located in Xinjiang,China.This caused three 660 MW synchronous generating units,which were located in a thermal power plant 300 km away,to trip the shaft system torsional vibration protection camera [9-10].Since these events,several researchers have extensively focused on the problem of SSOs.

Given the successive completion of 10 M∙kWh kilowatt wind power bases,the centralized grid connection of largescale wind turbines poses a significant challenge for power systems [11].In the process of simulating the grid-connected systems of wind turbines,there exists an unavoidable contradiction between ensuring the level of detail regarding the models for new energy sites and expanding the scale of the grid simulations.Hence,to study the operational states of large-scale wind power systems,the construction of aggregation models that accurately characterize the wind farms as a whole is fundamental [12].In this regard,the equivalence problem associated with wind farms has emerged as a key research direction worldwide.

A detailed model can be built by modeling each unit included in the wind farm,in parallel with the model of the collector system,such as the overhead lines or cables.The detailed modeling of each DFIG can help analyze the dynamic characteristics within a wind farm; however,the order of the resulting mathematical model is excessively high,the simulation calculations are vague,and the simulation conditions have more demanding requirements[13].Hence,to reduce the simulation time,it is necessary to build wind farm equivalent models that are easy to use and also accurately reflect the operation of the wind farms in real time.

In this context,single-machine equivalence,halfmachine equivalence,and multi-machine equivalence are commonly used.The single-machine equivalence method is based on the weighted average method of equating an entire wind farm to a single wind turbine.In this structure,if the wind speed is not identical at each part of the wind farm,the sum of the wind power obtained at each wind turbine is used as the wind power of the equivalent machine.This approach has been detailed in existing literature [14-17].However,the accuracy of this single-unit equivalence model is low;the model also gradually fails to meet the requirements for evaluating certain problems,including the operating state of a power system with large-scale wind farms,owing to the significant differences in the operating states of the units within the wind farm.Furthermore,the half-unit equivalence method is only suitable for wind turbine models with adjustable internal modules and is not applicable across all simulation software [18].Lastly,the multi-machine equivalence method involves the grouping of wind turbines with similar specifications,according to a certain standard,such that these wind turbines experience similar wind speeds.All the units within each group are then represented as a single machine,which essentially represents the entire wind farm with a multiple equivalence generator model.This approach has been discussed in detail elsewhere [19-21].The applicability of this method has been demonstrated;however,the rationality of such unit grouping has not been discussed.Accordingly,a multi-unit equivalence method considering a paddle pitch angle action case,the turbine speed,and the turbine transient voltage characteristics as a single clustering index has been proposed to overcome the limitations of the traditional single-unit equivalence method[22-24]; however,the actual equivalence effect was not as ideal as expected,when a single variable as the clustering index.Another study [25]proposed the clustering of units based on the state variables during turbine operation; a multi-unit equivalence model for wind farms was built using this clustering analysis.The effects of the wake and the collector system on the operating state of the wind turbine were also considered.However,calculating all 13 state variables during the operation of a turbine may not be feasible for an expanding wind farm.In another previous study [26],support vector machines were used to cluster wind farm operation data with respect to the unit type and the wind speed.Furthermore,based on the wind farm wake effect,support vector machines were used to cluster the units with similar wind speeds over several iterations [27];a set or a number of combinations of the units that could always be classified into a group was then obtained,and these combinations were used as fixed subgroups.This approach could help circumvent the tediousness associated with repeated subgroups as the wind speed varied.Using the DFIG data measured using a data acquisition system,a statistical Markov chain-based homogeneous group division method was proposed for wind farms with complex topographies and irregular distributions [28]; this approach essentially categorizes the units experiencing similar wind speeds into a group.

In this study,to address the shortcomings of the aforementioned methods,we consider the nature of the rotor equivalent resistance as a grouping principle to dynamically group the wind turbines; turbines with the same nature of the equivalent resistance were aggregated as a single turbine.A large wind farm was then equated to a small number of equivalent machine models,and the multi-machine equivalent modeling of large wind farms was performed.Lastly,we built an equivalence model for wind farms based on the rotor equivalent resistance property using Matlab/Simulink; the simulations verified that this method is effective and that the equivalence model is accurate.

1 Basis for equivalence modeling based on rotor equivalent resistance characteristics

The SSO mechanism in grid-connected wind farm systems can generally be classified into the following two categories: oscillations caused by the series compensation capacitors and oscillations caused by the power electronics and control systems in weak grids.In a grid-connected wind farm system with series compensation,the induction generator effect (IGE) and the sub-synchronous control interaction (SSCI) are typically the main causes of oscillations.The IGE indicates that,at a certain subsynchronous frequency,the system has a negative equivalent resistance,and the circuit experiences selfexcited oscillations with continuous current dissipation.

The IGE is caused by the self-excited oscillations of a circuit.When a system has a negative equivalent resistance,the voltage at the end of the machine increases continuously,resulting in a voltage runaway; this is also termed as “selfexcitation” [29].When the sub-synchronous current induces a disturbance component in the rotor,this disturbance component reacts on the stator winding and generates a new current component in the stator.When this new component maintains or enhances the initial sub-synchronous current,it becomes “self-excited” and the generator provides asynchronous power that is equivalent to that from an asynchronous generator; the equivalent circuit is presented in Fig.2.

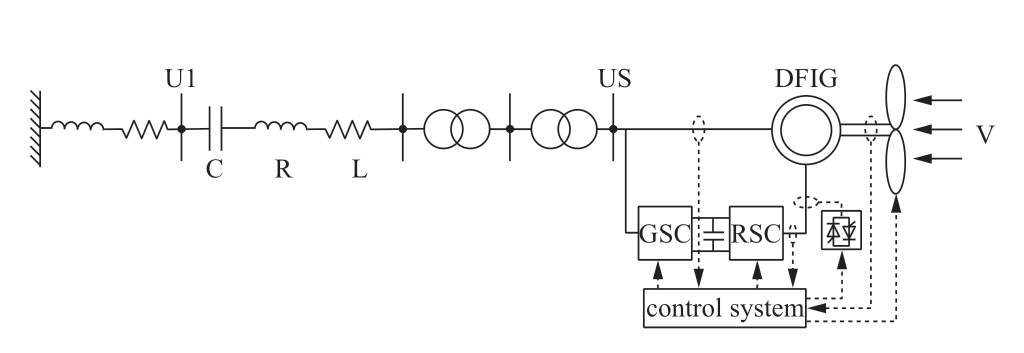
Fig.1 Single double-fed wind turbine output wind power system topology through series compensation

Fig.2 Equivalent circuit diagram of IGE

Here,s,Rr,Rs,Lr,and Ls indicate the slew rate,rotor resistance,stator resistance,rotor leakage inductance,and stator leakage inductance,respectively; fer and f denote the sub-synchronization and synchronization frequencies,respectively.

Typically,the line crosstalk degree < 1,and fer is lower than f,which is the rate of rotation difference.When the value tends to 0 from the negative direction,the rotor equivalent resistance tends to negative infinity; in this case,the equivalent resistance of the system is negative,and the resistance value varies with the oscillation frequency.Furthermore,the self-excited oscillation at this frequency increases the oscillations in the system.

When the system undergoes SSOs,its equivalent resistance is negative; furthermore,the rotor equivalent resistance at certain units may be positive,whereas those at the other units may be negative.Thus,turbines can be grouped according to the nature of the rotor equivalent resistance of the units in the sub-synchronous frequency domain.

The interaction between the control section of the wind turbine and the series compensation line can result in the SSCI; its oscillation frequency and decay rate are jointly determined by the series complementarity,including the controller and phase-locked loop parameters.When a disturbance current component with frequency i' is present in the line,the grid-side converter ensures a constant DC bus voltage; thus,the parameters of the GSC have a weak influence on the sub-synchronous oscillation phenomenon.This has been demonstrated previously.By sensing the disturbance component i',which is also produced on the rotor side,the reference values of the rotor current d and the q-axis components are introduced in the RSC control system and measured values,which in turn control the output voltage.Following the RSC control,a disturbance component u' also appears in the rotor voltage; u' influences the rotor current through an external circuit to induce a new sub-synchronous component i" at the stator.These newly generated sub-synchronous components are continuously superimposed with the occurrence of the disturbances.In this case,if suppression measures are not applied,the overall current will exhibit an oscillatory divergence positive feedback effect when the phase difference between the superimposed currents is less than 90°; this,in turn,will results in the SSCI within the system.

This study focuses on the clustering of multiple doubly fed wind turbines based on the nature of the rotor equivalent resistance,considering that the IGE and SSCI phenomena are generated in parallel.

2 Dynamic equivalence method based on rotor equivalent resistance characteristics

Dynamic equivalence refers to the process of simplifying a wind farm under the condition that the effect of the wind farm on the dynamics of the studied system remains unchanged [30].The dynamic equivalence modeling of the sub-synchronous frequency domain for a large wind farms entails the following guidelines:

(1) The equivalence model should reasonably describe the dynamic electrical behavior during normal operation with the external system,while maintaining the power balance both before and after equivalence.

(2) The equivalence model should reasonably describe the dynamic electrical behavior externally when the external system is disturbed.

(3) The equivalence model should require shorter simulation times than the detailed model and reflect the system operation more accurately than the stand-alone model.

2.1 DFIG model

A wind turbine can convert wind energy into mechanical energy.For this case,let v denote the wind speed and R denote the wind turbine blade radius.The wind energy captured by the DFIG cannot be converted into mechanical power entirely; thus,the wind energy utilization coefficient Cp is introduced to indicate the ability of capturing wind energy.The relationship between wind speed and power can be expressed as follows:

where,Pw is the wind power,ρ is the air density,β is the pitch angle,vw is the wind speed,CP is the wind energy utilization coefficient,and λ is the ratio of the linear speed of the impeller rotation to the wind speed.

CP can be changed by adjusting β and the leaf tip speed ratio λ,to obtain the maximum wind energy utilization:

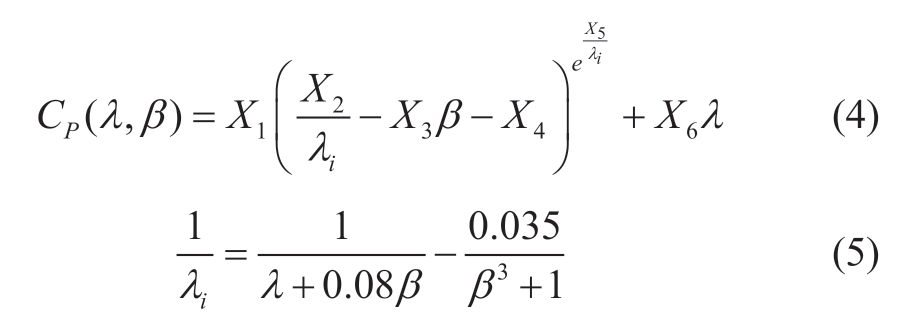
Here,X1=0.5176; X2=116,X3=0.4,X4=5,and X6=0.0068.

The Cp value for different tip speed ratios is not fixed and can be affected by the changes in β when λ is fixed.To ensure the maximum utilization of the wind energy at various wind speeds,for doubly fed turbines,the speed limit reflects the maximum power limit on the rotor side of the converter; however,when the wind speed is excessively low,the control system does not operate by changing the size of the pitch angle to stabilize it such that it captures the maximum wind energy.If the rated wind speed is lower than the wind speed,the pitch will change and affect the ability of the wind turbine to capture wind energy; this,in turn,will reduce the input mechanical power available for maintaining the wind turbine at the rated power.

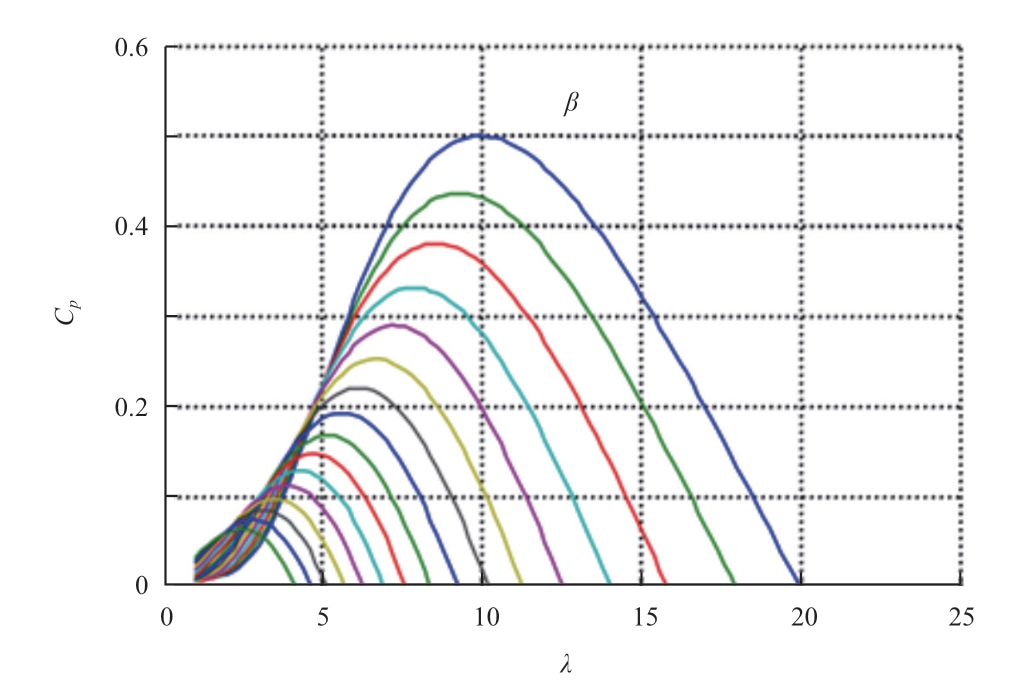
Fig.3 Cp curves

2.2 Pitch angle control

The pitch angle is controlled by a PI controller.When the power output of the DFIG is below the rated value,β is maintained at 0°.By contrast,if the power output exceeds the rated value,the PI controller will increase the β value and maintain the output at the rated value.A block diagram of this pitch angle control process is presented below.The input to this controller is obtained based on the difference between the output power and the rated power.

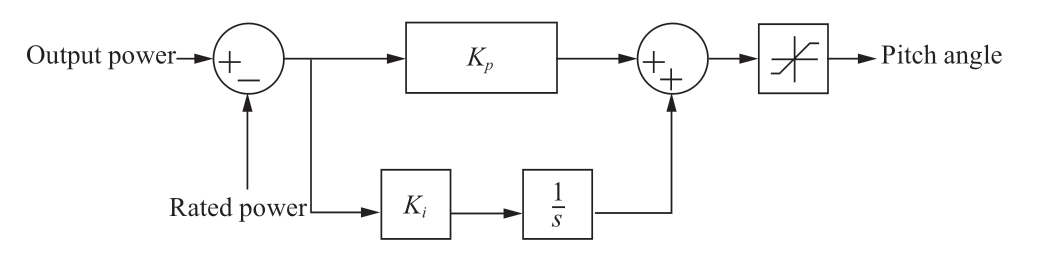
Fig.4 Block diagram for pitch angle controller

2.3 Aggregation of DFIGs

The aggregated equivalent machine parameters can be calculated using the weighted average method,where the weight factor is the ratio of the capacity of a single turbine to the sum of the capacities of all the turbines to be aggregated.

The capacity of the equivalent turbines before and after aggregation equals the sum of the capacities of the DFIGs,and the output mechanical torque is equal to the sum of the output torques of the turbines:

Here,Tm indicates the mechanical torque of the equivalent turbine,Tmi is the mechanical torque of each turbine,and n denotes the number of fans to be aggregated.

The capacity of the equivalent induction motor equals the sum of the capacities of each induction motor:

where SG indicates the capacity of the equivalent induction motor,SGi is the rated capacity of each induction motor,and n represents the number of induction motors to be aggregated.

All the impedance parameters of the equivalent induction motor can be calculated via the weighted average method:

where ZG is the equivalent impedance parameter of the equivalent induction motor and ZGi is the impedance parameter of the induction motor to be aggregated.

The rotational inertia and inertia time constants of the rotor of the equivalent induction motor are as follows:

where,JG indicates the rotor inertia of the equivalent induction motor,JGi is the rotor inertia of the induction motor with aggregation,and TG is the rotor inertia time constant of the equivalent machine.

3 Simulation analysis

3.1 Wind turbine model

Here,a wind farm comprising 20 identical DFIGs was considered; the single turbine capacity was 5 MW at 50 Hz,whereas the rated wind speed was 11.5 m/s.The output voltage was 690 V,and it was stepped up to 35 kV through a transformer located at the machine end; this voltage was then transferred to the bus through the transmission line and subsequently stepped up to 220 kV through the main transformer of the wind farm.This involved a line series compensation degree of 30%.The topology diagram is depicted in Fig.5,while the system parameters are listed in Table 1.

Table 1 Main system parameters

3.2 Analysis of Example 1

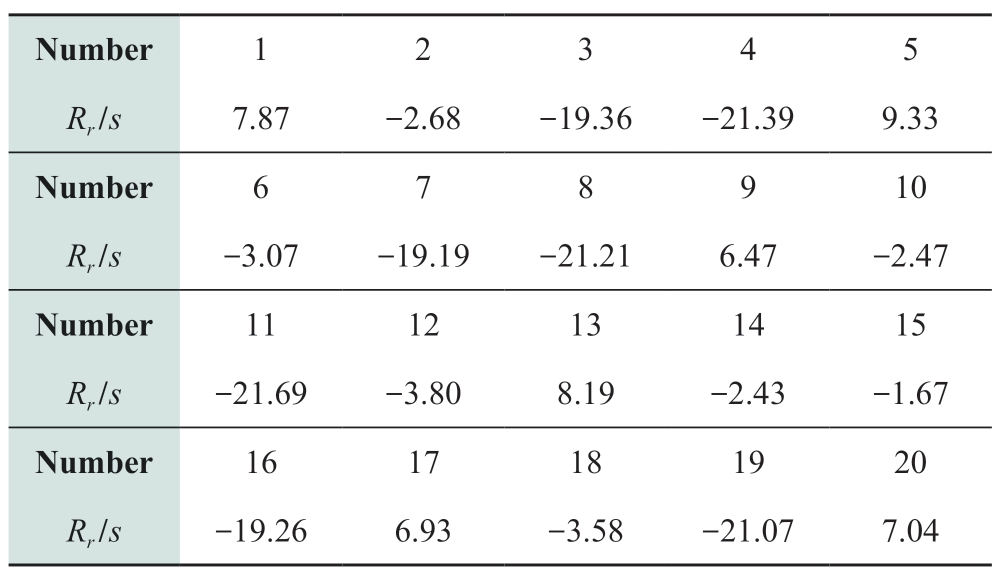
In this example,the 20 doubly fed turbines were numbered as shown in Fig.5.The equivalent resistance of each turbine under the sub-synchronous frequency was calculated according to the calculation method for the rotor equivalent impedance,as described in Section 2; the corresponding results are presented in Table 2.The rotor equivalent resistances of turbines 1,5,9,13,17,and 20 were positive.By contrast,the rotor equivalent resistances of turbines 2,6,10,12,14,16,and 18 were negative and smaller in magnitude,whereas those of turbines 3,4,7,8,11,15,and 19 were negative but larger in magnitude.According to this result,the units were classified into 3 categories.According to Eqs.(6–10),the units and lines were aggregated in each of the same classes,respectively.

Fig.5 Structural diagram of a wind power system

Table 2 Equivalent resistance of wind turbine rotor

Based on the calculated parameters above,an equivalent simplified model based on that shown in Fig.6 was established using Matlab/Simulink.A detailed model and a single-machine model were also established to compare the distributions of the active and reactive power and the SSO characteristics in the system when these three models are employed for the analyses.

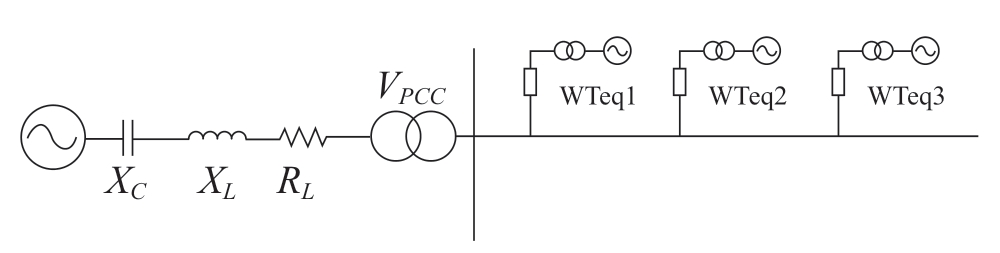
Fig.6 Simplified equivalence diagram of a wind farm

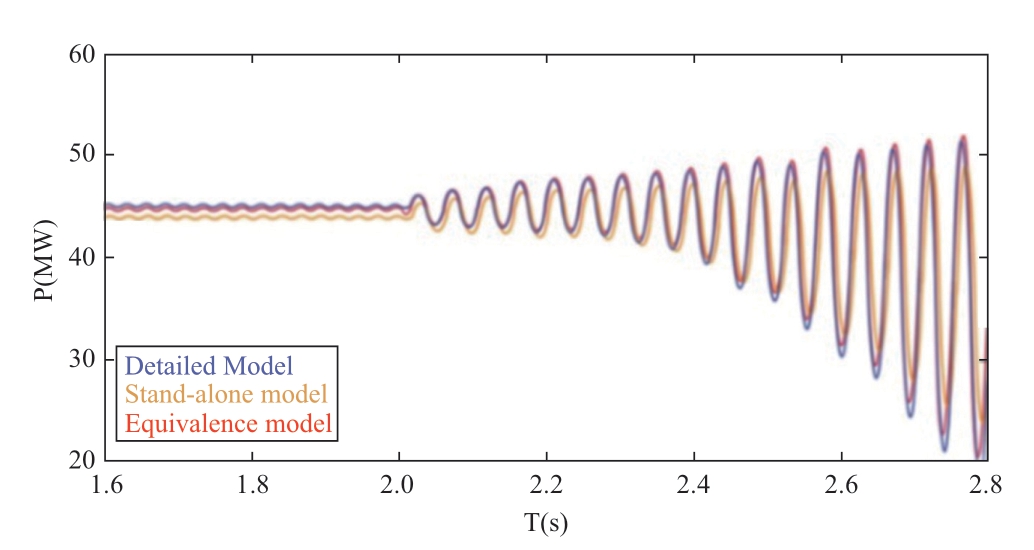
Fig.7 Comparison of wind farm active power for different models

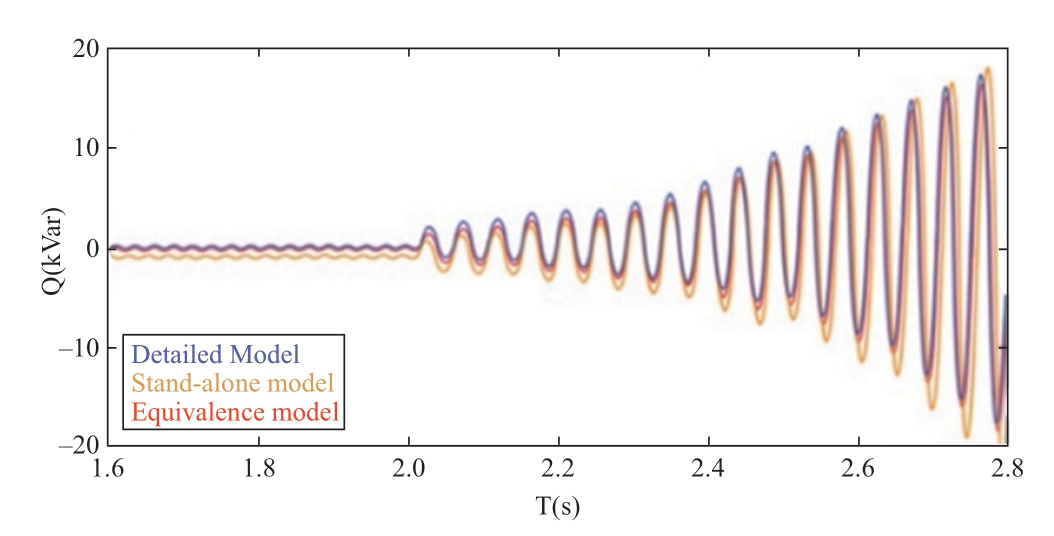
Fig.8 Comparison of wind farm reactive power for different models

Based on the figure above,the active and reactive powers of the three models were approximately equal when the models before and after equivalence were operated under the steady-state phase.Both the stand-alone and simplified models were better in terms of meeting the power balance requirements.When the system was operated up to 2.0 s,the series complement was introduced into the system,and SSOs were generated.The SSO components appeared in both the wind farm power and the current waveforms.The equivalence model was found to be more relevant than the single-machine model.Therefore,the proposed equivalence modeling method can reflect the actual conditions of the detailed model.When an SSO occurs in the wind farm,the equivalence model is better than the detailed model in terms of reflecting the dominant oscillation mode.This demonstrates the effectiveness of the equivalence method.

3.3 Analysis of Example 2

As the accuracy of the equivalence model was not apparent under Example 1,we included Example 2.For this case,the 20 doubly fed wind turbines were numbered as shown in Fig.5.A simplified equivalence diagram is presented in Fig.6.

FFT analyses of the current components of the detailed and equivalent models demonstrated that there existed a dominant sub-synchronous oscillation component of approximately 17.5 Hz in the output current of the wind farm,as shown in Fig.9.Based on Fig.10 and 11,the active and reactive power curves of the stand-alone model do not present the SSOs,whereas the power curves of the detailed and equivalent models display SSOs and are approximately equal.Therefore,this example demonstrates the validity of the equivalent model,further proving that the equivalent model is better than the stand-alone model.

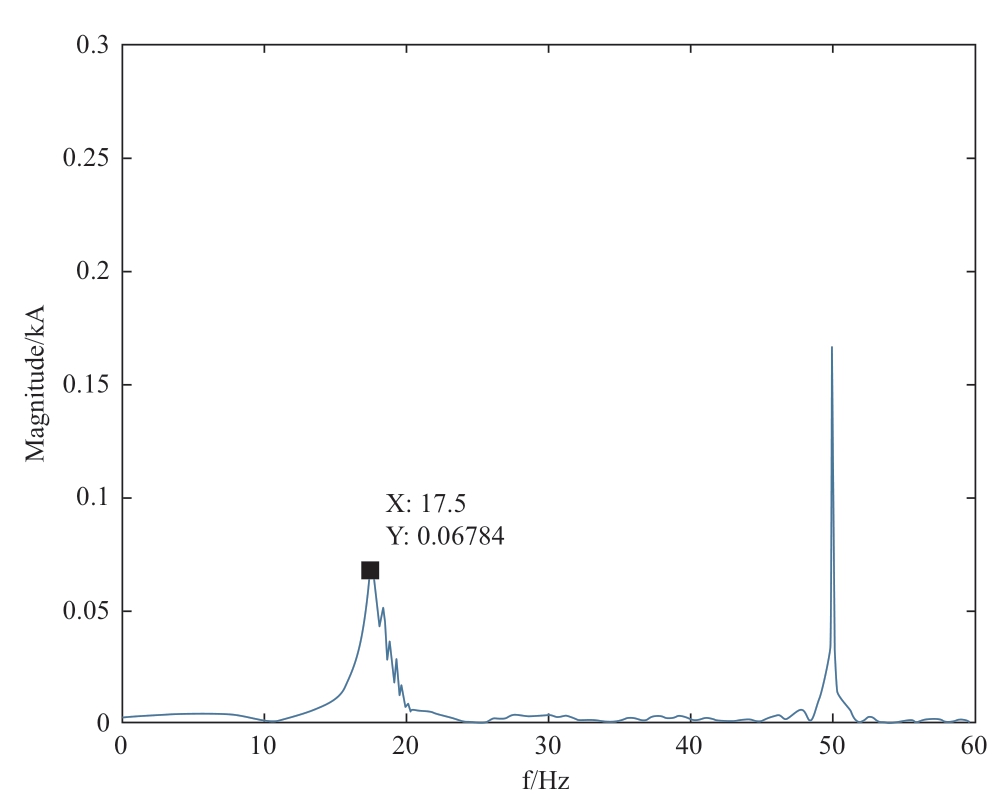
Fig.9 Spectrum analysis diagram

Fig.10 Wind farm active power comparison diagram

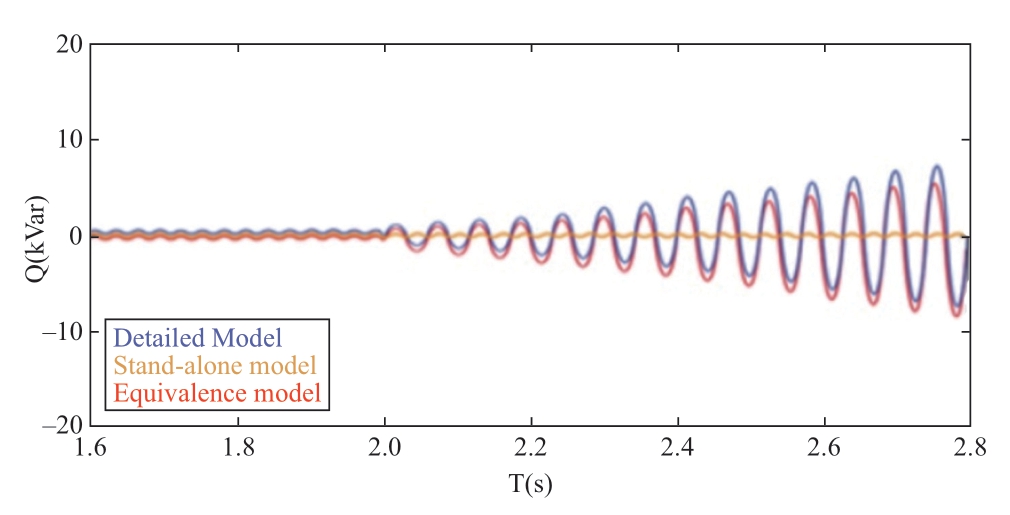
Fig.11 Comparison of reactive powers

4 Conclusion

In this study,a dynamic equivalence method considering the sub-synchronous frequency domain was developed for wind farms; this approach was based on the nature of the rotor equivalent resistance and was aimed at analyzing the sub-synchronous oscillation problem.Specifically,the nature of the rotor equivalent resistance in the subsynchronous frequency domain was adopted as the grouping principle to dynamically group the wind turbines.Furthermore,a detailed model,a single-machine model,and an equivalent model were established using the Matlab/Simulink platform.Simulation results revealed that the proposed model can describe the operating characteristics of large wind farms and better reflect the sub-synchronous oscillation characteristics during SSOs,as compared with the other model.This demonstrates that the equivalent model is accurate and that this method is effective.

Acknowledgements

This work was supported by the National Key R&D Program of China “Response-driven intelligent enhanced analysis and control for bulk power system stability” (No.2021YFB2400800).

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1]Outline of the National Medium-term and Long-Term Scientific and Technological Development Plan (2006-2020)

[2]Lauha F,Shruti S (2012) Global wind energy outlook 2012.GWEC

[3]Energy Research Institute of National Development and Reform Commission,Energy Foundation (2015) China 2050 Renewable Energy Development Situation and path Research.China,Beijing

[4]Adams J,Pappu VA,Dixit A (2012) ERCOT experience screening for Sub-Synchronous Control Interaction in the vicinity of series capacitor banks,IEEE PES Genral Meeting,San Diego,1-5 June 2012

[5]Moharana A,Vama RK (2021) Sub-synchronous resonace in single-cage self-excited-induction generator-based wind turbine for sub-synchronous resonace control.IET Renewable Power Generation 6(2): 92-98

[6]Zhu C,Hu M,Wu Z (2012) Parameters impact on the performance of a double-fed induction generator-based wind turbine for sub-synchronous resonance control.IET Renewable Power Generation 6(2): 92-98

[7]Wang L,Xie XR,Jiang QR (2015) Investigation of SSR in practical DFIG-based wind farms connected to a seriescompensated power system.IEEE Transactions on Power Systems 30(5): 2772-2779

[8]Li MJ,Yu ZX,Xu T,et al.(2017) Study of complex oscillation caused by renewable energy integration and its solution.Power System Technology,41(04): 1035-1042

[9]Chi YN,Tang BJ,Hu JB,et al.(2019) Overview of mechanism and mitigation measures on multi-frequency oscillation caused by large-scale integration of wind power.Csee Journal of Power and Energy Systems 5(4): 433-443

[10]Lin L,Zhao HL,Chen Y,et al.(2014) Research summary of wind farm modeling.Modern Electric Power 31(02): 1-10

[11]Gao C,Niu DX,Luo C,et al.(2018) Comparison of impact on sub-synchronous oscillation characteristics between single-and multi-generator equivalent model in DFIG wind farm.Electric Power Automation Equipment 38(08): 152-157

[12]Gu TY,Yang QJ,Lin CH,et al.(2020) A wind farm equivalent modeling method based on single-machine equivalent modeling and selection modal analysis.Power System Protection and Contro 48(1): 102-111

[13]Hu J,Yu YX (2006) A Practical Method of Parameter Aggregation for Power System Dynamic Equivalence.Power System Technology 24: 26-30

[14]Slootwer JG,Kling WL (2002) Modeling of Large Wind Farms in Power System Simulations.Proceedings of the IEEE PES Summer Meeting.Chicago 25-29

[15]Sun JF,Jiao LW,Wu JL,et al.(2004) Research on multi-machine dynamic aggregation in wind farm.Power System Technology(07):58-61

[16]Qiao JG,Lu ZX,Min Y,et al.(2009) New dynamic equivalence method for grid-connected wind farm.Transactions of China Electrotechnical Society 24(04):209-213

[17]Xu YQ,Liu D (2017) Equivalence of wind farms with DFIG based on two-step clustering method.Power System Protection and Control 45(6):108-114

[18]Mi ZQ,Su XW,Yang QX,et al.(2010) Multi-machine representation method for dynamic equivalent model of wind farms.Transactions of China Electrotechnical Society 25(05):162-169

[19]Fernandez LM,Garcia CA,Saenz JR,et al.(2009) Equivalent models of wind farms by using aggregated wind turbines and equivalent winds.Energy Conversion and Management 50(3):691-704

[20]Slootweg JG,Hann HSW,Polinder H,et al.(2003) General model for representing variable speed wind turbines in power system dynamic simulatin.IEEE Trans on Power Systems 18(1):1132-1139

[21]Mi ZQ,Su XW,Yu Y,et al.(2010) Study on dynamic equivalence model of wind farms withwind turbine driven doubly fed induction generator.Automation of Electric Power Systems 34(17):72-77

[22]Zhu QL,Han PP,Ding M,et al.(2014) Probabilistic equivalent model for wind farms based on clustering-discriminant analysis.Proceedings of the CSEE 34(28):4770-4780

[23]Xu YQ,Wang N (2013) Study on dynamic equivalence of wind farms with DFIG based on clustering analysis.Journal of North China Electric Power University 40(3):1-5

[24]Chen SY,Wang C,Shen H,et al.(2012) Dynamic equivalence for wind farms based on clustering algorithm.Proceedings of the CSEE 32(4):11-19

[25]Zhang Y,Hao LL,Dai JQ (2015) Overview of the equivalent model research for wind farms.Power System Protection and Control 43(6):138-146

[26]Wang X (2008) Study of dynamic equivalent model of wind farm.Beijing,China

[27]Ma Y,Jiang JN,Runolfsson T (2009) Cluster analysis of wind turbines of large wind farm.IEEE/PES Power Systems Conference and Exposition PSCE 09.Seattle

[28]Zhang K (2011) The study of wind farm equivalent model of Power System Simulation.Beijing,China

[29]Bizzarri F,Brambilla A,Milano F (2018) Simplified model to study the induction generator effect of the subsynchronous resonance phenomenon.IEEE Transactions on Energy Conversion 33(2):1-1

Received: 21 December 2021/Accepted: 28 March 2022/Published: 25 June 2022

Yanhui Xu xuyanhui23@sohu.com

Tianchu Gao 1103206267@qq.com

2096-5117/© 2022 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co.,Ltd.This is an open access article under the CC BY-NC-ND license (http://creativecommons.org/licenses/by-nc-nd/4.0/).

Biographies

Yanhui Xu received his PhD from North China Electric Power University in 2010,where he is currently working.His research interests include dynamic power system analyses and wind turbine equivalence.

Tianchu Gao is working towards her master’s degree at North China Electric Power University.Her research interests include wind turbine equivalence and grid stability analyses.

(Editor Yanbo Wang)