0 Introduction

A low-resistance grounding system is characterized by its superior capability to rapidly cut off fault current and thereby limit the resonance over-voltage and reduce the insulation level [1-4].Therefore, it is being gradually applied to the urban power distribution network.However, in a 10 kV system grounded by a marginal resistance, the widely used definite-time zero-sequence over-current protection has a low set action current (generally 40 A) [5-6].It can handle only faults with transition resistance less than approximately 130 Ω [7-8].Moreover, the marginal zero-sequence current under the condition of a highimpedance grounding fault (HIF) may cause the protection to malfunction and thereby endanger personal safety.In the cases where the fault exists for a long time, the scope and hazard of the accident may be increased further.This would impact the reliability of the power supply [9-11].

Many new protection methods have been developed by scholars to solve the above problems.However, certain problems remain to be solved.Considering that definitetime protection malfunctions straightforwardly in the case of HIF, inverse-time zero-sequence overcurrent protection was proposed in reference [12].It reduces the starting threshold of protection.However, it increases the action delay of high resistance faults.The authors of reference [13] presented an innovative and adaptive zero-sequence current protection by introducing the zero-sequence voltage to adaptively adjust the zero-sequence current.However, the method may not be applicable to the case of HIFs because zero-sequence voltage is affected significantly by transition resistance.References [14-15] used the projection relationship of the feeder current in the direction identical to that of the neutral branch current to select the line.In principle, it is not affected by the transition resistance.However, the amplitude and phase information need to be used simultaneously, which results in a large error in practical application.References [16-17] showed a line selection method based on zero-sequence current comparison.Although the principle is simple, all the lines need to communicate and calculate the ratio.In addition, the process is cumbersome.In reference [18], a new technique for evaluating the third and fifth harmonics to detect HIF was proposed [19].The authors of references [20-22] presented an HIF detection technology for distribution networks based on the discrete wavelet transform technique.A method based on energy entropy was proposed by the authors of reference [23].It is set to be the transient characteristic of single-phase high- resistance grounding fault.In reference [24], the authors proposed a method for selecting faulty lines based on signal injection after analyzing real-time data of distribution network parameters and the dynamic selection of injection frequency.However, the transient process of the HIF is short, whereby the transient information is significantly weak.This, in turn, hinders the utilization of the above information [25-27].

In this study, a single-phase-to-ground fault protection method for low-resistance grounding systems was proposed based on the zero-sequence current ratio coefficient.After the zero-sequence current ratio coefficient is calculated, the difference between the healthy line and faulty line is used to select the faulty line.For misoperations under normal working condition, this method can eliminate the influence of unbalanced current by setting the starting current.It shows high sensitivity and reliability under both lowresistance and high-resistance grounding fault conditions.In addition, a simulation verified the effectiveness of this method.

The remainder of this paper is organized as follows.The fault characteristics of a single-phase-to-ground fault in a low-resistance grounding system are introduced in Section 2.In Section 3, the principles and settings of the proposed protection method are presented.Then, the protection performance is analyzed in Section 4.In Section 5, the validity of the proposed protection method is verified using the simulation results.Section 6 presents the conclusion of the study.

1 Single-phase-to-ground fault characteristic

A typical structure of a low-resistance grounding system with N feeders is shown in Fig.1.Assuming that the component parameters in the network are symmetrical, the line impedance is omitted.

In Fig.1, Rg represents the grounding resistance connected to the neutral point by the Z-type transformer.To limit the grounding over-voltage and control the fault current, the grounding resistance is generally less than 20 Ω [28].In practical engineering, it is mostly set to 10 Ω [29].Therefore, Rg is selected as 10 Ω in this study.C01-C0N represent the single-phase-to-ground zero-sequence capacitances of Feeders 1-N, respectively, and C0Σ refers to their sum.f1 and f2 denote the fault points with the transition resistance Rf; they represent the locations where the grounding fault occurs.

The zero-sequence equivalent circuit schematic diagrams of the feeder fault and bus bar fault can be obtained according to Fig.1.These are shown in Figs.2 and 3.

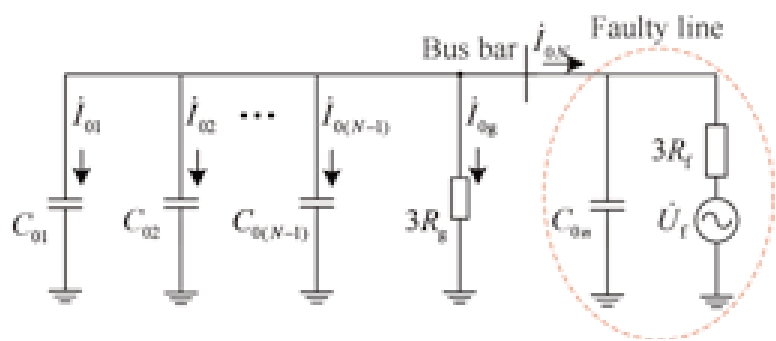
Fig.2 Zero-sequence equivalent circuit of a singlephase-to-ground fault

Fig.1 Typical structure of low-resistance grounding system

Fig.3 Zero-sequence equivalent circuit of bus bar 
grounding fault

1.1 Single-phase-to-ground fault on Feeder

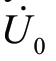In Fig.2, indicate the zero-sequence currents of the faulty feeder, healthy feeder, and neutral branch, respectively.is the zero-sequence voltage of the bus, and 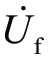is the virtual power supply of the fault point.The zero-sequence voltage and zero-sequence current show the following characteristics.

Based on Fig.2, the zero-sequence voltage of the bus bar is expressed as

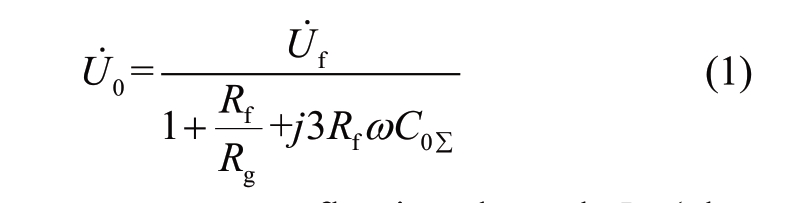
The zero-sequence current flowing through Rg (also known as the neutral-branch current) can be expressed as

The zero-sequence current of the healthy feeder is the capacitance current:

The zero-sequence current of the faulty feeder is the sum of those of the neutral branch and of all the non-faulty feeders.It is expressed as

The zero-sequence current ratio coefficient k of each line is defined as the ratio of its zero-sequence current to that of the neutral branch.According to equation (2) and equation (3), the zero-sequence current ratio coefficient of a nonfaulty feeder can be described as

Similarly, the zero-sequence current ratio coefficient of the faulty feeder is

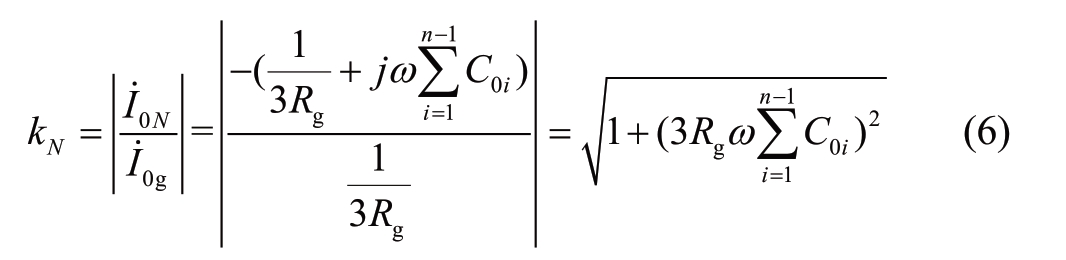
In a 10 kV power distribution system, the maximum capacitance current to the ground of a single line is 50 A.Furthermore, in general, the capacitance current to the ground of the system should be at most 200 A [29].Thus, the following formula can be obtained:

In this study, the neutral grounding resistance is 10 Ω, which is commonly used in engineering practice.The ranges of values of equation (5) and equation (6) can be obtained as follows:

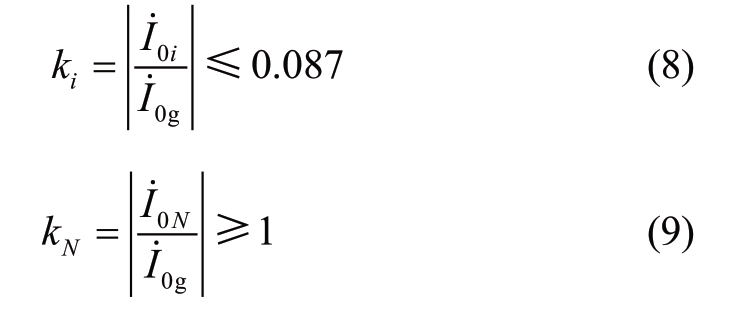
It is evident from equation (5) and equation (6) that for certain systems, the parameters Rg and ωC0i in the formula have definite values.Therefore, the zero-sequence current ratio coefficients are unrelated to the transition resistance.The requirements of equation (8) and equation (9) would be satisfied irrespective of the magnitude of the transition resistance.

1.2 Bus bar grounding fault

As shown in Fig.3, the parameters are identical to those considered when fault occurs on the feeder, except for those with the superscript “'.” In this study, the zero-sequence voltage and current show the following characteristics:

From Fig.3, the zero-sequence current of the healthy feeder can be expressed as

The zero-sequence current of the neutral branch is

The zero-sequence current ratio coefficient of the healthy feeder satisfies the following condition:

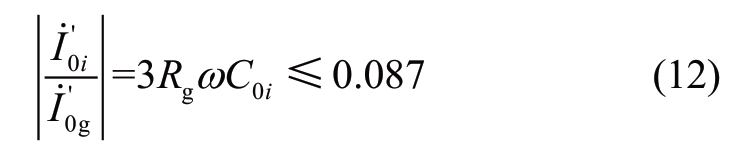
When bus bar grounding fault occurs, all the feeders are healthy.Each of their zero-sequence current ratio coefficients is at most 0.087.In this study, all the feeders are healthy, and the bus bar has a fault.Therefore, with the faults of the bus bar, the concept of using the zero-sequence current ratio coefficient is valid.

To summarize, the selection of the zero-sequence current coefficient as the characteristic quantity has the following advantages:

The zero-sequence current ratio coefficient is calculated based on the information of the feeder and neutral branch.It does not use the information of other feeders.Communication between feeders is unnecessary.Thus, the amount of data processed can be reduced, and the speed of information processing can be increased.The advantages are more significant when there are a large number of feeders.

There is a significant difference between the zerosequence current ratio coefficient of the faulty feeder and that of the healthy feeder.

The ultimately obtained zero-sequence current ratio coefficient is unrelated to the transition resistance.Therefore, its characteristics remain unaltered under different transition resistances.

2 Principle and setting of protection

2.1 Protection principle

Theoretical analysis revealed that the protection characteristically uses the zero-sequence current amplitude relationship of the non-faulty feeder, faulty feeder, and neutral branch.Their amplitude relationship can be better comprehended through the phasor diagram.

According to equations (2)-(4), the zero-sequence current of the neutral branch and the zero-sequence voltage are in the same direction, whereas the zero-sequence currents of the healthy feeder and neutral branch form an angle of 90°.In addition, the former is significantly smaller than the latter [14].The direction of the zero-sequence current of the faulty feeder is opposite to that of the sum of the neutral branch and all the healthy feeders.The direction relationship of these zero-sequence currents is shown in Fig.4.Here, the direction of the zero-sequence voltage is considered as the reference direction.

Fig.4 Phasor diagram of zero-sequence current of each feeder and neutral branch

As shown in Fig.4, the zero-sequence current of the healthy feeder is significantly less than those of the faulty feeder and neutral branch.Furthermore, the difference between the currents of the faulty feeder and neutral branch is marginal.

A comprehensive consideration of the theoretical derivation reveals the following: when a single-phase shortcircuit fault occurs in the small-resistance grounding system, the zero-sequence current ratio coefficient of the healthy feeder is at most 0.087.However, the ratio coefficient of the faulty feeder is at least one.In addition, the range of zerosequence current ratio coefficient of the healthy feeder and faulty feeder is unrelated to the transition resistance.

To eliminate the influence of the unbalanced current in the absence of fault, a start-up criterion is applied to maintain the system functional.

The final protection criterion is shown in equation (13):

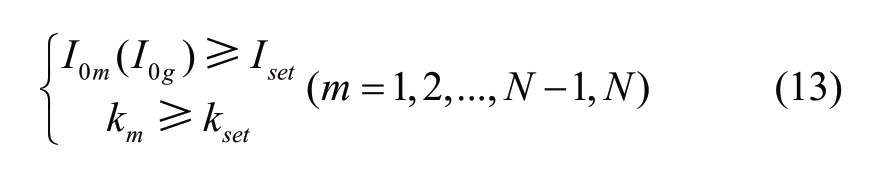
where Iset refers to the threshold current value and kset represents the action threshold of zero-sequence current ratio coefficient.

2.2 Setting of action value

According to the theoretical analysis of equation (8) and equation (9), the zero-sequence current ratio coefficients satisfy the following:

From equation (14), kset can be selected from within the range [0.087, 1].Considering that the protection is adequately reliable to operate without error in the case of grounding fault, the average of the two boundary values is set as kset in this study.That is, kset=0.5.

In addition, the starting threshold of the method must be set based on the maximum unbalanced zero-sequence current.In a 10 kV distribution network, the maximum unbalanced zero-sequence current of the overhead line and that of the cable line are approximately 0.37 A and 0.26 A, respectively [29].Therefore, the starting threshold is set to 0.4 A.That is, the protection would start only when the zero-sequence current is higher than 0.4 A.In general, the current of the protection device is three times the real zerosequence current.Therefore, the corresponding set value of the device is 1.2 A.

In that case, the protection criterion after setting is

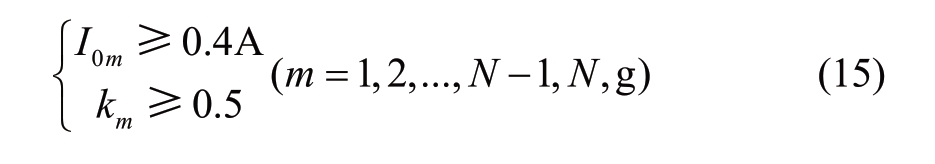
To facilitate the subsequent analysis, the first and second formulas in equation (14) are called the start criterion and action criterion, respectively.

The protection process is presented below: (1) It is assessed whether the zero-sequence current exceeds 0.4 A.If it does, the corresponding protection would start.(2) After the zero-sequence current of the neutral branch and all the feeders are obtained, the zero-sequence current ratio coefficient of each feeder is calculated using the above information.(3) The feeder whose zero-sequence current ratio coefficient is higher than 0.5 would be determined to be faulty.The feeder whose zero-sequence current ratio coefficient is lower than 0.5 would be determined to be healthy.In the cases where all the feeders are determined to be healthy, a grounding fault is considered to have occurred on the bus bar.

3 Performance analysis

3.1 Effect of transition resistance

(1) Influence on zero-sequence current ratio coefficient

According to equation (1), the effective value of the zero-sequence voltage is

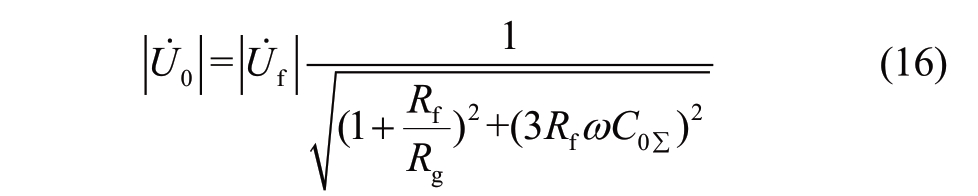
where the virtual voltage 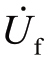is equal to the fault phase voltage at the fault time [29].That is,

The grounding resistance of the neutral point Rg is 10 Ω.Therefore, according to equation (16), the zero-sequence voltage is related only to the transition resistance and system admittance.

Assuming that the transition resistance is constant, the only variable in equation (16) is ωC0∑.Therefore, equation (16) can be expressed as

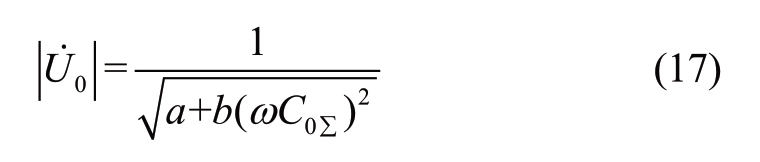
where Both these are constant.

From (16), the magnitude of the zero-sequence voltage is negatively correlated with the system admittance.Similarly, the zero-sequence voltage is negatively correlated with the transition resistance as well.

Fig.5 shows the variation in zero-sequence voltage with the variation in transition resistance and system capacitance.It is based on equation (16).

In Fig.5, the x-, y-, and z-axes represent the transition resistance, system admittance, and zero-sequence voltage, respectively.

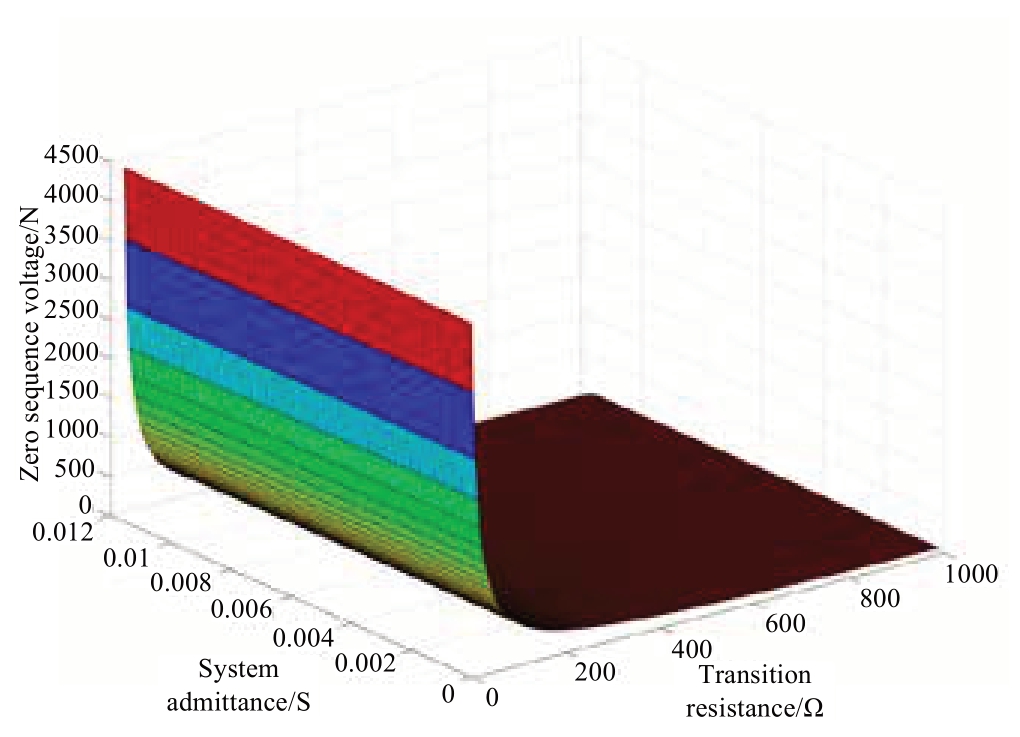
Fig.5 Variation in zero-sequence voltage with variation in transition resistance and system capacitance

As shown in Fig.5, when a single-phase-to-ground fault is grounded by a marginal transition resistance, the zero-sequence voltage decreases rapidly as the transition resistance increases.However, once the transition resistance exceeds 100 Ω, the zero-sequence voltage continues to decrease at a lower rate.When the transition resistance is considered to be constant, the variation in system admittance negligibly affects the zero-sequence voltage.That is, the zero-sequence voltage is determined mainly by the transition resistance.

According to equations (2)-(4), except for the zerosequence voltage, the zero-sequence currents of all the feeders and neutral branch would also be affected by the transition resistance.However, the zero-sequence voltage in the expression could be removed by calculating the zerosequence current ratio coefficient.Thereby, the influence of the transition resistance can be eliminated.

It is evident from equations (5)-(6) that the zerosequence current ratio coefficient is related only to the system admittance and not to the transition resistance.Hence, the transition resistance does not affect the action criterion in the protection criterion of equation (14).

(2) Influence on the starting criterion of protection

This study sets a starting value to ensure that the protection does not malfunction under the influence of the unbalanced current in the normal state.

The analysis reveals that the transition resistance impacts the zero-sequence current.Thereby, the starting criterion for the protection would also be affected.In that case, it is necessary to analyze the influence of the transition resistance on the threshold of the start criterion.

According to equation (14), the operation of the protection must first satisfy the requirements of the start criterion.Then, it is assessed whether the action criterion is satisfied.In the case of a low transition resistance, the zerosequence current of all the feeders satisfies the requirements of the start criterion, and the operation of the protectors is determined by the action criterion.

However, at a high transition resistance, the zerosequence current of certain healthy feeders may be lower than the starting value owing to the transition resistance.At this time, the corresponding line protection would not be activated.This prevents malfunction.For the feeders that satisfy the requirements of the start condition, the initiation of protection depends on the zero-sequence current ratio coefficient.Therefore, the correct faulty feeder can be selected by the protection as long as the zero-sequence current of the faulty feeder is higher than the starting value when high-resistance grounding fault occurs.

According to equation (1) and equation (4), the magnitude of the zero-sequence current of the faulty feeder is

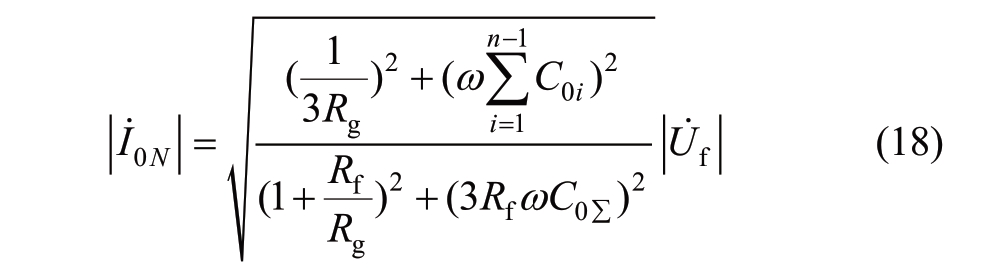
For the 10 kV distribution network, there is =5.77kV.For the high-resistance grounding fault, we could get Thus, equation (18) can be simplified as follows:

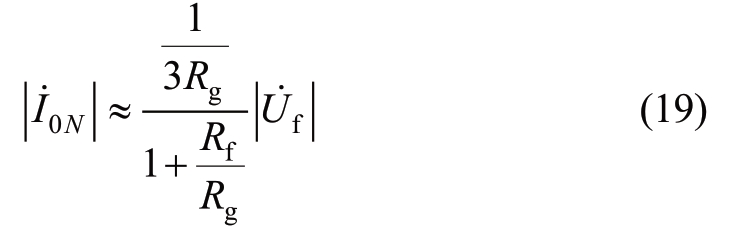
According to equation (19), the zero-sequence current of the faulty feeder decreases with the increase in transition resistance.In the case where the zero-sequence current of the faulty feeder is higher than the starting current of 0.4 A, the transition resistance Rf can be obtained as 4798 Ω.Therefore, when Rf ＜ 4798 Ω, the zero-sequence current of the faulty feeder would attain the threshold value specified by the starting criterion, and the protection can start.

To summarize, in principle, the action criterion of the protection is unrelated to the transition resistance.The transition resistance of this protection method can attain the maximum value of 4798 Ω after the starting current is set to prevent the influence of the unbalanced current.

3.2 Influence of unbalanced current

A zero-sequence current may also be generated in the system under normal operation.This may cause the protection to malfunction [30-32].Therefore, it is necessary to prevent the generation of this current.The maximum unbalanced zero sequence current in the overhead lines and the cable lines of a 10 kV low-resistance grounding system is approximately 0.37 A and 0.26 A, respectively [29].Furthermore, the starting current is set as 0.45 A in this study.It is higher than the maximum unbalanced zerosequence current.In this case, when there is no fault in the system, the protection would not malfunction.

4 Simulation results

A model of a typical 10 kV distribution network with four feeders is established using PSCAD simulation software, as shown in Fig.6.The neutral grounding resistance Rg is 10 Ω, and the lengths of Feeders 1-4 are 13 km, 10 km, 7 km, and 14 km, respectively.Table 1 shows the zero sequence parameters of the lines [33-34].

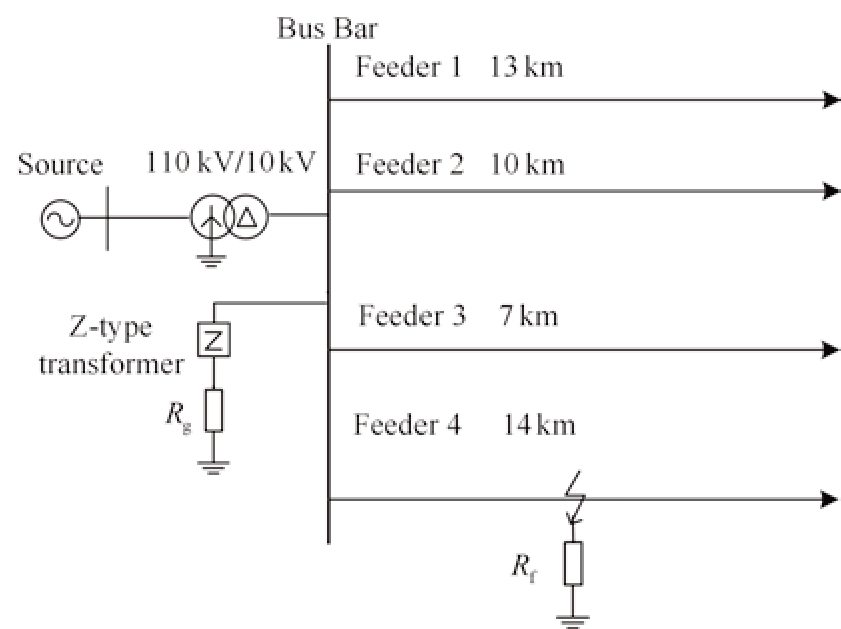
Fig.6 Single-phase-to-ground fault simulation model

Table 1 Line parameters

4.1 Simulation results of a feeder fault

It is assumed that a single-phase-ground fault occurs 8 km from the head of Feeder 4 with Phase C.Considering the transition resistances as 10 Ω, 500 Ω, and 2000 Ω, respectively, the zero-sequence current is shown in Fig.7.

As shown in Fig.7, when a single-phase-to-ground fault occurs in Feeder 4, the zero-sequence currents of the faulty feeder and neutral branch are approximately equal.Among the healthy feeders, a zero-sequence current of 20 times of the longest Feeder 1 is lower than the current mentioned earlier.This feature remains even when the transition resistance varies.

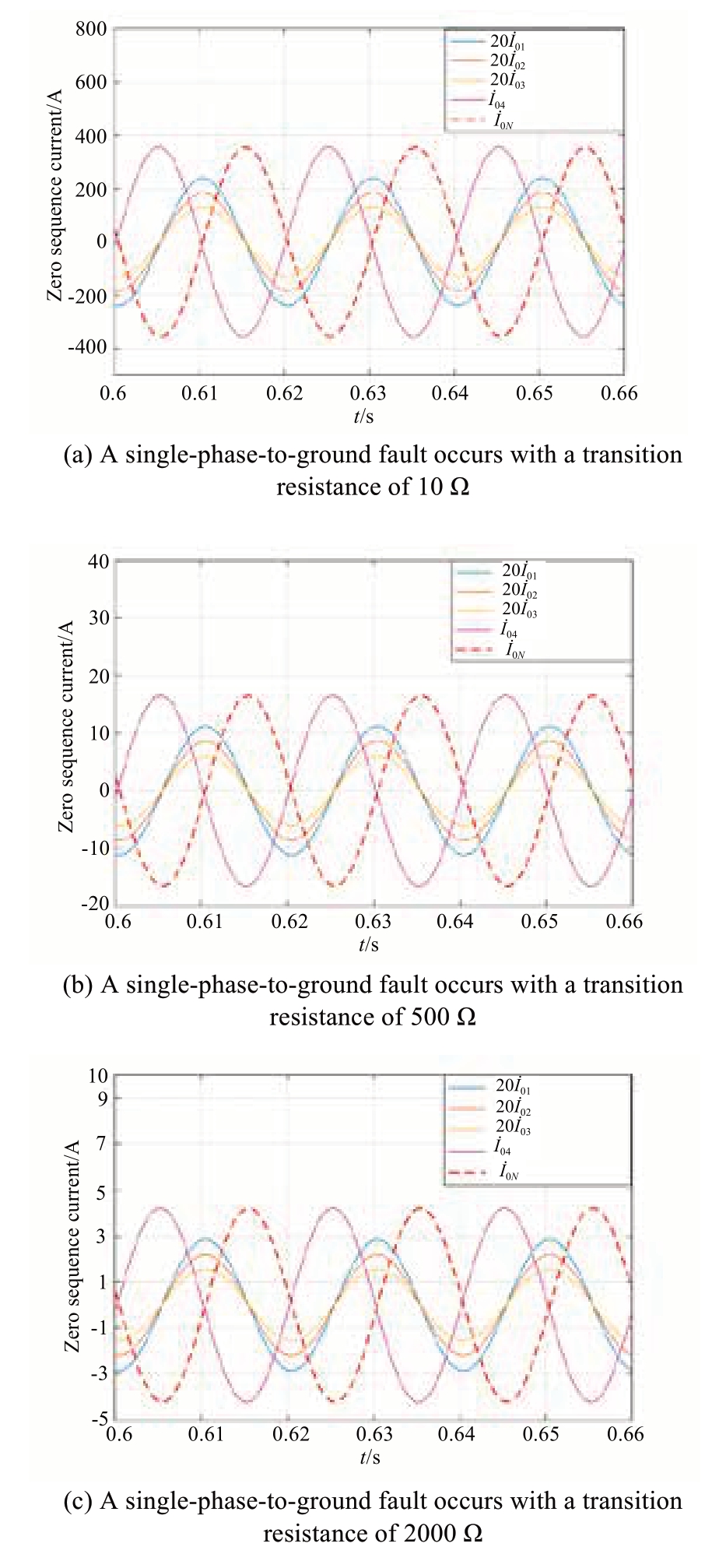
Fig.7 Simulation results of zero-sequence current under different transition resistances

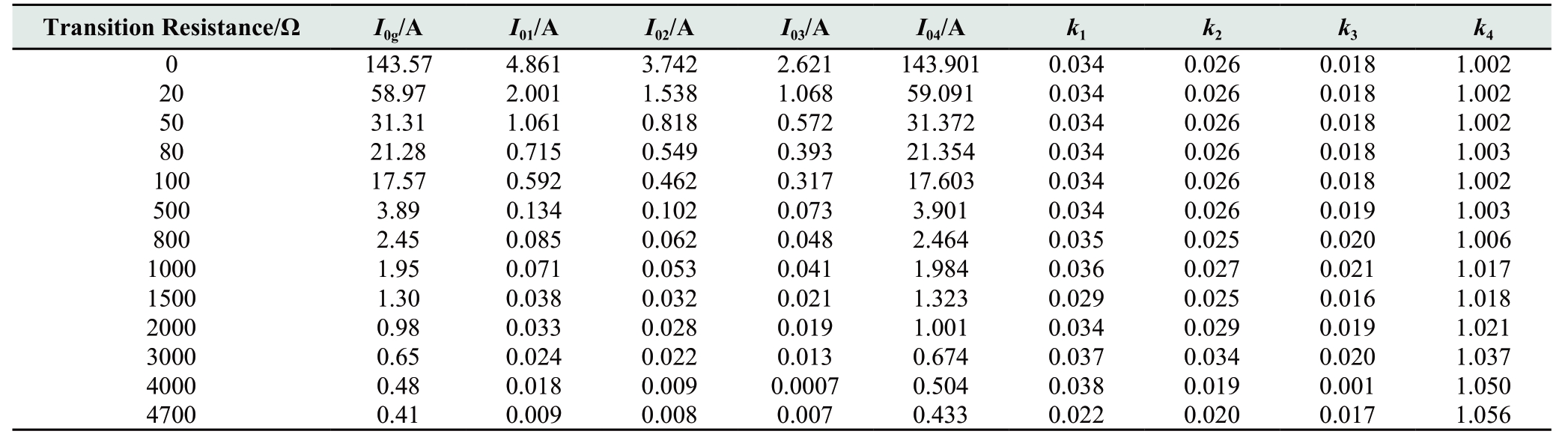
The simulation results at different transition resistance values are listed in Table 2.I0g represents the zero-sequence current of the neutral branch.I01, I02, and I03 represent the zero-sequence currents of the healthy Feeders 1-3, respectively.I04 represents the zero-sequence current of the faulty Feeder 4.

According to Table 2, when the transition resistance is below 100 Ω, the zero-sequence currents of all the feeders exceed the starting current.This enables the entire protection to start.However, the zero-sequence current ratio coefficient of Feeder 1 (approximately 0.034), which is the longest among the healthy feeders, is significantly smaller than the set value (0.5).In contrast, the zero-sequence current ratio coefficient of the faulty Feeder 4 is higher than the set value of the action criterion (0.5).Finally, the protection method selects the faulty Feeder 4 correctly.

However, in the case wherein the transition resistance exceeds 100 Ω, certain protections of healthy feeders may be blocked because their zero-sequence current does not attain the value of the starting current, whereas the protection of the faulty feeder can start normally owing to the significantly higher zero-sequence current.In addition, its zero-sequence current ratio coefficient also exceeds kset, which enables the protection to operate correctly.

As shown in Table 2, the zero-sequence current of each feeder decreases with the increase in the transition resistance, whereas the zero-sequence current ratio coefficient of each feeder essentially remains constant.In this case, the ratio coefficient is unrelated to the transition resistance.The method proposed is not affected by transition resistance.

To further verify the effect of the fault location on the protection, we have altered the fault locations and conducted an extensive verification.A large amount of data show that the zero-sequence current ratio coefficient displays the above characteristics even when the transition resistance varies.Moreover, owing to the small length of the feeder, the variation in fault position has a negligible effect on the zero-sequence current.Tables A1 and A2 in Appendix A list the data for the case wherein the fault occurs at the head and end of the feeder.Both tables indicate the same conclusions.

Table 2 Zero-sequence current and zero-sequence current ratio coefficient of each feeder with a feeder fault

4.2 Simulation analysis of bus bar fault

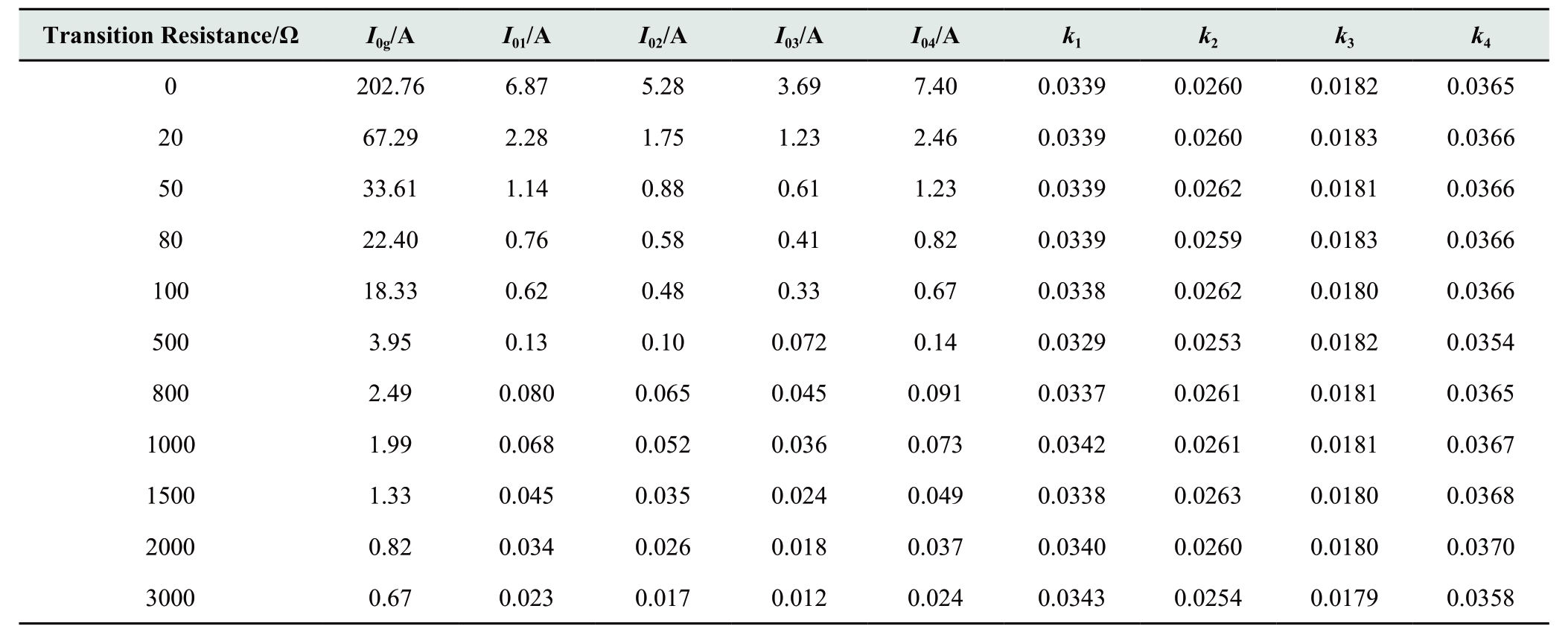
Table 3 shows the simulation results with different transition resistance values when a grounding fault occurs in the bus bar.I0g represents the zero-sequence current of the neutral branch.I01, I02, I03, and I04 represent the zerosequence currents of the healthy Feeders 1-4, respectively.

According to Table 3, when the transition resistance is below 100 Ω (which is identical to that during the feeder fault), the protection of all the feeders would be activated.The zero-sequence current ratio coefficient of the longest feeder (Feeder 4) is significantly smaller than 0.5.According to the action criterion, all the feeders are healthy.Therefore, it is concluded that the fault eventually occurs on the bus bar.

Table 3 Zero-sequence current and zero-sequence current ratio coefficient with the bus bar fault

4.3 Comparison of different methods by simulation

Considering the problem of definite-time zero-sequence over-current protection in high-resistance grounding faults, many scholars have proposed inverse-time zero-sequence over-current protections.These can effectively reduce the starting threshold of protection.Next, these two typical methods would be compared by simulation to further highlight the advantages of the protection proposed in this paper.

The expression for inverse-time zero-sequence overcurrent protection is

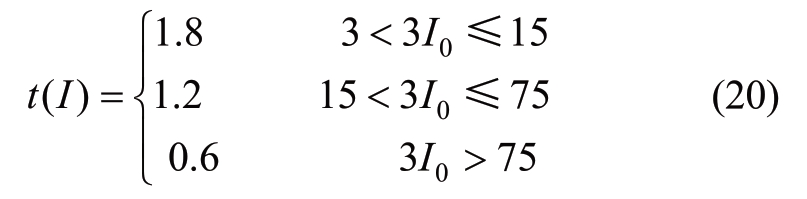
The zero-sequence current of the faulty feeder is higher than that of the healthy one.Hence, the protection of the faulty feeder would function first owing to the marginal delay [7].Because the fault location has a negligible effect on the selection results, only the results wherein the fault occurs at f1 are compared here.Different transition resistances are considered to ensure the credibility of the data.

Table 4 shows the zero-sequence current of the faulty feeder and the action time of inverse-time zero-sequence over-current protection under four transition resistances.

Table 4 Zero-sequence current of faulty feeder and the action time of inverse-time zero-sequence over-current protection under different transition resistances

Fig.8 shows the variation in zero-sequence current under different transition resistances.

The simulation sets the fault to occur at 0.4 s, i.e., t1 of Fig.8.After a period of transient process, the system attains the steady state again at t2.Δt represents the transition time from t1 to t2.

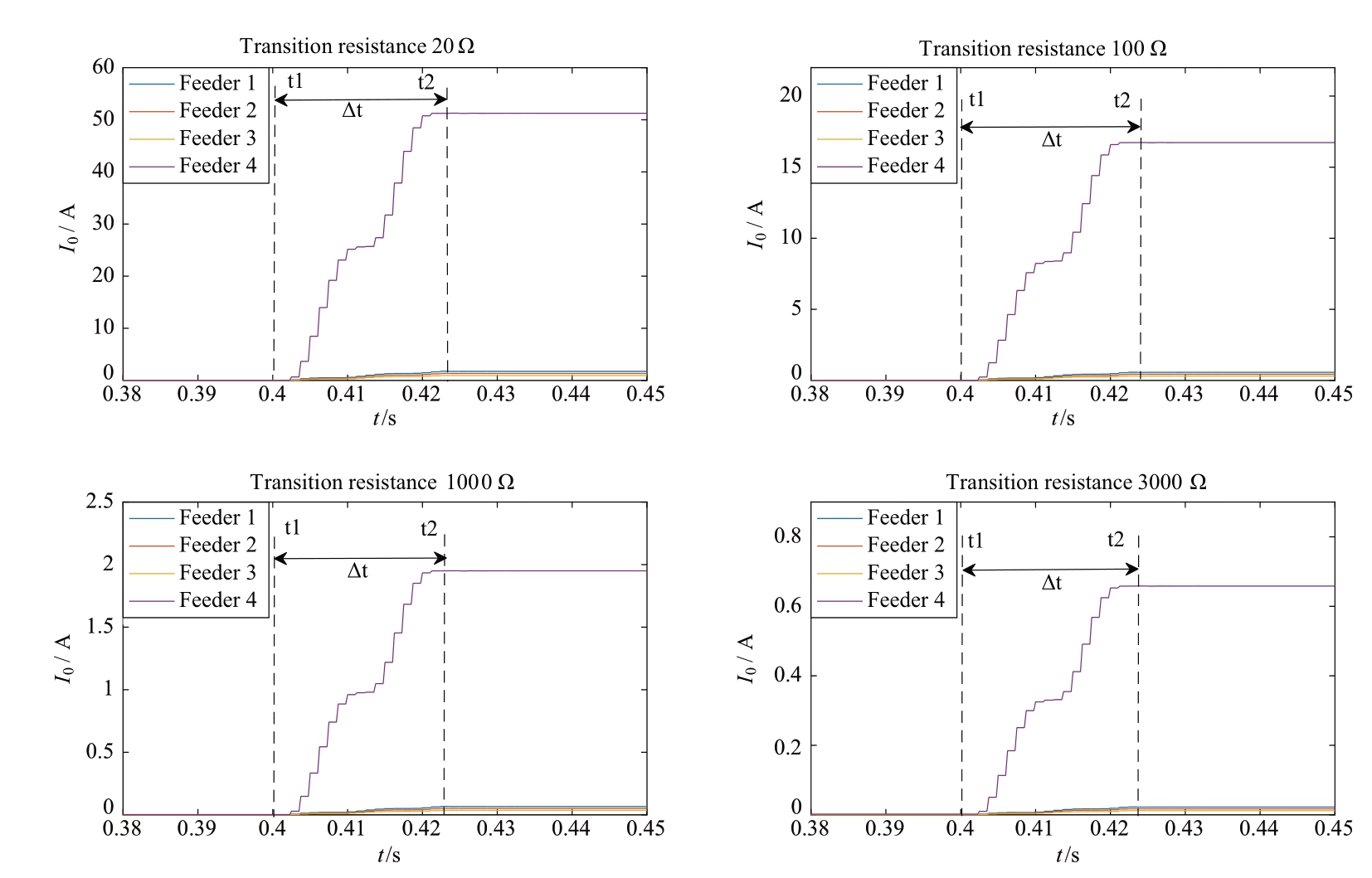
Fig.8 Simulation results of variation in zero-sequence current under different transition resistances

The protection proposed in this paper requires the fault steady-state signal.According to [35], the free oscillation frequency of transient capacitor current is generally 300-3000 Hz.Moreover, the attenuation is significantly rapid and generally endures for 0.5-1 power frequency cycle.From Fig.8, less than 0.04 s is required to regain the steady state after the occurrence of failure.Considering that the action time of the protection is generally less than 10 ms, the time required for the entire process is less than 50 ms.It is independent of the transition resistance.

Compared with inverse-time zero-sequence over-current protection, the newly proposed protection can reduce the action time and consider the rapidity of the action of protection while ensuring the accuracy of line selection.

5 Conclusion

In this study, a new protection based on the zerosequence current ratio coefficient for low-resistance grounding system was proposed.The conclusions are summarized below:

(1) The zero-sequence current ratio coefficient, which is independent of transition resistance, is used to distinguish the faulty feeder from the healthy ones.The significant difference between these ensures sensitivity in the event of high-resistance ground faults.

(2) The proposed method is simple and highly reliable.This is because only the zero-sequence currents of each feeder and the neutral branch are required (and not the information of other feeders).This reduces the amount of information collected and speeds up information processing.

(3) By setting the starting current, this protection can eliminate the influence of unbalanced current and would not malfunction during normal operation.This method is less likely to be affected by the degree of unbalance.

Appendix A

Table A1 Zero-sequence current and zero-sequence current ratio coefficient of each feeder with a fault at the head of Feeder 4

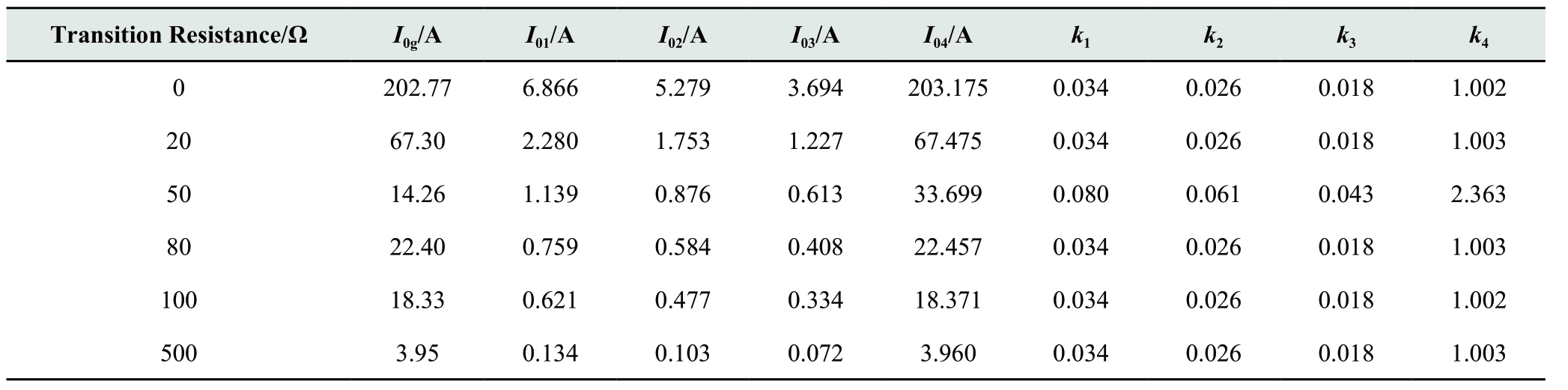
continue

Table A2 Zero-sequence current and zero-sequence current ratio coefficient of each feeder with a fault at the end of Feeder 4

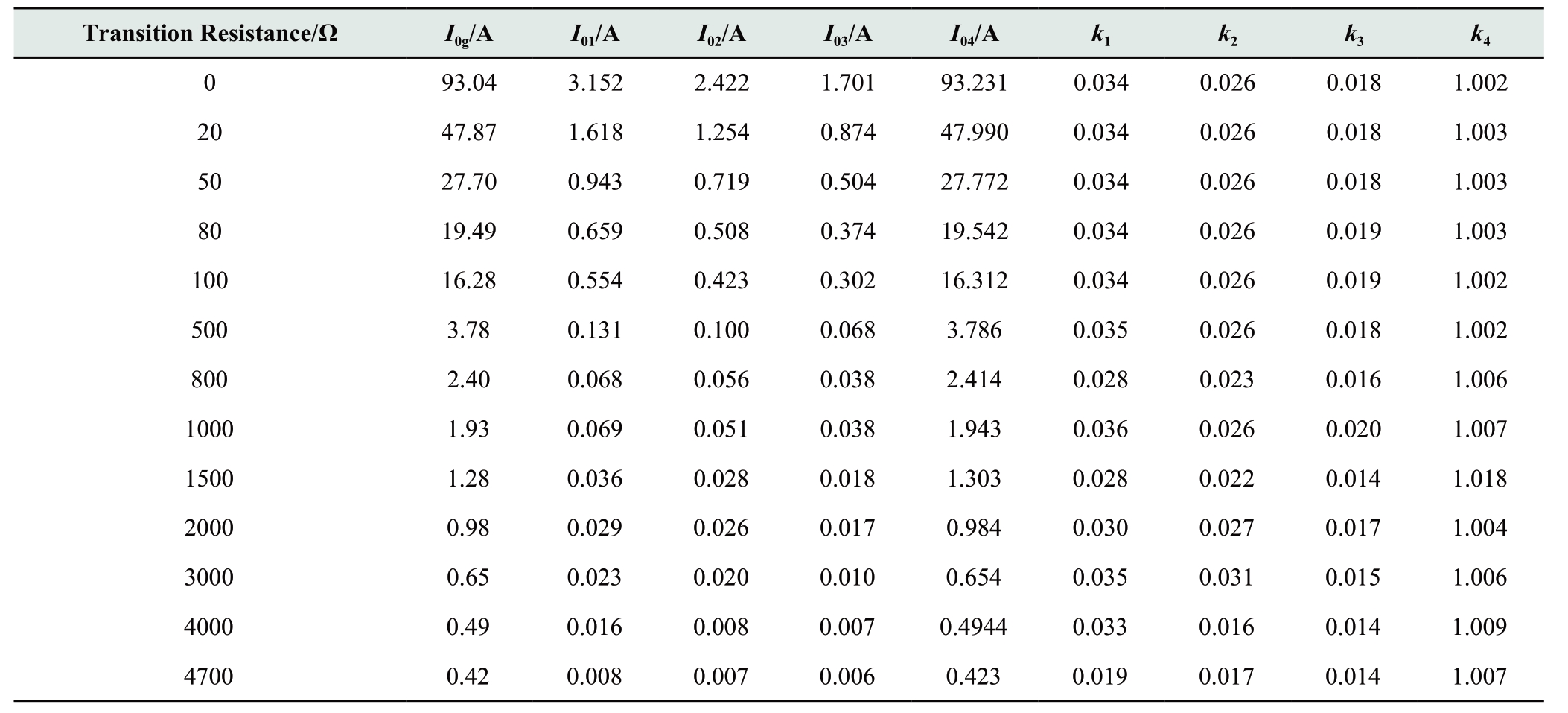
Acknowledgements

This work was supported in part by National Key Research and Development Program of China (2016YFB0900603) and Technology Projects of State Grid Corporation of China (52094017000W).

Declaration of Competing Interest

We declare that we have no conflict of interest.

References

[1] Liu Yuquan, Cai Yanchun, Deng Guohao, et al (2015) Operation and protection of low resistance grounding power distribution system.Power Supply, 32(06): 30-35

[2] Guo L W, Xue Y D, Xu B Y, et al (2014) Discussion about neutral grounding mode of Active Distribution Network.2014 China International Conference on Electricity Distribution (CICED).Shenzhen, China.IEEE, 1033-1036

[3] Guo M F, Zeng X D, Chen D Y, et al (2018) Deep-learning-based earth fault detection using continuous wavelet transform and convolutional neural network in resonant grounding distribution systems.IEEE Sensors Journal, 18(3): 1291-1300

[4] Cao J J, Qin L J, Li Y X, et al (2018) A new research on intelligent protection and positioning integration method of single phase grounding fault in small current grounding system.2018 2nd IEEE Conference on Energy Internet and Energy System Integration (EI2).Beijing, China.IEEE, 1-5

[5] Soheili A, Sadeh J (2017) Evidential reasoning based approach to high impedance fault detection in power distribution systems.IET Generation, Transmission & Distribution, 11(5): 1325-1336

[6] Le J, Wang C, Li X R, Zhou Q (2019) The Multi-Object Distributed Optimization Control Strategy of Medium Voltage Distribution Networks.Transactions of China Electrotechnical Society, 34(23): 4972-4981

[7] Dong K D, Cai Y C, Jin Z (2020) Research on improvement of zero sequence protection of small resistance grounded distribution network.Power Supply and Consumption, 37(06): 48-52+65

[8] Xu H Y, Liu B, Ye K, et al (2020) Identification of fault zones in distribution network based on zero sequence current distribution characteristics.Electric Power Engineering Technology, 39(1): 110-117,164

[9] Zhan Y, Xiao S W, Jiao S L, et al (2020) Synchronization of line fault recording data and fault location based on least square method.Electric Power Engineering Technology, 39(5):78-84

[10] Wang Y, Xue Y D, Xu B Y, et al (2018) Inverse time zero sequence overcurrent protection for ground faults in small resistance grounding systems.Automation of Electric Power Systems, 42(20): 150-157

[11] Li H F, Chen J Q, Zeng D H, et al (2018) High sensitivity zero sequence current protection for low resistance grounding system.Electric Power Automation Equipment, 38(09): 198-204

[12] Xue Y D, Wang Y, Xu B Y (2020) High sensitivity stage zero sequence overcurrent protection for low resistance grounding system.Proceedings of the Chinese Society of Electrical Engineering, 40(19): 6217-6227

[13] Xue Y D, Liu S, Wang Y S, et al (2016) Grounding protection for low resistance grounding system based on zero sequence voltage ratio braking.Automation of Electric Power Systems,40(16): 112-117

[14] Sheng Y R, Cong W, Bu X H, et al (2019) Low resistance grounding system high resistance grounding fault judgment method based on the difference of neutral point current and zero sequence current projection amount.Electric Power Automation Equipment, 39(03): 17- 22+29

[15] Yang F, Liu X X, Shen Y, et al (2020) Low-resistance grounding system high-resistance ground fault protection based on zero sequence current projection coefficient.Power System Technology, 44(03): 1128- 1133

[16] Lin Z C, Liu X X, Wang Y M, et al (2018) Ground fault protection of low resistance grounding system based on zero sequence current comparison.Power System Protection and Control, 46(22): 15-21

[17] Liao Y H, Chen Y L (2020) Zero sequence protection of 10 kV low resistance grounding system ratio rule.Journal of Electric Power System and Automation, 32(11): 50-56

[18] Suliman M Y, Ghazal M T (2019) Detection of high impedance fault in distribution network using fuzzy logic control.2019 2nd International Conference on Electrical, Communication, Computer, Power and Control Engineering (ICECCPCE).Mosul, Iraq.IEEE, 103-108

[19] Li Y J, Liu K Y, Meng X L (2016) A single-line-to-ground fault diagnosis method in small-current-grounding system based on fuzzy-integral decision fusion technique.2016 China International Conference on Electricity Distribution (CICED).Xi’an, China.IEEE, 1-5

[20] Jin Y, Shan C Z, Wu Y, et al (2019) Fault diagnosis of hydraulic seal wear and internal leakage using wavelets and wavelet neural network.IEEE Transactions on Instrumentation and Measurement, 68(4): 1026-1034

[21] Kim C H, Kim H, Ko Y H, et al (2002) A novel fault-detection technique of high-impedance arcing faults in transmission lines using the wavelet transform.IEEE Transactions on Power Delivery, 17(4): 921-929

[22] Saleem S M A, Sharaf A M (2007) A novel travelling wave based relaying scheme using wavelet transforms for arcing faults detection on series compensated transmission lines.2007 Canadian Conference on Electrical and Computer Engineering.Vancouver, BC, Canada.IEEE, 575-578

[23] Qin H, Li T Y (2018) High impedance fault line selection method for resonant grounding system based on wavelet packet analysis.2018 China International Conference on Electricity Distribution (CICED).Tianjin, China.IEEE, 1174-1179

[24] Niu L, Wu G Q, Xu Z S (2021) Single-phase fault line selection in distribution network based on signal injection method.IEEE Access, 9: 21567-21578

[25] Li Z W, Tang D, Xia Y X, et al.A summary of fault traveling wave protection for transmission lines.Electric Power Engineering Technology, 2020,39(5):49-58

[26] Ding P, Zhu K, Zhu Y Q, et al (2019) Determining the Permanent Fault in Distribution Lines Based on Model Recognition.Transactions of China Electrotechnical Society, 34(5): 1004-1012[27] Liu G Y, Dai R C, Lu Yi, et al (2020) Graph Computing Based Power Network Analysis Applications.Transactions of China Electrotechnical Society, 35(11): 2339-2348

[28] Liu H W, Zhu D P, Liu Jie, et al (2019) Selection of small resistance for neutral grounding of distribution network.Power grid and clean energy, 34 (07): 31-37

[29] Yang Fan, Jin Xin, Shen Yu, et al (2020) Ground fault direction identification algorithm of flexible grounding system based on zero sequence admittance change.Automation of Electric Power Systems, 44(17): 88-94

[30] Sun Z P, Tao S(2020) Calculation of distribution loss under three-phase unbalancebased on current phase estimation.Electric Power Engineering Technology, 39(3):114-119

[31] Qiu G X, Zhu P Y, Wang C, et al (2020) The compensation method of MMC-STATCOM under unbalanced load condition.Electric Power Engineering Technology, 2020, 39(2): 35-42

[32] Qu X, Li X R, Song J Y, et al (2018) Composite Load Model Considering Voltage Regulation of Distribution Network.Transactions of China Electrotechnical Society, 33(4): 759-77

[33] Zhu L (2011) Research on single phase short circuit fault and protection of small resistance grounding system in 10kV distribution network.(Master’s thesis, Hunan University)

[34] Yuan J H, Zhang X, Huang H, et al (2020) Multi-source distribution network fault location methodbased on current sequence component.Electric Power Engineering Technology, 39(5): 204-210

[35] Liu X X (2019) Study on reliability of small resistance grounding zero sequence protection in 10kV distribution network.(Master’s thesis, China University of mining and technology)

Received: June 25 2021 Accepted: October 17 2021 Published: December 25 2021

Jianrui Li

1144752058@qq.com

Yongli Li

lyltju@163.com

Yonghuan Wang

w18831182235@163.com

Jinzhao Song

1017234022@ tju.edu.cn

2096-5117/© 2021 Global Energy Interconnection Development and Cooperation Organization.Production and hosting by Elsevier B.V.on behalf of KeAi Communications Co., Ltd.This is an open access article under the CC BY-NC-ND license (http: //creativecommons.org/licenses/by-nc-nd/4.0/ ).

Biographies

Jianrui Li received her bachelor degree from Hebei University of Technology, Tianjin, China, in 2019.She is now pursuing her Master’s degree of Electrical Engineering in Tianjin University, Tianjin, China.Her research interests include Power system protection and control.

Yongli Li received the B.Sc.and M.Sc.degrees in electrical engineering from Tianjin University, Tianjin, China, in 1984 and 1987, respectively, and the Ph.D.degree in electrical engineering from the Université Libre de Bruxelles, Brussels, Belgium, in 1993.

She is currently a Professor with the School of Electrical and Information Engineering, Tianjin University.Her research interests include fault analysis of power systems and fault diagnosis of electrical equipment, protection, and adaptive reclosing of EHV/UHV transmission systems, and protection and control of the microgrids and distribution networks.Dr.Li is a member of CIGRE SC-B5.

Yonghuan Wang received her bachelor degree from Hebei University of Technology, Tianjin, China, in 2020.She is now pursuing her Master’s degree of Electrical Engineering in Tianjin University, Tanjin, China.Her research interests include Power system protection and control.

Jinzhao Song received the B.S and M.S degrees from Tianjin University, Tianjin, China, and is currently pursuing the Ph.D.degree at Tianjin University.His main research interests include power system fault detection, analysis and protection.

(Editor Dawei Wang)